A memristor–meminductor-based chaotic system with abundant dynamical behaviors

Abstract

In this paper, we introduce a memristor model and a meminductor model and design the corresponding emulator circuits for imitating their characteristics. By employing the two models, we propose a very simple chaotic circuit that contains only three elements in parallel: a memristor, a meminductor and a linear passive capacitor. The circuit is very simple, but has very abundant dynamical behaviors, including line equilibrium set, bursting, coexisting attractors, transient chaos, transient period and intermittency. Furthermore, we replace the memristor and meminductor with their corresponding emulators in the proposed circuit to make a hardware experiment, which illustrates the validity of the theoretical analysis.

1 Introduction

As a novel basic circuit element, a memristor was theoretically predicted by Chua [1]. In 1976, Chua and Kang [2] extended the definition of memristor and defined memristive systems and devices, which included a voltage-controlled memristor and a current-controlled memristor. In 2008, the physical implementation of memristor was reported in Nature by the researchers in Hewlett-Packard (HP) laboratories [3], which gained a wide interest in academic circles.

Some mathematical models of memristor were presented to describe precisely the characteristics of memristors. A mathematical model of HP memristor was proposed by HP laboratory [3]. Since the dopant drift of the HP memristor was nonlinear, Biolek et al. put forward some window functions to implement memristor models [4,5,6]. Although several window functions for the nonlinear dopant drift models of HP memristor have been studied, most of them are inadequate to capture the full characteristics of HP memristor. For improving this nonlinear dopant drift model, Wen et al. [7] proposed a unified window function to describe more precisely a general memristor with restrictions of its parameters given.

Since a voltage-controlled memristor was more suitable in parallel memristor-based application circuits, a voltage thrEshold adaptive memristor (VTEAM) model was proposed by Kvatinsky et al. [8]. Reference [9] presented a non-ideal active voltage-controlled memristor and designed a chua’s circuit with multiple attractors based on the memristor. For the convenience of applied research, SPICE models of memristor were proposed by Biolek et al. [4, 10], and its emulators were presented in Refs. [11, 12]. Yu et al. designed a memristor emulator consisting of one varactor diode, one capacitor, several current-feedback operational amplifiers and resistors. Sánchez-López and Aguila-Cuapio used the second-generation current conveyor to realize a 860 kHz memristor emulator.

Chua et al. extended the concept of memristive systems to memcapacitor and meminductor [13], which typically shows pinched hysteretic loops in the two constitutive variables: charge–voltage for the memcapacitor and current-flux for the meminductor. The properties of these memory devices depend on the state and history of the device. Recently, some mathematical models and equivalent circuits of meminductor were proposed. Reference [14] presented the mathematical model and equivalent circuit of a flux-controlled meminductor. Liang et al. [15] used several second-generation current conveyors and other devices to construct a floating meminductor emulator.

The memristor, memcapacitor and meminductor are collectively called as memory elements, which store information without need for a power supply and can be used for nonvolatile memory [13], artificial neural network [16], logic circuits [17], nonlinear circuits [18] and so on. Zhang et al. [19] used memristive synapse to improve neuron models. Within single new neuron model, the modes in electrical activities were controlled by the synapse with memory. For chain network with memristive synapse connection, continuous pulses induced regular patterns, whereas the complete synchronization was suppressed by the diversity in synapse current. Reference [20] presented memristive fully convolutional network, whose accuracy was over some existing machine learning methods about image segmentation. Wen et al. proposed memristor-based multilayer neural networks for machine learning, whose area consumption was 2–8% of the one of CMOS-only circuit [21]. A fuzzy method was employed to enable learning rate adjustment for multilayer neural networks, which increased the learning accuracy by 2–3% compared with a constant learning rate. Reference [22] put forward memristor-based echo state network, whose topological structure adopted NW small-world network. The proposed network successfully performed car evaluation and short-term power load forecasting.

Itoh and Chua firstly realized several memristor-based chaotic oscillators by using the piecewise linear memristors to replace Chua’s diodes in Chua’s circuit [23]. Afterward, many memristor-based and meminductor-based chaotic oscillators were presented [24,25,26,27,28]. Some simple memristive oscillators with three circuit elements were reported in Refs. [29,30,31,32]. Muthuswamy and Chua [29] successfully implemented the simplest autonomous chaotic circuit, in which an active current-controlled memristor connects a linear inductor and a linear capacitor in series. Reference [30] postulated a simple chaotic circuit containing a voltage-controlled memristor, an inductor and a capacitor in parallel. For increasing complexity of memristor-based systems, Teng et al. used a memristor of fourth-degree polynomial memristance to produce a multi-scroll chaotic attractor and further investigated its chaotic behaviors in integer order and fractional order [31]. Lozi and Abdelouahab [32] derived a fractional-order simple oscillator by replacing a memristor of fourth-degree polynomial memristance with the one of second-degree and found that it has rich nonlinear behavior, such as coexisting attractors. All these simple memristive systems were difficult to integrate them in ICs since an inductance element has larger volume. For avoiding to this shortcoming, Reference [33] proposed a simple chaotic circuit containing a non-ideal meminductor, a resister and a capacitor, whose behaviors also were complicated.

Recently, the system with coexisting attractors received much attention. The phenomenon of coexisting attractors is related to the emergence of multistability, which occurs in some dynamical systems, corresponding to the coexistence of multiple stable attractors for a set of fixed parameters. Li et al. [34] put forward symmetrical chaotic systems with multiple attractors. Xu et al. [35] found multistability in memristor-based circuit systems. The fractional-order simple oscillator presented by Lozi and Abdelouahab [32] also had coexisting attractors. Since multistability can result in unexpected behaviors, the system with coexisting attractors can be employed in information engineering.

However, all above simple chaotic oscillators included only one non-ideal memristor or meminductor and possess finite equilibrium points. Moreover, a simple chaotic system with two kinds of memory elements was not found by now. This paper presents a novel simple oscillator that has only a meminductor, a memristor and a capacitor.

The goal of this paper is to show how to design a simple oscillator with two different types of memory elements, which can exhibit more complex dynamics. For this end, we design a memristor–meminductor-based circuit, which is a simple Mr–Mi–C (memristor–meminductor–capacitor) parallel circuit and possesses complex dynamical behaviors, such as bursting, transient phenomenon, intermittency and so on. Bursting is originally used to describe a type of neuron activity in biological neurons and endocrine cells, which involves two time scales. Bursting oscillation has been found in some nonlinear systems. With proper parameters, the proposed oscillator contains two timescales, from which the chaotic bursting oscillation can be observed. In addition, transient phenomenon and intermittency are found in the system.

The rest of this paper is outlined as follows. Section 2 gives a memristor model and a meminductor model and explores their fingerprints by their equivalent circuits. In Sect. 3, we construct a simple chaotic system and investigate its nonlinear behaviors. Section 4 verifies the theoretical analyses by the circuit experiments. The conclusion is given in Sect. 5.

2 Memristor and meminductor models

2.1 A memristive model and its emulator circuit

The definition of memristor is generalized by Chua and Kang, which is defined as [2]:

$$\begin{aligned} \begin{array}{l} z(t)=G(y,x,t)x(t), \\ {\dot{y}}(t)=F(y,x,t), \\ \end{array} \end{aligned}$$

(1)

where x(t) and z(t) are the input and output of a memristor, respectively, and y(t) is the state variable of a memristor. F(.) and G(.) are functions related to the specific memristor.

In order to design a memristor-based chaotic system in parallel, a voltage-controlled memristor is proposed as:

$$\begin{aligned} \begin{array}{l} i_\mathrm{M} =(Ay^{2}-B)v_\mathrm{M} , \\ {\dot{y}}=-cv_\mathrm{M} -dy+ev_\mathrm{M}^2 y. \\ \end{array} \end{aligned}$$

(2)

where $i_{\mathrm{M}}$ and $v_{\mathrm{M}}$ denote the current and voltage across the memristor, and A, B, c, d and e are constants. To further investigate features of the memristor, the corresponding equivalent circuit is designed in Fig. 1. Let $R_{4}=R_{10}$, we can obtain

$$\begin{aligned} \begin{array}{l} i_\mathrm{M} =\frac{1}{R_1 }\left( 1-\frac{R_3 }{R_9 }+\frac{R_3 }{R_2 }y^{2}\right) v_\mathrm{M} , \\ {\dot{y}}=-\frac{1}{R_6 C{ }_1}v_\mathrm{M} -\frac{1}{R{ }_5C{ }_1}y+\frac{1}{R_7 C{ }_1}v_\mathrm{M}^2 y. \\ \end{array} \end{aligned}$$

(3)

Comparing Eq. (2) with Eq. (3), it can be obtained that $A=R_{3}/R_{1}R_{2}$, $B = (1/R_{1})(R_{3}/R_{9}-1)$, $c = 1/R_{6}C_{1}$, $d = 1/R_{5}C_{1}$, $e = 1/R_{7}C_{1}$.

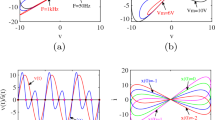
When the equivalent circuit parameters are taken as Fig. 1 and we apply a sinusoidal voltage signal of $v=\hbox {cos}$(2$\pi$ft) to the memristor, the v–i characteristics can be obtained as Fig. 2a, where a set of frequency-dependent pinched hysteresis loops are illustrated. Since the v–i characteristic curves exist in the second and fourth quadrants, the proposed memristor is an active memristor. Varying the value of $R_{9}$, two different v–i characteristics are described in Fig. 2b, where the v–i characteristic curve exists in the second and fourth quadrants as $R_{9}=12.5$ k$\Omega$, while the curve exists in the first and third quadrants as $R_{9} = 50$ k$\Omega$. Therefore, it is clear to observe that varying the value of $R_{9}$ can change the nature of the memristor. It means that the memristor is a passive memristor when $R_{9} = 50$ k$\Omega$, i.e., corresponding to B < 0; otherwise, it is active when $R_{9} = 12.5$ k$\Omega$, i.e., corresponding to parameter $B>$ 0. This paper utilizes an active memristor.

Fig. 1

Equivalent emulator circuit of the memristor

Fig. 2

v–i characteristic curves of the memristor a with different frequencies and b with different values of $R_{9}$. (Color figure online)

Fig. 3

Equivalent emulator circuit of the meminductor

Fig. 4

$\varphi$–i characteristic curves of the meminductor: the $\varphi$–i characteristic curves of $f= 100$ Hz, $f = 120$ Hz and $f = 300$ Hz are colored in blue, green and red, respectively. (Color figure online)

2.2 A meminductor model and its emulator circuit

The meminductor is postulated by Chua et al. in Ref. [13], where a flux-controlled meminductor is defined as

$$\begin{aligned} \begin{array}{l} i_{LM} =L^{-1}\hbox {(}\rho \hbox {)}\varphi \hbox {,} \\ {\dot{\rho }}=\varphi , \\ \end{array} \end{aligned}$$

(4)

where $L^{-1}(\rho )$ is the inverse meminductance and $\rho$ is the state variable of a meminductor.

The inverse meminductance is selected as $L^{-1}(\rho )=D+E\rho$ [14]. Its equivalent circuit is designed as shown in Fig. 3. Let $R_{14 }=R_{15}$, $R_{18 }=R_{19}$, $R_{22 }=R_{23}$, the flux-controlled meminductor is described as

$$\begin{aligned} \begin{array}{l} i_{LM} =\frac{1}{R_{11} }\left( \frac{R_{23} }{R_{20} }+\frac{R_{23} }{R_{21} }\rho \right) \varphi , \\ {\dot{\rho }}=\varphi . \\ \end{array} \end{aligned}$$

(5)

Comparing Eq. (4) with Eq. (5), the parameters of the mathematical model can be represented by $D =R_{23}$/($R_{20} \quad R_{11})$ and $E =R_{23}$/($R_{21} R_{11})$.

Similarly, when a sinusoidal voltage signal of $v = \hbox {cos}$(2$\pi$ft) is employed to stimulate this equivalent circuit, and its frequency is set to 100 Hz, 120 Hz and 300 Hz, respectively, the $\varphi$–i characteristics are displayed in Fig. 4, where the hysteresis loops depend on the frequency. These $\varphi$–i curves are in the second and fourth quadrants, whereupon indicating that the proposed meminductor is active.

Fig. 5

A simple chaotic circuit

3 A simple chaotic system based on memristor and meminductor

3.1 A simple chaotic oscillator

Based on the proposed memristor and meminductor models, a simple chaotic circuit that contains only three elements is constructed as shown in Fig. 5. Selecting the voltage $v_c$ across the capacitor, the state variable y of the memristor, the flux $\varphi$ of the meminductor and its state variable $\rho$ as state variables, the state equations of the system can be described as

$$\begin{aligned} \left\{ {{\begin{array}{l} {C{\dot{v}}_C =-(Ay^{2}-B)v_C -(D\rho +E)\varphi ,} \\ {{\dot{y}}=-cv_C -dy+ev_C^2 y,} \\ {{\dot{\varphi }}=v_C ,} \\ {{\dot{\rho }}=\varphi .} \\ \end{array} }} \right. \end{aligned}$$

(6)

Let $v_c =x$, $\varphi =z$, $\rho =u$, $\frac{A}{C}=a$, $\frac{B}{C}=b$, $\frac{D}{C}=\alpha$, and $\frac{E}{C}=\beta$,${\dot{w}}=\frac{dw}{d\tau } \quad (w\equiv x,y,z,u)$, $t=\tau$, the equations are expressed as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {{\dot{x}}=-(ay^{2}-b)x-(\alpha u+\beta )z,} \\ {{\dot{y}}=-cx-dy+ex^{2}y,} \\ {{\dot{z}}=x,} \\ {{\dot{u}}=z.} \\ \end{array} }} \right. \end{aligned}$$

(7)

When the system parameters are set as $a=0.1$, $b=0.5$, $c=0.5$, $d=10$, $e=4$, $\alpha =0.1$ and $\beta =1$, with the initial conditions as $(-\,1, -\,0.5, -\,0.5, -\,3)$, the system shows chaotic state. The Lyapunov exponents of the oscillator are $\hbox {LE}_1 =0.081$, $\hbox {LE}_2 =0$, $\hbox {LE}_3 =-\,0.040$ and $\hbox {LE}_4 =-\,4.290$, as well as the Lyapunov dimension is $D_L =3.010$. The chaotic attractors and the Poincaré mappings are exhibited in Figs. 6 and 7, respectively.

Fig. 6

Chaotic attractors of the simple chaotic oscillator ax–y phase portrait, by–z phase portrait, cz–u phase portrait, du–x phase portrait

Fig. 7

Poincaré map on $z = 0$

3.2 Basic dynamical analysis

The divergence of System (7) is written as

$$\begin{aligned} \nabla V= & {} \frac{\partial {\dot{x}}}{\partial x}+\frac{\partial \dot{y}}{\partial y}+\frac{\partial {\dot{z}}}{\partial z}+\frac{\partial {\dot{u}}}{\partial u}\nonumber \\= & {} -ay^{2}+b-d+ex^{2}. \end{aligned}$$

(8)

When the parameters are selected as $a=0.1$, $b=0.5$, $c=0.5$, $d=10$, $e=4$, $\alpha =0.1$ and $\beta =1$, under the initial condition of $(-\,1,-\,0.5,-\,0.5,-\,3)$, it has $\nabla V<0$, i.e., the system is dissipative, which implies that the attractor might be a chaotic attractor.

Let ${\dot{x}}={\dot{y}}={\dot{z}}={\dot{u}}=0$, a line equilibrium set O(0, 0, 0, u) of this circuit can be obtained. In other words, this system has infinite equilibria. Its Jacobian matrix is described as

$$\begin{aligned} \mathbf{J}=\left[ {{\begin{array}{llll} b&{} 0&{} {-(\alpha u+\beta )}&{} 0 \\ {-c}&{} {-d}&{} 0&{} 0 \\ 1&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 1&{} 0 \\ \end{array} }} \right] . \end{aligned}$$

(9)

The characteristic equation at equilibrium set consequently is written as

$$\begin{aligned}&F(\lambda )=\lambda [\lambda ^{3}+(d-b)\lambda ^{2} \nonumber \\&\qquad \qquad \quad +\,(\alpha u+\beta -bd)\lambda +d(\alpha u+\beta )]. \end{aligned}$$

(10)

By solving Eq. (10), we can yield one eigenvalue $\lambda _1 =0$, and one cubic equation of $\lambda$:

$$\begin{aligned} \lambda ^{3}+a_1 \lambda ^{2}+a_2 \lambda +a_3 =0, \end{aligned}$$

(11)

where $a_1 =d-b$, $a_2 =\alpha u+\beta -bd$, $a_3 =d(\alpha u+\beta )$.

Fig. 8

Lyapunov exponent spectrum and bifurcation portrait against a: a Lyapunov exponent spectrum and b bifurcation portrait. (Color figure online)

According to the Routh–Hurwitz stability criterion, System (7) is stable if $a_1 <0$, $a_3 <0$ and $a_1 a_2 >a_3$. For $a=0.1$, $b=0.5$, $c=0.5$, $d=10$, $e=4$, $\alpha =0.1$ and $\beta =1$, under the initial condition of $(-\,1,-\,0.5,-\,0.5,-\,3)$, the eigenvalues of the characteristic equation can be obtained as $\lambda _1 =\hbox { }0$, $\lambda _2 =-\,10$ and $\lambda _{3,4} =\hbox {0.2500}\pm \hbox { }j\hbox {0.7984}$. Thus the equilibrium is unstable saddle-focus equilibrium in this case.

3.3 The influences of parameters

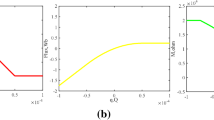
To explore the sensitivity of the simple oscillator with regard to the parameter a, the Lyapunov spectrum and the corresponding bifurcation portrait are calculated with the parameter a increasing from 0 to 1.2. When the other parameters and the initial conditions are chosen as Sect. 3.1, the Lyapunov exponent spectrum is depicted in Fig. 8a, where LE1-3 stand for the first three Lyapunov exponents, and the fourth Lyapunov exponent is trimmed out due to its large negative value. The corresponding bifurcation portrait is displayed in Fig. 8b.

Obviously, the system exhibits complex dynamical behaviors. In the region of $0<a\le 0.0059$, there is one positive Lyapunov exponent, which indicates the simple system is chaotic. When the parameter aincreases to 0.006, the system emerges periodic windows. If the parameter a is greater than 0.03, it goes into chaos. As a is the range of 1.118 to 1.2, the quasi-periodic state appears. In particular, two different chaotic attractors in the x–y plane are shown in Fig. 9a, c, whereas Fig. 9b, d demonstrate the periodic and quasi-periodic state of the system, respectively.

Fig. 9

Phase portraits in the x–y plane with the parameter a: a$a=0.00006$, b$a=0.02$, c$a=0.2$, and d$a=1.18$

Fig. 10

Dynamical map with a and b. (Color figure online)

In order to explore both a and b influencing on the system simultaneously, the dynamical map of the system is depicted in Fig. 10, where the other parameters and the initial conditions are set as Sect. 3.1. In the dynamical map, the system is in periodic state when the value of the parameters a and b is in the yellow regions, the system in chaotic state when the value in the blue region, and the system in unbounded state when the value in the brown region.

Fig. 11

Lyapunov exponent spectrum and bifurcation portrait against x(0): a Lyapunov exponent spectrum and b bifurcation portrait. (Color figure online)

Fig. 12

Phase portraits in the x–y plane with the parameter x(0): ax(0) $=1$, and bx(0) $=5$

3.4 Impacts of initial conditions

For analyzing the sensitivity of the initial condition, we fix the system parameters as Sect. 3.1, and exploit Lyapunov exponent spectrum, bifurcation portrait and dynamical map.

In order to explore the sensitivity of the initial condition x(0), and selecting the initial values as y(0) = 0, z(0) = 10.5 and u(0) = 0, the first three Lyapunov exponents and the corresponding bifurcation portrait are depicted in Fig. 11, where the initial value x(0) increases from 1 to 8. From Fig. 11, it is clear to observe that the state of the proposed oscillator depends on the initial value x(0). The simple oscillator starts from periodic state. The system jumps from periodic state into chaotic state at $x(0)=2.830$. In the region of $2.830\le x(0)\le 6.620$, there exist some periodic windows. The system jumps back periodic state as $x(0)=6.621$. In particular, the periodic attractor in the x–y plane is shown in Fig. 12a, whereas Fig. 12b demonstrates chaotic state of the system, respectively.

In order to observe the influence of x(0) and z(0) on the system dynamics at the same time, the dynamical map of the system is illustrated in Fig. 13, where the yellow region denotes chaotic state, as well as the blue one stands for periodic state. From Fig. 13, we can see that the initial values have an important influence on the dynamics of the system.

Fig. 13

Dynamical map with x(0) and z(0). (Color figure online)

Fig. 14

Lyapunov exponent spectrum and bifurcation portrait against y(0): a Lyapunov exponent spectrum and b bifurcation portrait. (Color figure online)

However, the dynamical behavior of the simple chaotic system is independent of the initial condition y(0). The Lyapunov exponent spectrum and bifurcation portrait with respect to initial condition y(0) are shown in Fig. 14, where the other initial conditions are set as $x(0) = -\,1$, $z(0) = -\,0.5$ and $u(0) = -\,3$. This phenomenon is named as sustained chaos in this paper, whose largest Lyapunov exponent keeps positive value and is approximate constant in the region of $y\left( \hbox {t} \right) \in \left[ {-\,1000,1000} \right]$. The bifurcation portrait also indicates that the system is sustained chaos state.

3.5 Bursting phenomenon

Bursting is an important neuronal activity of sending message [36, 37], which is a phenomenon of alternating between rest states and spiking states. Bursting phenomenon also is found in some nonlinear dynamical systems [38,39,40], which relates to Hopf bifurcation and fold bifurcation. When the system has two timescales, the fast variables are modulated by the slow variable, which leads to the emergence of bursting.

Fig. 15

Critical condition in the y–u plane

Fig. 16

Bursting phenomenon under the initial condition of (0, 2, 1, 0) a time-domain waveform of the variable x, b time-domain waveform of the variable y, cx–y phase portrait

Fig. 17

Coexisting attractors of bursting with the initial conditions of (1, 1.8, 1, 1) (blue) and (2, − 1, 1, 2) (red): a time-domain waveforms of the variable x, b time-domain waveforms of the variable y, cx–y phase portraits. (Color figure online)

Hence, a system, which has bursting phenomenon, can be divided into fast and slow subsystems such that the slow subsystem includes a single slow variable, and the fast subsystem includes the remaining variables, which are relatively fast [41, 42]. The fast subsystem of Eq. (7) is expressed as

$$\begin{aligned} \left\{ {{\begin{array}{ll} {{\dot{x}}=-(ay^{2}-b)x-(\alpha u+\beta )z,} \\ {{\dot{z}}=x,} \\ {{\dot{u}}=z,} \\ \end{array} }} \right. \end{aligned}$$

(12)

which consists of the first two equations and the fourth equation in Eq. (7), while the slow subsystem is the rest of the equations described as

$$\begin{aligned} {\dot{y}}=-cx-dy+ex^{2}y, \end{aligned}$$

(13)

which is the third equation of Eq. (7). For the fast subsystem, the variable y can be considered as a conventional parameter, and its equilibrium point is got as O(0, 0, u). The corresponding Jacobian matrix is expressed as

$$\begin{aligned} \mathbf{J}_{\mathrm{sub}} =\left[ {{\begin{array}{lll} {-(ay^{2}-b)}&{} {-(\alpha u+\beta )}&{} 0 \\ 1&{} 0&{} 0 \\ 0&{} 1&{} 0 \\ \end{array} }} \right] . \end{aligned}$$

(14)

Therefore, the characteristic equation is described as

$$\begin{aligned} \det (\lambda I-J_{\mathrm{sub}} )=\lambda [\lambda ^{2}+(ay^{2}-b)\lambda +(\alpha u+\beta )].\nonumber \\ \end{aligned}$$

(15)

Obviously, the characteristic equation has a zero eigenvalue, which means that there exists the fold bifurcation with the variable y taking any value.

The Hopf bifurcation is associated with the existence of a pair of pure imaginary eigenvalues, whereupon the critical condition at the Hopf bifurcation point is $(ay^{2}-b)=0$ and $(\alpha u+\beta )>0$. This critical condition is demonstrated in the y–u plane, which is the two red lines as shown in Fig. 15.

For the parameters as $a=0.1$, $b=0.4$, $c=0.2$, $d=0.1$, $e=4$, $\alpha =0.1$ and $\beta =3$, with the initial condition as (0, 2, 1, 0), the eigenvalues of the fast subsystem can be obtained as $\lambda _1 =\hbox { }0$, and $\lambda _{2,3} =\hbox {0}\pm \hbox {}j\hbox {1}.7321$. These eigenvalues indicate that fold bifurcation and Hopf bifurcation appear in this fast subsystem, and thus, the bursting oscillation occurs.

By simulating Eqs. (12) and (13), the time-domain waveforms of the state variables x and y are depicted in Fig. 16a, b, respectively, and the corresponding phase portrait in the x–y plane is displayed in Fig. 16c. The Lyapunov exponents of the oscillator are $\hbox {LE}_1 =0.023$, $\hbox {LE}_2 =0$, $\hbox {LE}_3 =-\,0.003$ and $\hbox {LE}_4 =-\,0.050$, whereupon this bursting can be regarded as chaotic bursting.

Moreover, fixing the above system parameters and changing initial conditions from (1, 1.8, 1, 1) to (2, − 1, 1, 2), the corresponding time-domain waveforms and the phase portrait for the state variables x and y are shown in Fig. 17, where the waveform (orbit) marked in blue starts from the initial condition (1, 1.8, 1, 1), while the other waveform (orbit) from (2, − 1, 1, 2). From Fig. 17, we can observe two coexisting attractors of bursting, which are approximately symmetrical about the y-axis.

Fig. 18

Coexisting attractors in the x–y and z–u planes with different b under the initial conditions of (2, $-\,1$, 1, 2) (blue), ($-\,2$, 0.7, $-\,1$, $-\,2$) (red), (0.1, 0, 0.2, 0) (green) and (0, 0, 0.2, 0.2) (yellow): a attractors in the x–y plane and b attractors in the z–u plane with $b = 0.0001$, c attractors in the x–y plane and d attractors in the z–u plane with $b = 0.1$, e attractors in the x–y plane and f attractors in the z–u plane with $b = 0.2$, g attractors in the x–y plane and h attractors in the z–u plane with $b = 0.5$, i attractors in the x–y plane and j attractors in the z–u plane with $b = 20$, k attractors in the x–y plane and l attractors in the z–u plane with $b = 100$. (Color figure online)

Fig. 19

Bifurcation portraits under the initial conditions: a bifurcation portraits under the initial conditions of (2, $-\,1$, 1, 2) (blue), ($-\,2$, 0.7, $-\,1$, $-\,2$) (red), b bifurcation portraits under the initial conditions (0, 0, 0.2, 0.2) (blue) and (0.1, 0, 0.2, 0) (red). (Color figure online)

Fig. 20

Attractive basins on the cross section of $a = 1$, $b = 0.1$, $c = 0.02$, $d = 5$, $e = 6$, $\alpha = 2$ and $\beta = 12$: a the attractive basin in the cross section of z(0) $= 0$ and u(0) $= 0$, b the attractive basin in the cross section of x(0) $= 2$ and y(0) $= 0$. (Color figure online)

Fig. 21

Coexisting attractors in the x–y and z–u planes with different initial conditions: ax–y plane bz–u plane. (Color figure online)

3.6 Coexistence of attractors

In recent years, attractor coexistence becomes a research focus, which is a special phenomenon in some special nonlinear systems, i.e., the coexistence of different attractor basins with the different initial conditions [43,44,45,46]. In Sect. 3.4, two coexisting attractors of bursting are demonstrated.

For further exploring this phenomenon, we fix $a = 1$, $c = 0.02$, $d = 5$, $e = 6$, $\alpha = 2$ and $\beta = 12$, with varying the parameter b and then watch the changes of this system’s state. The results of numerical simulation are demonstrated in Fig. 18, where the orbit colored in blue starts from the initial condition of (2, − 1, 1, 2), and the red, green and yellow ones start from the initial conditions of (− 2, 0.7, − 1, − 2), (0.1, 0, 0.2, 0) and (0, 0, 0.2, 0.2), respectively.

When $b = 0.0001$, the coexistence of four periodic attractors is shown in Fig. 18a, b, where the four periodic attractors are separated in the x–y and z–u planes, respectively.

For $b = 0.1$, 0.2 and 0.5, Fig. 18c, e, g, respectively, display the coexisting chaotic attractors on the x–y phase plane, as well as Fig. 18d, f, h shows the coexisting chaotic attractors in the z–u phase plane, respectively.

From Fig. 18c, e, g, it is clear to observe that four chaotic attractors are interlinked in the x–y plane, and the shape of the every existing attractor is slightly different. Moreover, the overlap of the attractor basins in the z–u plane also emerges with the increase of the parameter b.

Figure 18i, k visualizes two separated chaotic attractor basins in the x–y plane. However, green attractor is in the upper attractor basin as b=20, whereas green attractor is in the below attractor basin as b=100. Furthermore, the distance between two separated basins increases in the y-axis direction with the increase of the parameter b.

Four coexisting chaotic attractors in the z–u plane with $b = 20$, 100 are displayed in Fig. 18j, l, respectively, where the four chaotic attractors are separated again when $b = 100$. Hence, it is easy to see that the system has complex dynamics in this bifurcation with respect to both the parameter b and initial conditions.

In order to investigate the phenomenon of attractor coexistence, we draw the bifurcation portraits, which is shown in Fig. 19. Though there exits almost the same process from periodic oscillation to chaotic oscillation, the periodic windows in the chaotic region and the maximum of the oscillation are different.

The attractive basin, which changes with the system parameters, is an important tool to analyze coexistent attractors of circuits. Figure 20 gives the attractive basin in the cross section of $a = 1$, $b = 0.1$, $c = 0.02$, $d = 5$, $e = 6$, $\alpha = 2$ and $\beta = 12$. It includes four different color regions, representing four different types of attractors in the given value regions of the two parameters. From the graph of the attractive basin, we can see that the oscillation state varies with the increases of z(0) and u(0). Several detailed coexistent attractors are given in Figs. 21. Table 1 lists the initial values and the corresponding types of coexistent attractors.

Table 1 Initial conditions and color

Fig. 22

Transient chaos a time-domain waveform of the variable x in the time interval [0, 2000 s], b Lyapunov exponent spectrum, c phase portrait of transient chaos, d phase portrait of periodic oscillation, f time-domain waveform of the variable x in the time interval [1000, 1110 s]. (Color figure online)

Fig. 23

Intermittency for the initial conditions of a ($-\,1$, 0.7, 1, 1), and b ($-\,1$, $-\,0.8$, 1, 1)

Fig. 24

Transient process from period to chaos ax waveform from period to chaos in the time interval [0, 1000 s] b Lyapunov exponent spectrum with respect to time t in the time interval [0, 1000 s], c periodic waveform of x in the transient process for the time interval [0, 10 s], d phase portrait of transient period, f phase portrait of chaotic oscillation in the transient process. (Color figure online)

3.7 Transient phenomenon and intermittency

Transient phenomenon has been found in memristor-based or meminductor-based systems, which includes transient chaos [32, 47,48,49], transient hyperchaos [49, 50] and transient period [51]. Transient chaos is a familiar phenomenon, which is often observed in chaotic systems. The proposed system also generates transient chaos certainly. When the parameters are set as $a = 0.1$, $b = 1$, $c = 0.5$, $d = 10$, $e = 4$, $\alpha = 0.2$ and $\beta = 1$, and the initial condition is selected as (− 1, − 1.1, 1, 1), the time-domain waveform of the variable x is depicted in Fig. 22a, where the trajectory has a transition from transient chaos to periodic oscillation.

The Lyapunov exponent spectrum is displayed in Fig. 22b, where the largest Lyapunov exponent decreases to zero with time evolution, which verifies this transient phenomenon. In order to further illustrate this transient, the chaotic phase portrait is shown in Fig. 22c, whereas Fig. 22d displays the periodic phase portrait, and the waveform of the variable x in the time interval [1000, 1110 s] is shown in Fig. 22e.

Moreover, if the initial condition is taken as (− 1, 0.7, 1, 1), the intermittency on the route from chaos to period is displayed in Fig. 23a. Under different conditions, this system emerges different intermittency. Figure 23b demonstrates the different intermittency with the former, where the initial condition is (− 1, − 0.8, 1, 1).

This proposed system has infinite equilibria, whereupon this system maybe has transient period. Setting the parameters as $a = 1$, $b = 1$, $c = 0.5$, $d = 5$, $e = 4$, $\alpha = 2$ and $\beta = 10$, and taking initial condition as (− 1.4649, 0.5461, 0.1394, 8.9251), the time domain waveform of the variable x is displayed in Fig. 24a, which shows that this system starts from periodic oscillation and then switches to chaos with time evolution. The Lyapunov exponent spectrum is shown in Fig. 24b. For clarity, the waveform of the variable x in the time interval [0, 10s] is shown in Fig. 24c, which is a sinusoidal oscillation. Figure 24d, e demonstrates the transient process from periodic oscillation to chaotic oscillation by using phase portraits.

We remark that although the simple circuit contains only two dynamic circuit elements and a nonlinear resistor, i.e., a capacitor, a meminductor and a memristor, it can generate complex chaotic oscillation. The reason is that the circuit contains a local-active memristor which can provides the energy to sustain the oscillation. In addition, the memristor and the meminductor each has an internal variable, y and $\rho$, which each satisfies a differential equation. Therefore, the governing equations of the dynamic second-order circuit are actually described by a set of four differential equations, thereby yielding the complex dynamical behaviors for the second order circuit.

Fig. 25

Experimental circuit with a memristor and a meminductor

Fig. 26

Experimental bursting phenomenon observed from a digital storage oscilloscope a time-domain waveforms of $v_{\mathrm{c}}$ (brown) and y (pink), b$v_{\mathrm{c}}-y$ phase portrait

Fig. 27

Chaotic attractors observed from a digital oscilloscope: a$v_{\mathrm{c2}}$ versus y, by versus $\varphi$, c$\varphi$ versus $\rho$, d$\rho$ versus $v_{\mathrm{c2}}$

4 Circuit design and experiment results

Replacing the memristor and meminductor in Fig. 5 with their equivalent circuits (emulators) shown as Figs. 1 and 3, we can make a circuit experiment for verifying the proposed memristor–meminductor-based circuit, and the corresponding circuit is shown in Fig. 25. For controlling the speed of system evolution, the timescaling factor K is introduced into Eq. (7). Let $\tau =Kt$, Eq. (7) is rewritten as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {{\dot{x}}=K[-(ay^{2}-b)x-(\alpha u+\beta )z],} \\ {{\dot{y}}=K(-cx-dy+ex^{2}y),} \\ {{\dot{z}}=Kx,} \\ {{\dot{u}}=Kz.} \\ \end{array} }} \right. \end{aligned}$$

(16)

The dynamics of the circuit shown in Fig. 25 can be described by:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{v}}_{C2} =-\frac{1}{R_1 C_2 }\left( 1-\frac{R_3 }{R_9 }+\frac{R_3 }{R_2 }y^{2}\right) v_{C2} \\ -\frac{1}{R_1 C_2 }\left( \frac{R_{23} }{R_{20} }+\frac{R_{23} }{R_{21} }\rho \right) \varphi ,\\ {{\dot{y}}=-\frac{1}{R_6 C{ }_1}v_{c2} -\frac{1}{R{ }_5C{ }_1}y+\frac{1}{R_7 C{ }_1}v_{c2}^2 y,} \\ {{\dot{\varphi }}=\frac{1}{R_{12} C_3 }v_{c2} ,} \\ {{\dot{\rho }}=\frac{1}{R_{16} C_4 }\varphi .} \\ \end{array} }} \right. \end{aligned}$$

(17)

Comparing Eq. (16) with Eq. (17), and let their corresponding coefficients be equal, we have

$$\begin{aligned}&\frac{1}{R_1 C_2 }\frac{R_3 }{R_2 }=Ka,\frac{1}{R_1 C_2 }\left( \frac{R_3 }{R_9 }-1\right) \\&\quad =Kb,\frac{1}{R_1 C_2 }\frac{R_{23} }{R_{21} }=K\alpha ,\frac{1}{R_1 C_2 }\frac{R_{23} }{R_{20} }=K\beta \\&\frac{1}{R_6 C_1 }=Kc,\frac{1}{R_5 C_1 }=Kd,\frac{1}{R_7 C_1 }\\&\quad =Ke,\frac{1}{R_{12} C_3 }=K,\frac{1}{R_{16} C_4 }=K \\ \end{aligned}$$

When the parameters of Eq. (17) are $a = 0.1$, $b = 0.5$, $c = 0.5$, $d = 10$, $e = 4$, $\alpha = 0.1$ and $\beta = 1$, with $K=10000$, the parameter values of the electronic components are selected as shown in Fig. 25

Fig. 28

Experimental setup with experimental chaotic bursting

The experimental results of bursting obtained from the digital oscilloscope of the experimental setup are shown in Fig. 26, in which the brown and pink waveforms of Fig. 26a correspond to the time-domain waveforms of x and y in Fig. 16a, b, respectively, while Fig. 26b corresponds to Fig. 16c, describing the phase diagram of x versus y. Figure 27 shows chaotic attractors observed from oscilloscope of the physical circuit experiment, and Fig. 28 is the experimental setup with the experimental results of chaotic bursting. The physical circuit is constructed in a breadboard, whose area is about $8 \times 10\,\hbox {cm}^{2}$. The circuit includes four analog multiplier AD633s and three operational amplifier LF347Ns; thus, the power consumption of the circuit is approximate 1W.

5 Conclusion

In this work, we presented the mathematical models and their equivalent circuits of a memristor and a meminductor. Based on the two models, a simple chaotic oscillator containing a memristor and a meminductor is proposed. We have shown that this oscillator can exhibit some complex dynamical behaviors, including bursting, coexisting attractors, transient chaos, transient period and intermittency. Finally, an electronic circuit is designed by utilizing the equivalent circuits of the memristor and meminductor to substitute their mathematical models, with which the experimental results confirm its chaotic feature via hardware experiment. Due to rich dynamical behaviors of the simple chaotic system, it can be expected that it will have extensive prospects for memristive circuits in the future.