1 Introduction

Parametrically excited systems have been studied extensively in mathematics and engineering applications (see, e.g., [1,2,3,4,5]). A well-known example of a parametrically excited system is the Mathieu equation. It can describe the linearized equations of motion of a simple pendulum with a periodically moving support or the transverse oscillations of a beam with a pulsating axial load [6, 7]. The trivial solution of the Mathieu equation can be destabilized by parametric excitation. Another system with such a destabilizing effect due to parametric excitation is the Jeffcott rotor with a breathing crack [8]. Unstable parameter regions caused by parametric excitation are known as parametric resonances. This effect has also been studied in [1, 5, 9].

In systems with two or more degrees of freedom, a parametric excitation may have a stabilizing effect. This beneficial effect was discovered and described by Tondl in [4, 10]. This idea was generalized to the concept of damping by parametric excitation [11, 12] which describes the process of introducing a well-chosen parametric excitation to increase the overall system damping of a general system. As described in [11,12,13], this effect can be interpreted as a coupling of certain modal degrees of freedom which allows for a more efficient usage of the existing system damping. If the trivial solutions of an unstable linear time-invariant system can be stabilized in certain parameter regions by introducing parametric excitation, these regions are called parametric anti-resonances. Among others, the studies of interaction of self-excited and parametric vibrations have been continued in [11, 14,15,16].

In the physics literature, a similar effect of the parametric excitation was observed investigating unstable periodic orbits of a chaotic attractor. In [17], it is described that a well-chosen time-varying parameter can stabilize some of these periodic orbits, and therefore the trajectories settle on the stabilized periodic orbits. The method, however, relies on real-time exact state feedback, which is difficult to realize in an experimental setup. Adding a parametric excitation to the Duffing oscillator can also prevent the intersection of stable and unstable manifolds, as shown in [18] by Melnikovs method. This analysis, however, becomes infeasible for general high-dimensional systems. Experimental and numerical studies [19,20,21] have further shown that the phase difference between the unstable periodic orbit and the parametric excitation can be crucial for the success of stabilizing a periodic orbit. Analytical results, however, have not been reported. These methods are summarized as (phase) control of chaos.

Two well-known examples for self-excited vibrations in rotor dynamics are inner damping and the effects due to journal bearings (see e.g., [8]). Applications and numerical verifications of beneficial effects of parametric anti-resonances in rotor dynamics can be found in, e.g., [15, 22,23,24,25]. In particular, damping by parametric excitation has been implemented experimentally for a rotor in magnetic bearings during the passage through resonance [26]. Recent publications [27,28,29,30] indicate the potential to suppress the self-excited vibrations occurring in fluid-film bearings. Thereby, the operating range of rotors in journal bearings is enlarged. Further potential applications are the suppression of self-excited vibrations occurring in air bearings [31], clearance-excitations induced by air-gaps between rotating and non-rotating parts [32], or friction-induced vibrations such as break squeal [33].

Parametric resonance and parametric anti-resonance can only be observed if the frequency of parametric excitation is in the vicinity to either one of the fundamental parametric resonance frequencies or the parametric combination frequencies [3, 5]. This can be confirmed analytically by applying the method of averaging [11, 12, 16, 29], whereby the linear time-varying system is approximated by a linear time-invariant system on a certain time scale. Therefore, the stability analysis is performed by standard eigenvalue computation. In [11,12,13], the method of averaging has further been used to understand the occurrence of parametric anti-resonances and interpret the underlying physical reasons. Generally, the application of the method of averaging is computationally less costly compared to analysis relying on the numerical calculation of the monodromy matrix. This allows for parameter studies even in high-dimensional systems.

The studies [11, 12, 16] perform the averaging for equations of motion in second-order form with decoupled linear part. However, common rotor dynamic effects such as gyroscopic forces, inner damping or journal bearings are described by systems with non-symmetric system matrices [8], whereby the decoupling of the linear part in second-order form is infeasible. To overcome these limitations, an averaging process in the state-space representation (i.e., first-order form) has been developed recently [29, 34, 35]. Furthermore, in [29] numerical evidence was presented, that the averaging in the state-space representation leads to more accurate results than the more common approaches [11, 12, 16] even for systems with symmetric system matrices.

To perform the averaging process, a single parametric resonance frequency has to be chosen at the beginning of the approximation process. If the investigated frequency range of parametric excitation contains multiple parametric resonance frequencies, it is not trivial which one to choose. In higher-dimensional systems, this is more challenging, since for linear systems the number of parametric resonance frequencies increases quadratically with the number of degrees of freedom. If the eigenvalues of the system without parametric excitation are close to each other, the parametric resonance frequencies are also close. Restricting the frequency interval such that it contains only one parametric resonance frequency may lead to a limited interval for the frequency of parametric excitation. Recent investigations [34] indicate that treating each parametric resonance frequency independently might lead to contradictory results. In [29], it is highlighted that certain stability maps can only be explained by the interaction of multiple parametric resonance frequencies.

To analyze parametrically excited systems with non-symmetric system matrices in a frequency range of parametric excitation containing multiple parametric resonance frequencies, a novel approach is presented. Due to the non-symmetric system matrices, the procedure of [29] is applied, where the system is transformed to state space and the method of averaging is then applied. To account for interfering parametric resonance frequencies, the eigenvalues of the averaged system are investigated. Relying on this eigenvalues an algorithm is proposed to determine the stability of the system with interfering parametric resonance frequencies. Thereby, it is assumed that the averaged system results from applying the method of averaging in state space. However, the procedure can be easily adopted to alternative, more common averaging approaches. To illustrate the potential of the approach, two rotor systems from the literature are re-investigated.

2 The process of averaging

Starting with the equation of motion of a linear mechanical system, it is then transformed to a computationally convenient form to which the method of averaging is applied. Subsequently, the stability of the system is discussed.

2.1 Equation of motion

In engineering applications, the linearized equation of motion of a parametrically excited system is given by

$$\begin{aligned}&\mathbf {M} \;\!\ddot{\mathbf {q}}+\mathbf {B}(t)\;\!\dot{\mathbf {q}}+\mathbf {K}(t)\;\!\mathbf {q}=\mathbf {0},\nonumber \\&\quad \mathbf {B}(t+T)=\mathbf {B}(t), \qquad \mathbf {K}(t+T)=\mathbf {K}(t). \end{aligned}$$
(1)

The mass matrix \(\mathbf {M}\) is assumed to be non-singular and constant, t denotes the time and \(\mathbf {q}\) a vector of generalized coordinates. The matrices \(\mathbf {K}\) and \(\mathbf {B}\) correspond to the stiffness and damping coefficient matrix. These matrices are of general structure and can be non-symmetric. Examples for asymmetry in rotor systems are the presence of gyroscopic forces, inner damping or journal bearings [8]. The number of degrees of freedom of system (1) is denoted by N. The frequency of parametric excitation is given by \(\Omega _{P}=2\pi / T\). Utilizing the complex Fourier series expansion of the periodic matrices, Eq. (1) can be rewritten as

$$\begin{aligned}&\mathbf {M}\;\!\ddot{\mathbf {q}} + \mathbf {B}_0\;\!\dot{\mathbf {q}} + \mathbf {K}_0\;\!\mathbf {q} \nonumber \\&= -\varepsilon \;\!\sum \limits _{k=1}^{K} \left[ \left( \mathbf {K}^{k+} \mathrm{e}^{\mathrm {i}\;\!k\Omega _P t} +\,\mathbf {K}^{k-} \mathrm{e}^{-\mathrm {i}\;\!k\Omega _P t} \right) \;\!\mathbf {q}\right. \nonumber \\&\quad \left. +\left( \mathbf {B}^{k+} \mathrm{e}^{\mathrm {i}\;\!k\;\!\Omega _P t} +\, \mathbf {B}^{k-} \mathrm{e}^{-\mathrm {i}\;\!k\;\!\Omega _P t} \right) \;\!\dot{\mathbf {q}} \right] . \end{aligned}$$
(2)

The superscript k indicates the kth coefficient of the Fourier series expansion and ± the sign of the associated exponential. It is assumed that the time-varying part is small compared to the constant part, which is denoted by the small parameter  \(\varepsilon \). The eigenvalues \(\lambda _j\) and the state-space eigenvectors \(\mathbf {v}_j\) of the system (2) without parametric excitation (\(\varepsilon = 0\)) are defined by

$$\begin{aligned}&\left( \begin{bmatrix} \mathbf {0}&\quad \mathbf {I}\\ -\,\mathbf {M}^{-1}\mathbf {K}_0&\quad -\,\mathbf {M}^{-1}\mathbf {B}_0 \end{bmatrix} - \lambda _n\mathbf {I} \right) \mathbf {v}_n=\mathbf {0},\nonumber \\&\quad n=1,\ldots ,2N, \quad \mathbf {V} =\left[ \mathbf {v}_1,\ldots ,\mathbf {v}_{2N}\right] . \end{aligned}$$
(3)

The truncation of the Fourier series in Eq. (2) is chosen such that K is well above the double of the maximum imaginary part of the eigenvalues \(\lambda _n\) divided by the parametric excitation frequency \(\Omega _P\), i.e., \(K \gg 2\max _n\left( \mathrm {Im}\left[ \lambda _n\right] \right) /\Omega _{P}\). This truncation is chosen such that the ignored terms in the Fourier expansion do not contribute in the outlined averaging process of first order, which is discussed in the following section. The matrix \(\mathbf {V}\) consists of the eigenvectors of the time-invariant part of system (1), and therefore it decouples the time-invariant part. Defining the modal coordinates \(\mathbf {z} = \mathbf {V}[\mathbf {q}^\mathrm{T},\dot{\mathbf {q}}^\mathrm{T}]^\mathrm{T}\), Eq. (2) is transformed to

$$\begin{aligned}&\displaystyle \dot{\mathbf {z}} = \mathbf {\Lambda }\mathbf {z} - \varepsilon \sum \limits _{k=1}^{K}\left( \mathbf {P}^{k+} \mathrm{e}^{\mathrm {i}\;\!k\;\!\Omega _P t} + \mathbf {P}^{k-} \mathrm{e}^{-\mathrm {i}\;\!k\;\!\Omega _P t} \right) \;\!\mathbf {z},\nonumber \\&\mathbf {\Lambda }=\text{ diag }(\lambda _1,\ldots ,\lambda _{2N}), \end{aligned}$$
(4)

whereby it is assumed, that the constant state-space matrix is semi-simple, i.e., the matrix \(\mathbf {\Lambda }\) is diagonal. Its entries are the eigenvalues \(\lambda _n\) (cf. Eq. (3)). The transformation of the matrices \(\mathbf {K}^{k\pm }\) and \(\mathbf {B}^{k\pm }\) generates the matrices of parametric excitation \(\mathbf {P}^{k\pm }\). Generally, they are not diagonal and couple the modal degrees of freedom. Equation (4) for the nth modal degree of freedom is given by

$$\begin{aligned} \displaystyle {\dot{z}}_n= & {} \lambda _n z_n - \varepsilon \sum \limits _{m=1}^{2N}\sum \limits _{k=1}^{K} \left( P_{nm}^{k+} \mathrm{e}^{\mathrm {i}\;\!k\Omega _P t} \right. \nonumber \\&\quad \left. +\, P_{nm}^{k-} \mathrm{e}^{-\mathrm {i}\;\!k\;\!\Omega _P t} \right) z_m,\quad n=1,\ldots ,2N. \end{aligned}$$
(5)

Linear systems with time-periodic coefficients arise in the stability investigations of periodic orbits in general. Therefore, if the equation of variation along the periodic orbit can be expressed in the form of system (4) (diagonalizable constant part and small time-varying part), the outlined procedure can be applied. More specifically, in the case of (phase) control of chaos (c.f. [19,20,21]) the linearization about an unstable periodic orbit needs to be computed. In the following, the focus lies on parametrically excited mechanical systems.

In the literature [36,37,38], the method of averaging is formulated for second-order systems. Equation (5) is of first-order form; however, the averaging process can be adapted, as shown in the next section.

2.2 Transformation and averaging

In the following, the averaging procedure developed in [14, 16] is adapted to the state-space representation (cf. Eq. (5)), which allows the analysis of systems with non-symmetric stiffness and damping matrices. The standard procedure of averaging (see [36, 37]) introduces a small detuning \(\Delta \Omega _P\) of the excitation frequency, by

$$\begin{aligned} \Omega _P = \Omega _{P0} + \varepsilon \;\!\Delta \Omega _{P} + {\mathcal O}(\varepsilon ^2),\qquad \Omega _{P0}\ne 0 , \end{aligned}$$
(6)

where the frequency \(\Omega _{P0}\) determines a resonant manifold in whose vicinity the results of method of averaging are valid. Usually, this frequency is determined by systems frequencies [37], and in the upcoming derivations an explicit expression for choices of \(\Omega _{P0}\) is obtained. Furthermore, a dimensionless time \(\tau = \Omega _{P}t\) and normalized eigenvalues \({\bar{\lambda }}_n =\lambda _n/\Omega _{P0}\) are introduced. Utilizing these notations and the detuning (6), the Taylor series expansion of Eq. (5) for small \(\varepsilon \) can be computed to

(7)

where the prime denotes the derivative with respect to the dimensionless time. For system (7), a harmonic ansatz with a time-dependent amplitude of the form

$$\begin{aligned} \displaystyle z_n = u_n(\tau )\;\!\mathrm{e}^{ \mathrm {i}\tau \;\!\mathrm {Im}\left[ {\bar{\lambda }}_n\right] }, \end{aligned}$$
(8)

is made. It is the state-space equivalent to the amplitude-phase transformation [37], which is also applied in the method of slowly varying phase and amplitude (see [6, 38]). Rescaling the real part of each eigenvalue by the small systems parameter \(\varepsilon \) (\(\mathrm {Re}\left[ \lambda _n\right] \mapsto \varepsilon \mathrm {Re}\left[ \lambda _n\right] \)), the first-order approximation of system (7) is given by

(9)

Since the number of periodic functions in Eq. (9) is finite, the system of first-order differential equations (9) can be expressed in the standard form

$$\begin{aligned}&\dot{\mathbf {u}} = \varepsilon \mathbf {f}(\mathbf {u},t)=\varepsilon \sum _{k=1}^{\tilde{K}} \mathbf {f}^k(\mathbf {u},t)+\mathcal {O}(\varepsilon ^2)\nonumber \\&\mathbf {f}^k(\mathbf {u},t+T_k)=\mathbf {f}^k(\mathbf {u},t). \end{aligned}$$
(10)

The method of averaging can be applied to systems of the form of Eq. (10) [36]. The averaged system is given by averaging each of the periodic functions on the right-hand side of Eq. (10) over its period

$$\begin{aligned} \dot{\hat{\mathbf {u}}} = \varepsilon \sum \limits _{k=1}^{\tilde{K}}\frac{1}{T_k}\int \limits _{0}^{T_k}\mathbf {f}^k(\hat{\mathbf {u}},t)\;\!\mathrm{d}t. \end{aligned}$$
(11)

The difference of the solution of the averaged system (11) and the original system (10) is of order \(\varepsilon \) (\(\hat{\mathbf {u}} - \mathbf {u} = \mathcal {O}(\varepsilon )\)) on the time scale \(1/\varepsilon \). Proofs and further treatment can be found in, e.g., [36, 37] and higher-order approximations in [14, 34, 37]. Averaging the harmonic functions of Eq. (9) will always give zero, unless the exponent of the exponential function vanishes. This is the case if

$$\begin{aligned} {k}\Omega _{P0}= & {} {\mp \mathrm {Im}[\lambda _n]\pm \mathrm {Im}[\lambda _m]}. \end{aligned}$$
(12)

These frequencies are called parametric resonance frequencies in the following. The parameter k denotes the order of the parametric resonance frequency. The parametric resonance frequencies are determined by the imaginary parts of the eigenvalues of the underlying system with constant coefficients and not by the eigenfrequencies as they are defined in the literature (e.g., [3, 5]). The difference, however, is in second order in \(\varepsilon \). The averaged system will generally depend on the parametric resonance frequencies. Due to the definition (6), the parametric resonance frequencies are not zero.

The choice \(K \gg 2\max _n\left( \mathrm {Im}\left[ \lambda _n\right] \right) /\Omega _{P}\) in the Fourier expansion (2) is justified by assuming the existence of a parametric resonance frequencies above the truncation frequency, i.e., with \(k = k^* > K\). Eq. (12) yields

$$\begin{aligned} \Omega _{P0}= & {} \frac{\mp \mathrm {Im}\left[ \lambda _n\right] \pm \mathrm {Im}\left[ \lambda _m\right] }{k^*}\nonumber \\\le & {} \frac{2\max _{n=1,\ldots ,2N}\left( \mathrm {Im}\left[ \lambda _n\right] \right) }{K} \ll \Omega _{P}, \end{aligned}$$
(13)

which contradicts the closeness of \(\Omega _P\) and \(\Omega _{P0}\) from Eq. (6). For higher-order averaging, the truncation can be adjusted.

2.3 The averaged system

The parametric resonance frequency is given by the choice of two specific indices \(n = {\widetilde{n}}\) and \(m = {\widetilde{m}}\). Averaging yields to

$$\begin{aligned} \left[ \begin{array}{l} {\hat{u}}_{\bar{n}}' \\ {\hat{u}}_{\bar{m}}' \end{array}\right]= & {} -\frac{\varepsilon }{\Omega _{P0}} \left[ \begin{array}{ll} \sigma _{\bar{n}} &{}\quad P_{\bar{n},\bar{m}}^{k\pm } \\ P_{\bar{m},\bar{n}}^{k\mp } &{}\quad \sigma _{\bar{m}} \end{array}\right] \left[ \begin{array}{l} {\hat{u}}_{\bar{n}} \\ {\hat{u}}_{\bar{m}} \end{array}\right] ,\,\nonumber \\ \sigma _{{n}}= & {} \mathrm {i}\;\!\frac{ \mathrm {Im}\left[ \lambda _{{n}}\right] \;\!\Delta \Omega _P }{\Omega _{P0}} - \mathrm {Re}\left[ \lambda _{{n}}\right] . \end{aligned}$$
(14)
Table 1 Indices for system (14) depending on the parametric resonance frequency given by the eigenvalues \(\lambda _{{\tilde{n}}}\) and \(\lambda _{{\tilde{m}}}\); \(+N\) denotes the complex conjugated eigenvalue
Full size table

The indices \(\bar{n}\) and \(\bar{m}\) in Eq. (14) can be taken from Table 1. In the case of a fundamental parametric resonance frequency (first line of Table 1), two modal coordinates with complex conjugate eigenvalues are coupled (\({\hat{u}}_{{\tilde{n}}}\) and \({\hat{u}}_{{\tilde{n}}+N}\)). In the case of a parametric combination frequency, the replacements for \(\bar{n}\) and \(\bar{m}\) can be found in the line two (difference) and line three (sum) of Table 1. Two \(2 \times 2\) systems arise, for instance in the case of a parametric combination frequency of difference type, the coordinate \({\hat{u}}_{{\tilde{n}}}\) is coupled with \({\hat{u}}_{{\tilde{m}}}\) and \({\hat{u}}_{{\tilde{n}}+N}\) with \({\hat{u}}_{{\tilde{m}}+N}\), whereas the coordinates \({\hat{u}}_{{\tilde{m}}}\) and \({\hat{u}}_{{\tilde{n}}+N}\) are decoupled from \({\hat{u}}_{{\tilde{n}}+N}\) and \({\hat{u}}_{{\tilde{m}}+N}\). It can be shown that the two decoupled \(2 \times 2\) are complex conjugates [34], and therefore the stability type of the trivial fixed point is the same for both systems. This holds similarly for the summation type.

If the resonance condition for the upper sign in the second column of Table 1 is fulfilled, then the upper signs in Eq. (14) are valid. Analogous holds for the lower signs. Equation (14) is only valid if none of the other eigenvalues have the same imaginary part as \(\lambda _{{\widetilde{n}}}\) and \(\lambda _{{\widetilde{m}}}\). If this is the case, the averaged system will generally have more dimensions [34] and cannot be written in the form of Eq. (14). However, the proposed process can easily be adapted.

For all other coordinates \(n\ne \bar{n},\bar{m}\), the averaged system simplifies to

$$\begin{aligned} {\hat{u}}_{{n}}' = -\frac{\varepsilon }{\Omega _{P0}}\;\!\sigma _{{n}} \;\!{\hat{u}}_{{n}} . \end{aligned}$$
(15)

3 Stability analysis

In this section, the stability of the trivial solution of the averaged system is investigated. Since the averaged system is time invariant, an extension of the Hurwitz criterion for complex-valued polynomials [39] can be used to derive conditions for stability on the detuning \(\Delta \Omega _P\) (see e.g., [11, 14, 23]). In general, the influence of parametric excitation is observed in a vicinity of the parametric resonance frequencies (cf. e.g., [3, 4]). However, the coefficient matrix in Eq. (14) depends on the choice of \(\Omega _{P0}\) and its evaluation at different parametric resonance frequencies \(\Omega _{P0}\) might lead to a different stability conclusion. So, even contradictory stability maps might arise. To overcome this problem, an approach motivated in an engineering manner is proposed. It accounts for all relevant parametric resonance frequencies in a specific region of the stability map.

After transforming the averaged Eqs. (14) and (15) to the original time, their eigenvalues (\(\rho _n\)) are investigated. In the case of \(n =\bar{n}\) or \(n=\bar{m}\), these are determined by

$$\begin{aligned} \displaystyle \rho _{\bar{n},\bar{m}}= & {} \varepsilon \left[ \frac{\mathrm {Re} [\lambda _{\bar{n}}]+ \mathrm {Re} [\lambda _{\bar{m}}]}{2}-\mathrm {i}\Delta \Omega _P \frac{\mathrm {Im} [{\bar{\lambda }}_{\bar{n}}]+\mathrm {Im} [{\bar{\lambda }}_{\bar{m}}]}{2} \right. \nonumber \\&\quad \displaystyle \pm \left. \frac{1}{2}\sqrt{[ \mathrm {Re} [\lambda _{\bar{n}}]-\mathrm {Re} [\lambda _{\bar{m}}]-\mathrm {i}\Delta \Omega _P(\mathrm {Im} [{\bar{\lambda }}_{\bar{n}}]-\mathrm {Im} [{\bar{\lambda }}_{\bar{m}}]) ]^2+4P^{k\pm }_{\bar{n}\bar{m}}P^{k\mp }_{\bar{m}\bar{n}}}\right] \nonumber \\&\quad +\, {{\mathcal {O}}}(\varepsilon ^2)\nonumber \\= & {} \rho _{m,\mathfrak {R}}-\mathrm {i}\rho _{m,\mathfrak {I}}\pm \sqrt{\Delta \rho _{\mathfrak {R}} +i\Delta \rho _{\mathfrak {I}}} + {{\mathcal {O}}}(\varepsilon ^2). \end{aligned}$$
(16)

The indices for which the resonance condition is met are given in Table 1. For the other indices, \(\rho _n\) is computed from Eq. (15). Since the indices \(\bar{n}\) and \(\bar{m}\) depend on \(\Omega _{P0}\) and \(\Delta \Omega _{P}\), the eigenvalues \(\rho \) will generally also depend on these parameters. It can be observed that a parametric combination frequency determined by the indices \({\widetilde{n}}\) and \({\widetilde{m}}\) introduces damping in the modal coordinates \(u_{{\widetilde{n}}}\), \(u_{{\widetilde{m}}}\), \(u_{{\widetilde{n}}+N}\) and \(u_{{\widetilde{m}}+N}\). This is consistent with the observations [11]. Furthermore, investigating Eq. (16) reveals, if the parametric excitation lowers the real part of an eigenvalue, the real part of the another eigenvalue is always increased. The stability gain in some modal degree of freedom will always cause a stability loss in another modal coordinate. This matches with the observations and interpretations described in [11].

If the parametric resonance frequency (\(\Omega _{P0}\)) is fixed, only the parameter \(\Delta \Omega _P\) can be varied. From the linear Eq. (6), it is obvious that \(\Delta \Omega _P\) can be replaced by \(\Omega _P\). Therefore, the eigenvalues \(\rho _{n}\) can be visualized over the frequency of parametric excitation \(\Omega _P\), which is a physically meaningful parameter. A schematic drawing of several eigenvalues is given in Fig. 1. To distinguish between the eigenvalues \(\rho _n\) arising from different choices of \(\Omega _{P0}\), a new superscript r (\(r=1,\ldots ,R\)) is introduced. The eigenvalue \(\rho _n^{(r)}\) is the eigenvalue of nth modal degree of freedom of the averaged system due to the rth parametric resonance frequency (\(\Omega _{P0}^{(r)}\)).

Fig. 1
figure 1

Sketch of the eigenvalues of the averaged system (16) and the parameters defined in Eq. (18) for neighboring parametric combinations frequencies

Full size image

In Fig. 1, it is assumed that \(\lambda _{\max }\) and its complex conjugate are the only eigenvalues with positive real part, and thus the trivial equilibrium of system (1) without parametric excitation is unstable. As observed earlier, the real part of the eigenvalues of the averaged system \(\rho _n\) can change due to the parametric excitation. For stability of the averaged system (14), it is therefore necessary that the real parts of \(\rho ^{(r)}_{\max }\) and its complex conjugated cross the \(\mathrm {Re}[\rho ^{(r)}_{n}] = 0\) line. Then, a parametric resonance can be observed.

This is shown in Fig. 1, where the first parametric combination frequency \(\Omega _{P0}^{(1)}\) is determined by the eigenvalues \(\lambda _{\max }\) and \(\lambda _{n_1}\). If this frequency is chosen for \(\Omega _{P0}\) in the detuning (6), \(\rho ^{(1)}_{\max }\), \(\rho ^{(1)}_{max+N}\), \(\rho ^{(r)}_{n_1}\) and \(\rho ^{(r)}_{n_1+N}\) differ from the corresponding eigenvalues \(\lambda _n\) for non vanishing coefficients \(P^{\pm }_{nm}\) (cf. Eq. (16)). Such a case is indicated by the gray lines in Fig. 1. It can be shown that \(\rho ^{(r)}_{n}\) and \(\rho ^{(r)}_{n+N}\) are complex conjugates [34]. So it is sufficient to show one of them. If the frequency of parametric excitation is in the interval S\(^{(1)}\), then the trivial solution of averaged system is stable, whereas the trivial solution of the system without parametric excitation is unstable (\(\mathrm {Re}\left[ \lambda _{\max }\right] >0\)). Thus, a parametric anti-resonance is observed in this interval. The interval S\(^{(1)}\) can also be obtained by applying the Hurwitz criterion to Eq. (14), as this is done in, e.g., [11, 12, 29].

Investigating Eq. (16) for large \(\Delta \Omega _{P}\) and reversing the rescaling of \(\mathrm {Re}\left[ \lambda _n\right] \) reveals that \(\mathrm {Re}\left[ \rho _{n}^r\right] \) tends toward \(\mathrm {Re}\left[ \lambda _n\right] \). The parameter \(\Delta \Omega _{P0}\) is the difference between the choice of the parametric resonance frequency \(\Omega _{P0}\) and the actual frequency of parametric excitation \(\Omega _P\) (cf. Eq. (6)). The eigenvalues of the averaged system differ significantly from the corresponding eigenvalues \(\lambda _n\) if these are sufficiently close to a parametric resonance frequency. Only in this region, the stability of the system (1) is influenced by parametric excitation. Consequently, parametric anti-resonances and parametric resonances can be observed only in the vicinity of a parametric excitation frequency (see [3, 4, 7]).

The eigenvalues \(\lambda _{\max }\) and \(\lambda _{n_2}\) (\(n_1\ne n_2\)) contribute toward the second combination frequency \(\Omega _{P0}^{(2)}\). The dashed black lines in Fig. 1 indicate a schematic evolution of the real part of corresponding eigenvalues \(\rho ^{(2)}_{\max }\) and \(\rho ^{(2)}_{n_2}\). Choosing \(\Omega ^{(2)}_{P0}\) as parametric resonance frequency in the averaging process leads to the stability interval S\(^{(2)}\). Figure 1 illustrates that the stability intervals arising from different parametric resonance frequencies not necessarily coincide.

The difference between the real parts of the averaged system (\(\rho _n^{(r)}\)) and \(\lambda _n\) is defined by

$$\begin{aligned} \Delta \rho _{n}^{(r)}= & {} \mathrm {Re}\left[ \rho _{n}^{(r)}\right] -\mathrm {Re}\left[ \lambda _n\right] \nonumber \\ \quad= & {} \left\{ \begin{array}{ll} \displaystyle f^{(r)}_n(\Delta \Omega _P)&{}\quad \text{ if }\;\; \;\!n= \bar{n},\bar{m}\\ \displaystyle 0 &{}\quad \text{ if }\;\; n\ne \bar{n},\bar{m}. \end{array}\, \right. \end{aligned}$$
(17)

This parameter can be interpreted as a measure of damping (negative or positive) which is caused by the rth parametric resonance frequency at the nth coordinate. To account for possible interactions between different parametric resonance frequencies, the parameters \(\Delta \rho _{n}^{(r)}\) are added at constant values of the frequency \(\Omega _P\). The approximation

$$\begin{aligned} {\tilde{\rho }}_{n}=\mathrm {Re}\left[ \lambda _n\right] +\sum \limits _{r=1}^R\Delta \rho _{n}^{(r)}, \end{aligned}$$
(18)

determines the stability with respect to the overlying region between R parametric resonance frequencies. The trivial solution of system (1) is stable if \({\tilde{\rho }}_{n}\) is negative for all coordinates. Through the summation in Eq. (18), the influence of all interacting parametric resonance frequencies is approximated and resolves the contradictions in the stability intervals due to a different choice of \(\Omega _{P0}\). The parameter \({\tilde{\rho }}_{\max }\) is shown as black solid line in Fig. 1. It is highlighted that the overall stability interval is not simply the union of both stability intervals (\(S^{(1)}\) and \(S^{(2)}\)). In the example showed in Fig. 1, it is greater than the union of the individual stability intervals. If the \(\mathrm {Re}[\rho _m]=0\) line in Figure 1 is lowered, such that it does not intersect with the \(\mathrm {Re}[\rho ^{(1)}_{\max }]\) and \(\mathrm {Re}[\rho ^{(2)}_{\max }]\) curves but still with the \({\tilde{\rho }}_{\max }\) curve from the summation (18), the resulting parametric anti-resonance can only be explained by the interference of the two parametric resonance frequencies. An isolated treatment would fail to predict this parametric anti-resonance. Similar cases can be constructed for the arise of parametric resonances and significant interference of a neighboring parametric resonance and anti-resonance. Although reasoning is indicated by observing the eigenvalues of the averaged system, the outlined process is motivated empirically. A strict mathematical proof is subject to future research.

4 Numerical examples

Two rotor systems from the literature are re-investigated to highlight the potential of the proposed approach. The first one was proposed in [15]. The second system is a Jeffcott rotor in journal bearings with adjustable gap geometry as studied in [28,29,30].

Fig. 2
figure 2

Rigid rotor model with flexible bearing mounts

Full size image

The benchmark stability maps are based on the Floquet theory, which is summarized briefly in the following. Detailed treatments can be found in e.g., [6, 37, 40]. System (1) can be transformed to a 2N dimensional system with time-periodic coefficients of the form

$$\begin{aligned} \dot{\mathbf {x}}=\mathbf {A}(t)\mathbf {x},\quad \mathbf {A}(t)=\mathbf {A}(t+T). \end{aligned}$$
(19)

According to Floquet’s theorem, the system (19) can be transformed into an equivalent time-invariant system with the transformation \(\mathbf {x}(t)=\mathbf {L}(t)\mathbf {y}(t)\). The matrix \(\mathbf {L}(t)\) is time periodic, non-singular and equal to the identity at initial time \(t=t_0=0\). The resulting system is

$$\begin{aligned}&\dot{\mathbf {y}}=\mathbf {L}^{-1}(t)\left[ \mathbf {A}(t)\mathbf {L}(t)-\dot{\mathbf {L}}(t)\right] \mathbf {y}=\mathbf {C}\mathbf {y},\nonumber \\&\mathbf {L}(t+T)=\mathbf {L}(t),\quad \mathbf {L}(0)=\mathbf {I}. \end{aligned}$$
(20)

If computable, the stability of the resulting time-invariant system (20) can be determined by standard eigenvalue computations of the matrix \(\mathbf {C}\). In general, however, the transformation matrix \(\mathbf {L}(t)\) is not computable in closed form [40]. With the solution to linear time-invariant system (20), the solution to system (19) at \(t=T\) with initial condition \(\mathbf {x}_0\) is given by

$$\begin{aligned} \mathbf {x}(T)=\mathbf {L}(T)\mathrm{e}^{\mathbf {C}T}\mathbf {x}_0=\mathrm{e}^{\mathbf {C}T}\mathbf {x}_0=\varvec{\Phi }(T) \mathbf {x}_0, \end{aligned}$$
(21)

where the matrix \(\varvec{\Phi }(T)\) is the monodromy matrix. Equation (21) reveals \(\mathbf {C}=1/T\ln (\varvec{\Phi }(T))\), and therefore the eigenvalues of the matrix \(\mathbf {C}\), which determine the stability of system (20), respectively, the equivalent system (19), can be obtained by the eigenvalues of the monodromy matrix. The trivial solution of system (19) is asymptotically stable, if and only if all eigenvalues of the monodromy matrix are less than one in magnitude.

To solve Eq. (21) for the monodromy matrix, Eq. (19) is numerically integrated for a set of 2N linearly independent initial conditions for one period. Collecting these results and the initial conditions in the matrices \(\mathbf {X}_T\) and \(\mathbf {X}_0\), the monodromy matrix is obtained as \(\varvec{\Phi }(T)=\mathbf {X}_T\mathbf {X}_0^{-1}\). The numerical integration is carried out with the ode45 or ode15s numerical integration routines of the software package MATLAB.

4.1 Rotor system proposed by Tondl and Ecker

In [15], Tondl and Ecker propose a self-excited rotor system with parametric excitation, which is further studied in [41, 42]. The system served as a basic study to indicate the capability of damping by parametric excitation for self-excited rotor systems. Stability maps, however, have only been obtained numerically.

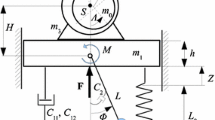
The rotor system, depicted in Fig. 2, consists of two bearing housings with mass \(m_{h}\) and one rigid rotor (\(m_\mathrm{r}\)). All three masses have two translational degrees of freedom perpendicular to the rotating axis of the rotor. In addition, the rotor mass has two rotational degrees of freedom (\(\phi _x\) and \(\phi _y\)), whose axis coincides with the transverse degrees of freedom. The moment of inertia of the rotor with respect to these axis is given by \(\Theta _a\), while the moment of inertia of the rotor with respect to the z-axis is given by \(\Theta _p\).

Fig. 3
figure 3

Comparison of different stability predictions for the rotor system [15]

Full size image

The vector of generalized coordinates is given by \(\mathbf {q}^T=[x_r, y_r, \phi _x, \phi _y, x_{b1}, y_{b1}, x_{b2}, y_{b2}]\). The symmetric system matrices and numerical values can be found in “Appendix A”. The skew-symmetric part of the damping matrix and the skew-symmetric part of the stiffness matrix, denoted by \(\mathbf {G}\) and \(\mathbf {N}\), are proportional to the rotor speed (\(\Omega \)) and are given by

$$\begin{aligned}&\mathbf {G}(\Omega ) = \frac{\Omega \Theta _p}{\Omega _\mathrm{r}} \begin{bmatrix} 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 1&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad -\,1&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0 \end{bmatrix},\nonumber \\&\mathbf {N}(\Omega )= \frac{\sigma _b \Omega }{\Omega _\mathrm{r}^2} c_\mathrm{b}\nonumber \\&\qquad \qquad \times \begin{bmatrix} 0&\quad 2&\quad 0&\quad 0&\quad 0&\quad -\,1&\quad 0&\quad -\,1\\ -\,2&\quad 0&\quad 0&\quad 0&\quad 1&\quad 0&\quad 1&\quad 0\\ 0&\quad 0&\quad 0&\quad 2l^2&\quad l&\quad 0&\quad -\,l&\quad 0\\ 0&\quad 0&\quad -\,2l^2&\quad 0&\quad 0&\quad l&\quad 0&\quad -\,l\\ 0&\quad -\,1&\quad -\,l&\quad 0&\quad 0&\quad 1&\quad 0&\quad 0\\ 1&\quad 0&\quad 0&\quad -\,l&\quad -\,1&\quad 0&\quad 0&\quad 0\\ 0&\quad -\,1&\quad l&\quad 0&\quad 0&\quad 0&\quad 0&\quad 1\\ 1&\quad 0&\quad 0&\quad l&\quad 0&\quad 0&\quad -\,1&\quad 0 \end{bmatrix},\nonumber \\ \end{aligned}$$
(22)

where l denotes the axial distance between the center of the rotor and the journal bearings. The parameter \(\Omega _\mathrm{r}\) denotes a reference frequency, \(c_\mathrm{b}\) the damping of the housing and \(\sigma _b\) controls the effect of self-excitation. Numerical values can be found in “Appendix A” . The asymmetry in the damping matrix arises due to the rotation of the center mass about the angles \(\phi _x\) and \(\phi _y\) (gyroscopic effect). The bearings forces are modeled phenomenologically having linear visco-elastic properties and non-conservative follower forces depending on the rotor speed. The follower forces are proportional to the stiffness forces, but shifted by 90-degree in phase in complex notation. The arising matrix of the follower forces in real-valued coordinates is skew-symmetric (see Eq. (22)). The asymmetric stiffness matrix \(\mathbf {N}\) destabilizes the trivial solution of the system.

It is assumed that the stiffness of the bearing supports can be varied with the frequency \(\Omega _P\) and the amplitude \(\varepsilon \) (\(k(t)=k_\mathrm{h}(1+\varepsilon \cos (\Omega _P t))\)), thereby the terms \(\mathbf {K}^{1\pm }=k_\mathrm{h}/(2\Omega _\mathrm{r}^2)\mathrm {diag}(0,0,0,0,1,1,1,1)\) in the Fourier series expansion in Eq. (2) arise. The systems equation of motion is in the form of Eq. (2). The derivation of the systems equation of motion, the detailed description of physical quantities and the set of parameters used can be found in [15]. The numerical values are also given in “Appendix A”.

The trivial solution of rotor system without parametric excitation (\(\varepsilon =0\)) is stable, if the dimensionless rotor speed is below a critical value of \({\bar{\Omega }}_{\mathrm{crit}}=0.82\). In the following, the bar indicates that the corresponding frequency was non-dimensionalized by the systems reference frequency. Following the procedure from [15], the stability is analyzed by numerical calculation of the monodromy matrix and the Floquet multipliers [6]. The resulting stability areas are plotted in Fig 3. A parametric anti-resonance at a dimensionless rotor speed of \({\bar{\Omega }}_P=2\) and a parametric resonance at \({\bar{\Omega }}_P=2.8\) can be observed.

Since two relevant parametric resonance frequencies are close to each other, an interaction is very likely and the proposed algorithm is utilized to analyze the stability. The frequencies for the evaluation of Eqs. (16), (17) and (18) are the parametric combination frequencies \({\bar{\Omega }}^{(1)}_{P0}=\mathrm {Im}[{\bar{\lambda }}_5]-\mathrm {Im}[{\bar{\lambda }}_1]\)and \({\bar{\Omega }}^{(2)}_{P0}=\mathrm {Im}[{\bar{\lambda }}_6]+\mathrm {Im}[{\bar{\lambda }}_1]\). The numbering of the eigenvalues is according to [15]. Above the thick solid line, the parameter \({\tilde{\rho }}_{1}\) is positive and the trivial equilibrium of the rotor is unstable. The proposed analytical prediction matches well with the numerical calculations.

Choosing the single frequency \({\bar{\Omega }}^{(1)}_{P0}\) to be parameter \(\Omega _{P0}\) in the averaging process and thereby ignoring a possible interference, the dashed stability boundary arises. It is predicted that the trivial solution of the rotor is unstable if the system configurations are above the dashed curve. The choice of \(\Omega _{P0}={\bar{\Omega }}^{(2)}_{P0}\) results in the dash-dotted stability boundaries. From the theory, the analytical prediction is valid for a small detuning from the reference \(\Omega _{P0}\). However, the proposed summation in Eq. (18) extends the validity by taking into account the interference.

4.2 Flexible rotor in adjustable journal bearings

The operating speed range of rotors in journal bearings is limited up to the onset speed of instability, which arises due to self-excitation induced by the journal bearings [8]. For rotors with flexible shafts, the oil whip phenomenon can occur, which leads to large deflections and thus represents a danger to such rotors. Promising results of damping by parametric excitation of rotor system through magnetic bearings [15, 23, 43], as well as experiments of rotors in journal bearings with a passively adjustable geometry [44], inspired extensive studies of a Jeffcott rotor in journal bearings with a semi-active adjustment of the gap geometry [25, 28,29,30]. The purpose of these studies is to increase the operating speed range through damping by parametric excitation. The gap geometry is varied periodically to parametrically excite the system and suppress the fluid induced instability. Experimental evidence was presented in [25], and industrial rotors have been further investigated in [27, 45].

The Jeffcott rotor is a simplified model of real-world rotors, which is frequently used to study elementary rotor dynamical phenomena [8]. Contrary to the rotor discussed in the previous section, the Jeffcott rotor consists of a flexible shaft (stiffness k) with a centered disk of mass \(m_s\). At both ends of the shaft, a journal of mass \(m_Z\) is mounted. It is assumed that all masses are perfectly balanced. The coordinates are \(v_W\) and \(w_W\) for the geometric center of the disk and \(v_L\) and \(w_L\) for the journals in the plane perpendicular to the rotor axis. The equation of motion for a constant rotational speed \(\Omega \) is given by

$$\begin{aligned}&\left[ \begin{array}{llll} m_S &{}\quad &{}\quad &{}\quad \\ &{}\quad m_S &{}\quad &{}\quad \\ &{}\quad &{}\quad 2\;\!m_Z &{}\quad \\ &{}\quad &{}\quad &{}\quad 2\;\!m_Z \end{array}\right] \left[ \begin{array}{l} \ddot{v}_W \\ \ddot{w}_W \\ \ddot{v}_L \\ \ddot{w}_L \end{array}\right] \nonumber \\&\quad + \left[ \begin{array}{llll} &{}\quad &{} \quad &{} \quad \\ &{}\quad &{}\quad &{}\quad \\ &{}\quad &{}\quad 2\;\!b_{yy}(t;\Omega ) &{}\quad 2\;\!b_{yz}(t;\Omega ) \\ &{}\quad &{}\quad 2\;\!b_{zy}(t;\Omega ) &{}\quad 2\;\!b_{zz}(t;\Omega ) \end{array}\right] \left[ \begin{array}{l} {\dot{v}}_W \\ {\dot{w}}_W \\ {\dot{v}}_L \\ {\dot{w}}_L \end{array}\right] \nonumber \\&\quad +\left[ \begin{array}{llll} k &{}\quad &{}\quad -\,k &{}\quad \\ &{}\quad k &{}\quad &{}\quad -\,k \\ -\,k &{}\quad &{}\quad k +2\;\!k_{yy}(t;\Omega ) &{}\quad 2\;\!k_{yz}(t;\Omega ) \\ &{}\quad -\,k &{}\quad 2\;\!k_{zy}(t;\Omega ) &{}\quad k+2\;\!k_{yy}(t;\Omega ) \end{array}\right] \left[ \begin{array}{l} v_W \\ w_W \\ v_L \\ w_L \end{array}\right] = \mathbf {0},\nonumber \\ \end{aligned}$$
(23)

where the stiffness coefficients \(k_{yy}\), \(k_{yz}\), \(k_{zy}\) and \(k_{zz}\) and the damping coefficients \(b_{yy}\), \(b_{yz}\), \(b_{zy}\) and \(b_{zz}\) arise through a linearization of the journal bearings forces. Figure 4 shows an adjustable lemon bore bearing in horizontal design [30]. While the lower segment is fixed, the upper one can be moved vertically. Due to a harmonic adjustment, the gap h is varied and as a consequence, the stiffness and damping properties of the fluid film change periodically.

Fig. 4
figure 4

Lemon bore bearing in horizontal construction design; adjustment of the upper segment [25, 30]

Full size image
Fig. 5
figure 5

Stability map for a rotor system in journal bearings with adjustable geometry (see also [28,29,30] or [34])

Full size image

The calculation of the bearing forces is performed for individual segments by numerical integration (finite volume method) of the Reynolds differential equation of lubricating film theory, see e. g., [46, 47]. It describes the pressure distribution \(p(\vartheta ,x)\) in the bearing as a function of the radial coordinate \(\vartheta \) and the axial coordinate x. Integrating the pressure distribution yields the forces acting on the journal, \(F_z\) and \(F_y\). The fluid-film forces depend on vertical and horizontal positions (\(v_L\) and \(w_L\)), and the corresponding velocities of the journal are in general expressed by a nonlinear relationship \(F_{z,y}=F_{z,y}(v_L,w_L,{\dot{v}}_L,{\dot{w}}_L)\).

For stability analysis, these forces are linearized around the equilibrium position \((v_{L,0},w_{L,0},0,0)\). Thereby, the stiffness coefficients \(k_{yy}\), \(k_{yz}\), \(k_{zy}\) and \(k_{zz}\) as well as the damping coefficients \(b_{yy}\), \(b_{yz}\), \(b_{zy}\) and \(b_{zz}\) arise, which alter periodically due to the harmonic adjustment (cf. Eq. (23)). All eight coefficients depend on geometrical and physical properties of the bearing (e.g., radii, width, oil viscosity, rotational speed and load) as well as on the amplitude of the adjustment. The cross-coupling stiffness is usually unequal (\(k_{yz}\ne k_{zy}\)) [8, 46, 47], therefore system (23) is non-symmetric. A detailed treatment and the set of parameters of the system can be found in [25, 28].

Utilizing the proposed approach, the stability of the system is analyzed and compared with numerical results in Fig. 5.Footnote 1 Again, the prediction according to Eq. (18) matches well with the results from numerical studies. The dimensionless onset speed of stability without parametric excitation is \({\bar{\Omega }}_{P}\approx 2.2\). A parametric anti-resonance arises in the vicinity of \({\bar{\Omega }}^{(1)}_{P0}=\mathrm {Im}[{\bar{\lambda }}_3]-\mathrm {Im}[{\bar{\lambda }}_1]\). The stability area is significantly shrunk by the presence of \({\bar{\Omega }}^{(2)}_{P0}=\mathrm {Im}[{\bar{\lambda }}_3]+\mathrm {Im}[{\bar{\lambda }}_1]\). The accuracy of the stability region estimated by treating \({\bar{\Omega }}^{(1)}_{P0}\) isolated is not satisfactory (see gray line in Fig. 5). Considering only \({\bar{\Omega }}^{(2)}_{P0}\) in the averaging process, no parametric anti-resonance or resonance is estimated. However, ignoring this frequency completely will lead to unsatisfactory results. Furthermore, the loss of stability around a dimensionless excitation frequency of \({\bar{\Omega }}_{P}\approx 3\) can be related to the fundamental parametric resonance consisting of \(\lambda _3\) and its complex conjugate. Also in the vicinity of this frequency, the analytic approximation matches well with the numerical results. To enhance the prediction further, the overdamped eigenvalue \({\bar{\lambda }}_7\) is considered as well. The system matrices differ from Eq. (14), but the algorithm is essentially the same and details can be found in [34].

The depicted analytic results in Fig. 5 arise from the method of averaging of first order. Higher-order terms are not considered (see also Sect. 2.2). The convergence of the perturbation method is concluded from the good agreement with the numerical results. Averaging of higher order does not qualitative change the stability boundaries of Fig. 5, and merely a convergence of the analytical predictions to the numerical result was observed in [34]. For instance, averaging of second order will perturb the obtained stability boundaries by \(\mathcal {O}(\varepsilon ^2)\) (see also [14]).

By applying the method of averaging, the enlarged stability interval can be related to the occurrence of two parametric combination frequencies. Furthermore, the computational effort is significantly reduced compared to the numerical studies because the calculation of the monodromy matrix relying on numerical integration is omitted.

The stability region of a parametric anti-resonance can be significantly shrunk if a second parametric resonance frequency is in the immediate vicinity. This can have critical impacts for design purposes. The interaction can be approximated by Eq. (18), but not by the isolated treatment of each parametric resonance frequency.

5 Conclusions

The method of averaging is applied to construct a time-invariant first-order approximation to a linear system with parametric excitation and non-symmetric stiffness and damping matrices. Performing the averaging in the state space, the limitation of common averaging approaches [11, 12, 16] to symmetric stiffness and damping matrices is circumvented. The location of the parametric anti-resonances and the coupling of modes by parametric excitation are confirmed analytically by studying the eigenvalues of the averaged system. An empirically motivated approach to account for multiple interacting parametric resonance frequencies is outlined. It relies on an summation of the eigenvalues of the averaged system. Its potential is verified by applying the approach to two rotor systems. The approximation of the interference of the stability areas of multiple parametric resonance frequencies matches well with numerical results and shows a clear improvement in the prediction compared to the stability boundaries relying on a single parametric resonance frequency. The interference of multiple parametric resonance frequencies is approximated sufficiently well.

The proposed algorithm is reasoned, and its power by numerical examples outlined. However, a mathematical proof needs to be provided, which is subject to future research.