Low-velocity impact response of geometrically nonlinear functionally graded graphene platelet-reinforced nanocomposite plates

Abstract

This paper investigates the low-velocity impact response of functionally graded multilayer nanocomposite plates reinforced with a low content of graphene nanoplatelets (GPLs) in which GPLs are randomly oriented and uniformly dispersed in the polymer matrix within each individual layer with GPL weight fraction following a layer-wise variation along the plate thickness. The micromechanics-based Halpin–Tsai model is used to evaluate the effective material properties of the GPL-reinforced composite (GPLRC), and the modified nonlinear Hertz contact theory is utilized to define the contact force between the spherical impactor and the GPLRC target plate. The equations of motion of the plate are derived within the framework of the first-order shear deformation plate theory and von Kármán-type nonlinear kinematics and are solved by a two-step perturbation technique. The present analysis is validated through a direct comparison with those in the open literature. A parametric study is then performed to study the effects of GPL distribution pattern, weight fraction, geometry and size, temperature variation as well as the radius and initial velocity of the impactor on the low-velocity impact response of functionally graded GPLRC plates.

1 Introduction

In recent years, using graphene as reinforcing nanofillers in polymer composites has attracted increasing attention. Previous studies demonstrated that graphene and its derivatives significantly outperform carbon nanotubes (CNTs) in improving the mechanical properties of polymer nanocomposites mainly due to their bigger surface area which provides much better load transfer capability. Rafiee et al. [1] reported in their experiments that the strength and stiffness of the epoxy nanocomposites reinforced with only 0.1% weight fraction (wt%) of GPLs are almost the same as those of the epoxy nanocomposites reinforced with 1.0 wt% of CNTs. Fang et al. [2] manufactured polystyrene/graphene nanocomposites and demonstrated that an addition of 0.9 wt% graphene sheets increases the tensile strength and Young’s modulus by 70% and 57%, respectively. Zhao et al. [3] added 1.8 wt% of graphene oxide in poly(vinyl alcohol) (PVA) matrix and found that the Young’s modulus of graphene-reinforced PVA composite film is almost ten times greater than that of the PVA matrix. In addition, graphene and its derivatives also offer relative lower manufacturing costs, better dispersion, and less agglomeration than CNTs, making them outstanding reinforcement materials in improving the mechanical properties of polymeric materials.

Owing to their lightweight and superior mechanical properties, graphene-reinforced polymer nanocomposites have emerged as one of the most promising areas in developing advanced lightweight engineering structures. Extensive theoretical and experimental investigations have been conducted on the manufacturing, characterization, and structural behavior of polymer nanocomposites, and in all these studies, the graphene nanofillers are randomly orientated and uniformly dispersed. Chandra et al. [4] studied the free vibration of graphene/polymer composites by using a multiscale finite element method that models graphene and polymer matrix with the atomistic and conventional continuum finite element methods, respectively. Cranford [5] investigated the buckling-induced delamination of mono- and bilayer graphene-based composites by employing a hybrid atomistic and molecular dynamics approach. Rissanou et al. [6] employed atomistic molecular dynamic simulation method to analyze the structural and dynamic behaviors of several graphene-based polymer nanocomposites with graphene sheets of different sizes. Rafiee et al. [7] presented an experimental study to measure the critical buckling loads of GPL/epoxy composite beams with fixed boundary conditions and observed that an addition of only 0.1 wt% of GPLs increases the critical buckling load by 52%. Their study also demonstrated that the theoretical results based on the classical Euler-buckling model are in reasonable agreement with the measured buckling loads, showing that the traditional continuum modeling method is desirable for GPL/Epoxy composite structures. Most recently, Yang and his co-workers [8,9,10,11,12,13,14,15,16,17] introduced the concept of multilayer functionally graded materials (FGMs) into graphene-reinforced polymer nanocomposites in which GPLs are uniformly distributed in polymer matrix within each individual layer with GPL weight fraction varying layer to layer along the thickness direction. They found that the mechanical properties of the polymer/GPL nanocomposites can be further improved if GPLs are non-uniformly distributed in the polymer matrix according to an appropriately chosen distribution pattern. They have investigated the free and forced vibrations [8], linear and nonlinear bending [9,10,11], buckling and postbuckling [11,12,13,14], dynamic stability [15], large-amplitude vibration [16, 17] of functionally graded multilayer GPL-reinforced composite (GPLRC) beams and plates. Guo et al. [18, 19] discussed the free vibration and nonlinear bending of laminated GPLRC quadrilateral plates based on the element-free IMLS-Ritz method.

By employing Reddy’s higher-order shear deformation theory, Shen et al. [20,21,22] studied the nonlinear bending, buckling and postbuckling, and nonlinear vibration of functionally graded composite laminated beams and plates reinforced with graphene sheets under a uniform temperature field. Kiani and Mirzaei [23,24,25] adopted a non-uniform rational B-spline-based isogeometric finite element method to analyze the buckling, postbuckling, and large-amplitude free vibration of composite laminated plates with graphene reinforcements in thermal environment. They also employed a conventional Ritz method and the simple polynomials as the basic functions to investigate the nonlinear thermal stability of temperature-dependent laminated beams reinforced with graphene sheets [26]. Sahmani and Aghdam [27, 28] used nonlocal strain gradient models to study nonlinear vibration and postbuckling of multilayer functionally graded GPLRC nanobeams and nanoshells.

The susceptibility to low-velocity impacts and the resulting internal damage is a critical issue for solid structures in aerospace, marine, automotive, and defense engineering applications as it may lead to crucial failure of the structure and, in some cases, even the loss of human lives. In order to improve the impact resistance of structures, extensive studies have been attempted to understand the low-velocity impact behavior of engineering structures. Timoshenko was first to use the Hertz contact theory to study the low-velocity impact response of an Euler beam subjected to an elastic sphere impactor. Wu and Springer [29] studied the impact-induced stresses and strains and delaminated in a fiber-reinforced composite rectangular plate. They calculated the stresses and strains in the plate during the impact by a three-dimensional, transient finite element method using 8-node brick element with incompatible modes and predicted the locations, lengths, and widths of delaminations inside the plate by means of a proposed failure criterion. Gong [30] developed a spring–mass contact force model to analyze the impact response of laminated open cylindrical shells. Olsson [31] pointed out that the impact response is governed by impactor versus target structure mass ratio and not by impact velocity. Khalili et al. [32] used the Navier solution-based technique to study the low-velocity impact response of functionally graded plates with temperature-dependent properties. Kiani et al. [33], and Jam and Kiani [34] applied the Ritz method to investigate the low-velocity impact response of FGM beams in thermal environment. Shariyat and Nasab [35] studied the effects of the hierarchical viscoelastic nature of the materials on the low-velocity impact responses of FGM plates using a new version of the differential quadrature method in conjunction with a novel time integration scheme. Song et al. [36] and Zhang et al. [37] used an analytical method to study the CNT-reinforced composite plate and shell, respectively, based on the Reddy’s high-order shear deformation theory (HSDT). Selim et al. [38] presented an IMLS-Ritz element-free model in association with Reddy’s HSDT to study the impact response of CNT-reinforced composite plates. Wang et al. [39] adopted a two-step perturbation technique to solve the governing equations of temperature-dependent CNT-reinforced composite plates subjected to a low-velocity impactor. The two-step perturbation technique was also used to analyze the low-velocity impact responses of matrix cracked hybrid plates [40], FGM plates [41], and curved panels [42] resting on an elastic foundation. Malekzadeh and Dehbozorgi [43] employed the finite element method in conjunction with Newmark’s time integration scheme and Newton–Raphson algorithm to investigate the low-velocity impact behavior of functionally graded CNT-reinforced skew plates. Boroujerdy and Kiani [44] analyzed the dynamic response of composite laminated beams subjected to multiple impacts in thermal filed. To the best of the authors’ knowledge, no previous study has been reported on the low-velocity impact analysis of functionally graded GPLRC structures.

The present work investigates, for the first time, the low-velocity impact characteristics of novel functionally graded multilayer GPLRC plates. It is assumed that each individual layer is a homogeneous mixture of polymer matrix and GPLs that are randomly oriented and uniformly dispersed in the matrix, while the GPL weight fraction follows a layer-wise variation along the thickness direction. The effective material properties of GPLRC are assumed to be temperature independent and estimated by using micromechanics-based Halpin–Tsai model. A modified Hertz model is used to describe the contact forces between the impactor and the plate. Theoretical formulations are based on the first-order shear deformation plate theory and von Kármán nonlinear kinematics. The governing equations are solved by a two-step perturbation technique for plates that are simply supported and freely moveable in the in-plane directions. Comprehensive numerical results are presented to provide the first-ever-known information regarding the effects of distribution, weight fraction, geometry, and size of GPLs as well as impactor’s radius and initial velocity on the low-velocity impact response of functionally graded GPLRC plates which is very important for engineering applications but has never been reported in any previous studies.

Fig. 1

Geometry and coordinate system of a functionally graded multilayer GPLRC plate under a spherical impactor

Fig. 2

Through-thickness GPL distribution patterns

2 Problem formulation

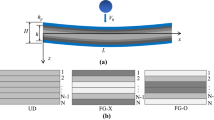
To the best of authors’ knowledge, the criterions of debonding and delamination of multilayered GPLRC structures have not been determined in the open literature yet, which is thus neglected in this paper. Figure 1 shows a functionally graded multilayer GPLRC rectangular plate composed of a total of N perfectly bonded GPLRC layers with the same thickness and subjected to a spherical impactor. The length, width, and total thickness of the plate are denoted as a, b, and h, respectively. The right-handed coordinate system (X, Y, Z) has its origin at the corner of the plate on the midplane. Within each individual layer, GPL reinforcements are randomly oriented and uniformly dispersed in the homogeneous and isotropic polymer matrix. Six different GPL distribution patterns shown in Fig. 2 are considered in the present analysis, including five functionally graded distributions (FG-O, FG-X, FG-B, FG-$\Lambda$, and FG-V) in which GPL volume fraction varies piecewise linearly from layer to layer along the thickness direction and uniform distribution (UD) as a special case. Without loss of generality, it is assumed that the plate consists of an even total number of layers. The GPL volume fraction at the kth layer for these distribution patterns follows [8]:

$$\begin{aligned} \left\{ {{\begin{array}{ll} {\hbox {UD}:} &{} {V_{\mathrm{GPL}}^{(k)} =V_{\mathrm{GPL}},\quad 1\le k\le N} \\ {\hbox {FG-O}:} &{} V_{\mathrm{GPL}}^{(k)} =\frac{4V_{\mathrm{GPL}} }{N+2}\left( {\frac{N+1}{2}-\left| {\frac{N+1}{2}-k} \right| } \right) , \\ &{} \qquad \qquad \qquad 1\le k\le N \\ {\hbox {FG-X}:} &{} V_{\mathrm{GPL}}^{(k)} =\frac{4V_{\mathrm{GPL}} }{N+2}\left( {\frac{1}{2}+\left| {\frac{N+1}{2}-k} \right| } \right) , \\ &{} \qquad \qquad \qquad 1\le k\le N \\ {\hbox {FG-B}:} &{} V_{\mathrm{GPL}}^{(k)} =\frac{NV_{\mathrm{GPL}} }{\frac{N^{2}}{4}+\frac{N}{2}-4s^{2}+4s} \\ &{} \qquad \quad \qquad \left( {2N-4s+\frac{5}{2}-3\left| {k-\frac{N+1}{2}} \right| } \right) , \\ &{} \qquad \qquad \qquad {1\le k\le s, \, N-s+1\le k\le N} \\ &{} V_{\mathrm{GPL}}^{(k)} =\frac{NV_{\mathrm{GPL}} }{\frac{N^{2}}{4}+\frac{N}{2}-4s^{2}+4s}\left( {\left| {\frac{N+1}{2}-k} \right| +\frac{1}{2}} \right) , \\ &{} \qquad \qquad \qquad s<k\le N-s \\ {\hbox {FG-}\Lambda :} &{} {V_{\mathrm{GPL}}^{(k)} =\frac{2V_{\mathrm{GPL}} k}{N+1}, \quad 1\le k\le N} \\ {\hbox {FG-V}:} &{} {V_{\mathrm{GPL}}^{(k)} =\frac{2V_{\mathrm{GPL}} (N+1-k)}{N+1}, \quad 1\le k\le N} \\ \end{array} }} \right. \end{aligned}$$

(1)

in which $V_{\mathrm{GPL}}$ is the total GPL volume fraction. It should be noted that FG-O, FG-X, and FG-B are all symmetric along the thickness direction and is GPL rich in the middle layers in FG-O and in the top and bottom layers in FG-X, and in the sth and ($N-s+1$)th layers in FG-B. It should be noted that when $s=1$, the FG-B GPL distribution pattern is reduced to the FG-X pattern. In the two non-symmetric distribution patterns, GPL weight fraction changes linearly from the minimum in the top layer to the maximum in the bottom layer of the FG-$\Lambda$ plate, while this is reversed in the FG-V plate.

2.1 Material properties of GPLRCs

The effective Young’s modulus of the kth GPLRC layer can be approximated by the modified Halpin–Tsai model [1]:

$$\begin{aligned} E^{(k)}= & {} \left[ {\frac{3}{8}\frac{1+\xi _\mathrm{L} \eta _{\mathrm{L}} V_{\mathrm{GPL}}^{(k)} }{1-\eta _{\mathrm{L}} V_{\mathrm{GPL}}^{(k)} }+\frac{5}{8}\frac{1+\xi _{\mathrm{W}} \eta _{\mathrm{W}} V_{\mathrm{GPL}}^{(k)} }{1-\eta _{\mathrm{W}} V_{\mathrm{GPL}}^{(k)} }}\right] \nonumber \\&\times \,E_{\mathrm{M}} \end{aligned}$$

(2)

where $V_{{\mathrm{GPL}}}^{(k)}$ is GPL volume fraction, $E_{{\mathrm{M}}}$ is Young’s modulus of the polymer matrix, and parameters $\eta _{\mathrm{L}}$ and $\eta _{{\mathrm{W}}}$ can be determined by:

$$\begin{aligned}&\eta _{\mathrm{L}} =\frac{E_{\mathrm{GPL}} -E_{\mathrm{M}} }{E_{\mathrm{GPL}} +\xi _L E_{\mathrm{M}} } \end{aligned}$$

(3a)

$$\begin{aligned}&\eta _{\mathrm{W}} =\frac{E_{\mathrm{GPL}} -E_{\mathrm{M}} }{E_{\mathrm{GPL}} +\xi _{\mathrm{W}} E_{\mathrm{M}} } \end{aligned}$$

(3b)

in which $E_{\mathrm{GPL}}$ is GPL’s Young’s modulus and $\xi _{\mathrm{L}}$ and $\xi _{\mathrm{W}}$ are geometry factors characterizing both the geometry and size of GPL nanofillers, defined as

$$\begin{aligned} \xi _L =2\left( {\frac{a_{\mathrm{GPL}} }{h_{\mathrm{GPL}} }} \right) , \quad \xi _{\mathrm{W}} =2\left( {\frac{b_{\mathrm{GPL}} }{h_{\mathrm{GPL}} }} \right) \end{aligned}$$

(4)

in which $a_{\mathrm{GPL}}$, $b_{\mathrm{GPL}}$, and $h_{\mathrm{GPL}}$ are the average length, width, and thickness of the GPLs, respectively. The GPL volume fraction of the kth GPLRC layer is related to GPL’s weight fraction $g_{\mathrm{GPL}}^{(k)}$ and the mass densities of polymer matrix ($\rho _{\mathrm{M}}$) and GPLs ($\rho _{\mathrm{GPL}}$) by

$$\begin{aligned} V_{\mathrm{GPL}}^{(k)} =\frac{\rho _{\mathrm{M}} g_{\mathrm{GPL}}^{(k)}}{\rho _{\mathrm{M}} g_{\mathrm{GPL}}^{(k)} +\rho _{\mathrm{GPL}} \left( {1-g_{\mathrm{GPL}}^{(k)} } \right) } \end{aligned}$$

(5)

The mass density $\rho ^{(k)}$, Poisson’s ratio $\nu ^{(k)}$, and thermal expansion coefficient $\alpha ^{(k)}$ of the kth GPLRC layer can be evaluated by the rule of mixture:

$$\begin{aligned} \rho ^{(k)}= & {} \rho _{\mathrm{GPL}} V_{\mathrm{GPL}}^{(k)} +\rho _{\mathrm{M}} V_{\mathrm{M}}^{(k)} \end{aligned}$$

(6a)

$$\begin{aligned} \nu ^{(k)}= & {} \nu _{\mathrm{GPL}} V_{\mathrm{GPL}}^{(k)} +\nu _{\mathrm{M}} V_{\mathrm{M}}^{(k)} \end{aligned}$$

(6b)

$$\begin{aligned} \alpha ^{(k)}= & {} \alpha _{\mathrm{GPL}} V_{\mathrm{GPL}}^{(k)} +\alpha _{\mathrm{M}} V_{\mathrm{M}}^{(k)} \end{aligned}$$

(6c)

where $\nu _{\mathrm{GPL}}$ and $\nu _{\mathrm{M}}$ are Poisson’s ratios and $\alpha _{\mathrm{GPL}}$ and $\alpha _{\mathrm{M}}$ are thermal expansion coefficients, in which the subscripts “GPL” and “M” refer to the GPL and matrix, respectively. $V_{\mathrm{M}}^{(k)}$ is the volume fraction of the matrix that is related to $V_{\mathrm{GPL}}^{(k)}$ by $V_{\mathrm{GPL}}^{(k)} +V_{\mathrm{M}}^{(k)} =1$.

It is worth noting that the accuracy of Halpin–Tsai micromechanics model for the estimation of the effective Young’s modulus of GPL/polymer nanocomposites was verified by the experiment taken by Rafiee et al. [1]. The Young’s modulus of GPL/polymer nanocomposites with 0.1 wt% GPL nanofillers predicted by Eq. (2) is just 2.7% higher than the experimental result, indicating that Halpin–Tsai micromechanics model provides quite good estimation.

2.2 Governing equation of the GPLRC plate

In accordance with the first-order shear deformation plate theory [45], the displacement field $\{{u,v,w}\}^{T}$ can be expressed as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {u({X,Y,Z,t})} \\ {v({X,Y,Z,t})} \\ {w({X,Y,Z,t})} \\ \end{array} }} \right\}= & {} \left\{ {{\begin{array}{l} {\bar{{U}}({X,Y,t})} \\ {\bar{{V}}({X,Y,t})} \\ {\bar{{W}}({X,Y,t})} \\ \end{array} }} \right\} \nonumber \\&+Z\cdot \left\{ {{\begin{array}{l} {{\phi }_X ({X,Y,t})} \\ {{\phi }_Y ({X,Y,t})} \\ 0 \\ \end{array} }} \right\} \end{aligned}$$

(7)

where $\bar{{U}}({X,Y,t})$, $\bar{{V}}({X,Y,t})$, and $\bar{{W}}({X,Y,t})$ are the displacements at the midplane of the plate in X, Y, and Z directions; ${\phi }_X$ and ${\phi }_Y$ are the rotations of a transverse normal about the Y- and X-axes, respectively; and t is time. The strain components are given by von Kármán-type nonlinear strain–displacement relationship as

$$\begin{aligned} \begin{aligned} {\varvec{\upvarepsilon }}_0&=\left\{ {{\begin{array}{l} {\varepsilon _{0X} } \\ {\varepsilon _{0Y} } \\ {\gamma _{0XY} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{c} {\frac{\partial \bar{{U}}}{\partial X}+\frac{1}{2}\left( {\frac{\partial \bar{{W}}}{\partial X}} \right) ^{2}} \\ {\frac{\partial \bar{{V}}}{\partial Y}+\frac{1}{2}\left( {\frac{\partial \bar{{W}}}{\partial Y}} \right) ^{2}} \\ {\frac{\partial \bar{{U}}}{\partial Y}+\frac{\partial \bar{{V}}}{\partial X}+\frac{\partial \bar{{W}}}{\partial X}\frac{\partial \bar{{W}}}{\partial Y}} \\ \end{array} }} \right\} , \\ {\varvec{\upvarepsilon }}_1&=\left\{ {{\begin{array}{l} {\varepsilon _{1X} } \\ {\varepsilon _{1Y} } \\ {\gamma _{1XY} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{l} {\frac{\partial {\phi }_X }{\partial X}} \\ {\frac{\partial {\phi }_Y }{\partial Y}} \\ {\frac{\partial {\phi }_X }{\partial Y}+\frac{\partial {\phi }_Y }{\partial X}} \\ \end{array} }} \right\} , \\ {\varvec{\upgamma }}_0&=\left\{ {{\begin{array}{l} {\gamma _{0YZ} } \\ {\gamma _{0XZ} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{l} {{\phi }_Y +\frac{\partial \bar{{W}}}{\partial Y}} \\ {{\phi }_X +\frac{\partial \bar{{W}}}{\partial X}} \\ \end{array} }} \right\} \\ \end{aligned} \end{aligned}$$

(8)

The equations of motion of the functionally graded GPLRC plate can be derived by Hamilton’s principle as

$$\begin{aligned}&\frac{\partial N_X }{\partial X}+\frac{\partial N_{XY} }{\partial Y}=\bar{{I}}_0 \frac{\partial ^{2}\bar{{U}}}{\partial t^{2}}+\bar{{I}}_1 \frac{\partial ^{2}{\phi }_X }{\partial t^{2}} \end{aligned}$$

(9a)

$$\begin{aligned}&\frac{\partial N_{XY} }{\partial X}+\frac{\partial N_Y }{\partial Y}=\bar{{I}}_0 \frac{\partial ^{2}\bar{{V}}}{\partial t^{2}}+\bar{{I}}_1 \frac{\partial ^{2}{\phi }_Y }{\partial t^{2}} \end{aligned}$$

(9b)

$$\begin{aligned}&\frac{\partial Q_X }{\partial X}+\frac{\partial Q_Y }{\partial Y}+\frac{\partial }{\partial X}\left( {N_X \frac{\partial \bar{{W}}}{\partial X}+N_{XY} \frac{\partial \bar{{W}}}{\partial Y}} \right) \nonumber \\&\quad + \frac{\partial }{\partial Y}\left( {N_{XY} \frac{\partial \bar{{W}}}{\partial X}+N_Y \frac{\partial \bar{{W}}}{\partial Y}} \right) \nonumber \\&\quad +\bar{{F}}_{\mathrm{c}} (t)\delta \left( {X-X_{\mathrm{c}} ,Y-Y_{\mathrm{c}} } \right) =\bar{{I}}_0 \frac{\partial ^{2}\bar{{W}}}{\partial t^{2}} \end{aligned}$$

(9c)

$$\begin{aligned}&\frac{\partial M_X }{\partial X}+\frac{\partial M_{XY} }{\partial Y}-Q_X =\bar{{I}}_2 \frac{\partial ^{2}{\phi }_X }{\partial t^{2}}+\bar{{I}}_1 \frac{\partial ^{2}\bar{{U}}}{\partial t^{2}} \end{aligned}$$

(9d)

$$\begin{aligned}&\frac{\partial M_{XY} }{\partial X}+\frac{\partial M_Y }{\partial Y}-Q_Y =\bar{{I}}_2 \frac{\partial ^{2}{\phi }_Y }{\partial t^{2}}+\bar{{I}}_1 \frac{\partial ^{2}\bar{{V}}}{\partial t^{2}} \end{aligned}$$

(9e)

where $\bar{{F}}_{\mathrm{c}} (t)$ is the contact force between the impactor and plate, $\delta$ is the Dirac delta function, and $(X_{\mathrm{c}}, Y_{\mathrm{c}})$ is the position where the impactor hits the plate. The stress resultants $\mathbf{N}=\left[ {N_X ,N_Y ,N_{XY}} \right] ^{T}$, moment resultants $\mathbf{M}=\left[ {M_X ,M_Y ,M_{XY}} \right] ^{T}$, and shear forces $\mathbf{Q}=\left[ {Q_Y ,Q_X } \right] ^{T}$ are defined by

$$\begin{aligned} \left\{ {{\begin{array}{l} \mathbf{N} \\ \mathbf{M} \\ \end{array} }} \right\}= & {} \left[ {{\begin{array}{ll} \mathbf{A}&{}\quad \mathbf{B} \\ \mathbf{B}&{}\quad \mathbf{D} \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {{\varvec{\upvarepsilon }}_0 } \\ {{\varvec{\upvarepsilon }}_1 } \\ \end{array} }} \right\} -\left\{ {{\begin{array}{l} {{\mathbf{N}}^{\mathrm {H}}} \\ {{\mathbf{M}}^{\mathrm {H}}} \\ \end{array} }} \right\} \end{aligned}$$

(10a)

$$\begin{aligned} \mathbf{Q}= & {} \kappa \mathbf{K} {\varvec{\upgamma }}_0 \end{aligned}$$

(10b)

The shear correction factor $\kappa =5/6$. The stiffness components $A_{ij}$, $B_{ij}$, $D_{ij}$, and $K_{ij}$ and the inertia-related terms $\bar{{I}}_i \, (i=0,1,2)$ are calculated by

$$\begin{aligned}&(\mathbf{A},\mathbf{B},\mathbf{D})=\sum _{k=1}^N {\int _{Z_k }^{Z_{k+1} } {{\mathbf{P}}^{(k)}\cdot (1,Z,Z^{2})\hbox {d}Z} } \end{aligned}$$

(11a)

$$\begin{aligned}&{} \mathbf{K}=\sum _{k=1}^N {\int _{Z_k }^{Z_{k+1}} {{\mathbf{Q}}^{(k)}\hbox {d}Z} } \end{aligned}$$

(11b)

$$\begin{aligned}&\bar{{I}}_i =\sum _{k=1}^N {\int _{Z_k }^{Z_{k+1} } {\rho ^{(k)}Z^{i}\hbox {d}Z}} \end{aligned}$$

(11c)

and

$$\begin{aligned} {\mathbf{P}}^{(k)}= & {} \frac{E^{(k)}}{1-\nu ^{(k)2}}\left[ {{\begin{array}{ccc} 1&{}\quad {\nu ^{(k)}}&{}\quad 0 \\ {\nu ^{(k)}}&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad {\frac{1-\nu ^{(k)}}{2}} \\ \end{array} }} \right] , \nonumber \\ {\mathbf{Q}}^{(k)}= & {} \frac{E^{(k)}}{2(1+\nu ^{(k)})}\left[ {{\begin{array}{cc} 1&{}\quad 0 \\ 0&{}\quad 1 \\ \end{array} }} \right] \end{aligned}$$

(12)

The thermal stress resultants ${\mathbf{N}}^{\mathrm {H}}=\left[ {N_X^{\mathrm{H}} ,N_Y^{\mathrm{H}} ,N_{XY}^{\mathrm{H}} } \right] ^{T}$ and thermal moment resultants ${\mathbf{M}}^{\mathrm {H}}=\left[ {M_X^{\mathrm{H}} ,M_Y^{\mathrm{H}}}\right. , \left. {M_{XY}^{\mathrm{H}} } \right] ^{T}$ are calculated from

$$\begin{aligned}&\left( {{\mathbf{N}}^{\mathrm {H}},{\mathbf{M}}^{\mathrm {H}}} \right) \nonumber \\&\quad =\sum _{k=1}^N \int _{Z_k }^{Z_{k+1}} \left( \mathbf{P}\cdot \left\{ {{\begin{array}{l} {\alpha ^{(k)}\Delta T} \\ {\alpha ^{(k)}\Delta T} \\ 0 \\ \end{array} }} \right\} , \right. \nonumber \\&\quad \left. \mathbf{P}\cdot \left\{ {{\begin{array}{l} {\alpha ^{(k)}\Delta T} \\ {\alpha ^{(k)}\Delta T} \\ 0 \\ \end{array} }} \right\} \cdot Z \right) \hbox {d}Z \end{aligned}$$

(13)

Let $\bar{{F}}$ be the stress function such that

$$\begin{aligned} \mathbf{N}= \{ {\bar{{F}}_{,YY} ,\bar{{F}}_{,XX} ,-\bar{{F}}_{,XY}}\}^{T} \end{aligned}$$

(14)

where a comma denotes partial differentiation with respect to the coordinates. Relationship (10a) can be rewritten in partial reverse form as

$$\begin{aligned} \left\{ {{\begin{array}{l} {{\varvec{\upvarepsilon }}_0 } \\ {{\mathbf{M}}^{{*}}} \\ \end{array} }} \right\} =\left[ {{\begin{array}{cc} {{\mathbf{A}}^{{*}}}&{}\quad {{\mathbf{B}}^{{*}}} \\ {-({\mathbf{B}}^{{*}})^{T}}&{}\quad {{\mathbf{D}}^{{*}}} \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {{\mathbf{N}}^{{*}}} \\ {{\varvec{\upvarepsilon }}_1 } \\ \end{array} }} \right\} \end{aligned}$$

(15)

where ${\mathbf{A}}^{{*}}= {\mathbf{A}}^{-1}$, ${\mathbf{B}}^{{*}}=-{\mathbf{A}}^{-1}{\mathbf{B}}$, ${\mathbf{D}}^{{*}}= {\mathbf{D}}- {\mathbf{BA}}^{-1} {\mathbf{B}}$, ${\mathbf{N}}^{*}= {\mathbf{N}}+{\mathbf{N}}^{\mathrm {H}}$, ${\mathbf{M}}^{*}={\mathbf{M}}+{\mathbf{M}}^{\mathrm {H}}$.

For a plate simply supported on all edges, the boundary conditions require

$X=0,a:$

$$\begin{aligned}&\bar{{W}}={\phi }_Y =0 \end{aligned}$$

(16a)

$$\begin{aligned}&M_X =0 \end{aligned}$$

(16b)

$$\begin{aligned}&\sigma _X bh+\int _0^b {N_X \hbox {d}Y} =0 \quad \hbox {(movable)} \end{aligned}$$

(16c)

$$\begin{aligned}&\bar{{U}}=0 \quad \hbox {(immovable)} \end{aligned}$$

(16d)

$Y=0,b:$

$$\begin{aligned}&\bar{{W}}={\phi }_X =0 \end{aligned}$$

(17a)

$$\begin{aligned}&M_Y =0 \end{aligned}$$

(17b)

$$\begin{aligned}&\sigma _Y ah+\int _0^a {N_Y \hbox {d}X} =0 \quad \hbox {(movable)} \end{aligned}$$

(17c)

$$\begin{aligned}&\bar{{V}}=0 \quad \hbox {(immovable)} \end{aligned}$$

(17d)

Since it is difficult to handle the immovable boundary conditions directly using the two-step perturbation technique, approximate treatment is usually employed. The immovable boundary conditions (Eqs. (16d) and (17d)) then be represented by weaker ones on the average sense in this study, i.e.,

$$\begin{aligned} \int _0^b {\int _0^a {\frac{\partial \bar{{U}}}{\partial X}\hbox {d}X\hbox {d}Y}}= & {} 0 \end{aligned}$$

(18a)

$$\begin{aligned} \int _0^a {\int _0^b {\frac{\partial \bar{{V}}}{\partial Y}\hbox {d}Y\hbox {d}X}}= & {} 0 \end{aligned}$$

(18b)

2.3 The modified nonlinear Hertz contact model

The low-velocity impact can be divided into two phases, i.e., the loading phase and the unloading phase. The loading phase starts from the moment when the impactor and the GPLRC plate are in contact, and ends when the maximum contact force is reached. For the low-velocity impact dynamics of laminated structures, the contact force between the impactor and the target can be given by the Hertz contact theory when the thickness of the impacted layer is large compared with the size of the contact zone [46]. Usually, the unloading path is different from that of the loading phase due to the loss of kinetic energy during the impact phase especially when the impactor is small. Yang and Sun thus proposed what is now called the modified nonlinear Hertz contact law which consists of different equations for the loading and unloading phases [47]. Till now, the modified Hertz law has been widely used for the analyses of low-velocity impact dynamics of engineering structures [38,39,40,41,42,43,44]. According to the modified nonlinear Hertz contact theory, the contact force during the loading phase is related to the contact stiffness $K_{\mathrm{c}}$ and local contact indentation $\theta (t)$ by [47]:

$$\begin{aligned} \bar{{F}}_{\mathrm{c}} (t)=K_{\mathrm{c}} \theta ^{\frac{3}{2}}(t) \end{aligned}$$

(19)

and

$$\begin{aligned} \theta (t)= & {} \bar{{S}}_{\mathrm{i}} (t)-\bar{{W}}_{\mathrm{c}} (t) \end{aligned}$$

(20)

$$\begin{aligned} K_{\mathrm{c}}= & {} \frac{4}{3}\sqrt{R_{\mathrm{i}} }\left( {\frac{1-v_{\mathrm{i}}^2 }{E_{\mathrm{i}} }+\frac{1-v_{\mathrm{t}}^2 }{E_{\mathrm{t}} }} \right) ^{-1} \end{aligned}$$

(21)

in which $\bar{{S}}_{\mathrm{i}}$ is the impactor’s displacement and $\bar{{W}}_{\mathrm{c}}$ is the deflection of the plate at the impact point. Besides, $R_{\mathrm{i}}$, $E_{\mathrm{i}}$, and $\nu _{\mathrm{i}}$ are the radius, Young’s modulus, and Poisson’s ratio of the impactor, respectively. $E_{\mathrm{t}}$ and $\nu _{\mathrm{t}}$ are the Young’s modulus and Poisson’s ratio of the top surface of the plate, respectively.

During the unloading phase, the contact force which decreases until the impactor and plate become separate from each other can be expressed as [47]:

$$\begin{aligned} \bar{{F}}_{\mathrm{c}} (t)=\bar{{F}}_{\mathrm{c}}^{\mathrm{m}} \left( {\frac{\theta -\theta _0 }{\theta _{\mathrm{m}} -\theta _0 }} \right) ^{\frac{5}{2}} \end{aligned}$$

(22)

where $\bar{{F}}_{\mathrm{c}}^{\mathrm{m}}$ and $\theta _{\mathrm{m}}$ are the maximum contact force and the corresponding maximum indentation during the loading phase, respectively. The permanent indentation $\theta _0$ equals to zero when $\theta _{\mathrm{m}}$ is below a critical indentation during the loading phase. Since there is still no previous study on the critical indentation for GPLRCs, $\theta _0$ is assumed to be zero in this study.

3 Analytical method and asymptotic solutions

Introducing the following dimensionless quantities

$$\begin{aligned}&({x,x_{\mathrm{c}}}) =\pi \frac{( {X,X_{\mathrm{c}} } )}{a}, \quad ( {y,y_{\mathrm{c}} } )=\pi \frac{( {Y,Y_{\mathrm{c}} } )}{b}, \nonumber \\&\beta =\frac{a}{b}, \quad ( {W,S_{\mathrm{i}} } )=\frac{( {\bar{{W}},\bar{{S}}_{\mathrm{i}} } )}{( {A_{11}^{*} A_{22}^{*} D_{11}^{*} D_{22}^*} )^{\frac{1}{4}}}, \nonumber \\&F=\frac{\bar{{F}}}{( {D_{11}^{*} D_{22}^*} )^{\frac{1}{2}}}, \nonumber \\&( {{\phi }_x ,{\phi }_y } ) =\frac{a}{\pi }\frac{( {{\phi }_X ,{\phi }_Y } )}{( {A_{11}^{*} A_{22}^{*} D_{11}^{*} D_{22}^*} )^{\frac{1}{4}}}, \nonumber \\&\gamma _{14} =\left( {\frac{D_{22}^{*} }{D_{11}^{*} }} \right) ^{\frac{1}{2}}, \nonumber \\&\gamma _{15} =\frac{A_{11}^*( {D_{11}^{*} D_{22}^*} )^{\frac{1}{2}}}{a^{2}}, \nonumber \\&\gamma _{24} =\frac{B_{11}^*( {A_{11}^{*} A_{22}^{*} D_{11}^{*} D_{22}^*})^{\frac{1}{4}}}{a^{2}}, \nonumber \\&\gamma _{25} =\frac{A_{12}^*}{A_{11}^*}, \, \gamma _{35} =\frac{B_{12}^*}{B_{11}^*}, \nonumber \\&I_0 =\frac{\bar{{I}}_0 a^{2}E_{\mathrm{M}} }{\pi ^{2}\rho _{\mathrm{M}} D_{11}^{*} }, \quad I=\frac{( {\bar{{I}}_0 \bar{{I}}_2 -\bar{{I}}_1^2 } )E_{\mathrm{M}} }{\bar{{I}}_0 \rho _{\mathrm{M}} D_{11}^{*} }, \nonumber \\&F_{\mathrm{c}} =\frac{a^{3}\bar{{F}}_{\mathrm{c}} }{\pi ^{2}bD_{11}^{*} ( {A_{11}^{*} A_{22}^{*} D_{11}^{*} D_{22}^*} )^{\frac{1}{4}}}, \nonumber \\&({M_x, M_y}) =\frac{a^{2}}{\pi ^{2}}\frac{( {M_X ,M_Y } )}{D_{11}^{*} ( {A_{11}^{*} A_{22}^{*} D_{11}^{*} D_{22}^*} )^{\frac{1}{4}}}, \nonumber \\&( {N_x^{\mathrm{H}} ,N_y^{\mathrm{H}} }) =\frac{( {A_{11}^{*} N_X^{\mathrm{H}} ,A_{12}^{*} N_Y^{\mathrm{H}}} )}{\pi ^{2}}, \nonumber \\&\lambda _{\mathrm{q}} =F_{\mathrm{c}} \delta ( {x-x_{\mathrm{c}} ,y-y_{\mathrm{c}} } ), \nonumber \\&({\lambda _x ,\lambda _y}) =\frac{( {P_X b,P_Y a})}{4\pi ^{2}( {D_{11}^{*} D_{22}^{*} } )^{\frac{1}{2}}}, \quad \tau =\frac{\pi t}{a}\sqrt{\frac{E_{\mathrm{M}} }{\rho _{\mathrm{M}} }}, \end{aligned}$$

(23)

substituting Eqs. (10a), (10b), and (14) into equilibrium Eqs. (9a)–(9e), with Eq. (15) in mind and considering the deformation compatibility requirement

$$\begin{aligned}&\frac{\partial ^{2}\varepsilon _X^{(0)} }{\partial Y^{2}}+\frac{\partial ^{2}\varepsilon _Y^{(0)} }{\partial X^{2}}-\frac{\partial ^{2}\gamma _{XY}^{(0)} }{\partial X\partial Y}=\left( {\frac{\partial ^{2}\bar{{W}}}{\partial X\partial Y}} \right) ^{2} \nonumber \\&\quad -\,\frac{\partial ^{2}\bar{{W}}}{\partial X^{2}}\frac{\partial ^{2}\bar{{W}}}{\partial Y^{2}} \end{aligned}$$

(24)

lead to the dimensionless nonlinear governing equations of motion of the plate in terms of W, ${\phi }_x$, ${\phi }_y$ and F as

$$\begin{aligned}&L_{11} (W)+L_{12} ({\phi }_x )+L_{13} ({\phi }_y) +\beta ^{2}\gamma _{14} L(W,F) \nonumber \\&\quad =I_0 {\ddot{W}}-\lambda _{\mathrm{q}} \end{aligned}$$

(25a)

$$\begin{aligned}&L_{21} ({\phi }_x )+L_{22} ({\phi }_y )+L_{23} (F) \nonumber \\&\quad =-\frac{1}{2}\beta ^{2}L(W,W) \end{aligned}$$

(25b)

$$\begin{aligned}&L_{31} (W)+L_{32} ({\phi }_x )+L_{33} ({\phi }_y )+L_{34} (F) \nonumber \\&\quad =I\ddot{{\phi }}_x \end{aligned}$$

(25c)

$$\begin{aligned}&L_{41} (W)+L_{42} ({\phi }_x )+L_{43} ({\phi }_y) +L_{44} (F) \nonumber \\&\quad =I\ddot{{\phi }}_y \end{aligned}$$

(25d)

where nonlinear partial differential operator $L(\,)=(\,)_{,xx} (\,)_{,yy} -2(\,)_{,xy} (\,)_{,xy} +(\,)_{,yy} (\,)_{,xx}$. The linear partial differential operators $L_{ij}$ are given in “Appendix A.” It should be noted that there are not longitudinal inertias in Eqs. (25a)–(25d). The reason lies in the fact that the introduction of Airy stress function F brings the dependence of longitudinal inertias on the rotary inertias.

The dimensionless boundary conditions can be expressed as

$$\begin{aligned}&x=0,\pi :\nonumber \\&W={\phi }_y =0 \end{aligned}$$

(26a)

$$\begin{aligned}&M_x =0 \end{aligned}$$

(26b)

$$\begin{aligned}&4\lambda _x +\frac{1}{\pi }\int _0^\pi {\frac{\partial ^{2}F}{\partial y^{2}}\hbox {d}y} =0 \,\, \hbox {(movable)} \end{aligned}$$

(26c)

$$\begin{aligned}&\int _0^\pi \int _0^\pi \left( \gamma _{15} \gamma _{25} \frac{\partial ^{2}F}{\partial x^{2}}+\beta ^{2}\gamma _{15} \frac{\partial ^{2}F}{\partial y^{2}} \right. \nonumber \\&\quad \qquad \qquad +\gamma _{24} \frac{\partial {\phi }_x }{\partial x} +\beta \gamma _{24} \gamma _{35} \frac{\partial {\phi }_y }{\partial y} \nonumber \\&\quad \qquad \qquad \left. +\,N_x^{\mathrm{H}} +N_y^{\mathrm{H}} \right) \hbox {d}x\hbox {d}y=0 \nonumber \\&\qquad \quad \hbox {(immovable)} \end{aligned}$$

(26d)

$y=0,\pi :$

$$\begin{aligned}&W={\phi }_x =0 \end{aligned}$$

(27a)

$$\begin{aligned}&M_y =0 \end{aligned}$$

(27b)

$$\begin{aligned}&4\lambda _y +\frac{1}{\pi }\int _0^\pi {\frac{\partial ^{2}F}{\partial x^{2}}\hbox {d}x} =0 \,\, \hbox {(movable)} \end{aligned}$$

(27c)

$$\begin{aligned}&\int _0^\pi \int _0^\pi \left( \gamma _{15} \gamma _{25} \frac{\partial ^{2}F}{\partial x^{2}}+\beta ^{2}\gamma _{15} \gamma _{25}^2 \frac{\partial ^{2}F}{\partial y^{2}}\right. \nonumber \\&\qquad \qquad +\gamma _{24} \gamma _{25} \gamma _{35} \frac{\partial {\phi }_x }{\partial x} +\beta \gamma _{24} \gamma _{25} \frac{\partial {\phi }_y }{\partial y} \nonumber \\&\qquad \qquad \left. +\gamma _{25}^2 N_x^{\mathrm{H}} +N_y^{\mathrm{H}} \right) \hbox {d}x\hbox {d}y=0 \nonumber \\&\quad \qquad \qquad \hbox {(immovable)}. \end{aligned}$$

(27d)

A two-step perturbation technique [48] is employed to solve Eqs. (25a)–(25d) to determine the low-velocity impact response of the functionally graded multilayer GPLRC plate. The solutions of Eqs. (25a)–(25d) are assumed to take the following forms

$$\begin{aligned} W(x,y,\bar{{\tau }},\varepsilon )= & {} \sum _{j=1} {\varepsilon ^{j}w_j (x,y,\bar{{\tau }})}, \nonumber \\ F(x,y,\bar{{\tau }},\varepsilon )= & {} \sum _{j=0} {\varepsilon ^{j}f_j (x,y,\bar{{\tau }})} , \nonumber \\ {\phi }_x (x,y,\bar{{\tau }},\varepsilon )= & {} \sum _{j=1} {\varepsilon ^{j}{\varphi }_{xj} (x,y,\bar{{\tau }})}, \nonumber \\ {\phi }_y (x,y,\bar{{\tau }},\varepsilon )= & {} \sum _{j=1} {\varepsilon ^{j}{\varphi }_{yj} (x,y,\bar{{\tau }})} , \nonumber \\ \lambda _q (x,y,\bar{{\tau }},\varepsilon )= & {} \sum _{j=1} {\varepsilon ^{j}\lambda _j (x,y,\bar{{\tau }})} \end{aligned}$$

(28)

where $\varepsilon$ is a small perturbation parameter and $\bar{{\tau }}=\varepsilon \tau$ is introduced to improve perturbation procedure. The first term of $w_j (x,y,\bar{{\tau }})$ is assumed to have the form

$$\begin{aligned} w_1 (x,y,\bar{{\tau }})=J_{\mathrm{w}11}^{[1]} (\bar{{\tau }})\sin mx\sin ny. \end{aligned}$$

(29)

Substituting Eq. (28) into Eqs. (25a)–(25d), and equating coefficients of like powers of $\varepsilon$, one has

Order $\varepsilon ^{0}$:

$$\begin{aligned} L_{23} (f_0 )=0 \end{aligned}$$

(30)

Order $\varepsilon ^{1}$:

$$\begin{aligned}&L_{11} (w_1 )+L_{12} ({\varphi }_{x1} )+L_{13} ({\varphi }_{y1})\nonumber \\&\quad +\beta ^{2}\gamma _{14} L(w_1 ,f_0 )=-\lambda _1 \end{aligned}$$

(31a)

$$\begin{aligned}&L_{21} (f_1 )=0 \end{aligned}$$

(31b)

$$\begin{aligned}&L_{31} (w_1 )+L_{32} ({\varphi }_{x1} )+L_{33} ({\varphi }_{y1}) \nonumber \\&\quad +L_{34} (f_1 )=0 \end{aligned}$$

(31c)

$$\begin{aligned}&L_{41} (w_1 )+L_{42} ({\varphi }_{x1} )+L_{43} ({\varphi }_{y1}) \nonumber \\&\quad +L_{44} (f_1 )=0 \end{aligned}$$

(31d)

Order $\varepsilon ^{2}$:

$$\begin{aligned}&L_{11} (w_2 )+L_{12} ({\varphi }_{x2} )+L_{13} ({\varphi }_{y2}) +\beta ^{2}\gamma _{14} L(w_2 ,f_0) \nonumber \\&\qquad +\beta ^{2}\gamma _{14} L(w_1 ,f_1)=-\lambda _2 \end{aligned}$$

(32a)

$$\begin{aligned}&L_{21} ({\varphi }_{x2} )+L_{22} ({\varphi }_{y2} )+L_{23} (f_2) \nonumber \\&\quad =-\frac{1}{2}\beta ^{2}L(w_1 ,w_1 ) \end{aligned}$$

(32b)

$$\begin{aligned}&L_{31} (w_2 )+L_{32} ({\varphi }_{x2} )+L_{33} ({\varphi }_{y2}) \nonumber \\&\quad +L_{34} (f_2 )=0 \end{aligned}$$

(32c)

$$\begin{aligned}&L_{41} (w_2 )+L_{42} ({\varphi }_{x2} )+L_{43} ({\varphi }_{y2}) \nonumber \\&\quad +L_{44} (f_2 )=0 \end{aligned}$$

(32d)

Order $\varepsilon ^{3}$:

$$\begin{aligned}&L_{11} (w_3 )+L_{12} ({\varphi }_{x3} )+L_{13} ({\varphi }_{y3})\nonumber \\&\qquad +\beta ^{2}\gamma _{14} L(w_3 ,f_0 ) +\beta ^{2}\gamma _{14} L(w_2 ,f_1 ) \nonumber \\&\qquad +\beta ^{2}\gamma _{14} L(w_1 ,f_2) =I_0 \ddot{w}_1 -\lambda _3 \end{aligned}$$

(33a)

$$\begin{aligned}&L_{21} ({\varphi }_{x3} )+L_{22} ({\varphi }_{y3} )+L_{23} (f_3) \nonumber \\&\quad =-\beta ^{2}L(w_1 ,w_2 ) \end{aligned}$$

(33b)

$$\begin{aligned}&L_{31} (w_3 )+L_{32} ({\varphi }_{x3} )+L_{33} ({\varphi }_{y3}) +L_{34} (f_3) \nonumber \\&\quad =I\ddot{{\varphi } }_{x1} \end{aligned}$$

(33c)

$$\begin{aligned}&L_{41} (w_3 )+L_{42} ({\varphi }_{x3} )+L_{43} ({\varphi }_{y3}) +L_{44} (f_3) \nonumber \\&\quad =I\ddot{{\varphi } }_{y1}. \end{aligned}$$

(33d)

Considering the boundary conditions in Eqs. (26a)–(27d), the solutions of $w_j$, $f_j$, ${\varphi }_{xj}$, and ${\varphi }_{yj}$ can be obtained by solving Eqs. (30)–(33d) from order $\varepsilon ^{0}$ to $\varepsilon ^{3}$. Then, the asymptotic solutions of the displacements and stress function of the plate are constructed as:

$$\begin{aligned}&W(x,y,\tau ,\varepsilon ) \nonumber \\&\quad =\varepsilon J_{\mathrm{w}11}^{[1]} \sin mx\sin ny \nonumber \\&\qquad +\,\varepsilon ^{3}\left( {J_{\mathrm{w}13}^{[3]} \sin mx\sin 3ny+J_{\mathrm{w}31}^{[3]} \sin 3mx\sin ny} \right) \nonumber \\&\qquad +\,O(\varepsilon ^{4}) \end{aligned}$$

(34a)

$$\begin{aligned}&F(x,y,\tau ,\varepsilon ) \nonumber \\&\quad =-J_{\mathrm{f}00}^{[0]} \frac{x^{2}}{2}-J_{\mathrm{F}00}^{[0]} \frac{y^{2}}{2} \nonumber \\&\qquad +\,\varepsilon \left( {J_{\mathrm{f}11}^{[1]} +{\ddot{J}}_{\mathrm{f}11}^{[3]} }\right) \sin mx\sin ny \nonumber \\&\qquad +\,\varepsilon ^{2}\left( -J_{\mathrm{f}00}^{[2]} \frac{x^{2}}{2}-J_{\mathrm{F}00}^{[2]} \frac{y^{2}}{2}+J_{\mathrm{f}20}^{[2]} \cos 2mx \right. \nonumber \\&\quad \qquad \qquad \left. +\,J_{\mathrm{f}02}^{[2]} \cos 2ny \right) \nonumber \\&\qquad +\,\varepsilon ^{3}\left( {J_{\mathrm{f}13}^{[3]} \sin mx\sin 3ny+J_{\mathrm{f}31}^{[3]} \sin 3mx\sin ny} \right) \nonumber \\&\qquad +\,O(\varepsilon ^{4})\end{aligned}$$

(34b)

$$\begin{aligned}&{\phi }_x (x,y,\tau , \varepsilon ) \nonumber \\&\quad =\varepsilon \left( {J_{\mathrm{x}11}^{[1]} +{\ddot{J}}_{\mathrm{x}11}^{[3]} } \right) \cos mx\sin ny+\varepsilon ^{2}J_{\mathrm{x}20}^{[2]} \sin 2mx \nonumber \\&\qquad +\,\varepsilon ^{3}\left( {J_{\mathrm{x}13}^{[3]} \cos mx\sin 3ny+J_{\mathrm{x}31}^{[3]} \cos 3mx\sin ny} \right) \nonumber \\&\qquad +\,O(\varepsilon ^{4}) \end{aligned}$$

(34c)

$$\begin{aligned}&{\phi }_y (x,y,\tau ,\varepsilon ) \nonumber \\&\quad =\varepsilon \left( {J_{\mathrm{y}11}^{[1]} +{\ddot{J}}_{\mathrm{y}11}^{[3]} } \right) \sin mx\cos ny+\varepsilon ^{2}J_{\mathrm{y}02}^{[2]} \sin 2ny \nonumber \\&\qquad +\,\varepsilon ^{3}\left( {J_{\mathrm{y}13}^{[3]} \sin mx\cos 3ny+J_{\mathrm{y}31}^{[3]} \sin 3mx\cos ny} \right) \nonumber \\&\qquad +\,O(\varepsilon ^{4}) \end{aligned}$$

(34d)

$$\begin{aligned}&\lambda _{\mathrm{q}} (x,y,\tau , \varepsilon ) \nonumber \\&\quad =\varepsilon \left( {J_{\mathrm{q}11}^{[1]} +{\ddot{J}}_{\mathrm{q}11}^{[3]} } \right) \sin mx\sin ny \nonumber \\&\qquad +\,\varepsilon ^{2}\left( {J_{\mathrm{q}20}^{[2]} \cos 2mx+J_{\mathrm{q}02}^{[2]} \cos 2ny} \right) \nonumber \\&\qquad +\,\varepsilon ^{3}J_{\mathrm{q}11}^{[3]} \sin mx\sin ny+O(\varepsilon ^{4}) \end{aligned}$$

(34e)

where $J_{\mathrm{w}\xi \zeta }^{[\eta ]} =g_{\xi \zeta \eta }^{\mathrm{w}} \left( {J_{\mathrm{w}11}^{[1]} } \right) ^{\eta }$, $J_{\mathrm{f}\xi \zeta }^{[\eta ]} =g_{\xi \zeta \eta }^{\mathrm{f}} \left( {J_{\mathrm{w}11}^{[1]} } \right) ^{\eta }$, $J_{\mathrm{x}\xi \zeta }^{[\eta ]} =g_{\xi \zeta \eta }^{\mathrm{x}} \left( {J_{\mathrm{w}11}^{[1]} } \right) ^{\eta }$, $J_{\mathrm{y}\xi \zeta }^{[\eta ]} =g_{\xi \zeta \eta }^{\mathrm{y}} \left( {J_{\mathrm{w}11}^{[1]} } \right) ^{\eta }$, $J_{\mathrm{q}\xi \zeta }^{[\eta ]} =g_{\xi \zeta \eta }^{\mathrm{q}} \left( {J_{\mathrm{w}11}^{[1]} } \right) ^{\eta }$, ${\ddot{J}}_{\mathrm{f}11}^{[3]} =\hat{{g}}_{113}^{\mathrm{f}} {\ddot{J}}_{\mathrm{w}11}^{[1]}$, ${\ddot{J}}_{\mathrm{x}11}^{[3]} =\hat{{g}}_{113}^{\mathrm{x}} {\ddot{J}}_{\mathrm{w}11}^{[1]}$, ${\ddot{J}}_{\mathrm{y}11}^{[3]} =\hat{{g}}_{113}^{\mathrm{y}} {\ddot{J}}_{\mathrm{w}11}^{[1]}$, and ${\ddot{J}}_{\mathrm{q}11}^{[3]} =\hat{{g}}_{113}^{\mathrm{q}} {\ddot{J}}_{\mathrm{w}11}^{[1]}$ in which $\xi$, $\zeta$, and $\eta$ are nonnegative integers, and coefficients $g_{\xi \zeta \eta }^{\mathrm{w}}$, $g_{\xi \zeta \eta }^{\mathrm{f}}$, $g_{\xi \zeta \eta }^{\mathrm{x}}$, $g_{\xi \zeta \eta }^{\mathrm{y}}$, $g_{\xi \zeta \eta }^{\mathrm{q}}$, $\hat{{g}}_{113}^{\mathrm{f}}$, $\hat{{g}}_{113}^{\mathrm{x}}$, $\hat{{g}}_{113}^{\mathrm{y}}$, and $\hat{{g}}_{113}^{\mathrm{q}}$ are given in “Appendix B.” Taking $(x,y)=(\pi /2,\pi /2)$, the relationship between the second perturbation parameter $J_{\mathrm{w}11}^{[1]} \varepsilon$ and maximum dimensionless deflection $w_{\mathrm{m}}$ can be obtained from Eq. (34a) by ignoring the small terms:

$$\begin{aligned} w_{\mathrm{m}} =J_{\mathrm{w}11}^{[1]} \varepsilon -\left( {g_{133}^{\mathrm{w}} +g_{313}^{\mathrm{w}} } \right) \left( {J_{\mathrm{w}11}^{[1]} \varepsilon } \right) ^{3}. \end{aligned}$$

(35)

Rewrite Eq. (35) as

$$\begin{aligned} J_{\mathrm{w}11}^{[1]} \varepsilon&=w_{\mathrm{m}} +\left( {g_{133}^{\mathrm{w}} +g_{313}^{\mathrm{w}} } \right) \left( {J_{\mathrm{w}11}^{[1]} \varepsilon } \right) ^{3} \\&=w_{\mathrm{m}} +\left( {g_{133}^{\mathrm{w}} +g_{313}^{\mathrm{w}} } \right) \\&\quad \times \left[ {w_{\mathrm{m}} +\left( {g_{133}^{\mathrm{w}} +g_{313}^{\mathrm{w}} } \right) \left( {J_{\mathrm{w}11}^{[1]} \varepsilon } \right) ^{3}} \right] ^{3} \\&=w_{\mathrm{m}} +\left( {g_{133}^{\mathrm{w}} +g_{313}^{\mathrm{w}} } \right) \\&\quad \times \left[ {w_{\mathrm{m}}^3 +3w_{\mathrm{m}}^2 \left( {g_{133}^{\mathrm{w}} +g_{313}^{\mathrm{w}} } \right) ^{3}\left( {J_{\mathrm{w}11}^{[1]} \varepsilon } \right) ^{3}} \right. \\&\quad \qquad +3w_{\mathrm{m}} \left( {g_{133}^{\mathrm{w}} +g_{313}^{\mathrm{w}} } \right) ^{2}\left( {J_{\mathrm{w}11}^{[1]} \varepsilon } \right) ^{6} \\&\quad \qquad \left. +\left( {g_{133}^{\mathrm{w}} +g_{313}^{\mathrm{w}} } \right) ^{3}\left( {J_{\mathrm{w}11}^{[1]} \varepsilon } \right) ^{9} \right] . \end{aligned}$$

Since the terms $3w_{\mathrm{m}}^2 \left( {g_{133}^{\mathrm{w}} +g_{313}^{\mathrm{w}} } \right) ^{3}\left( {J_{\mathrm{w}11}^{[1]} \varepsilon } \right) ^{3}$, $3w_{\mathrm{m}} \left( {g_{133}^{\mathrm{w}} +g_{313}^{\mathrm{w}} } \right) ^{2}\left( {J_{\mathrm{w}11}^{[1]} \varepsilon } \right) ^{6}$, and $\left( {g_{133}^{\mathrm{w}} +g_{313}^{\mathrm{w}} } \right) ^{3}\left( {J_{\mathrm{w}11}^{[1]} \varepsilon } \right) ^{9}$ are much smaller than $w_{\mathrm{m}}^3$ if $w_{\mathrm{m}} \ll 1$, the above equation can be simplified as

$$\begin{aligned} J_{\mathrm{w}11}^{[1]} \varepsilon =w_{\mathrm{m}} +\left( {g_{133}^{\mathrm{w}} +g_{313}^{\mathrm{w}} } \right) w_{\mathrm{m}}^3. \end{aligned}$$

(36)

Applying Galerkin procedure, one has

$$\begin{aligned} \ddot{w}_{\mathrm{m}} +\chi _1 w_{\mathrm{m}} +\chi _2 w_{\mathrm{m}}^2 +\chi _3 w_{\mathrm{m}}^3 =\chi _{\mathrm{f}} F_{\mathrm{c}} \end{aligned}$$

(37)

On the other hand, according to the Newton’s second law, the dimensionless equation of motion of the impactor can be written as:

$$\begin{aligned} m_{\mathrm{i}} {\ddot{S}}_{\mathrm{i}} =-F_{\mathrm{c}} \end{aligned}$$

(38)

with initial conditions

$$\begin{aligned} S_{\mathrm{i}} (0)=0, \, {\dot{S}}_{\mathrm{i}} (0)=V_0 \end{aligned}$$

(39)

where coefficients $\chi _1$, $\chi _2$, $\chi _3$, and $\chi _{\mathrm{f}}$ are given in “Appendix C.” The dimensionless variable $m_{\mathrm{i}} ={\beta E_{\mathrm{M}} \bar{{m}}_{\mathrm{i}} }/{\left( {\rho _{\mathrm{M}} D_{11}^{*} } \right) }$, in which $\bar{{m}}_{\mathrm{i}}$ is the mass of the impactor. Equations (37) and (38) are then solved by the variable-step fourth–fifth-order Runge–Kutta method [49] to determine the impact response of the plate and impactor, and the contact force.

4 Numerical results and discussion

In this section, the numerical procedure outlined in the previous sections is used to study the dynamic characteristics of functionally graded multilayer GPLRC plates under the action of a low-velocity steel spherical impactor. Isotropic epoxy is selected as the matrix material. Comparison studies are conducted to validate and demonstrate the accuracy and effectiveness of the present analysis, followed by a comprehensive parametric study to examine the influences of GPL distribution patterns, weight fraction, geometry and size as well as impactor’s initial velocity and radius on the contact force and central deflection of the plate.

Fig. 3

Comparison of contact force time history of a simply supported isotropic plate under a low-velocity impact

Fig. 4

Comparison of impactor displacement history of an isotropic plate under a low-velocity impact

4.1 Comparison studies

A simply supported isotropic square plate subjected to a low-velocity spherical impactor previously reported in Refs. [39, 50] is first considered. The size of the square plate is $200\,\hbox {mm}\times 200\,\hbox {mm}\times 8\,\hbox {mm}$. The plate and impactor are made of the same material with mass density $7810\,{\hbox {kg/m}}^{3}$, Young’s modulus 206.8 GPa, and Poisson’s ratio 0.3. The radius of the impactor is 10 mm,and the initial velocity of the impactor is 1 m/s. Figures 3 and 4 show the time histories of the contact force and impactor’s displacement, respectively. Our results agree reasonably well with those in Refs. [39, 50].

We then consider a simply supported square FGM plate struck by a low-velocity rigid spherical impactor. The mass, mass density, and initial velocity of the impactor are 0.075 kg, $3253.5\,{\hbox {kg/m}}^{3}$, and 1 m/s, respectively. The radius of the impactor is 17.66 mm, and the size of the FGM plate is $400\,\hbox {mm}\times 500\,\hbox {mm}\times 2\,\hbox {mm}$. The top and bottom of the plate are alumina and aluminum rich, respectively. The material properties of alumina and aluminum are [35]:

$$\begin{aligned}&\hbox {alumina:} \, E=380\,\hbox {GPa}, \quad \nu =0.22, \quad \rho =3800\hbox {kg/m}^{3} \\&\hbox {aluminum:} \, E=70\,\hbox {GPa}, \quad \nu =0.35, \quad \rho =2070\hbox {kg/m}^{3}. \end{aligned}$$

The effective material properties of the FGM plate are graded through the thickness according to

$$\begin{aligned} \vartheta (Z)=\vartheta _1 +(\vartheta _2 -\vartheta _1 )\left( {0.5+\frac{Z}{h}} \right) \end{aligned}$$

where $\vartheta _1$ and $\vartheta _2$ denote the properties of alumina and aluminum, respectively. According to the equivalent homogeneous laminated structure approach [51,52,53], the FGM plate is equivalent to a laminated plate with a finite number of isotropic and homogenous layers, in which the equivalent effective material property of the kth layer is defined in the mean sense [53]

$$\begin{aligned} \vartheta _{\mathrm{eq}}^{(k)} =\int _{Z_k }^{Z_{k+1} } {\frac{\vartheta (Z)}{Z_{k+1} -Z_k }} \hbox {d}Z, \quad k=1,2,\ldots ,N. \end{aligned}$$

Comparisons between the present central deflection results of the plate with varying total number of layers N and those by the differential quadrature method [35] in Fig. 5 show that convergent results can be obtained when $N = 10$. Excellent agreement is achieved.

Fig. 5

Comparison of central deflection time history of a simply supported functionally graded plate under a low-velocity impact

Table 1 Material properties of GPLs, epoxy, and steel spherical impactor [1, 14, 54, 55]

Fig. 6

Effect of GPL distribution pattern on the impact response of the functionally graded multilayer GPLRC plate: a contact force and b central deflection

Fig. 7

Effect of GPL weight fraction on the impact response of the functionally graded multilayer GPLRC plate: a contact force and b central deflection

Fig. 8

Effect of GPL length-to-width ratio on the impact response of the functionally graded multilayer GPLRC plate: a contact force and b central deflection

Fig. 9

Effect of GPL length-to-thickness ratio on the impact response of the functionally graded multilayer GPLRC plate: a contact force and b central deflection

Fig. 10

Effect of the impactor radius on the impact response of the functionally graded multilayer GPLRC plate: a contact force and b central deflection

Fig. 11

Effect of initial velocity on the impact response of the functionally graded multilayer GPLRC plate: a contact force and b central deflection

Fig. 12

Effect of initial uniaxial in-plane load $P_x /P_{\mathrm{cr}}$ on the impact response of the functionally graded multilayer GPLRC plate: a contact force and b central deflection

Fig. 13

Effect of temperature variation on the impact response of the functionally graded multilayer GPLRC plate: a contact force and b central deflection

Fig. 14

Effect of impact position on the impact response of the functionally graded multilayer GPLRC plate: a contact force and b central deflection

4.2 Parametric study

In what follows, it is assumed that a functionally graded GPLRC square plate of length 1000 mm and width-to-thickness ratio $b/h = 30$ is struck by a steel spherical impactor with radius of 10 mm and initial velocity 1.0 m/s. The material properties of GPLs, epoxy, and the impactor is given in Table 1. The GPL weight fraction is 1.0%, and its average length, width, and thickness are $a_{\mathrm{GPL}} =2.5\,\upmu \hbox {m}$, $b_{\mathrm{GPL}} =1.5\,{\upmu }\hbox {m}$, and $h_{\mathrm{GPL}} =1.5\,\hbox {nm}$ [1], respectively. The total number of GPLRC layers equals to 10, i.e., $N = 10$. Unless otherwise stated, the results are for functionally graded multilayer GPLRC plates simply supported on all edges but freely movable in both X and Y directions.

Figure 6 shows the effect of GPL distribution pattern on the time histories of the contact force and central deflection of functionally graded multilayer GPLRC plates, along with those of the pure epoxy plate for comparison. For the FG-B plate, the value of GPL weight fraction is maximum in the second and ninth layers. Compared with the pure epoxy plate, all GPL-reinforced composite plates have considerably higher peak contact force, shorter contact time, and smaller peak central deflection. For example, the FG-X plate has the smallest peak central deflection among the six GPL distribution patterns considered which is only 40% of that of the pure epoxy plate. This is attributed to the remarkably improved overall plate stiffness due to the addition of a small amount of GPLs and this reinforcing effect is the maximum in the FG-X plate. The contact force, however, is a different scenario. The FG-V and FG-$\Lambda$ patterns have the largest and smallest peak contact force, respectively. It can also be seen that compared to the FG-V plate, the peak contact force of the FG-X plate is slightly smaller. The reason for this phenomenon is that in both FG-V and FG-X patterns the plate is most GPL rich on the top surface, which leads to the the highest contact stiffness at the location where the impactor hits the plate consequently the largest contact force. For central deflection results, the FG-X and FG-B patterns have almost the same and the smallest center deflection, followed by the UD, FG-V, FG-$\Lambda$, and FG-O patterns, indicating that dispersing more GPL nanofillers near the top and bottom layers is the most effective way to reduce the impact deformation. It is interesting to find that the peak central deflection of the FG-$\Lambda$ plate is almost the same as that of the FG-V plate although the contact forces, as mentioned above, are quite different. Moreover, the FG-X and FG-V patterns have the shortest contact time between the impactor and the plate, while the FG-$\Lambda$ pattern has the longest contact time. It is worth noting that, compared to the FG-X plate, the peak center deflection of the FG-B plate is almost the same, but the peak contact force is significantly smaller, indicating that moving the maximum GPL concentration away from the top and bottom layers to the midplane by a short distance is an effective way to reduce both peak deflection and contact force, while the FG-X GPL distribution pattern does significantly bring down the deflection but also results in the largest peak contact force which is not desirable.

Figure 7 depicts the effect of total GPL weight fraction $g_{\mathrm{GPL}}$ on the time histories of the contact force and central deflection of the FG-X plate. It is seen that an increase in the GPL weight fraction results in a shorter contact time and larger peak contact force due to the increase in contact stiffness. Besides, the peak central deflection remarkably decreases as the GPL weight fraction increases. For example, the addition of only 0.25% weight fraction GPLs can yield a significantly smaller peak central deflection that is only 65% of that of the pure epoxy plate.

Figure 8 displays the effects of GPL length-to-width ratio $a_{\mathrm{GPL}} /b_{\mathrm{GPL}}$ on the time histories of contact force and central deflection of the FG-X plate with $a_{\mathrm{GPL}} /b_{\mathrm{GPL}}= 1.0, 3.0, 5.0$, and $a_{\mathrm{GPL}} /h_{\mathrm{GPL}} =2000$. Note that $a_{\mathrm{GPL}} /b_{\mathrm{GPL}} =1.0$ corresponds to square GPLs, while $a_{\mathrm{GPL}} /b_{\mathrm{GPL}} \ne 1.0$ corresponds to rectangular GPLs. Results show that the peak contact force decreases while the peak central deflection of the plate increases as the value of $a_{\mathrm{GPL}} /b_{\mathrm{GPL}}$ increases, indicating that the plate reinforced with GPLs with a smaller surface area has both lower overall stiffness and contact stiffness. In addition, the central deflections with different $a_{\mathrm{GPL}} /b_{\mathrm{GPL}}$are found to be almost identical when $t < 1.5\,\hbox {ms}$ beyond which the deflection gradually becomes different as $a_{\mathrm{GPL}} /b_{\mathrm{GPL}}$ changes from 1.0 to 3.0.

Figure 9 illustrates the effect of length-to-thickness ratio $a_{\mathrm{GPL}} /h_{\mathrm{GPL}}$ on the time histories of the contact force and central deflection of the FG-X plate. As can be seen, the peak contact force increases, while the peak central deflection decreases as the value of $a_{\mathrm{GPL}} /h_{\mathrm{GPL}}$ increases. This means that GPLs with less graphene monolayers offer greater contact stiffness and bending stiffness of the plate due to an increased effective Young’s modulus of the GPLRC. Similar to the observations in Fig. 8, the central deflections with different $a_{\mathrm{GPL}} /h_{\mathrm{GPL}}$ ratios are very close to each other when $t < 1.2\,\hbox {ms}$; then, the difference becomes bigger as the time further increases. Moreover, the effect of $a_{\mathrm{GPL}} /h_{\mathrm{GPL}}$ on the peak contact force and central deflection tends to be much less significant when $a_{\mathrm{GPL}} /h_{\mathrm{GPL}} >2000$.

Figure 10 depicts the effect of the impactor’s radius on the time histories of the contact force and central deflection of the FG-X plate. It is seen that an increase in the impactor’s radius leads to a longer contact time as well as larger contact force and central deflection. This is because a larger impactor’s radius results in a greater contact stiffness and a larger impactor mass.

Figure 11 shows the effect of the impactor’s initial velocity on the time histories of the contact force and central deflection of the FG-X plate. Three different initial velocities of $V_{0}= 1\,\hbox {m/s}$, 1.5 m/s, and 2 m/s are considered in this example. As expected, a larger initial velocity causes a greater contact force and central deflection but a shorter contact time. For instance, both the maximum contact force and central deflection increase about two times as the initial velocity raises from 1 to 2 m/s.

Figure 12 displays the effect of initial uniaxial in-plane force on the low-velocity impact characteristics of the FG-X plate. The initial uniaxial edge force considered herein is taken to be $P_{x}/P_{\mathrm{cr}} =-\,0.5, 0.0$, and 0.5, in which $P_{\mathrm{cr}}$ is the critical buckling load of the FG-X plate under uniaxial compression in the X direction. $P_{x}/ P_{\mathrm{cr}}=-\,0.5, 0.0$, and 0.5 refers to the case where the plate is under an initial tensile force, without initial force, and under an initial compressive force, respectively. Results show that although the contact force is not sensitive to the initial in-plane force, the application of an initial in-plane compressive force results in an increased central deflection of the plate, while the initial in-plane tensile force does the opposite. This is due to the fact that the in-plane tensile (compressive) force increases (decreases) the bending stiffness of the plate but does not affect the contact stiffness.

Since the thermally induced in-plane deformation can develop freely and obviously has no effect on the bending stiffness of the movable plate, the study of effect of temperature variation on the low-velocity impact characteristics is conducted for immovable plate. Taken the immovable FG-X plate as an example, Fig. 13 shows that there is no obvious difference in the contact force histories. That is because the temperature variation does not affect the material properties and consequently has no effect on the contact stiffness. In contrast, the temperature drop dramatically reduces the central deflection of the plate, while the temperature rise does the opposite. The reason for this phenomenon is that the temperature rise (drop) decreases (increases) the bending stiffness of the plate.

Figure 14 studies the effect of impact position on the time histories of both contact force and central deflection of the FG-X plate. Four cases are considered, in which the impact positions $(X_{\mathrm{c}}, Y_{\mathrm{c}})$ are taken as (a / 2, a / 8), (a / 2, a / 4), (a / 2, 3a / 8), and (a / 2, a / 2). It is seen that the effect of impact position on the contact force is almost negligible. The central deflection, however, increases as the impactor gets closer to the center of the plate as expected.

5 Conclusions

The dynamic behaviors of functionally graded multilayer GPLRC plates subjected to a low-velocity impact are investigated based on the first-order shear deformation plate theory, the modified nonlinear Hertz contact theory, and a two-step perturbation technique. The effects of the distribution pattern, weight fraction, geometry and size of GPL nanofillers, and the radius and initial velocity of the spherical impactor on the low-velocity impact characteristics of the plates are comprehensively studied. It is found that (1) adding a very small amount of GPLs into matrix material and dispersing more GPLs near the top surface can significantly reduce the peak central deflection and contact time, whereas it increases the peak contact force; (2) moving the maximum GPL concentration away from the top and bottom layers to the midplane by a short distance is a most effective way to reduce both peak deflection and contact force; (3) square GPLs with fewer monolayer graphene sheets are preferred than rectangular GPLs in suppressing the peak central deflection of the GPLRC nanocomposite plate; (4) an impactor with a higher initial velocity leads to a higher peak contact force and a larger central deflection but a shorter contact time; (5) the contact time, peak contact force, and central deflection increase as the impactor radius increases; (6) an initial in-plane tensile (compressive) load decreases (increases) the peak central deflection, but its effect on the contact force is negligible; (7) the central deflection of the immovable plate considerably increases/decreases when the temperature rise/drop.

Appendices

Appendix A

The differential operators in Eqs. (25a)–(25d) are

$$\begin{aligned} L_{11}= & {} \gamma _{110} \frac{\partial ^{2}}{\partial x^{2}}+\gamma _{112} \frac{\partial ^{2}}{\partial y^{2}}, \quad L_{12} =\gamma _{120} \frac{\partial }{\partial x}, \\ L_{13}= & {} \gamma _{131} \frac{\partial }{\partial y}, \\ L_{21}= & {} \gamma _{210} \frac{\partial ^{3}}{\partial x^{3}}+\gamma _{212} \frac{\partial ^{3}}{\partial x\partial y^{2}}, \\ L_{22}= & {} \gamma _{221} \frac{\partial ^{3}}{\partial x^{2}\partial y}+\gamma _{223} \frac{\partial ^{3}}{\partial y^{3}}, \\ L_{23}= & {} \frac{\partial ^{4}}{\partial x^{4}}+\gamma _{232} \frac{\partial ^{4}}{\partial x^{2}\partial y^{2}}+\gamma _{234} \frac{\partial ^{4}}{\partial y^{4}}, \\ L_{31}= & {} \gamma _{310} \frac{\partial }{\partial x}, \quad L_{32} =\frac{\partial ^{2}}{\partial x^{2}}+\gamma _{322} \frac{\partial ^{2}}{\partial y^{2}}+\gamma _{32} , \\ L_{33}= & {} \gamma _{331} \frac{\partial ^{2}}{\partial x\partial y}, \\ L_{34}= & {} \gamma _{340} \frac{\partial ^{3}}{\partial x^{3}}+\gamma _{342} \frac{\partial ^{3}}{\partial x\partial y^{2}}, \\ L_{41}= & {} \gamma _{411} \frac{\partial }{\partial y}, \quad L_{42} =\gamma _{421} \frac{\partial ^{2}}{\partial x\partial y}, \\ L_{43}= & {} \gamma _{430} \frac{\partial ^{2}}{\partial x^{2}}+\gamma _{432} \frac{\partial ^{2}}{\partial y^{2}}+\gamma _{43}, \\ L_{44}= & {} \gamma _{441} \frac{\partial ^{3}}{\partial x^{2}\partial y}+\gamma _{443} \frac{\partial ^{3}}{\partial y^{3}} \end{aligned}$$

where

$$\begin{aligned}&\left[ {\gamma _{110} ,\gamma _{112} } \right] ={\kappa a^{2}\left[ {K_{22} ,\beta ^{2}K_{11} } \right] }/{\left( {\pi ^{2}D_{11}^{*} } \right) }, \\&\gamma _{120} ={\kappa a^{2}K_{22} }/{\left( {\pi ^{2}D_{11}^{*} } \right) }, \\&\gamma _{131} ={\kappa \beta a^{2}K_{11} }/{\left( {\pi ^{2}D_{11}^{*} } \right) }, \\&\left[ {\gamma _{210} ,\gamma _{212} } \right] ={\gamma _6 \left[ {B_{21}^{*} ,\beta ^{2}\left( {B_{11}^{*} -B_{33}^{*} } \right) } \right] }/{A_{22}^{*} }, \\&\left[ {\gamma _{221} ,\gamma _{223} } \right] ={\gamma _6 \left[ {\beta \left( {B_{22}^{*} -B_{33}^{*} } \right) ,\beta ^{3}B_{12}^{*} } \right] }/{A_{22}^{*} }, \\&\left[ {\gamma _{232} ,\gamma _{234} } \right] ={\beta ^{2}\left[ {2A_{12}^{*} +A_{33}^{*} ,\beta ^{2}A_{11}^{*} } \right] }/{A_{22}^{*} }, \\&\gamma _{310} ={-\kappa a^{2}K_{22} }/{\left( {\pi ^{2}D_{11}^{*} } \right) }, \\&\left[ {\gamma _{322} ,\gamma _{32} } \right] ={\left[ {\pi ^{2}\beta ^{2}D_{33}^{*} ,-\kappa a^{2}K_{22} } \right] }/{\left( {\pi ^{2}D_{11}^{*} } \right) }, \\&\gamma _{331} ={\beta \left( {D_{12}^{*} +D_{33}^{*} } \right) }/{D_{11}^{*} }, \\&\left[ {\gamma _{340} ,\gamma _{342} } \right] ={\left[ {-B_{21}^{*} ,\beta ^{2}\left( {B_{33}^{*} -B_{11}^{*} } \right) } \right] }/{\left( {\gamma _6 D_{11}^{*} } \right) }, \\&\gamma _{411} ={-\kappa \beta a^{2}K_{11} }/{\left( {\pi ^{2}D_{11}^{*} } \right) }, \\&\gamma _{421} ={\beta \left( {D_{21}^{*} +D_{33}^{*} } \right) }/{D_{11}^{*} }, \\&\left[ {\gamma _{430} ,\gamma _{432} ,\gamma _{43} } \right] \\&\quad ={\left[ {\pi ^{2}D_{33}^{*} ,\pi ^{2}\beta ^{2}D_{22}^{*} ,-\kappa a^{2}K_{11} } \right] }/{\pi ^{2}D_{11}^{*} }, \\&\left[ {\gamma _{441} ,\gamma _{443} } \right] ={\left[ {\beta \left( {B_{33}^{*} -B_{22}^{*} } \right) ,-\beta ^{3}B_{12}^{*} } \right] }/{\left( {\gamma _6 D_{11}^{*} } \right) } \end{aligned}$$

in which $\gamma _6 = \left( {\frac{A_{11}^{*} A_{22}^{*} }{D_{11}^{*} D_{22}^{*} }} \right) ^{\frac{1}{4}}$.

Appendix B

Coefficients $g_{\xi \zeta \eta }^{\mathrm{w}}$, $g_{\xi \zeta \eta }^{\mathrm{f}}$, $g_{\xi \zeta \eta }^{\mathrm{x}}$, $g_{\xi \zeta \eta }^{\mathrm{y}}$, $g_{\xi \zeta \eta }^{\mathrm{q}}$, $\hat{{g}}_{113}^{\mathrm{f}}$, $\hat{{g}}_{113}^{\mathrm{x}}$, $\hat{{g}}_{113}^{\mathrm{y}}$, and $\hat{{g}}_{113}^{\mathrm{q}}$ are

$$\begin{aligned} g_{111}^{\mathrm{f}}= & {} \frac{1}{g_{11} }\left| {{\begin{array}{ccc} 0&{} {m^{3}\gamma _{210} +mn^{2}\gamma _{212} }&{}\quad {m^{2}n\gamma _{221} +n^{3}\gamma _{223} } \\ {m\gamma _{310} }&{}\quad {m^{2}+n^{2}\gamma _{322} -\gamma _{32} }&{}\quad {mn\gamma _{331} } \\ {n\gamma _{411} }&{}\quad {mn\gamma _{421} }&{}\quad {m^{2}\gamma _{430} +n^{2}\gamma _{432} -\gamma _{43} } \\ \end{array} }} \right| , \\ g_{111}^{\mathrm{x}}= & {} \frac{1}{g_{11} }\left| {{\begin{array}{ccc} {m^{4}+m^{2}n^{2}\gamma _{232} +n^{4}\gamma _{234} }&{}\quad 0&{}\quad {m^{2}n\gamma _{221} +n^{3}\gamma _{223} } \\ {m^{3}\gamma _{340} +mn^{2}\gamma _{342} }&{}\quad {m\gamma _{310} }&{}\quad {mn\gamma _{331} } \\ {m^{2}n\gamma _{441} +n^{3}\gamma _{443} }&{}\quad {n\gamma _{411} }&{}\quad {m^{2}\gamma _{430} +n^{2}\gamma _{432} -\gamma _{43} } \\ \end{array} }} \right| , \\ g_{111}^{\mathrm{y}}= & {} \frac{1}{g_{11} }\left| {{\begin{array}{ccc} {m^{4}+m^{2}n^{2}\gamma _{232} +n^{4}\gamma _{234} }&{}\quad {m^{3}\gamma _{210} +mn^{2}\gamma _{212} }&{}\quad 0 \\ {m^{3}\gamma _{340} +mn^{2}\gamma _{342} }&{}\quad {m^{2}+n^{2}\gamma _{322} -\gamma _{32} }&{}\quad {m\gamma _{310} } \\ {m^{2}n\gamma _{441} +n^{3}\gamma _{443} }&{}\quad {mn\gamma _{421} }&{}\quad {n\gamma _{411} } \\ \end{array} }} \right| , \end{aligned}$$

$$\begin{aligned} g_{111}^{\mathrm{q}}= & {} m^{2}\gamma _{110} +n^{2}\gamma _{112} +m\gamma _{120} g_{111}^{\mathrm{x}} +n\gamma _{131} g_{111}^{\mathrm{y}} \\&-\beta ^{2}\gamma _{14} \left( {n^{2}J_{\mathrm{f}00}^{[0]} +m^{2}J_{\mathrm{F}00}^{[0]} } \right) , \\ g_{202}^{\mathrm{f}}= & {} \frac{1}{2}\frac{\beta ^{2}m^{2}n^{2}\left( {\gamma _{32} -4m^{2}} \right) }{16m^{4}\left( {\gamma _{32} -4m^{2}} \right) +64m^{6}\gamma _{210} \gamma _{340} }, \\ g_{022}^{\mathrm{f}}= & {} \frac{1}{2}\frac{\beta ^{2}m^{2}n^{2}\left( {\gamma _{43} -4n^{2}\gamma _{432} } \right) }{16n^{4}\gamma _{234} \left( {\gamma _{43} -4n^{2}\gamma _{432} } \right) +64n^{6}\gamma _{223} \gamma _{443} }, \end{aligned}$$

$$\begin{aligned} g_{202}^{\mathrm{x}}= & {} -\frac{4\beta ^{2}m^{5}n^{2}\gamma _{340} }{16m^{4}\left( {\gamma _{32} -4m^{2}} \right) +64m^{6}\gamma _{210} \gamma _{340} }, \\ g_{022}^{\mathrm{y}}= & {} -\frac{4\beta ^{2}m^{2}n^{5}\gamma _{443} }{16n^{4}\gamma _{234} \left( {\gamma _{43} -4n^{2}\gamma _{432} } \right) +64n^{6}\gamma _{223} \gamma _{443} }, \\ g_{202}^{\mathrm{q}}= & {} m^{2}n^{2}\beta ^{2}\gamma _{14} g_{111}^{\mathrm{f}} -2m\gamma _{120} g_{202}^{\mathrm{x}} , \\ g_{022}^{\mathrm{q}}= & {} m^{2}n^{2}\beta ^{2}\gamma _{14} g_{111}^{\mathrm{f}} -2n\gamma _{131} g_{022}^{\mathrm{y}} , \\ \end{aligned}$$

$$\begin{aligned} g_{133}^{\mathrm{w}}= & {} \frac{2\beta ^{2}m^{2}n^{2}\gamma _{14} g_{022}^{\mathrm{f}} }{g_{13} } \\&\left| {{\begin{array}{ccc} {m^{4}+9m^{2}n^{2}\gamma _{232} +81n^{4}\gamma _{234} }&{}\quad {m^{3}\gamma _{210} +9mn^{2}\gamma _{212} }&{}\quad {3m^{2}n\gamma _{221} +27n^{3}\gamma _{223} } \\ {-m^{3}\gamma _{340} -9mn^{2}\gamma _{342} }&{}\quad {-m^{2}-9n^{2}\gamma _{322} +\gamma _{32} }&{}\quad {-3mn\gamma _{331} } \\ {-3m^{2}n\gamma _{441} -27n^{3}\gamma _{443} }&{}\quad {-3mn\gamma _{421} }&{}\quad {-m^{2}\gamma _{430} -9n^{2}\gamma _{432} +\gamma _{43} } \\ \end{array} }} \right| ,\\ g_{133}^{\mathrm{f}}= & {} -\frac{2\beta ^{2}m^{2}n^{2}\gamma _{14} g_{022}^{\mathrm{f}} }{g_{13} } \\&\left| {{\begin{array}{ccc} 0&{} {m^{3}\gamma _{210} +9mn^{2}\gamma _{212} }&{}\quad {3m^{2}n\gamma _{221} +27n^{3}\gamma _{223} } \\ {m\gamma _{310} }&{}\quad {-m^{2}-9n^{2}\gamma _{322} +\gamma _{32} }&{}\quad {-3mn\gamma _{331} } \\ {3n\gamma _{411} }&{}\quad {-3mn\gamma _{421} }&{}\quad {-m^{2}\gamma _{430} -9n^{2}\gamma _{432} +\gamma _{43} } \\ \end{array} }} \right| , \\ g_{133}^{\mathrm{x}}= & {} \frac{2\beta ^{2}m^{2}n^{2}\gamma _{14} g_{022}^{\mathrm{f}} }{g_{13} } \\&\left| {{\begin{array}{ccc} 0&{}\quad {m^{4}+9m^{2}n^{2}\gamma _{232} +81n^{4}\gamma _{234} }&{}\quad {3m^{2}n\gamma _{221} +27n^{3}\gamma _{223} } \\ {m\gamma _{310} }&{}\quad {-m^{3}\gamma _{340} -9mn^{2}\gamma _{342} }&{}\quad {-3mn\gamma _{331} } \\ {3n\gamma _{411} }&{}\quad {-3m^{2}n\gamma _{441} -27n^{3}\gamma _{443} }&{}\quad {-m^{2}\gamma _{430} -9n^{2}\gamma _{432} +\gamma _{43} } \\ \end{array} }} \right| , \\ g_{133}^{\mathrm{y}}= & {} -\frac{2\beta ^{2}m^{2}n^{2}\gamma _{14} g_{022}^{\mathrm{f}} }{g_{13} } \\&\left| {{\begin{array}{ccc} 0&{} {m^{4}+9m^{2}n^{2}\gamma _{232} +81n^{4}\gamma _{234} }&{}\quad {m^{3}\gamma _{210} +9mn^{2}\gamma _{212} } \\ {m\gamma _{310} }&{}\quad {-m^{3}\gamma _{340} -9mn^{2}\gamma _{342} }&{}\quad {-m^{2}-9n^{2}\gamma _{322} +\gamma _{32} } \\ {3n\gamma _{411} }&{}\quad {-3m^{2}n\gamma _{441} -27n^{3}\gamma _{443} }&{}\quad {-3mn\gamma _{421} } \\ \end{array} }} \right| , \\ g_{313}^{\mathrm{w}}= & {} \frac{2\beta ^{2}m^{2}n^{2}\gamma _{14} g_{202}^{\mathrm{f}} }{g_{31} } \\&\left| {{\begin{array}{ccc} {81m^{4}+9m^{2}n^{2}\gamma _{232} +n^{4}\gamma _{234} }&{}\quad {27m^{3}\gamma _{210} +3mn^{2}\gamma _{212} }&{}\quad {9m^{2}n\gamma _{221} +n^{3}\gamma _{223} } \\ {-27m^{3}\gamma _{340} -3mn^{2}\gamma _{342} }&{}\quad {-9m^{2}-n^{2}\gamma _{322} +\gamma _{32} }&{}\quad {-3mn\gamma _{331} } \\ {-9m^{2}n\gamma _{441} -n^{3}\gamma _{443} }&{}\quad {-3mn\gamma _{421} }&{}\quad {-9m^{2}\gamma _{430} -n^{2}\gamma _{432} +\gamma _{43} } \\ \end{array} }} \right| ,\\ g_{313}^{\mathrm{f}}= & {} -\frac{2\beta ^{2}m^{2}n^{2}\gamma _{14} g_{202}^{\mathrm{f}} }{g_{31} } \\&\left| {{\begin{array}{ccc} 0&{} {27m^{3}\gamma _{210} +3mn^{2}\gamma _{212} }&{}\quad {9m^{2}n\gamma _{221} +n^{3}\gamma _{223} } \\ {3m\gamma _{310} }&{}\quad {-9m^{2}-n^{2}\gamma _{322} +\gamma _{32} }&{}\quad {-3mn\gamma _{331} } \\ {n\gamma _{411} }&{}\quad {-3mn\gamma _{421} }&{}\quad {-9m^{2}\gamma _{430} -n^{2}\gamma _{432} +\gamma _{43} } \\ \end{array} }} \right| , \\ g_{313}^{\mathrm{x}}= & {} \frac{2\beta ^{2}m^{2}n^{2}\gamma _{14} g_{202}^{\mathrm{f}} }{g_{31} } \\&\left| {{\begin{array}{ccc} 0&{} {81m^{4}+9m^{2}n^{2}\gamma _{232} +n^{4}\gamma _{234} }&{}\quad {9m^{2}n\gamma _{221} +n^{3}\gamma _{223} } \\ {3m\gamma _{310} }&{}\quad {-27m^{3}\gamma _{340} -3mn^{2}\gamma _{342} }&{}\quad {-3mn\gamma _{331} } \\ {n\gamma _{411} }&{}\quad {-9m^{2}n\gamma _{441} -n^{3}\gamma _{443} }&{}\quad {-9m^{2}\gamma _{430} -n^{2}\gamma _{432} +\gamma _{43} } \\ \end{array} }} \right| , \\ \end{aligned}$$

$$\begin{aligned} g_{313}^{\mathrm{y}}= & {} -\frac{2\beta ^{2}m^{2}n^{2}\gamma _{14} g_{202}^{\mathrm{f}} }{g_{31}}\\&\left| {{\begin{array}{ccc} 0&{} {81m^{4}+9m^{2}n^{2}\gamma _{232} +n^{4}\gamma _{234} }&{}\quad {27m^{3}\gamma _{210} +3mn^{2}\gamma _{212} } \\ {3m\gamma _{310} }&{}\quad {-27m^{3}\gamma _{340} -3mn^{2}\gamma _{342} }&{}\quad {-9m^{2}-n^{2}\gamma _{322} +\gamma _{32} } \\ {n\gamma _{411} }&{}\quad {-9m^{2}n\gamma _{441} -n^{3}\gamma _{443} }&{}\quad {-3mn\gamma _{421} } \\ \end{array} }} \right| , \\ \hat{{g}}_{113}^{\mathrm{f}}= & {} \frac{I}{g_{11} }\left| {{\begin{array}{ccc} 0&{}\quad {m^{3}\gamma _{210} +mn^{2}\gamma _{212} }&{}\quad {m^{2}n\gamma _{221} +n^{3}\gamma _{223} } \\ {g_{111}^{\mathrm{x}} }&{}\quad {-m^{2}-n^{2}\gamma _{322} +\gamma _{32} }&{}\quad {-mn\gamma _{331} } \\ {g_{111}^{\mathrm{y}} }&{}\quad {-mn\gamma _{421} }&{}\quad {-m^{2}\gamma _{430} -n^{2}\gamma _{432} +\gamma _{43} } \\ \end{array} }} \right| , \end{aligned}$$

$$\begin{aligned} \hat{{g}}_{113}^{\mathrm{x}}= & {} \frac{I}{g_{11} }\left| {{\begin{array}{ccc} {m^{4}+m^{2}n^{2}\gamma _{232} +n^{4}\gamma _{234} }&{}\quad 0&{}\quad {m^{2}n\gamma _{221} +n^{3}\gamma _{223} } \\ {-m^{3}\gamma _{340} -mn^{2}\gamma _{342} }&{}\quad {g_{111}^{\mathrm{x}} }&{}\quad {-mn\gamma _{331} } \\ {-m^{2}n\gamma _{441} -n^{3}\gamma _{443} }&{}\quad {g_{111}^{\mathrm{y}} }&{}\quad {-m^{2}\gamma _{430} -n^{2}\gamma _{432} +\gamma _{43} } \\ \end{array} }} \right| , \\ \hat{{g}}_{113}^{\mathrm{y}}= & {} \frac{I}{g_{11} }\left| {{\begin{array}{ccc} {m^{4}+m^{2}n^{2}\gamma _{232} +n^{4}\gamma _{234} }&{}\quad {m^{3}\gamma _{210} +mn^{2}\gamma _{212} }&{}\quad 0 \\ {-m^{3}\gamma _{340} -mn^{2}\gamma _{342} }&{}\quad {-m^{2}-n^{2}\gamma _{322} +\gamma _{32} }&{}\quad {g_{111}^{\mathrm{x}} } \\ {-m^{2}n\gamma _{441} -n^{3}\gamma _{443} }&{}\quad {-mn\gamma _{421} }&{}\quad {g_{111}^{\mathrm{y}} } \\ \end{array} }} \right| , \\ g_{113}^{\mathrm{q}}= & {} 2\beta ^{2}m^{2}n^{2}\gamma _{14} \left( {g_{022}^{\mathrm{f}} +g_{202}^{\mathrm{f}} } \right) -\beta ^{2}\gamma _{14} \left( {n^{2}g_{002}^{\mathrm{f}} +m^{2}g_{002}^{\mathrm{F}} } \right) , \\ \hat{{g}}_{113}^{\mathrm{q}}= & {} m\gamma _{120} \hat{{g}}_{113}^{\mathrm{x}} +n\gamma _{131} \hat{{g}}_{113}^{\mathrm{y}} +I_0 \end{aligned}$$

in which

$$\begin{aligned} g_{11}= & {} \left| {{\begin{array}{ccc} {m^{4}+m^{2}n^{2}\gamma _{232} +n^{4}\gamma _{234} }&{}\quad {m^{3}\gamma _{210} +mn^{2}\gamma _{212} }&{}\quad {m^{2}n\gamma _{221} +n^{3}\gamma _{223} } \\ {m^{3}\gamma _{340} +mn^{2}\gamma _{342} }&{}\quad {m^{2}+n^{2}\gamma _{322} -\gamma _{32} }&{}\quad {mn\gamma _{331} } \\ {m^{2}n\gamma _{441} +n^{3}\gamma _{443} }&{}\quad {mn\gamma _{421} }&{}\quad {m^{2}\gamma _{430} +n^{2}\gamma _{432} -\gamma _{43} } \\ \end{array} }} \right| , \\ g_{13}= & {} \left| {{\begin{array}{l} {m^{2}\gamma _{110} +9n^{2}\gamma _{112} -\beta ^{2}\gamma _{14} \left( {m^{2}J_{\mathrm{F}00}^{[0]} +9n^{2}J_{\mathrm{f}00}^{[0]} } \right) } \\ 0 \\ {m\gamma _{310} } \\ {3n\gamma _{411} } \\ \end{array} }} \right. \\&\left. { \, {\begin{array}{ccc} 0&{}\quad {m\gamma _{120} }&{}\quad {3n\gamma _{131} } \\ {m^{4}+9m^{2}n^{2}\gamma _{232} +81n^{4}\gamma _{234} }&{}\quad {m^{3}\gamma _{210} +9mn^{2}\gamma _{212} }&{}\quad {3m^{2}n\gamma _{221} +27n^{3}\gamma _{223} } \\ {-m^{3}\gamma _{340} -9mn^{2}\gamma _{342} }&{}\quad {-m^{2}-9n^{2}\gamma _{322} +\gamma _{32} }&{}\quad {-3mn\gamma _{331} } \\ {-3m^{2}n\gamma _{441} -27n^{3}\gamma _{443} }&{}\quad {-3mn\gamma _{421} }&{}\quad {-m^{2}\gamma _{430} -9n^{2}\gamma _{432} +\gamma _{43} } \\ \end{array} }} \right| , \\ g_{31}= & {} \left| {{\begin{array}{l} {9m^{2}\gamma _{110} +n^{2}\gamma _{112} -\beta ^{2}\gamma _{14} \left( {9m^{2}J_{\mathrm{F}00}^{[0]} +n^{2}J_{\mathrm{f}00}^{[0]} } \right) } \\ 0 \\ {3m\gamma _{310} } \\ {n\gamma _{411} } \\ \end{array} }} \right. \\&\, \left. {{\begin{array}{ccc} 0&{}\quad {3m\gamma _{120} }&{}\quad {n\gamma _{131} } \\ {81m^{4}+9m^{2}n^{2}\gamma _{232} +n^{4}\gamma _{234} }&{}\quad {27m^{3}\gamma _{210} +3mn^{2}\gamma _{212} }&{}\quad {9m^{2}n\gamma _{221} +n^{3}\gamma _{223} } \\ {-27m^{3}\gamma _{340} -3mn^{2}\gamma _{342} }&{}\quad {-9m^{2}-n^{2}\gamma _{322} +\gamma _{32} }&{}\quad {-3mn\gamma _{331} } \\ {-9m^{2}n\gamma _{441} -n^{3}\gamma _{443} }&{}\quad {-3mn\gamma _{421} }&{}\quad {-9m^{2}\gamma _{430} -n^{2}\gamma _{432} +\gamma _{43} } \\ \end{array} }} \right| \\ \end{aligned}$$

The coefficients $J_{\mathrm{f}00}^{[0]}$ and $J_{\mathrm{F}00}^{[0]}$ can be obtained by substituting Eqs. (34b)–(34d) into Eqs. (26c) and (27c) or Eqs. (26d) and (27d).

Appendix C

Coefficients $\chi _1$, $\chi _2$, $\chi _3$ and $\chi _{\mathrm{f}}$ in Eq. (37) are

$$\begin{aligned} \chi _1= & {} \left[ m^{2}\gamma _{110} +n^{2}\gamma _{112} +m\gamma _{120} g_{111}^{\mathrm{x}} +n\gamma _{131} g_{111}^{\mathrm{y}}\right. \\&\left. -4\beta ^{2}\gamma _{14} \left( {m^{2}\lambda _x +n^{2}\lambda _y } \right) \right] \Big /{\hat{{g}}_{113}^{\mathrm{q}} }, \\ \chi _2= & {} {4\varGamma \left( {g_{202}^{\mathrm{q}} +g_{022}^{\mathrm{q}} } \right) }/{\left( {\pi ^{2}\hat{{g}}_{113}^{\mathrm{q}} } \right) }, \\ \chi _3= & {} {2\beta ^{2}m^{2}n^{2}\gamma _{14} \left( {g_{022}^{\mathrm{f}} +g_{202}^{\mathrm{f}} } \right) }/{\hat{{g}}_{113}^{\mathrm{q}} }, \\ \chi _{\mathrm{f}}= & {} {4\sin (mx_{\mathrm{c}} )\sin (ny_{\mathrm{c}} )}/{\left( {\pi ^{2}\hat{{g}}_{113}^{\mathrm{q}} } \right) } \end{aligned}$$

in which

$$\begin{aligned} \varGamma =\left\{ {{\begin{array}{ll} -\frac{4}{3mn},&{} m\hbox { and }n\hbox { are both odd numbers} \\ 0,&{} m\hbox { or }n\hbox { is an even number} \\ \end{array} }} \right. \end{aligned}$$