Distributed cooperative adaptive tracking control for heterogeneous systems with hybrid nonlinear dynamics

Abstract

The cooperative leader-following tracking for a group of heterogeneous mechanical systems with nonlinear hybrid order dynamics is studied. The controlled systems are considered to be composed of followers (agents) with hybrid first- and second-order time-varying dynamics. The leader is an unknown nonautonomous nonlinear system and can only give the state information of position and velocity to its neighboring followers. The followers are linked by the directed graph with fixed communication topology. And, not all of them have the information path to the leader directly. The directed information topology graph is required to have at least one spanning tree for position and velocity, respectively. Distributed cooperative adaptive control protocols are developed for all followers with first- or second-order dynamics to achieve the ultimate synchronization to the leader. The control protocols are designed based on the neural networks and the adaptive estimation algorithm for unknown time-varying functions and control coefficients. The convergence and boundedness of the synchronization error is proved by the Lyapunov theory. The simulation example verifies the correctness of the developed distributed control protocols.

1 Introduction

Research of the multi-agent systems (MAS) derives from the cooperative movement characteristics of some animals in nature, such as the swimming of fish cluster and the troops of ants [1]. For the past recent decades, cooperative control of MAS has got a lot of attention and many significant results has been achieved in the practical applications such as artificial satellite, spacecraft, unmanned underwater vehicles, robots, etc.

The main research directions of MAS contain consensus, formation, estimation, and optimization [2]. The problem of consensus refers to a kind of group behavior that all followers reach some agreements under certain distributed control protocols. Generally, the consensus of MAS includes two categories, cooperative consensus regulation, and cooperative consensus tracking [3]. For the former one, distributed consensus controllers are developed to drive the agents to an unprescribed consensus equilibrium which has a relationship with the agents’ initial states [4]. This problem is also called leaderless consensus. For the latter one, the real or virtual leader acts as the command reference for all followers. Not all of the followers have the direct information path to the leader in this situation, and all followers try to track the trajectory of the leader by the information from their neighbors. This problem can also be known as leader-following consensus or pinning control [5]. Many achievements on these two problems have been published including papers [4,5,6,7,8,9,10,11,12,13], surveys [2, 14] and books [1, 15,16,17].

In the previous studies of consensus control, the linear or nonlinear controlled objects are mostly considered to be MAS with the agents having homogeneous order such as first-, second- or higher-order. On this basis, the states which need to be synchronized are identical for each agent. In practice, however, the types of the agents to be controlled may be distinct. That is, the orders for different agents may be nonidentical. To our best knowledge, only few works have referred to the consensus tracking problem of MAS with hybrid-order dynamics, and the agents are generally defined by the models of simple linear single or double integrator [18,19,20,21,22,23], which is the main motivation of this paper.

In this study, we mainly consider the cooperative tracking problem of nonlinear heterogeneous mechanical systems. The agents in the systems are considered to be with hybrid first- or second-order dynamics and have unknown nonlinear time-varying control coefficients. The objective of control design is to achieve the ultimate synchronization of all agents to the leader. Here, the ultimate synchronization means that the positions of all agents synchronize to the leader’s position and the velocities of the second-order agents synchronize to the leader’s velocity, respectively. The distributed consensus control protocols based on neural networks and adaptive parameter estimation schemes are proposed for all agents with hybrid-order dynamics to achieve the ultimate synchronization. The neural networks and adaptive schemes are used mainly for estimating the unknown time-varying nonlinear functions and control parameters. Compared with the previous works, the following points need to be emphasized.

• 1. In the actual multi-agent mechanical systems, the agents may have different order dynamics. Different from the papers [3, 7,8,9,10,11,12,13, 24, 25] in which the dynamics orders for all agents are considered to be same, in this study, the cooperative control protocol is developed for the agents with hybrid first- or second-order dynamics.

• 2. Unlike [18,19,20,21,22,23] where the dynamics of agents with hybrid first- or second-order are considered to be known linear single or double integrator, in this study, we consider the dynamics of all agents to be unknown and nonlinear which is more applicable.

• 3. In practical mechanical systems, due to actuator dynamics, load fluctuation, power flow rate and drive mechanism, the coefficient of control item is generally time-varying and almost impossible to be one. Unlike the papers [3, 12, 24, 25] where the coefficient is considered as one, in this study, the agents with unknown heterogeneous dynamics are considered to have time-varying control coefficients which will be approximated by a singularity-avoided adaptive scheme.

The paper is structured as follows. In Sect. 2, basic algebraic graph theory is introduced. The consensus tracking of nonlinear multi-agent mechanical systems with hybrid orders is formulated in Sect. 3. Control protocol design and stability analysis are detailed in Sect. 4. Simulation case is presented in Sect. 5. And, some conclusions are given in Sect. 6.

2 Basic algebraic graph theory

In MAS, each agent (node) can communicate with its neighbors. Define a graph ${{\mathcal {G}}}=({{\mathcal {V}}},{{\mathcal {E}}})$ where ${{\mathcal {V}}}=\left\{ {{{\mathcal {V}}}_{1} ,\ldots , {{\mathcal {V}}}_n } \right\}$ is a nonempty set and edge set ${{\mathcal {E}}}\subseteq \mathcal{V}\times {{\mathcal {V}}}$. $\left( {{{\mathcal {V}}}_i ,{{\mathcal {V}}}_j } \right) \in {{\mathcal {E}}}$ denotes the edge from ${{\mathcal {V}}}_i$ to ${{\mathcal {V}}}_j$. The graph is assumed to be simple and there is no multiple edge or $\left( {{{\mathcal {V}}}_i ,{{\mathcal {V}}}_i } \right) \notin {{\mathcal {E}}}$. Define a weighted digraph (directed graph) ${{\mathcal {G}}}$ by adjacency matrix $A=\left[ {a_{ij} } \right] \in {{\mathcal {R}}}^{n\times n}$ where $a_{ij} >0$ if $\left( {{{\mathcal {V}}}_j ,{{\mathcal {V}}}_i } \right) \in {{\mathcal {E}}}$ and otherwise $a_{ij} =0$. The neighbor of node i is represented by ${{\mathcal {N}}}_i =\left\{ {j|\left( {{{\mathcal {V}}}_j ,{{\mathcal {V}}}_i } \right) \in {{\mathcal {E}}}} \right\}$, which means that i can get information from the nodes defined in set ${{\mathcal {N}}}_i$, but not vice versa. Define in-degree matrix as $D=\hbox {diag}\left\{ {d_i } \right\} \in {{\mathcal {R}}}^{n\times n}$ with $d_i =\sum _{j=1}^N {a_{ij} }$. Define the Laplacian matrix for the graph as $L=D-A$. Different from the conventional definitions that the spanning tree has to be defined based on the agent, here we consider the more general case that the agent may have first- or second-order dynamics and discuss the spanning tree for some specific state instead of the agent. Therefore, a spanning tree for jth-order state means that there is a direct or indirect path from the leader to every agent containing jth-order state. The topology is assumed to be fixed and L, D and A are all time-invariant.

Here, some notations are given as follows. $\mathrm{tr}\{\cdot \}$ is the trace of a matrix. $|\cdot |$ is the absolute value, $||\cdot ||$ denotes the Euclidean norm, $||\cdot ||_F$ denotes the Frobenius norm. Matrix $Q>0$ means it is positive definite. $I_n$ is the identity matrix in ${{\mathcal {R}}}^{n\times n}$, $0_{n\times m}$ denotes the zero matrix in ${{\mathcal {R}}}^{n\times m}$, $1_n$ is the unit column vector in ${{\mathcal {R}}}^{n}$. $\sigma (\cdot )$ denotes the set of singular values. $\bar{{\sigma }}(\cdot )$ and ${\underline{\sigma } }(\cdot )$ are the maximum and minimum singular values, respectively. Set $N=\left\{ {1,2,\ldots ,n} \right\}$.

3 Cooperative consensus tracking problem formulation

Consider a $n(n\ge 2)$ agents mechanical system where m agents have second-order nonlinear dynamics

$$\begin{aligned}&\left\{ {\begin{array}{l} {\dot{x}}_{p,i} =x_{v,i} \\ {\dot{x}}_{v,i} =f_i (\bar{{x}}_i )+g_i (\bar{{x}}_i ,t)u_i +w_i \\ \end{array}} \right. \bar{{x}}_i =[x_{p,i} ,x_{v,i} ]^\mathrm{T},\,\, i\in l_2 =\left\{ {1, 2, \ldots ,m} \right\} \nonumber \\ \end{aligned}$$

(1)

and other $n-m$ agents have first-order dynamics

$$\begin{aligned} {\dot{x}}_{p,i}= & {} f_i (\bar{{x}}_i )+g_i (\bar{{x}}_i ,t)u_i +w_i, \bar{{x}}_i =[x_{p,i} ,0]^\mathrm{T}, \quad \nonumber \\&i\in l_1 =\left\{ {m+1, m+2, \ldots ,n} \right\} \end{aligned}$$

(2)

where $x_{p,i}$ and $x_{v,i}$ represent position and velocity states of ith agent, respectively, $\bar{{x}}_i$ denotes the state vector, $u_i$ denotes the control input, $f_i (\cdot )$ and $g_i (\cdot )$ denote the state-dependent time-varying unknown nonlinear functions and are locally Lipschitz, $w_i$ denotes the unknown bounded external disturbance. Without loss of generality, we assume

$$\begin{aligned} g_i (\bar{{x}}_i ,t)\ge {\underline{g}}_i \end{aligned}$$

(3)

where ${\underline{g}}_i >0$ is the known lower bound.

The second-order agents in (1) can be globally defined by

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{x}}_p^{l_2 } =x_v \\ {\dot{x}}_v =f^{l_2 }(\bar{{x}}^{l_2 })+g^{l_2 }u^{l_2 }+w^{l_2 } \\ \end{array}} \right. \end{aligned}$$

(4)

and the first-order agents in (2) can be globally defined by

$$\begin{aligned} {\dot{x}}_p^{l_1 } =f^{l_1 }(\bar{{x}}^{l_1 })+g^{l_1 }u^{l_1 }+w^{l_1 } \end{aligned}$$

(5)

where $\left( \cdot \right) ^{l_1 }=\left[ {{\begin{array}{ll} {0_m }&{}\quad 0 \\ 0&{}\quad {I_{n-m} } \\ \end{array} }} \right] \left( \cdot \right)$, $\left( \cdot \right) ^{l_2 }=\left[ {{\begin{array}{ll} {I_m }&{}\quad 0 \\ 0&{}\quad {0_{n-m} } \\ \end{array} }} \right] \left( \cdot \right)$, $x_p =\left[ {x_{p,1}, \ldots , x_{p,n} } \right] ^\mathrm{T}$ is the global position vector, $x_v =\left[ {x_{v,1}, \ldots , x_{v,m}, 0_{1\times \left( {n-m} \right) } } \right] ^\mathrm{T}\in {{\mathcal {R}}}^{n}$ denotes the global velocity vector, $u=\left[ {u_1, u_2, \ldots , u_n } \right] ^\mathrm{T}$, $f(\bar{{x}})=\left[ {f_1 (\bar{{x}}_1 ), f_2 (\bar{{x}}_2 ), \ldots , f_n (\bar{{x}}_n )} \right] ^\mathrm{T}$, $\bar{{x}}=\big [ {\bar{{x}}_1, \bar{{x}}_2, }{\ldots , \bar{{x}}_n } \big ]^\mathrm{T}$, $g=\hbox {diag}\left\{ {g_i (\bar{{x}}_i ,t)} \right\} \in {{\mathcal {R}}}^{n\times n}$, $w=\left[ {w_1, w_2, \ldots , w_n } \right] ^\mathrm{T}$.

Define the leader (node 0) as

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{x}}_{p,0} =x_{v,0} \\ {\dot{x}}_{v,0} =f_0 (x_0 ,t) \\ \end{array}} \right. \end{aligned}$$

(6)

where $_{ }x_{p,0}$ and $x_{v,0}$ denote position and velocity, respectively. $f_0 (\cdot )$ is the unknown nonlinear function and locally Lipschitz, $x_0 =[x_{p,0} ,x_{v,0} ]^\mathrm{T}$ is the state vector. Here, the leader is considered as a generator of command or reference trajectory and can have unknown time-varying nonlinear dynamics.

Remark 1

In this paper, the aim of the cooperative tracking control design is to make all following agents with the dynamics given by (1) and (2) in graph ${{\mathcal {G}}}$ synchronize to the leader described by (6), i.e., $x_{p,i} (t)\rightarrow x_{p,0} (t), i\in N$ and $x_{v,i} (t)\rightarrow x_{v,0} (t), i\in l_2$.

The tracking error of ith agent is defined by

$$\begin{aligned} \begin{array}{ll} \delta _{p,i} =x_{p,i} -x_{p,0},&{}\quad i\in N \\ \delta _{v,i} =x_{v,i} -x_{v,0},&{}\quad i\in l_2 \\ \end{array} \end{aligned}$$

(7)

Then, the global position and velocity errors are $\delta _p =x_p -{\underline{1}}x_{p,0}$, $\delta _v =x_v -{\underline{1}}^{l_2 }x_{v,0}$, ${\underline{1}}=\left[ \hbox {1 },\ldots ,\hbox { 1} \right] ^\mathrm{T}\in \mathcal{R}^{n}$. In this study, the cooperative control protocols are developed for all following agents with first- and second-order dynamics to guarantee that $\delta _p$ and $\delta _v$ converge to zero. The notions of uniform ultimate boundedness [26] can be extended to the MAS control systems by the following definition.

Definition 1

Error $\delta _k \hbox { (}k=p,v)$ is cooperatively uniformly ultimately bounded (CUUB) if there exists a compact set $\varOmega _k \subset {{\mathcal {R}}}^{n}$, so that for $\forall \delta _k (t_0 )\in \varOmega _k$ there exists a bound $B_k >0$ and time $T_k (B_k ,\delta _p (t_0 ),\delta _v (t_0 ))$, such that $\left\| {\delta _k (t)} \right\| \le B_k ,\forall t\ge t_0 +T_k$ [3]. If $\delta _k$ is CUUB, the state $x_{k,i}$ is bounded within the neighborhood of $x_{k,0}$, and the agents can achieve the synchronization within limited time.

Remark 2

According to (7) and the graph theory, we have that not all agents can get the state information from the leader. That is, some agents may have only the information of their neighbors. The information of $x_{p,0}$ and $x_{v,0}$ may not be accessible for them. Therefore, we can not use $\delta _{p,i}$ and $\delta _{v,i}$ in the distributed control protocols design, but for stability analysis purpose.

The agents can only get the information from their neighbors. The local neighborhood synchronization error can be defined by [27]

$$\begin{aligned} e_{p,i}= & {} \sum _{j\in {{\mathcal {N}}}_i } a_{ij} (x_{p,j} -x_{p,i} )\nonumber \\&+\,b_i (x_{p,0} -x_{p,i} ), \quad i\in N \nonumber \\ e_{v,i}= & {} \sum _{j\in {{\mathcal {N}}}_i^2 } a_{ij} (x_{v,j} -x_{v,i} )\nonumber \\&+\,b_i (x_{v,0} -x_{v,i} ), \quad i\in l_2 \end{aligned}$$

(8)

where set ${{\mathcal {N}}}_i^2$ denotes the second-order neighbors of agent i, $b_i$ represents the weight between leader and node i. Since there is no need for the leader to receive the information from the following agents, $b_i$ is nonnegative. It should be noted that $b_i >0$ if and only if there is a communication edge from the leader to node i in the graph. Also, there is at least one agent whose $b_i >0$, which means at least one agent in the graph can receive the leader’s command.

Define the global synchronization error as

$$\begin{aligned} \begin{array}{l} e_p =-(L+B)(x_p -{\underline{1}}x_{p,0} ) \\ e_v =-(L+B)(x_v -{\underline{1}}^{l_2 }x_{v,0} ) \\ \end{array} \end{aligned}$$

(9)

where $e_p =\left[ {e_{p,1}, \ldots , e_{p,n} } \right] ^\mathrm{T}$, $e_v =\big [ {e_{v,1}, \ldots , e_{v,m},}{0_{1\times (n-m)} } \big ]^\mathrm{T}\in {{\mathcal {R}}}^{n}$, $B=\hbox {diag}\left\{ {b_i } \right\} \in {{\mathcal {R}}}^{n\times n}$.

Since $x_p =x_p^{l_1 } +x_p^{l_2 }$, differentiating (9) we have

$$\begin{aligned} {\dot{e}}_p= & {} -(L+B)({\dot{x}}_p^{l_1 } +x_v -{\underline{1}}x_{v,0} )\nonumber \\= & {} -(L+B)({\dot{x}}_p^{{l}_1 } -{\underline{1}}^{l_1 }x_{v,0} )+e_v \nonumber \\ {\dot{e}}_v= & {} -(L+B)\left( {{\dot{x}}_v -{\underline{1}}^{l_2 }f_0 (x_0 ,t)} \right) \end{aligned}$$

(10)

Define the sliding-mode error for node i as

$$\begin{aligned} r_i =\left\{ {{\begin{array}{l} {e_{p,i} \hbox { , }i\in l_1 } \\ {e_{v,i} +\lambda _i e_{p,i}, \quad i\in l_2 } \\ \end{array} }} \right. \end{aligned}$$

(11)

where $\lambda _i >0$.

Then, the error r can be given by

$$\begin{aligned} r=r_{n1} +r_{n2} \end{aligned}$$

(12)

where $r_{n1} =e_p^{l_1 }, r_{n2} =e_v +\Lambda e_p^{l_2 }$ and $\Lambda =\hbox {diag}\left( {\lambda _1,\ldots , \lambda _m, 0,\ldots , 0} \right) \in {{\mathcal {R}}}^{n\times n}$.

Differentiating (12), we have

$$\begin{aligned} {\dot{r}}= & {} {\dot{r}}_{n1} +{\dot{r}}_{n2} \nonumber \\ {\dot{r}}_{n1}= & {} {\dot{e}}_p^{l_1 } =-(L+B)({\dot{x}}_p^{l_1 } -{\underline{1}}^{l_1 }x_{v,0} ) \nonumber \\= & {} -(L+B)\left( f^{l_1 }(\bar{{x}}^{l_1 })\right. \nonumber \\&\left. +\,g^{l_1 }u^{l_1 }+w^{l_1 }-{\underline{1}}^{l_1 }x_{v, 0} \right) \nonumber \\ {\dot{r}}_{n2}= & {} {\dot{e}}_v +\Lambda e_v \nonumber \\= & {} -(L+B)({\dot{x}}_v -{\underline{1}}^{l_2 }f_0 (x_0 ,t))+\Lambda e_v \nonumber \\= & {} -(L+B)\left( f^{l_2 }(\bar{{x}}^{l_2 })+g^{l_2 }u^{l_2 }\right. \nonumber \\&\left. +\,w^{l_2 }-{\underline{1}}^{l_2 }f_0 (x_0 ,t) \right) +\Lambda e_v \end{aligned}$$

(13)

Remark 3

Define $\bar{{\mathcal {G}}}=(\bar{{\mathcal {V}}},\bar{{\mathcal {E}}})$ as the augmented communication graph including leader node 0, where $\bar{{\mathcal {V}}}=\left\{ {{{\mathcal {V}}}_0, \ldots , {{\mathcal {V}}}_n } \right\}$ and $\bar{{\mathcal {E}}}\subseteq \bar{{\mathcal {V}}}\times \bar{{\mathcal {V}}}$. Consider that $\bar{\mathcal{G}}$ contains at least a spanning tree for position and velocity, respectively. That means there is at least a path of the position or velocity state from the leader to each agent. And, $L+B$ is nonsingular M-matrix [17, 28].

Lemma 1

Let $\bar{{\mathcal {G}}}$ contain at least a spanning tree for position and velocity, respectively. Then, $B\ne 0$ and $L+B$ is nonsingular. According to (7) and (9), we have

$$\begin{aligned} \left\| {\delta _k } \right\|= & {} \left\| {(L+B)^{-1}e_k } \right\| \nonumber \\\le & {} \left\| {e_k } \right\| /{\underline{\sigma } }(L+B),k=p,v \end{aligned}$$

(14)

4 Distributed cooperative adaptive control protocol design

In this part, the cooperative controller is developed for the multi-agent mechanical system (1) and (2) to realize the ultimate synchronization of all followers to the leader.

4.1 Neural networks approximation

Here, the neural networks are used to estimate the unknown time-varying function $f_i (\bar{{x}}_i )$. According to the techniques of neural networks approximation in [26], assume that $f_i (\bar{{x}}_i )$ can be expressed by

$$\begin{aligned} f_i (\bar{{x}}_i )=W_i^T \phi _i (\bar{{x}}_i )+\varepsilon _i, \quad i\in N \end{aligned}$$

(15)

where $\phi _i (\bar{{x}}_i )\in {{\mathcal {R}}}^{v_i }$ denotes the basis function, $v_i$ denotes the number of neurons for ith node, $W_i \in {{\mathcal {R}}}^{v_i }$ denotes the ideal weight, $\varepsilon _i$ represents the estimation error.

Remark 4

The neural networks in (15) is linear in parameter. There exist a large enough positive $v_i^*$ and a compact set $\varOmega$, such that for any $v_i >v_i^*$, we can always find ideal $W_i$ and $\phi _i (\cdot )$, which makes (15) satisfy that $\max _{\bar{{x}}_i \in \varOmega } \left| {\varepsilon _i } \right|$ is small enough [29].

By the neural networks, each node will keep approximating the nonlinear function $f_i (\bar{{x}}_i )$ locally. Define the approximation of $f_i (\bar{{x}}_i )$ as

$$\begin{aligned} \hat{{f}}_i (\bar{{x}}_i )=\hat{{W}}_i^T \phi _i (\bar{{x}}_i ),\quad i\in N \end{aligned}$$

(16)

where $\hat{{f}}_i (\bar{{x}}_i )$ denotes the estimate of $f_i (\bar{{x}}_i )$, $\hat{{W}}_i \in {{\mathcal {R}}}^{v_i }$ is the estimate of weight $W_i$.

And, $f(\bar{{x}})$ can be globally described by

$$\begin{aligned} f(\bar{{x}})=W^\mathrm{T}\phi (\bar{{x}})+\varepsilon \end{aligned}$$

(17)

where $W=\hbox {diag}\left\{ {W_i } \right\} \in {{\mathcal {R}}}^{n\times n}$, $\phi (\bar{{x}})=\big [ {\phi _1^T (\bar{{x}}_1 ), \phi _2^T }{(\bar{{x}}_2 ), \ldots , \phi _n^T (\bar{{x}}_n )} \big ]^\mathrm{T}$, $\varepsilon =\left[ {\varepsilon _1, \varepsilon _2, \ldots , \varepsilon _n } \right] ^\mathrm{T}$.

Then, the approximation $\hat{{f}}(x)$ is given by

$$\begin{aligned} \hat{{f}}(\bar{{x}})=\hat{{W}}^\mathrm{T}\phi (\bar{{x}}) \end{aligned}$$

(18)

where $\hat{{f}}(\bar{{x}})=\left[ {\hat{{f}}_1 (\bar{{x}}_1 ), \hat{{f}}_2 (\bar{{x}}_2 ), \ldots , \hat{{f}}_n (\bar{{x}}_n )} \right] ^\mathrm{T}$, $\hat{{W}}=\hbox {diag}\left\{ {\hat{{W}}_i } \right\} \in {{\mathcal {R}}}^{n\times n}, i\in N$.

Remark 5

Define $\phi _{iM} =\max _{\bar{{x}}_i \in \varOmega } \left\| {\phi _i (\bar{{x}}_i )} \right\|$, $W_{iM} =\left\| {W_i } \right\|$ and $\varepsilon _{iM} =\left\| {\varepsilon _i } \right\|$. Then, there exist some upper bounds $\phi _M >0$, $W_M >0$ and $\varepsilon _M >0$ about the neural networks estimations, such that $\left\| {\phi (\bar{{x}})} \right\| \le \phi _M$, $\left\| W \right\| _F \le W_M$ and $\left\| \varepsilon \right\| \le \varepsilon _M$.

4.2 Distributed adaptive control protocols design

In this part, the local control protocols and adaptive updating laws will be presented for multi-agent mechanical system (1) and (2) to achieve the synchronization to the leader. Before proceeding further, the following assumptions about the bounds are required.

Assumption 1

Unknown disturbance w is bounded by $w_M >0$. Unknown nonlinear function $f_0 (x_0 ,t)$ is bounded by $f_M >0$. The state of the leader is bounded, such that $\left\| {x_0 } \right\| \le x_{0M}$. There exists finite $g_M >0$, such that $\left\| g \right\| _F \le g_M$. The control input u is bounded by $\left\| u \right\| \le u_M$, $u_M >0$.

Remark 6

Note that the bounds mentioned in Remark 5 and Assumption 1 are not necessary to be known and will not be used in the control protocols design but in the process of stability analysis.

Lemma 2

[17]. Consider that $\bar{{\mathcal {G}}}$ contains at least a spanning tree for position and velocity, respectively. That means $b_i >0$ for at least one agent and $L+B$ is nonsingular. Define

$$\begin{aligned} q= & {} (L+B)^{-1}{1}=\left[ {q_1, q_2,\ldots ,q_n } \right] ^\mathrm{T}\nonumber \\ P= & {} \mathrm{diag}\left\{ {p_i } \right\} =\mathrm{diag}\left\{ {1/q_i } \right\} ,\quad i\in N\nonumber \\ Q= & {} (L+B)^\mathrm{T}P+P(L+B)\nonumber \\ \end{aligned}$$

(19)

Then, P and Q are positive definite.

The distributed cooperative control protocols are designed as

$$\begin{aligned} u_i= & {} \frac{1}{\hat{{g}}_i }\left( {cr_i -\hat{{f}}_i (\bar{{x}}_i )} \right) \nonumber \\= & {} \frac{1}{\hat{{g}}_i }\left( {cr_i -\hat{{W}}_i^T \phi _i (\bar{{x}}_i )} \right) \hbox { , }i\in l_1 \nonumber \\ u_i= & {} \frac{1}{\hat{{g}}_i }\left( cr_i -\hat{{f}}_i (\bar{{x}}_i ) + \frac{1}{d_i +b_i }\lambda _i e_{v,i} \right) \nonumber \\= & {} \frac{1}{\hat{{g}}_i }\left[ cr_i -\hat{{W}}_i^T \phi _i (\bar{{x}}_i )+\frac{1}{d_i +b_i }\lambda _i e_{v,i} \right] , \quad i\in l_2 \nonumber \\ \end{aligned}$$

(20)

or globally

$$\begin{aligned} \hat{{g}}^{l_1 }u^{l_1 }= & {} cr_{n1} -\left( {\hat{{W}}^{l_1 }} \right) ^\mathrm{T}\phi ^{l_1 }(\bar{{x}}^{l_1 }) \nonumber \\ \hat{{g}}^{l_2 }u^{l_2 }= & {} cr_{n2} -\left( {\hat{{W}}^{l_2 }} \right) ^\mathrm{T}\phi ^{l_2 }(\bar{{x}}^{l_2 })+\left( {D+B} \right) ^{-1}\Lambda e_v \nonumber \\ \end{aligned}$$

(21)

where $\hat{{g}}_i$ is the estimate of $g_i (t)$, $\hat{{g}}=\hbox {diag}\left\{ {\hat{{g}}_i } \right\} \in {{\mathcal {R}}}^{n\times n}$, c is the control gain.

The gain c satisfies

$$\begin{aligned} c{\underline{\sigma } }(Q)>2\left( {\frac{\chi ^{2}}{\theta }+\frac{\vartheta ^{2}}{{\underline{\sigma } }(\Lambda )}\hbox {+}\frac{\varsigma ^{2}}{\kappa }\hbox {+}\psi } \right) \end{aligned}$$

(22)

with $\vartheta =-\frac{1}{2}-\frac{\bar{{\sigma }}\left( {\Lambda ^{2}} \right) \bar{{\sigma }}\left( {P^{l_2 }} \right) \bar{{\underline{\sigma } }}\left( A \right) }{2{\sigma }\left( {D+B} \right) }$, $\psi =\frac{\bar{{\sigma }}\left( \Lambda \right) \bar{{\sigma }}\left( A \right) \bar{{\sigma }}\left( {P^{l_2 }} \right) }{{\underline{\sigma } }\left( {D+B} \right) }$, $\varsigma =-\frac{1}{2}\phi _M \bar{{\sigma }}\left( P \right) \bar{{\sigma }}\left( A \right)$and $\chi =-\frac{1}{2}u_M \bar{{\sigma }}\left( P \right) \bar{{\sigma }}\left( A \right)$, where $\kappa$ is defined in (24) and $\theta$ is defined in (25).

Design the local adaptive tuning laws for $\hat{{W}}_i$ as

$$\begin{aligned} \dot{\hat{{W}}}_i =-F_i \left[ {\phi _i (\bar{{x}}_i )r_i p_i (d_i +b_i )+\kappa \hat{{W}}_i } \right] \hbox {, }i\in N \end{aligned}$$

(23)

or globally

$$\begin{aligned} \dot{\hat{{W}}}=-F\left[ {\phi (\bar{{x}})r^\mathrm{T}P(D+B)+\kappa \hat{{W}}} \right] \end{aligned}$$

(24)

where $F_i >0$ and $\kappa >0$, $F=\hbox {diag}\left\{ {F_i } \right\} \in {{\mathcal {R}}}^{n\times n},i\in N$.

To avoid singularity, the updating law of control coefficient $\hat{{g}}$ is designed as

$$\begin{aligned}&\dot{\hat{{g}}}=-\eta \theta \hat{{g}}- \hbox {diag}\left( {\Delta _1 ,\Delta _2 ,\ldots ,\Delta _n } \right) \nonumber \\&\Delta _i = \nonumber \\&\left\{ {\begin{array}{ll} \eta _i u_i r_i p_i (d_i +b_i ),&{}\quad \hbox { if }\hat{{g}}_i >{\underline{g}}_i, \quad i\in N \\ \eta _i u_i r_i p_i (d_i +b_i ),&{}\quad \hbox { if }\hat{{g}}_i ={\underline{g}}_i \hbox { and }u_i r_i p_i (d_i +b_i )<0, \quad i\in N \\ 0,&{}\quad \hbox { if }\hat{{g}}_i ={\underline{g}}_i \hbox { and }u_i r_i p_i (d_i +b_i )\ge 0,\quad i\in N \\ \end{array}} \right. \nonumber \\ \end{aligned}$$

(25)

where $\theta$ is a positive scalar gain, $\eta =\hbox {diag}\left\{ {\eta _i } \right\} \in {{\mathcal {R}}}^{n\times n}$ and $\eta _i >0\hbox { },i\in N$.

4.3 Stability analysis

To make the notations simple, denote $f^{l_1 }(\bar{{x}}^{l_1 })$ as $f^{l_1 }$, $f^{l_2 }(\bar{{x}}^{l_2 })$ as $f^{l_2 }$, $f_0 (x_0 ,t)$ as $f_0$, $\phi ^{l_1 }(\bar{{x}}^{l_1 })$ as $\phi ^{l_1 }$, $\phi ^{l_2 }(\bar{{x}}^{l_2 })$ as $\phi ^{l_2 }$ and $\phi (\bar{{x}})$ as $\phi$. Using (4), (5), (17) and (21), (13) becomes

$$\begin{aligned} {\dot{r}}_{n1}= & {} -(L+B)\left( f^{l_1 }+g^{l_1 }u^{l_1 }+w^{l_1 }-{\underline{1}}^{l_1 }x_{v, 0}\right. \nonumber \\&\left. +\,\hat{{g}}^{l_1 }u^{l_1 }-\hat{{g}}^{l_1 }u^{l_1 } \right) \nonumber \\= & {} -(L+B)\left( \left( {W^{l_1 }} \right) ^\mathrm{T}\phi ^{l_1 }+\varepsilon ^{l_1 }+{\tilde{g}}^{l_1 }u^{l_1 }\right. \nonumber \\&\left. +\,cr_{n1} -\left( {\hat{{W}}^{l_1 }} \right) ^\mathrm{T}\phi ^{l_1 }+w^{l_1 }-{\underline{1}}^{l_1 }x_{v, 0} \right) \nonumber \\= & {} -(L+B)\left( \left( {{\tilde{W}}^{l_1 }} \right) ^\mathrm{T}\phi ^{_{l_1 } }+\varepsilon ^{l_1 }+{\tilde{g}}^{l_1 }u^{l_1 }\right. \nonumber \\&\left. +\,cr_{n1} +w^{l_1 }-{\underline{1}}^{l_1 }x_{v,0} \right) \nonumber \\ {\dot{r}}_{n2}= & {} -(L+B)\left( f^{l_2 }+g^{l_2 }u^{l_2 }+w^{l_2 }-{\underline{1}}^{l_2 }f_0\right. \nonumber \\&\left. +\,\hat{{g}}^{l_2 }u^{l_2 }-\hat{{g}}^{l_2 }u^{l_2 } \right) +\Lambda e_v \nonumber \\= & {} -(L+B)\left( \left( {W^{l_2 }} \right) ^\mathrm{T}\phi ^{l_2 }+\varepsilon ^{l_2 }+{\tilde{g}}^{l_2 }u^{l_2 }\right. \nonumber \\&\left. +\,cr_{n2} -\left( {\hat{{W}}^{l_2 }} \right) ^\mathrm{T}\phi ^{l_2 }+\left( {D+B} \right) ^{-1}\Lambda e_v \right. \nonumber \\&\left. +\,w^{l_2 }-{\underline{1}}^{l_2 }f_0 \right) +\Lambda e_v \nonumber \\= & {} -(L+B)\left( \left( {{\tilde{W}}^{l_2 }} \right) ^\mathrm{T}\phi ^{l_2 }+\varepsilon ^{l_2 }+{\tilde{g}}^{l_2 }u^{l_2 }+cr_{n2} \right. \nonumber \\&\left. +\,\left( {D+B} \right) ^{-1}\Lambda e_v +w^{l_2 }-{\underline{1}}^{l_2 }f_0 \right) +\Lambda e_v \nonumber \\= & {} -(L+B)\left( \left( {{\tilde{W}}^{l_2 }} \right) ^\mathrm{T}\phi ^{_{l_2 } }+\varepsilon ^{l_2 }\right. \nonumber \\&\left. +\,cr_{n2} +{\tilde{g}}^{l_2 }u^{l_2 }+w^{l_2 }-{\underline{1}}^{l_2 }f_0 \right) \nonumber \\&+\,A\left( {D+B} \right) ^{-1}\Lambda e_v \nonumber \\ \end{aligned}$$

(26)

Theorem 1

Consider the leader (6) and the networked mechanical system (1) and (2) under Assumption 1. $\bar{{\mathcal {G}}}$ has at least a spanning tree with the leader being node 0 for position and velocity, respectively. Using the protocol (20) and the adaptive tuning laws (24) and (25), we have the results

• 1. There exists a $\bar{{v}}_i >0$, such that for $v_i >\bar{{v}}_i ,\forall i\in N$, the tracking error $\delta _p$ and $\delta _v$ are CUUB. All nodes in ${{\mathcal {G}}}$ can synchronize to node 0.

• 2. For $\forall t\ge t_0$, states $x_{p,i} ,\hbox { }i\in N$ and$_{ }x_{v,i} ,i\in l_2$ are bounded.

Proof

See “Appendix.” $\square$

Remark 7

The fact that $F_i$ is arbitrary positive design gain implies $F_i p_i (d_i +b_i )$ and $F_i \kappa$ can be chosen as arbitrary positive parameters. This means that we can arbitrarily design positive gains $F_i p_i (d_i +b_i )$ and $F_i \kappa _i$ for adaptive tuning law in (23). Similarly, $\eta _i p_i (d_i +b_i )$ and $\eta _i \theta$ can also be arbitrarily designed in (25).

5 Simulation example

In this part, the simulation is conducted to verify the correctness of the proposed control protocols and adaptive updating laws. Consider the mechanical system with one leader and five followers, in which nodes $0,1,\hbox { 2 },5$ are second-order and nodes 3, 4 are first-order. The dynamics of the first-order following nodes are

$$\begin{aligned} {\dot{x}}_{p,i} =f_i (\bar{{x}}_i )+g_i (\bar{{x}}_i ,t)u_i +w_i \cos (t), \quad i\in 3, 4 \end{aligned}$$

and the dynamics of the second-order following nodes are

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{x}}_{p,i} =x_{v,i} \\ {\dot{x}}_{v,i} =f_i (\bar{{x}}_i )+g_i (\bar{{x}}_i ,t)u_i +w_i \cos (t) \\ \end{array}} \right. ,\quad i\in 1, 2, 5 \end{aligned}$$

where $w_i$ is the random disturbance between 0 and 0.1, $f_i (\bar{{x}}_i )=\cos (ix_{p,i} )+\sin (ix_{p,i} )$ is the nonlinear function of the states, $g_i (\bar{{x}}_i ,t)=i\left( {1+0.5\sin (tx_{p,i} )} \right)$ is the time-varying control coefficient.

The dynamics of the leader is

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{x}}_{p,0} =x_{v,0} \\ {\dot{x}}_{v,0} =-\sin (t) \\ \end{array}} \right. \end{aligned}$$

with the initial value $\left[ {x_{p,0} (0),x_{v,0} (0)} \right] \hbox {=}\left[ {1, 1} \right]$.

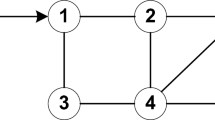
The communication topology is a fixed digraph as shown in Fig. 1. Node 0 is the leader and nodes 1, 2, 3, 4 and 5 are the following agents. It is obvious that there is a spanning tree of position or velocity for each following agent. And, all agents can receive the corresponding state information from the leader directly or from their neighbors indirectly. The edge weights of the communication topology in Fig. 1 are all chosen as 1 and the sampling period is chosen as 0.001 s.

Fig. 1

Topology of digraph $\bar{{{{\mathcal {G}}}}}$

Fig. 2

Position tracking errors $\delta _{p,i}$

In simulation, the disturbances $w_i$ and the nonlinear dynamics $f_i (\bar{{x}}_i )$ of the nodes are all assumed to be unknown and time-varying. The control coefficient $g_i (t)$ is also considered to be time-varying and nonlinear. Five neurons are used for the neural networks of each node. The weights of neural networks are initialized as $\hat{{W}}_i (0)=\left[ {0,\ldots ,0} \right] ^\mathrm{T}\in {{\mathcal {R}}}^{5}$. Hyperbolic tangent is used as the basis function of neural networks. Choose the known lower bound of the control coefficient for all agents as ${\underline{g}}_i =0.5$.

Fig. 3

Position tracking profiles $x_{p,i}$

Fig. 4

Velocity tracking errors $\delta _{v,i}$

The developed control law (20), adaptive laws (23) and (25) are absolutely distributed. The design parameters are chosen as $v_i =5$, $c=100$, $F_i =5000$, $\kappa =0.001$, $\eta _i =1$, $\theta =0.001$, $\lambda _i =5$. Based on the designed control protocols (20), (23) and (25), the simulation is performed on the given mechanical system and the leader under the communication digraph shown in Fig. 1. Despite the hybrid order nonlinear dynamics and external disturbances included in the controlled mechanical system, the simulation results show promising control performance. The position tracking error $\delta _{p,i}$ of the followers are compared in Fig. 2 and the position tracking profiles $x_{p,i}$ for all nodes are presented in Fig. 3. We can see that the overall synchronization errors of position converge to zero rapidly in about 2 s. Only agent 1 can receive the information from node 0 directly and all other agents have to follow agent 1 according to the topology digraph. Agents 3 and 4 can only get the position information from nodes 2 and 5, and their position trajectories are more affected by agent 2 from the beginning. Agent 5 can only receive the information from agent 1 and is not influenced by other agents.

The velocity tracking error $\delta _{v,i}$ of agents 1, 2 and 5 are given in Fig. 4 and the velocity tracking profiles $x_{v,i}$ for the nodes with second-order dynamics are compared in Fig. 5. Under the effect of initial velocity synchronization errors, there are some fluctuations of the velocity tracking for agents 1, 2 and 5. Agent 1’s velocity fluctuation is smallest and agent 5 has the largest about 9 m/s. Despite some fluctuations, the velocity tracking of all second-order agents is rapid and the tracking errors converge to approximate zero in 1.5 s. The tracking results show that the velocity fluctuations have no great impact on the position tracking for second-order agents 1, 2 and 5. The profiles of the control inputs for all following nodes are shown in Fig. 6. From these figures, it can be seen that the first- and second-order states of all followers synchronize to the trajectory of the leader accurately and rapidly. Under the developed control protocols and adaptive updating laws, the simulated nonlinear multi-agent mechanical control system with unknown, hybrid order dynamics and time-varying control coefficient is demonstrated to be stable, and the effectiveness of the proposed distributed cooperative control protocols is verified.

Fig. 5

Velocity tracking profiles $x_{v,i}$

Fig. 6

Control inputs $u_i$

6 Conclusion

This paper studied the problem of cooperative tracking control of multi-agent mechanical systems with hybrid first- and second-order dynamics. The agents have unknown nonidentical nonlinear dynamics. The coefficients of the control input item are nonlinear and time-varying. The distributed neural adaptive control protocols were proposed to achieve the synchronization of position and velocity to the leader. The protocols are completely distributed and can be calculated locally for all agents with only the neighbors’ information. Simulation example verifies the effectiveness of the proposed control protocols, and the results show that each agent can synchronize to the leader accurately and quickly. The future work will be concentrated on the time-varying actuator faults of hybrid order multi-agent mechanical systems.

Appendix: Proof of Theorem 1

Define the Lyapunov function as

$$\begin{aligned} V=V_r +V_W +V_g +V_e \end{aligned}$$

(27)

where $V_r =\frac{1}{2}r^\mathrm{T}Pr$, $V_W =\frac{1}{2}{\tilde{W}}^\mathrm{T}F^{-1}{\tilde{W}}$, $V_g =\frac{1}{2}{\tilde{g}}^\mathrm{T}\eta ^{-1}{\tilde{g}}$, $V_e =\frac{1}{2}\left( {e_p^{l_2 } } \right) ^\mathrm{T}e_p^{l_2 }$.

According to (26), by differentiating $V_r$, we have

$$\begin{aligned} {\dot{V}}_r= & {} r^\mathrm{T}P{\dot{r}}=r_{n1}^T P^{l_1 }{\dot{r}}_{n1} +r_{n2}^T P^{l_2 }{\dot{r}}_{n2} \nonumber \\= & {} -r_{n1}^T P^{l_1 }(L+B)\left( \left( {{\tilde{W}}^{l_1 }} \right) ^\mathrm{T}\phi ^{_{l_1 } }+\varepsilon ^{l_1 }+{\tilde{g}}^{l_1 }u^{l_1 }\right. \nonumber \\&\left. +\,cr_{n1} +w^{l_1 }-{\underline{1}}^{l_1 }x_{v,0} \right) \nonumber \\&-\,r_{n2}^T P^{l_2 }(L+B)\left( \left( {{\tilde{W}}^{l_2 }} \right) ^\mathrm{T}\phi ^{_{l_2 } }+\varepsilon ^{l_2 }+cr_{n2} \right. \nonumber \\&\left. +\,{\tilde{g}}^{l_2 }u^{l_2 }+w^{l_2 }-{\underline{1}}^{l_2 }f_0 \right) \nonumber \\&+\,r_{n2}^T P^{l_2 }A\left( {D+B} \right) ^{-1}\Lambda e_v \nonumber \\= & {} -r^\mathrm{T}P(L+B)\left[ {{\tilde{W}}^\mathrm{T}\phi +cr+{\tilde{g}}u} \right] \nonumber \\&-\,r_{n1}^T P^{l_1 }(L+B)\left[ {w^{l_1 }+\varepsilon ^{l_1 }-{\underline{1}}^{l_1 }x_{v,0} } \right] \nonumber \\&-\,r_{n2}^T P^{l_2 }(L+B)\left[ {w^{l_2 }+\varepsilon ^{l_2 }-{\underline{1}}^{l_2 }f_0 } \right] \nonumber \\&+\,r_{n2}^T P^{l_2 }A\left( {D+B} \right) ^{-1}\Lambda e_v \nonumber \\= & {} -r^\mathrm{T}P(D+B){\tilde{W}}^\mathrm{T}\phi +r^\mathrm{T}PA{\tilde{W}}^\mathrm{T}\phi \nonumber \\&-\,r^\mathrm{T}P(L+B)cr-r^\mathrm{T}P(D+B){\tilde{g}}u \nonumber \\&+r^\mathrm{T}PA{\tilde{g}}u \nonumber \\&-\,r_{n1}^T P^{l_1 }(L+B)\left[ {w^{l_1 }+\varepsilon ^{l_1 }-{\underline{1}}^{l_1 }x_{v,0} } \right] \nonumber \\&-\,r_{n2}^T P^{l_2 }(L+B)\left[ {w^{l_2 }+\varepsilon ^{l_2 }-{\underline{1}}^{l_2 }f_0 } \right] \nonumber \\&+\,r_{n2}^T P^{l_2 }A\left( {D+B} \right) ^{-1}\Lambda e_v \end{aligned}$$

(28)

Considering the fact that $x^\mathrm{T}y=\mathrm{tr}\left\{ {yx^\mathrm{T}} \right\}$, we have

$$\begin{aligned} {\dot{V}}_r= & {} -\mathrm{tr}\left\{ {{\tilde{W}}^\mathrm{T}\phi r^\mathrm{T}P(D+B)} \right\} \nonumber \\&+\,r^\mathrm{T}PA{\tilde{W}}^\mathrm{T}\phi -r^\mathrm{T}P(L+B)cr \nonumber \\&-\,\mathrm{tr}\left\{ {{\tilde{g}}^\mathrm{T}ur^{T}P(D+B)} \right\} +r^\mathrm{T}PA{\tilde{g}}u\nonumber \\&-\,r_{n1}^T P^{l_1 }(L+B)\left[ {w^{l_1 }+\varepsilon ^{l_1 }-{\underline{1}}^{l_1 }x_{v,0} } \right] \nonumber \\&-\,r_{n2}^T P^{l_2 }(L+B)\left[ {w^{l_2 }+\varepsilon ^{l_2 }-{\underline{1}}^{l_2 }f_0 } \right] \nonumber \\&+\,r_{n2}^T P^{l_2 }A\left( {D+B} \right) ^{-1}\Lambda e_v \end{aligned}$$

(29)

Differentiating $V_W$, $V_g$ and $V_e$, we have

$$\begin{aligned} {\dot{V}}_W +{\dot{V}}_g +{\dot{V}}_e= & {} \mathrm{tr}\left\{ {{\tilde{W}}^\mathrm{T}F^{-1}\dot{{\tilde{W}}}} \right\} \nonumber \\&+\,\mathrm{tr}\left\{ {{\tilde{g}}^\mathrm{T}\eta ^{-1}\dot{{\tilde{g}}}} \right\} +\left( {e_p^{l_2 } } \right) ^\mathrm{T}e_v \nonumber \\= & {} -\,\mathrm{tr}\left\{ {{\tilde{W}}^\mathrm{T}F^{-1}\dot{\hat{{W}}}} \right\} -tr\left\{ {{\tilde{g}}^\mathrm{T}\eta ^{-1}\dot{\hat{{g}}}} \right\} \nonumber \\&+\,\left( {e_p^{l_2 } } \right) ^\mathrm{T}e_v \end{aligned}$$

(30)

Combining (29) and (30), we have

$$\begin{aligned} {\dot{V}}= & {} {\dot{V}}_r +{\dot{V}}_W +{\dot{V}}_g +{\dot{V}}_e \nonumber \\= & {} -\mathrm{tr}\left\{ {{\tilde{W}}^\mathrm{T}\phi r^\mathrm{T}P(D+B)} \right\} \nonumber \\&+\,r^\mathrm{T}PA{\tilde{W}}^\mathrm{T}\phi -r^\mathrm{T}P(L+B)cr \nonumber \\&-\,\mathrm{tr}\left\{ {{\tilde{g}}^\mathrm{T}ur^{T}P(D+B)} \right\} +r^\mathrm{T}PA{\tilde{g}}u\nonumber \\&-\,r_{n1}^T P^{l_1 }(L+B)\left[ {w^{l_1 }+\varepsilon ^{l_1 }-{\underline{1}}^{l_1 }x_{v,0} } \right] \nonumber \\&-\,r_{n2}^T P^{l_2 }(L+B)\left[ {w^{l_2 }+\varepsilon ^{l_2 }-{\underline{1}}^{l_2 }f_0 } \right] \nonumber \\&+\,r_{n2}^T P^{l_2 }A\left( {D+B} \right) ^{-1}\Lambda e_v \nonumber \\&-\,\mathrm{tr}\left\{ {{\tilde{W}}^\mathrm{T}F^{-1}\dot{\hat{{W}}}} \right\} -tr\left\{ {{\tilde{g}}^\mathrm{T}\eta ^{-1}\dot{\hat{{g}}}} \right\} +\left( {e_p^{l_2 } } \right) ^\mathrm{T}e_v \nonumber \\= & {} -\mathrm{tr}\left\{ {{\tilde{W}}^\mathrm{T}\left[ {F^{-1}\dot{\hat{{W}}}+\phi r^\mathrm{T}P(D+B)} \right] } \right\} \nonumber \\&+\,r^\mathrm{T}PA{\tilde{W}}^\mathrm{T}\phi -r^\mathrm{T}P(L+B)cr \nonumber \\&-\,\mathrm{tr}\left\{ {{\tilde{g}}^\mathrm{T}\left[ {\eta ^{-1}\dot{\hat{{g}}}+ur^\mathrm{T}P(D+B)} \right] } \right\} \nonumber \\&+\,r^\mathrm{T}PA{\tilde{g}}u-r_{n1}^T P^{l_1 }(L+B)\left[ {w^{l_1 }+\varepsilon ^{l_1 }-{\underline{1}}^{l_1 }x_{v,0} } \right] \nonumber \\&-\,r_{n2}^T P^{l_2 }(L+B)\left[ {w^{l_2 }+\varepsilon ^{l_2 }-{\underline{1}}^{l_2 }f_0 } \right] \nonumber \\&+\,r_{n2}^T P^{l_2 }A\left( {D+B} \right) ^{-1}\Lambda e_v +\left( {e_p^{l_2 } } \right) ^\mathrm{T}e_v \end{aligned}$$

(31)

The error ${\tilde{g}}_i =g_i -{\underline{g}}_i \ge 0$ if $\hat{{g}}_i ={\underline{g}}_i$. Then, substituting (24) and (25) into (31), we have

$$\begin{aligned} {\dot{V}}= & {} \mathrm{tr}\left\{ {{\tilde{W}}^\mathrm{T}\kappa \hat{{W}}} \right\} +r^\mathrm{T}PA{\tilde{W}}^\mathrm{T}\phi -r^\mathrm{T}P(L+B)cr \nonumber \\&+\,r^\mathrm{T}PA{\tilde{g}}u-r_{n1}^T P^{l_1 }(L+B)\left[ {w^{l_1 }+\varepsilon ^{l_1 }-{\underline{1}}^{l_1 }x_{v,0} } \right] \nonumber \\&-\,r_{n2}^T P^{l_2 }(L+B)\left[ {w^{l_2 }+\varepsilon ^{l_2 }-{\underline{1}}^{l_2 }f_0 } \right] \nonumber \\&+\,r_{n2}^T P^{l_2 }A\left( {D+B} \right) ^{-1}\Lambda e_v +\left( {e_p^{l_2 } } \right) ^\mathrm{T}e_v \nonumber \\&+\,\mathrm{tr}\left\{ {{\tilde{g}}^\mathrm{T}\theta \hat{{g}}} \right\} \nonumber \\&-\left\{ {\begin{array}{ll} 0,&{}\quad \hbox {if }\hat{{g}}_i >{\underline{g}}_i \\ 0,&{}\quad \hbox {if }\hat{{g}}_i ={\underline{g}}_i \hbox { and }u_i r_i p_i (d_i +b_i )<0 \\ \mathrm{tr}\left\{ {\hbox {diag}\left\{ {{\tilde{g}}_i u_i r_i p_i (d_i +b_i )} \right\} } \right\} ,&{}\hbox { if }\hat{{g}}_i ={\underline{g}}_i \hbox { and }u_i r_i p_i (d_i +b_i )\ge 0 \\ \end{array}} \right. \nonumber \\\le & {} \mathrm{tr}\left\{ {{\tilde{W}}^\mathrm{T}\kappa \hat{{W}}} \right\} \nonumber \\&+\,r^\mathrm{T}PA{\tilde{W}}^\mathrm{T}\phi -r^\mathrm{T}P(L+B)cr \nonumber \\&+\,\mathrm{tr}\left\{ {{\tilde{g}}^\mathrm{T}\theta \hat{{g}}} \right\} +r^\mathrm{T}PA{\tilde{g}}u\nonumber \\&-\,r_{n1}^T P^{l_1 }(L+B)\left[ {w^{l_1 }+\varepsilon ^{l_1 }-{\underline{1}}^{l_1 }x_{v,0} } \right] \nonumber \\&-\,r_{n2}^T P^{l_2 }(L+B)\left[ {w^{l_2 }+\varepsilon ^{l_2 }-{\underline{1}}^{l_2 }f_0 } \right] \nonumber \\&+\,r_{n2}^T P^{l_2 }A\left( {D+B} \right) ^{-1}\Lambda e_v +\left( {e_p^{l_2 } } \right) ^\mathrm{T}e_v \ \end{aligned}$$

(32)

Then, according to Lemma 2, we have

$$\begin{aligned} {\dot{V}}\le & {} -\frac{1}{2}cr^\mathrm{T}Qr+\mathrm{tr}\left\{ {{\tilde{W}}^\mathrm{T}\kappa (W-{\tilde{W}})} \right\} \nonumber \\&+\,r^\mathrm{T}PA{\tilde{W}}^\mathrm{T}\phi +\mathrm{tr}\left\{ {{\tilde{g}}^\mathrm{T}\theta (g-{\tilde{g}})} \right\} +r^\mathrm{T}PA{\tilde{g}}u \nonumber \\&-\,r_{n1}^T P^{l_1 }(L+B)\left[ {w^{l_1 }+\varepsilon ^{l_1 }-{\underline{1}}^{l_1 }x_{v,0} } \right] \nonumber \\&-\,r_{n2}^T P^{l_2 }(L+B)\left[ {w^{l_2 }+\varepsilon ^{l_2 }-{\underline{1}}^{l_2 }f_0 } \right] \nonumber \\&+\,\left[ {\left( {e_p^{l_2 } } \right) ^\mathrm{T}+r_{n2}^T P^{l_2 }A\left( {D+B} \right) ^{-1}\Lambda } \right] \nonumber \\&\left( {r_{n2} -\Lambda e_p^{l_2 } } \right) \end{aligned}$$

(33)

Taking norm on (33), we have

$$\begin{aligned} {\dot{V}}\le & {} -\frac{1}{2}c{\underline{\sigma } }\left( Q \right) \left\| r \right\| ^{2}+\kappa W_M \left\| {{\tilde{W}}} \right\| _F -\kappa \left\| {{\tilde{W}}} \right\| _F^2 \nonumber \\&+\,\phi _M \bar{{\sigma }}\left( P \right) \bar{{\sigma }}\left( A \right) \left\| r \right\| \left\| {{\tilde{W}}} \right\| _F \nonumber \\&+\,\theta g_M \left\| {{\tilde{g}}} \right\| _F -\theta \left\| {{\tilde{g}}} \right\| _F^2 +u_M \bar{{\sigma }}\left( P \right) \bar{{\sigma }}\left( A \right) \left\| r \right\| \left\| {{\tilde{g}}} \right\| _F \nonumber \\&+\,\bar{{\sigma }}\left( P \right) \bar{{\sigma }}(L+B)B_M \left\| r \right\| -{\underline{\sigma } }\left( \Lambda \right) \left\| {e_p^{l_2 } } \right\| ^{2} \nonumber \\&+\,\frac{\bar{{\sigma }}\left( \Lambda \right) \bar{{\sigma }}\left( {P^{l_2 }} \right) \bar{{\sigma }}\left( A \right) }{{\underline{\sigma } }\left( {D+B} \right) }\left\| r \right\| ^{2}\nonumber \\&+\,\left[ {1+\frac{\bar{{\sigma }}\left( {\Lambda ^{2}} \right) \bar{{\sigma }}\left( {P^{l_2 }} \right) \bar{{\sigma }}\left( A \right) }{{\underline{\sigma } }\left( {D+B} \right) }} \right] \left\| {e_p^{l_2 } } \right\| \left\| r \right\| \end{aligned}$$

(34)

where $B_M =\varepsilon _M +w_M +f_M +x_{0M}$.

Write (34) as

$$\begin{aligned} {\dot{V}}\le -z^\mathrm{T}Sz+K^\mathrm{T}z=-V_z (z) \end{aligned}$$

(35)

where $z=\left[ {{\begin{array}{llll} {\left\| r \right\| }&{}\quad {\left\| {{\tilde{W}}} \right\| _F }&{}\quad {\left\| {e_p^{l_2 } } \right\| }&{}\quad {\left\| {{\tilde{g}}} \right\| _F } \\ \end{array} }} \right] ^\mathrm{T}$, $K=\left[ {{\begin{array}{llll} {\bar{{\sigma }}\left( P \right) \bar{{\sigma }}(L+B)B_M }&{}\quad {\kappa W_M }&{}\quad 0&{}\quad {\theta g_M } \\ \end{array} }} \right] ^\mathrm{T}$,

$$\begin{aligned} S=\left[ {{\begin{array}{llll} {\frac{1}{2}c{\underline{\sigma } }\left( Q \right) -\psi }&{} \varsigma &{} \vartheta &{} \chi \\ \varsigma &{} \kappa &{} 0&{} 0 \\ \vartheta &{} 0&{} {{\underline{\sigma } }\left( \Lambda \right) }&{} 0 \\ \chi &{} 0&{} 0&{} \theta \\ \end{array} }} \right] . \end{aligned}$$

Then, $V_z (z)$ is positive definite if $S>0$ and $\left\| z \right\| >\frac{\left\| K \right\| }{{\underline{\sigma } }(S)}$.

With Sylvester’s criterion, $S>0$ if

$$\begin{aligned}&\frac{1}{2}c{\underline{\sigma } }\left( Q \right) -\psi>0 \nonumber \\&\quad \kappa \left( {\frac{1}{2}c{\sigma }\left( Q \right) -\psi } \right) -\varsigma ^{2}>0 \nonumber \\&\quad {\underline{\sigma } }\left( \Lambda \right) \left[ {\kappa \left( {\frac{1}{2}c{\underline{\sigma } }\left( Q \right) -\psi } \right) -\varsigma ^{2}} \right] -\kappa \vartheta ^{2}>0 \nonumber \\&\quad \theta \left\{ {{\underline{\sigma } }\left( \Lambda \right) \left[ {\kappa \left( {\frac{1}{2}c{\underline{\sigma } }\left( Q \right) -\psi } \right) -\varsigma ^{2}} \right] -\kappa \vartheta ^{2}} \right\} \nonumber \\&\qquad -\kappa \chi ^{2}{\underline{\sigma } }\left( \Lambda \right) >0 \end{aligned}$$

(36)

Solve the above inequalities, we can get the condition (22).

Define $B_d$ as

$$\begin{aligned} B_d =\frac{\left\| K \right\| _1 }{{\underline{\sigma } }(S)}=\frac{B_M \bar{{\sigma }}(P)\bar{{\sigma }}(L+B)+\kappa W_M +\theta g_M }{{\underline{\sigma } }(S)} \nonumber \\ \end{aligned}$$

(37)

Then, if $z\ge B_d$, $\left\| z \right\|>\frac{\left\| K \right\| _1 }{{\underline{\sigma }}(S)}>\frac{\left\| K \right\| }{{\underline{\sigma }}(S)}$ holds. Under condition (22), we have ${\dot{V}}\le -V_z (z)$ with $V_z (z)$ being positive definite.

By [3], we have

$$\begin{aligned} {\underline{\sigma }}(\Gamma )\left\| z \right\| ^{2}\le V\le \bar{{\sigma }}(\varphi )\left\| z \right\| ^{2} \end{aligned}$$

(38)

where $\Gamma =\hbox {diag}\left( {\frac{{\underline{\sigma } }(P)}{2},\hbox { }\frac{1}{2\bar{{\sigma }}(F)},\frac{1}{2}\hbox { },\frac{1}{2\bar{{\sigma }}(\eta )}} \right)$ and $\varphi =\hbox {diag}\left( {\frac{\bar{{\sigma }}(P)}{2},\hbox { }\frac{1}{2{\sigma }(F)},\frac{1}{2},\hbox { }\frac{1}{2{\sigma }(\eta )}} \right)$.

According to Theorem 4.18 in [30], we can conclude that for any $z(t_0 )$ there exists a $T_0$ such that

$$\begin{aligned} \left\| {z(t)} \right\| \le \sqrt{\frac{\bar{{\sigma }}(\varphi )}{{\underline{\sigma } }(\Gamma )}}B_d ,\forall t\ge t_0 +T_0 \end{aligned}$$

(39)

Define $d=\min _{\left\| z \right\| \ge B_d } V_z (z)$, then according to [30]

$$\begin{aligned} T_0 =\frac{V(t_0 )-\bar{{\underline{\sigma } }}(\phi )B_d^2 }{d} \end{aligned}$$

(40)

With z, (39) implies that the synchronization error r is ultimately bounded. Then, according to Lemma 1, $\delta _p$ and $\delta _v$ are CUUB and all nodes in ${{\mathcal {G}}}$ achieve the synchronization to the leader.

For part (2) of Theorem 1, the state $x_{p,i} ,i\in N$ and$_{ }x_{v,i} ,i\in l_2$ are bounded $\forall t\ge t_0$. From (35), we have

$$\begin{aligned} {\dot{V}}\le -{\sigma }(S)\left\| z \right\| ^{2}+\left\| K \right\| \left\| z \right\| \end{aligned}$$

(41)

According to (38) and (41), we have

$$\begin{aligned} \frac{d}{dt}(\sqrt{V})\le -\frac{{\underline{\sigma } }(S)}{2\bar{{\sigma }}(\varphi )}\sqrt{V}+\frac{\left\| K \right\| }{2\sqrt{{\underline{\sigma } }(\Gamma )}} \end{aligned}$$

(42)

Then, we can conclude that V(t) is bounded for $t\ge t_0$ under Corollary 1.1 in [31]. Since (27) implies $\left\| r \right\| ^{2}\le \frac{2V(t)}{{\underline{\sigma } }(P)}$, r(t) is bounded. And, $x_0$ is bounded by $x_{0M}$ in Assumption 1. $x_{p,i} \hbox { },i\in N$ and$_{ }x_{v,i} ,i\in l_2$ are bounded $\forall t\ge t_0$. The proof is done. $\square$