1 Introduction

Rogue wave (RW), also called freak wave, monster wave or killer wave, is one kind of common nonlinear local waves, which receives significant attention recently. The RW is usually used to describe colossal spontaneous ocean waves, which lead to the generation of water walls taller than 20–30 m so that the RW is even a threaten to a big ship [1,2,3]. Researches on RW have been boosted and confirmed experimentally by several laboratory observations in nonlinear fiber [4, 5], water tank [6], plasma, super fluid, capillary flow, Bose–Einstein condensate and atmosphere [7,8,9,10,11].

Theoretically, the RW solution is an ubiquitous phenomenon in nonlinear integrable system. The RW model was first derived from a solution of the famous nonlinear Schrödinger equation (NLSE)

$$\begin{aligned} \mathbf{i}q_t+q_{xx}+2|q|^2q=0, \end{aligned}$$

in 1983 [12], and have a rational form

$$\begin{aligned} q=\left[ 1-\dfrac{4(1+4\mathbf{i}t)}{1+4x^2+16t^2}\right] \mathrm{e}^{2\mathbf{i}t}. \end{aligned}$$

Generally, the RW is generated from a nonzero boundary condition when the period of breather solution goes to infinity [13]. Like soliton solutions, the higher-order RWs are constructed to illustrate the collisions of multiple RWs [14,15,16], which display many interesting patterns. In addition to the NLSE, there are numerous nonlinear equations admitting RW and higher-order RWs such as derivative-type NLSE [17,18,19,20,21], the Hirota equation [22, 23] and so on.

In the real world, the oceanic and ultra-short optical RWs are evident \((2+1)\)-dimensional phenomena [24,25,26], so extensions of RW to higher spatiotemporal dimension are inevitable. In this work, we will consider a new \((2+1)\)-dimensional nonlinear evolution equation, namely the Kadomtsev–Petviashvili (KP)-based system, which is an extension of the well-known KP equation [27].

The KP equation, an integrable \((2+1)\)-dimensional extension of the famous Korteweg–de Vries (KdV) equation, has the form

$$\begin{aligned} {u_{xt}+u_{xxxx}+su_{yy}-3(u^2)_{xx}=0,\quad s=\pm \,1,} \end{aligned}$$
(1.1)

and it plays an important role in nonlinear wave theory. The KdV equation describes the evolution of strictly one-dimensional long water waves of small amplitude, while the KP equation describes the evolution of weakly two-dimensional long water waves of small amplitude. This means that the KP equation plays the same role in \((2+1)\) dimensions that the KdV equation plays in \((1+1)\) dimensions. The KP equation is one of the classical prototype problems in the field of exactly solvable equations and arises generically in physical contexts, such as the plasma physics and surface water waves.

The KP equation allows the formation of stable soliton and rational localized solution pertinent to systems involving quadratic nonlinearity, weak dispersion, and slow transverse variation [28]. Up to now, this equation has been well applied in a wide class of physical areas, including the ion-acoustic wave in plasma [29] and the 2-D shallow water wave [30], nonlinear optics, Bose–Einstein condensate, string theory [31,32,33]. The RW solution of the KP equation is derived in [34, 35]. However, unlike the \((1+1)\)-dimensional equations, the KP equation admits another rational solution–lump solution when \(s=-1\) [36, 37].

In [27], Maccari introduces the following transformations to the KP equation (1.1)

$$\begin{aligned} \begin{aligned}&\xi =\epsilon ^{p_1}(x-V_1t),\,\eta =\epsilon ^{p_2}(y-V_2t),\\&\tau =\epsilon ^{q}t,\,p_1,p_2,q>0,\\&u(x,y,t)=\sum \limits _{n=-\infty }^{+\infty }\epsilon ^{\gamma _n}\Psi _n(\xi ,\eta ,\tau ;\epsilon )\\&\qquad \times \exp \{\mathbf{i}n(K_1x+K_2y-\omega t)\},\\&\Psi _{-n}(\xi ,\eta ,\tau ,\epsilon )=\Psi _n^*(\xi ,\eta ,\tau ,\epsilon ),\,\gamma _{n}=|n|,\\&\qquad \qquad \qquad \qquad \qquad n=\pm 1, \pm 2, \cdots , \end{aligned} \end{aligned}$$
(1.2)

where

$$\begin{aligned}&V_1=V(K_1,K_2)=-3K_1^2-s\frac{K_2^2}{K_1^2},V_2=V(K_1,K_2)=2s\frac{K_2}{K_1}, \end{aligned}$$

mean components of the group velocity \(V=(V_1,V_2)\) of the linear dispersive part of the KP equation (1.1), and \(\gamma _0=1+r\) is a real number to be determined. For convenience, through taking further ansatz

$$\begin{aligned}&\xi \rightarrow x,\,\eta \rightarrow y,\,\tau \rightarrow t,\\&\Psi _{1}(\xi ,\eta ,\tau ;\epsilon \rightarrow 0)=u(x,y,t),\\&\Psi _{0}(\xi ,\eta ,\tau ;\epsilon \rightarrow 0)=v(x,y,t), \end{aligned}$$

a new \((2 + 1)\)-dimensional complex nonlinear evolution equation is obtained as follows:

$$\begin{aligned} \begin{aligned}&\mathbf{i}u_{t}+ u_{xx}+uv=0,\\&v_{t}+v_y+(|u|^2)_x=0, \end{aligned} \end{aligned}$$
(1.3)

which is just the integrable KP-based system. (The parameters x, y, t are just \(\xi ,\eta ,\tau \) in [27], and \(u,\,v\) mean \(\Psi _1,\,\Psi _0\) in [27], respectively.) The Lax pair of these equations were first constructed in [27], the Painlevé property was investigated in [38], the doubly periodic solutions were constructed in [39] by utilizing the extended Jacobian elliptic function expansion method, and its N-soliton solutions were derived in [40] with the help of the Hirota method. Besides, several other solutions had been derived by applying different methods, such as rational solutions and traveling wave solutions [41,42,43,44]. In particular, an integrable semi-discrete analog of the KP-based system was investigated in [40]. In this work, we will present the nonsingular rational and semi-rational solutions of KP-based system by utilizing the bilinear method. The rational solutions consist of lumps and line rogue waves; the semi-rational solutions describe interactions between line rogue waves, lumps, dark solitons, and breathers.

The outline of this paper is organized as follows: In Sect. 2, the formulae of N-th order rational solutions of the KP-based system are derived by employing the bilinear method and a long-wave limit. In Sect. 3, typical dynamics of lump and RW solutions of the KP-based system are demonstrated vividly. In Sect. 4, three types of semi-rational solutions are investigated in detail. The summary and discussion are given in Sect. 5.

2 Rational solution of the Kadomtsev–Petviashvili-based system

In this section, we derive explicit formulae of rational solutions of the KP-based system. Through using the dependent variable transformations

$$\begin{aligned} \begin{aligned} u=\rho \mathrm{e}^{\mathbf{i}(kx+(\epsilon -k^2)t)}\frac{g}{f},\,v=\epsilon +2( \mathrm{log} f)_{xx}, \end{aligned} \end{aligned}$$
(2.1)

Equation (1.3) can be transformed into the following bilinear forms:

$$\begin{aligned} \begin{aligned}&(D_{x}^2+2\mathbf{i}k D_x+\mathbf{i}D_{t}) g \cdot f =0\,,\\&D_x(D_t+D_y)f \cdot f=\rho ^{2}(f^2-gg^{*}). \end{aligned} \end{aligned}$$
(2.2)

Here, f is a real function, g is a complex function, \(\rho ,\,k,\,\epsilon \) are real parameters, the asterisk means complex conjugation, and the operator D is the Hirota’s bilinear differential operator [45] defined by

$$\begin{aligned} \begin{aligned}&P(D_{x},D_{y},D_{t}, )F(x,y,t\cdot \cdot \cdot )\cdot G(x,y,t,\cdot \cdot \cdot )\\&\quad =P(\partial _{x}-\partial _{x^{'}},\partial _{y}-\partial _{y^{'}}, \partial _{t}-\partial _{t^{'}},\cdot \cdot \cdot )\\&\quad \times F(x,y,t,\cdot \cdot \cdot )G(x^{'},y^{'},t^{'},\cdot \cdot \cdot )|_{x^{'}=x,y^{'}=y,t^{'}=t}, \end{aligned} \end{aligned}$$

where P is a polynomial of \(D_{x}\), \(D_{y}\), \(D_{t}\).

To obtain N-th order soliton solutions by the Hirota’s bilinear method and the perturbation expansion [45], one needs to expand f and g in terms of power series of a small parameter \(\epsilon \):

$$\begin{aligned} \begin{aligned} f=1+\epsilon f_1+ \epsilon ^2 f_2+ \epsilon ^3 f_3+\cdots ,\\ g=1+\epsilon g_1+ \epsilon ^2 g_2+ \epsilon ^3 g_3+\cdots . \end{aligned} \end{aligned}$$
(2.3)

Substituting functions f and g into bilinear equations (2.2) yields a series of equations corresponding to different orders of \(\epsilon \). After solving these equations, functions f and g are expressed as

$$\begin{aligned} \begin{aligned} f=&\sum _{\mu =0,1}\exp \left( \sum _{j<s}^{(N)}\mu _{j}\mu _{k}A_{jk}+\sum _{j=1}^{N}\mu _{j}\eta _{j}\right) ,\\ g=&\sum _{\mu =0,1}\exp \left( \sum _{j<s}^{(N)}\mu _{j}\mu _{k}A_{jk}+\sum _{j=1}^{N}\mu _{j}(\eta _{j}+\mathbf{i}\phi _{j})\right) , \end{aligned} \end{aligned}$$
(2.4)

where

$$\begin{aligned}&\eta _{j}=P_{j}\,x+Q_{j}\,y+\Omega _{j}t+\eta _{j}^{0}\,,\\&Q_{j}=-\frac{\Omega _{j}P_{j}^{4}+\Omega _{j}(2P_{j}k+\Omega _{j})^2-2\rho ^2 P_{j}^{3}}{P_{j}^4+(2P_{j}k+\Omega _{j})^2}\,,\\&\exp (A_{js})=\frac{P_{j}^{2}P_{s}^{2}(P_{j}-P_{s})^2+(\Omega _{j}P_s-\Omega _{s}P_{j})^2}{P_{j}^{2}P_{s}^{2}(P_{j}+P_{s})^2+(\Omega _{j}P_s-\Omega _{s}P_{j})^2}\,,\\&\sin (\phi _{j})=\frac{2P_{j}^2(2P_{j}k+\Omega _{j})}{P_{j}^{4}+(2P_{j}k+\Omega _{j})^2},\\&\cos (\phi _{j})=\frac{-P_{j}^4+(2P_{j}k+\Omega _{j})^2}{P_{j}^{4}+(2P_{j}k+\Omega _{j})^2}, \end{aligned}$$

\(P_{j}\,,\Omega _{j}\,,\eta ^0_j\) are arbitrary real parameters, the notation \(\sum _{\mu =0}\) indicates summation over all possible combinations of \(\mu _{1}=0,1\,,\mu _{2}=0,1\,,...,\mu _{N}=0,1\), and the \(\sum _{j<s}^{(N)}\) summation over all possible combinations of the N elements with the specific condition \(j<s\).

Similar to earlier works in the literatures [46,47,48,49,50,51,52,53,54], general n-breather solutions of the KP-based system can be generated by taking the following constraints in (2.4)

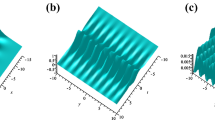
$$\begin{aligned} \begin{aligned} N=2n,\,P_{n+j}=P^*_{j},\,\Omega _{n+j}=\Omega ^*_{j},\,\eta _{n+j}^{0}=\eta _{j}^{0^{*}}. \end{aligned} \end{aligned}$$
(2.5)

For example, let \(N=2\) and

$$\begin{aligned}&P_{2}=P^*_{1}=k_{1}-\mathbf{i}k_{2}\,,\Omega _{2}=\Omega ^*_{1}=q_{1}-\mathbf{i}q_{2}\,,\nonumber \\&\quad \eta _{2}^{0}=\eta _{1}^{0^{*}}=0, \end{aligned}$$
(2.6)

then the first-order breather solution can be obtained, and its three types are shown in Fig. 1. Besides, mixed solution consisting of breather and soliton can also be derived by taking parameters in (2.4) as

$$\begin{aligned}&P_{n+j}=P^*_{j}\,,\Omega _{n+j}=\Omega ^*_{j}\,,\eta _{n+j}^{0}=\eta _{j}^{0^{*}}, P_{s}=P^*_{s},\nonumber \\&\Omega _{s}=\Omega ^*_{s} (2n<N,2n+1\le s\le N). \end{aligned}$$
(2.7)

This mixed solution describes collision of dark soliton and breather, which leads to several interesting dynamics in physical system. Particularly, the mixed solution has many intriguing dynamical behaviors, which are important in forming different wave structures such as lump soliton, rogue wave, and so on. To demonstrate this kind of mixed solution in detail, we consider the case of \(N=3\) and choose

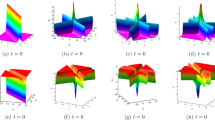
$$\begin{aligned} \begin{aligned}&P_{2}=P^*_{1}=k^{'}_{1}-\mathbf{i}k^{'}_{2},\,\Omega _{2}=\Omega ^*_{1}=q^{'}_{1}-\mathbf{i}q^{'}_{2},\\&\quad \eta _{2}^{0}=\eta _{1}^{0^{*}}=0,P_3=k^{'}_3,\,\Omega _{3}=q^{'}_{3}, \end{aligned} \end{aligned}$$
(2.8)

where \(k^{'}_{1},k^{'}_{2},k^{'}_{3},q^{'}_{1},q^{'}_{2},q^{'}_{3}\) are arbitrary real constants. Three types of interesting wave structures are shown in Fig. 2.

Fig. 1
figure 1

(Color online) Three types of first-order breather solutions of the KP-based system with parameters \(\rho =1,\epsilon =0,k=0\) at time \(t=0\). a\((k_1,k_2)=(0,1),\, (q_1,q_2)=(1,0)\). b\((k_1,k_2)=(0,1), \,(q_1,q_2)=(2,2)\). c\((k_1,k_2)=(0,\frac{2}{3}), \, (q_1,q_2)=(1,3)\)

Full size image
Fig. 2
figure 2

(Color online) Three types of mixed solutions of the KP-based system with parameters \(\rho =1,\epsilon =0,k=0,\eta _3^{0}=0\) at time \(t=0\). a\((k^{'}_1,k^{'}_2,k^{'}_{3})=(0,1,1),\, (q^{'}_1,q^{'}_2,q^{'}_{3})=(1,0,1)\). b\((k^{'}_1,k^{'}_2,k^{'}_{3})=(1,\frac{1}{2},\frac{1}{10}),\, (q^{'}_1,q^{'}_2,q^{'}_{3})=(\frac{1}{2},1,\frac{1}{20000})\). c\((k^{'}_1,k^{'}_2,k^{'}_{3})=(1,\frac{1}{2},1),\)\((q^{'}_1,q^{'}_2,q^{'}_{3})=(\frac{1}{3},\frac{1}{3},1)\)

Full size image

Now we will generate rational solution of the KP-based system by taking a long-wave limit of f and g in (2.4). In order to eliminate the exponential functions in (2.4), we set

$$\begin{aligned} \Omega _{j}=\lambda _{j}P_{j},\,\eta _{j}^{0}=\mathbf{i}\,\pi \quad (1\le j\le N). \end{aligned}$$
(2.9)

In this case, taking \(P_{i} \rightarrow 0\) in (2.4) implies that \(Q_j \) and \(\Omega _j\) also go to zero. By applying L’Hospital’s rule, the formulae of rational solutions of the KP-based system are obtained.

Theorem 1

The KP-based system has rational solutions defined by (2.1) with f and g given by

$$\begin{aligned} f=&\prod _{j=1}^{N}\theta _{j}+\frac{1}{2}\sum _{j,k}^{(N)}a_{jk}\prod _{l\ne j,k}^{N}\theta _{l}+\cdots \nonumber \\&+\frac{1}{M!2^{M}}\sum _{j,s,...,m,n}^{(N)}\overbrace{a_{js}a_{jr}\cdots a_{mn}}^{M}\nonumber \\&\times \prod _{p\ne j,s,...m,n}^{N}\theta _{p}+\cdots ,\nonumber \\ g=&\prod _{j=1}^{N}(\theta _{j}+\beta _{j})+\frac{1}{2}\sum _{j,s}^{(N)}a_{js}\prod _{l\ne j,s}^{N}(\theta _{l}+\beta _{l}) +\cdots \nonumber \\&+\frac{1}{M!2^{M}}\sum _{j,s,...,m,n}^{(N)}\overbrace{a_{js}a_{jr}\cdots a_{mn}}^{M}\nonumber \\&\times \prod _{p\ne j,s,...m,n}^{N}(\theta _{p}+\beta _{p})+\cdots , \end{aligned}$$
(2.10)

where

$$\begin{aligned} \theta _{j}= & {} x+\left[ -\lambda _{j}+\frac{2\rho ^2}{(2k+\lambda _{j})^2}\right] y + \lambda _{j} t\,, \beta _{j}=\frac{2\mathbf{i}}{2k+\lambda _{j}},\\ a_{js}= & {} -\frac{4}{(\lambda _{j}-\lambda _{s})^2}\,, \end{aligned}$$

\(\lambda _{j}\) is an arbitrary complex constant, and \(k\,,\rho \) are real constants.

Remark 1

The proof for Theorem 1 can be found in [48]. By applying the similar method in [37], we can prove that the rational solutions given by Theorem 1 are nonsingular when \(N=2n,\,\lambda _{j+n}=\lambda _j^*\).

3 Dynamics of rational solutions

This section focuses on the typical dynamics of rational solutions of the KP-based system generated by Theorem 1.

Let \(N=2, \, \lambda _{1}=a+\mathbf{i}b, \,\lambda _2=a-\mathbf{i}b\) in (2.10), then functions f and g can be rewritten as

$$\begin{aligned} \begin{aligned} f=&\theta _{1}\theta _{1}^{*}+a_{12},\\ g=&(\theta _{1}+\delta _1+\mathbf{i}\delta _2)(\theta ^*_{1}-\delta _1+\mathbf{i}\delta _2)+a_{12}, \end{aligned} \end{aligned}$$
(3.1)

where

$$\begin{aligned}&\theta _1=l_1+\mathbf{i}l_2,\nonumber \\&l_{1}=x+\left\{ 2\rho ^2\dfrac{(2k+a)^2-b^2}{[(2k+a)^2+b^2]^2}-a\right\} y+at,\nonumber \\&l_{2}=-\left\{ b+\dfrac{4\rho ^2 b(a+2k)}{[(2k+a)^2+b^2]^2}\right\} y+bt,\nonumber \\&\delta _{1}=\dfrac{2b}{(a+2k)^2+b^2},\,\delta _{2}=\dfrac{2(a+2k)}{(a+2k)^2+b^2},\nonumber \\&a_{12}=\dfrac{1}{b^2}\quad (b\ne 0). \end{aligned}$$
(3.2)

According to (2.1), a rational solution can be constructed as

$$\begin{aligned} \begin{aligned} u=&\rho e^{\mathbf{i}(kx+(\epsilon -k^2)t)}\left[ 1-\dfrac{2\mathbf{i}(\delta _{1}l_{2}-\delta _{2}l_{1})+\delta _{1}^2+\delta _{2}^2}{l_1^{2}+l_{2}^2+a_{12}}\right] ,\\ v=&\epsilon +4\dfrac{l_{2}^2-l_{1}^2+a_{12}}{(l_1^2+l_2^2+a_{12})^2}, \end{aligned} \end{aligned}$$
(3.3)

where \(a,\,b,\,k,\,\epsilon ,\,\rho \) are arbitrary real constants. Obviously, solutions u and v are regular.

For convenience, we define

$$\begin{aligned} \Delta =b+\dfrac{4\rho ^2 b(a+2k)}{[(2k+a)^2+b^2]^2}. \end{aligned}$$
(3.4)

After simple analysis, we find that rational solution given by (3.3) has two different structures depending on whether \(\Delta \) equals to zero or not.

Fig. 3
figure 3

(Color online) The lump solution of the KP-based system given by Eq. (3.3) with parameters \(\rho =1,\epsilon =0,k=0\) at time \(t=0\). a Dark lump: \((a,b)=(1,\frac{1}{3})\). b Mixed lump: \((a,b)=(1,1)\). c Bright lump: \((a,b)=(1,3)\)

Full size image

A: Lump solution When \(\Delta \ne 0\), we find that \(u,\,v\) given by (3.3) preserve constant along the following trajectory:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}x+\left\{ 2\rho ^2\dfrac{(2k+a)^2-b^2}{[(2k+a)^2+b^2]^2}-a\right\} y+at=0, \\ &{}-\left\{ b+\dfrac{4\rho b(a+2k)}{[(2k+a)^2+b^2]^2}\right\} y+bt=0\,. \end{array}\right. \end{aligned}$$
(3.5)

On the trajectory, u(x, y, t) arrives at its amplitude. Actually, solving the above linear equations implies that the location of amplitude is related to time t, i.e., u(x, y, t) can arrive at its amplitude on this trajectory at any time. This is different from the RW in \((1+1)\)-dimensional system that only exists for a very short while. In addition, the lump solution can be classified into three classes according to the number of extreme point.

  1. 1.

    Dark lump When \(0\le (b-k)^2\le \frac{1}{3}a^2\), |u| has two global maximum points and one global minimum point, shown in Fig. 3a.

  2. 2.

    Mixed lump When \(\frac{1}{3}a^2 < (b-k)^2\le 3a^2\), |u| has two global maximum points and two global minimum points, shown in Fig. 3b.

  3. 3.

    Bright lump When \((b-k)^2> 3a^2\), |u| has two global minimum points and one global maximum point, shown in Fig. 3c.

B: Rogue wave solution When \(\Delta =0\), the rational solution given by (3.3) displays a line-style RW, which is similar to the Davey–Stewartson (DS) equation, the Fokas system, and Yajima–Oikawa systems [25, 26, 55, 56]. This line-style RW solution is different from the classic soliton, which maintains a perfect profile without any decay during its propagation. Like the RW in \((1+1)\)-dimension, the RW solution \((u,\,v)\) generated by (3.3) approaches to its amplitude from background \((\rho ,\,\epsilon )\) at certain time quickly and disappears into background extremely fast. Like the previous case of lump, the RW can be classified into three classes according to its number of extreme point.

  1. 1.

    Dark RW When \(0\le (b-k)^2\le \frac{1}{3}a^2\), |u| has two global maximum lines and one global minimum line, shown in Fig. 4.

  2. 2.

    Mixed RW When \(\frac{1}{3}a^2 < (b-k)^2\le 3a^2\), |u| has one global maximum line and one global minimum line, shown in Fig. 5.

  3. 3.

    Bright RW When \((b-k)^2> 3a^2\), |u| has two global minimum lines and one global maximum line, shown in Fig. 6.

In brief, \(\Delta \) plays an extremely important role in determining the type of the rational solution given by (3.3). When \(\Delta \ne 0\), it yields the lump solution, and the RW solution otherwise. Both the lump and RW solutions are classified into three classes related to \((a,\,b)\). To illustrate these phenomena explicitly, Fig. 7 and Table 1 are given, which present the relationships between the status of rational solution and parameters \((a,\,b)\), i.e., dark case \(0\le (b-k)^2\le \frac{1}{3}a^2\), mixed case \(\frac{1}{3}a^2 < (b-k)^2\le 3a^2\), and bright case \((b-k)^2> 3a^2\).

Fig. 4
figure 4

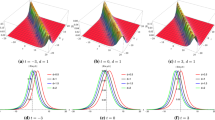
(Color online) The evolution of dark RW solution of KP-based system given by (3.3) with parameters \(\rho =3/5,\,\epsilon =0,\,k=0,\,a=-1,\,b=\sqrt{5}/5\). a\(t=-\,5\). b\(t=-\,1\). c\(t=-\,0.5\). d\(t=0\). e\(t=1\). f\(t=5\)

Full size image
Fig. 5
figure 5

(Color online) The evolution of mixed RW of KP-based system given by (3.3) with parameters \(\rho =1,\,k=0,\,\epsilon =0,\,a=-1,\,b=1\). a\(t=-\,5\). b\(t=-\,1\). c\(t=-\,0.5\). d\(t=0\). e\(t=1\). f\(t=5\)

Full size image
Fig. 6
figure 6

(Color online) The evolution of bright RW of KP-based system given by (3.3) with parameters \(\rho =9,\,k=0,\,\epsilon =0,\,a=-\,1,\,b=\sqrt{17}\). a\(t=-\,5\). b\(t=-\,1\). c\(t=-\,0.5\). d\(t=0\). e\(t=1\). f\(t=5\)

Full size image

If one sets

$$\begin{aligned} N=2n (n>1), \lambda _{n+j}^{*}=\lambda _{j}=a_{j}+\mathbf{i}b_{j}\,(2 \le j\le n), \end{aligned}$$

in (3.1), then the higher-order nonsingular rational solutions can be obtained, which describe the interactions of n individual lump or RW solutions. Similarly, introducing \(\Delta _j\)

$$\begin{aligned} \Delta _j=b_{j}+\dfrac{4\rho ^2 b_{j}(a_{j}+2k)}{(2k+a_{j})^2+b_{j}^2},\qquad j=1,2,3,\cdots ,n, \end{aligned}$$
(3.6)

we obtain different types of higher-order rational solutions.

For instance, when \(N=4,\,\lambda _3^*=\lambda _1=a_1+\mathbf{i}b_1,\,\lambda _4^*=\lambda _2=a_2+\mathbf{i}b_2\), the second-order rational solution can present two-lump, two-RW, and mixture of one lump and one RW based on the values of parameters \(\rho ,\,k,\,a_j,\,b_j\,(j=1,2).\) Here, we only discuss the case of two-RW solution, since the discussions related to another two cases can be conducted similarly. As \(\Delta _j=0,\,(j=1,2)\), the second-order rational solution illustrates the collision of two line RWs. In addition, the second-order rational solution presents six types of status as follows:

  • Dark–Dark status when \((b_j-k)^2\le \frac{a_j^2}{3}\,(j=1,2)\);

  • Dark–mixed status when \((b_1-k)^2\le \frac{a_1^2}{3}\) and \(\frac{a_2^2}{3}<(b_2-k)^2\le 3a_2^2\), or \(\frac{a_1^2}{3}<(b_1-k)^2\le 3a_1^2\) and \((b_2-k)^2\le \frac{a_2^2}{3}\);

  • Dark–bright status when \((b_1-k)^2\le \frac{a_1^2}{3}\) and \(3a_2^2<(b_2-k)^2\), or \(3a_1^2<(b_1-k)^2\) and \((b_2-k)^2\le \frac{a_2^2}{3}\);

  • Mixed–mixed status when \(\frac{a_j^2}{3}<(b_j-k)^2\le 3a_j^2\,(j=1,2)\);

  • Mixed–bright status when \(\frac{a_1^2}{3}<(b_1-k)^2\le 3a_1^2\) and \(3a_2^2<(b_2-k)^2\), or \(3a_1^2<(b_1-k)^2\) and \(\frac{a_2^2}{3}<(b_2-k)^2\le 3a_2^2\);

  • Bright–bright case when \(3a_j^2<(b_j-k)^2\,(j=1,2)\).

To express explicitly, the bright–bright pattern is shown in Fig. 8. Similarly, according to the above conditions, another five patterns can also be obtained.

Table 1 The classification of fundamental solution
Full size table

4 Semi-rational solutions

In [57], our group constructed a family of semi-rational solutions of three types of nonlocal DS equations. Here, we will use the similar method to consider the semi-rational solutions of the KP-based system, which describe the interactions of RW and bound-state multi-dark soliton, interactions of breather and RW, and interactions of lump and bound-state multi-dark soliton.

In order to obtain the semi-rational solutions, the long-time limit technique will be applied to deal with the higher-order solutions. Indeed, choosing

$$\begin{aligned} N=4,\,Q_{1}=\lambda _1\, P_1,\, Q_2=\lambda _2 P_2,\, \eta _1^0=\eta _2^0=\mathbf{i}\pi , \end{aligned}$$

and further taking \(P_1,P_2\rightarrow 0\) in (2.4), we transform f and g into a semi-rational form (a combination of rational function and exponential function, not just the exponential function), rewritten as

$$\begin{aligned} f=\,&e^{A_{34}}(a_{13}a_{23}+a_{13}a_{24}+a_{13}\theta _{2}+a_{14}a_{23}\nonumber \\&+a_{14}a_{24}+a_{14}\theta _{2}+a_{23}\theta _{1}\nonumber \\&+ a_{24}\theta _{1}+\theta _{1}\theta _{2}+a_{12})e^{\eta _{3}+\eta _{4}}+(a_{13}a_{23}+a_{13}\theta _{2}\nonumber \\&+a_{23}\theta _{1}+\theta _{1}\theta _{2}+a_{12})e^{\eta _{3}}\nonumber \\&+(a_{14}a_{24}+a_{14}\theta _{2}+a_{24}\theta _{1}\nonumber \\&+\theta _{1}\theta _{2}+a_{12})e^{\eta _{4}}+\theta _{1}\theta _{2}+a_{12}\,,\nonumber \\ g=\,&e^{A_{34}}[a_{13}a_{23}+a_{13}a_{24}+a_{13}(\theta _{2}+\beta _{2})\nonumber \\&+a_{14}a_{23}+a_{14}a_{24}+a_{14}(\theta _{2}\nonumber \\&+\beta _{2})+a_{23}(\theta _{1}+\beta _{1})+a_{24}(\theta _{1}+\beta _{1})\nonumber \\&+(\theta _{1}+\beta _{1})(\theta _{2}+\beta _{2})+a_{12}]e^{\eta _{3}+\mathbf{i}\phi _{3}+\eta _{4}+\mathbf{i}\phi _{4}}\nonumber \\&+[a_{13}a_{23}+a_{13}(\theta _{2}+\beta _{2})+a_{23}(\theta _{1}+\beta _{1})\nonumber \\&+(\theta _{1}+\beta _{1})(\theta _{2}+\beta _{2})+a_{12}]e^{\eta _{3}+\mathbf{i}\phi _{3}}\nonumber \\&+[a_{14}a_{24}+a_{14}(\theta _{2}+\beta _{2})+a_{24}(\theta _{1}+\beta _{1})\nonumber \\&+(\theta _{1}+\beta _{1})(\theta _{2}+\beta _{2})+a_{12}]e^{\eta _{4}+\mathbf{i}\phi _{4}}\nonumber \\&+(\theta _{1}+\beta _{1})(\theta _{2}+\beta _{2})+a_{12}, \end{aligned}$$
(4.1)

where \(\theta _1,\theta _2,\beta _1,\beta _2,a_{12}\) are defined in Theorem 1, and

$$\begin{aligned} a_{sl}=-\frac{P_l^3}{P_{l}^4+(\lambda _s-\Omega _l)^2} (\,s=1,2\,,l=3,4\,). \end{aligned}$$

Taking the similar procedure as above, we will consider the classification of the semi-rational solution next.

Fig. 7
figure 7

(Color online) The regions of \((a,\,b)\) related to the three patterns: bright, mixed, and dark, with \(k=0\)

Full size image
Fig. 8
figure 8

(Color online) The evolution of bright–bright second-order rational solution of KP-based system with parameters \(\rho =9,k=0,\epsilon =0,(a_1,b_{1})=(-1,\sqrt{17}),(a_2,b_2)=(-\frac{2}{3},\sqrt{-\frac{4}{9}+6\sqrt{6}})\). a\(t=-\,5\). b\(t=-\,1\). c\(t=-\,0.5\). d\(t=0\). e\(t=1\). f\(t=5\)

Full size image
Fig. 9
figure 9

(Color online) The evolution of semi-rational solution consisting of a line bright RW and a breather generated by (4.1) with parameters given by (4.2). a\(t=-\,3\). b\(t=-\,1\). c\(t=-0.5\). d\(t=0\). e\(t=1\). f\(t=3\)

Full size image
Fig. 10
figure 10

(Color online) The evolution of semi-rational solution consisting of a line RW and two bound-state dark solitons generated by (4.1) with parameters given by (4.3). a\(t=-3\). b\(t=-1\). c\(t=0\). d\(t=3\)

Full size image

A: The mixture of a breather and a line RW Assuming

$$\begin{aligned}&\lambda _1=a+\mathbf{i}b,\,\lambda _2=a-\mathbf{i}b,\, P_4^*=P_3,\,\Omega _{4}^{*}=\Omega _{3},\\&{\eta _{4}^{0}}^{*}=\eta _{3}^{0}, \end{aligned}$$

and

$$\begin{aligned} \Delta =b+\dfrac{4\rho ^2 b(a+2k)}{[(2k+a)^2+b^2]^2}, \end{aligned}$$

we obtain a kind of semi-rational solution of the KP-based system when \(\Delta =0\), which consists of a breather and a line RW. To interpret clearly, we choose the following parameters

$$\begin{aligned} \begin{aligned}&\epsilon =0,\,k=0,\,\rho =9,\,\lambda _1=-1+\mathbf{i}\sqrt{17},\\&\lambda _2=-1-\mathbf{i}\sqrt{17},\\&P_3=\mathbf{i},\,P_4=-\mathbf{i},\,\Omega _3=4,\,\Omega _4=4,\,\eta ^0_3=0,\,\eta ^0_4=0, \end{aligned} \end{aligned}$$
(4.2)

and show the corresponding solution |u| in Fig. 9. Obviously, the line bright RW only exists for a short period, while the breather keeps permanent moving on the constant background. During this short period, the line RW interacts with the breather apparently, and the wave structures of the line RW and breather are strongly destroyed (see the panel at \(t=0\)). After passing through the breather, the maximum amplitude of the line RW becomes lower than before, and apparent phase shifts occur to both the line RW and the breather. In fact, the phase shift of the RW is observed clearly by comparing with the RW shown in Fig. 6, which is derived by the same parameters. Furthermore, the period of the breather becomes smaller during the interaction and then recovers the same period as before. These facts indicate that energy transfer happens between the rogue wave and the breather during the interactions.

B: The mixture of a line RW and bound-state two dark soliton By taking the following parameters in (4.1),

$$\begin{aligned} \Delta =0,\,\mathrm{Im}(P_3)=0,\,\mathrm{Im}(P_{4})=0, \end{aligned}$$

where \(\mathrm{Im}\) represents the imaginary part of a complex number, the corresponding solution of the KP-based system behaves as a mixture of a line RW and two dark solitons. In particular, when the parameters satisfy

$$\begin{aligned} \frac{\Omega _3}{P_3}=\frac{\Omega _4}{P_4},\,\frac{\Omega _3}{q_3}=\frac{\Omega _4}{q_4}, \end{aligned}$$

these two dark solitons have the same velocity. (The solitons with same velocity are usually called “bound-state solitons”.) In this case, these solutions can describe dynamical profiles of a line RW arising from a two-soliton background and then decaying back to the same two-soliton background. The solution with

$$\begin{aligned} \begin{aligned}&\epsilon =0,\,k=0,\,\rho =9,\,\lambda _1=-1+\mathbf{i}\sqrt{17},\\&\lambda _2=-1-\mathbf{i}\sqrt{17},\\&P_3=\frac{2}{3},\,P_4=\frac{2}{3},\,\Omega _3=1,\,\Omega _4=-1,\\&\eta ^0_3=3\pi ,\,\eta ^0_4=-3\pi , \end{aligned} \end{aligned}$$
(4.3)

is shown in Fig. 10. When |t| is big enough, the semi-rational solution only has two dark solitons (see the panels at \(t=\pm \,3\)). During the intermediate time, a line RW arises and interacts with these two dark solitons (see the panels at \(t=-1,0\)). Obviously, the interaction does not destroy the structures of the line solitons and the RW, which is different from the above situation where the wave structures are strongly destroyed (shown in Fig. 9). Furthermore, to the best of our knowledge, this kind of solution with a semi-rational form has never been reported before.

Fig. 11
figure 11

(Color online) The evolution of semi-rational solution consisting of a lump and two bound-state dark solitons generated by (4.1) with parameters given by (4.4). a\(t=-3\). b\(t=-1\). c\(t=0\). d\(t=3\)

Full size image

C: The mixture of a lump and bound-state two dark soliton Assuming

$$\begin{aligned} \Delta \ne 0,\,\mathrm{Im}P_3=0,\, \mathrm{Im}P_4=0,\,\frac{\Omega _3}{P_3}=\frac{\Omega _4}{P_4},\, \frac{\Omega _3}{q_3}=\frac{\Omega _4}{q_4}, \end{aligned}$$

we obtain a solution of the KP-based system including a lump and bound-state two dark soliton. By choosing

$$\begin{aligned}&\epsilon =0,\,k=0,\,\rho =3,\,\lambda _1=\frac{1}{5}+3\mathbf{i},\,\lambda _2=\frac{1}{5}-3\mathbf{i},\nonumber \\&P_3=\frac{3}{2},\,P_4=\frac{3}{2},\,\Omega _3=1,\,\Omega _4=-1,\,\eta ^0_3=3\pi ,\nonumber \\&\eta ^0_4=-3\pi , \end{aligned}$$
(4.4)

this type of solution is shown in Fig. 11. Compared to the semi-rational solution shown in Fig. 10, this semi-rational solution not only consists of bound-state two dark soliton but also a lump when |t| is big enough (see the panels at \(t=\pm \,3\)), while only bound-state two dark soliton is presented in the Case B (see the panel at \(t=\pm \,3\) in Fig. 10). In Fig. 11, the wave structure of the semi-rational solution does not change during the interactions of the lump and two dark soliton (see the panel at \(t=0\)). In addition, the lump and two dark soliton do not change any more including phase shift or darkness, which may imply that these is no energy transfer between these two dark solitons or between the two dark soliton and the lump before and after collision.

D: Other types of semi-rational solutions The semi-rational solution consisting of lump and bound-state multi-dark soliton has been discussed for the nonlocal DS equation in [58]. This solution shows the process of annihilation (production) of two lumps into (from) multi-dark soliton. Besides, choosing

$$\begin{aligned} \Delta \ne 0,\,P_4^*=P_3,\,\Omega _{4}^{*}=\Omega _{3},\,{\eta _{4}^{0}}^{*}=\eta _{3}^{0}, \end{aligned}$$

we can get a kind of semi-rational solution displaying a hybrid of one lump and one breather, and this type of solution has been considered for the third-type nonlocal DS equation by our group in [57]. Hence, we will not investigate these two types of solutions of the KP-based system in this work.

5 Conclusions

By employing the bilinear method and a long-time limit, the general solutions of the KP-based system are generated, which include the breather solution, the rational solution and the semi-rational solution. The rational solution consists of two types: lump and RW. Both of them have three types of status: dark state, mixed state, and bright state. The RW has a line style arising from constant background and disappearing into the constant background again after a very short time. The profiles for the breather, lump, and RW solution of the KP-based system are shown in Figs. 1, 2, 3, 4, 5 and 6.

Parameters a and b are critical for the generation of these three types of status. The related regions about \((a,\,b)\) corresponding to these three types of status are shown in Fig. 7 and Table 1 explicitly. Higher-order rational solutions describe the interactions of several individual fundamental solutions, and they possess more interesting profiles. As an example, the second-order RW is considered, and it is classified into six types of status.

For the semi-rational solutions, this work gives three types of them in detail. The first one describes the collision between a line RW and a breather, and the wave structures of the line RW and the breather are destroyed during the interaction, shown in Fig. 9; the second one is an elastic collision of a line rogue wave and bound-state two dark soliton, shown in Fig. 10; the last one features an elastic collision of a lump and bound-state two dark soliton, shown in Fig. 11. Except for these three types of semi-rational solutions, a parallel way can be used to single out other types of semi-rational solutions, including mixtures of lumps and periodic line waves, mixtures of breathers, lumps, and RWs. Finally, it is worth to emphasize that the technique presented in this paper may also succeed to other nonlinear integrable (1 + 1) and higher-dimensional systems, such as negative-order modified KdV equation [59, 60], and the local KP-based system. The related results will be reported elsewhere.