Resonant 1:2 double Hopf bifurcation in an oscillator with delayed feedback

Abstract

In this work, the dynamics of an oscillator with delayed feedback is analyzed. It is found that for certain values of the parameters, the system exhibits a phenomenon known as double Hopf bifurcation with 1:2 resonance. This singularity provokes the interaction between two oscillatory solutions, one of frequency $\omega$ and the other with frequency $2\omega$. By using the graphical Hopf bifurcation theorem, the system dynamics in a neighborhood of this singularity is explored. Also, with the aid of the package DDE-Biftool, some global bifurcations are detected in order to provide a better understanding of the whole scenario.

1 Introduction

The appearance of smooth oscillations under the stability change in the equilibrium point, when a critical parameter is varied, is now a well-known phenomenon. When a single pair of complex eigenvalues resulting from the linearization of equilibrium point crosses the imaginary axis, an emergence of a unique limit cycle is born under the Hopf bifurcation mechanism [1]. This rich scenario has been captured by many articles and books, and recovered with fine and exquisite numerical methods [2, 3]. As a building block in complexity, when two pairs of complex eigenvalues cross the frontier of stability the appearance of two periodic branches can interact themselves and generate quasiperiodic motion after suitable perturbation in two parameters. This type of singularity is now called double Hopf bifurcation or simply Hopf–Hopf phenomenon [4]. Besides ordinary differential equations, a quite similar scenario is present in equations with delays [5]; to be more specific, see [6] and the references therein for Hopf bifurcation, and Xu et al. [7] for double Hopf singularity. Similarly, the advance in numerical continuation methods permits now the computation of periodic branches by varying one parameter in delay differential equations [8, 9] in order to complete a global result for Hopf and double Hopf bifurcations.

The present paper inscribes in the lines traced out by Tsypkin [10] in order to extend the stability test for systems with delayed feedback, and in the contributions of [11, 12] in order to recover the branch of periodic oscillations from Hopf bifurcation using feedback control methods, such as Nyquist diagrams and harmonic balance techniques. As a natural extension, the computation of the periodic solutions starting from Hopf bifurcations in a type of delayed feedback systems has been reported in [13, 14]. This technique has been efficient also to compute the periodic branches of double Hopf bifurcations [15] in ordinary differential equations (ODEs). So, the current paper starts from an example of a resonant 1:2 double Hopf bifurcation, i.e., the relation between both frequencies is 1:2, taken from [16].

Roughly speaking, the resonant 1:2 double Hopf bifurcation provokes the interaction between two oscillatory solutions, one of frequency $\omega$ and the other with frequency $2\omega$. However, the dynamics around this singularity can be fully described by varying two or three parameters, depending on its complexity. In other words, the singularity can be co-dimension two or co-dimension three. This difference has been pointed out in [17] for ODEs, where the authors used the multiple timescales method. By using the same theoretical framework, some conditions to determine if the resonance is co-dimension two or co-dimension three have been derived in [18] for time-delay systems. The former case is considered a weak resonance and the latter a strong resonance. So, it is worth mentioning that the 1:2 resonance can be weak even if it is low order.

In this paper, the dynamic behavior arising near the 1:2 resonance is analyzed by a combination of analytical techniques for local results using the frequency domain formulation [12, 19] and DDE-Biftool [8, 9] when considering some global results. More precisely, the main objective is to capture analytically the periodic solutions arising from the Hopf bifurcation branches near the resonance, and additionally, to compute some bifurcations of limit cycles numerically. The main advantage of the theoretical method employed is that the stability of both the equilibrium points and the periodic solutions can be deduced without dealing with an exponential polynomial. Moreover, there is no need for changing and scaling the state variables to apply the method. On the other hand, the main disadvantage is that the obtained formulas do not have a direct match with the normal form of the 1:2 resonance, so the classification into weak and strong resonances is not straightforward.

Other papers focused on some special types of resonances, for example, Revel et al. [20] for resonant 1:2 double Hopf bifurcation in ODEs, or Xu et al. [7] and Ji et al. [21] for delay differential equations. Recently, a model of a maglev system has been analyzed through an extensive exploration in the parameter space [22], showing a presence of a resonant 1:2 double Hopf bifurcation. Moreover, the celebrated technique of stabilization of periodic solutions by means of Pyragas time-delayed feedback control has found rich dynamic scenarios of double Hopf bifurcation, quasiperiodic oscillations and secondary bifurcations in order to delimit the domain of stability of the target periodic orbit [23]. These articles act as a true motifs of genuine research in order to characterize the unfoldings of this singularity with an hybrid method, such as the one reported in this paper.

2 The problem

Consider the following system proposed in [16]:

$$\begin{aligned} \ddot{u}+\alpha \dot{u}+\frac{5}{2}u=f\left( u(t-\tau )\right) , \end{aligned}$$

(1)

where $u,\alpha \in \mathbb {R}, \tau \in \mathbb {R}^+$ and $f:\mathbb {R}\rightarrow \mathbb {R}$ is a smooth function. Equation (1) is an oscillator with damping $\alpha$ and forced by the control law $f(u(t-\tau ))$, where $\tau$ is the time-delay. It is assumed that there is at least one value $u^*$ such that $\frac{5}{2}u^*=f(u^*)$, which means the existence of an equilibrium point of (1). By considering a perturbation around this equilibrium, one replaces the trial $z(t)=u^*+\epsilon \,\hbox {e}^{rt}$ in (1) to obtain the characteristic equation:

$$\begin{aligned} P(r,\mu )=r^2+\alpha r+\frac{5}{2}-f_1\hbox {e}^{-r\tau }=0, \end{aligned}$$

(2)

where $f_1\triangleq f'(u^*)$ and $\mu \triangleq (f_1,\tau ,\alpha )$ represents a vector of parameters. A necessary condition for the existence of a Hopf bifurcation is obtained when a pair of complex conjugate solutions of (2) crosses the imaginary axis, when a single parameter is varied. The critical condition is stated as $P(i\omega _0,\mu _0)=0$, with $\omega _0\ne 0$. The singularity known as resonant 1:2 double Hopf occurs when two couples of complex conjugate solutions of (2) cross the imaginary axis, while parameters are varied, and the ratio between their imaginary parts is 2 at criticality. At least two real parameters should be varied to provoke this situation. The necessary conditions for this phenomenon are

$$\begin{aligned} P(i\omega _0,\mu _0)=P(i2\omega _0,\mu _0)=0,\quad \omega _0\ne 0. \end{aligned}$$

(3)

The appearance of that singularity in system (1) will be studied in the next section, under the framework of the graphical Hopf bifurcation theorem (GHBT), see [11].

Fig. 1

Block system representation

2.1 Analysis using the GHBT

Letting $x_1=\dot{u}$ and $x_2=u$, system (1) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}_1&{}=&{}-\alpha x_1-\frac{5}{2}x_2+f\left( x_2(t-\tau )\right) ,\\ \dot{x}_2&{}=&{}x_1. \end{array} \right. \end{aligned}$$

(4)

In order to apply the GHBT formulation, (4) must be represented in a standard feedback form, as

$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{x}(t)&{}=&{}A\,x(t)+B\,g(y(t-\tau )),\\ y(t)&{}=&{}Cx(t), \end{array} \right. \end{aligned}$$

which is a linear subsystem whose output is y(t), with a nonlinear feedback $g(\cdot )$. To do so, the following matrices are considered

$$\begin{aligned} \begin{array}{c} A=\left( \begin{array}{cc}-\alpha &{}\quad -5/2\\ 1 &{}\quad 0\end{array}\right) ,\quad B=\left( \begin{array}{c}1\\ 0\end{array}\right) ,\quad C=\left( 0\quad 1\right) . \end{array} \end{aligned}$$

With this choice, the output of the linear block is $y=x_2$, and the nonlinear feedback is $g(y)=f(-y)$. The linear subsystem has a transfer function

$$\begin{aligned} G(s)=C(sI-A)^{-1}B\hbox {e}^{-s\tau }=\displaystyle \frac{\hbox {e}^{-s\tau }}{\varDelta (s)}, \end{aligned}$$

where

$$\begin{aligned} \varDelta (s)\triangleq s^2+\alpha s+5/2, \end{aligned}$$

since the feedback depends on $y(t-\tau )$, so the delay dynamics can be considered in the linear part. The feedback system can be seen in Fig. 1, where $d=0$ (zero external reference or disturbance) means that the system is autonomous. The stability of the equilibrium point is deduced from a linearized analysis, considering $J(\mu ) \triangleq g^{\prime }(y)|_{y=y^*}=-\,f_1$, where $y^*$ ($=u^*$) is the equilibrium value of the output y(t). The linear loop gain is given by

$$\begin{aligned} \lambda (s,\mu )\triangleq G(s)J(\mu )=-\,\frac{f_1 \hbox {e}^{-s\tau }}{\varDelta (s)}, \end{aligned}$$

(5)

where $\lambda (s;\mu )$ is known as the characteristic function. It is convenient to consider the following result.

Lemma 1

[19] If the characteristic Eq. (2) has a pair of imaginary complex conjugate solutions $\pm i \omega _0$ for $\mu =\mu _{0}$, then the characteristic function $\lambda (i\omega _{0},\mu _{0})$ in the frequency domain assumes the value $-1+i0$.

For a given value of $\mu$, the characteristic locus $\lambda (i\omega ,\mu )$ describes a curve in the complex plane, parametrized on the frequency $\omega$. The former Lemma establishes that the necessary condition for a Hopf bifurcation in the frequency domain is detected when this geometrical locus passes through $-1$ for $\omega =\omega _0$, when the parameter assumes the fixed value $\mu =\mu _0$. This graphical interpretation will be further explored in Sect. 3.1.

2.2 Conditions for the Hopf and resonant double Hopf bifurcations

By applying Lemma 1 for the characteristic function (5), the Hopf condition $\lambda (i\omega ,\mu )=-\,1$ leads to

$$\begin{aligned} f_1\cos (\omega \tau )&=\frac{5}{2}-\omega ^2, \end{aligned}$$

(6a)

$$\begin{aligned} f_1\,\sin (\omega \tau )&=-\,\alpha \omega . \end{aligned}$$

(6b)

Moreover, for the occurrence of a resonant 1:2 double Hopf, condition (3) also implies $\lambda (i2\omega ;\mu )=-\,1$, which gives

$$\begin{aligned} f_1\cos (2\omega \tau )&=\frac{5}{2}-4\omega ^2, \end{aligned}$$

(7a)

$$\begin{aligned} f_1\,\sin (2\omega \tau )&=-\,2\alpha \omega . \end{aligned}$$

(7b)

From (6b) and (7b), it is obtained

$$\begin{aligned} f_1\,\sin (2\omega \tau )=2f_1\sin (\omega \tau )\cos (\omega \tau ), \end{aligned}$$

which implies $-\,2\alpha \omega =-\,2\alpha \omega \cos (\omega \tau )$. Then $\alpha =0$, $\omega =0$ or $\cos (\omega \tau )=1\Rightarrow \omega \tau =2k\pi , k\in \mathbb {N}$. Discarding $\omega =0$, if $\omega \tau =2k\pi$, from (6a) and (7a) one obtains $5/2-\omega ^2=5/2-4\omega ^2$, then $\omega =0$. Thus, it should be $\alpha =0$. Considering again (6b), it results $\omega \tau =k\pi$. But if k is even, it is obtained again that $\omega =0$. Thus, k should be odd. By using (6a) and (7a) again, as $\cos (\omega \tau )=-\,1$ and $\cos (2\omega \tau )=1$, one obtains $f_1=5/2-4\omega ^2=\omega ^2-5/2$, then $\omega =1$. Finally, it is found that $f_1=-\,3/2$ and $\tau =k\pi$, with k odd. Thus, the possible double Hopf points in the parameter space will have the form $\mu _k=(f_1,\tau ,\alpha )=(-\,3/2,k\pi ,0)$, $k\in \mathbb {N}$, k odd. In the following, the neighborhood of $\mu _1=(-3/2,\pi ,0)$ will be studied by varying parameters $f_1$ and $\tau$. A three-parameter variation will not be considered in this work. Thus, the parameter $\alpha$ will be considered to be zero hereinafter.

3 A particular system

As suggested by the previous analysis, let $\alpha =0$ and $f(u)=f_1\,u+0.9\,u^2$, then (1) results in $\ddot{u}+\frac{5}{2}u=f_1u(t-\tau )+0.9u^2(t-\tau )$. With this choice of f(u), there are two equilibrium points, one at $u^*=0$ and the other at $u^*=(5/2-f_1)/0.9$. By considering the equilibrium at the origin, the characteristic function (5) reduces to

$$\begin{aligned} \lambda (s,\mu )=\frac{-f_1 \hbox {e}^{-s\tau }}{s^2+5/2}, \end{aligned}$$

(8)

and the condition for the Hopf bifurcation (6) takes the simpler form

$$\begin{aligned} \left\{ \begin{array}{rcl} f_1\cos (\omega \tau )&{}=&{}\frac{5}{2}-\omega ^2,\\ f_1\sin (\omega \tau )&{}=&{}0. \end{array} \right. \end{aligned}$$

(9)

By solving (9), one obtains explicit expressions for the Hopf curves in the parameter plane $(\tau ,f_1)$ as

$$\begin{aligned} \text {H}_k:\;\;f_{1(k)}=(-1)^{k+1}\left( \frac{k^2\pi ^2}{\tau ^2}-\frac{5}{2}\right) , \end{aligned}$$

(10)

where the pointwise frequency is given by $\omega =k\pi /\tau$.

Fig. 2

Left: Nyquist contour in the s-plane. Right: Image of the contour under the function $\lambda (s,\mu )$, for $f_1=-\,3/2$ and $\tau =\pi$. Only the image for Im$(s)\ge 0$ is shown

3.1 Stability of the equilibrium point

The poles of $\lambda (s,\mu )$ lie on the imaginary axis, at points $\pm \,i\sqrt{5/2}$. Thus, the closed-loop stability analysis is not trivial (see [24]). Consider the modified Nyquist contour shown in Fig. 2, in which the imaginary poles are avoided with a semi-circumference of small radius $\epsilon \ll 1$. This contour is parametrized on the frequency $\omega$. The portion corresponding to positive frequencies is shown in dark solid line, and the portion of negative frequencies is shown in dashed line. The image of the Nyquist contour under the function $\lambda (s;\mu )$ is only shown for positive frequencies. Recall that the goal is to analyze a neighborhood of the double Hopf bifurcation point, then it is assumed that $f_1<0$ and $\tau$ takes values close to $\pi$. Then, every portion of the curve is analyzed using (8), as follows:

• (a) $s=i\omega , 0<\omega <\sqrt{5/2}$. Thus, $|\lambda |=|f_1|/|5/2-\omega ^2|$, $\text {Arg}(\lambda )=-\,\omega \tau$. With $\omega =0$ one has $\text {Arg}(\lambda )=0$, and the image starts on the positive real axis, at point $2|f_1|/5$. As $\omega$ increases, the modulus grows, and when $\omega \rightarrow \sqrt{5/2}$, the argument approaches $-\sqrt{5/2}\,\tau$. If $\tau =\pi$, the curve crosses the negative real axis for $\omega =1$, at point $-2|f_1|/3$, which is the critical point $(-1)$ if $f_1=-\,3/2$.

• (c) $s=i\omega , \sqrt{5/2}<\omega <\infty$. In this case $\text {Arg}(\lambda )=-\,\omega \tau +\pi$, which decreases linearly as $\omega$ increases, then the image turns infinitely many times around the origin in the clockwise sense, as $|\lambda |$ decreases. If $\tau =\pi$, the curve crosses the negative real axis for $\omega =2$, at point$-2|f_1|/3$, as in case (a).

• (b) $s=\sqrt{5/2}\;i+\epsilon \hbox {e}^{i\theta }$, $-\,\pi /2\le \theta \le \pi /2$, with $\epsilon \ll 1$. In this case, from (8)

  $$\begin{aligned} \begin{array}{ccl} \lambda (s,\mu )&{}=&{}\displaystyle -\frac{f_1\;\hbox {e}^{-\tau \left( \sqrt{5/2}\;i+\epsilon \hbox {e}^{i\theta }\right) }}{\left( \sqrt{5/2}\;i+\epsilon \hbox {e}^{i\theta }\right) ^2+5/2}\\ &{}=&{}\displaystyle -\frac{f_1\;\hbox {e}^{-\tau \left( \sqrt{5/2}\;i+\epsilon \hbox {e}^{i\theta }\right) }}{2\sqrt{5/2}\epsilon i\hbox {e}^{i\theta }+\epsilon ^2 \hbox {e}^{i2\theta }}\\ &{}\simeq &{}\displaystyle -\frac{f_1\,\hbox {e}^{-\tau (\sqrt{5/2}\;i+\epsilon \hbox {e}^{i\theta })-i(\theta +\pi /2)}}{\sqrt{10}\epsilon }, \end{array} \end{aligned}$$

  so

  $$\begin{aligned} |\lambda |= & {} \frac{|f_1|}{\sqrt{10}\epsilon }\hbox {e}^{-\epsilon \tau \cos {\theta }},\\ \text {Arg}(\lambda )= & {} -\tau \sqrt{5/2}-\epsilon \tau \sin {\theta }-\theta -\pi /2\\\simeq & {} -\tau \sqrt{5/2}-\theta -\pi /2. \end{aligned}$$

Thus, when $\theta$ varies from $-\,\pi /2$ to $\pi /2$, $\text {Arg}(\lambda )$ varies between $-\sqrt{5/2}\tau$ and $-\,\sqrt{5/2}\tau -\pi$, respectively.

Fig. 3

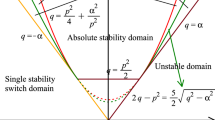
Hopf curves in the ($\tau ,\,f_1$) plane. H$^{(-)}$ corresponds to $\sigma _0<0$ (supercritical Hopf) and H$^{(+)}$ corresponds to $\sigma _0>0$ (subcritical Hopf). The number in each region corresponds to the number of solutions of (2) in the right-half plane. The three representative cases of Hopf bifurcations appearing for this example are shown below schematically

The image of the Nyquist contour under the function $\lambda (s,\mu )$ can be seen schematically in Fig. 2. The case depicted corresponds to $(f_1,\tau )=(-3/2,\pi )$, since two portions of the curve, namely (a) and (c), pass both through $-1$. According to the Nyquist stability criterion, if the image of the curve does not enclose the point $-1$, the closed-loop system is stable. Figure 3 shows the Hopf curves H$_k$ in the $(\tau ,f_1)$ obtained from (10), for $k=1,2$. In each region determined by these curves, it is simple to deduce, based on the Nyquist stability criterion, if the equilibrium point is stable or unstable. Also, for clarity, the number of encirclements of $\lambda (i\omega ,\mu )$ around $-1$ is indicated, which is equivalent to the number solutions of (2) with positive real part. Then, only the region with the number “0” has an stable equilibrium point; the other three regions, delimited by Hopf bifurcation curves, have unstable equilibrium points, i.e., there are 2 or 4 encirclements of the critical point $-1$ by the geometrical locus of $\lambda (s,\mu )$ (recall that only the image of $\lambda (i\omega ,\mu )$ for positive frequencies is shown in Fig. 2, since $\lambda (-i\omega ,\mu )=\overline{\lambda (i\omega ,\mu )}$). Then, in the regions with 2 or 4 encirclements, it means that 2 or 4 solutions of (2) are located in the right-half complex plane.

3.2 Direction and stability of the emerging periodic solutions

The direction and stability of the periodic solutions emerging from the Hopf points are determined by both the sign of the curvature coefficient and the stability changes in the equilibrium point.

For the block system in Fig. 1, the closed-loop transfer function is given by

$$\begin{aligned} H(s)=\frac{G(s)}{1+G(s)J(\mu )}=\frac{1}{\varDelta (s)\hbox {e}^{s\tau }-f_1}. \end{aligned}$$

Also by introducing the compact notation

$$\begin{aligned} \eta (k)= & {} \varDelta (i k \omega )\hbox {e}^{i k \omega \tau }-f_1\\= & {} \left[ 5/2-(k\omega )^2\right] \hbox {e}^{i k \omega \tau }-f_1, \end{aligned}$$

one can write $H(i k \omega )=1/\eta (k)$. As the linear system represented by G(s) is single input–single output (SISO), the loop gain $G(s)J(\mu )$ is scalar and its left and right eigenvectors are simply $v=w=1$. Thus, the following formulas are much simpler than in the general case of having multiple inputs and multiple outputs (MIMO). For the sake of simplicity, the simpler formulas are provided here, while the reader is referred to [11, 19] for the general ones.

The values representing the zero and second harmonics are given by

$$\begin{aligned} \begin{array}{rcl} v_{02}&{}=&{} -\frac{1}{4}H(0)f^{\prime \prime }(u^*)=-\,\frac{0.45}{\eta (0)},\\ v_{22}&{}=&{} -\frac{1}{4}H(i2\omega )f^{\prime \prime }(u^*)=-\,\frac{0.45}{\eta (2)}. \end{array} \end{aligned}$$

Thus, one obtains the vector which involves the components of fundamental frequency, given by

$$\begin{aligned} \begin{array}{rcl} p_1(\omega )&{}=&{}f^{\prime \prime }(u^*)\left( v_{02}+\frac{1}{2}v_{22}\right) +\frac{1}{8}f^{\prime \prime \prime }(u^*)\\ &{}=&{}-0.405\left( \frac{2}{\eta (0)} +\frac{1}{\eta (2)}\right) , \end{array} \end{aligned}$$

(11)

and the auxiliar complex quantity

$$\begin{aligned} \xi _1(\omega )= & {} -G(i\omega )p_1(\omega )\nonumber \\= & {} \displaystyle \frac{0.405\,\hbox {e}^{-i\omega \tau }}{(5/2-\omega ^2)}\left( \frac{2}{\eta (0)} +\frac{1}{\eta (2)}\right) . \end{aligned}$$

(12)

The last expression is needed for computing the amplitude and frequency of the bifurcated periodic solutions. Moreover, the stability of those solutions is determined algebraically by the curvature coefficient, defined as

$$\begin{aligned} \sigma _0\!=\! \text {Re}\left\{ \frac{\xi _1(\omega _0)}{G^{\prime }(i\omega _0)J(\mu )}\right\} , \end{aligned}$$

where $\omega _0$ represents the critical Hopf frequency, $\text {Re}\left\{ \,\cdot \,\right\}$ is the real part of a complex quantity and $G^{\prime }(i\omega _0)\triangleq \text {d}G(s)/\text {d}s|_{s=i\omega _0}$. Considering condition (9), it results that $\omega _0\tau =k\pi$, then $\hbox {e}^{i2\omega _0\tau }=1$, and $\omega _0^2=5/2+(-1)^{k+1} f_1$, thus

$$\begin{aligned}&\xi _1(\omega _0)\\&\quad =\frac{0.405}{f_1}\left( \frac{2}{5/2-f_1} -\frac{1}{15/2+f_1[4(-1)^{k+1}+1]}\right) . \end{aligned}$$

If k is odd, one obtains

$$\begin{aligned} \xi _{1,\mathcal {O}}(\omega _0)=\frac{0.405}{f_1}\left( \frac{11/5\,f_1+5/2}{(5/2-f_1)(3/2+f_1)}\right) , \end{aligned}$$

(13)

which leads to

$$\begin{aligned} \xi _{1,\mathcal {O}}(\omega _0)=\left\{ \begin{array}{ll}<0&{}\quad f_1<-3/2,\\ >0&{}\quad -3/2<f_1<-25/22,\\<0&{}\quad -25/22<f_1<0, \end{array}\right. \end{aligned}$$

and if k is even,

$$\begin{aligned} \xi _{1,\mathcal {E}}(\omega _0)=\frac{0.675}{f_1(5/2-f_1)}<0. \end{aligned}$$

Taking into account that $G(s)=\hbox {e}^{-s\tau }/\varDelta (s)$ and $J(\mu )=-f_1$, it results

$$\begin{aligned} \begin{array}{rcl} G^{\prime }(s)J(\mu )&{}=&{} \displaystyle f_1\hbox {e}^{-s\tau }\;\frac{(\tau \varDelta (s)+\varDelta ^{\prime }(s))}{\varDelta ^2(s)}\\ &{}=&{}\displaystyle f_1\hbox {e}^{-s\tau }\left( \frac{\tau }{s^2+5/2}+\frac{2s}{(s^2+5/2)^2}\right) . \end{array} \end{aligned}$$

By using (9) again, after some simple calculations, one has $G^{\prime }(i\omega _0)J(\mu )=\tau +2i\omega _0(-1)^k/f_1$, and the curvature coefficient finally results in this compact expression:

$$\begin{aligned} \begin{array}{rcl} \sigma _0=\displaystyle \text {Re}\left\{ \frac{\xi _1(\omega _0)}{\tau +\frac{2i\omega _0(-1)^k}{f_1}}\right\} =\frac{\xi _1(\omega _0)\; \tau }{\tau ^2+(2\omega _0/f_1)^2}, \end{array} \end{aligned}$$

(14)

thus the sign of $\sigma _0$ coincides with the sign of $\xi _1(\omega _0)$. So, the stability of the periodic solutions bifurcated from the curves H$_1$ and H$_2$ can be deduced replacing $\xi _1(\omega _0)$ in (14) by $\xi _{1,\mathcal {O}}(\omega _0)$ and $\xi _{1,\mathcal {E}}(\omega _0)$, respectively. Notice that (13) is not defined for $f_1=-\,3/2$, which corresponds exactly to the 1:2 resonance point. It means that the direction of birth of the limit cycle cannot be deduced exactly at this point, but in any neighborhood of it. Also note that the 1:2 double Hopf bifurcation is the only one which provokes this situation, because for any other ratio between the frequencies different from 1/2, the quantity $H(i2\omega _0)$ is well defined (more specifically, for 1:3 and 1:4 resonances).

The local bifurcation diagram of Fig. 3 shows the Hopf curves H$_1$ and H$_2$ in the $(\tau ,f_1)$ plane. H$^{(-)}$ represents supercritical bifurcations ($\sigma _0<0$) and H$^{(+)}$, subcritical bifurcations ($\sigma _0>0$). On the other hand, dashed lines correspond to supercritical bifurcations with no stability change in the equilibrium point (the emerging cycles are unstable). Three representative cases of Hopf bifurcations appearing for this example are shown below schematically as cross sections of the bifurcation diagram. For the diagrams below in Fig. 3, heavy line represents a stable equilibrium, dashed line represents unstable equilibrium, dark solid circles are stable limit cycles, and white circles are unstable limit cycles. It can be seen that when $\sigma _0<0$, the Hopf bifurcation is supercritical, and the emerging limit cycle exists when the associated pair of complex conjugate eigenvalues lie on the right half of the complex plane. Moreover, if the equilibrium point losses its stability, then the emerging limit cycle is stable (aa$^{\prime }$ cross section). If the stability of the equilibrium does not change, the limit cycle is unstable (cc$^{\prime }$ cross section). If $\sigma _0>0$, the Hopf bifurcation is subcritical, and the emerging periodic orbit exists when the associated pair of complex conjugate eigenvalues lie on the left half of the complex plane. Moreover, the emerging limit cycle is unstable (bb$^{\prime }$ cross section). Then, in simpler terms, if there is no stability change in the equilibrium point, $\sigma _0$ indicates only the direction, but not the stability, of the appearing cycle (which will be unstable).

3.3 Approximation of the periodic solutions

The former curvature coefficient is derived from a second-order Fourier representation of the periodic solutions. In order to compute the amplitude and frequency of those solutions, the same Fourier series may be used, but clearly the results will be more accurate if a higher (fourth)-order harmonic balance is employed (see [12]). Thus, the requested approximation of the periodic solutions can be achieved by solving

$$\begin{aligned} \lambda (i\omega ,\mu )=-\,1+\xi _1({\omega _0})\theta ^2+\xi _2({\omega _0})\theta ^4, \end{aligned}$$

(15)

where $\xi _1$ is given in (12), $\xi _2(\omega )=-G(i\omega )p_2$, and $p_2$ is given by

$$\begin{aligned} p_2=\frac{f^{\prime \prime }(u^*)}{2}\left[ 2v\,v_{04}+\bar{v}_{22}\,v_{33}+\bar{v}\,v_{24}\right] +\hbox {H.O.T.}, \end{aligned}$$

(16)

where H.O.T. represents terms involving higher-order derivatives, which are null in the current example since the nonlinearity is quadratic. Equation (16) has been also simplified considering that the system is SISO. The complete formulas can be seen in [19]. Coefficients $v_{33}, v_{04}$ and $v_{24}$ are given by the following expressions (also simplified):

$$\begin{aligned} \begin{array}{rcl} v_{33}&{}=&{}\displaystyle -\frac{1}{2}H(i3\omega )f^{\prime \prime }(u^*)v\,v_{22},\\ v_{04}&{}=&{}\displaystyle -\frac{1}{4}H(0)f^{\prime \prime }(u^*)\left[ 2v_{02}^2+v_{22}\bar{v}_{22}\right] ,\\ v_{24}&{}=&{}\displaystyle -\frac{1}{2}H(i2\omega )f^{\prime \prime }(u^*)\left[ 2v_{02}v_{22}+\overline{v}\,v_{33}\right] . \end{array} \end{aligned}$$

(17)

Now it is necessary to distinguish two cases related with the orbits coming from H$_1$ or H$_2$, whose frequencies are close to $\omega =\pi /\tau$ or $\omega =2\pi /\tau$, respectively.

Consider the first instance. By applying (16) and (17), and replacing the critical frequency associated with H$_1$ Hopf points, i.e., $\omega _0=\pi /\tau$, one obtains

$$\begin{aligned} \begin{array}{rcl} p_2(\omega _0)&{}=&{}-\,0.164025\\ &{}&{}\times \left\{ \frac{\left( 2\left| \eta (2)\right| ^{2}+3\left[ \eta (0)\right] ^{2}\right) \eta (3)+3\left[ \eta (0)\right] ^{3}}{\left[ \eta (0)\right] ^{3}\left| \eta (2)\right| ^{2}\eta (3)}\right\} . \end{array} \end{aligned}$$

(18)

As $\xi _1({\omega _0})$ and $\xi _2({\omega _0})$ result to be real numbers, the frequency which solves (15) can be obtained letting $\text {Im}(\lambda )=0$, which implies $\omega =\omega _0=\pi /\tau$. Then, (15) can be written as

$$\begin{aligned} p_2(\omega _0) \theta ^4+p_1(\omega _0) \theta ^2 +c=0, \end{aligned}$$

(19)

where $c=-f_1-\frac{5}{2}+\left( \frac{\pi }{\tau }\right) ^2$. The amplitude can be obtained as

$$\begin{aligned} \theta ^2=\frac{-p_1\pm \sqrt{p_1^2-4p_2 c}}{2p_2}. \end{aligned}$$

(20)

Let N be the number of real positive solutions of (19). It is mandatory to know the signs of $p_1$, $p_2$ and c, at least in a rectangle of the plane $(\tau ,f_{1})$, namely $\varOmega : [2,4]\times [-2,-0.5]$ (which can be observed in Fig. 4, where six regions of interest are labeled for convenience).

Consider (18). One has $\eta (0)=5/2-f_{1}>0$ since $f_{1}<0$ and $\eta (3)=\left[ \left( 3\pi /\tau \right) ^{2}-5/2\right] -f_{1}>0$ in $\varOmega$. In this way, both numerator and denominator in (18) are positive and $p_{2}(\omega _0)<0$. Also, from (11), it is also simple to deduce that $p_1$ is negative in regions I, II, V and VI and positive in regions III and IV of Fig. 4. The curve when $p_1$ vanishes is indicated in the figure. On the other hand, the coefficient c is negative in regions I, III and V and positive in regions II, IV and VI. Also, the discriminant $D=p_{1}^{2}-4p_2 c$ is positive in regions II, IV and VI. So, in regions I and V, from the signs of coefficients of (19) and the Descartes’ rule of signs, there are no positive solutions of (19). In region III, applying the same rule one gets that there are zero or two positive solutions. The above results are summarized in Table 1.

Fig. 4

The $\varOmega$ rectangle in the $(\tau ,f_{1})$ plane

Table 1 Signs of the expressions involved in (20) (symbol “?” means that the sign is not known) and number N of local periodic orbits emerging from H$_1$ in the six regions of Fig. 4

For the remaining case, namely the cycles associated with H$_2$, a similar study is performed with frequency $\omega _0=2\pi /\tau$. In this case the analysis is simpler since the curvature coefficient does not vanish along the curve H$_2$. It is shown in “Appendix A” that there is one periodic solution on regions V and VI, and there are no solutions on the other regions.

These results will become clearer in the framework of the next section, where the analysis of global bifurcations is going to be included.

Fig. 5

Comparison between DDE-Biftool (numerical) and GHBT (analytical, using a fourth-order harmonic balance) results in the detection of the SN of limit cycles bifurcation curve in region III

4 Analysis of global bifurcations

In Fig. 3, it can be seen that there is a point belonging to the Hopf curve H$_1$ where the curvature coefficient vanishes, at

$$\begin{aligned} (f_1,\tau )=(-25/22,\pi \sqrt{11/15})\simeq (-1.1364,\,2.6903) \end{aligned}$$

This point, known as Bautin bifurcation, is a degenerate Hopf singularity from which emerges a bifurcation curve of saddle-node of limit cycles, i.e., a singularity joining two periodic solutions [4]. This global bifurcation curve is detected both numerically using the package DDE-Biftool [8], as well as analytically through the fourth-order approximation (19) (see Fig. 5). The last one is defined as the vanishing of the discriminant in (20), since the existence of a solution of multiplicity two of (20) represents the coalescence of two periodic solutions. The slight difference in the location of the saddle-node of limit cycles between GHBT and DDE-Biftool is due to the local nature of approximation of the first method.

Fig. 6

Amplitude of the periodic orbits emerging from the subcritical Hopf bifurcation with $\tau =2.8$ (see Fig. 4, region III). The turning point corresponds to the saddle-node of limit cycles. There is a comparison between the numerical result of DDE-Biftool and the analytical prediction of the GHBT

Fig. 7

Numerical simulations for $\tau =3.4$ and a $f_1=-\,1.05$; b $f_1=-\,1.2$. The effect of the PD bifurcation is illustrated

Fig. 8

Numerical simulations for $\tau =3.55$ and $f_1=-\,1.2$. a Time evolution of $x_1(t)$, b phase diagram. The effect of the Neimark–Sacker bifurcation can be observed

Fig. 9

a Bifurcation diagram. It shows saddle-nodes (SN) of limit cycles, period-doubling (PD) bifurcations and two Neimark–Sacker curves, NS$_1$ (detected from the cycles emerging from H$_1$) and NS$_2$ (exhibited by the cycles emerging from H$_2$). b Enlarged area, in which the interaction between the mentioned curves can be appreciated more clearly. c Amplitudes of the periodic solutions obtained using DDE-Biftool via cross sections of the bifurcation diagrams (a) and (b) for constant values of $\tau$. Solid lines represent stable periodic solutions, and dashed lines represent unstable ones

The SN curve indicates that the unstable limit cycles emerging from the subcritical Hopf bifurcations (in region III of Fig. 4) collide with stable ones (of larger amplitude) and disappear. This is the reason why Eq. (19) can have two or zero solutions in region III (see Table 1). In fact, (19) has two solutions under the SN curve, and no solution above this curve. This phenomenon is illustrated in Fig. 6, in which the amplitude of the limit cycles emerging from the subcritical Hopf bifurcation (region III in Fig. 4) is shown. This figure also provides a comparison between the analytical results obtained from (20) and the numerical results via DDE-Biftool.

 The limit cycles emerging from the H$_2$ curve (whose period is close to $\pi$) can develop period-doubling (PD) or Neimark–Sacker (NS) bifurcations. The PD bifurcation provokes the loss of stability of these orbits, giving way to periodic solutions of period close to $2\pi$. This effect is illustrated in Fig. 7, where $\tau =3.4$ (see Fig. 4) is considered. In case (a), one has $f_1=-\,1.05$ (a point above the PD curve), and the existing limit cycle is shown, which emerges from the H$_2$ curve. In case (b), with $f_1=-\,1.2$ (below the PD curve), a periodic solution whose period is approximately twice the period of the former orbit appears. The detection of the PD bifurcation is performed numerically, and the determining condition is the appearance of a Floquet multiplier crossing the unit circle at point $-1$ (see [4]).

On the other hand, the periodic solutions developing Neimark–Sacker bifurcations become unstable, giving way to quasiperiodic orbits. This can be seen in Fig. 8, where the solution from numerical simulation is shown for $\tau =3.55$ and $f_1=-\,1.2$. The interaction between two frequencies can be appreciated, which provokes a stable torus in the phase diagram of Fig. 8b. In this case, the bifurcation is determined by the crossing of a pair of complex conjugate Floquet multipliers through the unit circle at points $\hbox {e}^{\pm i\omega }$, when a parameter is varied. Limit cycles emerging from H$_1$ and H$_2$ may exhibit both NS bifurcations, labeled as NS$_1$ and NS$_2$, respectively, in the bifurcation diagram of Fig. 9a, b. As also shown in Fig. 9a, b, the PD curve is tangent to the H$_2$ curve at the double Hopf point, as expected according by LeBlanc and Langford [25]. One branch of the PD curve collides with both the NS$_1$ and NS$_2$, at a point which represents itself a resonance point, since two Floquet multipliers of the periodic orbit coalesce at point $-1$. Figure 9c shows the amplitudes of the periodic solutions obtained using DDE-Biftool under cross sections of the bifurcation diagram, for constant values of $\tau$. A $2\tau$-periodic solution emerging from H$_1$ can be seen in Fig. 9c-I for $\tau =3.0020$. As $\tau$ increases, this solution interacts through a period-doubling bifurcation with the $\tau$-periodic solution emerging from H$_2$, as shown in Fig. 9c-II with $\tau =3.2504$. If $\tau$ increases further, the SN point approaches the PD as shown in Fig. 9c-III for $\tau =3.3301$. Finally, there is no SN bifurcation in Fig. 9c-IV, where $\tau =3.4001$. Then, even if the resonance cannot be named as strong, the interaction between $\tau$ and $2\tau$-period solutions through a period-doubling bifurcation becomes evident.

5 Conclusions

A second-order differential system with time delay having a 1:2 resonant double Hopf bifurcation has been presented. In the unfolding of the singularity saddle-node of limit cycles, Neimark–Sacker bifurcations and period-doubling are found using a combination of an analytical approach, rooted in harmonic balance method and Nyquist stability diagrams, and numerical continuation software DDE-Biftool. This type of hybrid method seems very powerful in order to discover the intricacies of period and quasiperiodic orbits around Hopf–Hopf bifurcations in delayed feedback systems.

Number of periodic solutions associated with H\(_2\)

It is necessary to study the number N of positive solutions of

$$\begin{aligned} p_{2}\theta ^{4}+p_{1}\theta ^{2}+d=0, \end{aligned}$$

(21)

now for $\omega _{0}=2\pi /\tau$, where

$$\begin{aligned}&p_{2}(\omega _{0})\\&\quad =-0.164025 \displaystyle \left\{ \frac{2\left| \bar{\eta }(2)\right| ^{2}\bar{\eta }(3)+3\left[ \bar{\eta }(0)\right] ^{2}( \bar{\eta }(3)+\bar{\eta }(0))}{\left[ \bar{\eta }(0)\right] ^{3}\left| \bar{\eta }(2)\right| ^{2}\bar{\eta }(3)}\right\} \\&p_{1}(\omega _{0})=\displaystyle -0.405\left\{ \frac{2}{\bar{ \eta }(0)}+\frac{1}{\bar{\eta }(2)}\right\} ,\\&d=-f_{1}+\frac{5}{2}-4\left( \frac{\pi }{\tau }\right) ^{2}, \end{aligned}$$

and

$$\begin{aligned} \displaystyle \bar{\eta }(k)=\left[ 5/2-\left( 2k\pi /\tau \right) ^{2} \right] (-1)^{k}-f_{1}. \end{aligned}$$

Again, it is necessary to analyze the sign of every coefficient in (21) in order to determine N. By replacing the formulas of $\bar{\eta }(0)$ and $\bar{\eta }(2)$ in $p_{1}(\omega _{0})$, one obtains

$$\begin{aligned} p_{1}(\omega _0)=-0.405\left\{ \frac{\frac{15}{2}- \frac{32\pi ^{2}}{\tau ^{2}}-3f_{1}}{\left( \frac{5}{2}-f_{1}\right) \left( \frac{5}{2}-\frac{16\pi ^{2}}{\tau ^{2}}-f_{1}\right) }\right\} , \end{aligned}$$

and $p_{1}<0$ in all regions labeled in Fig. 4. On the other hand, d is negative in regions I, II, III and IV and positive in regions V and VI. It remains to analyze the sign of $p_{2}(\omega _0)$ in region $\varOmega$. Consider the following expressions:

• 1. $\bar{\eta }(0)=5/2-f_{1}>0$ since $f_{1}$ $<0$.

• 2. $\ \bar{\eta }(3)=5/2-36\pi ^2/\tau ^2-f_{1}<0$ in $\varOmega$.

• 3. $2\left| \bar{\eta }(2)\right| ^{2}\bar{\eta }(3)+3\left[ \bar{\eta }(0)\right] ^{2}( \bar{\eta }(3)+\bar{\eta }(0))$.

In the last expression, the first term is negative in $\varOmega$ and the sign of the second term agrees with

$$\begin{aligned} \bar{\eta }(3)+\bar{\eta }(0)=5-\frac{36\pi ^{2}}{\tau ^{2}}-2f_{1}<0\;\;\text {in}\;\; \varOmega . \end{aligned}$$

Then it follows that $p_{2}(\omega _0)<0$ in $\varOmega$. Hence, the number N of positive solutions of (21) can be determined, which is summarized in Table 2.

Table 2 Signs of the expressions involved in (21) and number N of local periodic orbits emerging from H$_2$ in the six regions of Fig. 4

This means that in regions V and VI of Fig. 4, there is only one periodic solution associated with the frequency $\omega _0 =2\pi /\tau$.