1 Introduction

Standard spectral methods have vital roles in numerical analysis in general. These methods are capable of providing numerical solutions to various kinds of differential equations. They employ global polynomials as trial functions. Moreover, they provide very accurate approximate solutions with a relatively small number of unknowns. Many important problems in applied science and engineering can be treated by employing the different versions of spectral methods. For some of these applications, one can consult [1,2,3,4,5]. There are three popular versions of spectral methods; they are the collocation, tau and Galerkin methods. The choice of the suitable version of these methods depends on the type of the differential equation under investigation and also on the initial/boundary conditions governed by it. For some articles employ spectral methods for solving different kinds of differential equations, see [6,7,8,9].

Fractional calculus is a pivotal branch of mathematical analysis. This kind of calculus deals with derivatives and integrals to an arbitrary order (real or complex). Due to the frequent appearance of differential equations of fractional order in various disciplines such as fluid mechanics, biology, engineering and physics, many researchers focused on studying them from theoretical and practical points of view. It is rarely that we can obtain analytical solutions of fractional differential equations (FDEs), so it a challenging problem to develop efficient and applicable numerical algorithms to handle them. In this regard, serval numerical schemes are proposed to investigate different kinds of FDEs. Some of these schemes are, the Taylor collocation method [10]; Adomian’s decomposition method [11, 12]; finite difference method [13]; variational iteration method [14], homotopy analysis and homotopy perturbation methods [15] and [16]. For some relevant recent papers in the area of FDEs and their applications, one can be referred to [17,18,19,20,21,22,23,24].

It is well known that many number and polynomial sequences can be generated by recurrence relations of second order. Of these important sequences are the celebrated sequences of Fibonacci and Lucas. These sequences of polynomials and numbers are of great importance in a variety of branches such as number theory, combinatorics and numerical analysis. These sequences have been studied in several papers from a theoretical point of view (see, [25,26,27,28]). However, there are very few articles that employ these sequences practically. In this regard, a collocation procedure based on using the Fibonacci operational matrix of derivatives is implemented and presented for solving BVPs in [29, 30]. Recently, a numerical approach with error estimation to solve general integro-differential–difference equations using Dickson polynomials is introduced in [31].

Various kinds of differential equations were handled by employing spectral methods along with utilization of operational matrices of various orthogonal polynomials. This approach has many advantages. It is simple, applicable and yields very efficient solutions. Many articles follow this approach. For example, Abd-Elhameed in [32, 33] has established and used novel operational matrices of derivatives for solving linear and nonlinear even-order BVPs. In addition, Napoli and Abd-Elhameed in [34] have developed another harmonic numbers operational matrix of derivatives to solve initial value problems of any order. The operational matrices are not only used to solve ordinary differential equations, but they are also fruitfully employed to solve FDEs. For some articles in this direction, one can be referred for example to [18, 35,36,37,38,39].

The principal aims of this research article can be summarized in the following items:

  1. (i)

    Establishing operational matrices for integer and fractional derivatives of the generalized Lucas polynomials.

  2. (ii)

    Constructing two numerical algorithms for solving multi-term fractional-order differential equations based on employing spectral methods together with the introduced operational matrices of derivatives.

The rest of the paper is as follows. The next section is devoted to presenting some fundamentals and also some formulae of the generalized Lucas polynomials which are useful in the sequel. Section 3 is interested in establishing operational matrices of integer and fractional derivatives of generalized Lucas polynomials. Treatment of multi-term fractional-order differential equations is discussed in detail in Sect. 4 via presenting two spectral algorithms for solving the linear and nonlinear fractional differential equations. In Sect. 5, we investigate carefully the convergence and error analysis of the proposed generalized Lucas expansion. Some numerical tests and comparisons are given in Sect. 6 to validate the efficiency and applicability of the proposed algorithms. Finally, Sect. 7 displays some conclusions.

2 Fundamentals and used formulae

This section is devoted to presenting some fundamentals of the fractional calculus. Besides, some relevant properties and formulae of the introduced generalized Lucas polynomials are stated and proved.

2.1 Some definitions and properties of fractional calculus

Definition 1

The Riemann–Liouville fractional integral operator \(_0I_t^{\nu }\) of order \(\nu \) on the usual Lebesgue space \(L_1[0, 1]\) is defined as: for all \(t\in (0,1)\)

$$\begin{aligned} (_0I_t^{\nu }f)(t)={\left\{ \begin{array}{ll}\frac{1}{\Gamma (\nu )}\displaystyle \int _0^t(t-\tau )^{\nu -1}\,f(\tau )\,\mathrm{d}\tau ,&{} \nu >0,\\ f(t),&{}\nu =0. \end{array}\right. }\nonumber \\ \end{aligned}$$
(1)

Definition 2

The right side Riemann–Liouville fractional derivative of order \(\nu >0\) is defined by

$$\begin{aligned} (D_*^{\nu }f)(t)= & {} \left( \frac{\mathrm{d}}{\mathrm{d}t}\right) ^n(_0I_t^{n-\nu }f)(t),\,n-1\le \nu <n,\nonumber \\&n\in {\mathbb {N}}. \end{aligned}$$
(2)

Definition 3

The fractional differential operator in Caputo sense is defined as

$$\begin{aligned} (D^{\nu }f)(t)= & {} \frac{1}{\Gamma (n-\nu )}\displaystyle \int _0^t(t-\tau )^{n-\nu -1} \,f^{(n)}(\tau )\,\mathrm{d}\tau ,\ \nonumber \\&\,\nu>0,\, t>0, \end{aligned}$$
(3)

where \( \,n-1\le \nu <n, n\in {\mathbb {N}}\).

Remark 1

It is worthy to note here that the fractional derivative in the Caputo sense is the most commonly used definition among the definitions of the fractional derivative. The definition of Caputo is mathematically rigorous than the Riemann–Liouville definition (see, Changpin et al. [40] and Li and Zhao [41]). The Caputo derivative exists in the whole interval (0, 1). In addition, Caputo definition is very welcome in applied science and engineering (Changpin et al. [42]). Furthermore, properties of the Caputo derivative are helpful in translating the higher fractional-order differential systems into lower ones ([43]). For a comparison between Caputo and Riemann–Liouville operators, the interested reader is referred to [44].

The following properties are satisfied by the operator \(D^{\nu }\) for \(n-1\le \nu <n,\)

$$\begin{aligned}&(D^{\nu }I^{\nu }f)(t)=f(t),\nonumber \\&(I^{\nu }D^{\nu }f)(t)=f(t)- \displaystyle \sum _{k=0}^{n-1}\frac{f^{(k)}(0^{+})}{k!}(t-a)^k,\,t>0,\nonumber \\&D^{\nu }\,t^{k}=\displaystyle \frac{\Gamma (k+1)}{\Gamma (k+1-\nu )}\,t^{k-\nu },\nonumber \\&\quad k\in {\mathbb {N}}, k\ge \lceil \nu \rceil , \end{aligned}$$
(4)

where \(\lceil \nu \rceil \) denotes the smallest integer greater than or equal to \(\nu \). For more properties of fractional derivatives and integrals, see for example, [45, 46].

2.2 Relevant properties and relations of generalized Lucas polynomials

The sequence of Lucas polynomials \(L_{i}(t)\) may be constructed by means of the recurrence relation:

$$\begin{aligned} L_{i+2}(t)= & {} t\, L_{i+1}(t)+L_{i}(t),\quad L_{0}(t)=2,\nonumber \\ L_{1}(t)= & {} t,\ i\ge 0. \end{aligned}$$
(5)

The Binet’s form of Lucas polynomials is

$$\begin{aligned} L_{i}(t)=\displaystyle \frac{\left( t+\sqrt{t^2+4}\right) ^i+ \left( t-\sqrt{t^2+4}\right) ^i}{2^i},\quad i\ge 0. \end{aligned}$$

Also, the Lucas polynomials have the following power form representation:

$$\begin{aligned} L_{i}(t)=i\ \displaystyle \sum _{k=0}^{\left\lfloor \frac{i}{2}\right\rfloor }\displaystyle \frac{1}{i-k}\, \genfrac(){0.0pt}1{i-k}{k}\ t^{i-2k},\quad i\ge 1, \end{aligned}$$
(6)

and the notation \(\left\lfloor z\right\rfloor \) represents the largest integer less than or equal to z.

The first few Lucas polynomials \(L_{i}(t)\) are:

In this paper, we aim to generalize the sequence of Lucas polynomials. For this purpose, let a, b be any nonzero real constants, we define the so-called generalized Lucas polynomials which may be generated with the aid of the following recurrence relation:

$$\begin{aligned} \psi ^{a,b}_{i}(t)=a\, t\, \psi ^{a,b}_{i-1}(t)+b\, \psi ^{a,b}_{i-2}(t),\quad i\ge 2, \end{aligned}$$
(7)

with the initial values: \(\psi ^{a,b}_{0}(t)=2\) and \(\psi ^{a,b}_{1}(t)=a\, t\).

The first few generalized Lucas polynomials \(\psi ^{a,b}_{i}(t)\) are:

It is worthy to mention here that the generalized Lucas polynomials \(\psi ^{a,b}_{i}(t)\) generalize the Lucas polynomials \(L_{i}(t)\). In fact, Lucas polynomials can be deduced form \(\psi ^{a,b}_{i}(x)\) for the case: \(a=b=1\). In addition, some other important polynomials can be deduced as special cases of \(\psi ^{a,b}_{i}(x)\). Explicitly, we have

$$\begin{aligned}&Q_{i}(t)=\psi ^{2,1}_{i}(t),&f_{i}(t)=\psi ^{3,-2}_{i}(t),\\&2\, T_{i}(t)=\psi ^{2,-1}_{i}(t),&D_{i}(t,\alpha )=\psi ^{1,-\alpha }_{i}(t), \end{aligned}$$

where \(Q_{i}(t), f_{i}(t),T_{i}(t)\) and \(D_{i}(t,\alpha )\) are, respectively, the Pell–Lucas, Fermat–Lucas, first kind Chebyshev and first kind Dickson polynomials, each of degree i.

The power form representation of \(\psi ^{a,b}_{i}(t)\) can be written explicitly in the following two equivalent forms

$$\begin{aligned} \psi ^{a,b}_{i}(t)=i\, \displaystyle \sum _{m=0}^{\left\lfloor \frac{i}{2}\right\rfloor }\frac{a^{i-2m}\, b^{m}\left( {\begin{array}{c}i-m\\ m\end{array}}\right) }{i-m}\, t^{i-2m}, \end{aligned}$$
(8)

and

$$\begin{aligned} \psi ^{a,b}_{i}(t)=2\, i\, \displaystyle \sum _{k=0}^{i}\frac{a^k\, b^{\frac{i-k}{2}}\, \xi _{i+k}\, \left( {\begin{array}{c}\frac{i+k}{2}\\ \frac{i-k}{2}\end{array}}\right) }{i+k}\ t^k \end{aligned}$$
(9)

where

$$\begin{aligned} \xi _{r}={\left\{ \begin{array}{ll} 1,&{}\ r\ \text {even},\\ 0,&{}\ r\ \text {odd}.\end{array}\right. } \end{aligned}$$

Moreover, the Binet’s form for \(\psi ^{a,b}_{i}(t)\) is

$$\begin{aligned} \psi ^{a,b}_{i}(t)= & {} \displaystyle \frac{\left( a\, t+\sqrt{a^2\, t^2+4\, b}\right) ^i+ \left( a\, t-\sqrt{a^2\, t^2+4\, b}\right) ^i}{2^i},\\&i\ge 0. \end{aligned}$$

Now, the following two theorems are of fundamental importance in establishing our proposed algorithms in this paper. The first theorem gives an inversion formula to the power form representation given in (8), while the second introduces an expression for the first derivative of the generalized Lucas polynomials in terms of their original polynomials .

Theorem 1

For every nonnegative \(\ell \), the following inversion formula is valid

$$\begin{aligned} t^\ell =\ell !\, a^{-\ell }\,\ \displaystyle {\mathop {\mathop {\mathop {\sum }\limits _{j=0}}\limits _{(j+\ell )\, even}}\limits ^{\ell }}\frac{ (-1)^{\frac{\ell -j}{2}} \, b^{\frac{\ell -j}{2}}\, \delta _{j}}{\left( \frac{\ell -j}{2}\right) !\, \left( \frac{\ell +j}{2}\right) !}\ \psi ^{a,b}_{j}(t), \end{aligned}$$
(10)

where \(\delta _{j}\) is defined as

$$\begin{aligned} \delta _{j}= {\left\{ \begin{array}{ll} \frac{1}{2}&{}j=0,\\ 1,&{}j>0. \end{array}\right. } \end{aligned}$$
(11)

Proof

To prove relation (10), it is enough to prove its alternative form

$$\begin{aligned} t^{\ell }=a^{-\ell }\, \displaystyle \sum _{i=0}^{\left\lfloor \frac{\ell }{2}\right\rfloor } (-1)^i\, \left( {\begin{array}{c}\ell \\ i\end{array}}\right) \, b^i\, \delta _{\ell -2i}\ \psi ^{a,b}_{\ell -2i}(t). \end{aligned}$$
(12)

We proceed by induction on \(\ell \). Identity (12) is obviously satisfied for \(\ell =0\). Now, assume the validity of (12), and therefore to complete the proof, we have to show the validity of the following identity:

$$\begin{aligned}&t^{\ell +1}=a^{-\ell -1}\, \displaystyle \sum _{i=0}^{\left\lfloor \frac{\ell +1}{2}\right\rfloor } (-1)^i\, \left( {\begin{array}{c}\ell +1\\ i\end{array}}\right) \, b^i\,\nonumber \\&\quad \delta _{\ell -2i+1}\ \psi ^{a,b}_{\ell -2i+1}(t). \end{aligned}$$
(13)

If we multiply both sides of (12) by t, and make use of the recurrence relation (7), then we get

$$\begin{aligned} \begin{aligned} t^{\ell +1}&=a^{-\ell -1}\, \displaystyle \sum _{i=0}^{\left\lfloor \frac{\ell }{2}\right\rfloor }(-1)^i\, \left( {\begin{array}{c}\ell \\ i\end{array}}\right) \, b^{i}\, \delta _{\ell -2i}\ \psi ^{a,b}_{\ell -2i+1}(t)\\&\quad \, +b\, a^{-\ell -1}\displaystyle \sum _{i=0}^{\left\lfloor \frac{\ell }{2}\right\rfloor }(-1)^i\, \left( {\begin{array}{c}\ell \\ i\end{array}}\right) \, b^{i}\, \delta _{\ell -2i}\ \psi ^{a,b}_{\ell -2i-1}(t). \end{aligned} \end{aligned}$$
(14)

The last relation can be written alternatively—after performing some manipulations—as

$$\begin{aligned} \begin{aligned}&t^{\ell +1}=\displaystyle \sum _{i=1}^{\left\lfloor \frac{\ell }{2}\right\rfloor }\left[ (-1)^i\, a^{-\ell -1}\, \left( {\begin{array}{c}\ell \\ i\end{array}}\right) \, b^i\, \delta _{\ell -2i}\right. \\&\left. +(-1)^i\, a^{-\ell -1}\, \left( {\begin{array}{c}\ell \\ i-1\end{array}}\right) \, b^i\, \delta _{\ell -2i+2}\right] \, \psi ^{a,b}_{\ell -2i+1}(t)\\&+a^{-\ell -1}\, \delta _{\ell }\, \psi ^{a,b}_{\ell +1} +(-1)^{\left\lfloor \frac{\ell }{2}\right\rfloor +1}\, \delta _{\ell -2\, \left\lfloor \frac{\ell }{2}\right\rfloor }\ a^{-\ell -1}\, b^{\left\lfloor \frac{\ell }{2}\right\rfloor +1}\\&\,\left( {\begin{array}{c}\ell \\ \left\lfloor \frac{\ell }{2}\right\rfloor \end{array}}\right) \ \psi ^{a,b}_{\ell -2\, \left\lfloor \frac{\ell }{2}\right\rfloor -1}(t). \end{aligned} \end{aligned}$$
(15)

After some rather algebraic computations, it can be shown that formula (15) takes the form

$$\begin{aligned}&t^{\ell +1}=a^{-\ell -1}\, \displaystyle \sum _{i=0}^{\left\lfloor \frac{\ell +1}{2}\right\rfloor } (-1)^i\,\\&\quad \left( {\begin{array}{c}\ell +1\\ i\end{array}}\right) \, b^i\, \delta _{\ell -2i+1}\ \psi ^{a,b}_{\ell -2i+1}(t). \end{aligned}$$

Theorem 1 is now proved. \(\square \)

Theorem 2

The first derivative of the generalized Lucas polynomials \(\psi ^{a,b}_{j}(t)\) can be expressed as:

$$\begin{aligned} \displaystyle \frac{\mathrm{d} \psi ^{a,b}_{j}(t)}{\mathrm{d}t}=a\, j\ \displaystyle \sum _{\ell =0}^{\left\lfloor \frac{j-1}{2}\right\rfloor }(-1)^\ell \, b^\ell \, \delta _{j-2\ell -1}\ \psi ^{a,b}_{j-2\ell -1}(t).\nonumber \\ \end{aligned}$$
(16)

Proof

First, we differentiate the power form representation of the generalized Lucas polynomials \(\psi ^{a,b}_{j}(t)\) given in (9) with respect to t to get

$$\begin{aligned} \displaystyle \frac{\mathrm{d} \psi ^{a,b}_{j}(t)}{\mathrm{d}t}=j\ \displaystyle \sum _{k=0}^{\left\lfloor \frac{j-1}{2}\right\rfloor }\left( {\begin{array}{c}j-k-1\\ k\end{array}}\right) \, b^k\, a^{j-2k}\, t^{j-2k-1}.\nonumber \\ \end{aligned}$$
(17)

Making use of the inversion formula (10), Eq. (17) can be written equivalently as

$$\begin{aligned} \displaystyle \frac{\mathrm{d} \psi ^{a,b}_{j}(t)}{\mathrm{d}t}= & {} j\ \displaystyle \sum _{k=0}^{\left\lfloor \frac{j-1}{2}\right\rfloor }b^k\, a^{j-2k}\ \left( {\begin{array}{c}j-k-1\\ k\end{array}}\right) \, \displaystyle \nonumber \\&\sum _{s=0}^{\left\lfloor \frac{j-1}{2}\right\rfloor -k} (-1)^s\, b^s\, a^{2k-j+1}\, \left( {\begin{array}{c}j-2k-1\\ s\end{array}}\right) \,\nonumber \\&\delta _{j-2k-2s-1} \ \psi ^{a,b}_{j-2k-2s-1}(t). \end{aligned}$$
(18)

Expanding the right-hand side of the latter formula and rearranging the similar terms lead to the following relation

$$\begin{aligned} \displaystyle \frac{\mathrm{d} \psi ^{a,b}_{j}(t)}{\mathrm{d}t}=\displaystyle \sum _{\ell =0}^{\left\lfloor \frac{j-1}{2}\right\rfloor }H_{j,\ell } \ \psi ^{a,b}_{j-2\ell -1}(t), \end{aligned}$$
(19)

where \(H_{j,\ell }\) is given by

$$\begin{aligned}&H_{j,\ell }=j\, a\, \delta _{j-2\ell -1}\displaystyle \sum _{p=0}^{\ell }(-1)^{\ell +p}\, b^\ell \,\\&\quad \left( {\begin{array}{c}j-2p-1\\ \ell -p\end{array}}\right) \, \left( {\begin{array}{c}j-p-1\\ p\end{array}}\right) . \end{aligned}$$

In order to obtain a reduction formula for \(H_{j,\ell }\), we note that it can be written equivalently as

$$\begin{aligned}&H_{j,\ell }= (-1)^\ell \, a\, b^\ell \, \left( {\begin{array}{c}j\\ \ell \end{array}}\right) \,(j-\ell )\, \, \delta _{j-2\ell -1}\nonumber \\&\quad \ _{2}F_{1} \left. \left( \begin{array}{cc} -\ell ,-j+\ell +1\\ 1-j\end{array} \right| 1\right) . \end{aligned}$$
(20)

Based on Chu-Vandermonde identity (see Koepf [47]), the hypergeometric \(_2F_{1}\) in (20) can be summed to give

$$\begin{aligned} \ _{2}F_{1}\left. \left( \begin{array}{cc} -\ell ,-j+\ell +1\\ 1-j\end{array} \right| 1\right) =\displaystyle \frac{(j-\ell -1)!\, \ell !}{(j-1)!}, \end{aligned}$$
(21)

and therefore, \(H_{j,\ell }\) takes the following simplified form

$$\begin{aligned} H_{j,\ell }=(-1)^\ell \, \,a\, b^\ell \, \, j\ \delta _{j-2\ell -1}. \end{aligned}$$

Theorem 2 is now proved. \(\square \)

3 Generalized Lucas operational matrix of integer and fractional derivatives

This section is dedicated to establishing operational matrices for both integer and fractional derivatives of the generalized Lucas polynomials. These operational matrices serve to approximate integer and fractional derivatives.

3.1 Operational matrix of integer derivatives

Let u(t) be a square Lebesgue integrable function on (0, 1), and assume that it can be written as a combination of the linearly independent generalized Lucas polynomials, i.e.,

$$\begin{aligned} u(t)=\displaystyle \sum _{j=0}^{\infty }c_j\,\psi ^{a,b}_j(t). \end{aligned}$$

Assume that u(t) can be approximated as

$$\begin{aligned} u(t)\approx u_M(t)=\displaystyle \sum _{k=0}^{M}c_k\,\psi ^{a,b}_k(t)=\mathbf C ^T\, {\varvec{{\Psi }}}(t), \end{aligned}$$
(22)

where

$$\begin{aligned} \mathbf C ^T=[c_0, c_1,\dots , c_{M}], \end{aligned}$$
(23)

and

$$\begin{aligned} {\varvec{{\Psi }}}(t)=[\psi ^{a,b}_0(t), \psi ^{a,b}_1(t),\dots , \psi ^{a,b}_{M}(t)]^T. \end{aligned}$$
(24)

In order to approximate the successive derivatives of the vector \({\varvec{{\Psi }}}(t)\), first note that \(\displaystyle \frac{\mathrm{d}\,{\varvec{{\Psi }}}(t)}{\mathrm{d}\,t}\) can be expressed as

$$\begin{aligned} \frac{\mathrm{d}\,{\varvec{{\Psi }}}(t)}{\mathrm{d}\,t}=G^{(1)}\, {\varvec{{\Psi }}}(t), \end{aligned}$$
(25)

where \(G^{(1)}=\left( g^{(1)}_{ij}\right) \), is the \((M+1)\times (M+1)\) operational matrix of derivatives. With the aid of Theorem 2, the entries of this matrix are given explicitly as

$$\begin{aligned} g^{(1)}_{ij}={\left\{ \begin{array}{ll} (-1)^{\frac{i-j+1}{2}}\, i\, ab^{\frac{i-j-1}{2}}\, \delta _{j},&{} \quad \text {if}\ i>j,\ (i+j)\ \text {odd},\\ 0,&{}\quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

Equation (25) enables one to express \(\displaystyle \frac{\mathrm{d}^\ell \,{\varvec{{\Psi }}}(t)}{\mathrm{d}\,t^\ell },\, \ell \ge 1\) as powers of the operational matrix \(G^{(1)}\). In fact, for all \(\ell \ge 1\), one has

$$\begin{aligned} \frac{\mathrm{d}^\ell \,{\varvec{{\Psi }}}(t)}{\mathrm{d}\,t^\ell }=G^{(\ell )}\,{\varvec{{\Psi }}}(t) =\left( G^{(1)}\right) ^\ell \,{\varvec{{\Psi }}}(t). \end{aligned}$$
(26)

3.2 Operational matrix of fractional derivatives

We establish in this section an operational matrix of the fractional derivatives which generalizes the operational matrix of integer derivatives. The following theorem displays the fractional derivatives of the vector \({\varvec{{\Psi }}}(t)\), from which a new operational matrix of fractional derivatives can be obtained.

Theorem 3

If \({\varvec{{\Psi }}}(t)\) denotes the generalized Lucas polynomial vector which defined in Eq. (24), then the following relation holds for all \(\alpha >0\)

$$\begin{aligned} D^{\alpha }{\varvec{{\Psi }}}(t)=\displaystyle \frac{\mathrm{d}^\alpha {\varvec{{\Psi }}}(t)}{\mathrm{d}t^\alpha }=t^{-\alpha }\,G^{(\alpha )}\,{\varvec{{\Psi }}}(t), \end{aligned}$$
(27)

where \(G^{(\alpha )}=(g^{\alpha }_{i,j})\) is a lower triangular matrix of order \((M+1)\times (M+1)\). This matrix is the operational matrix of fractional derivatives of order \(\alpha \) in the Caputo sense. The entries of this matrix can be written explicitly in the form

$$\begin{aligned} G^{(\alpha )}= \left( \begin{array}{ccccc} 0 &{} 0 &{} 0 &{} \dots &{} 0 \\ \vdots &{} \vdots &{}\vdots &{} &{}\vdots \\ \theta _{\alpha }(\lceil \alpha \rceil ,0) &{} \theta _{\alpha }(\lceil \alpha \rceil ,\lceil \alpha \rceil ) &{} 0 &{} \dots &{} 0 \\ \vdots &{} \vdots &{}\vdots &{} &{}\vdots \\ \theta _{\alpha }(i,0) &{}\dots &{} \theta _{\alpha }(i,i) &{} \dots &{}0 \\ \vdots &{} \vdots &{}\vdots &{} &{}\vdots \\ \theta _{\alpha }(M,0) &{} \theta _{\alpha }(M,1) &{} \theta _{\alpha }(M,2) &{} \dots &{}\theta _{\alpha }(M,M) \\ \end{array} \right) .\nonumber \\ \end{aligned}$$
(28)

Moreover, the elements \(\left( g^{\alpha }_{i,j}\right) \) are given explicitly in the form

$$\begin{aligned} g^{\alpha }_{i,j}=\left\{ \begin{array}{ll} \theta _{\alpha }(i,j), &{} \qquad i\ge \lceil \alpha \rceil ,\, i\ge j; \\ 0, &{} \qquad \text {otherwise}. \\ \end{array} \right. \end{aligned}$$

where

$$\begin{aligned}&\theta _{\alpha }(i,j)\nonumber \\&=\displaystyle \sum _{k=\lceil \alpha \rceil }^i \displaystyle \frac{i\,k!\, \xi _{i+k}\, \xi _{j+k}\,\delta _j\, (-1)^{\frac{k-j}{2}}\, b^{\frac{i-j}{2}}\,\left( \frac{i+k}{2}-1\right) !}{ \left( \frac{i-k}{2}\right) !\, \left( \frac{k-j}{2}\right) !\, \left( \frac{j+k}{2}\right) !\, \Gamma (1+k-\alpha )}.\nonumber \\ \end{aligned}$$
(29)

Proof

The application of the fractional differential operator \(D^{\alpha }\) to Eq. (9) together with relation (4) yields

$$\begin{aligned}&D^{\alpha }\,\psi ^{a,b}_i(t)\nonumber \\&=\displaystyle \sum _{k=\lceil \alpha \rceil }^{i}\frac{i\,a^k\, b^{\frac{i-k}{2}}\, \xi _{i+k}\, (k+1)_{\frac{i-k-2}{2}}\,k!}{\left( \frac{i-k}{2}\right) !\,\Gamma (k+1-\alpha )}\,t^{k-\alpha }, \end{aligned}$$
(30)

which in turn with the aid of the inversion formula in (10) gives

$$\begin{aligned} D^{\alpha }\,\psi ^{a,b}_i(t)=t^{-\alpha }\displaystyle \sum _{j=0}^{i} \theta _{\alpha }(i,j)\,\psi ^{a,b}_j(t), \end{aligned}$$
(31)

where \( \theta _{\alpha }(i,j)\) is given in (29).

The last relation can be rewritten in the following vector form:

$$\begin{aligned} D^{\alpha }\psi ^{a,b}_i(t)= & {} t^{-\alpha }\left[ \theta _{\alpha }(i,0), \theta _{\alpha }(i,1),\dots ,\right. \nonumber \\&\left. \theta _{\alpha }(i,i),0,0,\dots ,0\right] \,{\varvec{{\Psi }}}(t),\nonumber \\&\lceil \alpha \rceil \le i\le M+1, \end{aligned}$$
(32)

Moreover, we can write

$$\begin{aligned} D^{\alpha }\psi ^{a,b}_i(t)= & {} t^{-\alpha }\left[ 0,0,\dots ,0\right] ,\nonumber \\&0\le i\le \lceil \alpha \rceil -1. \end{aligned}$$
(33)

Now, Merging Eq. (32) with Eq. (33), the desired formula can be obtained. \(\square \)

4 Treatment of FDEs based on the introduced operational matrix

This section focuses on constructing two numerical algorithms for treating linear and nonlinear FDEs. For this purpose, the two spectral methods, namely tau and collocation methods, are utilized. To be more precise, we propose a generalized Lucas tau method (GLTM) for handling linear FDEs, while a generalized Lucas collocation method (GLCM) is proposed for handling nonlinear FDEs.

4.1 Handling linear FDEs

In this section, we are interested in solving the following linear fractional differential equation with variable coefficients

$$\begin{aligned}&D^{\alpha _q}\,u(t)+\displaystyle \sum _{i=1}^{q-1}\lambda _i(t)\,D^{\alpha _{i}}\,u(t) +\mu (t)\,u(t)\nonumber \\&\quad =f(t),\, t\in (0,1), \end{aligned}$$
(34)

where

$$\begin{aligned} \alpha _{i}<\alpha _{i+1},\quad \text {and}\quad i<\alpha _i\le i+1,\quad i=1,2,\dots , q-1, \end{aligned}$$

governed by the following initial conditions

$$\begin{aligned} u^{(i)}(0)=a_i,\quad i=0,1,\dots , q-1, \end{aligned}$$
(35)

where \(\lambda _i(t), \mu (t)\) and f(t) are known continuous functions. From (22), it can be assumed that u(t) has the following approximation

$$\begin{aligned} u(t)\approx u_M(t)=\mathbf C ^T\,{\varvec{{\Psi }}}(t). \end{aligned}$$
(36)

Thanks to Theorem 3, \(D^{\alpha _i}\,u(t)\) can be approximated as

$$\begin{aligned} D^{\alpha _i}\,u(t)\approx t^{-\alpha _i}\,\mathbf C ^T\,G^{(\alpha _i)}\,{\varvec{{\Psi }}}(t). \end{aligned}$$
(37)

With the aid of the approximations in (36) and (37), the residual of (34) can be calculated by the formula

$$\begin{aligned} \begin{aligned} t^{\alpha _q}\,R(t)&=\mathbf C ^T\,G^{(\alpha _q)}\,{\varvec{{\Psi }}}(t)\\&\quad +\displaystyle \sum _{i=1}^{q-1}t^{\alpha _q-\alpha _i}\,\lambda _i(t)\,\mathbf C ^T\,G^{(\alpha _i)}\,{\varvec{{\Psi }}}(t)\\&\quad +t^{\alpha _q}\,\mu (t)\,\mathbf C ^T\,{\varvec{{\Psi }}}(t) -t^{\alpha _q}\,f(t). \end{aligned} \end{aligned}$$
(38)

As a result of tau method (see for example [48]), the following system of equations can be obtained

$$\begin{aligned} \displaystyle \int _0^1t^{\alpha _q}\,R(t)\,\psi ^{a,b}_i(t)\,\mathrm{d}t=0,\quad i=0,1,2,\ldots M-q.\nonumber \\ \end{aligned}$$
(39)

In addition, the initial conditions (35) give

$$\begin{aligned} \mathbf C ^T\,G^{(i)}\,{\varvec{{\Psi }}}(0)=a_i,\quad i=0,1,\ldots , q-1. \end{aligned}$$
(40)

Now, Eqs. (39) and (40) constitute a linear system of algebraic equations in the unknown expansion coefficients \(c_i\) of dimension \((M+1)\). The solution of this system can be obtained through employing any suitable numerical algorithm.

4.2 Handling nonlinear FDEs

In this section, we are interested in solving he following nonlinear fractional-order differential equation:

$$\begin{aligned} D^{\alpha _q}\,u(t)= & {} \Omega \big (t, u(t),\nonumber \\&D^{\alpha _1}\,u(t), D^{\alpha _2}\,u(t),\ldots , D^{\alpha _{q-1}}\,u(t)\big ),\nonumber \\&t\in (0,1), \end{aligned}$$
(41)

where

$$\begin{aligned} \alpha _{i}<\alpha _{i+1},\; \text {and}\; i<\alpha _i\le i+1,\quad i=1,2,\ldots , q-1, \end{aligned}$$

governed by the following initial conditions

$$\begin{aligned} u^{(i)}(0)=a_i,\quad i=0,1,\ldots , q-1. \end{aligned}$$

If \(u(t), D^{\alpha _i}\,u(t)\) are approximated as in Sect. 4.1, then the residual \(\tilde{R}(t)\) of Eq. (41) takes the form

$$\begin{aligned} \tilde{R}(t)= & {} t^{-\alpha _q}\,\mathbf C ^T\,G^{(\alpha _q)}\,{\varvec{{\Psi }}}(t)\nonumber \\&-\Omega \left( t, \mathbf C ^T\,{\varvec{{\Psi }}}(t), t^{-\alpha _1}\,\mathbf C ^T\,G^{(\alpha _1)}\,{\varvec{{\Psi }}}(t),\dots ,\right. \nonumber \\&\quad \left. t^{-\alpha _{q-1}}\,\mathbf C ^T\,G^{(\alpha _{q-1})}\,{\varvec{{\Psi }}}(t)\right) . \end{aligned}$$
(42)

The philosophy of the application of collocation method is based on enforcing the residual to vanish at certain interior points. There are several choices for these points. For example, they may be selected as: \(\left( \frac{i}{M+1}\right) ,\quad i=1,2,\ldots M-q,\) and therefore

$$\begin{aligned} \tilde{R}\left( \frac{i}{M+1}\right) =0,\quad i=1,2,\ldots M-q+1. \end{aligned}$$
(43)

Now, Eqs. (43) with (40) constitute a nonlinear system of equations in the unknown expansion coefficients \(c_i\) of dimension \((M+1)\), which may be solved via Newton’s iterative technique, and accordingly, the desired approximate solution can be obtained from (36).

5 Investigation of convergence and error analysis

In this section, we investigate carefully the convergence and error analysis of the proposed generalized Lucas expansion. In order to proceed in our study, the following lemmas are required.

Lemma 1

Let f(t) be an infinitely differentiable function at the origin. Then, it has the following generalized Lucas expansion

$$\begin{aligned} f(t){=}\!\displaystyle \sum \limits _{k=0}^\infty \displaystyle \sum _{j=0}^{\infty } \displaystyle \frac{(-1)^j\,\delta _k\,a^{-k-2j}\,b^j\,f^{(k+2j)}(0)}{j!\,(k{+}j)!}\,\psi ^{a,b}_{k}(t).\nonumber \\ \end{aligned}$$
(44)

Proof

First, we expand f(t) as

$$\begin{aligned} f(t)=\displaystyle \sum _{n=0}^{\infty }a_{n}\, t^n,\quad a_{n}=\displaystyle \frac{f^{(n)}(0)}{n!}. \end{aligned}$$
(45)

Inserting the inversion formula (10) into (45) enables one to write

$$\begin{aligned} f(t)=\displaystyle \sum _{n=0}^{\infty }a_{n}\displaystyle {\mathop {\mathop {\mathop {\sum }\limits _{r=0}}\limits _{(n+r)\ even}}\limits ^{n}} \eta _{r,n}\, \psi ^{a,b}_{r}(t), \end{aligned}$$
(46)

where \(\eta _{r,n}=\displaystyle \frac{(-1)^{\frac{n+r}{2}}\, \delta _{r}\, a^{-n}\, b^{\frac{n-r}{2}}\, n!}{(\frac{n-r}{2})!\, (\frac{n+r}{2})!}\).

Expanding the right-hand side of (46), and rearranging the similar terms, the following expansion is obtained

$$\begin{aligned} f(t)=\displaystyle \sum _{k=0}^\infty \displaystyle \sum _{j=0}^{\infty } a_{k+2j}\, \eta _{k,k+2j}\,\psi ^{a,b}_{k}(t). \end{aligned}$$
(47)

This immediately proves (44). \(\square \)

Lemma 2

[49] Let \(I_{\mu }(t)\) denote the modified Bessel function of order \(\mu \) of the first kind. The following identity is valid

$$\begin{aligned} \displaystyle \sum _{j=0}^{\infty }\displaystyle \frac{t^{k+2j}}{j!\,(j+k)!}=I_{k}(2\, t). \end{aligned}$$
(48)

Lemma 3

[50] The following inequality is satisfied by the modified Bessel function of the first kind \(I_{\mu }(t)\)

$$\begin{aligned} |I_{\mu }(t)|\le \displaystyle \frac{t^{\mu }\, \cosh (t)}{2^{\mu }\,\Gamma (\mu +1)},\quad \forall \ t>0. \end{aligned}$$
(49)

Lemma 4

For all \(t\in [0,1]\), the following inequality holds for generalized Lucas polynomials

$$\begin{aligned} |\psi ^{a,b}_{k}(t)|\le 2\,\left( a+\sqrt{a^2+b}\right) ^{k}.\ \end{aligned}$$
(50)

Proof

The above inequality follows from the Binet’s formula along with the triangle inequality. \(\square \)

Now, we are in a position to state and prove the following two theorems concerning the convergence and error analysis of the proposed generalized Lucas expansion.

Theorem 4

If f(t) is defined on [0, 1] and \(|f^{(i)}(0)|\le L^i\), \(i\ge 0\), where L is a positive constant, and if f(t) has the expansion \(f(t)=\sum _{k=0}^{\infty }c_k\,\psi ^{a,b}_{k}(t)\), then one has:

  1. 1.

    \(|c_k|\le \displaystyle \frac{|a|^{-k}\,L^k\,\cosh (2\,|a|^{-1}\,b^{\frac{1}{2}}\,L)}{k!}\).

  2. 2.

    The series converges absolutely.

Proof

Lemma 1 implies that

$$\begin{aligned} |c_k|=\left| \displaystyle \sum _{j=0}^{\infty }\displaystyle \frac{(-1)^j \,\delta _k\,a^{-k-2j}\,b^{j}\,f^{(2j+k)}(0)}{j!\,(j+k)!}\right| , \end{aligned}$$

and accordingly, and based on the assumption \(|f^{(i)}(0)|\le L^i,\ i\ge 0\), the following inequality holds

$$\begin{aligned} |c_k|\le \displaystyle \sum _{j=0}^{\infty }\displaystyle \frac{|a|^{-k-2j}\,|b|^j\,L^{2j+k}}{j!\,(j+k)!}, \end{aligned}$$
(51)

which in turn, after the application of Lemma 2 leads to the inequality

$$\begin{aligned} |c_k|\le |b|^{-\frac{k}{2}}\,I_{k}(2\,|a|^{-1}\,|b|^{\frac{1}{2}}\,L). \end{aligned}$$

If we make use of the last inequality along with Lemma 3, then the following estimate for the expansion coefficients is obtained

$$\begin{aligned} |c_k|\le \displaystyle \frac{|a|^{-k}\,L^k\,\cosh (2\,|a|^{-1}\,b^{\frac{1}{2}}\,L)}{k!}. \end{aligned}$$
(52)

The first part of Theorem 4 is now proved.

Now, we prove the second part of the theorem. Starting with the inequality in (52), we have

$$\begin{aligned}&\left| c_{k}\, \psi ^{a,b}_{k}(t)\right| \\&\le \left| \displaystyle \frac{|a|^{-k}\,L^k\,\cosh (2\,|a|^{-1}\,b^{\frac{1}{2}}\,L)}{k!}\,\psi ^{a,b}_{k}(t)\right| , \end{aligned}$$

and therefore, the application of Lemma 4 yields

$$\begin{aligned}&|c_k\,\psi ^{a,b}_{k}(t)|\\&\le \left| \displaystyle \frac{2\,|a|^{-k}\,L^k\left( a+\sqrt{a^2+b}\right) ^k \cosh (2\,|a|^{-1}\,b^{\frac{1}{2}}\,L)}{k!}\right| . \end{aligned}$$

Now since \(\sum \nolimits _{k=0}^{\infty }\left| \displaystyle \frac{|a|^{-k}\,L^k\,\,\left( a+\sqrt{a^2+b}\right) ^k}{k!} \right| =e^{|a^{-1}\,L\,\left( a+\sqrt{a^2+b}\right) |},\) so the series converges absolutely. \(\square \)

Theorem 5

Let f(t) satisfy the assumptions stated in Theorem 4. Moreover, let \(e_M(t)=\sum \nolimits _{k=M+1}^{\infty }c_k\,\psi ^{a,b}_{k}(t),\) be the global error. The following inequality holds for \(|e_M(t)|\)

$$\begin{aligned} |e_M(t)|<\displaystyle \frac{2\, e^{L\,\left( 1+\sqrt{1+a^{-2}\,b}\right) }\, \cosh \left( 2\,L\,\big (1+\sqrt{1+a^{-2}\,b}\big )\right) \, \big (1+\sqrt{1+a^{-2}\,b}\big )^{M+1}}{(M+1)!}. \end{aligned}$$

Proof

The first part of Theorem 4 enables one to write

$$\begin{aligned}&|e_M(t)|\le 2\,\cosh \left( 2\,L\,\big (1+\sqrt{1+a^{-2}\,b}\big )\right) \displaystyle \\&\quad \sum _{k=M+1}^{\infty } \displaystyle \frac{\left( L(1+\sqrt{1+a^{-2}\,b})\right) ^{k}}{k!}, \end{aligned}$$

and therefore, we have

$$\begin{aligned}&|e_M(t)|\le 2\,e^{L\,\big (1+\sqrt{1+a^{-2}\,b}\big )}\,\nonumber \\&\cosh \left( 2\, L\,\big (1+\sqrt{1+a^{-2}\,b}\big )\right) \nonumber \\&\quad \left( 1-\displaystyle \frac{\Gamma (M+1,L\,\big (1+\sqrt{1+a^{-2}\,b}\big ))}{\Gamma (M+1)}\right) , \end{aligned}$$
(53)

where \(\Gamma (.)\) and \(\Gamma (.,.)\) are the so-called gamma and the incomplete gamma functions, respectively, (see [51]). The integral representations of gamma and incomplete gamma functions together with the inequality, \(e^{-t}<1,\ \forall \ t>0,\) lead to the inequality

$$\begin{aligned}&|e_M(t)| <\displaystyle \frac{2\, e^{L\,\left( 1+\sqrt{1+a^{-2}\,b}\right) }\, \cosh \left( 2\,L\,\big (1+\sqrt{1+a^{-2}\,b}\big )\right) \, \big (1+\sqrt{1+a^{-2}\,b}\big )^{M+1}}{(M+1)!}. \end{aligned}$$

\(\square \)

Remark 2

If we let \(s=1+\sqrt{1+a^{-2}\,b}\) and \(n=M+1\), we have now \(|e_{n-1}(t)|=\mathcal {O}(s^n/n!)\). From Stirling approximation of factorial function [52], we have

$$\begin{aligned} \sqrt{2\pi }<\frac{n!}{n^{n+\frac{1}{2}}\,e^{-n}}<e, \end{aligned}$$

so, it is easy to see that \(|e_{n-1}(t)|=\mathcal {O}((s\,e)^n/n^{n+\frac{1}{2}}),\) which is a very rapid rate of convergence.

6 Numerical examples

This section concentrates on presenting some numerical results accompanied with comparisons with some numerical results in literature in order to validate the efficiency, high accuracy and applicability of the two proposed algorithms. In the following tests, the error is evaluated in maximum norm namely,

$$\begin{aligned} E=\displaystyle \max _{t\in [0,1]}|u(t)-u_N(t)|. \end{aligned}$$

Example 1

[53] Consider the following linear fractional initial value problem:

$$\begin{aligned}&D^2\,u(t)+D^{\alpha }\,u(t)+u(t)=\frac{6\, t^{3-\alpha }}{\Gamma (4-\alpha )}+t^3+6\, t,\nonumber \\&t\in (0,1),\, 0<\alpha <1, u(0) = u'(0)=0. \end{aligned}$$
(54)

The exact solution of the above equation is \(u(t)=t^3\). If GLTM (generalized Lucas tau method) is applied with \(N=3\), then the residual of Eq. (54) is calculated by the formula

$$\begin{aligned} t^{\alpha }\, R(t)= & {} t^\alpha \,\mathbf C ^T\,G^{(2)}\,{\varvec{{\Psi }}}(t)\\&+\mathbf C ^T\,G^{(\alpha )}\,{\varvec{{\Psi }}}(t)+t^{\alpha }\,\mathbf C ^T\, {\varvec{{\Psi }}}(t)\\&-\frac{6 t^{3}}{\Gamma (4-\alpha )}-t^{3+\alpha }-6\, t^{1+\alpha }, \end{aligned}$$
Table 1 Maximum absolute error E for Example 3
Full size table

and the operational matrices \(G^{(2)}\) and \(G^{(\alpha )}\) are given explicitly as follows:

$$\begin{aligned} G^{(2)}= & {} \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ \frac{a}{2} &{} 0 &{} 0 &{} 0 \\ 0 &{} 2 a &{} 0 &{} 0 \\ -\frac{3\, a\, b}{2} &{} 0 &{} 3\, a &{} 0 \\ \end{array} \right) ,\\ G^{(\alpha )}= & {} \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \frac{1}{\Gamma (2-\alpha )} &{} 0 &{} 0 \\ -\frac{2\, b}{\Gamma (3-\alpha )} &{} 0 &{} \frac{2}{\Gamma (3-\alpha )} &{} 0 \\ 0 &{} \frac{3\, b(\alpha -5) \alpha }{\Gamma (4-\alpha )} &{} 0 &{} \frac{6}{\Gamma (4-\alpha )} \\ \end{array} \right) . \end{aligned}$$

The application of GLTM yields the following two equations

$$\begin{aligned}&35 \sqrt{\pi } \left( 39\, a^3 c_3+28\, a^2 c_2\right. \nonumber \\&\quad \left. +6 a (3 b c_3+c_1)+24 b c_2+24 c_0-39\right) \nonumber \\&\quad +16 \left( 24 a^3 c_3+28\, a^2 c_2+35\, a (3 b c_3+c_1)-24\right) =0,\nonumber \\&21 \sqrt{\pi } \left( 132\, a^3 c_3+75\, a^2 c_2+20\, a (3 b c_3+c_1)\right. \nonumber \\&\quad \left. +60\, b c_2+60 c_0-132\right) \nonumber \\&\quad +16 \left( 56\, a^3 c_3+60\, a^2 c_2+63\, a (3 b c_3+c_1)-56\right) =0.\nonumber \\ \end{aligned}$$
(55)

Moreover, the initial conditions (55) yield

$$\begin{aligned} \begin{aligned}&b\, c_2+c_0=0,\\&3\, b\, c_3+c_1=0. \end{aligned} \end{aligned}$$
(56)

Equations (55) and (56) can be immediately solved to give

$$\begin{aligned} c_0= 0,\,c_1= -\frac{3 b}{a^3},\,c_2=0,\,c_3= \frac{1}{b^3}, \end{aligned}$$

and consequently \(u(t)=t^3,\) which is the exact solution.

Note 1

It is worthy to note here that the maximum pointwise error obtained in [53] for \(N=512\),and \(\alpha =\frac{1}{2},\, \alpha =\frac{3}{4}\) are, respectively, \(1.8626\,\times 10^{-9},\, 1.8624\,\times 10^{-9}\). while our method yields the exact solution with \(N=3\). This ascertains the advantage of our algorithm if compared with the other algorithms.

Example 2

[53] Consider the following multi-term nonlinear higher-order nonhomogeneous initial value problem:

$$\begin{aligned} \begin{aligned}&D^{\frac{11}{2}}\,u(t)+D^{\frac{5}{4}}\,u(t)+D^{\frac{3}{4}}\,u(t)+u^3(t)\\&=\frac{128\, t^{9/4}}{45\, \Gamma \left( \frac{1}{4}\right) }+\frac{32\, t^{7/4}}{21\, \Gamma \left( \frac{3}{4}\right) }+\frac{5\, t^{4/5}}{2\, \Gamma \left( \frac{4}{5}\right) }+\frac{t^9}{27},\\&t\in (0,1),\\&u(0)=u'(0)=u''(0)=0, \end{aligned} \end{aligned}$$
(57)

where \(0<\alpha <1\), with the exact smooth solution \(u(t)=t^3/3\). We apply the GLCM which is proposed in Sect. 4.2 for the case corresponds to \(N=3\). The residual of Eq. (57) takes the form

$$\begin{aligned} \begin{aligned} t^{\frac{11}{5}}\, R(t)&=\mathbf C ^T\,G^{(\frac{11}{5})}\,{\varvec{{\Psi }}}(t)+t^{\frac{19}{20}} \,\mathbf C ^T\,G^{(\frac{5}{4})}\,{\varvec{{\Psi }}}(t)\\&+t^{\frac{29}{20}}\,\mathbf C ^T\,G^{(\frac{3}{4})}\,{\varvec{{\Psi }}}(t) +t^{\frac{11}{5}}\,\left( \mathbf C ^T\,{\varvec{{\Psi }}}(t)\right) ^3\\ {}&-\frac{t^{56/5}}{27}-\frac{128\, t^{89/20}}{45\, \Gamma \left( \frac{1}{4}\right) }-\frac{32\, t^{79/20}}{21\, \Gamma \left( \frac{3}{4}\right) }-\frac{5 t^3}{2\, \Gamma \left( \frac{4}{5}\right) }, \end{aligned} \end{aligned}$$
(58)

and the operational matrix \(G^{(\alpha )}\) is given by:

$$\begin{aligned} G^{(\alpha )}=\left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \frac{1}{\Gamma (2-\alpha )} &{} 0 &{} 0 \\ -\frac{2\, b}{\Gamma (3-\alpha )} &{} 0 &{} \frac{2}{\Gamma (3-\alpha )} &{} 0 \\ 0 &{} \frac{3\,b (\alpha -5) \alpha }{\Gamma (4-\alpha )} &{} 0 &{} \frac{6}{\Gamma (4-\alpha )} \\ \end{array} \right) . \end{aligned}$$

The application of the collocation method yields the following real solution

$$\begin{aligned} c_0= 0,\,c_1= -\frac{b}{a^3},\,c_2=0,\,c_3= \frac{1}{3 a^3}, \end{aligned}$$

and two refused conjugate complex solutions, and consequently \(u(t)=t^3/3\) which is the exact solution.

Note 2

It is worthy to note here that the maximum pointwise error obtained in [53] for the case \(N=256\) is \(2.392\,\times 10^{-6}\), while we obtained the exact solution with \(N=3\). To the best of our knowledge, this is the first numerical algorithm yield the exact solution for nonlinear fractional problems.

Example 3

Consider the following linear Riccati FDE:

$$\begin{aligned} D^{\frac{1}{2}}\,u(x)+u(x)= & {} e^x \left( \text {erf} \left( \sqrt{x}\right) +1\right) ,\nonumber \\&x\in (0,1),\, u(0)=1. \end{aligned}$$
(59)

The exact solution of (59) is \(u(x)=e^x,\) where \(\text {erf}(x)\) is the well-known error function, namely

$$\begin{aligned} \text {erf}(x)=\frac{2}{\sqrt{\pi }}\displaystyle \int _0^x\, e^{-u^2}\,\mathrm{d}u. \end{aligned}$$

We apply GLTM. Table 1 lists the maximum pointwise error of Eq. (59) for different values of a and b. Figure 1 illustrates the absolute error for the case \(a=b=1\) and \(M=15\).

Fig. 1
figure 1

Absolute error of Example 3

Full size image
Table 2 Comparison between CLMM and [54] for Example 4
Full size table

Example 4

[54] Consider the following nonlinear Riccati FDE:

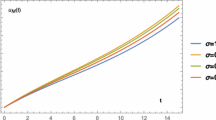
$$\begin{aligned} D^{\alpha }\,u(x)+u^2(x)= & {} 1,\qquad x\in (0,1),\quad \alpha \in (0,1],\nonumber \\ u(0)= & {} 0. \end{aligned}$$
(60)

The exact solution of (60) in case \(\alpha =1\) is \(u(x)=\tanh x.\) GLCM is applied for the case \(a=b=1\). Table 2 compares our results with those obtained in [54]. Figure 2 indicates that the approximate solutions for various values of \(\alpha \) near the value 1 have a similar behavior.

Example 5

[55, 56] Consider the following linear fractional oscillator equation

$$\begin{aligned} D^{q}\,u(t)+\omega ^2\,u(t)=0,t\in (0,L),q\in (1,2), \end{aligned}$$
(61)

subject the initial conditions

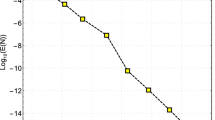
$$\begin{aligned} u(0)=0\qquad u'(0)=\omega . \end{aligned}$$
(62)

The exact solution of (61) for \(q=2\) is \(u(t)=\sin (\omega \,t).\) In this example, and due to the nonavailability of the exact solution in case of \(q\in (1,2)\) , we evaluate the stepwise error \(e_N=\max \nolimits _{t\in [0,1]}|u_N(t)-u_{N+1}(t)|\). Now, We consider the following two cases:

Case 1: \(L=1\)

Fig. 2
figure 2

Different solutions of Example 4

Full size image
Table 3 Comparison between GLTM and LTSM for Example 5—Case 1
Full size table
Table 4 Values of \(e_N\) for Example 5—Case 1
Full size table
Table 5 Maximum pointwise error of Example 5—Integer Case (\(q=2\))
Full size table

In Table 3, we compare GLTM for the case: \(a=b=\omega =1\), with the Legendre tau spectral method (LTSM), \(\tau \) denote the computational time of each algorithm. In addition, in Table 4, we list the values of \(e_N\) for different values of q, N.

Case 2: \(L>1\)

We apply GLTM, in order to show the influence of the values of L on the accuracy of the resulted numerical solutions; we list in Table 5 the maximum pointwise errors for the case \(a=b=\omega =1, N=20\) and \(q=2\) for different values of L . In addition, we plot Figs. 3, 4 and 5 to display the behavior of the numerical solutions for the three cases corresponds to: \(L=1,5,25\) for different values of q. The results of these figures along with the results of Table 5 show that the accuracy of the numerical solutions decreases as the values of L increases.

Remark 3

It is worthy to mention here that the definition of the stepwise error used in the above example for measuring error in case of the unavailability of exact solution of the FDE. This definition is used in many articles, see for example [57].

Example 6

[58] Consider the following nonlinear fractional initial value problem:

$$\begin{aligned} \begin{aligned}&D^2\,u(x)+x^{\frac{7}{2}}\,D^{\frac{3}{2}}\,u(x)+u^2(x)\\&\quad =\frac{4 x^4}{\sqrt{\pi }}+x^4+2,\quad x\in (0,1),\\&u(0)=u'(0)=0, \end{aligned} \end{aligned}$$
(63)

whose exact solution is: \(u(x)=x^2.\) We apply GLCM for the case \(M=2\) to get

$$\begin{aligned} u(x)\approx u_2(x)=2\,c_0+a\,c_1\,x+c_2(2b+a^2\,x^2). \end{aligned}$$
Fig. 3
figure 3

Different solutions of Example 5—\(L=1\)

Full size image
Fig. 4
figure 4

Different solutions of Example 5—\(L=5\)

Full size image
Fig. 5
figure 5

Different solutions of Example 5—\(L=25\)

Full size image
Table 6 Comparison between the method in [59] and GLTM for Example 7
Full size table

The expansion coefficients can be calculated by solving the nonlinear system:

$$\begin{aligned} \left. \begin{aligned}&a\,c_1=0,\\&c_0+b\, c_2=0,\\&\left( \frac{1}{9} \left( c_2 \left( a^2+18 b\right) +3 a c_1\right) +2 c_0\right) ^2\\ {}&\quad +\frac{4 a^2 c_2}{81 \sqrt{\pi }}+2 a^2 c_2=\frac{1}{81} \left( 163+\frac{4}{\sqrt{\pi }}\right) .\end{aligned}\right\} \end{aligned}$$

The above nonlinear system can be solved exactly to give

$$\begin{aligned} c_0=-\displaystyle \frac{b}{a^2},\, c_1=0,\, c_2=\displaystyle \frac{1}{a^2}, \end{aligned}$$

and therefore

$$\begin{aligned} u_2(x)=-2\displaystyle \frac{b}{a^2}+\displaystyle \frac{1}{a^2}(2b+a^2\,x^2)=x^2, \end{aligned}$$

which is the exact solution.

Example 7

[59] Consider the following linear fractional boundary value problem:

$$\begin{aligned} \begin{aligned}&4(1+x)\,D^{\frac{4}{3}}\,u(x)+4\,D^{\frac{1}{4}}\,u(x)+(1+x)^{-\frac{1}{2}}\,u(x)\\&=f(x),\qquad x\in (0,1),\\&u(0)=\sqrt{\pi }\qquad u(1)=\sqrt{2\pi }. \end{aligned} \end{aligned}$$
(64)

where f(x) is chosen such that the exact solution of (64) is given by

$$\begin{aligned} u(x)=\sqrt{\pi (1+x)}. \end{aligned}$$

We apply GLTM. Table 6 displays a comparison between the numerical scheme presented in [59] and GLTM for different values of M. The displayed results in this table ascertain that our approximations are closer to the exact one than those obtained by the method derived in [59] in almost all cases. This demonstrates that our method is advantageous if compared with the method developed in [59].

Remark 4

Aiming to illustrate the steps for the implementation of our two proposed algorithms, we add two algorithms. In Algorithm 1, we summarize the steps required for solving the nonlinear FDE in Example 4 by the method, namely GLCM, while in Algorithm 2, we summarize the steps required for solving the linear FDE in Example 5—Case 1 by the method, namely GLTM. The Mathematica program version 10 is employed for executing the required computations.

figure a
figure b

7 Conclusions

In this paper, the operational matrix of fractional derivatives of generalized Lucas polynomials is established. This operational matrix is novel, and it is fruitfully employed for handling multi-term linear and nonlinear fractional differential equations. Spectral solutions are obtained via the application of the collocation and tau methods. The convergence and error analysis are discussed using a new approach. Furthermore, the numerical results indicate that the proposed algorithms are efficient, applicable and easy in implementation. We do believe that the proposed algorithms can be applied to treat other kinds of fractional differential equations.