Analysis of nonlinear aeroelastic characteristics of a trapezoidal wing in hypersonic flow

Abstract

Nonlinear aeroelastic behavior of a trapezoidal wing in hypersonic flow is investigated. The aeroelastic governing equations are built by von Karman large deformation theory and the third-order piston theory. The Rayleigh–Ritz approach combined with the affine transformation is formulated and employed to transform the equations of a trapezoidal wing structure, modeled as a cantilevered wing-like plate, into modal coordinates. And then the modal equations are solved by numerical integrations. Several typical cases are studied to validate the capability of the proposed method for linear and nonlinear aeroelastic analysis of trapezoidal cantilever plate in hypersonic flow. The effects of Rayleigh–Ritz mode truncation for various wing-plate geometrical characteristics, i.e., sweep angle of leading edge, taper ratio and span, are examined to determine the appropriate mode number for accurate modeling and fast calculation. Meanwhile, the effects of various geometries of trapezoidal cantilever plates on the flutter stability are investigated. The nonlinear dynamic behaviors of the model with three typical geometries, namely, the rectangular, parallelogram and trapezoidal wing-like plate, are simulated numerically. Furthermore, complex dynamic behaviors are observed and identified via the phase plot, the Poincare map and the largest Lyapunov exponent. The results demonstrate that geometrical parameters of trapezoidal wing have significant effects on the nonlinear aeroelastic behaviors of wing structure. In particular, the evolution processes of chaos exhibit remarkable difference for these three wing configurations.

1 Introduction

Panel flutter is a self-excitation oscillation with aerodynamic pressure, inertia force and elastic loading functioning together. Flutter characteristics and nonlinear dynamic behaviors of panels in supersonic or hypersonic flow have been investigated by many researchers. Dowell et al. [1, 2] firstly used Rayleigh–Ritz approach to investigate the nonlinear aeroelastic behaviors of two-dimensional and three-dimensional panels. Dowell [3] also discussed qualitative and quantitative features of panel flutter and classified panel flutter analysis problems into four basic types based on the structural and aerodynamic theories adopted. Based on nonlinear piston theory applied in the hypersonic panel flutter analysis, Gray and Mei [4] proposed the fifth type of panel flutter analysis, in which both structural and aerodynamic nonlinearities were included, but material nonlinearity was not considered. Because the aerodynamic heating needs to be considered in hypersonic regime, more complex aeroelastic phenomena of panels may be observed. The sixth type of nonlinear panel analysis was also proposed with precise computational aerodynamic approaches based on CFD technique [5]. These panel flutter analysis categories are listed in Table 1.

Table 1 Panel flutter analysis types [5]

To solve the nonlinear aeroelastic governing equations of panels efficiently, Rayleigh–Ritz approximation is used for the modal representation of panel transverse deflections, and the obtained ordinary differential equations (ODEs) in modal coordinates can be integrated numerically. Ye and Dowell [6] applied Rayleigh–Ritz method to study the limit cycle oscillation (LCO) of a cantilever plate and analyzed the effect of length-to-width ratio on the nonlinear oscillations, as well as the effect of the number of modes on the amplitude of LCOs in numerical calculation. Using this model, Xie et al. [7] extended the work of Ye and Dowell, and adopted this method to observe the chaotic motions and the routes to chaos with the increase of dynamic pressure. Bakhtiari-Nejad and Nazari [8] investigated the nonlinear vibration of an isotropic cantilever plate with viscoelastic laminate. The semi-analytical nonlinear mode shapes of transverse vibration of this plate were obtained by using Ritz method. Dai et al. [9,10,11] developed a highly efficient global nonlinear Galerkin method for the analysis of the large-deflection problem of plates under combined loads and for the solution of von Karman nonlinear plate equations. In addition, Dai et al. [12, 13] proposed a time domain collocation method to solve nonlinear oscillatory problems, which is promising in the analysis of the von Karman fluttering plate. Li et al. [14] studied nonlinear dynamics and bifurcations of a two-dimensional thin panel with an external forcing in the presence of incompressible subsonic flow by using the Galerkin method, and obtained the regions of different motion types of the panel system in different parameter spaces. Zhou and Yang [15] applied the Galerkin method to study the flutter stability of heated panel with aeroelastic loading on both surfaces. Later, Yang and Zhou [16] proposed a modified local piston theory to analyze the static/dynamic aeroelasticity of curved panels.

Except for the semi-analytical Galerkin/Rayleigh–Ritz method, the finite element method (FEM) has been proposed and applied extensively to the studies of nonlinear panel flutter [4, 5, 17,18,19]. In particular, the FEM is convenient to solve the composite panel problems. Mei [17] applied FEM to study the LCO behavior of a fluttering plate at supersonic flow. Mei et al. [4, 18] predicted the nonlinear flutter characteristics of simply supported and clamped composite panels by FEM in frequency domain and time domain, respectively. The thermal effects have been considered in the hypersonic panel flutter analysis by Cheng and Mei [5]. However, the large number of degrees of freedom (DOFs) in the FEM analysis leads to the difficulty of solving flutter equations. To save computational costs, the reduced-order approach has been proposed and applied by researchers. Guo and Mei [20, 21] developed the aeroelastic modes for nonlinear panel flutter and achieved the DOFs reduction and computational cost saving greatly. Wang and Yang [22] applied Mei’s method [20] to analyze the aerothermoacoustic response of metallic panels in supersonic flow and the aeroelastic effect on dynamic behavior was considered for fatigue life prediction of panel structures. Recently, Xie et al. [23,24,25] constructed a proper orthogonal decomposition (POD) reduced-order model with a Galerkin projection to analyze the supersonic nonlinear oscillations of a simply supported plate and cantilever plate with remarkable computational savings. Furthermore, the POD method was available for the analysis of chaotic responses of nonlinear panel, and the results of existing studies demonstrated that the POD method with few modes could obtain the chaos solutions.

Fig. 1

a Schematic of trapezoidal wing-like plate geometry; b the transformed non-dimensional square-plate model

Due to the simple geometries of skin panels on a wing or fuselage, a rectangular plate model has been adopted in most of the studies. Few works focus on the cantilever plates with complex geometries with back-swept angles and taper ratios especially in hypersonic flow. Meanwhile, rekindled focus on hypersonic aircraft has resulted in the need to better understand the aeroelastic characteristics of wing model in hypersonic flow. Tang and Dowell [26,27,28] investigated a low-aspect-ratio delta wing-plate aeroelastic model at low subsonic flow, in which the flutter and LCOs of the model were observed and agreed well with experiment results. Their structure was modeled by von Karman plate theory and the reduced-order aerodynamic technique with vortex lattice aerodynamics. Shokrollahi and Bakhtiari-Nejad [29] investigated the stability and LCOs of the back-swept trapezoidal wing model at low subsonic flow. Their analysis was available for an estimation of wing structure at the conceptual design stages. Furthermore, such a model with wing-plate structural deformations has geometric strain-displacement nonlinearities and it exhibits nonlinear dynamic behaviors including LCO, bifurcation and chaos. Consequently, the exploration of nonlinear behaviors of cantilever plates has significant value for wing structures. However, to the best of authors’ knowledge, Rayleigh–Ritz approach has seldom been used for a wing-like plate with irregular geometries. And the nonlinear aeroelastic characteristics, e.g., LCO, bifurcation or chaos, for a trapezoidal cantilever plate in hypersonic flow, especially the effects of geometrical parameters on the evolution processes of chaos, have not been studied by researchers.

In the present study, we explore the nonlinear aeroelastic characteristics of a trapezoidal wing in hypersonic flow. The nonlinear third-order piston theory is used in conjunction with von Karman large deformation theory to obtain the governing equations. In order to utilize the ordinary mode functions to analyze a trapezoidal wing-like plate with different geometries, the affine transformation is proposed to combine with the Rayleigh–Ritz approach, which transforms the equations of a trapezoidal wing-like plate into modal coordinates. For wing-plate models with various geometrical characteristics, i.e., sweep angle of leading edge, taper ratio and span, the effects of mode truncation are examined by calculating LCO responses using an increasing number of retained modes, and its purpose is to determine the appropriate mode number for accurate modeling and fast calculation. Therefore, this paper firstly investigates the flutter stability and complex nonlinear dynamic responses of trapezoidal cantilever plate, and the exploration of this issue will contribute to a better understanding of the wing aeroelastic design in hypersonic flow. It is noted that a rectangular or parallelogram cantilever plate as a specific case of trapezoidal wing-like plate model are also under consideration in this study.

2 Theoretical analyses

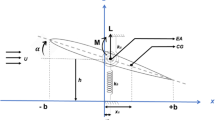
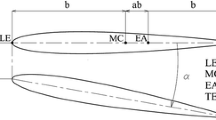
A schematic of the geometry of cantilevered trapezoidal wing-plate is shown in Fig. 1a. Here, the wing is fixed along the $y=0$ edge and free on other edges. The sweep angle of leading edge is denoted as $\alpha$. The wing taper ratio TR is defined as a ratio of the tip chord $c_\mathrm{t}$ to the root chord $c_\mathrm{r}$. The aspect ratio AR is defined in terms of the semi span l, root chord $c_\mathrm{r}$ and taper ratio TR as $\hbox {AR}={4(l/{c_\mathrm{r} })}/{(1+\hbox {TR})}$.

The nonlinear governing equations are derived from Lagrange’s equations based on the von Karman plate theory using kinetic and potential energies and the work done by applied aerodynamic loads on the plate.

2.1 Energy expressions

The von Karman nonlinear strain–displacement relation can be expressed as

$$\begin{aligned} \varepsilon _x= & {} \frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}-z\frac{\partial ^{2}w}{\partial x^{2}}=\varepsilon _x^0 -z\frac{\partial ^{2}w}{\partial x^{2}} \nonumber \\ \varepsilon _y= & {} \frac{\partial v}{\partial y}+\frac{1}{2}\left( {\frac{\partial w}{\partial y}} \right) ^{2}-z\frac{\partial ^{2}w}{\partial y^{2}}=\varepsilon _y^0 -z\frac{\partial ^{2}w}{\partial y^{2}} \nonumber \\ \gamma _{xy}= & {} \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}+\frac{\partial w}{\partial x}\frac{\partial w}{\partial y}-2z\frac{\partial ^{2}w}{\partial x\partial y}=\gamma _{xy}^0 \nonumber \\&-2z\frac{\partial ^{2}w}{\partial x\partial y} \end{aligned}$$

(1)

where $\varepsilon _x^0$ and $\varepsilon _y^0$ are the strain of the mid-plane surface in the x and y directions, respectively, and $\gamma _{xy}^0$ is the shear strain of the mid-plane surface in the xy plane.

The stress components can be obtained as:

$$\begin{aligned} \sigma _x= & {} \frac{E}{1-\upsilon ^{2}}(\varepsilon _x +\nu \varepsilon _y ) \nonumber \\ \sigma _y= & {} \frac{E}{1-\upsilon ^{2}}(\varepsilon _y +\nu \varepsilon _x ) \nonumber \\ \tau _{xy}= & {} \frac{E}{2(1+\upsilon )}\gamma _{xy} \end{aligned}$$

(2)

The potential energy of a plate is given by

$$\begin{aligned} U=\iiint {(\sigma _x \varepsilon _x +\sigma _y \varepsilon _y +\tau _{xy} \gamma _{xy} )\mathrm{d}x\mathrm{d}y\mathrm{d}z} \end{aligned}$$

(3)

Substituting the strain and stress components into Eq. (3), and integrating along the z direction, the elastic energy can be written as:

$$\begin{aligned} U= & {} \frac{h}{2}\iint {\left( \sigma _x^0 \varepsilon _x^0 +\sigma _y^0 \varepsilon _y^0 +\tau _{xy}^0 \gamma _{xy}^0 \right) \mathrm{d}x\mathrm{d}y} \nonumber \\&+\,\frac{D}{2}\iint \left[ \left( {\frac{\partial ^{2}w}{\partial x^{2}}} \right) ^{2}+\left( {\frac{\partial ^{2}w}{\partial y^{2}}} \right) ^{2}+2\nu \frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial ^{2}w}{\partial y^{2}}\right. \nonumber \\&\left. +\,2(1-\nu )\left( {\frac{\partial ^{2}w}{\partial x\partial y}} \right) ^{2} \right] \mathrm{d}x\mathrm{d}y \end{aligned}$$

(4)

where the first and second integrations denote the stretching energy $U_S$ and the bending energy $U_B$, respectively. The expressions of $U_S$ and $U_B$ can be written as:

$$\begin{aligned} U_S= & {} \frac{Eh}{2(1-\nu ^{2})}\iint \left\{ \left[ {\frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial ^{2}w}{\partial x^{2}}} \right) } \right] ^{2}\right. \nonumber \\&+\left[ {\frac{\partial v}{\partial y}+\frac{1}{2}\left( {\frac{\partial ^{2}w}{\partial y^{2}}} \right) } \right] ^{2}+2\nu \left[ {\frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial ^{2}w}{\partial x^{2}}} \right) } \right] \nonumber \\&\cdot \left[ {\frac{\partial v}{\partial y}+\frac{1}{2}\left( {\frac{\partial ^{2}w}{\partial y^{2}}} \right) } \right] \nonumber \\&\left. {+\frac{1-\nu }{2}\left[ {\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}+\frac{\partial w}{\partial x}\frac{\partial w}{\partial y}} \right] ^{2}} \right\} \mathrm{d}x\mathrm{d}y \end{aligned}$$

(5)

$$\begin{aligned} U_B= & {} \frac{D}{2}\iint \left[ \left( {\frac{\partial ^{2}w}{\partial x^{2}}} \right) ^{2}+\left( {\frac{\partial ^{2}w}{\partial y^{2}}} \right) ^{2}\right. \nonumber \\&\left. +2\nu \frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial ^{2}w}{\partial y^{2}}+2(1-\nu )\left( {\frac{\partial ^{2}w}{\partial x\partial y}} \right) ^{2} \right] \mathrm{d}x\mathrm{d}y \end{aligned}$$

(6)

The kinetic energy of the plate is expressed as:

$$\begin{aligned} T=\frac{1}{2}\iint {\rho _m h\left( {\frac{\partial w}{\partial t}} \right) ^{2}\mathrm{d}x\mathrm{d}y} \end{aligned}$$

(7)

2.2 Mode functions and expansions

Based on the Rayleigh–Ritz method, the chordwise, spanwise, and transverse deflections in non-dimensional form can be expressed through modal expansions as follows:

$$\begin{aligned} \bar{{u}}= & {} \sum _{i=1}^I {\sum _{j=1}^J {a_{ij} u_i (\xi )v_j (\eta )} } \nonumber \\ \bar{{v}}= & {} \sum _{r=1}^R {\sum _{s=1}^S {b_{rs} u_r (\xi )v_s (\eta )} } \nonumber \\ \bar{{w}}= & {} \sum _{m=1}^M {\sum _{n=1}^N {q_{mn} \varphi _m (\xi )\psi _n (\eta )} } \end{aligned}$$

(8)

For a rectangular cantilever plate, the mode function of a free-free beam and cantilever beam can be used as the mode functions of a cantilever plate in x and y directions, respectively [6]. The combination of them can satisfy the geometric boundary conditions of cantilever plate. The expressions of the mode functions are

$$\begin{aligned}&u_i (\xi )=\cos i\pi \xi , v_j (\eta )=\sin \frac{2j-1}{2}\pi \xi \nonumber \\&u_r (\xi )=\cos r\pi \xi , v_s (\eta )=\sin \frac{2s-1}{2}\pi \xi \nonumber \\&\varphi _m (\xi ) =\left\{ {{\begin{array}{l@{\quad }l} 2 &{} {m=1} \\ {2\left( {1-\xi } \right) } &{} {m=2} \\ {\sqrt{2}\sin \left( {\beta _m \xi +{3\pi }/4} \right) +\exp \left( {-\beta _m \xi } \right) +(-1)^{m+1}\exp \left[ {-\beta _m \left( {1-\xi } \right) } \right] } &{} {m>2} \\ \end{array} }} \right. \nonumber \qquad \qquad \qquad \qquad \qquad \quad \;\\&\psi _n (\eta )=\sqrt{2}\sin \left( {\beta _n \eta -\pi /4} \right) +\exp \left( {-\beta _n \eta } \right) \nonumber \\&\quad +(-1)^{n+1}\exp \left[ {-\beta _n \left( {1-\eta } \right) } \right] +(-1)^{n}\exp \left( {-\beta _n } \right) \end{aligned}$$

(9)

with $\beta _m =(m-3/2)\pi$, $\beta _n =(n-1/2)\pi$.

where $\varphi _m (\xi )$ and $\psi _n (\eta )$ are free-free and cantilever beam mode functions, respectively.

To facilitate the utilization of mode functions for a cantilever beam and free-free beam, the affine transformation is used to map a trapezoidal plate into a non-dimensional square-plate model as shown in Fig. 1b. Here, the affine transformation can be written as:

$$\begin{aligned} \xi =\frac{x/{c_\mathrm{r} }-({\hbox {AR}}/4)(1+\hbox {TR})\tan \alpha (y/l)}{1-(1-\hbox {TR})(y/l)}, \quad \eta =\frac{y}{l} \end{aligned}$$

(10)

According to Eq. (10), the transformation matrix can be obtained as:

$$\begin{aligned} \mathbf{J}= & {} \left[ {{\begin{array}{ll} {{\partial x}/{\partial \xi }}&{} {{\partial x}/{\partial \eta }} \\ {{\partial y}/{\partial \xi }}&{} {{\partial y}/{\partial \eta }} \\ \end{array} }} \right] \nonumber \\= & {} \left[ {{\begin{array}{ll} {c_\mathrm{r} \left[ {1-\left( {1-\hbox {TR}} \right) \eta } \right] }&{} {\frac{\hbox {AR}}{4}(1+\hbox {TR})\tan \alpha } \\ 0&{} l \\ \end{array} }} \right] \end{aligned}$$

(11)

2.3 Governing equations in state-space form

The governing equation of a trapezoidal cantilever plate can be reduced to that of a square plate with unit side length non-dimensionally based on the Rayleigh–Ritz method combined with affine transformation. Substituting the kinetic and potential energy equations into Lagrange’s equation,

$$\begin{aligned} \left\{ {{\begin{array}{l} {\frac{\partial L}{\partial a_{ij} }=0,} \\ {\frac{\partial L}{\partial b_{rs} }=0,} \\ {\frac{\mathrm{d}}{\mathrm{d}t}\left( {\frac{\partial L}{\partial \dot{q}_{mn} }} \right) -\frac{\partial L}{\partial q_{mn} }+Q_{mn} ,} \\ \end{array} }} \right. \end{aligned}$$

(12)

where $L=T-U$ is the Lagrangian and $Q_{mn} =\iint {\Delta p(x,y,t)\frac{\partial w}{\partial q_{mn} }\mathrm{d}x\mathrm{d}y}$ is the generalized force. We get,

$$\begin{aligned}&\frac{\partial U_S }{\partial a_{ij} }=0 \end{aligned}$$

(13a)

$$\begin{aligned}&\frac{\partial U_S }{\partial b_{rs} }=0 \end{aligned}$$

(13b)

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t}\left( {\frac{\partial T}{\partial \dot{q}_{mn} }} \right) +\frac{\partial U_B }{\partial q_{mn} }+\frac{\partial U_S }{\partial q_{mn} }+Q_{mn}=0. \end{aligned}$$

(13c)

It is assumed that all the non-conservative forces only work in the z direction and the in-plane inertia can be ignored [6]. Thus, the in-plane motion equations of motion are obtained from Eqs. (13a) and (13b). The non-dimensional in-plane motion equations are

$$\begin{aligned} \left[ {{\begin{array}{ll} {\mathbf{C}_\mathbf{a} }&{} {\mathbf{C}_\mathbf{b} } \\ {\mathbf{D}_\mathbf{a} }&{} {\mathbf{D}_\mathbf{b} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} \mathbf{a} \\ \mathbf{b} \\ \end{array} }} \right\} =\left[ {{\begin{array}{l} \mathbf{C} \\ \mathbf{D} \\ \end{array} }} \right] \end{aligned}$$

(14)

where the elements of matrices $\mathbf C _{\mathbf{a}}$, $\mathbf{C}_{\mathbf{b}}$, $\mathbf{D}_{\mathbf{a}}$, $\mathbf{D}_{\mathbf{b}}$ are given in Eqs. (15) and (16). Matrices $\mathbf{C}$, $\mathbf{D}$ are nonlinear (quadratic) functions of the transverse deflection as given in “Appendix.” Equation (14) can be solved to determine $a_{ij}$ and $b_{rs}$ in terms of $q_{mn}$.

$$\begin{aligned}&C_{kp}^{ij} =2\left( {\frac{h}{c_\mathrm{r} }} \right) ^{2}\int _0^1 {{u}'_k {u}'_i \mathrm{d}\xi } \int _0^1 {v_p v_j H^{2}{J}'\mathrm{d}\eta } \nonumber \\&\quad +(1-\nu )\left( {\frac{h}{l}} \right) ^{2} \left[ \int _0^1 {{u}'_k {u}'_i G^{2}\mathrm{d}\xi } \int _0^1 {v_p v_j H^{2}{J}'\mathrm{d}\eta }\right. \nonumber \\&\quad +\int _0^1 {{u}'_k u_i G\mathrm{d}\xi } \int _0^1 {v_p {v}'_j H{J}'\mathrm{d}\eta } \nonumber \\&\quad + \int _0^1 {u_k {u}'_i G\mathrm{d}\xi } \int _0^1 {{v}'_p v_j H{J}'\mathrm{d}\eta } \nonumber \\&\quad \left. +\int _0^1 {u_k u_i \mathrm{d}\xi } \int _0^1 {{v}'_p {v}'_j {J}'\mathrm{d}\eta } \right] \end{aligned}$$

(15a)

$$\begin{aligned}&C_{gf}^{ij} =2\nu \frac{h}{c_\mathrm{r} l}\left[ \int _0^1 {{u}'_g {u}'_i G\mathrm{d}\xi } \int _0^1 {v_f v_j H^{2}{J}'\mathrm{d}\eta } \right. \nonumber \\&\quad \left. +\int _0^1 {u_g {u}'_i \mathrm{d}\xi } \int _0^1 {{v}'_f v_j H{J}'\mathrm{d}\eta } \right] \nonumber \\&\quad {+(1-\nu )} \frac{h}{c_\mathrm{r} l}\left[ \int _0^1 {{u}'_g {u}'_i G\mathrm{d}\xi } \int _0^1 {v_f v_j H^{2}{J}'\mathrm{d}\eta } \right. \nonumber \\&\quad \left. +\int _0^1 {{u}'_g u_i \mathrm{d}\xi } \int _0^1 {v_f {v}'_j H{J}'\mathrm{d}\eta } \right] \end{aligned}$$

(15b)

$$\begin{aligned}&D_{kp}^{rs} =2\nu \frac{h}{c_\mathrm{r} l}\left[ \int _0^1 {{u}'_k {u}'_r G\mathrm{d}\xi } \int _0^1 {v_p v_s H^{2}{J}'\mathrm{d}\eta }\right. \nonumber \\&\quad \left. +\int _0^1 {{u}'_k u_r \mathrm{d}\xi } \int _0^1 {v_p {v}'_s H{J}'\mathrm{d}\eta } \right] \nonumber \\&\quad +(1-\nu )\frac{h}{c_\mathrm{r} l}\left[ \int _0^1 {{u}'_k {u}'_r G\mathrm{d}\xi } \int _0^1 {v_p v_s H^{2}{J}'\mathrm{d}\eta } \right. \nonumber \\&\quad \left. +\int _0^1 {u_k {u}'_r \mathrm{d}\xi } \int _0^1 {{v}'_p v_s H{J}'\mathrm{d}\eta } \right] \end{aligned}$$

(16a)

$$\begin{aligned}&D_{gf}^{rs} =2\left( {\frac{h}{l}} \right) ^{2}\left[ \int _0^1 {{u}'_g {u}'_r G^{2}\mathrm{d}\xi } \int _0^1 {v_f v_s H^{2}{J}'\mathrm{d}\eta }\right. \nonumber \\&\quad +\int _0^1 {{u}'_g u_r G\mathrm{d}\xi } \int _0^1 {v_f {v}'_s H{J}'\mathrm{d}\eta } \nonumber \\&\quad +\int _0^1 {u_g {u}'_r G\mathrm{d}\xi } \int _0^1 {{v}'_f v_s H{J}'\mathrm{d}\eta } \nonumber \\&\quad \left. +\int _0^1 {u_g u_r \mathrm{d}\xi } \int _0^1 {{v}'_f {v}'_s {J}'\mathrm{d}\eta } \right] \nonumber \\&\quad +(1-\nu )\left( {\frac{h}{c_\mathrm{r} }} \right) ^{2}\int _0^1 {{u}'_g {u}'_r \mathrm{d}\xi } \int _0^1 {v_f v_s H^{2}{J}'\mathrm{d}\eta }\nonumber \\ \end{aligned}$$

(16b)

In Eqs. (15) and (16),

$$\begin{aligned} H(\eta )=\frac{1}{1-c_2 \eta }, \quad G(\xi )=c_2 \xi -c_1, \quad {J}'(\eta )=1-c_2 \eta \end{aligned}$$

(17)

where $c_1 =\frac{\hbox {AR}}{4}(1+\hbox {TR})\tan \alpha$ and $c_2 =1-\hbox {TR}$.

The non-dimensional transverse motion equation can be obtained from Eq. (13c) as follows:

$$\begin{aligned} \mathbf{A}\ddot{\mathbf{q}}+\mathbf{Bq}+\mathbf{F}+\mathbf{Q}=0 \end{aligned}$$

(18)

where $\mathbf{A}$ and $\mathbf{B}$ are coefficient matrices and $\mathbf{F}$ is a nonlinear term that depends on the transverse deflection. $\mathbf{Q}$ is the generalized aerodynamic force. In this paper, the nonlinear third-order piston aerodynamics are adopted and the aerodynamic pressure $\Delta p$ is

$$\begin{aligned} \Delta p= & {} \frac{2q}{Ma}\left[ {\gamma \left( {\frac{\partial w}{\partial x}+\frac{1}{V_\infty }\frac{\partial w}{\partial t}} \right) } \right. \nonumber \\&+\frac{\kappa +1}{4}Ma\gamma ^{2}\left( {\frac{\partial w}{\partial x}+\frac{1}{V_\infty }\frac{\partial w}{\partial t}} \right) ^{2} \nonumber \\&\left. {+\frac{\kappa +1}{12}Ma^{2}\gamma ^{3}\left( {\frac{\partial w}{\partial x}+\frac{1}{V_\infty }\frac{\partial w}{\partial t}} \right) ^{3}} \right] \end{aligned}$$

(19)

where the first term, which includes the stiffness and damping components, is linear. And the second and third terms are both nonlinear.

Thus, Q can be rewritten as

$$\begin{aligned} \mathbf{Q}=\mathbf{Q}_{\mathbf{L1}} \mathbf{q}+\mathbf{Q}_{\mathbf{L2}} {\dot{\mathbf{q}}}+\mathbf{Q}_\mathbf{N} \end{aligned}$$

(20)

where $\mathbf{Q}_{\mathbf{L1}}$ and $\mathbf{Q}_{\mathbf{L2}}$ are the stiffness and damping matrices of the linear term of generalized aerodynamics, respectively. $\mathbf{Q}_{\mathbf{N}}$ is the nonlinear term of generalized aerodynamics.

Pre-multiplying Eq. (18) by the inverse of matrix A, a set of nonlinear ODEs in state-space matrix form can be written as follows:

$$\begin{aligned} {\dot{\mathbf{y}}}(\tau )= & {} \left[ {{\begin{array}{ll} \mathbf{0}&{} \mathbf{I} \\ {-\mathbf{A}^{\mathbf{-1}}{} \mathbf{(B+Q}_{\mathbf{L1}} \mathbf{)}}&{} {-\mathbf{A}^{\mathbf{-1}}{} \mathbf{Q}_{\mathbf{L2}} } \\ \end{array} }} \right] \mathbf{y}(\tau )\nonumber \\&+\left[ {{\begin{array}{ll} \mathbf{0}&{} \mathbf{0} \\ \mathbf{0}&{} {-\mathbf{A}^{\mathbf{-1}}} \\ \end{array} }} \right] \mathbf{R} \end{aligned}$$

(21)

Herein the state vector and system matrices can be represented as

$$\begin{aligned} {\dot{\mathbf{y}}}(\tau )=\left[ {{\begin{array}{l} {\mathbf{q}(\tau )} \\ {{\dot{\mathbf{q}}}(\tau )} \\ \end{array} }} \right] , \quad \mathbf{R}=\left[ {{\begin{array}{l} \mathbf{0} \\ {\mathbf{F}+\mathbf{Q}_\mathbf{N} } \\ \end{array} }} \right] \end{aligned}$$

(22)

The expressions of the matrices and vectors A, B, $\mathbf{Q}_{\mathbf{L1}}$, $\mathbf{Q}_{\mathbf{L2}}$, $\mathbf{Q}_{\mathbf{N}}$ and F are given in “Appendix.” This set of ODEs can be solved by numerical integration, and then the transverse deflection $\bar{{w}}$ can be calculated by Eq. (8).

2.4 Thermal stress and its effects

The aerodynamic heating cannot be ignored at high Mach number in hypersonic flow. The thermal effects arising from the aerodynamic heating can significantly affect the dynamic behaviors of wing. Generally, two main thermal effects should be considered: (a) the thermal expansion of structures generates in-plane thermal stresses, and may change the stiffness distribution and (b) the temperature evolution of structure may change the material properties. For such a wing-like plate model with even distributed heating, its one side is restricted and other sides are free. Thus, thermal stresses can be released from free boundaries and only little exists at the root of the plate. Therefore, the impact of thermal stresses on the cantilever plate model is usually neglected in dynamic analysis. Thus, the temperature dependence of structural material is much more significant relatively.

The aerodynamic heating can degenerate the elastic modulus of material. However, due to non-dimension expression of dynamic pressure, $\lambda {=2q_\infty c_\mathrm{r}^3 }/D$, the terms of the elastic modulus are not explicitly involved in the non-dimensional transverse equation [see Eq. (18)]. Hence, the thermal effects do not change the non-dimensional results of the flutter stability and nonlinear dynamic responses. Thus, the discussion of the following results will not refer to the thermal effects.

3 Validation of the Formulation

In the present work, the Rayleigh–Ritz approach is extended to analyze the nonlinear aeroelastic behavior of trapezoidal plates in hypersonic flow. The trapezoidal cantilever plates with different geometrical parameters, i.e., taper ratio TR, sweep angle of leading edge $\alpha$ and root chord-to-semi span ratio ${c_\mathrm{r} }/l$ are studied, respectively. In all the cases, we assume that $c_\mathrm{r} = 1.0, h= 0.01,\mu =0.1$ and $\nu =0.33$.

To validate the feasibility of the present method, the trapezoidal plate will be degenerated as a rectangular plate at first, in which $\alpha = 0^{\circ }, \hbox {TR}=1$ and ${c_\mathrm{r} }/l=1$. The first-order piston aerodynamics $\Delta p=\frac{2q}{\sqrt{Ma^{2}-1}}\left( {\frac{\partial w}{\partial x}+\frac{Ma^{2}-2}{Ma^{2}-1}\frac{1}{V_\infty }\frac{\partial w}{\partial t}} \right)$ is also adopted for comparisons. The structure and aerodynamic parameters of the plate are taken from Xie et al. [7]. The transverse deflections of LCOs at various dynamic pressures for this rectangular plate are compared with those obtained by Xie et al. [7]. The comparison of LCO behavior of this plate shown in Fig. 2 indicates a good agreement.

Fig. 2

Comparison of LCO behavior of the rectangular cantilever plate at $Ma=2$

Table 2 Modal frequencies of the trapezoidal cantilever plate model obtained by FEM and the present method ($\hbox {TR} = 0.5, \alpha = 30^{\circ }$ and ${c_\mathrm{r} }/l= 1$)

Fig. 3

Eigenvalue solutions for linear trapezoidal cantilever plate model ($\hbox {TR} = 0.5, \alpha = 30^{\circ }$ and ${c_\mathrm{r} }/l= 1$) with non-dimensional dynamic pressure $\lambda$ by using FEM and the present method

Then, to further validate the accuracy of the present computational model, the modal characteristics of the trapezoidal cantilever plate are compared with those obtained by using FEM [20]. When the nonlinear term F in Eq. (11) is set to be zero, Eq. (11) is reduced to describe a linear aeroelastic model. Table 2 lists the modal frequencies of the linear trapezoidal cantilever plate by using FEM and the present method, in which $\hbox {TR}= 0.5, \alpha = 30^{\circ }$ and ${c_\mathrm{r} }/l= 1$. The maximum error in the modal frequencies is 3.99% at the tenth mode. The flutter characteristics are calculated with the first-order piston theory at $Ma=2$, and the corresponding eigenvalue solutions with non-dimensional dynamic pressure $\lambda$ are shown in Fig. 3. It can be seen that the critical flutter dynamic pressure $\lambda _\mathrm{cr}$ obtained by using FEM and the present method is 68.93 and 67.65, respectively. These results show that the flutter boundary of the model obtained by the present method agrees well with that by FEM. The LCO amplitudes calculated by using FEM and the present method are plotted in Fig. 4. It exhibits good agreement of LCO responses obtained by using the two methods. The aforementioned results demonstrate that the derivation of formulas is precise enough in predicting the aeroelastic stability and LCO responses. It is also confirmed that the ordinary beam modes can be used for the aeroelastic analysis of a cantilever plate-like wing with various geometries.

Fig. 4

Comparison of LCO amplitudes obtained by FEM and the present method for the trapezoidal cantilever plate model ($\hbox {TR}= 0.5,\alpha = 30^{\circ }$ and ${c_\mathrm{r} }/l= 1$)

Table 3 The number of retained Rayleigh–Ritz modes for the trapezoidal cantilever plate of $\hbox {TR}=1$ and ${c_\mathrm{r} }/l=1$ with different sweep angles of leading edge

Fig. 5

LCO amplitude versus dynamic pressure for several numbers of retained modes along the airflow and the span directions for $\hbox {TR} = 1, {c_\mathrm{r} }/l=1$ and $\alpha =5^{\circ }$

Fig. 6

LCO amplitude versus dynamic pressure for several numbers of retained modes along the airflow and span directions for $\hbox {TR}=1, {c_\mathrm{r} }/l=1$ and $\alpha =45^{\circ }$

Fig. 7

LCO amplitude versus dynamic pressure for several numbers of retained modes along the airflow and span directions for $\hbox {TR}=1, {c_\mathrm{r} }/l=1$ and $\alpha =60^{\circ }$

Table 4 The number of retained Rayleigh–Ritz modes for the trapezoidal cantilever plate of $\hbox {TR} = 0.75$ with different sweep angles of leading edge

Table 5 The number of retained Rayleigh–Ritz modes for the trapezoidal cantilever plate of $\hbox {TR}=0.5$ with different sweep angles of leading edge

4 Effects of mode truncation

The effects of Rayleigh–Ritz mode truncation on the response of the system are examined to determine the appropriate number of modes to be used for a given configuration. Obviously, the predicted dynamic characteristics are closer to the real values by using more modes, but it will spend more computational time on solving the nonlinear dynamic responses. Therefore, it is expected to make a good compromise between accuracy of results and computational costs. In the present study, calculation experience shows that $J=S=2$ retained in the $\eta$ direction for in-plane displacement u and v are sufficient for cantilever plates, which also have been employed in Xie et al. [7].

Table 3 shows the number of Rayleigh–Ritz modes retained in the calculation on LCO amplitude for the trapezoidal cantilever plate of $\hbox {TR}=1$ and ${c_\mathrm{r} }/l=1$ with different sweep angles of leading edge. It can be seen that the number of retained modes along the airflow direction has little effect for the configuration with different sweep angles, but more modes along the span direction are needed with the increasing of sweep angles. The effect of the number of retained modes on the LCO amplitude for the sweep angle of leading edge $\alpha =5^{\circ }$ is shown in Fig. 5. In Fig. 5a, when two modes are used along the span direction, the amplitude obtained by six modes along the airflow direction is close to that by eight modes. Figure 5b shows that two modes along the span direction are sufficient to achieve a converged LCO amplitude. Similarly, the effects of the number of retained modes on the LCO amplitude for $\alpha =45^{\circ }$ and $\alpha =60^{\circ }$ are illustrated in Figs. 6 and 7, respectively.

To explore the effects of the number of retained modes on the response of LCO for different taper ratio TR, the number of retained Rayleigh–Ritz modes for the trapezoidal cantilever plate of $\hbox {TR}=0.75$ and $\hbox {TR}=0.5$ are listed in Tables 4 and 5, respectively. Tables 4 and 5 show that seven modes along the airflow direction are enough to obtain the dynamic characteristic of the trapezoidal cantilever plate with $\hbox {TR}=0.75$ or $\hbox {TR}=0.5$. For example, the effect of the number of retained modes on the LCO amplitude for $\hbox {TR}=0.5$ and $\alpha =5^{\circ }$ is shown in Fig. 8. It can be seen from Fig. 8a that the LCO amplitudes obtained by using $M = 7, N = 2$ agree well with those by using $M = 8, N = 2$. Thus, it can be concluded that more modes along the span direction should be used for solving nonlinear responses with the increasing of sweep angle of leading edge. In Fig. 8b, there is a slight difference between the results obtained by using $M = 4, N = 4$ and $M = 4, N = 5$. It suggests that 4 modes along the airflow direction are sufficient to achieve a converged LCO amplitude for this configuration.

Fig. 8

LCO amplitude versus dynamic pressure for several numbers of the retained modes along the airflow and span directions for $\hbox {TR}=0.5$ and $\alpha =5^{\circ }$

Table 6 The number of retained Rayleigh–Ritz modes for the trapezoidal cantilever plate of ${c_\mathrm{r} }/l=0.5$

Similarly, the effects of the number of retained Rayleigh–Ritz modes are examined using the configuration with ${c_\mathrm{r} }/l= 0.5$ and ${c_\mathrm{r} }/l= 2$ to explore whether the numbers of mode truncation will have a significant change for different ${c_\mathrm{r} }/l$. The number of retained Rayleigh–Ritz modes for the configuration with ${c_\mathrm{r} }/l= 0.5$ and ${c_\mathrm{r} }/l= 2$ are listed in Table 6 and 7, respectively. Tables 3, 4, 5, 6 and 7 demonstrate that, (1) with the increasing of sweep angle of leading edge, the number of retained modes along the span direction increases gradually for fixed ${c_\mathrm{r} }/l$ and TR, (2) as TR varies from 1.0 to 0.5, the numbers of retained modes along the airflow and span direction both increase gradually for fixed ${c_\mathrm{r} }/l$ and $\alpha$, and 3) more modes along the airflow and span directions are needed as ${c_\mathrm{r} }/l$ varies from 1.0 to 0.5.

Table 7 The number of retained Rayleigh–Ritz modes for the trapezoidal cantilever plate of ${c_\mathrm{r} }/l=2$

Fig. 9

Flutter stability of linear trapezoidal cantilever plate model for ${c_\mathrm{r} }/l= 1$

Fig. 10

Flutter stability of linear trapezoidal cantilever plate model for ${c_\mathrm{r} }/l= 0.5$

From the above discussion, it is noted that the effects of the number of retained mode on the LCO response for different configurations should be considered. In the present study, for a given geometric configuration, the appropriate retained mode number is selected from Tables 3, 4, 5, 6, and 7 to achieve a good compromise between computational accuracy and efficiency.

Fig. 11

Flutter stability of linear trapezoidal cantilever plate model for ${c_\mathrm{r} }/l= 2$

Fig. 12

Geometries of a rectangular plate, b parallelogram plate and c trapezoidal plate

5 Linear flutter analysis

When the nonlinear force F in Eq. (18) and the nonlinear term of generalized aerodynamics in Eq. (12) are neglected, it leads to a linear aeroelastic model of the trapezoidal cantilever plate and the problem of linear flutter stability in hypersonic flow can be analyzed. For all the cases studied, the parameters are $h=0.01$ m, $\mu =0.1$, $Ma=6$, unless otherwise noted. To analyze the effect of geometrical parameters, including $\alpha$, TR and ${c_\mathrm{r} }/l$, on the flutter characteristics, Figs. 9, 10 and 11 show the critical flutter dynamic pressure $\lambda _\mathrm{cr}$ and flutter frequency $\omega _\mathrm{cr}$ of the model with a variety of combinations of TR, $\alpha$ and ${c_\mathrm{r} }/l$. For such an isotropic trapezoidal plate, the linear flutter motion is dominated by the coupling of the first two natural modes, i.e., the spanwise bending mode and the chordwise torsional mode. For ${c_\mathrm{r} }/l= 1$, $\lambda _\mathrm{cr}$ is initially decreased and then increased by increasing the sweep angle of leading edge with three different TR values, while the variation trend of flutter frequency is contrary. As TR varies from 0.5 to 1.0, $\lambda _\mathrm{cr}$ and $\omega _\mathrm{cr}$ are both decreased under the same sweep angle of leading edge and this variation trend is also suitable for the cases of ${c_\mathrm{r} }/l= 0.5$ and 2. For ${c_\mathrm{r} }/l= 0.5$, $\lambda _\mathrm{cr}$ is decreased gradually by increasing the sweep angle of leading edge for these three TR values. As ${c_\mathrm{r} }/l$ is equal to 2, $\lambda _\mathrm{cr}$ is increased dramatically, but its evolution with the variation of sweep angles of leading edge is irregular. The reason of this phenomenon is that the variations of geometrical parameters change the structural and aerodynamic characteristics of the system simultaneously, that both have remarkable effects on the flutter stability. Therefore, these results can serve as a reference of parameter selection in the subsequent nonlinear aeroelastic analysis.

6 Nonlinear aeroelastic analysis

In this section, with the structural and aerodynamic nonlinearities are both considered, nonlinear aeroelastic analysis of the trapezoidal wing-like plate are simulated by using numerical integration method. All the figures are drawn with respect to a typical point $\xi =0.75$, $\eta =1.0$ of the plate. Here, a parameter marching procedure using the solution of the previous dynamic pressure as the initial conditions for the next dynamic pressure is employed in the bifurcation analysis. The bifurcation diagrams are plotted with dynamic pressure increment $\Delta \lambda =2$ in the range of periodic motions and $\Delta \lambda =0.5$ in the range of quasi-periodic or chaotic motions. The dynamic behaviors of the plate in hypersonic flow are revealed and identified via the phase plot, the power spectra, the Poincare map and the largest Lyapunov exponent. It should be mentioned that the Poincare map is plotted by recording the deflection and velocity of the typical point $\xi =0.75$, $\eta =1.0$ when the deflection time histories of the point $\xi =0.15$, $\eta =1.0$ reaches zero with a positive velocity. The Lyapunov exponent, which is computed by using the algorithm of Wolf et al. [30], is used to quantify the dynamic responses. To explore the effect of the geometry of model on nonlinear dynamic behaviors, we employ the analytical models with three typical geometries, i.e., rectangular, parallelogram and trapezoidal wing-like plates, as discussed below. These analytical models are shown in Fig. 12, and their geometrical parameters are listed in Table 8.

Table 8 Geometrical parameters of analytical models

Fig. 13

Bifurcation diagram in terms of local amplitude extreme for a rectangular cantilever plate

Fig. 14

Phase plots for a rectangular cantilever plate under several dynamic pressures in the bifurcation diagrams: a $\lambda =700$; b $\lambda =900$; c $\lambda =906$ and d $\lambda =940$

6.1 Rectangular wing-like plate

When the sweep angle of leading edge is reduced to zero, the trapezoidal plate will degenerate into a rectangular plate, which is illustrated in Fig. 12a. The bifurcation diagram of a rectangular cantilever plate, which is plotted as the local amplitude extreme with respect to the dynamic pressure $\lambda$, is shown in Fig. 13. The motion of the system converges to a stable equilibrium point for $\lambda <160$, and the dynamic pressure of the bifurcation point is in agreement with the critical flutter dynamic pressure $\lambda _\mathrm{cr} =159.43$. For dynamic pressure $160<\lambda <820$, the system exhibits a period-1 motion, and a typical phase plot is shown in Fig. 14a for $\lambda =700$. It can be seen from Fig. 13 that a sudden change takes place at $\lambda =890$ and then period-3 motions are observed between $891<\lambda <904.5$. A second bifurcation appears at $\lambda =904.5$, after which the motion becomes period-6 between $160<\lambda <820$. With the further increasing of dynamic pressure, chaotic motions are observed, a typical Poincare map of which is shown in Fig. 15d for $\lambda =940$. The Poincare map has a set of organized points, which indicates chaotic motion. The phase plots and Poincare maps for period-1, period-3, period-6 and chaotic motions are presented in Figs. 14 and 15, respectively, which reveal the evolution process of chaos of the plate dynamic responses. To sum up, these results show that the period-doubling of periodic motion is a possible approach to chaos. Using the first piston theory aerodynamics, Xie et al. [7] showed that panel oscillates in period-1, period-2, and period-4 motions and finally it goes to chaos for this model at $Ma=2$, and they concluded that the route to chaos is via period-doubling. Similar to the conclusion of Xie et al, the present study shows that the route to chaos is also via period-doubling with the nonlinear third-order piston aerodynamics.

Fig. 15

Poincare maps for a rectangular cantilever plate under several dynamic pressures in the bifurcation diagrams: a $\lambda =700$; b $\lambda =900$; c $\lambda =906$ and d $\lambda =940$

Figure 16 presents a partially enlarged bifurcation diagram of the upper branch shown in Fig. 11. The regions of chaos are separated by several periodic windows in the regions of $969.5<\lambda <985.5$, $1004<\lambda <1006$, $1018<\lambda <1020$, $1026<\lambda <1031$ and $1065.5<\lambda <1077$. Typical phase plots for $\lambda =1070$ and $\lambda =1075$ at the periodic windows are presented in Fig. 17a, b, respectively. Obviously, the phase plots show periodic responses. Furthermore, period-doubling bifurcations are also found at these periodic windows as shown in Fig. 16, and then the responses of the system go to chaos with the increasing of dynamic pressure.

Fig. 16

Partially enlarged bifurcation diagram of the upper branch for a rectangular cantilever plate

Fig. 17

Phase portraits at the periodic windows between $1065.5<\lambda <1077$ of the bifurcation diagram: a $\lambda =1070$ and b $\lambda =1076$

6.2 Parallelogram wing-like plate

When $\hbox {TR}=1$ and $\alpha >0$, the trapezoidal plate is simplified into a parallelogram plate. In this case, we will discuss the nonlinear dynamic behaviors of a parallelogram wing-like plate, of which the geometrical parameters are given in Table 8. The numbers of retained modes are taken as $I=R=14, M=6, N=3$ for this model with ${c_\mathrm{r} }/l=1, \hbox {TR}=1.0$ and $\alpha =30^{\circ }$ based on the result of mode truncation in Sect. 4. Its bifurcation diagram in terms of local amplitude extreme with respect to dynamic pressure $\lambda$ is shown in Fig. 18.

Fig. 18

Bifurcation diagram in terms of local amplitude extreme for a parallelogram cantilever plate

Fig. 19

Phase plots for a parallelogram cantilever plate under several dynamic pressure: a $\lambda =450$; b $\lambda =650$; c $\lambda =700$ and d $\lambda =750$

Fig. 20

Partially enlarged bifurcation diagram of the upper branch for the parallelogram cantilever plate

For dynamic pressure $120<\lambda <398$, the responses present single periodic motions. Then, the first bifurcation takes place at $\lambda =398$ and causes a transition from period-1 motion to period-3 motion. Unlike the rectangular cantilever plate, the parallelogram cantilever plate model does not go to chaos via period-doubling directly, but the route to chaos exhibits more complex process. Between dynamic pressure $398<\lambda <795$, the system presents period-1 and complex LCOs alternately. The four typical phase plots are shown in Fig. 19. With the increasing of $\lambda$, the responses exhibit quasi-periodic motions and complex LCOs, and finally trend to chaotic motions. Figure 20 presents the partially enlarged bifurcation diagram shown in Fig. 18. Here, a quasi-periodic motion for $\lambda =796$ and a complex LCO for $\lambda =806$ are demonstrated in Fig. 21 as representations before chaos. In Fig. 21b, the Poincare map for $\lambda =796$ shows two closed loops, which indicate a quasi-periodic motion. In particular, Fig. 21c, d shows a complex LCO for $\lambda =806$, although the response is in complex dynamic response region. Between $797.5<\lambda <811$, the motion of the system mainly exhibits quasi-period and complex LCOs. For larger dynamic pressure $\lambda >811$, the motion of the system goes to chaos. The time history, phase plot, and Poincare map of chaotic responses for $\lambda =830$ are shown in Fig. 22a–c, respectively. All of them indicate a typical chaotic motion.

Fig. 21

Dynamic responses for the parallelogram cantilever plate under given dynamic pressures: a phase plot at $\lambda =796$; b Poincare maps at $\lambda =796$; c phase plot at $\lambda =806$ and d Poincare maps at $\lambda =806$

6.3 Trapezoidal wing-like plate

For a trapezoidal wing-like plate shown in Fig. 12c, its bifurcation diagram is shown in Fig. 23. To examine the approach to chaos, the partially enlarged bifurcation diagram of the lower branch of Fig. 23 in the region of $1150<\lambda <1550$ is presented in Fig. 24. In this case, the Lyapunov exponent is employed to identify the chaotic motions. The corresponding LLE values for $1150<\lambda <1550$ are shown in Fig. 25, in which a positive LLE value indicates a chaotic motion while a zero or negative LLE value indicates a periodic/quasi-periodic motion. Based on Fig. 25, chaotic response is predicted in regions of $1232.5<\lambda <1257$ and $\lambda >1264$, but a periodic window exists between these two chaotic regions. These results keep a good consistency with the bifurcation diagram shown in Fig. 24.

Furthermore, it is observed from Fig. 24 that the motion of the system also exhibits complex response in several regions of $1150<\lambda <1232.5$. However, a converged zero or negative LLE value is calculated in these regions. For several typical dynamic pressures, the phase plot and Poincare map are presented to estimate the motion type shown in Fig. 26. For $\lambda =1178$, the phase plot in Fig. 26a presents a narrow band and the Poincare map in Fig. 26b shows a closed loop. Both of them indicate a quasi-periodic response. For $\lambda =1190$ and $\lambda =1228$, the closed loops in the Poincare maps mean that they are also quasi-periodic motions rather than chaotic motions. Therefore, the route to chaos for this trapezoidal cantilever plate model in the current study is via the quasi-periodic motion. Meanwhile, several periodic windows exist before the occurrence of chaotic motions.

Fig. 22

Chaotic response at $\lambda =830$ for the parallelogram cantilever plate: a time history; b phase portrait; c Poincare map

Fig. 23

Bifurcation diagram in terms of local amplitude extreme for a trapezoidal cantilever plate

Fig. 24

Partially enlarged bifurcation diagram of the lower branch for the trapezoidal cantilever plate

Fig. 25

The largest Lyapunov exponent versus the dynamic pressure $\lambda$ for the trapezoidal cantilever plate

Moreover, to find out the approach to chaos, several dynamic pressures in chaotic regions of $1232.5<\lambda <1257$ and $\lambda >1264$ are taken as examples shown in Fig. 27. It can be observed from the results of $\lambda =1235$, $\lambda =1300$ and $\lambda =1500$ that the phase plots exhibit more complex responses with the increasing of dynamic pressure $\lambda$. From the comparison of the Poincare maps shown in Figs. 26f and 27d–f, it is observed that a quasi-periodic torus in Fig. 26f breaks, and then turns into a cloud of points gradually with the increasing of dynamic pressure $\lambda$. Therefore, the evolution process from period-1, quasi-periodic to chaotic motions reflects the broken of quasi-periodic torus.

Fig. 26

Phase portraits and Poincare maps for the trapezoidal cantilever plate under given dynamic pressures: a phase plot at $\lambda =1178$; b Poincare maps at $\lambda =1178$; c phase plot at $\lambda =1190$; d Poincare maps at $\lambda =1190$; e phase plot at $\lambda =1228$ and f Poincare maps at $\lambda =1228$

Fig. 27

Phase plots and Poincare maps for the trapezoidal cantilever plate under given dynamic pressures: a–c phase plots for $\lambda =1235$, $\lambda =1300$ and $\lambda =1500$; d–f Poincare maps for $\lambda =1235$, $\lambda =1300$ and $\lambda =1500$

7 Conclusions

To utilize the ordinary mode functions to analyze a trapezoidal cantilever plate with various geometries in hypersonic flow, the Rayleigh–Ritz approach is combined with the affine transformation. The von Karman plate theory and nonlinear third-order piston theory aerodynamics are used to establish the governing equations, which are solved by numerical integration. The validity of this approach for linear and nonlinear model has been provided by comparing current results with results from the literature. The effects of Rayleigh–Ritz mode truncation on the response of the system are examined to determine the appropriate number of modes to be used for a given geometry and achieve a good compromise between accuracy of results and the efficiency of the present method.

For plates with different geometries, the flutter stability and nonlinear dynamic behaviors are analyzed. The combination of time history, phase plot, Poincare map and the largest Lyapunov exponent are employed to identify the type of dynamic behaviors. The following conclusions can be drawn from the numerical examples:

• (a) The geometrical parameters have significant effects on flutter boundary of the system. For fixed root chord-to-semi span ratio ${c_\mathrm{r} }/l$ and sweep angle $\alpha$ of leading edge, the flutter speed and frequency decrease with the increasing of taper ratio TR. For different ${c_\mathrm{r} }/l$, the variations of the flutter boundary have detectable difference with the increasing of $\alpha$.

• (b) For the rectangular wing-like plate of ${c_\mathrm{r} }/l= 1, \hbox {TR} = 1$ and $\alpha = 0^{\circ }$, the route to chaos is through period-doubling, i.e., period-1, period-3, and period-6 responses. The chaotic regions are separated by several periodic windows.

• (c) For the parallelogram wing-like plate of ${c_\mathrm{r} }/l= 1, \hbox {TR}=1$ and $\alpha = 30^{\circ }$, unlike period-doubling bifurcation of the rectangular cantilever plate, the parallelogram cantilever plate shows more complex process of the route to chaos. In particular, the responses of the system mainly exhibit the quasi-periodic motions and complex LCOs before the occurrence of chaos.

• (d) For the trapezoidal wing-like plate of ${c_\mathrm{r} }/l= 1, \hbox {TR}=0.5$ and $\alpha = 30^{\circ }$, the route from periodic motions to chaos is via the broken of quasi-periodic torus. The quasi-periodic and chaotic regions are also separated by periodic windows.

Appendix

Elements of matrix A:

$$\begin{aligned} A_{mn}^{ij} =\frac{1}{6}\int _0^1 {\phi _m \phi _i } \mathrm{d}\xi \int _0^1 {\psi _n \psi _j {J}'\mathrm{d}\eta } \end{aligned}$$

Elements of matrix B:

$$\begin{aligned}&B_{mn}^{ij} = \frac{1}{6}\left\{ {\int _0^1 {{{\phi ''}_m}{{\phi ''}_i}\mathrm{d}\xi } \int _0^1 {{\psi _n}{\psi _j}{H^4}J'\mathrm{d}\eta } } \right. \\&+ {\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^4}\int _0^1 {{{\phi ''}_m}{{\phi ''}_i}{G^4}\mathrm{d}\xi } \int _0^1 {{\psi _n}{\psi _j}{H^4}J'\mathrm{d}\eta } \\&+ 2\nu {\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^2}\int _0^1 {{{\phi ''}_m}{{\phi ''}_i}{G^2}\mathrm{d}\xi } \int _0^1 {{\psi _n}{\psi _j}{H^4}J'\mathrm{d}\eta } \\&+ 2(1 - \nu ){\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^2}\int _0^1 {{{\phi ''}_m}{{\phi ''}_i}{G^2}\mathrm{d}\xi } \int _0^1 {{\psi _n}{\psi _j}{H^4}J'\mathrm{d}\eta }\\&+ {{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) }^4}\int _0^1 {{\phi _m}{\phi _i}\mathrm{d}\xi } \int _0^1 {{{\psi ''}_n}{{\psi ''}_j}J'\mathrm{d}\eta }\\&+ {\left( {2{c_2}} \right) ^2}{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^4}\int _0^1 {{{\phi '}_m}{{\phi '}_i}{G^2}\mathrm{d}\xi } \int _0^1 {{\psi _n}{\psi _j}{H^4}J'\mathrm{d}\eta } \\&+ 2(1 - \nu ){c_2}^2{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^2}\int _0^1 {{{\phi '}_m}{{\phi '}_i}\mathrm{d}\xi } \int _0^1 {{\psi _n}{\psi _j}{H^4}J'\mathrm{d}\eta }\\&+ 4{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^4}\int _0^1 {{{\phi '}_m}{{\phi '}_i}{G^2}\mathrm{d}\xi } \int _0^1 {{{\psi '}_n}{{\psi '}_j}{H^2}J'\mathrm{d}\eta } \\&+ 2(1 - \nu ){\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^2}\int _0^1 {{{\phi '}_m}{{\phi '}_i}\mathrm{d}\xi } \int _0^1 {{{\psi '}_n}{{\psi '}_j}{H^2}J'\mathrm{d}\eta }\\&+ {\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^4}\left[ \int _0^1 {{{\phi ''}_m}{\phi _i}{G^2}\mathrm{d}\xi } \int _0^1 {{\psi _n}{{\psi ''}_j}{H^2}J'\mathrm{d}\eta } \right. \\&\left. + \int _0^1 {{\phi _m}{{\phi ''}_i}{G^2}\mathrm{d}\xi } \int _0^1 {{{\psi ''}_n}{\psi _j}{H^2}J'\mathrm{d}\eta } \right] \\&+ v{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^2}\left[ \int _0^1 {{\phi _m}{{\phi ''}_i}\mathrm{d}\xi } \int _0^1 {{\psi ''}_n}{\psi _j}{H^2}J'\mathrm{d}\eta \right. \\&\left. + \int _0^1 {{\phi _m}{{\phi ''}_i}\mathrm{d}\xi } \int _0^1 {{{\psi ''}_n}{\psi _j}{H^2}J'\mathrm{d}\eta } \right] \\&+ 2{c_2}{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^4}\left[ \int _0^1 {{{\phi ''}_m}{{\phi '}_i}{G^3}\mathrm{d}\xi } \int _0^1 {{\psi _n}{\psi _j}{H^4}J'\mathrm{d}\eta } \right. \\&\left. + \int _0^1 {{{\phi '}_m}{{\phi ''}_i}{G^3}\mathrm{d}\xi } \int _0^1 {{\psi _n}{\psi _j}{H^4}J'\mathrm{d}\eta } \right] \\&+ 2{c_2}{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^2}\left[ \int _0^1 {{{\phi ''}_m}{{\phi '}_i}G\mathrm{d}\xi } \int _0^1 {\psi _n}{\psi _j}{H^4}J'\mathrm{d}\eta \right. \\&\left. + \int _0^1 {{{\phi '}_m}{{\phi ''}_i}G\mathrm{d}\xi } \int _0^1 {{\psi _n}{\psi _j}{H^4}J'\mathrm{d}\eta } \right] \\&+ 4{c_2}{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^4}\left[ \int _0^1 {{{\phi '}_m}{{\phi '}_i}{G^2}\mathrm{d}\xi } \int _0^1 {\psi _n}{{\psi '}_j}{H^3}J'\mathrm{d}\eta \right. \\&\left. + \int _0^1 {{{\phi '}_m}{{\phi '}_i}{G^2}\mathrm{d}\xi } \int _0^1 {{{\psi '}_n}{\psi _j}{H^3}J'\mathrm{d}\eta } \right] \\&+ 2{c_2}(1 - \nu ){\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^2}\left[ \int _0^1 {{{\phi '}_m}{{\phi '}_i}\mathrm{d}\xi } \int _0^1 {\psi _n}{{\psi '}_j}{H^4}J'\mathrm{d}\eta \right. \\&\left. + \int _0^1 {{{\phi '}_m}{{\phi '}_i}\mathrm{d}\xi } \int _0^1 {{{\psi '}_n}{\psi _j}{H^4}J'\mathrm{d}\eta } \right] \\&+ 2{c_2}{{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) }^4}\left[ \int _0^1 {{\phi _m}{{\phi '}_i}G\mathrm{d}\xi } \int _0^1 {{\psi ''}_n}{\psi _j}{H^2}J'\mathrm{d}\eta \right. \\&\left. + \int _0^1 {{{\phi '}_m}{\phi _i}G\mathrm{d}\xi } \int _0^1 {{\psi _n}{{\psi ''}_j}{H^2}J'\mathrm{d}\eta } \right] \\&+ 2{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^4}\left[ \int _0^1 {{{\phi ''}_m}{{\phi '}_i}{G^3}\mathrm{d}\xi } \int _0^1 {\psi _n}{{\psi '}_j}{H^3}J'\mathrm{d}\eta \right. \\&\left. + \int _0^1 {{{\phi '}_m}{{\phi ''}_i}{G^3}\mathrm{d}\xi } \int _0^1 {{{\psi '}_n}{\psi _j}{H^3}J'\mathrm{d}\eta } \right] \\&+ 2{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) ^2}\left[ \int _0^1 {{{\phi ''}_m}{{\phi '}_i}G\mathrm{d}\xi } \int _0^1 {\psi _n}{{\psi '}_j}{H^3}J'\mathrm{d}\eta \right. \\&\left. + \int _0^1 {{{\phi '}_m}{{\phi ''}_i}G\mathrm{d}\xi } \int _0^1 {{{\psi '}_n}{\psi _j}{H^3}J'\mathrm{d}\eta } \right] \\&+ 2{{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) }^4}\left[ \int _0^1 {{\phi _m}{{\phi '}_i}G\mathrm{d}\xi } \int _0^1 {{\psi ''}_n}{{\psi '}_j}HJ'\mathrm{d}\eta \right. \\&\left. \left. + \int _0^1 {{{\phi '}_m}{\phi _i}G\mathrm{d}\xi } \int _0^1 {{{\psi '}_n}{{\psi ''}_j}HJ'\mathrm{d}\eta } \right] \right\} \end{aligned}$$

Elements of matrices C, D

$$\begin{aligned}&C^{ij}=-\left( {\frac{h}{c_\mathrm{r} }} \right) ^{3}\sum _m^M {\sum _n^N {\sum _p^M {\sum _l^N {q_{mn} q_{pl} } } } } \int _0^1 {{\phi }'_m {\phi }'_p {u}'_i \mathrm{d}\xi } \nonumber \\&\quad \times \int _0^1 {\psi _n \psi _l v_j H^{3}{J}'\mathrm{d}\eta } \\&\quad {-\,\nu } \left( {\frac{h}{l}} \right) ^{2}\left( {\frac{h}{c_\mathrm{r} }} \right) \sum _m^M \sum _n^N \sum _p^M \sum _l^N q_{mn} q_{pl} \nonumber \\&\quad \left[ \int _0^1 {{\phi }'_m {\phi }'_p {u}'_i G^{2}\mathrm{d}\xi } \right. \nonumber \\&\quad \times \int _0^1 {\psi _n \psi _l v_j H^{3}{J}'\mathrm{d}\eta } +2\int _0^1 {{\phi }'_m \phi _p {u}'_i G\mathrm{d}\xi } \\&\quad \times \int _0^1 {\psi _n {\psi }'_l v_j H^{2}{J}'\mathrm{d}\eta }\nonumber \\&\quad \left. +\,{\int _0^1 {\phi _m \phi _p {u}'_i \mathrm{d}\xi } \int _0^1 {{\psi }'_n {\psi }'_l v_j H{J}'\mathrm{d}\eta } } \right] \\&\quad -(1-\nu )\left( {\frac{h}{l}} \right) ^{2}\left( {\frac{h}{c_\mathrm{r} }} \right) \sum _m^M \sum _n^N \sum _p^M \sum _l^N q_{mn} q_{pl} \nonumber \\&\quad \left[ \int _0^1 {{\phi }'_m {\phi }'_p {u}'_i G^{2}\mathrm{d}\xi } \int _0^1 {\psi _n \psi _l v_j H^{3}{J}'\mathrm{d}\eta } \right. \\&\quad \left. +\,\int _0^1 {{\phi }'_m {\phi }'_p u_i G\mathrm{d}\xi } \int _0^1 {\psi _n \psi _l {v}'_j H^{2}{J}'\mathrm{d}\eta } \right. \\&\quad +\, \int _0^1 {{\phi }'_m \phi _p {u}'_i G\mathrm{d}\xi } \int _0^1 {\psi _n {\psi }'_l v_j H^{2}{J}'\mathrm{d}\eta } \\&\quad \left. +\,\int _0^1 {{\phi }'_m \phi _p u_i \mathrm{d}\xi } \int _0^1 {\psi _n {\psi }'_l {v}'_j H{J}'\mathrm{d}\eta } \right] \\&D^{rs}=-\left( {\frac{h}{l}} \right) ^{3}\sum _m^M \sum _n^N \sum _p^M \sum _l^N q_{mn} q_{pl} \\&\quad \left[ \int _0^1 {{\phi }'_m {\phi }'_p {u}'_r G^{3}\mathrm{d}\xi } \int _0^1 {\psi _n \psi _l v_s H^{3}{J}'\mathrm{d}\eta } \right. \\&\quad \left. +\int _0^1 {{\phi }'_m {\phi }'_p u_r G^{2}\mathrm{d}\xi } \int _0^1 {\psi _n \psi _l {v}'_s H^{2}{J}'\mathrm{d}\eta } \right. \\&\quad +\,2\int _0^1 {{\phi }'_m \phi _p {u}'_r G^{2}\mathrm{d}\xi } \int _0^1 {\psi _n {\psi }'_l v_s H^{2}{J}'\mathrm{d}\eta } \\&\quad +\,2\int _0^1 {{\phi }'_m \phi _p u_r G\mathrm{d}\xi } \int _0^1 {\psi _n {\psi }'_l {v}'_s H{J}'\mathrm{d}\eta } \\&\quad +\, \int _0^1 {\phi _m \phi _p {u}'_r G\mathrm{d}\xi } \int _0^1 {{\psi }'_n {\psi }'_l v_s H{J}'\mathrm{d}\eta } \\&\quad \left. +\,\int _0^1 {\phi _m \phi _p u_r \mathrm{d}\xi } \int _0^1 {{\psi }'_n {\psi }'_l {v}'_s {J}'\mathrm{d}\eta } \right] \\&\quad -\,\nu \left( {\frac{h}{l}} \right) \left( {\frac{h}{c_\mathrm{r} }} \right) ^{2}\sum _m^M {\sum _n^N {\sum _p^M {\sum _l^N {q_{mn} q_{pl} } } } } \\&\quad \left[ \int _0^1 {{\phi }'_m {\phi }'_p {u}'_r G\mathrm{d}\xi }\right. \\&\int _0^1 {\psi _n \psi _l v_s H^{3}{J}'\mathrm{d}\eta } +\int _0^1 {{\phi }'_m {\phi }'_p u_r \mathrm{d}\xi } \\&\quad \left. \int _0^1 {\psi _n \psi _l {v}'_s H^{2}{J}'\mathrm{d}\eta } \right] \\&\quad -(1-\nu )\left( {\frac{h}{l}} \right) \left( {\frac{h}{c_\mathrm{r} }} \right) ^{2}\sum _m^M {\sum _n^N {\sum _p^M {\sum _l^N {q_{mn} q_{pl} } } } } \nonumber \\&\quad \left[ \int _0^1 {{\phi }'_m {\phi }'_p {u}'_r G\mathrm{d}\xi }\right. \\&\int _0^1 {\psi _n \psi _l v_s H^{3}{J}'\mathrm{d}\eta } +\int _0^1 {{\phi }'_m \phi _p {u}'_r \mathrm{d}\xi } \nonumber \\&\quad \left. \int _0^1 {\psi _n {\psi }'_l v_s H^{2}{J}'\mathrm{d}\eta } \right] \end{aligned}$$

Elements of matrices $\mathbf{Q}_{\mathbf{L1}}$, $\mathbf{Q}_{\mathbf{L2}}$, $\mathbf{Q}_{\mathbf{N}}$:

$$\begin{aligned}&Q_{kl}^{ij} =\frac{\lambda }{6}\frac{\gamma }{M_\infty }\int _0^1 {{\phi }'_k \phi _i \mathrm{d}\xi } \int _0^1 {\psi _l \psi _j H{J}'\mathrm{d}\eta }\\&Q_{\mathrm{mn}}^{ij} =\frac{\lambda }{6}\frac{\gamma }{M_\infty }\sqrt{\frac{\mu }{\lambda }}\int _0^1 {\phi _m \phi _i \mathrm{d}\xi } \int _0^1 {\psi _n \psi _j {J}'\mathrm{d}\eta }\\&Q_{\mathrm{N}}^{ij} =\frac{\lambda }{6}\left\{ \frac{\kappa +1}{4}\gamma ^{2}\frac{h}{c_\mathrm{r} }\left[ \sum _m^M \sum _n^N \sum _k^M \sum _l^N q_{mn} q_{kl} \right. \right. \nonumber \\&\quad \left. \left. \int _0^1 {{\phi }'_m {\phi }'_k \phi _i \mathrm{d}\xi \int _0^1 {\psi _n \psi _l \psi _j H^{2}{J}'} } \mathrm{d}\eta \right. \right. \\&\quad +\,2\sqrt{\frac{\mu }{\lambda }}\sum _m^M \sum _n^N \sum _k^M \sum _l^N q_{mn} \dot{q}_{kl} \int _0^1 {\phi }'_m \phi _k \phi _i \mathrm{d}\xi \nonumber \\&\int _0^1 {\psi _n \psi _l \psi _j H{J}'} \mathrm{d}\eta \\&\quad +\,\frac{\mu }{\lambda }\sum _m^M \sum _n^N \sum _k^M \sum _l^N \dot{q}_{mn} \dot{q}_{kl} \int _0^1 \phi _m \phi _k \phi _i \mathrm{d}\xi \nonumber \\&\quad \left. \times \int _0^1 {\psi _n \psi _l \psi _j {J}'} \mathrm{d}\eta \right] \\&\quad +\,\frac{\kappa +1}{12}M_\infty \gamma ^{3}\left( {\frac{h}{c_\mathrm{r} }} \right) ^{2}\\&\quad \times \left[ \sum _k^M \sum _l^N \sum _m^M \sum _n^N \sum _r^M \sum _s^N q_{kl} q_{mn} q_{rs} \right. \nonumber \\&\int _0^1 {{\phi }'_k {\phi }'_m {\phi }'_r \phi _i \mathrm{d}\xi \int _0^1 {\psi _l \psi _n \psi _s \psi _j H^{3}{J}'} } \mathrm{d}\eta \\&\quad +\,3\sqrt{\frac{\mu }{\lambda }}\sum _k^M \sum _l^N \sum _m^M \sum _n^N \sum _r^M \sum _s^N q_{kl} q_{mn} \dot{q}_{rs} \nonumber \\&\quad \times \int _0^1 {{\phi }'_k {\phi }'_m \phi _r \phi _i \mathrm{d}\xi \int _0^1 {\psi _l \psi _n \psi _s \psi _j H^{2}{J}'} } \mathrm{d}\eta \\&\quad +\,3\frac{\mu }{\lambda }\sum _k^M \sum _l^N \sum _m^M \sum _n^N \sum _r^M \sum _s^N q_{kl} \dot{q}_{mn} \dot{q}_{rs} \nonumber \\&\int _0^1 {{\phi }'_k \phi _m \phi _r \phi _i \mathrm{d}\xi \int _0^1 {\psi _l \psi _n \psi _s \psi _j H{J}'} } \mathrm{d}\eta \\&\quad +\,\left( {\sqrt{\frac{\mu }{\lambda }}} \right) ^{3}\sum _k^M \sum _l^N \sum _m^M \sum _n^N \sum _r^M \sum _s^N \dot{q}_{kl} \dot{q}_{mn} \dot{q}_{rs} \\&\left. \left. \int _0^1 {\phi _k \phi _m \phi _r \phi _i \mathrm{d}\xi \int _0^1 {\psi _l \psi _n \psi _s \psi _j {J}'} } \mathrm{d}\eta \right] \right\} \end{aligned}$$

Elements of matrix F:

$$\begin{aligned}&{F^{ij}} = 2\left( {\frac{{{c_\mathrm{r}}}}{h}} \right) \sum \limits _m^I \sum \limits _n^J \sum \limits _k^M \sum \limits _l^N {a_{mn}}{q_{kl}}\int _0^1 {{u'}_m}{{\phi '}_k}{{\phi '}_i}\mathrm{d}\xi \\&\times \int _0^1 {{v_n}{\psi _l}{\psi _j}{H^3}J'} \mathrm{d}\eta \\&+ \sum \limits _k^M \sum \limits _l^N \sum \limits _m^M \sum \limits _n^N \sum \limits _r^M \sum \limits _s^N {q_{kl}}{q_{mn}}{q_{rs}}\\&\times \int _0^1 {{{\phi '}_k}{{\phi '}_m}{{\phi '}_r}{{\phi '}_i}\mathrm{d}\xi \int _0^1 {{\psi _l}{\psi _n}{\psi _s}{\psi _j}{H^4}J'} } \mathrm{d}\eta \\&+ 2{{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) }^3}\left( {\frac{{{c_\mathrm{r}}}}{h}} \right) \sum \limits _r^R \sum \limits _s^S \sum \limits _k^M \sum \limits _l^N {b_{rs}}{q_{kl}}\\&\left[ \int _0^1 {{{u'}_r}{{\phi '}_k}{{\phi '}_i}{G^3}\mathrm{d}\xi \int _0^1 {{v_s}{\psi _l}{\psi _j}{H^3}J'} } \mathrm{d}\eta \right. \\&+ \int _0^1 {{{u'}_r}{{\phi '}_k}{\phi _i}{G^2}\mathrm{d}\xi \int _0^1 {{v_s}{\psi _l}{{\psi '}_j}{H^2}J'} } \mathrm{d}\eta \\&+\int _0^1 {{{u'}_r}{\phi _k}{{\phi '}_i}{G^2}\mathrm{d}\xi \int _0^1 {{v_s}{{\psi '}_l}{\psi _j}{H^2}J'} } \mathrm{d}\eta \\&+ \int _0^1 {{{u'}_r}{\phi _k}{\phi _i}G\mathrm{d}\xi \int _0^1 {{v_s}{{\psi '}_l}{{\psi '}_j}HJ'} } \mathrm{d}\eta \\&+\int _0^1 {{u_r}{{\phi '}_k}{{\phi '}_i}{G^2}\mathrm{d}\xi \int _0^1 {{{v'}_s}{\psi _l}{\psi _j}{H^2}J'} } \mathrm{d}\eta \\&+ \int _0^1 {{u_r}{{\phi '}_k}{\phi _i}G\mathrm{d}\xi \int _0^1 {{{v'}_s}{\psi _l}{{\psi '}_j}HJ'} } \mathrm{d}\eta \\&+ \int _0^1 {{u_r}{\phi _k}{{\phi '}_i}G\mathrm{d}\xi \int _0^1 {{{v'}_s}{{\psi '}_l}{\psi _j}HJ'} } \mathrm{d}\eta \\&\left. + \int _0^1 {{u_r}{\phi _k}{\phi _i}\mathrm{d}\xi \int _0^1 {{{v'}_s}{{\psi '}_l}{{\psi '}_j}J'} } \mathrm{d}\eta \right] \\&+ {{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) }^4}\sum \limits _k^M \sum \limits _l^N \sum \limits _m^M \sum \limits _n^N \sum \limits _r^M \sum \limits _s^N {q_{kl}}{q_{mn}}{q_{rs}}\\&\left[ \int _0^1 {{{\phi '}_k}{{\phi '}_m}{{\phi '}_r}{{\phi '}_i}{G^4}\mathrm{d}\xi \int _0^1 {{\psi _l}{\psi _n}{\psi _s}{\psi _j}{H^4}J'} } \mathrm{d}\eta \right. \\&+ 3\int _0^1 {{{\phi '}_k}{{\phi '}_m}{\phi _r}{{\phi '}_i}{G^3}\mathrm{d}\xi \int _0^1 {{\psi _l}{\psi _n}{{\psi '}_s}{\psi _j}{H^3}J'} } \mathrm{d}\eta \\&+3\int _0^1 {{{\phi '}_k}{\phi _m}{\phi _r}{{\phi '}_i}{G^2}\mathrm{d}\xi \int _0^1 {{\psi _l}{{\psi '}_n}{{\psi '}_s}{\psi _j}{H^2}J'} } \mathrm{d}\eta \\&+ \int _0^1 {{\phi _k}{\phi _m}{\phi _r}{{\phi '}_i}G\mathrm{d}\xi \int _0^1 {{{\psi '}_l}{{\psi '}_n}{{\psi '}_s}{\psi _j}HJ'} } \mathrm{d}\eta \\&+ \int _0^1 {{{\phi '}_k}{{\phi '}_m}{{\phi '}_r}{\phi _i}{G^3}\mathrm{d}\xi \int _0^1 {{\psi _l}{\psi _n}{\psi _s}{{\psi '}_j}{H^3}J'} } \mathrm{d}\eta \end{aligned}$$

$$\begin{aligned}&+3\int _0^1 {{{\phi '}_k}{{\phi '}_m}{\phi _r}{\phi _i}{G^2}\mathrm{d}\xi \int _0^1 {{\psi _l}{\psi _n}{{\psi '}_s}{{\psi '}_j}{H^2}J'} } \mathrm{d}\eta \\&\mathrm{{ + }}3\int _0^1 {{{\phi '}_k}{\phi _m}{\phi _r}{\phi _i}G\mathrm{d}\xi \int _0^1 {{\psi _l}{{\psi '}_n}{{\psi '}_s}{{\psi '}_j}HJ'} } \mathrm{d}\eta \\&\left. + \int _0^1 {{\phi _k}{\phi _m}{\phi _r}{\phi _i}\mathrm{d}\xi \int _0^1 {{{\psi '}_l}{{\psi '}_n}{{\psi '}_s}{{\psi '}_j}J'} } \mathrm{d}\eta \right] \\&+ 2\nu {{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) }^2}\left( {\frac{{{c_\mathrm{r}}}}{h}} \right) \sum \limits _m^I \sum \limits _n^J \sum \limits _k^M \sum \limits _l^N {a_{mn}}{q_{kl}}\\&\left[ \int _0^1 {{{u'}_m}{{\phi '}_k}{{\phi '}_i}{G^2}\mathrm{d}\xi \int _0^1 {{v_n}{\psi _l}{\psi _j}{H^3}J'} } \mathrm{d}\eta \right. \\&+ \int _0^1 {{{u'}_m}{\phi _k}{{\phi '}_i}G\mathrm{d}\xi \int _0^1 {{v_n}{{\psi '}_l}{\psi _j}{H^2}J'} } \mathrm{d}\eta \\&\mathrm{{ + }}\int _0^1 {{{u'}_m}{{\phi '}_k}{\phi _i}G\mathrm{d}\xi \int _0^1 {{v_n}{\psi _l}{{\psi '}_j}{H^2}J'} } \mathrm{d}\eta \\&\left. + \int _0^1 {{{u'}_m}{\phi _k}{\phi _i}\mathrm{d}\xi \int _0^1 {{v_n}{{\psi '}_l}{{\psi '}_j}HJ'} } \mathrm{d}\eta \right] + \nu {{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) }^2}\\&\sum \limits _k^M \sum \limits _l^N \sum \limits _m^M \sum \limits _n^N \sum \limits _r^M \sum \limits _s^N {q_{kl}}{q_{mn}}{q_{rs}}\\&\left[ 2\int _0^1 {{\phi '}_k}{{\phi '}_m}{{\phi '}_r}{{\phi '}_i}{G^2}\mathrm{d}\xi \right. \\&\int _0^1 {{\psi _l}{\psi _n}{\psi _s}{\psi _j}{H^4}J'} \mathrm{d}\eta + \int _0^1 {{\phi '}_k}{{\phi '}_m}{\phi _r}{{\phi '}_i}G\mathrm{d}\xi \\&\int _0^1 {{\psi _l}{\psi _n}{{\psi '}_s}{\psi _j}{H^3}J'} \mathrm{d}\eta \\&+2\int _0^1 {{{\phi '}_k}{\phi _m}{{\phi '}_r}{{\phi '}_i}G\mathrm{d}\xi \int _0^1 {{\psi _l}{{\psi '}_n}{\psi _s}{\psi _j}{H^3}J'} } \mathrm{d}\eta \\&+\int _0^1 {{\phi _k}{\phi _m}{{\phi '}_r}{{\phi '}_i}\mathrm{d}\xi \int _0^1 {{{\psi '}_l}{{\psi '}_n}{\psi _s}{\psi _j}{H^2}J'} } \mathrm{d}\eta \\&+\int _0^1 \phi _k^\prime \phi _m^\prime \phi _r^\prime \phi _i G\mathrm{d}\xi \int _0^1\psi _l \psi _n\psi _s\psi _j^\prime H^3J^\prime \mathrm{d}\eta \\&\left. +\int _0^1 \phi _k^\prime \phi _m^\prime \phi _r\phi _i \mathrm{d}\xi \int _0^1\psi _l \psi _n\psi _s^\prime \psi _j^\prime H^2J^\prime \mathrm{d}\eta \right] \\&+\, 2v\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) \left( {\frac{{{c_\mathrm{r}}}}{h}} \right) \sum \limits _r^R \sum \limits _s^S \sum \limits _k^M \sum \limits _l^N {b_{rs}}{q_{kl}}\\&\left[ \int _0^1 {{{u'}_r}{{\phi '}_k}{{\phi '}_i}G\mathrm{d}\xi \int _0^1 {{v_s}{\psi _l}{\psi _j}{H^3}J'} } \mathrm{d}\eta \right. \\&\left. + \int _0^1 {{u_r}{{\phi '}_k}{{\phi '}_i}\mathrm{d}\xi \int _0^1 {{{v'}_s}{\psi _l}{\psi _j}{H^2}J'} } \mathrm{d}\eta \right] \\&+ (1 - v)\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) \left( {\frac{{{c_\mathrm{r}}}}{h}} \right) \sum \limits _r^R \sum \limits _s^S \sum \limits _k^M \sum \limits _l^N {b_{rs}}{q_{kl}}\\&\left[ 2\int _0^1 {{{u'}_r}{{\phi '}_k}{{\phi '}_i}G\mathrm{d}\xi \int _0^1 {{v_s}{\psi _l}{\psi _j}{H^3}J'} } \mathrm{d}\eta \right. \\&+ \int _0^1 {{{u'}_r}{{\phi '}_k}{\phi _i}\mathrm{d}\xi \int _0^1 {{v_s}{\psi _l}{{\psi '}_j}{H^2}J'} } \mathrm{d}\eta \\&\left. {\mathrm{{ + }}\int _0^1 {{{u'}_r}{\phi _k}{{\phi '}_i}\mathrm{d}\xi \int _0^1 {{v_s}{{\psi '}_l}{\psi _j}{H^2}J'} } \mathrm{d}\eta } \right] \\&+ (1 - v){{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) }^2}\left( {\frac{{{c_\mathrm{r}}}}{h}} \right) \sum \limits _m^I \sum \limits _n^J \sum \limits _k^M \sum \limits _l^N {a_{mn}}{q_{kl}}\\&\left[ 2\int _0^1 {{{u'}_m}{{\phi '}_k}{{\phi '}_i}{G^2}\mathrm{d}\xi \int _0^1 {{v_n}{\psi _l}{\psi _j}{H^3}J'} } \mathrm{d}\eta \right. \\&+ \int _0^1 {{{u'}_m}{{\phi '}_k}{\phi _i}G\mathrm{d}\xi \int _0^1 {{v_n}{\psi _l}{{\psi '}_j}{H^2}J'} } \mathrm{d}\eta \\&+ 2\int _0^1 {{u_m}{{\phi '}_k}{{\phi '}_i}G\mathrm{d}\xi \int _0^1 {{{v'}_n}{\psi _l}{\psi _j}{H^2}J'} } \mathrm{d}\eta \\&+ \int _0^1 {{u_m}{{\phi '}_k}{\phi _i}\mathrm{d}\xi \int _0^1 {{{v'}_n}{\psi _l}{{\psi '}_j}HJ'} } \mathrm{d}\eta \\&+ \int _0^1 {{{u'}_m}{\phi _k}{{\phi '}_i}G\mathrm{d}\xi \int _0^1 {{v_n}{{\psi '}_l}{\psi _j}{H^2}J'} } \mathrm{d}\eta \\&\left. + \int _0^1 {{u_m}{\phi _k}{{\phi '}_i}\mathrm{d}\xi \int _0^1 {{{v'}_n}{{\psi '}_l}{\psi _j}HJ'} } \mathrm{d}\eta \right] \\&+ (1 - v){{\left( {\frac{{{c_\mathrm{r}}}}{l}} \right) }^2}\sum \limits _k^M \sum \limits _l^N \sum \limits _m^M \sum \limits _n^N \sum \limits _r^M \sum \limits _s^N {q_{kl}}{q_{mn}}{q_{rs}}\\&\left[ 2\int _0^1 {{{\phi '}_k}{{\phi '}_m}{{\phi '}_r}{{\phi '}_i}{G^2}\mathrm{d}\xi \int _0^1 {{\psi _l}{\psi _n}{\psi _s}{\psi _j}{H^4}J'} } \mathrm{d}\eta \right. \\&+ \int _0^1 {{{\phi '}_k}{{\phi '}_m}{{\phi '}_r}{\phi _i}G\mathrm{d}\xi \int _0^1 {{\psi _l}{\psi _n}{\psi _s}{{\psi '}_j}{H^3}J'} } \mathrm{d}\eta \\&+2\int _0^1 {{{\phi '}_k}{\phi _m}{{\phi '}_r}{{\phi '}_i}G\mathrm{d}\xi \int _0^1 {{\psi _l}{{\psi '}_n}{\psi _s}{\psi _j}{H^3}J'} } \mathrm{d}\eta \\&+\int _0^1 {{{\phi '}_k}{\phi _m}{{\phi '}_r}{\phi _i}\mathrm{d}\xi \int _0^1 {{\psi _l}{{\psi '}_n}{\psi _s}{{\psi '}_j}{H^2}J'} } \mathrm{d}\eta \\&+ \int _0^1 {{{\phi '}_k}{{\phi '}_m}{\phi _r}{{\phi '}_i}G\mathrm{d}\xi \int _0^1 {{\psi _l}{\psi _n}{{\psi '}_s}{\psi _j}{H^3}J'} } \mathrm{d}\eta \\&\left. + \int _0^1 {{{\phi '}_k}{\phi _m}{\phi _r}{{\phi '}_i}\mathrm{d}\xi \int _0^1 {{\psi _l}{{\psi '}_n}{{\psi '}_s}{\psi _j}{H^2}J'} } \mathrm{d}\eta \right] \end{aligned}$$