1 Introduction

It is well known that parallel mechanisms have significant advantages over serial mechanisms in terms of accuracy, rigidity and payload ability [1–4]. Compared with serial open-loop mechanisms, the kinematics of parallel mechanisms is more complex due to their multi-closed-loop structures. The complexity of kinematics leads to quite complicated dynamic model because dynamics is a natural extension of kinematics [5, 6]. Therefore, the derivation of explicit dynamic equations in the actuation space for parallel mechanisms is often difficult except several particular manipulators. However, the precise dynamic equations in the actuation space play an important role in design and operation of robotic devices. In design, dynamic equations are employed as the dynamic constraints for an optimal design process or as a tool to test performance indexes of a robot. As regards robot operations, dynamic equations are the most important part to develop control laws and determine controller’s parameters; inverse dynamics are always used to compute the actuation forces as feedforward information in order to achieve desired motions, which are called the internal model control or model-based control. The trajectory tracking performance of most commercial parallel robots is limited because they are controlled by simple single-joint feedback controller ignoring the coupled dynamics. Unlike the serial mechanisms that have well-established modeling and control methods, most studies of the parallel mechanisms focus on kinematics and optimal design issues. To the best of our knowledge, the dynamic modeling of parallel mechanisms is still an open problem. Therefore, we aim for an efficient method for the derivation of the control-oriented dynamic model, i.e., the explicit closed-form dynamic equations in the actuation space.

The literature on the dynamic modeling is rather vast, and it will be impossible to mention all of them. For parallel mechanisms, there are mainly four kinds of methods to build the dynamic equations for them. The first one is the Newton–Euler method. Dasgupta and Mruthyunjaya [7] obtained the dynamic equations of two types of the Stewart platform via Newton–Euler method. Using this approach, the acceleration of every isolated rigid body should be obtained. All constraint forces and moments between the joints also should be obtained because of the application of the Newton–Euler equations for each rigid body, whereas the internal forces and moments of interaction between elements of a robot are useless for the control of a manipulator. The second method that is widely used is Kane’s method. Kane proposed Kane’s dynamical equations for robotics applications to formulate explicit equations of motion [8, 9]. This approach uses Lagrange’s form of d’Alembert’s principle, as exposited by Houston and Passerello in [10–13]. Lagrange’s form of d’Alembert’s principle states that the sum of the total generalized active force and the total generalized inertia force, for each generalized coordinate of the system, is zero, which are Kane’s dynamical equations. Kane’s dynamical equations have the advantage of automatically eliminating “no-working” internal constraint forces. In order to efficiently obtain the generalized forces needed for Kane’s equations, the concepts of partial angular velocity and partial velocity are introduced by Kane [8, 9]. Subsequently, Houston and Amirouche made great contribution to the development of Kane’s method [14–23]. As for dynamic modeling of parallel mechanisms, they employed the combination of Kane’s dynamic equations and constrained kinematic equations or undetermined multipliers embedded in Kane’s equations. Then, in order to derive the explicit dynamic equations with respect to the independent coordinates, the zero eigenvalue decomposition and pseudo-uptriangular decomposition methods are proposed by Houston and Amitouche, respectively, to eliminate the undetermined multipliers. Their method is an efficient method especially when the dimension of the constraint equations is large due to a large number of rigid bodies of the multi-body system. However, the derivation of partial velocities and accelerations are inevitable, which needs a bit of tedious calculations. Lieh [24] studied Kane’s method employed by Wang and Huston [15] and indicated that they didn’t generate the closed-form dynamic equations. Then, he successfully used the principle of virtual work to get the closed-form dynamic model for closed-loop systems [24, 25]. Currently, the principle of virtual work has been a very popular method to derive dynamic models of parallel mechanisms [26–29]. The principle of virtual work states that the work done by a dynamically equilibrium system undergoing arbitrarily displacement vanishes. It is salient that the “no-working” forces can be dropped out from the virtual work equation, which is very similar with Kane’s method. The calculation of every body’s acceleration is also demanded in this approach. Different to the Newton–Euler approach, the characteristic of the principle of virtual work for a system equaling zero is applied to combine all dynamic equations of isolated bodies into one dynamic equation of the total manipulator. However, Guo and Li [30] think the method based on principle of virtual work delivers only an implicit model of inverse dynamics. The last one is Lagrangian formulation. Traditionally, Lagrange’s method considers the system as a whole instead of isolating each body as the other methods mentioned above. Lagrange’s method is very successful for serial mechanisms since the Lagrangian function is simply expressed by the actuator variables for serial mechanisms, whereas quite a few of literature have used the Lagrangian formulation for parallel mechanisms due to the constraints introduced by the closed loops. In [31–34], because of the complexity of the kinematics, dynamic model simplification was suggested, like neglecting Coriolis terms or inertia tensors. In [35], the passive joint variables are involved in generalized coordinates, which increases the dimension of dynamic equations. So, the result in [35] is not the expected explicit form of dynamics. Additionally, most of the previous works just consider the primary rigid body dynamics of a manipulator while neglect the friction even the actuator dynamics. However, for an actual physical prototype, the actuator dynamics and friction frequently play a large part in the governing equations of motion. It was demonstrated in [36] that for some systems, friction compensation yields significant improvement of control performance. Obviously, a precise dynamic model without neglecting any parts of the dynamic equations would benefit the perception of the system and controller design. Below we contribute to remove all these drawbacks. The novelty of this paper is the combination of Lagrangian formulation and the virtual work principle for being free of the complicated computation of acceleration and internal forces and moments. This is an important advantage of the modeling approach over the Newton–Euler formulation.

In this paper, the Lagrangian formulation is restudied in order to determine the explicit closed-form dynamic equations in the actuation space of parallel mechanisms by combining the Lagrangian formulation with the principle of virtual work. The closed-loop structure of the manipulator is opened into several serial subchains in order to form explicit energy functions of subsystems with respect to their local coordinates for the convenience of the subsequent differentiating calculation. The dynamics of subsystems corresponding to different local generalized coordinates can be easily obtained through Lagrange’s equations of the second type because of the conveniences of the Lagrange formulation for serial robots. However, the dynamic equations of subsystems should be grouped into the closed-form dynamic equations of the manipulator corresponding to the active generalized coordinates. The virtual work principle could transform the generalized joint torques into another joint space according to the relationship between different generalized coordinates. The Jacobian and Hessian matrices, which represent the key of robot’s kinematics, play the transformation bridge roles in combining different dynamic equations of isolated body subsystems. The cube Hessian matrices are only utilized in the study of kinematics in [37, 38]. Here, we introduce them into dynamic equations, which make the equations more concise. Additionally, the inclusion of friction in the derived rigid body dynamic equations is also discussed.

The goal of this paper is to propose an alternative dynamic modeling method for parallel robots. This method is embedded with four desired merits. (1) Accuracy the use of virtual work principle to deal with kinematic constraints makes the Lagrangian formulation available for parallel robots without neglecting any parts of dynamic equations; hence, the derived dynamic model is an accurate rigid body dynamic model without any simplification. (2) Convenient implementation there are only five steps to obtain the final dynamic model for any non-redundant parallel robots and the process is easy to be implemented by computer algebra program. (3) Explicit expression the derived dynamic equations are explicit with respect to active joints, which is important for the solution of forward dynamics. (4) High efficiency the derivation process for the explicit closed-form dynamic equations is high efficiency, and the computational cost for solution of inverse dynamics is low enough for online model-based control.

The paper is organized as follows. The problems of using the Lagrangian formulation to derive dynamic equations for parallel mechanisms are discussed in detail in Sect. 2. The proposed approach is then developed in Sect. 3. In Sect. 4, as an application example, the inverse kinematics of a 3-DOF parallel manipulator is analyzed. Then, the dynamic equations of motion are formulated through the proposed approach. In Sect. 5, the dynamic equations are verified by the commercial software ADAMS and experiments on a test bed. Some conclusions and future research directions are given in Sect. 6. Although the 3-DOF manipulator is used as an example to illustrate the modeling approach, the methodology can be used for other types of parallel manipulators.

2 Problem formulation

When neglecting the friction and other disturbances, for non-redundant N-DOF mechanisms, the explicit closed-form dynamic equations is a N-dimensional set of differential equations as

$$\begin{aligned} \mathbf{D}\ddot{\mathbf{q}}_a +\mathbf{C}\dot{\mathbf{q}}_a +\mathbf{G}={\varvec{\uptau }}_a, \end{aligned}$$
(1)

where \(\mathbf{q}_{a}\in \mathbf{R}^{N}\) is the vector of the active generalized coordinates that is the coordinates of the actuators. \(\varvec{\uptau }_{a}\) denotes the vector of the corresponding active forces. The inertia matrix, the Coriolis and centrifugal terms, and the gravitational forces are denoted by \(\mathbf{D}\), \(\mathbf{C}\) and \(\mathbf{G}\), respectively. Eq. (1) is given in the actuation space responding to \(\mathbf{q}_{a}\), which is very useful for internal model control, dynamic simulation and real-time application. Eq. (1) can be directly derived by Lagrange’s equations of the second type

$$\begin{aligned} \frac{d}{dt}\frac{\partial E_k (\mathbf{q}_a )}{\partial \mathbf{q}_a }-\frac{\partial E_k (\mathbf{q}_a )}{\partial \mathbf{q}_a }+\frac{\partial E_p (\mathbf{q}_a )}{\partial \mathbf{q}_a }={\varvec{\uptau } }_a, \end{aligned}$$
(2)

where \(E_k (\mathbf{q}_a )\) and \(E_p (\mathbf{q}_a )\) denote the kinetic energy and potential energy of the whole system, respectively. \(E_k (\mathbf{q}_a )\) and \(E_p (\mathbf{q}_a )\) are expressed by \(\mathbf{q}_a \) that are the vector of active variables responding to time. For serial mechanisms, all coordinates are active joint variables. So the kinetic energy and potential energy are naturally expressed in terms of \(\mathbf{q}_a \). For parallel mechanisms, the active joints are commonly prismatic joints, and the kinetic energy and potential energy are conveniently expressed by a set of general coordinates \(\mathbf{q}\) composed of both active and passive joint variables, rather than only expressed by active joint variables. Therefore, the kinetic energy and potential energy of parallel mechanisms denoted by \(E_k (\mathbf{q})\) and \(E_p (\mathbf{q})\), respectively, are in function of \(\mathbf{q}\) and time t. Hence, the partial derivatives with respect to \(\mathbf{q}_a \), i.e., \(\partial E_k (\mathbf{q})/\partial \mathbf{q}_a \) and \(\partial E_p (\mathbf{q})/\partial \mathbf{q}_a \), are very hard to be computed. This is the special problem of parallel mechanisms in contrast to serial mechanisms. The most common way to solve this problem is to obtain the relationship between \(\mathbf{q}_a \) and \(\mathbf{q}\) by the geometrical constraints of the parallel mechanism, i.e.,

$$\begin{aligned} f(\mathbf{q}_a,\mathbf{q})=0. \end{aligned}$$
(3)

In the best case, Eq. (3) could be transformed into an explicit form where every general coordinate could be determined by functions of the active general coordinates. Unfortunately, Eq. (3) always cannot be transformed into an explicit form, which makes it impossible to determine of \(E_k (\mathbf{q}_a )\) and \(E_p (\mathbf{q}_a )\) explicitly. As for traditional Lagrangian formalism, one must perform unnecessary labor in introducing and subsequently eliminating Lagrange multipliers. That is the drawback of the usual way to apply the traditional Lagrangian formalism for dynamic modeling of parallel mechanisms. When using Kane’s equations to obtain the dynamic model, as mentioned before, the pseudo-uptriangular decomposition [18], the zero eigenvalue theorem [14], and the singular value decomposition method [39] are employed to eliminate the undetermined multipliers in Kane’s equations. However, we are trying to make the Lagrangian formalism for parallel mechanisms to overcome this obstacle. In the following sections, we will show how the principle of virtual work provides an efficient approach to solve the abovementioned problems.

3 Lagrangian formalism for parallel mechanisms

Assume that the manipulator can be divided into several isolated rigid bodies. The vector of the generalized coordinates corresponding to \(i\hbox {th} (i=1, \ldots , m)\) isolated rigid body denotes \(\mathbf{q}_i \). The Jacobian matrix between \(\mathbf{q}_i \) and \(\mathbf{q}\) can be obtained by kinematic analysis. So the velocity mapping relationship has the following equation,

$$\begin{aligned} \dot{\mathbf{q}}_i =\mathbf{J}_i \dot{\mathbf{q}}. \end{aligned}$$
(4)

where \(\mathbf{q}_i \in \mathbf{R}^{n_i }\), \(\mathbf{q}\in \mathbf{R}^{N}\), \(\mathbf{J}_i \in \mathbf{R}^{n_i \times N}\). The generalized forces corresponding to \(\mathbf{q}_i \) are defined as \(\mathbf{f}_i \). According to the virtual work principle, the following forces transformation exists,

$$\begin{aligned} {\varvec{\uptau }}_i =\mathbf{J}_i^T \mathbf{f}_i, \end{aligned}$$
(5)

where \({\varvec{\uptau }}_i \) indicates the mapping from \(\mathbf{f}_i \) to another generalized coordinates, i.e., \(\mathbf{q}\). Eq. (5) for forces transformation gives us a new idea to formulate the dynamics of multi-body systems.

Firstly, we use the Lagrangian formulation to derive the dynamics of isolated bodies with respect to their local generalized coordinates, as follows,

$$\begin{aligned} \mathbf{M}_i (\mathbf{q}_i )\ddot{\mathbf{q}}_i +\mathbf{C}_i (\mathbf{q}_i,\dot{\mathbf{q}}_i )\dot{\mathbf{q}}_i +\mathbf{G}_i (\mathbf{q}_i )=\mathbf{f}_i, \end{aligned}$$
(6)

where \(\mathbf{f}_i \) is the vector of generalized forces. Left multiplying Eq. (6) by \(\mathbf{J}_i^T \), the following equation is obtained,

$$\begin{aligned} \mathbf{J}_i^T \mathbf{M}_i (\mathbf{q}_i )\ddot{\mathbf{q}}_i +\mathbf{J}_i^T \mathbf{C}_i (\mathbf{q}_i,\dot{\mathbf{q}}_i )\dot{\mathbf{q}}_i +\mathbf{J}_i^T \mathbf{G}_i (\mathbf{q}_i )={\varvec{\uptau }}_i. \end{aligned}$$
(7)

Eq. (7) reveals the contribution to the generalized forces \({\varvec{\uptau }}_i \) of the motion of the ith isolated rigid body. Here, the Coriolis and centrifugal terms \(\mathbf{C}_i (\mathbf{q}_i ,\dot{\mathbf{q}}_i )\dot{\mathbf{q}}_i \) can be rewrite as follows,

$$\begin{aligned} \mathbf{C}_i (\mathbf{q}_i,\dot{\mathbf{q}}_i )\dot{\mathbf{q}}_i =\dot{\mathbf{q}}_i^T {*}\,\mathbf{H}_{ci} (\mathbf{q}_i ) \dot{\mathbf{q}}_i, \end{aligned}$$
(8)

where \(\mathbf{H}_{ci} (\mathbf{q}_i )\in \mathbf{R}^{n_i \times n_i \times n_i }\)is the cubic Hessian matrix; the sign “\({*}\)” denotes a generalized scalar product [37, 38]. And \(n_i \) denotes the dimension of \(\mathbf{q}_i \). The generalized scalar product of two matrices \(\mathbf{X}\in \mathbf{R}^{m\times n}\) and \(\mathbf{Y}\in \mathbf{R}^{n\times p\times p}\) are defined as follows,

$$\begin{aligned} \left[ {\mathbf{XY}} \right] _{k::} =\sum _{l=1}^n {\mathbf{X}_{k:l} \mathbf{Y}_{l::} } \in \mathbf{R}^{p\times p},\quad k=1,2, \ldots ,m\nonumber \\ \end{aligned}$$
(9)

where \(\mathbf{XY}\in \mathbf{R}^{m\times p\times p}\). Equation (9) means that only when the column number of \(\mathbf{X}\) is equal to the layer number of \(\mathbf{Y}\), the two matrices \(\mathbf{X}\) and \(\mathbf{Y}\) can be multiplied using the generalized scalar product.

Afterward, substituting Eq. (8) to (7), yields,

$$\begin{aligned}&{} \mathbf{J}_i^T \mathbf{M}_i (\mathbf{q}_i )\ddot{\mathbf{q}}_i + \dot{\mathbf{q}}_i^T {*}\,[\mathbf{J}_i^T {*}\,\mathbf{H}_{ci} (\mathbf{q}_i )]\dot{\mathbf{q}}_i\nonumber \\&\quad +\, \mathbf{J}_i^T \mathbf{G}_i (\mathbf{q}_i )={\varvec{\uptau }}_i . \end{aligned}$$
(10)

where \(\mathbf{J}_i^T \in {} \mathbf{R}^{N\times n_i }\). Therefore, \(\mathbf{J}_i^T {*}{} \mathbf{H}_{ci} (\mathbf{q}_i )\in \mathbf{R}^{N\times n_i \times n_i }\) according to Eq. (9). However, \(\mathbf{q}_i^T \in \mathbf{R}^{1\times n_i }\). This implies that only when \(n_i =N\) is satisfied, Eq. (10) can be used. Otherwise, please don’t use Hessian matrix and keep using \(\mathbf{C}_i (\mathbf{q}_i,\dot{\mathbf{q}}_i )\). Hereinafter, assume that \(n_i \) is equal to N. The application of Hessian matrix separates \(\dot{\mathbf{q}}_i \) from \(\mathbf{C}_i (\mathbf{q}_i,\dot{\mathbf{q}}_i )\), which brings convenience to transform Eq. (10) to standard form of Eq. (1).

Next, differentiating Eq. (4) with respect to time, yields,

$$\begin{aligned} \ddot{\mathbf{q}}_i =\mathbf{J}_i \ddot{\mathbf{q}}+\dot{\mathbf{J}}_i \dot{\mathbf{q}}=\mathbf{J}_i \ddot{\mathbf{q}}+\dot{\mathbf{q}}^{T}{*}\,\mathbf{H}_i \dot{\mathbf{q}}. \end{aligned}$$
(11)

Similarly, if \(n_i \) is not equal to N, please keep using \(\dot{\mathbf{J}}_i \) and don’t use \(\mathbf{H}_i \).

Substituting Eqs. (4) and (11) to Eq. (10), the following equation is obtained,

$$\begin{aligned}&{} \mathbf{J}_i^T \mathbf{M}_i (\mathbf{q}_i )\mathbf{J}_i \ddot{\mathbf{q}}+\dot{\mathbf{q}}^{T}{*}[\mathbf{J}_i^T \mathbf{M}_i (\mathbf{q}_i ){*}\,\mathbf{H}_i \nonumber \\&\quad +\,\mathbf{J}_i^T \mathbf{J}_i^T {*}\,\mathbf{H}_{ci} (\mathbf{q}_i )\mathbf{J}_i ]\dot{\mathbf{q}} + \, \mathbf{J}_i^T \mathbf{G}_i (\mathbf{q}_i )={\varvec{\uptau }}_i. \end{aligned}$$
(12)

The dynamic equations with respect to the generalized coordinates \(\mathbf{q}\) of the full manipulator can be derived by summing Eq. (12) with respect to each isolated rigid body, as follows,

$$\begin{aligned}&\left[ \sum _{i=1}^m {\mathbf{J}_i^T \mathbf{M}_i (\mathbf{q}_i )\mathbf{J}_i } \right] \ddot{\mathbf{q}}+\dot{\mathbf{q}}^{T}\nonumber \\&\quad {*}\,\left[ \sum _{i=1}^m {(\mathbf{J}_i^T \mathbf{M}_i (\mathbf{q}_i ){*}\,\mathbf{H}_i +\mathbf{J}_i^T \mathbf{J}_i^T {*}\,\mathbf{H}_{ci} (\mathbf{q}_i )\mathbf{J}_i } )\right] \dot{\mathbf{q}}\nonumber \\&\quad +\sum _{i=1}^m {\mathbf{J}_i^T \mathbf{G}_i (\mathbf{q}_i )} =\sum _{i=1}^m {{\varvec{\uptau }}_i } ={\varvec{\uptau }}. \end{aligned}$$
(13)

Let \(\mathbf{q}\) be the vector of the active generalized coordinates. Thus, Eq. (13) takes the form of Eq. (1), as follows,

$$\begin{aligned}&\left[ \sum _{i=1}^m {\mathbf{J}_i^T \mathbf{M}_i (\mathbf{q}_i )\mathbf{J}_i } \right] \ddot{\mathbf{q}}_a +\dot{\mathbf{q}}_a^T\nonumber \\&\quad {*}\,\left[ \sum _{i=1}^m {(\mathbf{J}_i^T \mathbf{M}_i (\mathbf{q}_i ){*}\,\mathbf{H}_i +\mathbf{J}_i^T \mathbf{J}_i^T {*}\,\mathbf{H}_{ci} (\mathbf{q}_i )\mathbf{J}_i } )\right] \dot{\mathbf{q}}_a\nonumber \\&\quad +\sum _{i=1}^m {\mathbf{J}_i^T \mathbf{G}_i (\mathbf{q}_i )} ={\varvec{\uptau }}_a. \end{aligned}$$
(14)

If \(\mathbf{q}\) is not the vector of the active generalized coordinates, it is possible to find the relationships. Introductions,

$$\begin{aligned}&\dot{\mathbf{q}}=\mathbf{J}\dot{\mathbf{q}}_a, \end{aligned}$$
(15)
$$\begin{aligned}&{\varvec{\uptau }}_a =\mathbf{J}^{T}{\varvec{\uptau }}, \end{aligned}$$
(16)
$$\begin{aligned}&\ddot{\mathbf{q}}=\mathbf{J}\ddot{\mathbf{q}}_a +\dot{\mathbf{q}}_a^T {*}\,\mathbf{H}\dot{\mathbf{q}}_a. \end{aligned}$$
(17)

Introducing Eqs. (15)–(17) into Eq. (13) yields,

$$\begin{aligned}&\left[ \sum _{i=1}^m {\mathbf{J}^{T}{} \mathbf{J}_i^T \mathbf{M}_i (\mathbf{q}_i )\mathbf{J}_i } \mathbf{J}\right] \ddot{\mathbf{q}}_a +\dot{\mathbf{q}}_a^T\nonumber \\&\quad {*}\,\left[ \sum _{i=1}^m {\mathbf{J}^{T}{} \mathbf{J}_i^T \mathbf{M}_i (\mathbf{q}_i ){*}\,\mathbf{HJ}_i }+\sum _{i=1}^m (\mathbf{J}^{T}{} \mathbf{J}^{T}{} \mathbf{J}_i^T \mathbf{M}_i (\mathbf{q}_i ) {*}\,\mathbf{H}_i \mathbf{J}\right. \nonumber \\&\quad \left. +\,\mathbf{J}^{T}{} \mathbf{J}^{T}{} \mathbf{J}_i^T \mathbf{J}_i^T{*}\,\mathbf{H}_{ci} (\mathbf{q}_i )\mathbf{J}_i \mathbf{J})\right] \dot{\mathbf{q}}_a+\sum _{i=1}^m {\mathbf{J}^{T}{} \mathbf{J}_i^T \mathbf{G}_i (\mathbf{q}_i )} ={\varvec{\uptau }}_a.\nonumber \\ \end{aligned}$$
(18)

Equation (18) is the explicit closed-form dynamic equations in the actuation space of a general parallel mechanism. The abovementioned algorithm giving the dynamic model of parallel mechanisms can be summarized to the following five steps.

  1. Step 1.

    A multi-closed-chain manipulator can be divided into several open-chain isolated rigid body by cutting selected joints.

  2. Step 2.

    Derive the dynamic equations of the isolated subchains with respect to the local generalized coordinates \(\mathbf{q}_i \) by the direct Lagrangian formulation.

  3. Step 3.

    Transform dynamic equations of each subchain into equations with respect to the same generalized coordinates \(\mathbf{q}\) (maybe the active generalized coordinates \(\mathbf{q}_a\)) through the virtual work principle.

  4. Step 4.

    Use Jacobian and Hessian matrices to transform local generalized coordinates to the same generalized coordinates.

  5. Step 5.

    Sum all the equations of subsystems to obtain the closed-form dynamic equations of the full manipulator. If \(\mathbf{q}\ne \mathbf{q}_a \), transform the full dynamic equations with respect to \(\mathbf{q}\) to equations with respect to \(\mathbf{q}_a \) by the approach mentioned in steps 3 and 4.

4 Dynamics of a 3-DOF spatial parallel manipulator

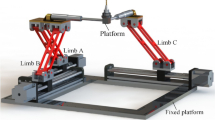
There have been a great number of practical applications of parallel mechanisms, such as the aircraft simulator [40], the force/torque sensor [41], and the acceleration sensor [42]. In recent years, the limited-DOF manipulators that both maintain the inherent advantages of parallel mechanisms and possess several other advantages in terms of the total cost reduction in manufacturing [43] and wider workspace are attracting more attentions of researchers, for instance the Delta robot [44], and Tricept robot and TriVariant robot [45]. In this paper, the 3-DOF spatial parallel manipulator presented in reference [46], which contains 1-UP chain and 2-UPS chains, is used as an example to verify the effectiveness of the proposed modeling approach. U, P, and S denote universal, prismatic, and spherical joint respectively. P pair is the actuated joint driven by an actuator. This 3-DOF parallel manipulator can be used as cutting robot or grabbing robot after assembling corresponding terminal effectors. The CAD model of the 3-DOF manipulator is represented in Fig. 1.

Fig. 1
figure 1

Spatial 3-DOF parallel manipulator with three linear actuators

Full size image
Fig. 2
figure 2

Schematic diagram of the 1-UP&2-UPS manipulator

Full size image

4.1 Kinematics

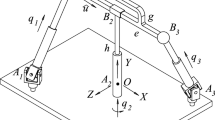
Figure 2 shows the schematic diagram of the 3-DOF manipulator, which can be decomposed into six isolated rigid bodies. The six isolated rigid bodies are called Link 1 to 6, respectively, and their corresponding center of mass is defined as \(c1,{\ldots }, c6\) as shown in Fig. 2. \(U_i (i=1,2,3)\) represents the center of the U joint. \(S_i (i=2,3)\) represents the center of the S joint. A denotes the end point of the UP limb. \(O_1 \) is the intersection of the axis of the UP limb and the normal plane in which \(S_i (i=2,3)\) are located. \(\Delta U_1 U_2 U_3 \) and \(\Delta O_1 S_2 S_3 \) are isosceles triangles. \(\theta _i (i=1,\ldots 6)\) denotes the rotational angle of U joint. Frame \(U_1 -x_0 y_0 z_0 \) is fixed on the base, while \(y_0 \) axis is coincident with the first rotational axis of \(U_1 \), i.e., the rotational axis of \(\theta _1 \); \(z_0 \) axis is parallel to the second rotational axis, i.e., the rotational axis of \(\theta _2 \); the \(x_0 \) axis satisfies the right-hand rule. The axial axis of the UP limb is coincident with \(x_1 \). \(y_1 \) lies in the plane of \(\Delta O_1 S_2 S_3 \) and is normal to the \(S_2 S_3 \). \(\mathbf{l}_1 \equiv \overrightarrow{U_1 O_1 }\), \(\mathbf{l}_2 \equiv \overrightarrow{U_2 S_2 }\) and \(\mathbf{l}_3 \equiv \overrightarrow{U_3 S_3 }\) are defined as components in the base frame \(U_1 -x_0 y_0 z_0 \). Define the following vectors of generalized coordinates,

$$\begin{aligned}&{} \mathbf{q}_a =[{\begin{array}{lll} {l_1 }&{} {l_2 }&{} {l_3 } \\ \end{array} }]^{T}, \quad \mathbf{q}=[{\begin{array}{lll} {\theta _1 }&{} {\theta _2 }&{} {l_1 } \\ \end{array} }]^{T}, \\&{} \mathbf{q}_1 =[{\begin{array}{lll} {\theta _3 }&{} {\theta _4 }&{} {l_2 } \\ \end{array} }]^{T}, \quad \mathbf{q}_2 =[{\begin{array}{lll} {\theta _5 }&{} {\theta _6 }&{} {l_3 } \\ \end{array} }]^{T}. \end{aligned}$$

\(\mathbf{q}, \quad \mathbf{q}_1, \quad \mathbf{q}_2 \) are the local generalized coordinates for three open-chains respectively, i.e., the UP chain and two UPS chains. According to the proposed approach in Sect. 3, the dynamics of every isolated part can be solved by the direct Lagrangian formulation with respect to the local generalized coordinates.

Firstly, as usual, the relationship between the position of point A at the tip and the position of actuators should be derived to implement trajectory tracking. We can obtain the coordinate transformation matrix between frames \(U_1 -x_0 y_0 z_0 \) and \(O_1 -x_1 y_1 z_1 \), as follows,

$$\begin{aligned} \begin{array}{l} { }_1^0 \mathbf{T}=Rot(y_0,\theta _1 )Rot(z_0,\theta _2 )Trans(x_0,l_1 ) \\ \quad =\left[ {{\begin{array}{llll} {c_1 c_2 }&{} {-c_1 s_2 }&{} {s_1 }&{} {l_1 c_1 c_2 } \\ {s_2 }&{} {c_2 }&{} 0&{} {l_1 s_2 } \\ {-s_1 c_2 }&{} {s_1 s_2 }&{} {c_1 }&{} {-l_1 s_1 c_2 } \\ 0&{} 0&{} 0&{} 1 \\ \end{array} }} \right] , \\ \end{array} \end{aligned}$$
(19)

where \(l_1 \) denotes \(\left| {\mathbf{l}_1 } \right| \); \(s_i \) and \(c_i \hbox { (i=1,2)}\) denote \(\sin \theta _i \) and \(\cos \theta _i \), respectively. Then, the position vector of the tip A in frame \(U_1 -x_0 y_0 z_0 \) can be derived,

$$\begin{aligned} { }^0\mathbf{p}_A =\left[ {{\begin{array}{l} {{ }^0x_A } \\ {{ }^0y_A } \\ {{ }^0z_A } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {(l_1 +d)c_1 c_2 } \\ {(l_1 +d)s_2 } \\ {-(l_1 +d)s_1 c_2 } \\ \end{array} }} \right] , \end{aligned}$$
(20)

where d denotes the length between the tip A and point \(O_1 \). According to Eq. (20), the following equation is obtained,

$$\begin{aligned} \left\{ {\begin{array}{l} l_1 =\sqrt{{ }^0x_A^2 +{ }^0y_A^2 +{ }^0z_A^2 }-d, \\ \theta _2 = arc\sin \left( \frac{{ }^0y_A }{l_1 +d}\right) , \\ \theta _1 =arc\sin \left( \frac{-{ }^0z_A }{(l_1 +d)c_2 }\right) . \\ \end{array}} \right. \end{aligned}$$
(21)

According to geometrical relationship, we can obtain,

$$\begin{aligned} \left\{ {\begin{array}{l} \left[ {{\begin{array}{l} {\mathbf{l}_2 } \\ 0 \\ \end{array} }} \right] ={ }_1^0 \mathbf{T}\left[ {{\begin{array}{l} {{ }^1\mathbf{p}_{S_2 } } \\ 1 \\ \end{array} }} \right] -\left[ {{\begin{array}{l} {{ }^0\mathbf{p}_{U_2 } } \\ 1 \\ \end{array} }} \right] , \\ \\ \left[ {{\begin{array}{l} {\mathbf{l}_3 } \\ 0 \\ \end{array} }} \right] ={ }_1^0 \mathbf{T}\left[ {{\begin{array}{l} {{ }^1\mathbf{p}_{S_3 } } \\ 1 \\ \end{array} }} \right] -\left[ {{\begin{array}{l} {{ }^0\mathbf{p}_{U_3 } } \\ 1 \\ \end{array} }} \right] . \\ \end{array}} \right. \end{aligned}$$
(22)

where \({ }^0\mathbf{P}_{U_2 } =[{\begin{array}{lll} 0&{} {a_y }&{} {a_z } \\ \end{array} }]^{T}\), \({ }^0\mathbf{P}_{U_3 } =[{\begin{array}{lll} 0&{} {a_y }&{} {-a_z } \\ \end{array} }]^{T}\), \({ }^1\mathbf{P}_{S_2 } =[{\begin{array}{lll} 0&{} {b_y }&{} {b_z } \\ \end{array} }]^{T}\), \({ }^1\mathbf{P}_{S_3 } =[{\begin{array}{lll} 0&{} {b_y }&{} {-b_z } \\ \end{array} }]^{T}\). Substituting Eq. (19) into Eq. (22), leads to

$$\begin{aligned} \left\{ {\begin{array}{l} \mathbf{l}_2 =\left[ {{\begin{array}{l} {-b_y c_1 s_2 +b_z s_1 +l_1 c_1 c_2 } \\ {b_y c_2 +l_1 s_2 -a_y } \\ {b_y s_1 s_2 +b_z c_1 -l_1 s_1 c_2 -a_z } \\ \end{array} }} \right] , \\ \mathbf{l}_3 =\left[ {{\begin{array}{l} {-b_y c_1 s_2 -b_z s_1 +l_1 c_1 c_2 } \\ {b_y c_2 +l_1 s_2 -a_y } \\ {b_y s_1 s_2 -b_z c_1 -l_1 s_1 c_2 +a_z } \\ \end{array} }} \right] . \\ \end{array}} \right. \end{aligned}$$
(23)

Thus, the displacements of \(l_2 \) and \(l_3 \) can be calculated as

(24)
(25)

The inverse kinematics is given by Eqs. (21), (24) and (25). The velocity and acceleration equations can be derived by differentiating Eqs. (20), (24) and (25) as follows,

$$\begin{aligned}&{ }^0\dot{\mathbf{p}}_A =\mathbf{J}_A \dot{\mathbf{q}}\nonumber \\&\quad =\left[ {{\begin{array}{lll} {-(l_1 +d)s_1 c_2 }&{} {-(l_1 +d)c_1 s_2 }&{} {c_1 c_2 } \\ 0&{} {(l_1 +d)c_2}&{} {s_2 } \\ {-(l_1 +d)c_1 c_2 }&{} (l_1 +d)s_1 s_2 &{} {-s_1 c_2 } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\dot{\theta }_1 } \\ {\dot{\theta }_2 } \\ {\dot{l}_1 } \\ \end{array} }} \right] , \end{aligned}$$
(26)
$$\begin{aligned}&\dot{\mathbf{q}}_a =\mathbf{J}_a \dot{\mathbf{q}}\nonumber \\&\quad =\left[ {{\begin{array}{lll} 0&{} \quad 0&{}\quad 1 \\ {\frac{a_z b_z s_1 -a_z b_y c_1 s_2 +a_z l_1 c_1 c_2 }{l_2 }}&{} {\frac{a_y b_y s_2 -a_y l_1 c_2 -a_z b_y s_1 c_2 -a_z l_1 s_1 s_2 }{l_2 }}&{}{} \mathbf{} {\frac{l_1 -a_y s_2 +a_z s_1 c_2 }{l_2 }} \\ {\frac{a_z b_z s_1 +a_z b_y c_1 s_2 -a_z l_1 c_1 c_2 }{l_3 }}&{} {\frac{a_y b_y s_2 -a_y l_1 c_2 +a_z b_y s_1 c_2 +a_z l_1 s_1 s_2 }{l_3 }}&{} {\frac{l_1 -a_y s_2 -a_z s_1 c_2 }{l_3 }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\dot{\theta }_1 } \\ {\dot{\theta }_2 } \\ {\dot{l}_1 } \\ \end{array} }} \right] . \end{aligned}$$
(27)

Then, we can obtain the following equation,

$$\begin{aligned} { }^0\dot{\mathbf{P}}_A =\mathbf{J}_{leg} \dot{\mathbf{q}}_a =\mathbf{J}_A \mathbf{J}_a^{-1} \dot{\mathbf{q}}_a, \end{aligned}$$
(28)

where \(\mathbf{J}_{leg} \) is the overall velocity Jacobian matrix of the manipulator. Then, the acceleration mapping relationship can be obtained by differentiating Eq. (28), as follows,

$$\begin{aligned} { }^0\ddot{\mathbf{P}}_A =\mathbf{J}_{leg} \ddot{\mathbf{q}}_a +\dot{\mathbf{q}}_a^T {*}\,\mathbf{H}_{leg} \dot{\mathbf{q}}_a. \end{aligned}$$
(29)

Next, we derive the relationship between \(\mathbf{q}\) and \(\mathbf{q}_i (i=1,2)\). \(\mathbf{q}_1 \) can be determined making \(U_1 O_1 S_2 U_2 \) a closed-chain, as follows,

$$\begin{aligned}&{ }^0\mathbf{p}_{S_2 }\nonumber \\&\quad =\left[ {{\begin{array}{l} {l_2 c_3 c_4 } \\ {l_2 s_4 } \\ {-l_2 s_3 c_4 } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {-b_y c_1 s_2 +b_z s_1 +l_1 c_1 c_2 } \\ {b_y c_2 +l_1 s_2 -a_y } \\ {b_y s_1 s_2 +b_z c_1 -l_1 s_1 c_2 -a_z } \\ \end{array} }} \right] .\nonumber \\ \end{aligned}$$
(30)

According to Eq. (30) we can obtain

$$\begin{aligned} \theta _3= & {} \arctan \frac{b_y s_1 s_2 +b_z c_1 -l_1 s_1 c_2 -a_z }{b_y c_1 s_2 -b_z s_1 -l_1 c_1 c_2 }, \end{aligned}$$
(31)
$$\begin{aligned} \theta _4= & {} \arcsin \frac{b_y c_2 +l_1 s_2 -a_y }{l_2 }. \end{aligned}$$
(32)

Similarly, \(\mathbf{q}_2 \) can be solved through the closed-chain \(U_1 O_1 S_3 U_3 \), as follows,

$$\begin{aligned} \theta _5= & {} \hbox {arctan}\frac{b_y s_1 s_2 -b_z c_1 -l_1 s_1 c_2 +a_z }{b_y c_1 s_2 +b_z s_1 -l_1 c_1 c_2 }, \end{aligned}$$
(33)
$$\begin{aligned} \theta _6= & {} \hbox {arcsin} \frac{b_y c_2 +l_1 s_2 -a_y }{l_3 }. \end{aligned}$$
(34)

Secondly, the Jacobian and Hessian matrices should be obtained for dynamic modeling. The Jacobian matrix \(\mathbf{J}_a \) for \(\mathbf{q}_a \) and \(\mathbf{q}\) has been given in Eq. (27). The Hessian matrix \(\mathbf{H}_a \) can be obtained by differentiation of Eq. (26). It should be noted that all of the calculations can be implemented using a symbolic algebra package as MAPLE, which can help us to simplify the calculations, and to calculate \(\mathbf{J}_i \) and \(\mathbf{H}_i \) for \(\mathbf{q}\) and \(\mathbf{q}_i\, (i=1,2)\) by differentiating Eqs. (24), (25) and (31)–(34).

4.2 Dynamic modeling using Lagrangian formulation

As shown in Fig. 2, according to the proposed approach, we need to obtain the dynamic equations for each link using the Lagrangian formulation. Here, we take the computation of dynamic equations for Link 1 as an example. The kinetic energy and potential energy of Link 1 with respect to \(\mathbf{q}\) are as follows,

$$\begin{aligned} E_{k1} (\mathbf{q})= & {} \frac{1}{2}(m_1 { }^0\dot{\mathbf{p}}_{c1}^T (\mathbf{q}){ }^0\dot{\mathbf{p}}_{c1} (\mathbf{q})+{\varvec{\upomega } }_1^T \mathbf{I}_{c1} {\varvec{\upomega } }_1 ), \end{aligned}$$
(35)
$$\begin{aligned} E_{p1} (\mathbf{q})= & {} m_1 { }^0\mathbf{g}^{T}{} \mathbf{P}_{c1} (\mathbf{q}), \end{aligned}$$
(36)

where

$$\begin{aligned}&{ }^0\mathbf{P}_{c1} =\left[ {{\begin{array}{l} {x_{c1} c_1 c_2 -y_{c1} c_1 s_2 +z_{c1} s_1 } \\ {x_{c1} s_2 +y_{c1} c_2 } \\ {-x_{c1} s_1 c_2 +y_{c1} s_1 s_2 +z_{c1} c_1 } \\ \end{array} }} \right] , \\&\quad { }^0\mathbf{g}=\left[ {{\begin{array}{l} {g_x } \\ {g_y } \\ {g_z } \\ \end{array} }} \right] , \\&\quad \mathbf{I}_{c1} =\left[ {{\begin{array}{lll} {L_{1xx} }&{} {L_{1xy} }&{} {L_{1xz} } \\ {L_{1xy} }&{} {L_{1yy} }&{} {L_{1yz} } \\ {L_{1xz} }&{} {L_{1yz} }&{} {L_{1zz} } \\ \end{array} }} \right] , \end{aligned}$$

\(x_{c1}, y_{c1} \), and \(z_{c1} \) are constant variables, \(m_1 \) denotes the mass of Link 1, \(\mathbf{I}_{c1} \) means the moment of inertia of Link 1. Thus, introducing Eqs. (35) and (36) into Lagrange’s equations of the second type, i.e., Eq. (2), yields,

$$\begin{aligned} \mathbf{M}_1 (\mathbf{q})\ddot{\mathbf{q}}+\dot{\mathbf{q}}^{T}{*}\,\mathbf{H}_{c1} (\mathbf{q})\dot{\mathbf{q}}+\mathbf{G}_1 (\mathbf{q}) ={\varvec{\uptau }}_1. \end{aligned}$$
(37)

Similarly, the dynamic equations of Link \(k \,(k=2,\ldots 6)\) can be derived using the identical approach, as follows,

Link 2:

$$\begin{aligned} \mathbf{M}_2 (\mathbf{q})\ddot{\mathbf{q}}+\dot{\mathbf{q}}^{T}{*}\,\mathbf{H}_{c2} (\mathbf{q})\dot{\mathbf{q}}+\mathbf{G}_2 (\mathbf{q})={\varvec{\uptau }}_2. \end{aligned}$$
(38)

As an example, Appendix 1 gives the expressions of Eq. (38) in detail.

Link 3–4:

$$\begin{aligned}&{} \mathbf{M}_k (\mathbf{q}_1 )\ddot{\mathbf{q}}_1 +\dot{\mathbf{q}}_1^T {*}\,\mathbf{H}_{ck} (\mathbf{q}_1 )\dot{\mathbf{q}}_1 +\mathbf{G}_k (\mathbf{q}_1 )\nonumber \\&\quad =\mathbf{f}_k. (k=3,4) \end{aligned}$$
(39)

Link 5–6:

$$\begin{aligned}&{} \mathbf{M}_k (\mathbf{q}_2 )\ddot{\mathbf{q}}_2 +\dot{\mathbf{q}}_2^T {*}\,\mathbf{H}_{ck} (\mathbf{q}_2 )\dot{\mathbf{q}}_2 +\mathbf{G}_k (\mathbf{q}_2 )\nonumber \\&\quad =\mathbf{f}_k. (k=5,6) \end{aligned}$$
(40)

Then, the kinematic mapping between the local generalized coordinates \(\mathbf{q}_i \) and \(\mathbf{q}\) has been solved in Sect. 4.1, as follows,

$$\begin{aligned} \dot{\mathbf{q}}_i= & {} \mathbf{J}_i (\mathbf{q},\mathbf{q}_i )\dot{\mathbf{q}}.\,(i=1,2) \end{aligned}$$
(41)
$$\begin{aligned} \ddot{\mathbf{q}}_i= & {} \mathbf{J}_i (\mathbf{q},\mathbf{q}_i )\ddot{\mathbf{q}}+\dot{\mathbf{q}}^{T}{*}\,\mathbf{H}_i (\mathbf{q})\dot{\mathbf{q}}.\,(i=1,2) \end{aligned}$$
(42)

According to the virtual work principle, that implies

$$\begin{aligned} {\varvec{\uptau }}_k= & {} \mathbf{J}_1^T (\mathbf{q},\mathbf{q}_1 )\mathbf{f}_k ,\, (k=3,4) \end{aligned}$$
(43)
$$\begin{aligned} {\varvec{\uptau }}_k= & {} \mathbf{J}_2^T (\mathbf{q},\mathbf{q}_2 )\mathbf{f}_k .\,(k=5,6) \end{aligned}$$
(44)

Combining Eqs. (41)–(44) and (39), (40) leads to

$$\begin{aligned}&{} \mathbf{J}_1^T (\mathbf{q},\mathbf{q}_1 )\mathbf{M}_k (\mathbf{q}_1 )\mathbf{J}_1 (\mathbf{q},\mathbf{q}_1 )\ddot{\mathbf{q}} \nonumber \\&\qquad +\,\dot{\mathbf{q}}^{T}{*}\,[\mathbf{J}_1^T (\mathbf{q},\mathbf{q}_1 )\mathbf{M}_k (\mathbf{q}_1 ){*}\,\mathbf{H}_1 (\mathbf{q})\nonumber \\&\qquad +\mathbf{J}_1^T (\mathbf{q},\mathbf{q}_1 )\mathbf{J}_1^T (\mathbf{q},\mathbf{q}_1 ){*}\,\mathbf{H}_{ck} (\mathbf{q}_1 )\mathbf{J}_1 (\mathbf{q},\mathbf{q}_1 )]\dot{\mathbf{q}}\nonumber \\&\qquad +\,\mathbf{J}_1^T (\mathbf{q},\mathbf{q}_1 )\mathbf{G}_k (\mathbf{q}_1 ) \nonumber \\&\quad ={\varvec{\uptau }}_k\,, (k=3,4) \end{aligned}$$
(45)
$$\begin{aligned}&\qquad \mathbf{J}_2^T (\mathbf{q},\mathbf{q}_2 )\mathbf{M}_k (\mathbf{q}_2 )\mathbf{J}_2 (\mathbf{q},\mathbf{q}_2 )\ddot{\mathbf{q}} \nonumber \\&\qquad +\,\dot{\mathbf{q}}^{T}{*}\,[\mathbf{J}_2^T (\mathbf{q},\mathbf{q}_2 )\mathbf{M}_k (\mathbf{q}_2 ){*}\,\mathbf{H}_2 (\mathbf{q})\nonumber \\&\qquad +\,\mathbf{J}_2^T (\mathbf{q},\mathbf{q}_2 )\mathbf{J}_2^T (\mathbf{q},\mathbf{q}_2 ){*}\,\mathbf{H}_{ck} (\mathbf{q}_2 )\mathbf{J}_2 (\mathbf{q},\mathbf{q}_2 )]\dot{\mathbf{q}}\nonumber \\&\qquad +\,\mathbf{J}_2^T (\mathbf{q},\mathbf{q}_2 )\mathbf{G}_k (\mathbf{q}_2 ) ={\varvec{\uptau }}_k \,.(k=5,6) \end{aligned}$$
(46)

The dynamic equations with respect to \(\mathbf{q}\) can be derived by summing equations of all the links, i.e., Eqs. (37), (38), (45), (46), as follows,

$$\begin{aligned}&\mathbf{M}(\mathbf{q},\mathbf{q}_1,\mathbf{q}_2 )\ddot{\mathbf{q}}+\dot{\mathbf{q}}^{T}{*}\,\mathbf{H}(\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 )\dot{\mathbf{q}}\nonumber \\&\quad +\,\mathbf{G}(\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 )={\varvec{\uptau }}, \end{aligned}$$
(47)

where \(\mathbf{M}(\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 )=\mathop {\sum }\limits _{k=1}^2 {\mathbf{M}_k (\mathbf{q})} +\mathop {\sum }\limits _{k=3}^4 {\mathbf{J}_1^T (\mathbf{q},\mathbf{q}_1 )} \mathbf{M}_k (\mathbf{q}_1 )\mathbf{J}_1 (\mathbf{q},\mathbf{q}_1 )+\mathop {\sum }\limits _{k=5}^6 {\mathbf{J}_2^T } (\mathbf{q},\mathbf{q}_2 )\mathbf{M}_k (\mathbf{q}_2 )\mathbf{J}_2 (\mathbf{q},\mathbf{q}_2 )\),

$$\begin{aligned}&{} \mathbf{H}(\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 )=\sum _{k=1}^2 {\mathbf{H}_{ck} (\mathbf{q})}\\&\quad +\,\sum _{k=3}^4 \Big [\mathbf{J}_1^T (\mathbf{q},\mathbf{q}_1 )\mathbf{M}_k (\mathbf{q}_1 ){*}\,\mathbf{H}_1 (\mathbf{q})\\&\quad +\,\mathbf{J}_1^T (\mathbf{q},\mathbf{q}_1 )\mathbf{J}_1^T (\mathbf{q},\mathbf{q}_1 ){*}\,\mathbf{H}_{ck} (\mathbf{q}_1 )\mathbf{J}_1 (\mathbf{q},\mathbf{q}_1 )\Big ] \\&\quad +\,\sum _{k=5}^6 \Big [\mathbf{J}_2^T (\mathbf{q},\mathbf{q}_2 )\mathbf{M}_k (\mathbf{q}_2 ){*}\,\mathbf{H}_2 (\mathbf{q})\\&\quad +\,\mathbf{J}_2^T (\mathbf{q},\mathbf{q}_2 )\mathbf{J}_2^T (\mathbf{q},\mathbf{q}_2 ){*}\,\mathbf{H}_{ck} (\mathbf{q}_2 )\mathbf{J}_2 (\mathbf{q},\mathbf{q}_2 )\Big ] , \\&{} \mathbf{G}(\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 )=\sum _{k=1}^2 {\mathbf{G}_k (\mathbf{q})} +\sum _{k=3}^4 {\mathbf{J}_1^T (\mathbf{q},\mathbf{q}_1 )\mathbf{G}_k (\mathbf{q}_1 )}\\&\quad +\,\sum _{k=5}^6 {\mathbf{J}_2^T (\mathbf{q},\mathbf{q}_2 )\mathbf{G}_k (\mathbf{q}_2 )} ,\\&\quad {\varvec{\uptau }}=\sum _{k=1}^6 {{\varvec{\uptau }}_k } . \end{aligned}$$

Equation (47) is the dynamic equations of the whole system, however, which is not represented by the active generalized coordinates \(\mathbf{q}_a \). Similarly, use the force transformation matrices to derive the final dynamic model of the manipulator. The velocity and acceleration mapping between \(\mathbf{q}\) and \(\mathbf{q}_a \) have been obtained in Sect. 4.1, as follows,

$$\begin{aligned} \dot{\mathbf{q}}_a= & {} \mathbf{J}_a (\mathbf{q},\mathbf{q}_a )\mathbf{q}, \end{aligned}$$
(48)
$$\begin{aligned} \ddot{\mathbf{q}}_a= & {} \mathbf{J}_a (\mathbf{q},\mathbf{q}_a )\ddot{\mathbf{q}}+\dot{\mathbf{q}}^{T}{*}\,\mathbf{H}_a (\mathbf{q})\mathbf{q}. \end{aligned}$$
(49)

Therefore, the dynamic equations of the whole manipulator can be derived as

$$\begin{aligned}&{} \mathbf{M}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 )\ddot{\mathbf{q}}_a +\mathbf{C}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 ,\dot{\mathbf{q}}_a )\dot{\mathbf{q}}_a\nonumber \\&\quad +\,\mathbf{G}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 )={\varvec{\uptau }}_a , \end{aligned}$$
(50)

where \(\mathbf{M}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 ) =[\mathbf{J}_a^{-1} (\mathbf{q},\mathbf{q}_a )]^{T}{} \mathbf{M}(\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 ){} \mathbf{J}_a^{-1} (\mathbf{q},\mathbf{q}_a )\),

$$\begin{aligned}&{} \mathbf{C}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 ,\dot{\mathbf{q}}_a )\\&\quad =\dot{\mathbf{q}}_a^T {*}\,[[\mathbf{J}_a^{-1} (\mathbf{q},\mathbf{q}_a )]^{T}[\mathbf{J}_a^{-1} (\mathbf{q},\mathbf{q}_a )]^{T}\\&\quad {*}\,\mathbf{H}(q,q_1 ,q_2 )\mathbf{J}_a^{-1} (\mathbf{q},\mathbf{q}_a ) \\&\quad -\,[\mathbf{J}_a^{-1} (\mathbf{q},\mathbf{q}_a )]^{T}[\mathbf{J}_a^{-1} (\mathbf{q},\mathbf{q}_a )]^{T}\\&\quad \mathbf{M}(\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 )\mathbf{J}_a^{-1} (\mathbf{q},\mathbf{q}_a ){*}\,\mathbf{H}_a (\mathbf{q})\mathbf{J}_a^{-1} (\mathbf{q},\mathbf{q}_a )],\\&\quad \mathbf{G}_{a} (\mathbf{q}_{a}, \mathbf{q}, \mathbf{q}_{1}, \mathbf{q}_{2})= [{\mathbf{J}_{a}^{-1}(\mathbf{q}, \mathbf{q}_{a})}]^{T} \mathbf{G}(\mathbf{q}, \mathbf{q}_{1}, \mathbf{q}_{2}). \end{aligned}$$

Eq. (50) are the expected explicit closed-form dynamic equations for the analyzed 3-DOF spatial parallel manipulator, which is very useful for real-time control for a MIMO system. \({\varvec{\uptau }}_a =[{\begin{array}{lll} {f_1 }&{} {f_2 }&{} {f_3 } \\ \end{array} }]^{T}\) is the vector of the three linear actuators’ forces.

5 Simulation and experiment

5.1 Simulation validation

In this section, the inverse dynamics is used to validate the dynamic model. For the inverse dynamic problem, the time history of a predetermined trajectory is given. And the problem is to determine the active forces or torques required to produce that movement. That means the left parts of Eq. (50) can be calculated in terms of the movement.

In order to validate the correctness of the dynamic model, the results derived by the proposed approach and these obtained by ADAMS are compared. ADAMS is a mature and reliable commercial software which is based on numerical method for equation formulation [24]. ADAMS provides a good test bed for simulation. However, numerical expressions can’t clearly provide physical insight into the system structure and can be difficult for engineers to develop better control laws with less known physics. Additionally, the model in ADAMS cannot be used for real-time control on physical prototypes. Those are the reasons for why the dynamic equations should be derived by algebraic formulae rather than by ADAMS. The kinematic and dynamic parameters can be directly obtained from the virtual prototype in ADAMS. Table 1 shows the architecture and dynamic parameters of the 3-DOF manipulator depicted in Fig 1.

As shown in Fig. 3, we set the trajectory of the end-effector of the manipulator with respect to the inertial reference frame \(B-xyz\) as follows

$$\begin{aligned} \left\{ {\begin{array}{ll} x(t)=St/T-(S/2\pi )\sin (2\pi t/T)\quad &{}\quad t\in [0,T], \\ y(t)=0\quad &{}\quad t\in [0,T], \\ z(t)=2Ht/T-(H/2\pi )\sin (2\pi t/T)\quad &{}\quad t\in [0,T/2], \\ z(t)=2H-2Ht/T+(H/2\pi )\sin (4\pi t/T)\quad &{}\quad t\in [T/2,T], \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(51)

where T denotes the period of the movement, S and H determine the length and height of the movement. Set \(T=1 \hbox {s}, S=200 \hbox { mm }, H=100\hbox { mm}\). As shown in Fig. 3, \(U_1 -x_0 y_0 z_0 \) has a \(30^{\circ }\) angle with respect to the vertical plane. Thus, the vector of gravitational acceleration in \(U_1 -x_0 y_0 z_0 \) is \({ }^0\mathbf{g}=[{\begin{array}{lll} {-g\cdot \sin 30^{\circ }}&{} {g\cdot \cos 30^{\circ }}&{} 0 \\ \end{array} }]^{T}\). The simulation results are shown in Fig. 4. From Fig. 4, we can see a good agreement between the results derived by ADAMS and those obtained from algebraic formulae, which validates the correctness of the dynamic equations and further means our method is right.

Fig. 3
figure 3

Schematic diagram for simulation

Full size image
Fig. 4
figure 4

Active forces computed by the proposed method and ADAMS

Full size image
Fig. 5
figure 5

Simulation results decomposed into three terms: a inertial forces, b coriolis and centrifugal forces, and c gravitational forces

Full size image

In addition, the dynamic model in the joint space is useful for optimization of motion planning, since the motion planning is affected by the capabilities of motors. Of course, some software, e.g.,ADAMS and Solidworks, also can finish that work. As mentioned before, another role of the dynamic equations that the commercial software can’t replace is that the model can be used to analyze the actuator forces with respect to the physical nature. The inertial forces, the Coriolis and centrifugal forces, and the gravitational forces can be determined from Eq. (50), respectively, impossibly from ADAMS. Figure 5 shows the three different terms for the chosen trajectory of Eq. (51). We can see that the Coriolis and centrifugal forces are very small compared with the other two terms. Thus, in some cases, according to the simulation results, the terms which give small contribution on the active forces can be neglected in order to simplify the computations [47]. However, when the dynamic model is employed in model-based control, the neglecting for any part of dynamic equations will affect the control performance largely, which will be shown in Sect. 5.3.

5.2 Computational efficiency

In order to compare our method with existing methods, we also used the Newton–Euler method to obtain the dynamic equations of the 3-DOF manipulator. Figure 6 shows the comparison of simulation results obtained by Newton–Euler method and our method. Obviously, if the results are not identical, one of the methods must be wrong under the precondition of no miscalculation. The computer algebra program MAPLE is employed to implement the algorithms of dynamic modeling using these two methods. The programs are executed in a computer with Windows 8.1 equipped with Intel Core i7-4700HQ CPU. The computation time of our method to obtain the final dynamic equations is 22.461 s, whereas the time consumption of Newton–Euler method is 24.213 s.

Fig. 6
figure 6

Active forces computed by the proposed method and Newton–Euler method

Full size image
Fig. 7
figure 7

Computed-torque control scheme

Full size image

In the earlier studies, some researchers [51–54] compared computational cost for different algorithms using the number of floating point operations, i.e., multiplications and additions. Gosselin [52] even parallelize the computation on several processors in order to improve the computational speed. Tsai [53], Khalil and Guegan [54] only derived the implicit models rather than the explicit models with very little computational cost. However, as it is recognized in [54], implicit dynamic model cannot be used for solving forward dynamics in simulation of motion control. Since the process of dynamic modeling is an offline work, we think it is not necessary to pursue faster computational efficiency. Moreover, some convenient software, such as MAPLE and MATLAB, can liberate researchers from complex computations. It’s more important to obtain precise explicit closed-form dynamics in the actuation space because of their crucial role for model-based control. In Sect. 5.3, we will demonstrate that the inverse and forward dynamics derived from our method could be used in online model-based control.

5.3 Implementation in model-based control

Computed-force control is chosen as the model-based control scheme to track the desired trajectory mentioned in Sect. 5.1, i.e., the profile \(\mathbf{X}=[{\begin{array}{lll} {x(t)}&{} {y(t)}&{} {z(t)} \\ \end{array} }]^{T}\) represented by Eq. (51). As shown in Fig. 7, the control scheme is implemented in joint space based on the dynamic equations in the actuation space. The control law is

$$\begin{aligned} \mathbf{u}=\mathbf{M}_a (\ddot{\mathbf{q}}_a^d +\mathbf{K}_P \mathbf{e}+\mathbf{K}_D \dot{\mathbf{e}})+\mathbf{C}_a \dot{\mathbf{q}}_a +\mathbf{G}_a , \end{aligned}$$
(52)

where \(\mathbf{K}_p =diag(k_p )_{3\times 3} \), \(\mathbf{K}_D =diag(k_D )_{3\times 3} \). For a given control input \(\mathbf{u}\), the resulting motion can be determined by the numerical integration of the actuator accelerations. As for the 3-DOF manipulator, we can obtain the discrete state space model according to Eq. (50), as follows,

$$\begin{aligned} \left\{ {\begin{array}{l} \mathbf{q}(k+1)= \hbox {diag}(T_s )_{3\times 3}\dot{\mathbf{q}}(\hbox {k})+\mathbf{q}(\hbox {k}), \\ \dot{\mathbf{q}}(k+1)=\hbox {diag}(T_s )_{3\times 3} \mathbf{M}_a^{-1} (k)\\ \left[ {\mathbf{u}-\mathbf{C}_a (\hbox {k})\dot{\mathbf{q}}_a (\hbox {k})-\mathbf{G}_a (\hbox {k})} \right] , \\ \end{array}} \right. \end{aligned}$$
(53)

where \(T_s =1ms\) denotes the sample period.

Fig. 8
figure 8

Trajectory tracking error using precise inverse dynamics

Full size image

According to the simplified dynamic model suggested in literature [31–34], the control law has to use an inaccurate inverse dynamic model to compute the control input. Obviously, for a set of parameters of feedback gains, i.e., \(\mathbf{K}_P \) and \(\mathbf{K}_D \), the more precise the inverse dynamic model is, the better control performance becomes. That is validated by the simulation results as shown in Figs. 8 and 9. With the same feedback gains \(k_P =160\), \(k_D =10\), the trajectory tracking performance based on precise inverse dynamics is much better than that depended on inverse dynamics neglecting Coriolis and centrifugal terms, which indicates the importance to obtain a precise dynamic model for the use of model-based control. As for other manipulators with larger inertia or tracking faster trajectories, the effect of model accuracy on control performance will be highlighted. The control simulation algorithm is executed by MATLAB on the same computer mentioned in Sect. 5.2. Functions “tic” and “toc” of MATLAB give the run time of the control cycle, which is 0.66646 ms. Several tasks, such as motion planning and the computation of inverse dynamics, should be accomplished in the control cycle. Among a control cycle, the computation time for inverse dynamics is 0.52695 ms. Generally, the servo control cycle for a commercial control-hardware is between 1 ms and tens of milliseconds. Therefore, the dynamic model derived by our modeling method is feasible for online control.

Fig. 9
figure 9

Trajectory tracking error using inaccurate inverse dynamic without Coriolis and centrifugal part

Full size image

5.4 Experiment analysis

Similar to the CAD model displayed in Fig. 1, a test bed has been built as shown in Fig. 10. The linear actuator is composed of a 400 W DC servo motor, a timing belt transmission with 2:1 reduction ratio and a ball screw with 5 mm lead. The parameters of the test bed are identical to those shown in Table 1 with the exception of the mass parameters. Here, the parameters of mass and moment of inertia are a bit smaller than those shown in Table 1. The motors are driven by Elmo’s motor drives (G-MOLWHI15/100EE), which are connected to an embedded controller (CX2030) made by the company Beckhoff through an EtherCAT bus. Each motor drive has three control modes: position loop mode, velocity loop mode and torque loop mode. Additionally, the motor drives can provide real-time values of displacement, velocity, acceleration and torque. We have done two experiments using the position loop mode and the torque loop mode respectively.

Fig. 10
figure 10

Photograph of the test bed

Full size image
Table 1 Parameters of the 3-DOF parallel manipulator
Full size table

The sever motor drive can give real-time torques of motors, whereas Eq. (50) gives the push/pull forces of prismatic joints. There is a transformation relationship between motor torque and push/pull force in a linear actuator composed of timing belt transmission and ball screw, as follows,

$$\begin{aligned} \tau _{mi} =\frac{L}{2\pi R}\tau _{ai} , \quad (i=1,2,3) \end{aligned}$$
(54)

where L is the lead of the ball screw; R is the reduction ratio of the timing belt transmission; \(\tau _{mi} \) denotes the motor torque of each linear actuator; \(\tau _{ai} \) denotes the active forces of prismatic joints. Therefore, Eq. (50) can be transformed into the following style in terms of motor torques,

$$\begin{aligned}&(\mathbf{M}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 )\ddot{\mathbf{q}}_a +\mathbf{C}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 ,\mathbf{q}_a )\dot{\mathbf{q}}_a\nonumber \\&\quad +\,\mathbf{G}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 ))L/(2\pi R)={\varvec{\uptau }}_m . \end{aligned}$$
(55)
Fig. 11
figure 11

Measured motion of P1 in the first experiment using position loop mode: a displacement, b velocity, c acceleration

Full size image

The friction contributions must be incorporated into the rigid body dynamic equations given in Eq. (55) because friction effects are usually important for actual industrial robots [48]. It has been observed that friction can cause more than 50 % error in some heavy industrial manipulators [49]. The classical Stribeck friction model [50] is adopted in this paper. Including friction the dynamic equations of a manipulator can be written as

$$\begin{aligned}&(\mathbf{M}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 )\ddot{\mathbf{q}}_a +\mathbf{C}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 ,\mathbf{q}_a )\dot{\mathbf{q}}_a\nonumber \\&\quad +\,\mathbf{G}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 ))L/(2\pi R) +{\varvec{\uptau }}_f ={\varvec{\uptau }}_m , \end{aligned}$$
(56)

where \({\varvec{\uptau }}_f \) is the friction torque vector. However, identifying the friction parameters for each joint is very difficult. The friction forces of passive joints are much smaller than those of active joints because of the prestress force on the ball screw. Thus, after neglecting the friction of passive joints, Eq. (54) is rewritten as

$$\begin{aligned}&(\mathbf{M}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 )\ddot{\mathbf{q}}_a +\mathbf{C}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 ,\mathbf{q}_a )\dot{\mathbf{q}}_a\nonumber \\&\quad +\,\mathbf{G}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 ))L/(2\pi R)+{\varvec{\uptau }}_{fa} ={\varvec{\uptau }}_m , \end{aligned}$$
(57)

where \({\varvec{\uptau }}_{fa} =[{\begin{array}{lll} {\tau _{fa1} }&{} {\tau _{fa2} }&{} {\tau _{fa3} } \\ \end{array} }]^{T}\) is the friction torque vector of the three linear actuators. The Stribeck friction model for each prismatic joint is as follows,

$$\begin{aligned} \tau _{fai}= & {} [F_c +(F_s -F_c )e^{-|\dot{l}_i /v_s |^{\delta }}]\hbox { sgn }(\dot{l}_i )\nonumber \\&+\,F_v \dot{l}_i ,\quad (i=1,2,3) \end{aligned}$$
(58)

where the unit of \(\tau _{fai} \) is \(\hbox {N}\cdot \hbox {m}\); the unit of \(\dot{l}_i \) is \(\hbox {mm/s}\). The friction model is identified by some experimental data using least square method, as follows,

$$\begin{aligned} \tau _{fai}= & {} [0.059+(0.07-0.059)e^{-|\dot{l}_i /0.3|^{1.5}}]\hbox { sgn }(\dot{l}_i )\nonumber \\&+\,0.002\dot{l}_i.\quad ( i=1,2,3) \end{aligned}$$
(59)

Moreover, the inertia of motor’s shaft and of the ball screw should be added, and these two contributions are defined as \(\mathbf{I}_m \). Then, the complete dynamic equations of the manipulator explicitly showing the motor torques for the convenience of experiments can be expressed as follows,

$$\begin{aligned}&(\mathbf{M}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 )\ddot{\mathbf{q}}_a+\,\mathbf{C}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 ,\mathbf{q}_a )\dot{\mathbf{q}}_a\nonumber \\&\quad +\,\mathbf{G}_a (\mathbf{q}_a ,\mathbf{q},\mathbf{q}_1 ,\mathbf{q}_2 ))\hbox {L}/(2\pi \hbox {R})\nonumber \\&\quad +\,{\varvec{\uptau }}_{fa} +\mathbf{I}_m \ddot{\varvec{\uptheta }}_m ={\varvec{\uptau }}_m , \end{aligned}$$
(60)

where \(\ddot{\varvec{\uptheta }}_m =[{\begin{array}{lll} {\ddot{\theta }_{m1} }&{} {\ddot{\theta }_{m2} }&{} {\ddot{{\theta } }_{m3} } \\ \end{array} }]^{T}\) is the angular acceleration vector of the three motors, and \(\ddot{{\uptheta } }_{mi} =2\pi R\ddot{l}_i /L (i=1,2,3)\). \({\varvec{\uptau }}_m =[{\begin{array}{lll} {\tau _{m1} }&{} {\tau _{m2} }&{} {\tau _{m3} } \\ \end{array} }]^{T}\) is the torque vector of the three motors.

Fig. 12
figure 12

Comparison between measured and estimated torques in the first experiment

Full size image
Fig. 13
figure 13

Measured motion of P1 in the second experiment using torque loop mode: a displacement, b velocity, c acceleration

Full size image

In the first experiment, the motor of P1 worked under the position loop mode. Set the motion of P1 as a sine function, while P2 and P3 are locked. As shown in Fig. 11, the motion of P1 measured by an encoder is very smooth. The simulated motor torques can be obtained by introducing the motion data shown in Fig. 11 into Eqs. (50) and (60). As depicted in Fig. 12, the torque of the motor shows some fluctuation while the result calculated by the dynamic model is very smooth. The reason for the fluctuation of the measured value is that the controller of the driver should change the torque to follow the motion function since the friction is varying during a rotational circle of the ball screw. In the second experiment, the P1 motor works under the torque loop mode, then the motor drive will try to guarantee the predetermined profile of the motor torque. The measured torque and simulated torque are shown in Fig. 14. In contrast to the results of the first experiment, the motion of P1 shows large fluctuation as shown in Fig. 13 while the actual torque is smooth. The explanation of the fluctuation in this second experiment also indicates the variation of friction over the rotational circle of the ball screw. In the same way, the model-computed torque of the second experiment can be obtained by introducing the measured displacement, velocity and acceleration data into the dynamic equations. Neglecting the fluctuation caused by friction, the measured results and dynamic model outputs have a good fitting in both two experiments, which validates the correctness of the dynamic model as well. However, if it is desired to increase the precision of the simulated results, the variation of the friction with the rotation of the motor shaft should be taken into account. Whereas the main purpose of this paper is to derive the multi-rigid-body dynamics, a more accurate model of friction will be discussed in the future work.

5.5 Trajectory tracking experiments

In this section, the trajectory planned in Sect. 5.1, i.e., the profile \(\mathbf{X}=[{\begin{array}{lll} {x(t)}&{} {y(t)}&{} {z(t)} \\ \end{array} }]^{T}\)represented by Eq. (51), was tracked by using classic PD control and computed-torque control, respectively. Classic PD controller is implemented in each single motor with the same parameters of \(k_P =500\) and \(k_D =20\). The friction model represented by Eq. (59) is added to the computed-torque controller motioned in Sect. 5.3. Other parameters of the

Fig. 14
figure 14

Comparison between measured and estimated torques in the second experiment

Full size image
Fig. 15
figure 15

Comparison of trajectory tracking control errors in experiments by using classical PID control and model-based control: a classic PID control, b computed-torque control

Full size image

computed-torque controller are identical with those in Sect. 5.3. Control programs are explored using ST language that is similar to C language. The servo control cycle in the control-hardware CX2030 produced by Beckhoff is 1 ms, which is enough to accomplish all tasks including motion planning and the computation of inverse kinematics and dynamics for computed-torque control. The control performance is shown in Fig. 15. As shown in Fig.15, the peak error occurs in the middle, because motor’s rotary direction changes around that time. As expected, model-based control outperforms the classic PD control significantly due to the compensation of dynamic model.

6 Conclusions

This paper presents a systematic methodology for determining the inverse dynamics equations of complex non-redundant parallel manipulators by the combination of the Lagrangian formulation and the virtual work principle. Based on the proposed algorithm which is summarized as five steps, the dynamic equations of a 3-DOF spatial parallel manipulator have been obtained and shown to be valid by comparison with \(3^{\mathrm{rd}}\) parts software and by experiments. The determination of the dynamic equations of a complex multi-closed-loop mechanism can be simplified by splitting the system into independent substructures with respect to suitable generalized coordinates. The constraints are introduced by the way of Jacobian and Hessian matrices. The Jacobian and Hessian matrices keep the explicit attributes of the dynamic equations, when they are transformed into different coordinate subsystems according to the virtual work principle. The study presented here provides a sound basis for future work on the context of model-based control. Moreover, the modeling approach and valid verification method can also be applied to other parallel mechanisms. In the future, the model-based control will be studied using the derived dynamic equations of the manipulator.