1 Introduction

Aeroelastic instabilities are important matters in aerospace structure’s design. The flexible characteristics of aeroelastic structures can result in catastrophic behavior of the system. When the inherent structural flexibility of an airplane interplays with the aerodynamic and inertial forces, different aeroelastic phenomena such as flutter, divergence, limit cycle oscillations (LCO), quasi-periodic behavior and chaos can result. In fact, for this kind of systems, there is a limit velocity above which the structure cannot damp the received energy, so the system tends to a deformation or instabilities.

Many passive and active control methods for suppressing the aeroelastic instabilities have been introduced. While active control has been shown to be effective in suppressing LCOs, these methods require the use of external energy for actuating. Active methods also require sensors capable of constantly providing accurate measurements of the system’s state for feedback into the controller, and the control devices are also high maintenance, so using of passive devices with efficient performance is desirable due to their inherent characteristics. They are maintenance free, without any need to external energy input. Using the isolators and vibration absorbers is examples of the passive approaches.

Linear vibration absorbers are consisting of small masses, linear springs and dissipation elements that can be in different series and parallel configurations. On the other hand, nonlinear vibration absorbers which are introduced and developed recently have some nonlinear stiffness or damping elements. According to previous studies, these nonlinear vibration absorbers can be effective in broadband frequency and act as a nonlinear energy sink based on the nonlinear energy pumping, which is the one-way transferring of the vibration energy from the main system to the passive nonlinear vibration absorber [1]. Nonlinear energy sinks (NESs) are single or multi-degree of freedom systems, composed of essentially nonlinear damped oscillators that are attached to the main system in order to absorb and dissipate the energy through targeted energy transfers (TETs).

The previous researches have shown that NES can be designed to act as passive sinks of unwanted vibrations generated by external impulsive excitations in a linear subsystem [2]. The energy pumping is due to resonance capture and the stiffness nonlinearity, which enables NES to resonate with any mode of the linear subsystem regardless of its frequency [3]. The investigations on the effectiveness of passive TET to mitigate the rotary vibration amplitude in rotor systems at the critical velocities are performed by applying NES to the rotor systems in [4]. It is shown that the NES absorbs shock energy in a one-way, irreversible fashion and dissipates this energy locally, without spreading it back to the linear beam. Moreover, it is shown numerically that an appropriately designed and placed NES can passively absorb and dissipate a major part of the shock energy of the beam, up to an optimal value of 87 % [5]. The steady-state dynamics of linear, Euler–Bernoulli beam under harmonic excitation coupled to an NES with nonlinear stiffness of order three is considered in [6]. To compare with the performance of NES, a linear tuned mass damper (TMD) is designed. The results show that the performance of NES is dependent on designed force amplitude. The effect of NES on the amplitude reduction of the forced system is investigated in [7], and the results showed that the NES results an increase in the vibration amplitude of the linear subsystem, especially when the damping is low. They demonstrate that there is no observation of nonlinear energy pumping, which means the NES is not sufficient for mitigating the vibrations of the linear primary system.

Similar to other engineering studies, the effectiveness of the NES in aeroelastic systems has been investigated in some researches. The triggering mechanism of LCOs of a wing due to aeroelastic instability was studied in [8, 9]. Mitigation of limit cycle oscillations (LCO) in a 2-DOF rigid in-flow wing with nonlinear heave and pitch stiffness in quasi-steady flow, through the TET, is studied in [9, 10]. With the addition of the NES to the system they have predicted three different mechanisms for suppressing the LCO. It was found that the passive TETs are activated by transient resonant interactions between the NES and the aeroelastic modes. The passive nonlinear targeted energy transfer between a 2-DOF model of a long-span bridge with an SDOF NES prone to coupled flutter is studied in [11]. This study demonstrated that an NES could be able to control the aeroelastic instability of a structure using TET. Moreover, they showed that analytical method’s results lead to an NES design which is able to efficiently control the aeroelastic instability of the bridge. The suppression of aeroelastic instabilities in a 2-DOF wing system by means of passive, broadband, nonlinear targeted energy transfers was investigated in [12]. It has been shown that it is possible to partially or completely suppress aeroelastic instability by transferring vibration energy from the wing to the SDOF NES in a one-way irreversible energy transfer. The robustness in suppression of LCO to initial conditions and the parameters of the system were shown, accordingly. In the second part of this study, the experimental results are presented in [13]. The NES was attached to the heave degree of freedom of a rigid airfoil which was supported in a low-velocity wind tunnel. The experimental results validate some aspects of the theoretical analysis.

In a contrary and different research, the parameters of the NES varied in order to test the passive device efficiency in suppressing undesirable aeroelastic behavior [14]. The results showed that the nonlinearity of the NES influences the system behavior and can cause undesirable responses. It was concluded that the nonlinear energy sink influences the nonlinear dynamics of the aeroelastic system. It changes the type of Hopf bifurcation depending on its location and nonlinear parameters. A multi-degree of freedom (MDOF) NES is applied to a 2-DOF wing model by [15]. The results demonstrate that MDOF NES can enhance the robustness of limit cycle oscillation suppression, compared with SDOF NES under identical situations. The effects of different system parameters on the LCO of the system were investigated according to the bifurcation analysis. They have shown that the reduced velocity for the Hopf bifurcation monotonously increases as the mass ratio increases for a fixed offset and is almost insensitive to the changes of the damping and essential nonlinearity. A new method, which is the combination of the harmonic balance and multiple scale methods, is applied to an aeroelastic model and was presented by Luongo and Zulli [16]. This method was applied to a 2-DOF wing with an NES attached to it, which is subjected to steady wind. The results obtained by the application of this method to the aeroelastic model showed good agreement with previous researches.

As previously mentioned, in the work presented by Lee et al. [15], a detailed investigation of how the nonlinear energy sink affects the aeroelastic characteristic of the model is provided. But surveys conducted in [15] show that the nonlinear term has no effect on the flutter velocity, and the important effect on the flutter velocity is depended upon the mass and damping parameters of the absorbers. The results presented in [15] represent subcritical bifurcation behaviors. Hence, the stability range added by NES is not reliable, because in this subcritical range, there would be limit cycle oscillation or any other type of nonlinear behaviors. Therefore, although there is an improvement in the flutter velocity range (i.e., linear stability), this range is not reliable because in this added range, the system would have high-amplitude oscillations for large initial conditions. Ineffectiveness of the NES stiffness parameter on the flutter velocity is a motivation to compare the performance of linear and nonlinear absorbers.

In this study, different types of linear dynamic vibration absorbers (DVAs) are attached to the wing model in order to compare their performance such as flutter velocity, limit cycle oscillations (LCOs) and other types of nonlinear behaviors with two types of NES considered in [15]. In order to achieve a higher flutter velocity, an optimization method is presented to obtain system parameter’s values. The method of optimization provided here is to find parameters of different types of NES such that the magnitudes of system’s eigenvalues in higher reduced velocity with desired stable eigenvalues are minimized.

In the following, at first modeling of the wing model with different types of DVAs is presented. Then, continuously, flutter analysis is carried out and optimization problem is presented to find optimum parameters of DVAs. Finally, by using Poincare section, nonlinear time response analysis is presented to compare the performance of NES and DVA at velocities higher than flutter. All the system’s time responses and bifurcation diagrams are derived from numerical analysis, using MATLAB software. For this purpose the “event” option in “odeset” of MATLAB ODE solver can be used. This is an efficient option in ODE solver of MATLAB, which can simply be used. For obtaining the bifurcation diagrams, after diminishing the transient response, the steady-state response is obtained and the amplitude of related displacement is recorded at times with zero velocity. With continuously changing reduced velocity, the bifurcation diagram can be obtained. For reducing the computational time needed in constructing this bifurcation diagram, the transient period of response must be reduced. Hence the final state of the previously obtained response is used as the initial condition for simulation with new reduced velocity. Accordingly system will settle down in the steady state as soon as possible.

2 System formulation

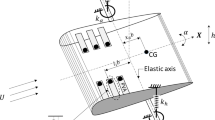
The model considered here is a two degree of freedom, heave (positive downward) and pitch (positive clockwise), wing model which is subjected to the quasi-steady aerodynamic model as shown in Fig. 1. The quasi-steady aerodynamic model is a simple aerodynamic model in which compressibility and viscosity are ignored. The resultant lift force (L) and the moment (M) about the elastic axis could be written as

$$\begin{aligned}&L=qS\frac{\partial C_\mathrm{L} }{\partial \alpha }\alpha \nonumber \\&M=eL \end{aligned}$$
(1)

As clear, there are different types of linear and nonlinear vibration absorbers; among them some more familiar cases are considered here.

Fig. 1
figure 1

Two DOF wing model coupled with DVA

Full size image
Fig. 2
figure 2

Kelvin–Voigt model DVA

Full size image

2.1 Linear parallel DVA (Kelvin–Voigt model)

Kelvin–Voigt model DVA is an SDOF DVA with a linear spring and damper attached in parallel to a single mass as shown in Fig. 2. Referring to [17], the coupled equations of motions for wing and absorber are as follows:

$$\begin{aligned}&m\ddot{h} + S_{\alpha } \ddot{\alpha } + K_\mathrm{h} \left( h + c_\mathrm{h}h^3 \right) + qS C_{L\cdot \alpha }\nonumber \\&\quad \left( {\alpha + \frac{{\dot{h}}}{U}} \right) + c\left( {\dot{h} - \mathrm{d}\dot{\alpha }- \dot{z}} \right) \nonumber \\&\quad + k\left( {h - \mathrm{d}\alpha - z} \right) = 0\nonumber \\&{I_{\alpha } }\ddot{\alpha }+ {S_{\alpha } }\ddot{\alpha }+ {K_{\alpha } }\left( {\alpha + {C_{\alpha } }{\alpha ^3}} \right) \nonumber \\&\quad - qeS{C_{L\cdot \alpha }}\left( {\alpha + \frac{{\dot{h}}}{U}} \right) + dC \left( \mathrm{d}\dot{\alpha } + \dot{z} - \dot{h} \right) \nonumber \\&\quad + dK\left( {\mathrm{d}\alpha + z - h} \right) = 0\nonumber \\&m_\mathrm{s}\ddot{z} + C\left( \mathrm{d}\dot{\alpha } + \dot{z} - \dot{h} \right) + K\left( \mathrm{d}\alpha + z - h\right) = 0 \end{aligned}$$
(2)

and by introducing dimensionless parameters the equations are written to following form.

$$\begin{aligned}&y^{\prime \prime }+x_{\alpha } \alpha + \varOmega ^2 y + \xi _y y^3\nonumber \\&\quad + \mu C_{L\cdot \alpha } \Theta \left( y^{\prime } + \Theta \alpha \right) + \epsilon \lambda \left( y^{\prime }- \delta \alpha ^{\prime } -\nu ^{\prime }\right) \nonumber \\&\quad + C_1\left( y - \delta \alpha - \nu \right) = 0\nonumber \\&r_{\alpha }^2\alpha ^{\prime \prime } +x_{\alpha } y^{\prime \prime } \nonumber \\&\quad + r_{\alpha }^2\alpha + \xi _{\alpha } \alpha ^3\nonumber \\&\quad - \gamma \mu C_{L\cdot \alpha }\Theta \left( y^{\prime } + \Theta \alpha \right) + \delta \epsilon \lambda \left( \delta \alpha ^{\prime } + \nu ^{\prime } - y^{\prime }\right) \nonumber \\&\quad + \delta C_1\left( \delta \alpha + \nu - y \right) = 0\nonumber \\&\epsilon \nu + \epsilon \lambda \left( \nu ^{\prime } + \delta \alpha ^{\prime } - y^{\prime } \right) \nonumber \\&\quad + {C_1}\left( \nu + \delta \alpha - y \right) = 0 \end{aligned}$$
(3)

2.2 Maxwell model DVA

The Maxwell model is a simple model which consists of a linear spring and a damper that is attached in series to a mass as depicted in Fig. 3. The dimensionless equations of motion for the wing coupled with this DVA could be derived as the previous model and are presented as follows.

$$\begin{aligned}&y^{\prime \prime } +x_{\alpha } \alpha + \Omega ^2 y + \xi _y y^3 + \mu C_{L\cdot \alpha } \Theta \left( y^{\prime } + \Theta \alpha \right) \nonumber \\&\quad + C_1 \left( y - \delta \alpha - \nu _2\right) = 0\nonumber \\&r_{\alpha }^2\alpha +x_{\alpha } y + r_{\alpha }^2\alpha + \xi _{\alpha }\alpha ^3 - \gamma \mu C_{L\cdot \alpha }\nonumber \\&\quad \Theta \left( y^{\prime } + \Theta \alpha \right) + \delta C1\left( \delta \alpha + \nu _2 - y \right) = 0\nonumber \\&\epsilon \nu _1^{\prime \prime } + \epsilon \lambda \left( \nu _1^{\prime } - \nu _2^{\prime } \right) = 0\nonumber \\&\nu _1^{\prime } - \nu _2^{\prime } - \frac{C_1}{\epsilon \lambda } \left( \nu _2 + \delta \alpha - y \right) = 0 \end{aligned}$$
(4)
Fig. 3
figure 3

Maxwell model DVA

Full size image

2.3 Two degrees of freedom DVA

Another model which is attached to the airfoil model is a 2-DOF DVA with two linear springs, one damper and two masses as shown in Fig. 4. In fact, this model is the combination of a linear spring and a Kelvin–Voigt element which is attached in series. The dimensionless system’s equations of motion are presented as follows.

$$\begin{aligned}&y^{\prime \prime }+x_{\alpha } \alpha + \varOmega ^2 y + \xi _y y^3 + \mu C_{L\cdot \alpha } \Theta \left( y^{\prime } + \Theta \alpha \right) \nonumber \\&\quad + C_1\left( y - \delta \alpha - \nu _1 \right) = 0\nonumber \\&r_{\alpha } ^2\alpha +x_{\alpha } y+ r_{\alpha } ^2\alpha + \xi _{\alpha } \alpha ^3 \nonumber \\&\quad - \gamma \mu C_{L\cdot \alpha } \Theta \left( y^{\prime } + \Theta \alpha \right) + \delta C1\left( \delta \alpha + \nu _1 - y \right) = 0\nonumber \\&\frac{1}{2}\epsilon {\ddot{\nu }_1} +\epsilon \lambda \left( \dot{\nu }_1 - \dot{\nu _2} \right) \nonumber \\&\quad + C_1\left( \nu _1 + \delta \alpha - y \right) + C_2\left( \nu _1 - \nu _2\right) = 0\nonumber \\&\frac{1}{2}\epsilon {\ddot{\nu }_2} + \epsilon \lambda \left( \dot{\nu }_2 - \dot{\nu }_1 \right) + C_2\left( \nu _2 - \nu _1 \right) = 0 \end{aligned}$$
(5)
Fig. 4
figure 4

Two degree of freedom model DVA

Full size image
Fig. 5
figure 5

Maxwell–Voigt model DVA

Full size image
Fig. 6
figure 6

Linear spring parallel to the Maxwell element model DVA

Full size image

2.4 Maxwell–Voigt DVA

As shown in Fig. 5, this type of DVA consists of both Maxwell and Kelvin–Voigt elements, which are attached in parallel. The equations of motion of the wing-absorber system can be derived similar to previous models and can be written in the following form.

$$\begin{aligned}&y^{\prime \prime }+x_{\alpha } \alpha ^{\prime \prime } + \varOmega ^2 y + \xi _y y^3 + \mu C_{L\cdot \alpha } \Theta \left( y^{\prime } + \Theta \alpha \right) \nonumber \\&\quad + C_1\left( y - \delta \alpha - \nu _1 \right) +\epsilon \lambda _1\left( y^{\prime } - \delta \alpha ^{\prime } - \nu _1^{\prime } \right) \nonumber \\&\quad + C_2\left( y - \delta \alpha - \nu _2 \right) = 0\nonumber \\&r_\alpha ^2\alpha +x_{\alpha } y + r_\alpha ^2\alpha + \xi _\alpha \alpha ^3 - \gamma \mu C_{L\cdot \alpha } \Theta \left( y^{\prime } + \Theta \alpha \right) \nonumber \\&\quad +\delta C_1 \left( \delta \alpha + \nu _1 - y \right) \nonumber \\&\quad + \delta \epsilon \lambda _1\left( \delta \alpha ^{\prime } + \nu _1^{\prime } - y^{\prime } \right) + \delta C_2\left( \delta \alpha + \nu _2 - y \right) = 0\nonumber \\&\epsilon \nu _1^{\prime \prime } + C_1 \left( \delta \alpha + \nu _1 - y \right) + \epsilon \lambda _1\left( \delta \alpha ^{\prime } + \nu _1^{\prime } - y^{\prime } \right) \nonumber \\&\quad +\epsilon \lambda _2\left( \nu _1^{\prime } - \nu _2^{\prime } \right) = 0\nonumber \\&\nu _1^{\prime } - \nu _2^{\prime } = \frac{C_2}{\epsilon \lambda _2} \left( \delta \alpha +\nu _2 - y \right) \end{aligned}$$
(6)

2.5 Linear spring and Maxwell DVA

As depicted in Fig. 6, this absorber is the combination of a linear spring and the Maxwell element that is attached in parallel.

$$\begin{aligned}&y^{\prime \prime } + x_{\alpha } \alpha ^{\prime \prime } + \varOmega ^2 y + \xi _y y^3 + \mu C_{L\cdot \alpha } \Theta \left( y^{\prime } + \Theta \alpha \right) \nonumber \\&\quad + C_1\left( y - \delta \alpha - \nu _1 \right) + C_2\left( y - \delta \alpha - \nu _2 \right) = 0\nonumber \\&r_\alpha ^2\alpha +x_{\alpha } y + r_\alpha ^2\alpha + \xi _\alpha \alpha ^3 \nonumber \\&\quad -\gamma \mu C_{L\cdot \alpha } \Theta \left( y^{\prime } + \Theta \alpha \right) + \delta C_1 \left( \delta \alpha + \nu _1 - y \right) \nonumber \\&\quad + \delta C_2\left( \delta \alpha + \nu _2 - y \right) = 0\nonumber \\&\epsilon \nu _1^{\prime \prime } + C_1\left( \delta \alpha + \nu _1 - y \right) \nonumber \\&\quad + \epsilon \lambda _2\left( \nu _1^{\prime } - \nu _2^{\prime } \right) = 0\nonumber \\&\nu _1^{\prime } - \nu _2^{\prime } - \frac{C_2}{\epsilon \lambda _2}\nonumber \\&\quad \left( \delta \alpha + \nu _2 - y \right) = 0 \end{aligned}$$
(7)

2.6 Single degree of freedom NES

This nonlinear absorber consists of a cubic nonlinear spring, linear damper and a single mass. Figure 7 shows the configuration of this nonlinear absorber. The vibration energy dissipates in a one-way transfer to this absorber.

Fig. 7
figure 7

Single degree of freedom NES model

Full size image

Dimensionless equations of motion for the wing coupled with SDOF NES are as follows

$$\begin{aligned}&y^{\prime \prime } + x_\alpha \alpha ^{\prime \prime } + \Omega ^2y + \xi _y y^3 + \mu C_{L\cdot \alpha } \Theta \left( y^{\prime } + \Theta \alpha \right) \nonumber \\&\quad + \epsilon \alpha \left( y^{\prime } - \delta \alpha ^{\prime } - v^{\prime } \right) \nonumber \\&\quad + C\left( y - \delta \alpha - v \right) ^3 = 0\nonumber \\&r_\alpha ^2\alpha ^{\prime \prime } + x_{\alpha } y^{\prime \prime } + r_\alpha ^2\alpha + \xi _\alpha \alpha ^3 \nonumber \\&\quad - \gamma \mu C_{L\cdot \alpha } \Theta \left( y^{\prime } + \Theta \alpha \right) + \delta \epsilon \lambda \left( \delta \alpha ^{\prime } + \nu ^{\prime } - y^{\prime }\right) \nonumber \\&\quad + \delta C\left( \delta \alpha + \nu - y \right) ^3 = 0\nonumber \\&\epsilon \nu ^{\prime \prime } + \epsilon \lambda \left( \nu ^{\prime } + \delta \alpha ^{\prime } - y^{\prime } \right) + C(\nu + \delta \alpha - y)^3 = 0 \end{aligned}$$
(8)

2.7 Multi-degrees of freedom NES

The multi-degree of freedom NES (MDOF NES) is another type of nonlinear absorber, which is introduced and applied to the wing model in [15]. This type of NES is consisted on some SDOF NESs which are coupled in series and attached to the wing through a linear spring as depicted in Fig. 8.

Fig. 8
figure 8

Multi-degree of freedom NES model

Full size image

The total mass of the MDOF NES is equal to total mass of the SDOF NES, and the nonlinear coupling between masses 1 and 2 should be greater than the one between 2 and 3.

$$\begin{aligned}&y^{\prime \prime } + x_\alpha \alpha ^{\prime \prime } + \Omega ^2y + \xi _y y^3 + \mu C_{L\cdot \alpha } \Theta \left( y^{\prime } + \Theta \alpha \right) \nonumber \\&\quad + C_1\left( y - \delta \alpha - \nu _1 \right) = 0\nonumber \\&r_\alpha ^2\alpha ^{\prime \prime } + x_\alpha y^{\prime \prime } + r_\alpha ^2\alpha + \xi _\alpha \alpha ^3 - \gamma \mu C_{L\cdot \alpha }\Theta \nonumber \\&\quad \left( y^{\prime } + \Theta \alpha \right) + \delta C_1\left( \delta \alpha + \nu _1 - y \right) = 0\nonumber \\&\frac{1}{3}\epsilon \nu _1^{\prime \prime } + \epsilon \lambda \left( \nu _1^{\prime } - \nu _2^{\prime } \right) \nonumber \\&\quad + C_1\left( \nu _1 + \delta \alpha - y \right) + C\left( \nu _1 - \nu _2\right) ^3 = 0\nonumber \\&\frac{1}{3}\epsilon \nu _2^{\prime \prime } +\epsilon \lambda \left( \nu _2^{\prime } - \nu _1^{\prime } \right) + \epsilon \lambda \left( \nu _2^{\prime } - \nu _3^{\prime } \right) \nonumber \\&\quad + C\left( \nu _2 - \nu _1 \right) ^3 + \frac{1}{{50}}C\left( \nu _2 - \nu _3 \right) ^3 = 0\nonumber \\&\frac{1}{3}\epsilon \nu _3^{\prime \prime } + \epsilon \lambda \left( \nu _3^{\prime } - \nu _2^{\prime } \right) \nonumber \\&\quad + \frac{1}{50}C\left( \nu _3 - \nu _2 \right) ^3 = 0 \end{aligned}$$
(9)

Up to now, different forms of linear and nonlinear DVAs are introduced, and the corresponding governing equations are derived. There could be numerous configurations of absorbers, which can be used in different systems, but for the comparison study, few of them that have acceptable perform on the considered aeroelastic model are presented here.

3 Results and discussion

In this section, performance of different types of DVAs in aeroelastic systems is compared with single and multi-degree of freedom NESs reported in [15].

3.1 Linear stability analysis

Transforming equations of motion to the state space form, the eigenvalues of the wing-absorber system can be obtained. Flutter is a dynamic instability and happens due to the interactions of the inertial, elastic and aerodynamic forces. Flutter point is the point at which the structure is undergoing a harmonic motion, i.e., eigenvalues are purely imaginary. Hence the point where the real part of eigenvalues passes through the reduced velocity axis and has pure imaginary eigenvalue, gives flutter velocity.

Fig. 9
figure 9

Variations of eigenvalues of wing model with reduced velocity, a real part of eigenvalues versus reduced velocity (filled circle denotes the flutter points) and b imaginary part of eigenvalues versus their real parts

Full size image
Table 1 Flutter margin of wing model for different DVAs with parameters mentioned in [15]
Full size table

The eigenvalues of the aeroelastic model with no absorber are shown in Fig. 9. As it is seen from Fig. 9a, by changing the velocity, at first there would be an increase in the negative value of the real part of eigenvalues, so that in \(\Theta =0.585\) eigenvalues have the largest negative real parts. In this situation, based on the concepts of linear control, since the system’s dominant poles are in the greatest distance from the imaginary axis, system is in its most stable situation. By changing the velocity, the negative value of the real part of the eigenvalues decreases, and the eigenvalues tend to the positive values gradually. There is a bifurcation in the intersection point of the eigenvalue branches with velocity axis. This point, which is denoted by black dot point in Fig. 9a, could be either a flutter (Hopf) or divergence (saddle node) instability. If in the intersection point of real part of eigenvalues with real axis, the imaginary part is nonzero, flutter instability will occur, but if eigenvalue becomes zero, divergence will occur. For the case shown in Fig. 9b, system has purely imaginary eigenvalues; hence, its real part is zero and at flutter velocity sustained oscillation will occur. After that, system has complex eigenvalues with positive real part, and the amplitude of system oscillatory grows with time. Type of instability can be determined from Fig. 9b, in which real and imaginary parts of eigenvalues are displayed. Form Fig. 9b, it can be understood that instability is a flutter. For this figure, flutter velocity of \(\Theta _\mathrm{F} =0.87\) is determined and shown by black dot point. More increase in the velocity causes the system to be linearly instable, and its amplitude tends to infinity, but because of the presence of structural nonlinearity, limit cycle behavior or other type of nonlinear behaviors would be occurred in the system, which would be discussed in the following.

In Fig. 9b the direction of change in imaginary part of eigenvalues is shown with arrow. As it is clear from this figure, for \(\Theta =0\), since aerodynamics damping is zero, the only damping presented in the system is due to the effect of linear damper, and eigenvalues are located close to the imaginary axis, but with increase in reduced velocity, more damping induces to the system, and at \(\Theta =0.585\) eigenvalues have the greatest negative real part and system is in higher state of stability. But with increase in reduced velocity, eigenvalues move toward the imaginary axis and at \(\Theta =0.585\) intersect with it, and flutter occurs. After flutter, linear system is unstable. The flutter point is denoted by a black dot in Fig. 9a.

To compare the performance of different linear DVAs with NESs, in this part the optimum values determined in [15] are applied to obtain the flutter of linear absorbers. The obtained flutter values are shown in Table 1.

Fig. 10
figure 10

Dominate eigenvalues of different linear absorbers and two types of NESs, a Kelvin–Voigt, b Maxwell, c two DOF linear, d Maxwell–Voigt, e linear spring parallel to the Maxwell

Full size image
Table 2 The optimized value of the system’s parameters
Full size table

It is observed from the results that the presented linear absorber models have a better performance in comparison with the single degree of freedom NES, and except the Maxwell model, other four types of linear absorbers also have a better performance comparing multi-degree of freedom NES. It can be concluded here that using the parameter values presented by Lee et al [15], linear absorbers can be designed such that to have a better performance comparing both SDOF NES and MDOF NES in order to improve the stability characteristics of the system.

According to the results shown in Table 1, it is necessary to give point on the role of linear and nonlinear stiffnesses and linear damping on flutter velocity. The flutter is linear instability, and flutter instability can be determined from linear system. After flutter velocity, the amplitude of vibration for linear system continuously grows with time, but for nonlinear systems, limit cycle oscillations will occur. So the nonlinear part of the system does not play a role in the flutter point. This has been mentioned in page 1376 of Ref. [15] that is “The bifurcation sets (Hopf and LPC) are almost insensitive to the coefficient of the essential nonlinearity. The robustness of instability suppression is not much affected by the essential nonlinearity if its magnitude is sufficiently large. The main role of the essential nonlinearity is to provide broadband nonlinear resonant interaction between the primary and NES subsystems.” This statement in Refs. [8, 10, 12] and [15] confirmed our result in the role of essential nonlinearity on flutter velocity. The increase in flutter velocity in the works done by these authors is due to the effect of damper and not essential stiffness nonlinearity. With linearization, the nonlinear stiffness term of NES will be diminished and it has no role in the linear region of stability, and this is in confirmation with the above-mentioned sentence in Ref. [15]. On the other hand, in linear DVAs, both the stiffness and dissipation element are effective in the flutter velocity. This cause the linear DVAs to perform better from the flutter point of view.

Changes in real part of eigenvalues versus the reduced velocity for mentioned DVAs are presented in Fig. 10, and flutter velocity points of each DVA are compared with both types of NESs.

In order to optimize the systems parameter values, first parameter’s value ranges are defined, which means the upper and lower values can be considered for the parameters. Then, a set of stable eigenvalues from the primary system is considered. For a higher flutter velocity achievement, it is necessary to optimize parameters of DVA. For this purpose, an achievable targeted flutter velocity \(\theta _\mathrm{F} \) is considered, and then the norm of eigenvalues difference at \(\theta _\mathrm{F} \) with some desirable eigenvalues set is minimized. The set of targeted eigenvalues could be considered as the most stable point of the primary system (i.e., \(\Theta =0.585)\). This point can be seen in Fig. 9a. Attaching different type of absorbers to the system and adding some degree of freedom to the system, it is essential to add some extra eigenvalues to the targeted eigenvalues set which is obtained from the primary system. For this purpose, other stable eigenvalues can be added to the eigenvalues set. This approach is to some extent similar to the pole assignment technique used in modern control theory. Hence, if \(D_\mathrm{T}\) is assumed to be the set of targeted eigenvalues, which is obtained from the stable point of the primary system, and \(D_\mathrm{s} \) to be the system’s eigenvalues set at desired flutter velocity \(\theta _\mathrm{F} \), the optimization cost function will be:

$$\begin{aligned} f=\sum \left| {\left( {D_\mathrm{s} -D_\mathrm{T} } \right) ^{2}} \right| \end{aligned}$$
(10)

and the DVA parameters are obtained such that to minimize the f.

Fig. 11
figure 11

Real and imaginary parts of eigenvalues for wing model with different linear and nonlinear DVAs. a SDOF NES. b MDOF NES. c Kelvin–Voigt DVA. d Maxwell DVA. e Two DOF DVA. f Maxwell–Voigt DVA. g Linear spring parallel to the Maxwell DVA

Full size image

The optimization procedure is based on the following strategy. First we defined the parameter’s values range, which means the upper and lower values can be considered for the parameters. The bond of each value is selected according to the parameters mentioned in Refs. [8, 10, 12] and [15]. Then, a set of the most stable eigenvalues of the primary system was taken. This set of stable eigenvalues is assumed to be targeted eigenvalue set and is denoted by \(D_\mathrm{T}\). The flutter velocity is selected as \(\Theta _\mathrm{F} \), whose eigenvalues are denoted by \(D_\mathrm{s} \). Then according to the cost function mentioned in Eq. (8), parameters of DVAs are selected. From Fig. 9 it is clear that at \(\Theta =0.585\), system has the best state of stability, since in this reduced velocity, eigenvalues have the greatest negative real parts. These eigenvalues are selected as \(D_\mathrm{s} \). \(\Theta _\mathrm{F} \) must be selected, as our desired flutter velocity, and \(D_\mathrm{T}\) is determined from the eigenvalue solution for linear parts of equation of motion in the selected \(\Theta _\mathrm{F} \). Then with cost function of Eq. (8) and using gradient-based optimization algorithm such as MATLAB fmicon or fminsearch commands, parameters of DVAs are determined.

It is necessary to point out, with DVAs according to cost function of (8), it is tried to use passive absorber to optimize the locations of poles of total system. It should be noticed that, with using passive vibration absorber, complete pole assignment cannot occurred. This point is described by Mottershead et al. [18]. They described procedures for pole placement by passive modification and active control using measured receptance. For passive modification, they mentioned that with passive structures, limited numbers of poles can be assigned. For example, they pointed out that a single added spring can assign only one eigenvalue exactly and the other eigenvalues are then given by solving the characteristic equation. Also they mentioned that since most practical passive modifications have considerably higher rank, limitation of passive structures for accurate pole assignment will be increased. Hence, they proposed active control for pole assignment.

The limitation of passive absorber in complete pole assignment is presented here. The main focus of the work done by Mottershead et al. [18] is to accurately assign the desired poles at some specific locations; hence, finally they proposed active control for complete pole assignment. Form modern control theory, complete pole assignment is only possible, when the controllability matrix has full rank, but this is not possible here, since passive vibration absorber is used.

In state space, the considered wing model with attached linear and nonlinear absorbers has dimension greater than 6, and with increase in degrees of freedom of absorber, dimension of total system will be increased; accordingly, with limited number of parameters for absorber, complete assignments of eigenvalues are impossible. Since there are infinite choices for selection of absorber parameters, an optimization procedure is proposed to obtain the parameters of different absorbers. In this optimization, at first some desirable eigenvalues and desired flutter velocity \(\theta _\mathrm{F} \) are selected, and according to the cost function mentioned in Eq. (8), the parameters of absorbers are obtained. The flutter velocity \(\theta _\mathrm{F} \) can be extended without limitation. But it should be noticed that the desired \(\theta _\mathrm{F} \) must be in the domain of validity of aerodynamics model, and the obtained parameters of linear DVAs are in the range of parameters given for NES, since with arbitrary selection of linear DVAs, the flutter may extensively postponed, but the parameters of DVAs may not comparable with NES parameters mentioned in Ref. [15].

In Eq. (8), \({D}_{\mathrm{T}} \) assumed to be the set of targeted eigenvalues, which is obtained from the stable point of the primary system, and \(D_\mathrm{s} \) to be the system’s eigenvalues set at desired flutter velocity \(\theta _\mathrm{F}\). These are not the same at all, since for \(D_\mathrm{T}\) the distribution of eigenvalues is such that the maximum margin of stability is obtained, i.e., they have eigenvalues with greatest negative real part, while for \(D_\mathrm{s} \) the eigenvalues are located close to the imaginary axis, and eigenvalue assignment cannot occurred here. In Eq. (8) it is tried to optimize the distance between the best stable conditions of system with condition in which system is in the verge of instability. In this optimization, upper and lower bonds for absorber parameters are considered.

Fig. 12
figure 12

Phase angle of dominant eigenvalues (filled circle denotes the flutter points). a SDOF NES. b MDOF NES. c Kelvin–Voigt. d Maxwell. e Two DOF linear DVA. f Maxwell–Voigt. g Linear and Maxwell

Full size image

Based on this method, the optimized parameter values will be obtained and the corresponding flutter velocity, limit cycle oscillations and other nonlinear responses are compared.

The optimal parameter’s values for linear DVAs and the equivalent flutter velocities are presented in the next table. It is obvious from Table 2 that after the optimization, higher values in the system’s flutter velocities are obtained. It should be mentioned that the NES values which are presented in Table 1 are the optimized values, as mentioned in [15].

It is obvious from the analysis of this section that the linear DVAs can delay the flutter velocity in a better way than both types of NESs, which means for considered wing model attached to these mentioned linear DVAs; flutter occurs in higher velocity. It should be pointed that since for presented equations of motion the equilibrium state is equal to zero, the nonlinear stiffness term is ineffective on the flutter velocity The flutter velocity range order for the absorbers is as \(\Theta _{\mathrm {MV}}>\Theta _{\mathrm {KV}}>\Theta _{\mathrm {LSPM}}>\Theta _{\mathrm{M}}>\Theta _{2\mathrm{DOF}}>\Theta _{\mathrm {MDOF NES}} >\Theta _{\mathrm {SDOF NES}} \).

Following the work done by Mottershead et al. [18], it can be stated that the forced applied from DVAs to the wing model is composed of stiffness and damping terms (i.e., damping and stiffness injection); hence, DVAs can change both of these terms in the host structure, while the NES induces damping and nonlinear stiffness terms. Since flutter is linear phenomenon, DVAs can better control the flutter, due to change in both linear stiffness and damping terms, while since NES can only change linear damping term of the primary system, hence it has lower authority to the flutter margin.

The real and imaginary parts of eigenvalues for systems are presented in Fig. 11. Real part of the eigenvalues is plotted on the horizontal axis, and imaginary part of the eigenvalues is plotted on the vertical axis. The stability of the systems can be analyzed from these figures. Since none of the plot’s branches passes through the real axis line, it can be concluded that the instabilities of the systems are flutter and there is no happening of other types of instability such as divergence.

The phase angle of the system’s dominant poles varying with the reduced velocity is illustrated in Fig. 12. Flutter occurs when the phase angle of the dominant poles is equal to \(\pm \pi /2\). These points are also denoted in Fig. 12. The flutter speeds obtained by this analysis are identical to previously obtained flutter velocity’s values.

Fig. 13
figure 13

Time response comparisons for heave and pitch modes for different types of linear DVAs with two types of NESs at \(\Theta =1\), all initial conditions are zero except \(y' (0)=0.01\). a Kelvin–Voigt, b 2-DOF linear, c Maxwell–Voigt, d linear spring and Maxwell, and e Maxwell DVAs

Full size image
Fig. 14
figure 14

Bifurcation diagram for LCO amplitude of pitch mode

Full size image
Fig. 15
figure 15

Heave mode LCO amplitude. a Without absorber. b MDOF NES. c SDOF NES. d Linear spring parallel to Maxwell DVA. e Kelvin–Voigt DVA. f Maxwell DVA. g Two DOF linear DVA. h Maxwell–Voigt DVA

Full size image

3.2 Nonlinear response analysis

In the previous section, it was demonstrated that properly designed linear absorbers can have a better stability range. In this section, the time responses and bifurcation diagrams of the nonlinear system would be analyzed in order to compare the linear and nonlinear vibration absorber’s performances in different specific reduced velocities. Numerical method is applied to obtain the systems time responses and bifurcation diagrams. Time responses of the wing-DVA systems are derived for both heave and pitch modes and compared with the wing-NES systems shown in Fig. 13. For linear and nonlinear absorbers, the optimal values of parameters are considered. All the initial conditions set to be zero except the heave mode initial velocity, which is considered to be \(y'(0)=0.01\).

It is obvious from the figures that according to [15], MDOF NES performs better than SDOF NES, but what is more important is that for \(\Theta =1\), the time response amplitude for all the linear absorbers tends to zero, while the nonlinear absorbers have limit cycle oscillations of higher periods.

Now the nonlinear behaviors of linear and nonlinear absorbers are investigated accurately. Since the system of study has structural nonlinearities, different nonlinear behaviors such as limit cycle, quasi-periodic behaviors and multi-frequency behaviors could be occurred. Hence, the performances of linear and nonlinear absorbers are examined in this case to be addressed to closer analysis.

In order to analyze the nonlinear behaviors of considered aeroelastic model, variation in pitch and heave oscillation amplitudes versus reduced velocity of \(\Theta \) is shown in Figs. 13 and 14. It is clear from the figures that the presented linear DVAs could delay the Hopf bifurcation points and Pitch mode LCOs occurrence. As mentioned in [15] and seen in Fig. 13, both types of NESs tend to subcritical behaviors. It is clear that for the system with absorbers, the pitch limit cycle amplitude is smaller than the primary system with no absorber.

The heave mode LCO amplitudes varying with reduced velocity are illustrated in Fig. 15. Despite the pitch mode, quasi- periodic, high frequency and maybe chaotic behaviors may occur in heave mode for some cases of DVA. Although there are chaotic behaviors in SDOF NES, this nonlinear absorber could not perform as well in delaying the flutter velocity and controlling the LCOs.

It is obvious from the figures that the heave amplitude of the primary system with no absorber increases gradually. Initially, the frequency content of the primary system is one. As the reduced velocity increases, its frequency content would be three, and all of these three amplitudes increase. For the system with MDOF NES there is a sudden jump in the heave amplitude response after the flutter velocity, and hence there is a nonlinear resonance. Increasing the velocity causes a three frequency or three amplitude behaviors in the system. Comparing the MDOF NES system results with the primary system, clearly up to \(\Theta =1\cdot 5\), the MDOF NES system’s response is greater than the primary system. For the SDOF NES model the heave amplitude is greater than the primary system but smaller than MDOF NES model. However, in SDOF NES system the response’s frequency content is more than two past systems which have three frequencies.

The heave mode behaviors for Maxwell DVA, linear spring parallel to Maxwell DVA and two DOF linear DVA are close to the MDOF NES. Hence, their performances are similar. There is little difference in these absorber’s response amplitudes that is after the flutter point the MDOF NES response is greater than the linear spring parallel to Maxwell DVA ones, but after the flutter takes to happen this behavior change and the linear spring parallel to Maxwell DVA response would be greater. For Kelvin–Voigt DVA model, after the flutter the heave mode amplitude increases gradually and for the \(\Theta \ge 1.3\) the amplitude value tends to a constant value. The Maxwell–Voigt DVA performance is similar to the Kelvin–Voigt model. It can be claimed from the results that only the Kelvin–Voigt and Maxwell–Voigt models would have single-frequency limit cycle behaviors in the velocities after the flutter, while other absorber models have higher-frequency content behaviors.

4 Conclusion

Both linear and nonlinear types of vibration absorbers delay the flutter happening. From this point of view, the linear vibration absorbers can perform better. Subcritical bifurcation behaviors occur in the analyzed nonlinear absorbers with the essentially third-order stiffness nonlinearities; therefore, they should be designed and used accurately. For the primary system without any absorber, as the reduced velocity rises, the heave and pitch mode amplitudes increase. In velocities over the flutter, every type of absorbers has smaller pitch amplitudes than the primary system. Similar to the stability range, linear absorbers perform in a better way than nonlinear absorbers of study. In heave mode, the absorber’s behaviors are different. In systems with SDOF NES, increase in reduced velocity causes a gradual increase in its maximum amplitudes, and the frequency content would increase in some parts and decrease in other. This clearly shows the incidence of quasi-periodic behaviors due to the frequency content increase, existence of periodic windows as a result of decrease in the frequency content and the system tendency to chaotic behaviors due to high-density frequency content in some parts. For MDOF NES model, a nonlinear resonance behavior occurs right after the flutter, and afterward the amplitude suddenly reduces. Then with appearing a periodic behavior with three frequency contents, amplitude increases slowly. Similar behaviors are observed for two DOF linear DVA, linear spring parallel to Maxwell DVA and Maxwell model DVA.