Effectiveness of a nonlinear energy sink in the control of an aeroelastic system

Abstract

The effectiveness of the nonlinear energy sink in controlling the limit cycle oscillations of a nonlinear aeroelastic system is assessed. The system consists of a rigid airfoil elastically mounted on linear and nonlinear springs. The coupled equations of the airfoil and sink are derived using Lagrange’s equations. The nonlinear quasi-steady aerodynamics are used to model the aerodynamic loads. Parameters including the mass and placement of the passive controller are varied in order to test its efficiency in suppressing undesirable aeroelastic behavior under varying conditions. The nonlinear normal form governing the responses of the airfoil and the energy sink is derived. The contribution of the aerodynamic, structural and sink nonlinearities to the type of instability is quantified. The results show that the nonlinear energy sink has a limited impact on the system’s response in terms of effectively delaying the onset of flutter, changing the type of instability or reducing the amplitude of the limit cycle oscillations.

1 Introduction

Flutter control and suppression of limit cycle oscillations have been objectives of many investigations of aeroelastic systems. The interest is in expanding the flight boundary and enhancing aircraft performance. Furthermore, successful robust control strategies can be used to reduce the number of required flight tests for different configurations. Different strategies, including active and passive controls, have been proposed to increase the flutter speed or suppress limit cycle oscillations. The use of active control strategies requires external actuators and sensors. These requirements are not needed in passive control strategies. This is an important advantage in terms of keeping the payload to a minimum and avoiding issues associated with control surfaces.

We focus in this work on one mechanism that has been proposed as a passive control strategy, namely the nonlinear energy sink (NES), to suppress or reduce the amplitude of limit cycle oscillations of aeroelastic systems. The NES has been proposed to suppress the vibrations of different mechanical systems. It is composed of a secondary system with a nonlinear stiffness that is attached to the main system. The idea behind it is to pump the energy of the main system to the NES and, as such, limit the amplitude of its motion. One advantage of having a nonlinear stiffness is that the passive pumping of energy would take place irrelevant of the frequency of the motion of the main system. Although successful in some applications, the NES has been shown to have some shortcomings in terms of yielding multiple solutions and practicality especially when it comes to specific types of instabilities. Lee et al. [1] showed that the NES causes a delay in flutter and a reduction in the amplitudes of oscillations. Jiang et al. [2] experimentally and theoretically investigated the dynamics of an NES that is weakly coupled to a linear structure that was harmonically forced. They determined that, due to the nonlinearity, the NES can vibrate with any mode of the primary system. Malatkar and Nayfeh [3] investigated the system considered by Jiang et al. [2] and showed that multiple solutions for undamped or slightly damped linear subsystems exist. They also showed that, for lightly damped subsystems, the NES increases the amplitude of oscillations when increasing the mass. Recently, Mehmood et al. [4] investigated the use of the NES to suppress the vortex-induced vibrations of a circular cylinder. They determined that there is a critical mass ratio 3 % below which the NES is ineffective. When the mass ratio was set between 3 and 6 %, the results showed multiple solutions and a strong dependence on the initial conditions such as gust, which eliminates its effectiveness. As the mass ratio was increased to 10 %, the vibrations were significantly reduced. However, this reduction may be more due to the change in the density ratio of the combined cylinder and NES masses to the density of the surrounding fluid, which affects the lock-in region of the vortex-induced vibrations. They also determined that placing the secondary mass within the main cylinder may be impractical.

The above studies and notions about the response of systems controlled by an NES show that there is a need for careful examination of the response of aeroelastic systems including aircraft wings when combined with a nonlinear energy sink. This is especially true because the payload increase in terms of the mass of the NES and its placement along the chord must be carefully considered. Furthermore, gust effects could cause a change in the initial conditions and unexpected or undesirable responses. The introduction of the NES, which is essentially a cubic nonlinearity to the aeroelastic system, could lead to multiple stable responses depending on such conditions. The objective of this work is to assess the effectiveness of the NES in controlling the flutter and ensuing limit cycle oscillations of a two-dimensional aeroelastic system. Particular attention is placed on its effects on the flutter delay, type of instability and reduction of the ensuing LCO amplitudes. This will be achieved by investigating the dependence of controlled responses on the placement location along the chord of the NES, its mass and the initial conditions. In the following section, we use the energy approach to derive the governing coupled equations of the airfoil-NES system. The aerodynamics are modeled using the nonlinear quasi-steady aerodynamics. In Sect. 3, we perform a linear analysis to determine the effects of the NES on the onset of flutter. We use, in Sect. 4, the normal form to analytically determine the nonlinear response characteristics of the coupled system and the effects of combining the sink nonlinearity with the system’s nonlinearities. In Sect. 5, we present and discuss the results for different systems and NES parameters. Finally, we give in Sect. 6 the conclusions and some remarks.

2 Aeroelastic model

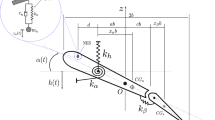
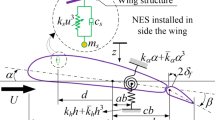
The aeroelastic system under investigation is composed of a rigid wing supported by torsional and flexural springs, as shown in Fig. 1. This wing is allowed to move with two degrees of freedom: (a) a vertical translational motion referred to as plunge and denoted by h and (b) a clockwise rotational motion referred to as pitch and denoted by $\theta$. The relative displacement of the NES mass with respect to the wing is denoted by $y_2$. In Fig. 1, the plunge is considered positive in the downward direction and the pitch is assumed positive in the clockwise direction. The position of the center of gravity, leading and trailing edges, etc. are measured with respect to the elastic axis which is the origin of the translating frame. The parameters $k_h (h)$, $k_{\theta } (\theta )$ and $k_{n} (y_2)$ are used to respectively represent the stiffness of the plunge, pitch and NES. The pitch and plunge stiffness are assumed to have polynomial forms and given by

$$\begin{aligned} \begin{aligned} k_h (h)&= k_{h_0} + k_{h_1}\,h+ k_{h_2}\,h^2 \\ k_{\theta } (\theta )&= k_{\theta _0} + k_{\theta _1}\, \theta + k_{\theta _2}\, \theta ^2 \end{aligned} \end{aligned}$$

and the NES stiffness is of the form

$$\begin{aligned} k_{n} (y_2) = k_{n_2}\, y_2^2 \end{aligned}$$

Next, we use the energy approach to derive the equations of motion governing the coupled wing/NES system. The details of the derivation are given in the “Appendix”. Based on this derivation, the following set of ordinary differential equations is obtained:

$$\begin{aligned}&{\ddot{h}} \, \left[ m_1+m_2 \right] +{\ddot{\theta }}\, \left[ e \,m_1+m_2\,d\right] \,\cos (\alpha _0+\theta ) + m_2\, \ddot{y_2}\nonumber \\&\quad -\, e\, {\dot{\theta }}^2\,m_1\, \sin (\alpha _0+\theta )-m_2\,d\,{\dot{\theta }}^2\,\sin (\alpha _0+\theta )\nonumber \\&\quad +\, k_{h_0}\,h + k_{h_1}\,h^2 + k_{h_2}\,h^3 + C_h \, {\dot{h}} = - L \end{aligned}$$

(1)

$$\begin{aligned}&{\ddot{h}} \, \left[ m_1\,e+m_2\,d\right] \,\cos (\alpha _0+\theta )\,+\, \ddot{y_2}\,m_2\,d\,\cos (\alpha _0+\theta ) \nonumber \\&\quad +\,{\ddot{\theta }}\, \left[ m_1\, e^2 +I_\mathrm{{cg}}+m_2\,d^2\right] \nonumber \\&\quad + \,k_{\theta _0}\, \theta + k_{\theta _1}\, \theta ^2 + k_{\theta _2}\, \theta ^3 + C_{\theta } \,{\dot{\theta }} = M \end{aligned}$$

(2)

$$\begin{aligned}&m_{2} \, {\ddot{h}}+ {\ddot{\theta }} \left[ m_2\,d\,\cos (\alpha _0+\theta ) \right] \nonumber \\&\quad +\, m_2\,\ddot{y_2}\,-\,2\,m_2\,d\,{\dot{\theta }}^2\, \sin (\alpha _0+\theta ) \nonumber \\&\quad + \,k_{n_2}\, y_2^3 + C_{y_2} \,\dot{y_2} = 0 \end{aligned}$$

(3)

Fig. 1

Schematic of the airfoil-NES system

These equations were derived assuming that $y_2$ is computed from the mid thickness of the airfoil. However, if we assume that $y_2$ is computed from a fixed point (i.e. the origin of the frame), the following equations are obtained

$$\begin{aligned}&m_1{\ddot{h}} + e{{\ddot{\theta }}} m_1\cos \left( \theta \right) + k_{h_0} h + k_{h_1} h^2+k_{h_2} h^3 \nonumber \\&\quad -\,k_n \left( - y_2 -d \sin {\theta }+h\right) ^{3}\nonumber \\&\quad +\, C_h{\dot{h}} - C_{y_2} \left( {\dot{y}}_2+\mathrm{{d}}{{\dot{\theta }}}\cos {\theta }-{\dot{h}} \right) = -L \end{aligned}$$

(4)

$$\begin{aligned}&\left( I_\mathrm{cg} +\,m_1e^2 \right) {{\ddot{\theta }}}+ m_1e{\ddot{h}}\cos \left( \theta \right) \nonumber \\&\quad +\, m_2d^2{{\ddot{\theta }}} +k_{\theta _0}\theta + k_{\theta _1} \theta ^2+k_{\theta _2} \theta ^3\nonumber \\&\quad -\,k_n d\cos {\theta } \left( - y_2 -d \sin {\theta }+h\right) ^3 + C_\theta {{\dot{\theta }}} \nonumber \\&\quad + C_{y_2} d\cos {\theta }\left( \dot{y}_2+\mathrm{d}{{\dot{\theta }}}\cos {\theta }-{\dot{h}} \right) = M \end{aligned}$$

(5)

$$\begin{aligned}&\quad m_2{\ddot{y}}_2 + k_n \left( y_2 +d \sin {\theta }-h\right) ^{3}\nonumber \\&\quad +\,C_{y_2} \left( {\dot{y}}_2+\mathrm{d}{{\dot{\theta }}}\cos {\theta }-{\dot{h}} \right) = 0 \end{aligned}$$

(6)

When non-dimensionalized, these equations yield:

$$\begin{aligned}&h^{''} + e^{*} \theta ^{''} \cos \left( \theta \right) + \frac{\sigma ^2}{V^2} \left( h + \eta _1^{h} h^2+ \eta _2^{h} h^3\right) \nonumber \\&+\,{\overline{\eta }} \frac{\sigma ^{2}}{V^{2}} \left( - y_2 -d^{*} \sin {\theta }+h\right) ^{3}+ \frac{\overline{C_1}}{V} h^{'} \nonumber \\&+\,\overline{C_{y_2}} \frac{\sigma }{V} \left( y_2^{'}+d^{*} \theta ^{'}\cos {\theta }- h^{'} \right) = - {\overline{L}} \end{aligned}$$

(7)

$$\begin{aligned}&r^2 \theta ^{''} + e^{*}\cos \left( \theta \right) h^{''}+ {\overline{\epsilon }} {d^{*}}^2 \theta ^{''} \nonumber \\&+\,\frac{r^2}{V^2}\left( \theta + \eta _{1}^{\theta } \theta ^{2} +\eta _{2}^{\theta } \theta ^{3} \right) \nonumber \\&-\,{\overline{\eta }} \frac{\sigma ^{2}}{V^{2}} d^{*}\cos {\theta } \left( - y_2 -d \sin {\theta }+h\right) ^{3} \frac{\overline{C_2} }{V} \theta ^{'} \nonumber \\&+\,\overline{C_{y_2}} \frac{\sigma }{V} d^{*} \cos {\theta }\left( y_2^{'}+d^{*} \theta ^{'}\cos {\theta }- h^{'} \right) = {\overline{M}} \end{aligned}$$

(8)

$$\begin{aligned}&{\overline{\epsilon }} y_2^{''} + {\overline{\eta }} \frac{\sigma ^2}{V^2} \left( y_2 +d^{*} \sin {\theta }-h\right) ^{3} \nonumber \\&+\,\overline{C_{y_2}} \frac{\sigma }{V} \left( y_2^{'}+d^{*} \theta ^{'}\cos {\theta }- h^{'} \right) = 0 \end{aligned}$$

(9)

where ${\overline{\epsilon }}$ is the mass ratio of the NES relative to the total mass of the system, $\sigma$ is the frequency ratio, V is the reduced velocity, d is the nondimensional location of the NES with respect to the elastic axis, ${\overline{\eta }}$ is the nondimensional stiffness associated with the NES, $e^{*}$ is the eccentricity, $\eta _{i=1,2}^{h}$ are the quadratic and cubic plunging stiffness, $\eta _{i=1,2}^{\theta }$ are the quadratic and cubic pitching stiffness, ${\overline{L}}$ is the nondimensional lift and ${\overline{M}}$ is the nondimensional moment.

Figure 2 shows a comparison of the amplitudes of the limit cycle oscillations obtained using the models of Lee et al. [1] and Guo et al. [5] and the current model for an NES mass ratio of 5 %. The observed differences in the amplitude values are due to the different assumptions made regarding the representation of the aerodynamic forces and moments. In the current work, we use a nonlinear quasi-steady representation. Lee et al. used a linear quasi-steady aerodynamic model while Guo et al used the aerodynamic formulation of Fung et al. [6]. This difference along with the difference in the approximations of the $\cos {\theta }$ and $\sin {\theta }$ terms and the solution approach yield the observed differences in the LCO amplitudes. Still, the common observation from the three models is that the effect of the NES on delaying flutter is negligible.

Fig. 2

Comparison of the results of Lee et al. [1] ($-o-$), Guo et al. [5] ($-*-$) and the current model ($-+-$) for the a plunge and b pitch response

In the rest of the work, we make use of Eqs. (1), (2) and (3), assume zero preset angle of attack $\alpha _0$ (i.e. $\alpha _0 = 0$) and a small pitch angle ($\theta$) to obtain

$$\begin{aligned}&{\ddot{h}} \, \left[ m_1+m_2 \right] +{\ddot{\theta }}\, \left( 1-\frac{\theta ^2}{2}\right) \,\left[ e \,m_1+m_2\,d\right] \, \nonumber \\&\quad +\,m_2\, \ddot{y_2} - e\, {\dot{\theta }}^2\,m_1\, \theta -m_2\,d\,{\dot{\theta }}^2\,\theta + k_{h_0}\,h + k_{h_1}\,h^2\nonumber \\&\quad + k_{h_2}\,h^3 + C_h \, {\dot{h}} = - L \nonumber \\\end{aligned}$$

(10)

$$\begin{aligned}&{\ddot{h}} \,\left( 1-\frac{\theta ^2}{2}\right) \, \left[ m_1\,e+m_2\,d\right] \,+\, \ddot{y_2}\,m_2\,d\, \left( 1-\frac{\theta ^2}{2}\right) \nonumber \\&\quad +\,{\ddot{\theta }}\, \left[ m_1\, e^2 +I_\mathrm{cg}+m_2\,d^2\,\right] \nonumber \\&\quad +\, k_{\theta _0}\, \theta + k_{\theta _1}\, \theta ^2 + k_{\theta _2}\, \theta ^3 + C_{\theta } \,{\dot{\theta }} = M \end{aligned}$$

(11)

$$\begin{aligned}&m_{2} \, {\ddot{h}}+ {\ddot{\theta }}\,\left( 1-\frac{\theta ^2}{2}\right) \, \left[ m_2\,d \right] + m_2\,\ddot{y_2}\,-\,2\,m_2\,d\,{\dot{\theta }}^2\, \theta \nonumber \\&\quad +\,k_{n_2}\, y_2^3 + C_{y_2} \,\dot{y_2} = 0 \end{aligned}$$

(12)

To model the limit cycle oscillations, one needs to account for the aerodynamic nonlinearities resulting from flow separation, which depends on the effective angle of attack. For accurate evaluation of the nonlinear effects, one would need to solve the Navier-Stokes equations and couple them with the equations of motion of the nonlinear energy sink and airfoil section. Still, such a high-fidelity approach would need to be validated and is computationally expensive. More importantly, it would be impossible to pinpoint underlying physics from such simulations that have a large number of degrees of freedom. As such, we opted for using a reduced-order model of the aerodynamic loads that would allow for the evaluation of the underlying stability and effects of different parameters of the NES, which is the objective of this work. Reduced-order models have their own shortcomings. For instance, unsteady aerodynamic models are mostly linear and are, thus, limited to small angles of attack, which may limit their applicability to the problem considered in this study. As such, we model the aerodynamic loads by a nonlinear quasi-steady approximation [7, 8], where the lift and moment are given by:

$$\begin{aligned} \begin{aligned}&L=\rho \, U^{2} \, b \,C_{\mathrm{l}_{\alpha }} \, \left( \alpha _\mathrm{{eff}} - c_s \,\alpha _\mathrm{{eff}}^3\right) \\&M= \rho \, U^{2} \, b^{2}\, C_{m_{\alpha }} \, \left( \alpha _\mathrm{{eff}} - c_s \,\alpha _\mathrm{{eff}}^3\right) \end{aligned} \end{aligned}$$

(13)

where $c_s$ is the nonlinear aerodynamic coefficient, $C_{\mathrm{l}_{\alpha }} = 2\,\pi$ is the lift coefficient, $C_{m_{\alpha }}=\left( \frac{1}{2}+a\right) \,C_{\mathrm{l}_{\alpha }}$ is the moment coefficient, and $\alpha _\mathrm{{eff}} = \theta + \frac{{\dot{h}}}{U}+\left( \frac{1}{2}-a \right) \, \frac{b}{U} {\dot{\theta }}\,$ is the effective angle of attack.

3 Linear analysis

To study the effects of the NES parameters on the onset of flutter, we eliminate all nonlinear terms of the equations, which yields

$$\begin{aligned}&\overbrace{\left( \begin{array}{ccc} m_1+m_2 &{} m_1\,e+m_2\,d &{} m_2\\ m_1\,e+m_2\,d &{} m_1\,e^2+I_\mathrm{cg}+m_2\,d^2 &{} m_2\,d\\ m_2 &{} m_2\,d &{} m_2 \end{array} \right) }^{M_\mathrm{{mat}}}\left( \begin{array}{c} {\ddot{h}}\\ {\ddot{\theta }}\\ \ddot{y_2} \end{array} \right) \nonumber \\&+\overbrace{\left( \begin{array}{ccc} k_{h_0} &{} 0 &{} 0\\ 0 &{} k_{\theta _0} &{} 0\\ 0 &{} 0 &{} 0 \end{array} \right) }^{{K_\mathrm{{mat}}}}\left( \begin{array}{c} h\\ \theta \\ y_2 \end{array} \right) \nonumber \\&+\underbrace{\left( \begin{array}{ccc} C_{h} &{} 0 &{} 0\\ 0 &{} C_{\theta } &{} 0\\ 0 &{} 0 &{} C_{y_2} \end{array} \right) }_{{C_\mathrm{{mat}}}}\left( \begin{array}{c} {\dot{h}}\\ {\dot{\theta }}\\ \dot{y_2} \end{array} \right) = \underbrace{\left( \begin{array}{ccc} 0 &{} \rho U^2 b C_{\mathrm{l}_\alpha } &{} 0\\ 0 &{} \rho U^2 b^2 C_{m_\alpha } &{} 0\\ 0 &{} 0 &{} 0 \end{array} \right) }_{{K^a_\mathrm{{mat}}}}\left( \begin{array}{c} h\\ \theta \\ y_2 \end{array} \right) \nonumber \\&+\underbrace{\left( \begin{array}{ccc} \rho U b C_{\mathrm{l}_\alpha } &{} \rho U b^2 C_{\mathrm{l}_\alpha } (\frac{1}{2}-a) &{} 0\\ \rho U b^2 C_{\mathrm{m}_\alpha } &{} \rho U b^3 C_{\mathrm{m}_\alpha } (\frac{1}{2}-a) &{} 0\\ 0 &{} 0 &{} 0 \end{array} \right) }_{{C^a_\mathrm{{mat}}}}\left( \begin{array}{c} {\dot{h}}\\ {\dot{\theta }}\\ \dot{y_2} \end{array} \right) \end{aligned}$$

(14)

Using the state variable

$$\begin{aligned} Y=\left( \begin{array}{cccccc} h&\theta&y_2&{\dot{h}}&{\dot{\theta }}&\dot{y_2} \end{array} \right) ^\mathrm{{T}} \end{aligned}$$

(15)

we rewrite Eq. (14) as

$$\begin{aligned} {\dot{Y}}=B(U) \, Y \end{aligned}$$

(16)

where

$$\begin{aligned}&B(U)=\nonumber \\&\left( \begin{array}{cc} 0_{3\times 3} &{}\quad I_{3\times 3}\\ -M^{-1}_\mathrm{{mat}}\times (K_\mathrm{{mat}}-K^a_{mat})&{}\quad -M^{-1}_\mathrm{{mat}}\times (C_\mathrm{{mat}}-C^a_{mat}) \end{array} \right) \nonumber \\ \end{aligned}$$

(17)

Figure 3 shows the variations of the real and imaginary parts of the eigenvalues of the aeroelastic system, having the parameters presented in Table 1, as the freestream velocity U is increased. The plot shows that the flutter speed is $18.16 \,\frac{m}{s}$.

Fig. 3

Variation of the eigenvalues of the aeroelastic system for $U \in$ [$0, 30 \frac{m}{s}$]

To investigate further the behavior of the system when the NES is attached, we conduct various simulations. Figures 4a–c, show the effects of the mass $m_2$ and location of the NES relative to the elastic axis of the airfoil, as defined by the parameter d in semi-chords on the flutter speed, for damping coefficients $C_{y_2} = 0.01,\,0.1$ and $1\, \frac{\mathrm{Ns}}{\mathrm{m}}$, respectively. It is noted that all of these parameters affect the onset of the flutter. Although increasing the mass causes a small delay in the flutter speed when the NES is placed in front of the elastic axis, the increased mass actually causes the flutter to take place at a lower speed when the NES is placed behind the elastic axis. However, a general observation is that the impact of the NES on the flutter speed is negligible.

Table 1 Numerical parameters of the aeroelastic system

Fig. 4

Effect of the mass ratio $\frac{m_2}{m_1}$, 1 %(-*-), 3 %(-+-), 5 %(-o-) and location of the NES on the flutter speed of the airfoil-NES system for a $C_{y_2} = 0.01$, b $C_{y_2} = 0.1$ and c $C_{y_2} = 1$

4 Nonlinear analysis: normal form of the Hopf bifurcation

To determine the effects of the different nonlinear terms on the type of instability, the energy exchange between the wing and the NES and the amplitude of the limit cycle oscillations, we derive the normal form of the Hopf bifurcation [9] of the coupled airfoil-NES system near $U_{{ f}}$. For this purpose, we add a perturbation term $\epsilon ^2 \,\sigma _{U} \,U_{{ f}}$ to $U_{{ f}}$ and seek a first order solution of the form:

$$\begin{aligned} X=\epsilon \,X_1+\epsilon ^2 \,X_2+\epsilon ^3 \,X_3 \end{aligned}$$

(18)

where $\sigma _{U}$ is a variable small positive number and X stands for any of the outputs of the system (i.e. $X=h$,$\theta$ or $y_2$). We also rewrite the time derivative as:

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}t}=\frac{\partial }{\partial \tau _0}+\epsilon ^2 \, \frac{\partial }{\partial \tau _2}=D_{0}+\epsilon ^2 \,D_{2} \end{aligned}$$

(19)

where $\tau _n=\epsilon ^{n} \,t$.

Next, we introduce the matrix F whose columns are the eigenvectors of $B(U_{{ f}})$, the corresponding eigenvalues are ${\pm }j\,\omega _{1}-\mu _{1}$, ${\pm }j\,\omega _{2}$, ${-}\mu _2$ and 0. Then, we define the vector ${\mathbf {V}}$ such that ${\mathbf {Y}}=F\,{\mathbf {V}}$. Under these assumptions, and using the state variable ${\mathbf {Y}}$ defined in Eq. (15), Eqs. (10), (11), (12) and (13) lead to a set of three nonlinear coupled ordinary differential equations defined by the order of $\epsilon$, namely $\epsilon$, $\epsilon ^2$ and $\epsilon ^3$ and written as:

Order ($\epsilon$)

$$\begin{aligned} D_0\,V_1=J_U \, V_1 \end{aligned}$$

(20)

Order ($\epsilon ^2$)

$$\begin{aligned} D_0\,V_2=J_U \, V_2 + Q^{\epsilon ^2}(V_1,V_1) \end{aligned}$$

(21)

Order ($\epsilon ^3$)

$$\begin{aligned} D_0\,V_3&= - D_2\,V_1 + J_U \, V_3 + \sigma _U R \, V_1 + C^{a}(V_1,V_1,V_1) \nonumber \\&\quad +\,C^{b}(D_{0}\,V_1,V_1,V_1) \end{aligned}$$

(22)

where $J_{U}{=}F^{-1}\,B(U_{{ f}})\,F$ is a diagonal matrix whose elements are the eigenvalues of $B(U_{f})$ namely : $\pm j\,\omega _{1}-\mu _{1}$, $\pm j\,\omega _{2}$ , $- \mu _2$ and 0, $R=F^{-1}\,B_{1}(U_{{ f}})\,F$. We note that $V_i(2)=\overline{V_i(1)}$ and $V_i(4)=\overline{V_i(3)}$ (where $i=1,2,3$ and $V_i(j)$ is the $j\mathrm{{th}}$ component of the vector $V_i$); the homogenous solution of $V_i(1)$ and $V_i(5)$ are decaying solutions. Consequently, Eqs. (20), (21) and (22) are simplified to

Order ($\epsilon$)

$$\begin{aligned} \begin{aligned} D_0\,v_{13}-j\,\omega _2\,v_{13} = 0\\ D_0\,v_{16} = 0 \end{aligned} \end{aligned}$$

(23)

Order ($\epsilon ^2$)

$$\begin{aligned} \begin{aligned} D_0\,v_{23}-j\,\omega _2\,v_{23}&=\hat{Q^{\epsilon ^2}_3}(v_{13},v_{13})\\ D_0\,v_{26}&=\hat{Q^{\epsilon ^2}_6}(v_{16},v_{16}) \end{aligned} \end{aligned}$$

(24)

Order ($\epsilon ^3$)

$$\begin{aligned}&D_0\,v_{33}-j\,\omega _2\,v_{33}=-D_2\,v_{13} + \sigma _U R \, v_{1}\nonumber \\&\quad +\,\hat{Q^{\epsilon ^3}_3}(v_{13},v_{23})+ \hat{C^{a}_3}(v_{13},v_{13},\overline{v_{13}}) \nonumber \\&\quad +\,\hat{C^{b}_3}(D_{0}\,v_{13},v_{13},\overline{v_{13}})+cc+NST\nonumber \\&D_0\,v_{36}=-D_2\,v_{16} + \sigma _U R \, v_1 + \hat{Q^{\epsilon ^3}_6}(v_{16},v_{26})\nonumber \\&\qquad \qquad \,\,+\, \hat{C^{c}_6}(v_{16},v_{16},\overline{v_{16}}) \nonumber \\&\quad +\,\hat{C^{d}_6}(D_{0}\,v_{16},v_{16},\overline{v_{16}})+cc+NST \end{aligned}$$

(25)

where $v_{ij}=V_i(j)$, $\hat{Q^{\epsilon ^i}_{3}}(v,v)$ and $\hat{C^{a,b,c,d}_3}(v,v,v)$ are bilinear and trilinear functions of v, respectively and where NST stands for nonsecular terms and cc stands for complex conjugate of the preceding terms in the equation. The solution of Eq. (23) is given by:

$$\begin{aligned} \begin{aligned} v_{13}(\tau _0)&= G(T_2) e^{j\omega _{2}\,\tau _0}\\ v_{16}(\tau _0)&= H(T_2) \end{aligned} \end{aligned}$$

(26)

where G denotes the complex amplitudes of the pitch and plunging motions of the airfoil section and H denotes the amplitude of the NES oscillations. Substituting Eqs. (26) into (24) and solving for the particular solution, we obtain:

$$\begin{aligned} \begin{aligned} v_{23}&= e^{j\omega _{2}\,\tau _0} \int {e^{-j\omega _{2}\,x}\, \hat{Q^{\epsilon ^2}_3}(v_{13}(x),v_{13}(x))\,\mathrm{d}x}\\ v_{26}&= \hat{Q^{\epsilon ^2}_6}(v_{16},v_{16})\, \tau _0 \end{aligned} \end{aligned}$$

(27)

Substituting Eqs. (27) into (25) and removing the secular terms, the complex-valued normal form of the Hopf bifurcation is obtained as

$$\begin{aligned} D_{2} \,G= & {} \eta G + \phi _{e}\, G^{2} \, {\overline{G}}+ \gamma \,H^2\,G \end{aligned}$$

(28)

$$\begin{aligned} D_{2} \,H= & {} \kappa \, G \, {\overline{G}} \, H+\lambda \,H^3 \end{aligned}$$

(29)

The complex coefficient $\eta$ represents the growth rate and frequency of the oscillations of the airfoil section. The effective nonlinearity $\phi _{e}$ denotes the role of the different system’s nonlinearities in limiting the amplitude of the motion of the airfoil section. H is a real number and, as such, $\lambda$ is directly related to the nonlinear stiffness of the energy sink. The parameters $\gamma$ and $\kappa$ are related to the energy exchange between the airfoil section and the nonlinear energy sink.

By letting $G(T_2)=\frac{1}{2}\,w\,e^{i\zeta (T_2)}$ and separating the real and imaginary parts of Eqs. (28) and (29), we obtain the following real-valued normal form of the Hopf bifurcation:

$$\begin{aligned}&w^{'}=\eta _{r}\,w+\frac{1}{4}\, \phi _\mathrm{er}\,w^{3}+\frac{1}{2}\,\gamma _r\,H^2\,w \end{aligned}$$

(30)

$$\begin{aligned}&\zeta ^{'}=\eta _{i}+\frac{1}{4}\, \phi _\mathrm{ei}\,w^{2}+\gamma _i\,H^2 \end{aligned}$$

(31)

$$\begin{aligned}&H^{'}=\frac{1}{4}\, \kappa _r \,w^2\,H+\frac{1}{4}\, \lambda _r\,H^3 \end{aligned}$$

(32)

$$\begin{aligned}&0=\frac{1}{4}\, \kappa _i \,w^2+\lambda _i\,H^2 \end{aligned}$$

(33)

where w is the amplitude of oscillations and $\zeta$ is the shifting angle whose time variation is related to the frequency of the oscillations. The signs of $\eta _r$ and $\phi _\mathrm{er}$ determine the type of bifurcation Nayfeh et al. [10]. A supercritical Hopf bifurcation is obtained for $\eta _r > 0$ and $\phi _\mathrm{er} > 0$ and a subcritical Hopf bifurcation is obtained for $\eta _r < 0$ and $\phi _\mathrm{er} > 0$. The two parameters, $\gamma _r$ and $\kappa _r$ are of particular importance to the current problem because they represent the rate of energy exchange between the airfoil section and the nonlinear sink. As expected, both of these parameters would depend on the nonlinear stiffness of the energy sink with a coefficient that depends on the mass ratio and the amplitude of the limit cycle oscillations.

5 Results and discussion

We consider the effects of a nonlinear energy sink on a wing section having the parameters shown in Table 1. For this wing the expression of the effective nonlinearity and growth rate without NES are given by

$$\begin{aligned}&\eta _r =0.433987\,\sigma _U\,U_{{ f}}\nonumber \\&\phi _\mathrm{er}=0.0000213689 - 0.00657702\,\mathrm{cs}\nonumber \\&-\,1.24153\times 10^{-15}\,k_{h_1}^2 - 1.68515\times 10^{-10}\,k_{h_2}\nonumber \\&-\,7.14763\times 10^{-10} \,k_{h_1}\,k_{\theta _1} \nonumber \\&-\,0.0000171762\,k_{\theta _1}^2 + 0.000213956\,k_{\theta _2} \end{aligned}$$

(34)

As explained above, the signs of $\eta _r$ and $\phi _\mathrm{er}$ determine whether the instability is supercritical or subcritical. We note that the cubic pitch nonlinearity $k_{\theta _2}$ contributes to a subcritical Hopf bifurcation since it contributes to a positive $\phi _\mathrm{er}$. However, the pitch quadratic nonlinearity, $k_{\theta _1}$, as well as the cubic aerodynamic nonlinearity, $c_s$, have a negative contribution to $\eta _r$ which lead to a supercritical instability.

Next we add a nonlinear energy sink to the airfoil section. Two different cases of mass ratios, namely, 5 and 3 % are considered. For each of these cases, three cases for the location of the sink along the chord are considered. These include placing the sink at the elastic axis, $d=0$, ahead of the elastic axis, $d=-0.3\,b$, and behind the elastic axis, $d=0.3\,b$. The growth rates of the amplitudes of the oscillations for these cases are $\eta _r =0.267653\times \sigma _U\,U_f$ for $d=0$, $\eta _r = 0.272251\times \sigma _U\,U_f$, for $d=-0.3\,b$ and $\eta _r = 0.265612\times \sigma _U\,U_f$, for $d=0.3\, b$.

5.1 Case of 5 $\%$ mass ratio

The coefficients of the effective nonlinearity of the system and the other terms of the normal form as derived above for an NES mass of 5 $\%$ are given by

$$\begin{aligned} \begin{aligned} \phi _\mathrm{er}&= -0.00157815 - 0.0181067\, cs - 7.94452 \\&\quad \times \,10^{-12}\, k_{h_1}^2 - 1.59542\times 10^{-7}\, k_{h_2} \\&\quad -\,3.86976\times 10^{-7} \,k_{n_2} - 5.2063\times 10^{-8} \,k_{h_1}\, k_{\theta _1} \\&\quad -\,0.0000218303 \, k_{\theta _1}^2+\,0.000502663 \,k_{\theta _2}\\ \gamma _{r}&= -0.00476769\,k_{n_2}\\ \kappa _r&= -0.000973996\,k_{n_2}\\ \lambda _r&= -2\,k_{n_2}\\ \kappa _i&=0\\ \lambda _i&= 0 \end{aligned} \end{aligned}$$

(35)

for $d= - 0.3\, b$,

$$\begin{aligned} \begin{aligned} \phi _\mathrm{er}&= -0.00154919 - 0.0179625 \,\mathrm{cs} - 7.5623 \\&\quad \times \,10^{-12} \, k_{h_1}^2 - 1.53456\times 10^{-7} \,k_{h_2} \\&\quad -\, 7.11105\times 10^{-8} \,k_{n_2} - 5.13344\times 10^{-8} \,k_{h_1} \,k_{\theta _1} \\&\quad -\,0.0000216527\, k_{\theta _1}^2 +0.000494614\, k_{\theta _2}\\&\gamma _{r} = -0.00146539\,k_{n_2}\\&\kappa _r = -0.000582321 \,k_{n_2}\\&\lambda _r = -2\,k_{n_2}\\&\kappa _i = 0\\&\lambda _i = 0 \end{aligned} \end{aligned}$$

(36)

for $d= 0$, and

$$\begin{aligned} \begin{aligned} \phi _\mathrm{er}&= -0.00154374 - 0.0180555 \,\mathrm{cs} - 7.40378 \\&\quad \times \,10^{-12} \,k_{h_1}^2 - 1.5157\times 10^{-7} \,k_{h_2} \\&\quad -\,8.40011\times 10^{-9}\, k_{n_2} - 5.13289\times 10^{-8}\, k_{h_1}\, k_{\theta _1} \\&\quad -\,0.0000216049\, k_{\theta _1}^2+0.000491564 \, k_{\theta _2}\\&\gamma _{r} = -0.000344654\,k_{n_2}\\&\kappa _r = -0.000292471 \,k_{n_2}\\&\lambda _r = -2\,k_{n_2}\\&\kappa _i = 0\\&\lambda _i = 0 \end{aligned} \end{aligned}$$

(37)

for $d= 0.3\, b$

In all cases, the energy sink is helpful in terms of contributing toward a supercritical bifurcation. As for the energy transfer between the airfoil section and the nonlinear sink, we note that the value of $\gamma _r$ is negative in all cases indicating that the nonlinear energy sink can reduce the growth rate of the oscillations, depending on the value of the nonlinear stiffness of the energy sink and the amplitude of the limit cycle oscillations and the sink’s oscillations. It is important to note here that the sink does not contribute to decreasing the amplitude of oscillations unless the system starts to oscillate. Furthermore, this contribution is dependent on the amplitude of the NES itself. So, it does not delay the flutter point. Rather, it can, once the oscillations of the wing and NES have grown, reduce the amplitude of the oscillations. On the other hand, the values of $\kappa _r$ and $\lambda _r$ are negative which indicates that the amplitude of the NES is decaying at the same time that it draws energy from the wing. This decay impacts its effectiveness in continuously drawing energy from the wing to act like a sink. The reason is that once the amplitudes go below a specific value, the sink stops drawing energy which results in a recovery of the original amplitudes of the wing oscillations. So, the wing response exhibits modulated rather than controlled characteristics as will be shown below.

5.2 Case of 3 $\%$ mass ratio

The expression of the effective nonlinearity of the system and the other parameters of the normal form when the NES mass is 3 % are

$$\begin{aligned} \begin{aligned} \phi _\mathrm{er}&= -0.00156868 - 0.0181215 \, cs - 7.9393 \\&\quad \times \,10^{-12} \,k_{h_1}^2 - 1.5957\times 10^{-7}\, k_{h_2} \\&\quad -\,4.60049\times 10^{-7} \,k_{n_2} - 5.2163\times 10^{-8} \, k_{h_1} \,k_{\theta _1} \\&\quad -\,0.0000218307 \,k_{\theta _1}^2+0.000502073 \,k_{\theta _2}\\ \gamma _{r}&= -0.0062891\,k_{n_2}\\ \kappa _r&= -0.000877802 \,k_{n_2}\\ \lambda _r&= -2\,k_{n_2}\\ \kappa _i&= 0\\ \lambda _i&= 0 \end{aligned} \end{aligned}$$

(38)

for $d= - 0.3\, b$,

$$\begin{aligned} \begin{aligned} \phi _\mathrm{er}&= -0.00155343 - 0.0180097 \, cs - 7.6002 \\&\quad \times \,10^{-12} \,k_{h_1}^2 - 1.53984\times 10^{-7} \, k_{h_2} \\&\quad -\,1.81754\times 10^{-8} \,k_{n_2} - 5.15074\times 10^{-8} \, k_{h_1} \,k_{\theta _1} \\&\quad -\,0.0000217267 \,k_{\theta _1}^2+0.000496234 \,k_{\theta _2}\\ \gamma _{r}&= -0.000416306\,k_{n_2}\\ \kappa _r&= -0.000523905 \,k_{n_2}\\ \lambda _r&= -2\,k_{n_2}\\ \kappa _i&= 0\\ \lambda _i&= 0 \end{aligned} \end{aligned}$$

(39)

Fig. 5

Bifurcation diagrams of the a plunge and b pitch responses for the aeroelastic system having the parameters presented in Table 1 and without NES ($k_{\theta _1} = 9.967\,\mathrm{Nm},\,k_{\theta _2} = 67.685\,\mathrm{Nm},$). The continuous lines represent the stable solution, the dotted line, the unstable solution

for $d= 0$, and

$$\begin{aligned} \begin{aligned} \phi _\mathrm{er}&= -0.00154457 - 0.0181065 \,\mathrm{cs} - 7.46618 \\&\quad \times \,10^{-12} \, k_{h_1}^2 - 1.52212\times 10^{-7} \, k_{h_2} \\&\quad +\,4.60067\times 10^{-8} \,k_{n_2} - 5.15131\times 10^{-8} \, k_{h_1} \,k_{\theta _1} \\&\quad -\,0.0000217138 \,k_{\theta _1}^2+0.000494204 \,k_{\theta _2}\\&\gamma _{r} =0.00209951\,k_{n_2}\\&\kappa _r = -0.000262956 \,k_{n_2}\\&\lambda _r =-2\,k_{n_2}\\&\kappa _i = 0\\&\lambda _i = 0 \end{aligned} \end{aligned}$$

(40)

for $d= 0.3\, b$

The results of this case, 3 %, show similar responses to those of the 5 % case except for the case where the NES is placed behind the elastic axis. Under these conditions, the NES contributes to a subcritical response as exhibited by the positive coefficient of $k_{n_2}$ in Eq. 40. We should also note the positive sign of $\gamma _r$ in the same equation indicating that the energy can not be transferred to the NES under these conditions.

Fig. 6

Bifurcation diagrams for a the plunge, b the pitch and c NES responses, when the NES is activated in the airfoil-NES system having the parameters presented in Table 1 with $k_{\theta _1} = 9.967\,\mathrm{Nm},\,k_{\theta _2} = 67.685\,\mathrm{Nm},$ and $k_{n_2} = 150,000 \,\frac{\mathrm{{N}}}{{\mathrm{m}}^2}$. The mass of the NES is 3 % of the total mass of the wing. The dots are numerical simulations and the solid line is the normal form (valid only near bifurcation point)

Fig. 7

Bifurcation diagrams for a the plunge, b the pitch and c NES responses, when the NES is activated in the airfoil-NES system having the parameters presented in Table 1 with $k_{\theta _1} = 9.967\,\mathrm{Nm},\,k_{\theta _2} = 67.685\,\mathrm{Nm},$ and $k_{n_2} = 150000 \,\frac{\mathrm{N}}{{\mathrm{m}}^2}$. The mass of the NES is 5 % of the total mass of the wing. The dots are numerical simulations and the solid line is the normal form (valid only near bifurcation point)

5.3 Case of the original system exhibiting subcritical behavior

In this section, we choose the nonlinear parameters of the system without NES such that a subcritical Hopf bifurcation is obtained (i.e. $k_{\theta _1}=9.97$ Nm, $k_{\theta _2}=67.69$ Nm and $k_{h_1}=k_{h_2}=0$) We present in Fig.  5 the bifurcation diagram for the system when the NES is deactivated. The response is subcritical. which means that a reduction of the freestream velocity does not lead to a decay of the amplitudes of oscillations. This response is dependent on the initial conditions. In fact, for velocities below flutter and for proper initial conditions, the system can exhibit large amplitudes limit cycle oscillations.

Table 2 Numerical nonlinear parameters of the NES

Activating the NES, and using the parameters presented in Table 2 we obtain the results plotted in Figs. 6a–c and 7a–c for the cases of $m_2 = 0.03\,m_1$ and $m_2 = 0.05\,m_1$ respectively. The results show that adding the NES changed the subcritical response to a supercritical one over a small region of velocities near flutter. Unlike the subcritical response, the supercritical response is characterized by a progressive increase in the amplitudes of the LCOs as the freestream velocity is increased. The main feature of this response is the recovery, by the airfoil-NES system, of the decaying solution when the freestream velocity is decreased. On the other hand, the numerical solutions shows that although the NES changed the type of instability near the bifurcation point, the system recovered its subcritical property as the speed was increased slightly beyond the initial region of supercritical instability. That is the effect of the NES in changing the type of instability was limited to a small region near the flutter speed. We should note here that for the NES mass of $m_2 = 0.01\, m_1$ the type of the Hopf bifurcation remained subcritical. Therefore, the NES with a low mass is ineffective. It is also noted that for the NES to be effective a large value of the nonlinear stiffness $k_{n_2}$ is needed ($1.5 \times 10^5$).

Figure 8 shows the time series and phase portraits of the plunge, pitch and NES responses at a speed of 18.37 m/s. The plots show a periodic response with one frequency. However, as the speed is slightly increased to 18.43  m/s, we observe a totally different response as shown in Fig. 9. Particularly, as the pitch and plunge amplitudes increase, the amplitude of the NES increases, which indicates that the NES is drawing energy from the motions of the primary system. However, and as shown in the normal form analysis presented above, once enough energy is drawn and the amplitudes of the pitch and plunge oscillations decrease, the NES does not draw any energy from the main oscillations, which results in an increase of the amplitudes of these oscillations of the primary system. As such, these responses exhibit modulated behaviors as predicted by the analysis presented in Sect. 5.1. It is important to note that the coupled systems responses exhibited different characteristics over the small region between 18.26 and 18.5 m/s.

Fig. 8

Phase portrait and time series for the system with NES mass of 5 % when $U=\,18.3861\,\mathrm{m/s}$, $d=-0.3\times b$ and system parameters of Fig. 7

Fig. 9

Phase portrait and time series for the system with NES mass of 5 % when $U=\,18.4261\,\mathrm{m/s}$, $d=-0.3\times b$ and system parameters of Fig. 7

Fig. 10

Bifurcation diagrams for a the plunge, b the pitch responses, when the NES is deactivated. The airfoil-NES system parameters are presented in Table 1 with $k_{\theta _1}=90\,\mathrm{Nm}$

Fig. 11

Bifurcation diagrams for a the plunge, b the pitch and c NES responses, when the NES is activated. The airfoil-NES system parameters are presented in Table 1 with NES mass of 3 %

Fig. 12

Bifurcation diagrams for a the plunge, b the pitch and c NES responses, when the NES is activated. The airfoil-NES system parameters are presented in Table 1 with NES mass of 5 %

5.4 Case of the original system exhibiting supercritical behavior

In this section, we consider the case of an aeroelastic system that exhibits a supercritical Hopf bifurcation when the NES is deactivated. The consided parameters are: $k_{\theta _1}=90$ Nm and $k_{\theta _2}=k_{h_2}=k_{h_1}=0$. Figure 10 shows the bifurcation diagram for the system without NES. The plots in Figs. 11 and 12 show the bifurcation diagram when the NES is activated for the cases of 3 and 5 % respectively. A comparison of the plots in the three figures as presented in Fig. 13 shows that the NES can reduce the amplitude of the wing oscillations as the freestream velocity is increased. However, this reduction is effective over a very small region of incrased freestream velocity. Beyond this limited region, the wing oscillations recover their original amplitude values indicating the limited region of effectiveness of the NES in terms of reducing the LCO amplitudes of the original system.

Fig. 13

Superposition of bifurcation diagrams for a the plunge and b the pitch, when the NES is de/activated in the airfoil-NES system having the parameters presented in Table 1 with $k_{\theta _1} = 90,\,k_{\theta _2} = 0,$ and $k_{n_2} = 150,000$. The mass of the NES is 0 % ($+$), 3 $\%$ ($*$) and 5 % (o) of the total mass of the wing

6 Conclusions

We investigated the effectiveness of using a nonlinear energy sink to passively control the response of a pitching–plunging airfoil section. We used the normal form to quantify the contribution of the sink to the system’s nonlinear response. We used numerical integration to determine the system’s response over a wide range of operating conditions. The results show that depending on its mass and location along the airfoil, the nonlinear sink can be more effective in terms of changing a subcritical bifurcation to a supercritical one. However, the change is very limited in that the system recovers the subcritical response as the freestream velocity is increased. For the case where the original system exhibits supercritical behavior the results show that the NES can reduce the pitch and plunge amplitudes. However, this reduction is limited to a very small region of freestream velocities above the flutter speed. The results of the normal form show that the nonlinear sink has a decaying characteristics and as such cannot maintain the energy it draws from the airfoil section. This results in modulated responses of both the airfoil section and nonlinear sink.

Appendix: Derivation of the equations of motion

Position of the center of gravity of the airfoil:

$$\begin{aligned} \mathbf{R }_1&= h\mathbf{z } + e\mathbf{i }\nonumber \\ \text {where}& \mathbf{i } = \cos \left( \alpha _0 + \theta \right) \mathbf{x } + \sin \left( \alpha _0 + \theta \right) \mathbf{z }\nonumber \\ \mathbf{R }_1&= \left[ h + e\sin \left( \alpha _0 + \theta \right) \right) \mathbf{z } + e \cos \left( \alpha _0 + \theta \right) \mathbf{x } \end{aligned}$$

(41)

The velocity then given by

$$\begin{aligned} \mathbf{V }_1&= \left[ {\dot{h}} + e{{\dot{\theta }}} \cos \left( \alpha _0 + \theta \right) \right] \mathbf{z } - e{{\dot{\theta }}} \sin \left( \alpha _0 + \theta \right) \mathbf{x } \end{aligned}$$

(42)

which yields

$$\begin{aligned} V^{2}_1&= \left[ {\dot{h}} + e{{\dot{\theta }}} \cos \left( \alpha _0 + \theta \right) \right] ^{2} + e^{2}{{\dot{\theta }}}^{2}\sin ^{2}\left( \alpha _0 + \theta \right) \\ V^{2}_1&= {\dot{h}}^{2} + e^{2}{{\dot{\theta }}}^{2}\cos ^{2}\left( \alpha _0 + \theta \right) + 2e{\dot{h}}{{\dot{\theta }}} \cos \left( \alpha _0 + \theta \right) \\&\quad +\,e^{2}{{\dot{\theta }}}^{2} \sin ^{2}\left( \alpha _0 + \theta \right) \end{aligned}$$

The position of the NES mass is given by

$$\begin{aligned} \mathbf{R }_2&= h\mathbf{z } + d\mathbf{i } + y_2\mathbf{z }\nonumber \\ \mathbf{R }_2&= h\mathbf{z } + d\cos \left( \alpha _0 + \theta \right) \mathbf{x } \nonumber \\&\quad +\,d\sin \left( \alpha _0 + \theta \right) \mathbf{z }+ y_2\mathbf{z }\nonumber \\ \mathbf{R }_2&= \left[ h+d\sin \left( \alpha _0 + \theta \right) + y_2\right] \mathbf{z } \nonumber \\&\quad +\,d\cos \left( \alpha _0 + \theta \right) \mathbf{x } \end{aligned}$$

(43)

its velocity is given by

$$\begin{aligned} \mathbf{V }_2 =&\left[ {\dot{h}} + \mathrm{d}{{\dot{\theta }}} \cos \left( \alpha _0 + \theta \right) + {\dot{y}}_2\right] \mathbf{z } \nonumber \\&\quad - \mathrm{d}{{\dot{\theta }}} \sin \left( \alpha _0 + \theta \right) \mathbf{x } \end{aligned}$$

(44)

which yields

$$\begin{aligned} V^{2}_2&= \left( {\dot{h}} + \mathrm{d}{{\dot{\theta }}} \cos \left( \alpha _0 + \theta \right) + {\dot{y}}_2\right) ^{2} \\&\quad +\,d^{2}{{\dot{\theta }}}^{2}\sin ^{2}\left( \alpha _0 + \theta \right) \\ V^{2}_2&= {\dot{h}}^{2} + d^{2}{{\dot{\theta }}}^{2} \cos ^{2} \left( \alpha _0 + \theta \right) + {\dot{y}}^{2}_2 + 2\mathrm{d}{{\dot{\theta }}} {\dot{h}} \\&\quad \cos \left( \alpha _0 + \theta \right) +\,2{\dot{h}}{\dot{y}}_2 + 2\mathrm{d}{{\dot{\theta }}} \cos \left( \alpha _0 + \theta \right) {\dot{y}}_2 \\&\quad +\,d^{2}{{\dot{\theta }}}^{2} \sin ^{2}\left( \alpha _0 + \theta \right) \end{aligned}$$

The distance separating $m_2$ and the elastic axis is given by

$$\begin{aligned} r^{2} = d^{2} + y^{2}_{2} + 2dy_{2}\sin \left( \alpha _0 + \theta \right) \end{aligned}$$

The kinetic energy of the system is

$$\begin{aligned} T = \frac{1}{2}m_1V^{2}_{1} + \frac{1}{2} m_{2} V^{2}_{2} + \frac{1}{2} I_\mathrm{cg} {{\dot{\theta }}}^{2} \end{aligned}$$

The potential energy of the system

$$\begin{aligned} \mathrm{PE} = \frac{1}{2}k_{h}\ h^{2} + \frac{1}{2} k_{\theta } \theta ^{2} + \frac{1}{2} k_{n} y^{2}_{2} \end{aligned}$$

Rayleigh’s friction function

$$\begin{aligned} {{{\mathcal {R}}}}=\frac{1}{2} C_{h}\ {\dot{h}}^{2} + \frac{1}{2} C_{\theta } {{\dot{\theta }}}^{2} + \frac{1}{2} C_{y_2} y^{2}_{2} \end{aligned}$$

The Lagrange’s function

$$\begin{aligned}&L= T-V \\&\quad = \frac{1}{2} m_1 \left[ {\dot{h}}^{2} + e^{2} {{\dot{\theta }}}^{2} + 2e{\dot{h}}{{\dot{\theta }}} \cos \left( \alpha _0 + \theta \right) \right] \\&\qquad + \frac{1}{2} m_{2}\bigg [{\dot{h}}^{2} + d^{2}{{\dot{\theta }}}^{2} + {\dot{y}}^{2}_{2} + 2\mathrm{d}{{\dot{\theta }}}{\dot{h}}\cos \left( \alpha _0 + \theta \right) \\&\qquad + 2{\dot{h}}{\dot{y}}_{2} + 2\mathrm{d}{{\dot{\theta }}}{\dot{y}}_{2}\cos \left( \alpha _0 + \theta \right) \bigg ] \\&\qquad + \frac{1}{2} I_\mathrm{cg}{{\dot{\theta }}}^{2}-\frac{1}{2} k_hh^{2} - \frac{1}{2} k_{\theta } \theta ^{2} - \frac{1}{2} k_ny^{2}_{2}\\&\frac{\partial L}{\partial {\dot{h}}} = \frac{1}{2} m_1\left[ 2{\dot{h}} + 2e{{\dot{\theta }}} \cos \left( \alpha _0 + \theta \right) \right] \\&\qquad \quad +\, \frac{1}{2} m_2 \left[ 2{\dot{h}} + 2\mathrm{d}{{\dot{\theta }}} \cos \left( \alpha _0 + \theta \right) + 2{\dot{y}}_2\right] \end{aligned}$$

thus:

$$\begin{aligned} \frac{\partial L}{\partial {{\dot{\theta }}}} =&\frac{1}{2} m_1\big [2e^{2}{{\dot{\theta }}} + 2e{\dot{h}} \cos \left( \alpha _0 + \theta \right) \big ] \\&+ \frac{1}{2} m_{2}\big [2d^{2}{{\dot{\theta }}} + 2d{\dot{h}}\cos \left( \alpha _0 + \theta \right) \\&+2d{\dot{y}}_{2} \cos \left( \alpha _0 + \theta \right) \big ] + I_\mathrm{cg}{{\dot{\theta }}} \end{aligned}$$

$$\begin{aligned} \frac{\partial L}{\partial {\dot{y}}_{2}} = \frac{1}{2} m_{2} \big [2\dot{y}_{2} + 2{\dot{h}} + 2\mathrm{d}{{\dot{\theta }}}\cos \left( \alpha _{0} + \theta \right) \big ] \end{aligned}$$

$$\begin{aligned} \frac{\partial L}{\partial \theta }&= \frac{1}{2} m_1\big [-2e{\dot{h}}{{\dot{\theta }}} \sin \left( \alpha _0 + \theta \right) \big ]\\&\qquad +\, \frac{1}{2}m_2\big [-2\mathrm{d}{{\dot{\theta }}}{\dot{h}} \sin \left( \alpha _0 + \theta \right) \\&\qquad -\,2\mathrm{d}{{\dot{\theta }}}{\dot{y}}_{2}\sin \left( \alpha _0 + \theta \right) \big ]-k_\theta \theta \end{aligned}$$

$$\begin{aligned} \frac{\partial L}{\partial y_{2}} = -k_{ny_2} \end{aligned}$$

The equations of motion of the aeroelastic system are:

$$\begin{aligned}&m_{1}{\ddot{h}} + e{{\ddot{\theta }}} m_{1}\cos \left( \alpha _{0} + \theta \right) - e{{\dot{\theta }}}^{2m}_{1}\sin \left( \alpha _0 + \theta \right) \nonumber \\&\quad +\, m_{2}{\ddot{h}} + m_{2d}{{\ddot{\theta }}} \cos \left( \alpha _{0} + \theta \right) \nonumber \\&\quad -\,m_{2d}{{\dot{\theta }}}^{2} \sin \left( \alpha _{0} + \theta \right) + m_{2}\ddot{y}_{2} + k_{hh} + C_{h}{\dot{h}} = -L\\&m_1e^{2}{{\ddot{\theta }}} + m_{1e}{\ddot{h}} \cos \left( \alpha _{0} + \theta \right) - m_{1e}{\dot{h}}{{\dot{\theta }}} \sin \left( \alpha _{0} +\theta \right) \nonumber \\&\quad +\, m_{2d}^{2}{{\ddot{\theta }}} +\,m_{2d}{\ddot{h}}\cos \left( \alpha _{0} + \theta \right) -\, m_{2d}{\dot{h}}{{\dot{\theta }}} \sin \left( \alpha _{0} +\theta \right) \nonumber \\&\quad +\, m_{2d}{\ddot{y}}_{2} \cos \left( \alpha _{0} + \theta \right) - m_{2d}{\dot{y}}_{2}{{\dot{\theta }}} \sin \left( \alpha _{0} + \theta \right) \nonumber \\&\quad + I_\mathrm{cg} {{\ddot{\theta }}} + m_{1e}{\dot{h}}{{\dot{\theta }}}\sin \left( \alpha _{0} + \theta \right) \nonumber \\&\quad +\,m_{2d}{{\dot{\theta }}}{\dot{h}}\sin \left( \alpha _{0} + \theta \right) + m_{2d}{{\dot{\theta }}}{\dot{y}}_{2}\sin \left( \alpha _{0} + \theta \right) \nonumber \\&\quad +\,k_{\theta }\theta + C_{\theta }{{\dot{\theta }}} = M\nonumber \\&\,m_{2}{\ddot{y}}_{2} + m_{2}{\ddot{h}} + m_{2d}{{\ddot{\theta }}} \cos \left( \alpha _{0} + \theta \right) \nonumber \\&\quad -\, 2m_{2d}{{\dot{\theta }}}^{2} \sin \left( \alpha _{0} + \theta \right) - m_{2}y_{2}{{\dot{\theta }}}^{2} + k_{n} y_{2} + Cy_{2}{\dot{y}}_{2} = 0. \nonumber \end{aligned}$$

(45)

which can be written as:

$$\begin{aligned}&m_1{\ddot{h}} + e{{\ddot{\theta }}} m_{1}\cos \left( \alpha _{0} + \theta \right) - e{{\dot{\theta }}}^{2m}_{1}\sin \left( \alpha _{0} + \theta \right) + m_{2}{\ddot{h}} \\&\quad +\,m_{2d}{{\ddot{\theta }}} \cos \left( \alpha _{0} + \theta \right) -m_{2d}{{\dot{\theta }}}^{2}\sin \left( \alpha _{0} + \theta \right) + m_{2}{\ddot{y}}_{2} \\&\quad + k_{h_0} h+\,k_{h_1} h^{2}+k_{h_2} h^{3}+ C_{h}{\dot{h}} = -L \\&m_1e^{2}{{\ddot{\theta }}} + m_{1e}{\ddot{h}}\cos \left( \alpha _{0} + \theta \right) + m_{2d}^{2}{{\ddot{\theta }}} m_{2d}{\ddot{h}} \cos \left( \alpha _{0} + \theta \right) \\&\quad +\,m_{2d}{\ddot{y}}_{2}\cos \left( \alpha _{0} + \theta \right) +I_\mathrm{cg}\ddot{\theta }+ k_{\theta _{0}}\theta + k_{\theta _1} \theta ^{2}\\ {}&\quad +k_{\theta _{2}} \theta ^{3}+ C_{\theta }{{\dot{\theta }}} = M \\&m_{2}{\ddot{y}}_{2} + m_{2}{\ddot{h}} + m_{2d}{{\ddot{\theta }}} \cos \left( \alpha _{0} + \theta \right) - 2m_{2d}\dot{\theta }^{2}\sin \left( \alpha _{0} + \theta \right) \\&\quad +\,k_{n_0} y_2 + k_{n_1} y_2^2+k_{n_2} y_2^3+ C_{y_2}{\dot{y}}_2 =0. \end{aligned}$$