Legendre wavelets Galerkin method for solving nonlinear stochastic integral equations

Abstract

In this paper, an efficient and accurate computational method based on the Legendre wavelets (LWs) together with the Galerkin method is proposed for solving a class of nonlinear stochastic Itô–Volterra integral equations. For this purpose, a new stochastic operational matrix (SOM) for LWs is derived. A collocation method based on hat functions (HFs) is employed to derive a general procedure for forming this matrix. The LWs and their operational matrices of integration and stochastic Itô-integration and also some useful properties of these basis functions are used to transform such problems into corresponding nonlinear systems of algebraic equations, which can be simply solved to achieve the solution of such problems. Moreover, the efficiency of the proposed method is shown for some concrete examples. The results reveal that the proposed method is very accurate and efficient. Furthermore as some useful applications, the proposed method is applied to obtain approximate solutions for some stochastic problems in the mathematics finance, biology, physics and chemistry.

1 Introduction

Approximation by orthogonal families of basis functions has found wide applications in sciences and engineering [1]. The main idea of using an orthogonal basis is that the problem under consideration is reduced into solving a system of algebraic equations which can be simply solved to achieve the solution of the problem under study. This can be done by truncated series of orthogonal basis functions for the solution of the problem and using the operational matrices of these basis functions [1]. Depending on their structure, the orthogonal functions may be mainly classified into three families [2]. The first family includes sets of piecewise constant orthogonal functions such as the Walsh functions, block pulse functions, etc. The second family consists of sets of orthogonal polynomials such as Laguerre, Legendre, Chebyshev, etc., and the third family is the widely used sets of sine-cosine functions. It is worth noting that approximating a continuous function with piecewise constant basis functions results in an approximation that is piecewise constant. On the other hand if a discontinuous function is approximated with continuous basis functions, the resulting approximation is continuous and can not properly model the discontinuities. In remote sensing, images often have properties that vary continuously in some regions and discontinuously in others. Thus, in order to properly approximate these spatially varying properties, it is necessary to use approximating functions that can accurately model both continuous and discontinuous phenomena. Therefore, neither continuous basis functions nor piecewise constant basis functions taken alone can efficiently and accurately model these spatially varying properties. However, wavelets basis functions are another basis set which offers considerable advantages over alternative basis sets and allows us to attack problems not accessible with conventional numerical methods. Their main advantages are [1]: the basis set can be improved in a systematic way, different resolutions can be used in different regions of space, the coupling between different resolution levels is easy, there are few topological constraints for increased resolution regions, the Laplace operator is diagonally dominant in an appropriate wavelet basis, the matrix elements of the Laplace operator are very easy to calculate and the numerical effort scales linearly with respect to the system size.

It is also well known that we can approximate any smooth function by the eigenfunctions of certain singular Sturm–Liouville problems such as Laguerre, Legendre or Chebyshev orthogonal polynomials. In this manner, the truncation error approaches zero faster than any negative power of the number of basis functions used in the approximation [3]. This phenomenon is usually referred to as “The spectral accuracy” [3]. But, in the case that the function under approximation is not analytic, these basis functions do not work well and therefore spectral accuracy does not happen. For these situations, wavelet functions will be more effective. In this communication, it is worth mentioning that the LWs have mutually spectral accuracy, orthogonality and other useful properties of wavelets.

Nonlinear stochastic functional equations have been extensively studied over a long period of time since they are fundamental for modeling science and engineering phenomena [4–8]. As the computational power increases, it becomes feasible to use more accurate functional equation models and solve more demanding problems. Moreover, the study of stochastic or random functional equations can be very useful in application, due to the fact that they arise in many situations. For example, stochastic integral equations arise in a wide range of problems such as the stochastic formulation of problems in reactor dynamics [9, 10], the study of the growth of biological populations [11], the theory of automatic systems resulting in delay-differential equations [12], and in many other problems occurring in the general areas of biology, physics and engineering. Also, nowadays, there is an increasing demand to investigate the behavior of even more sophisticated dynamical systems in physical, medical, engineering and financial applications [13–19]. These systems often depend on a noise source, like a Gaussian white noise, governed by certain probability laws, so that modeling such phenomena naturally involves the use of various stochastic differential equations (SDEs) [11, 20–26], or in more complicated cases, stochastic Volterra integral equations and stochastic integro-differential equations [27–34]. In most cases it is difficult to solve such problems explicitly. Therefore, it is necessary to obtain their approximate solutions by using some numerical methods [9–15, 20, 29–31].

In recent years, the LWs have been used to estimate solutions of some different types of functional equations, for instances see [1, 35–40]. In this paper, the LWs will be used for solving the following nonlinear stochastic Itô–Volterra integral equation:

$$\begin{aligned} X(t)= & {} h(t)+\int _{0}^{t}f(\tau )\mu \left( X(\tau )\right) \mathrm{d}\tau \nonumber \\&+ \int _{0}^{t}g(\tau )\sigma \left( X(\tau )\right) \mathrm{d}B(\tau ), \quad t\in [0,1], \end{aligned}$$

(1)

where X(t), f (t), g(t), h(t), are the stochastic processes defined on same probability space $(\Omega ,{\mathcal {F}},\mathbf {P})$, X(t) is an unknown stochastic function to be found, B(t) is a Brownian motion process and the second integral in (1) is an Itô integral. Moreover, it is assumed that $\mu$ and $\sigma$ are analytic functions.

It is worth mentioning that a real-valued stochastic process $B(t),~t\in [0,1]$ is called Brownian motion, if it satisfies the following properties [41]:

• (i) $B(0)=0$ (with the probability 1).

• (ii) For $0 \le s < t \le 1$ the random variable given by the increment $B(t)-B(s)$ is normally distributed with mean zero and variance $t-s$; equivalently, $B(t)-B(s)\sim \sqrt{t-s}~{\mathcal {N}}(0,1)$, where ${\mathcal {N}}(0,1)$ denotes a normally distributed random variable with zero mean and unit variance.

• (iii) For $0\le s< t < u < v \le 1$ the increments $B(t)-B(s)$ and $B(v)-B(u)$ are independent.

In order to compute an approximate solution for Eq. (1), we first obtain some new useful properties for the LWs and then derive an operational matrix of stochastic Itô-integration for these basis functions to eliminate the stochastic integral operation and reduce the problem into solving a system of algebraic equations. The operational matrix of stochastic Itô-integration for LWs can be expressed as:

$$\begin{aligned} \int _{0}^{t}\Psi (\tau )\mathrm{d}B(t)\simeq P_{s}\Psi (t), \end{aligned}$$

(2)

where B(t) is a Brownian motion process and $\Psi (t)=[\psi _{1}(t),\psi _{2}(t),\ldots ,\psi _{\hat{m}}(t)]^{T}$, in which $\psi _{i}(t)\,(i=1,2,\ldots ,\hat{m})$ are LWs and $P_{s}$ is the operational matrix of stochastic Itô-integration for LWs.

The proposed method is based on reducing the problem under study to a system of nonlinear algebraic equations by expanding the solution as LWs with unknown coefficients and using the operational matrices of integration and stochastic integration. Moreover, a new technique for computation of the nonlinear terms in such equations is presented.

This paper is organized as follows: In Sect. 2, the LWs and their properties are described. In Sect. 3, the proposed method is described for solving nonlinear stochastic Itô–Volterra integral equations. In Sect. 4, the proposed method is applied for solving some numerical examples. In Sect. 5, some applications of the proposed computational method are described. Finally, a conclusion is drawn in Sect. 6.

2 The LWs and their properties

In this section, we briefly review the LWs and their properties which are used further in this paper.

2.1 Wavelets and the LWs

Wavelets constitute a family of functions constructed from dilation and translation of a single function $\psi (t)$ called the mother wavelet. When the dilation parameter a and the translation parameter b vary continuously, we have the following family of continuous wavelets as [35]:

$$\begin{aligned} \psi _{ab}(t)=|a|^{-\frac{1}{2}}\psi \left( \frac{t-b}{a}\right) , \quad a,\,b\in {\mathbb {R}},\,\,a\ne 0. \end{aligned}$$

(3)

If we restrict the parameters a and b to discrete values as $a=a_{0}^{-k}$, $b=nb_{0}a_{0}^{-k}$, where $a_{0}>1$, $b_{0}>0$, we have the following family of discrete wavelets:

$$\begin{aligned} \psi _{kn}(t)=|a_{0}|^{\frac{k}{2}}\psi \left( a_{0}^{k}t-nb_{0}\right) , \quad k,\,n\in {\mathbb {Z}}, \end{aligned}$$

(4)

where the functions $\psi _{kn}(t)$ form a wavelet basis for $L^{2}({\mathbb {R}})$. In practice, when $a_{0}=2$ and $b_{0}=1$, the functions $\psi _{kn}(t)$ form an orthonormal basis.

The LWs $\psi _{nm}(t)=\psi (k,n,m,t)$ have four arguments, $n=1,2,\ldots ,2^{k}$, k is any arbitrary non-negative integer, m is the degree of the Legendre polynomials and independent variable t is defined on [0, 1]. They are defined on the interval [0, 1] by [1]:

$$\begin{aligned} \psi _{nm}(t)\!=\!\displaystyle \left\{ \begin{array}{lcc} \displaystyle \sqrt{2m\!+\!1}2^{\frac{k}{2}}P_{m}\left( 2^{k+1}t\!-\!2n\!+\!1\right) , &{} &{}t\in \left[ \frac{n-1}{2^{k}},\frac{n}{2^{k}}\right] , \\ 0, &{} &{} o.w. \end{array}\right. \end{aligned}$$

(5)

Here $P_{m}(t)$ are the well-known Legendre polynomials of degree m, which are orthogonal with respect to the wight function $w(t)=1$, on the interval $[-1,1]$ and satisfy the following recursive relation [3]:

$$\begin{aligned} P_{0}(t)= & {} 1, \quad P_{1}(t)=t, \quad P_{m+1}(t) = \frac{2m+1}{m+1}tP_{m}(t) \nonumber \\&- \frac{m}{m+1}P_{m-1}(t),\quad m=1,2,\ldots . \end{aligned}$$

(6)

The set of the LWs is an orthogonal set with respect to the weight function $w(t)=1$.

2.2 Function approximation

A function f(t) defined over [0, 1] may be expanded by the LWs as:

$$\begin{aligned} f(t)=\sum _{n=1}^{\infty }\sum _{m=0}^{\infty }{c_{nm}\psi _{nm}(t)}, \end{aligned}$$

(7)

where

$$\begin{aligned} c_{nm}=\left( f(t),\psi _{nm}(t)\right) =\int _{0}^{1}f(t)\psi _{nm}(t)\mathrm{d}t, \end{aligned}$$

(8)

and (., .) denotes the inner product in $L^{2}[0,1]$.

By truncating the infinite series in Eq. (7), we can approximate f(t) as follows:

$$\begin{aligned} f(t)\simeq \sum _{n=1}^{2^{k}}\sum _{m=0}^{M-1}{c_{nm}\psi _{nm}(t)=C^{T}\Psi (t)}, \end{aligned}$$

(9)

where T indicates transposition, C and $\Psi (t)$ are $\hat{m}=2^{k}M$ column vectors.

For simplicity, Eq. (9) can be also written as:

$$\begin{aligned} f(t)\simeq \sum _{i=1}^{\hat{m}}{c_{i}\psi _{i}(t)=C^{T}\Psi (t)}, \end{aligned}$$

(10)

where $c_{i}=c_{nm}$ and $\psi _{i}(t)=\psi _{nm}(t)$, and the index i is determined by the relation $i=M(n-1)+m+1$.

Thus we have:

$$\begin{aligned} C\triangleq \left[ c_{1},c_{2},\ldots ,c_{\hat{m}}\right] ^{T}, \end{aligned}$$

and

$$\begin{aligned} \Psi (t)\triangleq \left[ \psi _{1}(t),\psi _{2}(t),\ldots , \psi _{\hat{m}}(t)\right] ^{T}. \end{aligned}$$

(11)

By taking the collocation points:

$$\begin{aligned} t_{i}=\frac{i}{\hat{m}-1}, \quad i=0,1,\ldots ,\hat{m}-1, \end{aligned}$$

(12)

into Eq. (11), we define the LWs matrix $\Phi _{\hat{m}\times \hat{m}}$ as:

$$\begin{aligned} \Phi _{\hat{m}\times \hat{m}}\triangleq \left[ \Psi (0),\Psi \left( \frac{1}{\hat{m}-1}\right) ,\ldots ,\Psi (1)\right] . \end{aligned}$$

(13)

For example, for $k=1,\,M=3$, we have:

$$\begin{aligned} \Phi _{6\times 6}\!=\!\sqrt{2}\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1&{}1&{}1&{}0&{}0&{}0\\ -\sqrt{3}&{}-\frac{1}{5}\,\sqrt{3}&{}\frac{3}{5}\,\sqrt{3}&{}0&{}0&{}0\\ \sqrt{5} &{}-{\frac{11}{25}}\,\sqrt{5}&{}\frac{1}{25}\,\sqrt{5}&{}0&{}0&{}0 \\ 0&{}0&{}0&{}1&{}1&{}1\\ 0&{}0&{}0&{}-\frac{3}{5}\, \sqrt{3}&{}\frac{1}{5}\,\sqrt{3}&{}\sqrt{3}\\ 0&{}0&{}0&{}\frac{1}{25}\, \sqrt{5}&{}-{\frac{11}{25}}\,\sqrt{5}&{}\sqrt{5}\end{array} \right) . \end{aligned}$$

2.3 Operational matrix of stochastic Itô-integration

The stochastic Itô-integration of the vector $\Psi (t)$, defined in Eq. (11), may be expressed as:

$$\begin{aligned} \int _{0}^{t}\Psi (\tau )\mathrm{d}B(\tau )\simeq P_{s}\Psi (t), \end{aligned}$$

(14)

where $P_{s}$ is the $\hat{m}\times \hat{m}$ stochastic operational matrix (SOM) for the LWs.

In the sequel we express an explicit form of the matrix $P_{s}$. To this end, we need to introduce another family of basis functions, namely hat functions (HFs). An $\hat{m}$-set of these basis functions is defined on the interval [0, 1] as [42–44]:

$$\begin{aligned} \displaystyle \phi _{0}(t)= & {} \left\{ \begin{array}{cc} \displaystyle \frac{h-t}{h}, &{} 0\le t< h, \\ 0, &{} o.w, \end{array} \right. \end{aligned}$$

(15)

$$\begin{aligned} \displaystyle \phi _{i}(t)= & {} \left\{ \begin{array}{cc} \displaystyle \frac{t-(i-1)h}{h}, &{} (i-1)h\!\le \! t\!<\! ih, \\ \displaystyle \frac{(i\!+\!1)h-t}{h}, &{} ih\le t< (i+1)h, \\ 0, &{} o.w, \end{array} \quad i=1,2,\ldots ,\hat{m}-2, \right. \nonumber \\ \end{aligned}$$

(16)

and

$$\begin{aligned} \displaystyle \phi _{\hat{m}-1}(t)=\left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{t-(1-h)}{h}, &{} 1-h\le t\le 1, \\ 0, &{} o.w, \end{array} \right. \end{aligned}$$

(17)

where $h=\frac{1}{\hat{m}-1}$.

From the definition of the HFs, we have:

$$\begin{aligned} \displaystyle \phi _{i}(jh)=\left\{ \begin{array}{ll} 1, &{} \quad i=j, \\ 0, &{} \quad i\ne j. \end{array} \right. \end{aligned}$$

(18)

An arbitrary function X(t) defined over [0, 1] may be expanded by the HFs as:

$$\begin{aligned} X(t)\simeq \sum _{i=0}^{\hat{m}-1}x_{i}\phi _{i}(t)=X^{T}\Phi (t)=\Phi (t)^{T}X, \end{aligned}$$

(19)

where

$$\begin{aligned} X\triangleq [x_{0},x_{1},\ldots ,x_{\hat{m}-1}]^{T}, \end{aligned}$$

(20)

and

$$\begin{aligned} \Phi (t)\triangleq [\phi _{0}(t),\phi _{1}(t),\ldots , \phi _{\hat{m}-1}(t)]^{T}. \end{aligned}$$

(21)

The important aspect of using the HFs in approximating a function X(t) lies in the fact that the coefficients $x_{i}$ in Eq. (19) are given by:

$$\begin{aligned} x_{i}=X(ih),\,\, i=0,1,\ldots ,\hat{m}-1. \end{aligned}$$

(22)

Theorem 2.1

Suppose $\Psi (t)$ be the LWs vector, defined in Eq. (11). Then the stochastic Itô-integration of the vector $\Psi (t)$ can be expressed as follows:

$$\begin{aligned} \int _{0}^{t}\Psi (\tau )\mathrm{d}B(\tau )\simeq P_{s}\Psi (t)\simeq \left( \Phi _{\hat{m}\times \hat{m}}\hat{P}_{s}\Phi _{\hat{m}\times \hat{m}}^{-1}\right) \Psi (t), \end{aligned}$$

(23)

where $\Phi _{\hat{m}\times \hat{m}}$ is the LWs matrix which is defined in Eq. (13) and $\hat{P}_{s}$ is the operational matrix of stochastic Itô-integration for the HFs which is given in [44] by:

$$\begin{aligned} \int _{0}^{t}\Phi (\tau )\mathrm{d}B(\tau ) \simeq \hat{P}_{s}\Phi (t), \end{aligned}$$

(24)

where

$$\begin{aligned} \displaystyle \hat{P}_{s}=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} \alpha _{0}(h) &{} \alpha _{0}(h) &{} 0 &{}\ldots &{} \alpha _{0}(h) &{} \alpha _{0}(h) \\ 0 &{} B(h)+\alpha _{1}(h) &{} \beta _{1}(h) &{} 0&{}\ldots &{} \beta _{1}(h) &{} \beta _{1}(h) \\ 0 &{} 0 &{} B(2h)+\alpha _{2}(h) &{} \beta _{2}(h)&{} \ldots &{} \beta _{2}(h) &{} \beta _{2}(h) \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} 0 &{} \ldots &{}B\left( (\hat{m}-2)h\right) +\alpha _{\hat{m}-2}(h) &{} \beta _{\hat{m}-2}(h) \\ 0 &{} 0 &{} 0 &{} 0 &{} \ldots &{}0 &{} B(T)+\alpha _{\hat{m}-1}(h) \\ \end{array} \right) , \end{aligned}$$

(25)

and

$$\begin{aligned} \displaystyle \left\{ \begin{array}{ll} \displaystyle \alpha _{0}(h)= \frac{1}{h}\int _{0}^{h}B(\tau )\mathrm{d}\tau ,&{}\\ \displaystyle \alpha _{i}(h)=-\frac{1}{h}\int _{(i-1)h}^{ih}B(\tau )\mathrm{d}\tau ,&{} \quad i=1,2,\ldots ,\hat{m}-1, \\ \displaystyle \beta _{i}(h)=-\frac{1}{h}\left( \int _{(i-1)h}^{ih}B(\tau )\mathrm{d}\tau -\int _{ih}^{(i+1)h}B(\tau )\mathrm{d}\tau \right) ,&{}\quad i=1,2,\ldots ,\hat{m}-2. \end{array}\right. \end{aligned}$$

(26)

Proof

By considering Eqs. (19) and (22), it can be simply seen that the LWs can be expanded in terms of an $\hat{m}$-set of HFs as:

$$\begin{aligned} \Psi (t)\simeq \Phi _{\hat{m}\times \hat{m}}\Phi (t). \end{aligned}$$

(27)

Now, by considering Eq. (14), and using Eqs. (27) and (24), we obtain:

$$\begin{aligned} \int _{0}^{t}\Psi (\tau )\mathrm{d}B(\tau )\simeq & {} \int _{0}^{t} \Phi _{\hat{m}\times \hat{m}} \Phi (\tau )\mathrm{d}B(\tau ) \nonumber \\= & {} \Phi _{\hat{m}\times \hat{m}}\int _{0}^{t} \Phi (\tau )\mathrm{d}B(\tau ) \nonumber \\\simeq & {} \Phi _{\hat{m}\times \hat{m}}\hat{P}_{s}\Phi (t). \end{aligned}$$

(28)

Also from Eqs. (14) and (28), we have:

$$\begin{aligned} P_{s}\Psi (t)\simeq \Phi _{\hat{m}\times \hat{m}}\hat{P}_{s}\Phi (t). \end{aligned}$$

(29)

Then, by considering Eqs. (27) and (29), we obtain the LWs operational matrix of stochastic Itô-integration $P_{s}$ as:

$$\begin{aligned} P_{s}\simeq \Phi _{\hat{m}\times \hat{m}}\hat{P}_{s}\Phi _{\hat{m}\times \hat{m}}^{-1}, \end{aligned}$$

(30)

which completes the proof. $\square$

2.4 Operational matrix of integration

The integration of the vector $\Psi (t)$, defined in Eq. (11), can be expressed as:

$$\begin{aligned} \int _{0}^{t}\Psi (\tau )\mathrm{d}\tau \simeq P\Psi (t), \end{aligned}$$

(31)

where the $\hat{m}\times \hat{m}$ matrix P is called the operational matrix of integration for the LWs.

Remark 1

By considering the process of proving Theorem 2.1, we can approximate the matrix P as:

$$\begin{aligned} P\simeq \Phi _{\hat{m}\times \hat{m}}\hat{P}\Phi _{\hat{m}\times \hat{m}}^{-1}, \end{aligned}$$

(32)

where the $\hat{m}\times \hat{m}$ matrix $\hat{P}$ is called the operational matrix of integration for the HFs and is given in [43] as follows:

$$\begin{aligned} \displaystyle \hat{P}=\frac{h}{2}\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 1 &{} 1 &{} \ldots &{}1 &{} 1 \\ 0 &{} 1 &{} 2 &{} \ldots &{} 2 &{} 2 \\ 0 &{} 0 &{} 1 &{} \ldots &{} 2 &{} 2 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 2 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{array}\right) . \end{aligned}$$

(33)

2.5 Some new useful results for the LWs

In this section, we obtain some new useful results for the LWs which will be used further in this paper.

Lemma 2.2

Suppose $X^{T}\Phi (t)$ and $Y^{T}\Phi (t)$ be the expansions of X(t) and Y(t) by the HFs, respectively. Then we have:

$$\begin{aligned} X(t)Y(t)\simeq H^{T}\Phi (t), \end{aligned}$$

(34)

where $H=X\odot Y$, denotes pointwise product of X and Y, so that for any two matrices A and B of the same dimensions it yields a matrix of the same dimensions with elements $\left( A\odot B\right) _{ij}=\left( A\right) _{ij}\left( B\right) _{ij}$.

Proof

By considering Eqs. (19) and (22), we have:

$$\begin{aligned} X(t)\simeq & {} \sum _{i=0}^{\hat{m}-1}X(ih) \phi _{i}(t) = X^{T}\Phi (t), \\ Y(t)\simeq & {} \sum _{i=0}^{\hat{m}-1}Y(ih)\phi _{i}(t) = Y^{T}\Phi (t), \end{aligned}$$

and

$$\begin{aligned} X(t)Y(t)\simeq \sum _{i=0}^{\hat{m}-1}X(ih)Y(ih)\phi _{i}(t)=H^{T}\Phi (t), \end{aligned}$$

which completes the proof. $\square$

Corollary 2.3

Suppose $X^{T}\Phi (t)$ be the expansion of X(t) by the HFs. Then for any integer $q\ge 2$ we have:

$$\begin{aligned}{}[X(t)]^{q}\simeq [x_{0}^{q},x_{1}^{q},\ldots ,x_{\hat{m}-1}^{q}]\Phi (t). \end{aligned}$$

(35)

Proof

By considering Lemma 2.2, the proof will be straightforward. $\square$

Theorem 2.4

[45] Suppose F be an analytic function and $X^{T}\Phi (t)$ be the expansion of X(t) by the generalized hat basis functions. Then we have:

$$\begin{aligned} F\left( X(t)\right) \simeq F\left( X^{T}\right) \Phi (t), \end{aligned}$$

(36)

where $F\left( X^{T}\right) =[F(x_{0}),F(x_{1}),\ldots ,F(x_{\hat{m}-1})]$.

Theorem 2.5

Suppose F be an analytic function and $X^{T}\Psi (t)$ be the expansion of X(t) by the LWs. Then we have:

$$\begin{aligned} F\left( X(t)\right) \simeq F\left( \widetilde{X}^{T}\right) \Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (t), \end{aligned}$$

(37)

where $\widetilde{X}^{T}=X^{T}\Phi _{\hat{m}\times \hat{m}}$.

Proof

By considering Eq. (27) and Theorem 2.4, we have:

$$\begin{aligned} F\left( X(t)\right)\simeq & {} F\left( X^{T}\Psi (t)\right) \simeq F\left( X^{T}\Phi _{\hat{m}\times \hat{m}}\Phi (t)\right) \nonumber \\= & {} F\left( \widetilde{X}^{T}\Phi (t)\right) \simeq F\left( \widetilde{X}^{T}\right) \Phi (t). \end{aligned}$$

(38)

So from Eqs. (27) and (38), we have:

$$\begin{aligned} F\left( X(t)\right) \simeq F\left( \widetilde{X}^{T}\right) \Phi (t)\simeq F\left( \widetilde{X}^{T}\right) \Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (t), \end{aligned}$$

(39)

which completes the proof. $\square$

Corollary 2.6

Suppose $X^{T}\Psi (t)$ and $Y^{T}\Psi (t)$ be the expansions of X(t) and Y(t) by the LWs, respectively, and also F and G be two analytic functions. Then we have:

$$\begin{aligned}&F\left( X(t)\right) G\left( Y(t)\right) \nonumber \\&\quad \simeq \left( F\left( \widetilde{X}^{T}\right) \odot G\left( \widetilde{Y}^{T}\right) \right) \Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (t), \end{aligned}$$

(40)

Proof

By considering Theorem 2.5, Eq. (27) and Lemma 2.2, the proof will be straightforward. $\square$

3 Description of the proposed computational method

In this section, we apply the operational matrices of integration and stochastic Itô-integration of the LWs together with some of their useful properties of these basis functions for solving nonlinear stochastic Itô–Volterra integral equation:

$$\begin{aligned} X(t)= & {} h(t)+\int _{0}^{t}f(\tau )\mu \left( X(\tau )\right) \mathrm{d}\tau \\&+ \int _{0}^{t}g(\tau )\sigma \left( X(\tau )\right) \mathrm{d}B(\tau ), \quad t\in [0,1], \nonumber \end{aligned}$$

(41)

where X(t), f(t), g(t) and h(t) are the stochastic processes defined on the same probability space $(\Omega , {\mathcal {F}},\mathbf {P})$, X(t) is an unknown stochastic function to be found, B(t) is a Brownian motion process and the second integral in Eq. (41) is an Itô integral. Moreover it is assumed that $\mu$ and $\sigma$ are analytic functions.

For solving this equation, we approximate X(t), h(t), f(t) and g(t) by the LWS as follows:

$$\begin{aligned} X(t)\simeq & {} X^{T}\Psi (t), \end{aligned}$$

(42)

$$\begin{aligned} h(t)\simeq & {} H^{T}\Psi (t), \end{aligned}$$

(43)

and

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle f(t)\simeq C^{T}\Psi (t),\\ \displaystyle g(t)\simeq D^{T}\Psi (t), \end{array}\right. \end{aligned}$$

(44)

where X, H, C and D are the LWs coefficient vectors.

From Eq. (42) and Theorem 2.5, we have:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle \mu (X(\tau ))\simeq \mu \left( \widetilde{X}^{T} \right) \Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (\tau ), \\ \displaystyle \sigma (X(\tau ))\simeq \sigma \left( \widetilde{X}^{T}\right) \Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (\tau ), \end{array}\right. \end{aligned}$$

(45)

where $\widetilde{X}^{T}=X^{T}\Phi _{\hat{m}\times \hat{m}}$.

Now from Eqs. (44), (45) and Corollary 2.6, we have:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle f(\tau )\mu \left( X(\tau )\right) \simeq \left( \widetilde{C}^{T}\odot \mu \left( \widetilde{X}^{T}\right) \right) \Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (\tau ),\\ \displaystyle g(\tau )\sigma \left( X(\tau )\right) \simeq \left( \widetilde{D}^{T}\odot \sigma \left( \widetilde{X}^{T}\right) \right) \Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (\tau ), \end{array} \right. \end{aligned}$$

(46)

where $\widetilde{C}^{T}=C^{T}\Phi _{\hat{m}\times \hat{m}}$ and $\widetilde{D}^{T}=D^{T}\Phi _{\hat{m}\times \hat{m}}$.

So by substituting Eqs. (42), (43) and (46) into Eq. (41), and using operational matrices of integration and stochastic Itô-integration, we can write the residual function R(t) for stochastic integral equation (41) as follows:

$$\begin{aligned} R(t)= & {} \left( X^{T}- H^{T} - \left( \widetilde{C}^{T} \odot \mu \left( \widetilde{X}^{T}\right) \right) \Phi _{\hat{m}\times \hat{m}}^{-1}P \right. \nonumber \\&\left. -\, \left( \widetilde{D}^{T}\odot \sigma \left( \widetilde{X}^{T}\right) \right) \Phi _{\hat{m} \times \hat{m}}^{-1}P_{s}\right) \Psi (t). \end{aligned}$$

(47)

As in a typical Galerkin method [3], we generate $\hat{m}$ nonlinear algebraic equations:

$$\begin{aligned}&\left( R(t),\psi _{j}(t)\right) \nonumber \\&\quad =\int _{0}^{1}R(t)\psi _{j}(t)\mathrm{d}t=0, \quad j=1,2,\ldots ,\hat{m}, \end{aligned}$$

(48)

where $\psi _{j}(t)=\psi _{nm}(t)$, and the index j is determined by the relation $j=M(n-1)+m+1$.

Finally, by solving this system for the unknown vector X, we obtain an approximate solution for the problem by substituting X in Eq. (42).

The algorithm of the proposed method is presented as follows:

Algorithm 1

Input: $M,\,N\in {\mathbb {N}},\,k\in {\mathbb {Z}}^{+}$; Brownian motion process B(t); the functions $h,\,f,\, g\in L^{2}\left[ 0,1\right]$ and $\mu ,\,\sigma \in C^{\infty }\left[ 0,1\right]$.

Step 1: Define the LWs $\psi _{nm}(t)$ from Eq. (5).

Step 2: Construct the LWs vector $\Psi (t)$ from Eq. (11).

Step 3: Compute the LWs matrix $\Phi _{\hat{m}\times \hat{m}}\triangleq \left[ \Psi (0),\Psi \left( \frac{1}{\hat{m}-1}\right) ,\ldots ,\Psi (1)\right]$.

Step 4: Compute the integration operational matrix P using Eqs. (31)–(33) and SOM $\hat{P}_s$ using Eq. (25).

Step 5: Compute the LWs stochastic operational matrix $P_s=\Phi _{\hat{m}\times \hat{m}}\hat{P}_s\Phi ^{-1}_{\hat{m}\times \hat{m}}$.

Step 6: Compute the vectors $H,\,C$ and D in Eqs. (43) and (44) using Eq. (8).

Step 7: Compute the vectors $\widetilde{C}^{T}=C^{T}\Phi _{\hat{m}\times \hat{m}}$ and $\widetilde{D}^{T}=D^{T}\Phi _{\hat{m}\times \hat{m}}$.

Step 8: Put $R(t)=\left( X^{T}- H^{T}-\left( \widetilde{C}^{T}\odot \mu \left( \widetilde{X}^{T}\right) \right) \Phi _{\hat{m}\times \hat{m}}^{-1}P\right.$ $\left. - \left( \widetilde{D}^{T}\odot \sigma \left( \widetilde{X}^{T}\right) \right) \Phi _{\hat{m}\times \hat{m}}^{-1}P_{s}\right) \Psi (t)$.

Step 9: Construct the nonlinear system of algebraic equations:

$\qquad \displaystyle \int _{0}^{1}R(t)\psi _{j}(t)\mathrm{d}t=0, \quad j=1,2,\ldots ,\hat{m}.$

Step 10: Solve the nonlinear system of algebraic equations in Step 9 and obtain the unknown vector X.

Output: The approximate solution: $X(t)\simeq X^T\Psi (t)$.

4 Illustrative test problems

In this section, we consider some numerical examples to illustrate the efficiency and reliability of the proposed method. For computational purposes, it is useful to consider discretized Brownian motion, where B(t) is specified at t discrete values and employed an spline interpolation to construct B(t). We thus set $\Delta t = \frac{1}{N}$ for some positive integer N and let $B_{i}$ denote $B(t_{i})$ with $t_{i}=i\Delta t$. Condition (i) in introduction says that $B_{0} = 0$ with the probability 1, and Conditions (ii) and (iii) tell us that

$$\begin{aligned} B_{i}=B_{i-1}+dB_{i}, \quad i=1,2,\ldots ,N, \end{aligned}$$

where each $dB_{i}$ is an independent random variable of the form $\sqrt{\Delta t}{\mathcal {N}}(0,1)$.

Also we report the absolute errors in some points $t_{j}\in [0,1]$ as:

$$\begin{aligned} \left| e\left( t_{j}\right) \right| = \left| X^{T}\Psi \left( t_{j} \right) -X\left( t_{j}\right) \right| . \end{aligned}$$

Fig. 1

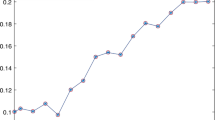
The graphs of the exact and approximate solutions for Example 1

Example 1

Let us first consider the following nonlinear stochastic Itô–Volterra integral equation [46]:

$$\begin{aligned} X(t)= & {} X_{0}+a^{2}\int _{0}^{t}\cos \left( X(\tau )\right) \sin ^{3} \left( X(\tau )\right) \mathrm{d}\tau \\&+\,a\int _{0}^{t}\sin ^{2}\left( X(\tau ) \right) \mathrm{d}B(\tau ), \end{aligned}$$

where X(t) is an unknown stochastic process defined on the probability space $(\Omega ,{\mathcal {F}},\mathbf {P})$, and B(t) is a Brownian motion process. The exact solution of this problem is given in [46] by:

$$\begin{aligned} X(t)={{\mathrm{arccot}}}\left( aB(t)+\cot \left( X_{0}\right) \right) . \end{aligned}$$

This problem is also solved by the proposed computational method for $X_{0}=a=\frac{1}{20}$. The graphs of the exact and approximate solutions for $\hat{m}=96\,(k=5, M=3)$ and $N=120$ are shown in Fig. 1. The absolute errors of the approximate solution at some different points $t\in [0,1]$, for $\hat{m}=24\,(k=3, M=3)$, $\hat{m}=48\,( k=4, M=3)$ and $\hat{m}=96\,(k=5, M=3)$ are shown in Table 1. From Fig. 1 and Table 1, it can be seen that the proposed method is very efficient and accurate in solving this problem.

Table 1 The absolute errors of the approximate solution at some different points for Example 1

Fig. 2

The graphs of the exact and approximate solutions for Example 2

Example 2

Consider the following nonlinear stochastic Itô–Volterra integral equation [46]:

$$\begin{aligned} X(t)= & {} X_{0}-\frac{a^{2}}{2}\int _{0}^{t}\tanh \left( X(\tau ) \right) {{\mathrm{sech}}}^{2}\left( X(\tau )\right) \mathrm{d}\tau \\&+a\int _{0}^{t} {{\mathrm{sech}}}\left( X(\tau )\right) \mathrm{d}B(\tau ), \end{aligned}$$

where X(t) is an unknown stochastic process defined on the probability space $(\Omega ,{\mathcal {F}},\mathbf {P})$, and B(t) is a Brownian motion process. The exact solution of this problem is given in [46] by:

$$\begin{aligned} X(t)={{\mathrm{arcsinh}}}\left( aB(t)+\sinh \left( X_{0}\right) \right) . \end{aligned}$$

This problem is also solved by the proposed computational method for $X_{0}=0$ and $a=\frac{1}{30}$. The graphs of the exact and approximate solutions for $\hat{m}=96$ and $N=82$ are shown in Fig. 2. The absolute errors of the approximate solution at some different points $t\in [0,1]$, for $\hat{m}=24$, $\hat{m}=48$ and $\hat{m}=96$ are shown in Table 2. From Fig. 2 and Table 2, it can be seen that the proposed method is very efficient and accurate in solving this problem.

Table 2 The absolute errors of the approximate solution at some different points for Example 2

Fig. 3

The graphs of the exact and approximate solutions for Example 3

Example 3

Consider the following nonlinear stochastic Itô–Volterra integral equation [46]:

$$\begin{aligned} X(t)= & {} X_{0}+\int _{0}^{t}\left( aX(\tau )+bX(\tau )^{2}\right) \mathrm{d}\tau \\&+\int _{0}^{t}cX(\tau )\mathrm{d}B(\tau ), \end{aligned}$$

where X(t) is an unknown stochastic process defined on the probability space $(\Omega ,{\mathcal {F}},\mathbf {P})$, and B(t) is a Brownian motion process. The exact solution of this problem is given in [46] by:

$$\begin{aligned} X(t)=\frac{U(t)}{\frac{1}{X_{0}}-b\int _{0}^{t}U(\tau )\mathrm{d}\tau }, \end{aligned}$$

where $U(t)=\exp \left( \left( a-\frac{c^{2}}{2}\right) t+cB(t)\right)$, and $a,\,b$ and c are constants. This problem is also solved by the proposed computational method for $X_{0}=\frac{1}{10}$, $a=\frac{1}{8}$, $b=\frac{1}{32}$ and $c=\frac{1}{20}$. The graphs of the exact solution and approximate solutions for $\hat{m}=96$ and $N=60$ are shown in Fig. 3. The absolute errors of the approximate solution at some different points $t\in [0,1]$, for $\hat{m}=24$, $\hat{m}=48$ and $\hat{m}=96$ are shown in Table 3. From Fig. 3 and Table 3, it can be seen that the proposed method is very efficient and accurate in solving this problem.

Table 3 The absolute errors of the approximate solution at some different points for Example 3

Fig. 4

The graphs of the exact and approximate solutions for Example 4

Example 4

Consider finally the following nonlinear stochastic Itô–Volterra integral equation [46]:

$$\begin{aligned} X(t)= & {} X_{0}-a^{2}\int _{0}^{t}X(\tau )\left( 1-X^{2}(\tau ) \right) \mathrm{d}\tau \\&+a\int _{0}^{t}\left( 1-X^{2}(\tau )\right) \mathrm{d}B(\tau ), \end{aligned}$$

where X(t) is an unknown stochastic process defined on the probability space $(\Omega ,{\mathcal {F}},\mathbf {P})$, and B(t) is a Brownian motion process. The exact solution of this problem is given in [46] by:

$$\begin{aligned} X(t)=\tanh \left( aB(t)+{{\mathrm{arctanh}}}(X_{0})\right) . \end{aligned}$$

This problem is also solved by the proposed computational method for $X_{0}=\frac{1}{100}$ and $a=\frac{1}{30}$. The graphs of the exact and approximate solutions for $\hat{m}=96$ and $N=65$ are shown in Fig. 4. The absolute errors of the approximate solution at some different points $t\in [0,1]$, for $\hat{m}=24$, $\hat{m}=48$ and $\hat{m}=96$ are shown in Table 4. From Fig. 4 and Table 4, it can be seen that the proposed method is very efficient and accurate in solving this problem.

Table 4 The absolute errors of the approximate solution at some different points for Example 4

5 Some applications of the proposed method

This section deals with the proposed computational method in Sect. 3, to obtain approximate solutions for some practical stochastic problems.

5.1 The mathematical finance

A well-known stochastic model which is used to stock prices, stochastic volatilities, and electricity prices is as follows [47]:

$$\begin{aligned}&\mathrm{d}S(t)=\kappa S(t)\left( \bar{\mu }-\ln (S(t))\right) \mathrm{d}t+\bar{\sigma } S(t) \mathrm{d}B(t), \nonumber \\&S(0)=S_{0}>0, \end{aligned}$$

(49)

where $\kappa >0,\,\bar{\mu }$ and $\bar{\sigma }$ are constants and also stochastic process S(t) for all $t>0$ is positive.

It is worth mentioning that stochastic volatility models have become popular for derivative pricing and hedging in the last decade as the existence of a non-flat implied volatility surface (or term-structure) has been noticed and become more pronounced, especially since the 1987 crash. This phenomenon, which is well-documented [48, 49], stands in empirical contradiction to the consistent use of a classical Black–Scholes (constant volatility) approach to pricing options and similar securities. However, it is clearly desirable to maintain as many of the features as possible that have contributed to this model’s popularity and longevity, and the natural extension pursued both in the literature and in practice has been to modify the specification of volatility in the stochastic dynamics of the underlying asset price model.

To solve stochastic model in Eq. (49), by the transformation $S(t)=X(t)+1$ in which X(t) is the unknown stochastic process, we transform Eq. (49) to the nonlinear stochastic differential equation:

$$\begin{aligned} \mathrm{d}X(t)= & {} \kappa \left( X(t)+1\right) \left( \bar{\mu }-\ln (1+X(t))\right) \mathrm{d}t \nonumber \\&+\bar{\sigma } \left( X(t)+1\right) \mathrm{d}B(t) \quad X(0)=X_{0}, \end{aligned}$$

(50)

where $X_{0}=S_{0}-1$.

However, we can write the integral form of the nonlinear SDE (50) as:

$$\begin{aligned} X(t)= & {} X_{0}+\kappa \int _{0}^{t} \left( X(\tau )+1\right) \left( \bar{\mu } - \ln (1+X(\tau ))\right) \mathrm{d}\tau \nonumber \\&+\,\bar{\sigma }\int _{0}^{t}\left( X(\tau )+1\right) \mathrm{d}B(\tau ) \end{aligned}$$

(51)

It is obvious that the proposed computational method can be used to obtain X(t) as the solution of (51). Finally, S(t) as the solution of original problem is $S(t)=1+X(t)$.

As a numerical example, we consider the nonlinear stochastic differential equation (49) with $S_{0}=0.1,\,\kappa =1,\,\bar{\mu }=0.5$ and $\bar{\sigma }=0.75$. This problem is also solved by the proposed computational method for $\hat{m}=96$ and $N=100$. The graph of the approximate solution is shown in Fig. 5.

Fig. 5

The graph of the approximate solution for stochastic finance problem

5.2 The biological systems

One of the most popular nonlinear systems in the biology is the Lotka–Volterra one [50]. As is well known, it was proposed by Volterra to account for the observed periodic variations in a predator–prey system. The Lotka–Volterra model can serve as a stepping stone toward the understanding of most realistic but still mathematically less tractable models of predator–prey systems [50]. The deterministic system which can be used to explain the problem is described by ordinary differential equations and is given by [50]:

$$\begin{aligned}&\left\{ \begin{array}{l} \displaystyle \dot{N}_{1}(t)=\frac{\mathrm{d}N_{1}(t)}{\mathrm{d}t} = \left( a-bN_{2}(t)\right) N_{1}(t), \\ \displaystyle \dot{N}_{2}(t)=\frac{\mathrm{d}N_{2}(t)}{\mathrm{d}t} = \left( -c-gN_{1}(t)\right) N_{2}(t), \end{array}\right. a,\,b,\,c,\,g>0,\nonumber \\ \end{aligned}$$

(52)

where $N_{1}(t)$ means the number of preys, and $N_{2}(t)$ the number of predators.

One of the most simple stochastic models for Eq. (52) is called stochastic Lotka–Volterra model and is given as follows [50]:

$$\begin{aligned}&\displaystyle \left\{ \begin{array}{lc} \displaystyle \mathrm{d}N_{1}(t)\!=\!\left( b_{1}\!-\!a_{1}N_{2}(t)\right) N_{1}(t)\mathrm{d}t\!+\!\bar{\sigma }_{1}N_{1}(t)\mathrm{d}B_{1}(t), &{} N_{1}(0)\!=\!N_{10},\\ \displaystyle \mathrm{d}N_{2}(t)\!=\!\left( b_{2}\!-\!a_{2}N_{1}(t)\right) N_{2}(t)\mathrm{d}t\!+\!\bar{\sigma }_{2}N_{2}(t)\mathrm{d}B_{2}(t), &{}N_{2}(0)\!=\!N_{20}, \end{array}\right. \nonumber \\ \end{aligned}$$

(53)

where $B_{1}(t)$ and $B_{2}(t)$ are independent Brownian motions.

We can write the integral form of the two-dimensional SDE (53) as follows:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{lc} \displaystyle N_{1}(t)=N_{10}+\int _{0}^{t}\left( b_{1} - a_{1}N_{2}(\tau )\right) N_{1}(\tau )\mathrm{d}\tau \\ \qquad \qquad +\,\bar{\sigma }_{1} \int _{0}^{t}N_{1}(\tau )\mathrm{d}B_{1}(\tau ),\\ \displaystyle N_{2}(t)=N_{20}+\int _{0}^{t}\left( b_{2} - a_{2}N_{1}(\tau )\right) N_{2}(\tau )\mathrm{d}\tau \\ \qquad \qquad +\,\bar{\sigma }_{2} \int _{0}^{t}N_{2}(\tau )\mathrm{d}B_{2}(\tau ). \end{array}\right. \end{aligned}$$

(54)

To solve Eq. (54) using the proposed computational method, we approximate $N_{1}(t)$ and $N_{2}(t)$ by the LWS as follows:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle N_{1}(t)\simeq N_{1}^{T}\Psi (t),\\ \displaystyle N_{2}(t)\simeq N_{2}^{T}\Psi (t), \end{array}\right. \end{aligned}$$

(55)

where $N_{1}$ and $N_{2}$ are the LWs coefficient vectors which should be found, and $\Psi (t)$ is the vector which is defined in Eq. (11).

Moreover, from Eq. (55) and Corollary 2.6, we have:

$$\begin{aligned} N_{1}(t)N_{2}(t)\simeq \left( \widetilde{N}_{1}^{T}\odot \widetilde{N}_{2}^{T}\right) \Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (t), \end{aligned}$$

(56)

where $\widetilde{N}_{1}^{T}=N_{1}^{T}\Phi _{\hat{m}\times \hat{m}}$ and $\widetilde{N}_{2}^{T}=N_{2}^{T}\Phi _{\hat{m}\times \hat{m}}$.

Moreover, by expanding $N_{10}$ and $N_{20}$ in terms of the Lws, we have:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{c} \displaystyle N_{10}\simeq N_{10}e^{T}\Psi (t),\\ \displaystyle N_{20}\simeq N_{20}e^{T}\Psi (t), \end{array}\right. \end{aligned}$$

(57)

where e is the LWs coefficients vector for the unit function.

Consequently by substituting Eqs. (55)–(57) into Eq. (54), and considering Eqs. (14) and (31), we have:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle N_{1}^{T}\Psi (t)\simeq \left( N_{10}e^{T} + \left( b_{1}N_{1}^{T}\right. \right. \\ \quad \left. \left. -a_{1}\left( \widetilde{N}_{1}^{T}\odot \widetilde{N}_{2}^{T}\right) \Phi _{\hat{m}\times \hat{m}}^{-1} \right) P+\bar{\sigma }_{1}N_{1}^{T}P_{s}\right) \Psi (t),\\ \displaystyle N_{2}^{T}\Psi (t)\simeq \left( N_{20}e^{T} + \left( b_{2}N_{2}^{T}\right. \right. \\ \quad \left. \left. -a_{2}\left( \widetilde{N}_{1}^{T}\odot \widetilde{N}_{2}^{T}\right) \Phi _{\hat{m}\times \hat{m}}^{-1} \right) P+\bar{\sigma }_{2}N_{2}^{T}P_{s}\right) \Psi (t). \end{array}\right. \end{aligned}$$

(58)

Now, from Eq. (58), we can write the residual functions $R_{1}(t)$ and $R_{2}(t)$ for system (54) as follows:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle R_{1}(t) =\left( N_{1}^{T}-N_{10}e^{T} - \left( b_{1}N_{1}^{T}\right. \right. \\ \quad \left. \left. -a_{1}\left( \widetilde{N}_{1}^{T}\odot \widetilde{N}_{2}^{T}\right) \Phi _{\hat{m}\times \hat{m}}^{-1} \right) P-\bar{\sigma }_{1}N_{1}^{T}P_{s}\right) \Psi (t),\\ \displaystyle R_{2}(t)=\left( N_{2}^{T}-N_{20}e^{T} - \left( b_{2}N_{2}^{T}\right. \right. \\ \quad \left. \left. -a_{2}\left( \widetilde{N}_{1}^{T}\odot \widetilde{N}_{2}^{T}\right) \Phi _{\hat{m}\times \hat{m}}^{-1} \right) P-\bar{\sigma }_{2}N_{2}^{T}P_{s}\right) \Psi (t). \end{array}\right. \end{aligned}$$

(59)

As in a typical Galerkin method [3], we generate $2\hat{m}$ nonlinear algebraic equations:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{c} \displaystyle \left( R_{1}(t),\psi _{j}(t)\right) = \int _{0}^{1}R_{1}(t)\psi _{j}(t)\mathrm{d}t=0, \quad j=1,2,\ldots ,\hat{m}, \\ \displaystyle \left( R_{2}(t),\psi _{j}(t)\right) = \int _{0}^{1}R_{2}(t)\psi _{j}(t)\mathrm{d}t=0, \quad j=1,2,\ldots ,\hat{m}, \end{array}\right. \end{aligned}$$

(60)

where $\psi _{j}(t)=\psi _{nm}(t)$, and the index j is determined by the relation $j=M(n-1)+m+1$.

Finally, by solving system (60) for the unknown vectors $N_{1}$ and $N_{2}$, we obtain the approximate solutions of the problem as $N_{1}(t)\simeq N_{1}^{T}\Psi (t)$ and $N_{2}(t)\simeq N_{2}^{T}\Psi (t)$.

The algorithm of the proposed computational method is presented as follows:

Algorithm 2

Input: $M\in {\mathbb {N}},\,k,N\in {\mathbb {Z}}^{+}$; Brownian motion processes $B_{1}(t)$ and $B_{2}(t)$; $a_{i},\,b_{i},\,\bar{\sigma }_{i},\,N_{i0}$ for $i=1,2$.

Step 1: Define the LWs $\psi _{nm}(t)$ from Eq. (5).

Step 2: Construct the LWs vector $\Psi (t)$ from Eq. (11).

Step 3: Compute the LWs matrix $\Phi _{\hat{m}\times \hat{m}}\triangleq \left[ \Psi (0),\Psi \left( \frac{1}{\hat{m}-1}\right) ,\ldots ,\Psi (1)\right]$.

Step 4: Compute the integration operational matrix P using Eqs. (31)–(33) and SOM $\hat{P}_s$ using Eq. (25).

Step 5: Compute the LWs stochastic operational matrix $P_s=\Phi _{\hat{m}\times \hat{m}}\hat{P}_s\Phi ^{-1}_{\hat{m}\times \hat{m}}$.

Step 6: Compute the vectors $e^{T}$ using Eq. (8).

Step 7: Compute the vectors $\widetilde{N}_{1}^{T}=N_{1}^{T}\Phi _{\hat{m}\times \hat{m}}$ and $\widetilde{N}_{2}^{T}=N_{2}^{T}\Phi _{\hat{m}\times \hat{m}}$.

Step 8: Put $\displaystyle \left\{ \begin{array}{l} \displaystyle R_{1}(t) \!=\!\left( N_{1}^{T}-N_{10}e^{T}\!-\!\left( b_{1}N_{1}^{T}\right. \right. \\ \left. \left. -a_{1}\left( \widetilde{N}_{1}^{T}\odot \widetilde{N}_{2}^{T}\right) \Phi _{\hat{m}\times \hat{m}}^{-1}\right) P\!-\!\bar{\sigma }_{1}N_{1}^{T}P_{s}\right) \Psi (t),\\ \displaystyle R_{2}(t)\!=\!\left( N_{2}^{T}\!-\!N_{20}e^{T}\!-\!\left( b_{2}N_{2}^{T}\right. \right. \\ \left. \left. -a_{2}\left( \widetilde{N}_{1}^{T}\odot \widetilde{N}_{2}^{T}\right) \Phi _{\hat{m}\times \hat{m}}^{-1}\right) P\!-\!\bar{\sigma }_{2}N_{2}^{T}P_{s}\right) \Psi (t). \end{array}\right.$.

Step 9: Construct the nonlinear system of algebraic equations:

$\displaystyle \left\{ \begin{array}{l} \displaystyle \left( R_{1}(t),\psi _{j}(t)\right) \!=\!\int _{0}^{1}R_{1}(t)\psi _{j}(t)\mathrm{d}t\!=\!0, \quad j\!=\!1,2,\ldots ,\hat{m}, \\ \displaystyle \left( R_{2}(t),\psi _{j}(t)\right) \!=\!\int _{0}^{1}R_{2}(t)\psi _{j}(t)\mathrm{d}t\!=\!0, \quad j\!=\!1,2,\ldots ,\hat{m}, \end{array}\right.$

Step 10: Solve the nonlinear system of algebraic equations in Step 9 and obtain the unknown vectors $N_{1}$ and $N_{2}$.

Output: The approximate solutions: $N_{1}(t)\simeq N_{1}^T\Psi (t)$ and $N_{2}(t)\simeq N_{2}^T\Psi (t)$.

Fig. 6

The graph of the approximate solution for stochastic biologic problem

As a numerical example, we consider the nonlinear system of stochastic integral equations (54) with $a_{1}=0.3,\,a_{2}=0.1, \,b_{1}=2.0,\,b_{2} = 1.5,\,\bar{\sigma }_{1}=0.2, \,\bar{\sigma }_{2}=0.4,\,N_{10}$ and $N_{20}=1.0$. This problem is also solved by the proposed method for $\hat{m}=48$ and $N=80$. The behavior of the numerical solutions is shown in Fig 6.

5.3 The Duffing–Van der Pol Oscillator

We investigate a simplified version of a Duffing–Van der Pol oscillator [46]:

$$\begin{aligned} \ddot{x}+\dot{x}-\left( \alpha -x^{2}\right) x=\bar{\sigma }x\xi , \end{aligned}$$

(61)

driven by multiplicative white noise $\xi (t)=\frac{\mathrm{d}B(t)}{\mathrm{d}t}$, where $\alpha$ is a real-valued parameter. The corresponding Itô stochastic differential equation is two-dimensional, with components $X_{1}$ and $X_{2}$ representing the displacement x and speed $\dot{x}$, respectively [46]:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l@{\quad }c} \displaystyle \mathrm{d}X_{1}(t)=X_{2}(t)\mathrm{d}t, &{} X_{1}(0)=X_{10},\\ \displaystyle \mathrm{d}X_{2}(t) = \left\{ X_{1}(t)\left( \alpha -X_{1}^{2} (t)\right) -X_{2}(t)\right\} \mathrm{d}t+\bar{\sigma } X_{1}(t)\mathrm{d}B(t),&{} X_{2}(0)=X_{20}, \end{array}\right. \end{aligned}$$

(62)

where B(t) is a one-dimensional standard Wiener process and $\bar{\sigma }$ controls the strength of the induced multiplicative noise.

We can write the integral form of the two-dimensional SDE (62) as follows:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle X_{1}(t)=X_{10}+\int _{0}^{t}X_{2}(\tau )\mathrm{d}\tau ,\\ \displaystyle X_{2}(t)\!=\!X_{20}\!+\!\int _{0}^{t}\left\{ X_{1}(\tau ) \left( \alpha \!-\!X_{1}^{2}(\tau )\right) \!-\!X_{2}(\tau )\right\} \mathrm{d}\tau \\ \qquad +\bar{\sigma } \int _{0}^{t}X_{1}(\tau )\mathrm{d}B(\tau ), \end{array}\right. \nonumber \\ \end{aligned}$$

(63)

To solve Eq. (63) using the proposed computational method, we approximate $X_{1}(t)$ and $X_{2}(t)$ by the LWS as follows:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle X_{1}(t)\simeq X_{1}^{T}\Psi (t),\\ \displaystyle X_{2}(t)\simeq X_{2}^{T}\Psi (t), \end{array}\right. \end{aligned}$$

(64)

where $X_{1}$ and $X_{2}$ are the LWs coefficient vectors which should be found, and $\Psi (t)$ is the vector which is defined in (11).

Also from Eq. (64) and Theorem 2.5, we have:

$$\begin{aligned} X_{1}^{3}(t)\simeq \left( \widetilde{X}_{1}^{T}\right) ^{3} \Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (t), \end{aligned}$$

(65)

where $\widetilde{X}_{1}^{T}=X_{1}^{T}\Phi _{\hat{m}\times \hat{m}}$.

Moreover, by expanding $X_{10}$ and $X_{20}$ in terms of the Lws, we have:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{c} \displaystyle X_{10}\simeq X_{10}e^{T}\Psi (t),\\ \displaystyle X_{20}\simeq X_{20}e^{T}\Psi (t), \end{array}\right. \end{aligned}$$

(66)

where e is the LWs coefficients vector for the unit function.

Therefore by substituting Eqs. (64)–(66) into (63), and considering Eqs. (14) and (31), we have:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle X_{1}^{T}\Psi (t)\simeq \left( X_{10}e^{T} + X_{2}^{T}P\right) \Psi (t),\\ \displaystyle X_{2}^{T}\Psi (t)\simeq \left( X_{20}e^{T} + \left( \alpha X_{1}^{T}-\left( \widetilde{X}_{1}^{T} \right) ^{3}\Phi _{\hat{m}\times \hat{m}}^{-1}\right. \right. \\ \qquad \left. \left. -X_{2}^{T}\right) P+\bar{\sigma } X_{1}^{T}P_{s}\right) \Psi (t). \end{array}\right. \nonumber \\ \end{aligned}$$

(67)

Now, from Eq. (67), we can write the residual functions $R_{1}(t)$ and $R_{2}(t)$ for system (63) as follows:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle R_{1}(t)= \left( X_{1}^{T}-X_{10}e^{T} - X_{2}^{T}P\right) \Psi (t), \\ \displaystyle R_{2}(t)\!=\! \left( X_{2}^{T}-X_{20}e^{T} \!-\! \left( \alpha X_{1}^{T}\!-\!\left( \widetilde{X}_{1}^{T}\right) ^{3}\Phi _{\hat{m} \times \hat{m}}^{-1}\right. \right. \\ \qquad \qquad \left. \left. -X_{2}^{T}\right) P-\bar{\sigma } X_{1}^{T}P_{s}\right) \Psi (t) . \end{array}\right. \nonumber \\ \end{aligned}$$

(68)

As in a typical Galerkin method, we generate $2\hat{m}$ nonlinear algebraic equations:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{c} \displaystyle \left( R_{1}(t),\psi _{j}(t)\right) = \int _{0}^{1} R_{1}(t)\psi _{j}(t)\mathrm{d}t=0, \quad j=1,2,\ldots ,\hat{m}, \\ \displaystyle \left( R_{2}(t),\psi _{j}(t)\right) = \int _{0}^{1} R_{2}(t)\psi _{j}(t)\mathrm{d}t=0, \quad j=1,2,\ldots ,\hat{m}. \end{array}\right. \end{aligned}$$

(69)

Finally, by solving system (69) with respect to the unknown vectors $X_{1}$ and $X_{2}$, we obtain the approximate solutions of the problem as $X_{1}(t)\simeq X_{1}^{T}\Psi (t)$ and $X_{2}(t)\simeq X_{2}^{T}\Psi (t)$.

The algorithm of the proposed computational method is presented as follows:

Algorithm 3

Input: $M\in {\mathbb {N}},\,k,N\in {\mathbb {Z}}^{+}$; Brownian motion process B(t); $\alpha ,\,\bar{\sigma },\,X_{10}$ and $X_{20}$.

Step 1: Define the LWs $\psi _{nm}(t)$ from Eq. (5).

Step 2: Construct the LWs vector $\Psi (t)$ from Eq. (11).

Step 3: Compute the LWs matrix $\Phi _{\hat{m}\times \hat{m}}\triangleq \left[ \Psi (0),\Psi \left( \frac{1}{\hat{m}-1}\right) ,\ldots ,\Psi (1)\right]$.

Step 4: Compute the integration operational matrix P using Eqs. (31)–(33) and SOM $\hat{P}_s$ using Eq. (25).

Step 5: Compute the LWs stochastic operational matrix $P_s=\Phi _{\hat{m}\times \hat{m}}\hat{P}_s\Phi ^{-1}_{\hat{m}\times \hat{m}}$.

Step 6: Compute the vectors $e^{T}$ using Eq. (8).

Step 7: Compute the vector $\widetilde{X}_{1}^{T}=X_{1}^{T}\Phi _{\hat{m}\times \hat{m}}$.

Step 8: Put $\displaystyle \left\{ \begin{array}{l} \displaystyle R_{1}(t)= \left( X_{1}^{T}-X_{10}e^{T}-X_{2}^{T}P\right) \Psi (t), \\ \displaystyle R_{2}(t)= \left( X_{2}^{T}-X_{20}e^{T}-\left( \alpha X_{1}^{T}\right. \right. \\ \left. \left. -\left( \widetilde{X}_{1}^{T}\right) ^{3}\Phi _{\hat{m}\times \hat{m}}^{-1}-X_{2}^{T}\right) P-\bar{\sigma } X_{1}^{T}P_{s}\right) \Psi (t) . \end{array}\right.$.

Step 9: Construct the nonlinear system of algebraic equations:

$\displaystyle \left\{ \begin{array}{c} \displaystyle \left( R_{1}(t),\psi _{j}(t)\right) =\int _{0}^{1}R_{1}(t)\psi _{j}(t)\mathrm{d}t=0, \quad j=1,2,\ldots ,\hat{m}, \\ \displaystyle \left( R_{2}(t),\psi _{j}(t)\right) =\int _{0}^{1}R_{2}(t)\psi _{j}(t)\mathrm{d}t=0, \quad j=1,2,\ldots ,\hat{m}, \end{array}\right.$

Step 10: Solve the nonlinear system of algebraic equations in Step 9 and obtain the unknown vectors $X_{1}$ and $X_{2}$.

Output: The approximate solutions: $X_{1}(t)\simeq X_{1}^T\Psi (t)$ and $X_{2}(t)\simeq X_{2}^T\Psi (t)$.

As a numerical example, we consider the Duffing–Van der Pol Oscillator (62) with $\alpha =0$ and the two different values $\bar{\sigma }=0.0$ and $\bar{\sigma }=0.0$ over the interval [0, 8], starting at $\left( X_{10},X_{20}\right) =(-\kappa \varepsilon ,0)$ for $\kappa =11,12,\ldots ,16$, and $\varepsilon =0.2$. This problem is also solved by the proposed method for $\hat{m}=80\,(k=4, M=5)$ and $N=16$. The behavior of the numerical solutions for $\bar{\sigma }=0.0$ (Deterministic solution) and $\bar{\sigma }=1.0$ (Stochastic solution) and some different values of $\kappa$ are shown in Figs. 7, 8 and 9. The behavior of the numerical solutions for the Duffing–Van der Pol Oscillator in the phase space is shown in Fig. 10.

Fig. 7

The graphs of the approximate solutions in the case $\kappa =11$ (left side) and $\kappa =12$ (right side)

Fig. 8

The graphs of the approximate solutions in the case $\kappa =13$ (left side) and $\kappa =14$ (right side)

Fig. 9

The graphs of the approximate solutions in the case $\kappa =15$ (left side) and $\kappa =16$ (right side)

Fig. 10

The graphs of the approximate solutions for the Duffing–Van der Pol Oscillator in the case $\bar{\sigma }=0.0$ (left side) and $\bar{\sigma }=1.0$ (right side)

Fig. 11

The graphs of the approximate solutions for the Brusselator problem in the case $\alpha =0.1$ (left side) and $\alpha =0.2$ (right side)

5.4 Stochastic Brusselator problem

The stochastic Brusselator problem is given in [51] as follows:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l@{\quad }l} \displaystyle dX(t)=\left\{ \left( \beta -1\right) X(t) + \left( X(t) + 1\right) ^{2}Y(t)\right\} \mathrm{d}t+\alpha X(t)\left( 1+X(t)\right) \mathrm{d}B(t), &{}X(0)=X_{0}, \\ \displaystyle \mathrm{d}Y(t)=-\left\{ \beta X(t)+\left( X(t)+1 \right) ^{2}Y(t)\right\} \mathrm{d}t-\alpha X(t)\left( 1+X(t)\right) dB(t),&{}Y(0)=Y_{0}, \end{array}\right. \end{aligned}$$

(70)

where $\alpha$ and $\beta$ are real constants.

The deterministic Brusselator ($\alpha =0$) equation was developed at the occasion of a scientific congress in Brussels, Belgium, to develop a simple model for bifurcations in chemical reactions [51].

We can write the integral form of the two-dimensional SDE (70) as follows:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle X(t)=X_{0}+\int _{0}^{t}\left\{ \left( \beta -1 \right) X(\tau )+\left( X(\tau )+1\right) ^{2}Y(\tau )\right\} \mathrm{d}\tau \\ \qquad \qquad +\,\alpha \displaystyle \int _{0}^{t}X(\tau )\left( 1+X(\tau )\right) \mathrm{d}B(\tau ), \\ \displaystyle Y(t)=Y_{0}-\int _{0}^{t}\left\{ \beta X(\tau ) + \left( X(\tau )+1\right) ^{2}Y(\tau )\right\} \mathrm{d}\tau \\ \qquad \qquad -\,\alpha \displaystyle \int _{0}^{t} X(\tau )\left( 1+X(\tau )\right) \mathrm{d}B(\tau ). \end{array}\right. \end{aligned}$$

(71)

To solve Eq. (71) using the proposed computational method, we approximate X(t) and Y(t) by the LWS as:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle X(t)\simeq X^{T}\Psi (t),\\ \displaystyle Y(t)\simeq Y^{T}\Psi (t), \end{array}\right. \end{aligned}$$

(72)

where X and Y are the LWs coefficient vectors which should be found and $\Psi (t)$ is the vector which is defined in (11).

Also from Eq. (72) and Theorem 2.5, we have:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle X^{2}(t)\simeq \left( \widetilde{X}^{T}\right) ^{2} \Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (t),\\ X(t)Y(t)\simeq \left( \widetilde{X}^{T}\odot \widetilde{Y}^{T}\right) \Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (t),\\ \displaystyle X^{2}(t)Y(t)\simeq \left( \left( \widetilde{X}^{T}\right) ^{2} \odot \widetilde{Y}^{T}\right) \Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (t), \end{array}\right. \end{aligned}$$

(73)

where $\widetilde{X}^{T}=X^{T}\Phi _{\hat{m}\times \hat{m}}$ and $\widetilde{Y}^{T}=Y^{T}\Phi _{\hat{m}\times \hat{m}}$.

Moreover, by expanding $X_{0}$ and $Y_{0}$ in terms of the Lws, we have:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{c} \displaystyle X_{0}\simeq X_{0}e^{T}\Psi (t),\\ \displaystyle Y_{0}\simeq Y_{0}e^{T}\Psi (t), \end{array}\right. \end{aligned}$$

(74)

where e is the LWs coefficients vector for the unit function.

Fig. 12

The graphs of the approximate solutions for the Brusselator problem in the case $\alpha =0.3$ (left side) and $\alpha =0.4$ (right side)

So by substituting Eqs. (72)–(74) into (63), and considering Eqs. (14) and (31), we have:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle X^{T}\Psi (t)\simeq \left( X_{0}e^{T} + \left\{ \left( \beta -1\right) X^{T}\right. \right. \\ \quad \left. \left. +\left[ \left( \left( \widetilde{X}^{T} \right) ^{2}\odot \widetilde{Y}^{T}\right) \right. \right. \right. \\ \quad \left. \left. \left. +2\left( \widetilde{X}^{T}\odot \widetilde{Y}^{T}\right) \right] \Phi _{\hat{m}\times \hat{m}}^{-1}+Y^{T} \right\} P\right. \\ \quad \left. +\alpha \left\{ X^{T}+\left( \widetilde{X}^{T}\right) ^{2} \Phi _{\hat{m}\times \hat{m}}^{-1}\right\} P_{s}\right) \Psi (t),\\ \displaystyle Y^{T}\Psi (t)\simeq \left( Y_{0}e^{T}- \left\{ \beta X^{T}+\left[ \left( \left( \widetilde{X}^{T}\right) ^{2}\odot \widetilde{Y}^{T}\right) \right. \right. \right. \\ \quad \left. \left. \left. +2\left( \widetilde{X}^{T}\odot \widetilde{Y}^{T}\right) \right] \Phi _{\hat{m}\times \hat{m}}^{-1} +Y^{T}\right\} P\right. \\ \quad \left. -\,\alpha \left\{ X^{T}+\left( \widetilde{X}^{T} \right) ^{2}\Phi _{\hat{m}\times \hat{m}}^{-1}\right\} P_{s}\right) \Psi (t). \end{array}\right. \end{aligned}$$

(75)

Now, from Eq. (75), we can write the residual functions $R_{1}(t)$ and $R_{2}(t)$ for system (71) as follows:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle R_{1}(t)=\left( X^{T}-X_{0}e^{T} - \left\{ \left( \beta -1\right) X^{T}\right. \right. \\ \quad \left. \left. +\left[ \left( \left( \widetilde{X}^{T} \right) ^{2}\odot \widetilde{Y}^{T}\right) \!+\!2\left( \widetilde{X}^{T} \odot \widetilde{Y}^{T}\right) \right] \Phi _{\hat{m}\times \hat{m}}^{-1} \!+\! Y^{T}\right\} P\right. \\ \quad \left. -\,\alpha \left\{ X^{T}\!+\!\left( \widetilde{X}^{T} \right) ^{2}\Phi _{\hat{m}\times \hat{m}}^{-1}\right\} P_{s}\right) \Psi (t),\\ \displaystyle R_{2}(t)= \left( Y^{T}-Y_{0}e^{T} + \left\{ \beta X^{T} + \left[ \left( \left( \widetilde{X}^{T}\right) ^{2} \odot \widetilde{Y}^{T}\right) \right. \right. \right. \\ \quad \left. \left. \left. +2\left( \widetilde{X}^{T} \odot \widetilde{Y}^{T}\right) \right] \Phi _{\hat{m}\times \hat{m}}^{-1}+Y^{T}\right\} P\right. \\ \quad \left. +\,\alpha \left\{ X^{T}+\left( \widetilde{X}^{T} \right) ^{2}\Phi _{\hat{m}\times \hat{m}}^{-1}\right\} P_{s}\right) \Psi (t). \end{array}\right. \end{aligned}$$

(76)

As in a typical Galerkin method, we generate $2\hat{m}$ nonlinear algebraic equations:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{c} \displaystyle \left( R_{1}(t),\psi _{j}(t)\right) =\int _{0}^{1} R_{1}(t)\psi _{j}(t)\mathrm{d}t=0, \quad j=1,2,\ldots ,\hat{m}, \\ \displaystyle \left( R_{2}(t),\psi _{j}(t)\right) =\int _{0}^{1} R_{2}(t)\psi _{j}(t)\mathrm{d}t=0, \quad j=1,2,\ldots ,\hat{m}. \end{array}\right. \end{aligned}$$

(77)

Finally, by solving system (77) with respect to the unknown vectors X and Y, we obtain the approximate solutions of the problem as $X(t)\simeq X^{T}\Psi (t)$ and $Y(t)\simeq Y^{T}\Psi (t)$.

The algorithm of the proposed computational method is presented as follows:

Algorithm 4

Input: $M\in {\mathbb {N}},\,k,N\in {\mathbb {Z}}^{+}$; Brownian motion process B(t); $\alpha ,\,\beta ,\,X_{0}$ and $Y_{0}$.

Step 1: Define the LWs $\psi _{nm}(t)$ from Eq. (5).

Step 2: Construct the LWs vector $\Psi (t)$ from Eq. (11).

Step 3: Compute the LWs matrix $\Phi _{\hat{m}\times \hat{m}}\triangleq \left[ \Psi (0),\Psi \left( \frac{1}{\hat{m}-1}\right) ,\ldots ,\Psi (1)\right]$.

Step 4: Compute the integration operational matrix P using Eqs. (31)–(33) and SOM $\hat{P}_s$ using Eq. (25).

Step 5: Compute the LWs stochastic operational matrix $P_s=\Phi _{\hat{m}\times \hat{m}}\hat{P}_s\Phi ^{-1}_{\hat{m}\times \hat{m}}$.

Step 6: Compute the vectors $e^{T}$ using Eq. (8).

Step 7: Compute the vectors $\widetilde{X}^{T}=X^{T}\Phi _{\hat{m}\times \hat{m}}$ and $\widetilde{Y}^{T}=Y^{T}\Phi _{\hat{m}\times \hat{m}}$.

Step 8: Put $\displaystyle \left\{ \begin{array}{l} \displaystyle R_{1}(t)=\left( X^{T}-X_{0}e^{T}-\left\{ \left( \beta -1\right) X^{T}\right. \right. \\ \left. \left. \!+\!\left[ \left( \left( \widetilde{X}^{T}\right) ^{2}\odot \widetilde{Y}^{T}\right) \!+\!2\left( \widetilde{X}^{T}\odot \widetilde{Y}^{T}\right) \right] \Phi _{\hat{m}\times \hat{m}}^{-1}\!+\!Y^{T}\right\} P\right. \\ \left. \qquad -\alpha \left\{ X^{T}+\left( \widetilde{X}^{T}\right) ^{2}\Phi _{\hat{m}\times \hat{m}}^{-1}\right\} P_{s}\right) \Psi (t),\\ \displaystyle R_{2}(t)\!=\! \left( Y^{T}-Y_{0}e^{T}\!+\!\left\{ \beta X^{T}\!+\!\left[ \left( \left( \widetilde{X}^{T}\right) ^{2}\odot \widetilde{Y}^{T}\right) \right. \right. \right. \\ \left. \left. \left. +2\left( \widetilde{X}^{T}\odot \widetilde{Y}^{T}\right) \right] \Phi _{\hat{m}\times \hat{m}}^{-1}+Y^{T}\right\} P\right. \\ \left. \qquad +\alpha \left\{ X^{T}+\left( \widetilde{X}^{T}\right) ^{2}\Phi _{\hat{m}\times \hat{m}}^{-1}\right\} P_{s}\right) \Psi (t). \end{array}\right.$.

Step 9: Construct the nonlinear system of algebraic equations:

$\displaystyle \left\{ \begin{array}{c} \displaystyle \left( R_{1}(t),\psi _{j}(t)\right) =\int _{0}^{1}R_{1}(t)\psi _{j}(t)\mathrm{d}t=0, \quad j=1,2,\ldots ,\hat{m}, \\ \displaystyle \left( R_{2}(t),\psi _{j}(t)\right) =\int _{0}^{1}R_{2}(t)\psi _{j}(t)\mathrm{d}t=0, \quad j=1,2,\ldots ,\hat{m}, \end{array}\right. .$

Step 10: Solve the nonlinear system of algebraic equations in Step 9 and obtain the unknown vectors X and Y.

Output: The approximate solutions: $X(t)\simeq X^{T}\Psi (t)$ and $Y(t)\simeq Y^T\Psi (t)$.

As a numerical example, we consider the stochastic Brusselator problem (70) with $\beta =2$ and some different values $\alpha$ over the interval [0, 6.5], starting at $\left( X_{0},Y_{0}\right) =(-0.1,0.0)$. This problem is also solved by the proposed method for $\hat{m}=80$ and $N=35$. The behavior of the numerical solutions for the stochastic Brusselator problem in the phase space are shown in Figs. 11 and 12. The non-noisy curve is the corresponding deterministic limit cycle.

6 Conclusion

Some SDEs can be written as nonlinear stochastic Volterra integral equations given in (1). It may be impossible to find exact solutions of such problems. So, it would be convenient to determine their numerical solutions using a stochastic numerical method. In this paper, the SOM of Itô-integration for the LWs was derived and applied for solving nonlinear stochastic Itô–Volterra integral equations. In the proposed method, a new technique for commuting nonlinear terms in problems under study was presented. Also some useful properties of the LWs were derived and used to solve problems under consideration. Applicability and accuracy of the proposed method were checked on some examples. Moreover, the results of the proposed method were in a good agreement with the exact solutions. Furthermore, as some applications, the proposed computational method was applied to obtain approximate solutions for some stochastic problems in the mathematics finance, biology, physics and chemistry.