Robust adaptive position and force controller design of robot manipulator using fuzzy neural networks

Abstract

This paper presents a robust adaptive position and force control scheme for an n-link robot manipulator under unknown environment. The robot manipulator’s model and the stiffness coefficient of contact environment are assumed to be not exactly known. Therefore, the traditional impedance force controller cannot be applied. We herein adopt the fuzzy neural networks (FNNs) to estimate the unknown model matrices of robot manipulator and the adaptive tracking position and force control is developed by the proposed adaptive scheme. Based on the Lyapunov stability theory, the stability of the closed-loop system and convergence of adjustable parameters are guaranteed. The corresponding update laws of FNNs’ parameters and estimated stiffness coefficient of contacting environment can be derived. Finally, simulation results of a two-link robot manipulator with environment constraint are introduced to illustrate the performance and effectiveness of our approach.

1 Introduction

Recently, various control strategies for treating the interaction control problem of robot manipulator are proposed, e.g., impedance control and the hybrid force control algorithms [1, 3, 5–13, 15, 16, 28–36, 38, 40]. The impedance control of robot manipulators is to adjust the end-effector position and sense the contact force in response to satisfy the target impedance behavior. Several robust control schemes and adaptive control strategies have been proposed for motion control of robot manipulator [1, 3, 4, 10, 31, 34–36, 38]. In the literature [5, 12, 13, 40], adaptive impedance control schemes using approximation technique for an n-link robot manipulator without regressor are introduced. The modifications of impedance function have been proposed to solve the force tracking problem on unknown environment [16].

As above, the purpose of this paper is to introduce a robust adaptive force and position tracking problem for robot manipulator with model uncertainties and the task environment is unknown. Many approaches are proposed to deal with the adaptive controller design for systems with uncertainties and disturbance. In [17–19], the neural network approach was proposed to treat the system uncertainties in force control problem. In addition, an on-line learning method was introduced to regulate all impedance parameters as well as desired trajectory [39]. Similarly, the fuzzy logic control was developed by human experience to implement nonlinear control algorithms [21–25]. Besides, the recurrent fuzzy neural network is introduced to deal with uncertainties and disturbances [33]. Therefore, the fuzzy neural networks (FNNs) are adopted to treat the tracking control of robot manipulator.

In this paper, a robust FNN-based adaptive force tracking control is proposed for robot manipulator with uncertainties and unknown stiffness coefficient. The dynamic model of the robot manipulator and the stiffness coefficient of contact environment are assumed to be unknown. Therefore, we cannot solve the force tracking control by using the traditional approaches. Thus, the FNN estimators are adopted to approximate the system’s dynamic model and to develop the proposed adaptive tracking control scheme. In addition, the adaptive force control law is established by gradient method. Based on the Lyapunov stability approach, the update laws of FNNs’ parameters and estimated stiffness coefficient are obtained. In addition, the stability of the closed-loop system and convergence of parameters are guaranteed. Finally, simulation results of a two-link robot manipulator with environment constraint are introduced to illustrate the performance and effectiveness of our approach.

The rest of this paper is as follows. Section 2 introduces the problem formulation and the used fuzzy neural network system. The proposed adaptive force control scheme is introduced in Sect. 3. The theoretical analysis is also introduced here. In Sect.  4, simulation results of a two-link robot manipulator are presented. Finally, conclusion is given.

2 Problem formulation

2.1 System description

The dynamic model of an n-link rigid robot manipulator in joint space coordinate is

$$\begin{aligned} \mathbf{D}(\mathbf{q})\ddot{\mathbf{q}}+\mathbf{C}\left( {\mathbf{q},\dot{\mathbf{q}}} \right) \dot{\mathbf{q}}+\mathbf{g}(\mathbf{q})=\varvec{{\uptau } }-\mathbf{J}^{T}{} \mathbf{F}_\mathrm{ext} \end{aligned}$$

(1)

where $\mathbf{q}\in \mathfrak {R}^{n}$ denotes the vector of generalized displacement in robot coordinates, $\varvec{{\uptau } }\in \mathfrak {R}^{n}$ is the vector of joint torque, $\mathbf{D}(\mathbf{q})\in \mathfrak {R}^{n\times n}$ is the inertia matrix, $\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}}\in \mathfrak {R}^{n}$ is the vector of centrifugal and Coriolis forces, $\mathbf{g}(\mathbf{q})\in \mathfrak {R}^{n}$ is the gravity vector. $\mathbf{J}(\mathbf{q})\in \mathfrak {R}^{n\times n}$ is the Jacobian matrix, which is assumed to be nonsingular, and $\mathbf{F}_\mathrm{ext} \in \mathfrak {R}^{n}$ is the external force at the end-effector. In the case of $n>6$, the manipulator is redundant; then, the inverse of Jacobian $(\mathbf{J}^{-1})$ should be replaced by pseudo-inverse $\mathbf{J}^{+}=\mathbf{J}^{T}(\mathbf{JJ}^{T})^{-1}$. System (1) can be transferred to the Cartesian space as

$$\begin{aligned} \mathbf{D}_\mathbf{x} (\mathbf{x})\ddot{\mathbf{x}}+\mathbf{C}_\mathbf{x} \left( {\mathbf{x},\dot{\mathbf{x}}} \right) \dot{\mathbf{x}}+\mathbf{g}_\mathbf{x} (\mathbf{x})=\mathbf{J}^{-T}\varvec{{\uptau } }-\mathbf{F}_\mathrm{ext} \end{aligned}$$

(2)

where $\mathbf{x}\in \mathfrak {R}^{n}$ is the location vector of the end-effector in Cartesian space and

$$\begin{aligned}&{} \mathbf{D}_\mathbf{x} (\mathbf{x})=\mathbf{J}^{-T}{} \mathbf{D}(\mathbf{q})\mathbf{J}^{-1} \end{aligned}$$

(3)

$$\begin{aligned}&{} \mathbf{C}_\mathbf{x} \left( {\mathbf{x},\dot{\mathbf{x}}} \right) =\mathbf{J}^{-T}{} \mathbf{(C}\left( {\mathbf{q},\dot{\mathbf{q}}} \right) -\mathbf{D(q)J}^{-\mathbf{1}}\dot{\mathbf{J}})\mathbf{J}^{-\mathbf{1}} \end{aligned}$$

(4)

$$\begin{aligned}&{} \mathbf{g}_\mathbf{x} \mathbf{(x)}=\mathbf{J}^{-\mathbf{T}}{} \mathbf{g(q)}. \end{aligned}$$

(5)

In most practical cases, the system dynamic model are not exactly known, thus identification or modeling of the robot manipulator model are needed for the controller design. In this paper, the FNN estimators solve this problem, i.e., the FNNs estimate the functions of $\mathbf{D}_{x},\, \mathbf{C}_{x}$, and $\mathbf{g}_{x}$.

The purpose of this paper is to provide proper control signals such that the end-effector of robot manipulator follows the desired trajectory for free space and tracks the desired force for contact space even the system with uncertainties and works under unknown environment (stiffness coefficient is unknown).

Fig. 1

Schematic diagram of fuzzy neural network [21–23]

2.2 Fuzzy neural network system

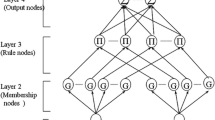
Herein, we introduce the FNN systems briefly as follows [21–23]. The schematic diagram of the used FNN with four layers is shown in Fig. 1, where “G” denotes the Gaussian fuzzy term set. Layer 1 is the input layer that accepts input variables and its nodes represent fuzzy input linguistic variables. The nodes in this layer only transmit input variables to the next layer directly, i.e., $O_i^{(1)} =x_i$. Layer 2 operates as the fuzzification; each node calculates the corresponding membership grade for input $x_{i}$

$$\begin{aligned} O_{ij}^{\left( 2 \right) } =e^{-\frac{\left( {x_i -m_{ij} } \right) ^{2}}{\left( {\sigma _{ij} } \right) ^{2}}} \end{aligned}$$

(6)

where $m_{ij}$ and $\sigma _{ij}$ are the center and the width of the Gaussian function, respectively. In layer 3 (rule layer), each node represents the fuzzy rule and the t-norm product operation is adopted. Links before layer 3 represent the preconditions of the rules, and the links after layer 3 represent the consequences of the fuzzy rule, the output of Layer 3 is

$$\begin{aligned} O_j^{(3)} =\prod _i {O_{ij}^{(2)} } . \end{aligned}$$

(7)

Layer 4 is the output layer. Each node is for actual output of FNN system that is connected by weighting value $w_{j}$, the $p^{\mathrm{th}}$ output is

$$\begin{aligned} y_p =O^{(4)} =\mathbf{w}^{T}\varvec{{\uppsi } }=\frac{\sum \nolimits _{j=1}^R {w_j O_j^{(3)} } }{\sum \nolimits _{j=1}^R {O_j^{(3)}} } \end{aligned}$$

(8)

where $\mathbf{w}=\left[ {w_1 w_2 ,\,\ldots ,w_R } \right] ^{T}$ is the weighting vector and $\varvec{{\uppsi } }=\left[ {\varvec{{\uppsi } }^{1}\,\varvec{{\uppsi } }^{2}, \ldots , \varvec{{\uppsi } }^{R}} \right] , \varvec{{\uppsi } }^{j}={O_j^{(3)} }\Big /{\sum \nolimits _j^R {O_j^{(3)}}}$ and R is the chosen rule number. As above, there is R adjustable parameters for a single output FNN with R rules. Herein, the FNN is adopted to estimate the unknown matrices of robot manipulator. In addition, the FNN realizes the fuzzy inference into the network structure. Assume that an FNN system has R rules and n inputs; the $j\hbox {th}$ rule can be expressed as

$$\begin{aligned}&\hbox {Rule }j:\hbox {IF }x_1 \hbox { is }A_{1j} \hbox { and }\ldots \,x_n \hbox { is }A_{nj} ,\hbox { THEN }y_1 \hbox { is } \nonumber \\&\quad \omega _{1j} \hbox { and }\ldots y_p \hbox { is }\omega _{pj} \end{aligned}$$

(9)

where $x_{j}$ denotes the input linguistic variable, $A_{1j}$ is the fuzzy set represented by the Gaussian fuzzy term set, and $\omega _{pj}$ is the consequent part parameter for inference output $y_{p}$. That is, the FNN provides the linguistic representation for the approximated function. In addition, as the mention of [21], the FNNs have the properties of universal approximator, fast convergence, less adjustable parameters, and parallel distribution scheme. The universal approximation theorem states “if the FNN has a sufficiently large number of fuzzy logical rules (or neurons), then it can approximate any continuous function in $C(\mathfrak {R}^{n})$ over a compact subset of $\mathfrak {R}^{n}$.” Therefore, the FNNs have the abilities of estimating the system dynamic matrices.

Fig. 2

The proposed adaptive tracking control scheme using FNNs

Fig. 3

Force tracking control scheme using FNNs

3 Robust adaptive position and force control scheme under unknown stiffness coefficient

As the results of traditional impedance control [2], the corresponding system parameters are exactly known, and then the closed-loop system satisfies the target impedance

$$\begin{aligned}&\mathbf{M}_m \left( {\ddot{\mathbf{x}}-\ddot{\mathbf{x}}_\mathrm{d} } \right) +\mathbf{B}_m (\dot{\mathbf{x}}-\dot{\mathbf{x}}_\mathrm{d} )+\mathbf{K}_m (\mathbf{x}-\mathbf{x}_\mathrm{d}) \nonumber \\&\quad =-\mathbf{F}_\mathrm{ext} \end{aligned}$$

(10)

where $\mathbf{M}_m ,\mathbf{B}_m$, and $\mathbf{K}_{m}$ are diagonal $n\times n$ matrices gain, $\mathbf{x}_\mathrm{d} \in \mathfrak {R}^{n}$ is the reference end-effector trajectory (reference location). However, system dynamic model is not exactly known, the proposed adaptive control utilizes the FNNs to approximate the system model matrices (denote as $\hat{\mathbf{D}}_\mathbf{x} ,\,\hat{\mathbf{C}}_\mathbf{x}$, and $\hat{\mathbf{g}}_\mathbf{x} )$ for solving the tracking control problem.

Herein, the control objective is divided into two cases; Case (a) is to design an adaptive controller such that $\mathbf{x}$ approaches to $\mathbf{x}_{d}$ asymptotically for free space ($\mathbf{F}_\mathrm{ext}=0$); Case (b), we should pay additional effort to design the adaptive force controller such that $\mathbf{F}_\mathrm{ext}$ is equal to the desired force $\mathbf{F}_{d}$ for contact space. However, the environment stiffness is not exactly known, then we cannot design the reference trajectory $\mathbf{x}$ to achieve the desired force directly. In this paper, we solve the problem by using FNN-based adaptive tracking controller firstly, shown in Fig. 2. Based on the Lyapunov stability approach, the stability analysis of the closed-loop system and the update laws of FNNs’ parameters are obtained. After solving the tracking control problem, the adaptive force tracking scheme is introduced for contact environment with unknown stiffness coefficient, shown in Fig. 3. The corresponding parameter estimator and update law are proposed based on the Lyapunov approach that guarantees the convergence. More details are introduced below.

3.1 Adaptive tracking controller design

Herein, we first consider the adaptive tracking control for free space. The system model matrices $\mathbf{D}_{\mathbf{x}},\, \mathbf{C}_{\mathbf{x}}$, and $\mathbf{g}_{\mathbf{x}}$ are not exactly known which are estimated by FNNs. Before introducing the proposed approach, we first define $\mathbf{e}=\mathbf{x}-\mathbf{x}_\mathbf{d}$ and $\mathbf{s}=\dot{\mathbf{e}}+\Lambda \mathbf{e}$, where $\Lambda =\hbox {diag}(\lambda _1 ,\lambda _2 ,\ldots ,\lambda _n )$ with $\lambda _i >0$ for $i=1,\, {\ldots }, n$. Rewrite system (2) as

$$\begin{aligned}&\hat{\mathbf{D}}_\mathbf{x} \dot{\mathbf{s}}+\hat{\mathbf{C}}_\mathbf{x} \mathbf{s}+\hat{\mathbf{g}}_\mathbf{x} +\hat{\mathbf{D}}_\mathbf{x} \ddot{\mathbf{x}}_\mathbf{d} -\hat{\mathbf{D}}_\mathbf{x} \varvec{\Lambda }\dot{\mathbf{e}}+\hat{\mathbf{C}}_\mathbf{x} \dot{\mathbf{x}}_\mathbf{d} -\hat{\mathbf{C}}_\mathbf{x} \varvec{\Lambda } \mathbf{e} \nonumber \\&\quad =\mathbf{J}^{-T}\varvec{{\uptau } }-\mathbf{F}_\mathrm{ext} \end{aligned}$$

(11)

where $\hat{\mathbf{D}}_\mathbf{x} =\hat{{\mathbf{w}}}_D^T \varvec{{\uppsi } }_D$, $\hat{\mathbf{C}}_\mathbf{x} =\hat{{\mathbf{w}}}_C^T \varvec{{\uppsi } }_C$, and $\hat{\mathbf{g}}_\mathbf{x} =\hat{{\mathbf{w}}}_g^T \varvec{{\uppsi } }_g$ are the estimations of $\mathbf{D}_{\mathbf{x}},\, \mathbf{C}_{\mathbf{x}}$, and $\mathbf{g}_{\mathbf{x}}$, respectively. $\hat{{\mathbf{w}}}$ denotes the weighting matrix of the FNN, and $\varvec{{\uppsi }}$ is the normalized firing strength of the corresponding fuzzy rules (it also viewed as basis function matrix). According to the universal approximation property of the FNNs, there exists optimal weighting matrix $\mathbf{w}^{*}$ such that the unknown functions are represented as follows with approximation error $\varepsilon$, i.e.,

$$\begin{aligned} \mathbf{D}_\mathbf{x}= & {} \mathbf{w}_D^{*T}\varvec{{\uppsi } }_D +\varepsilon _{\mathbf{D}_X } \end{aligned}$$

(12a)

$$\begin{aligned} \mathbf{C}_\mathbf{x}= & {} \mathbf{w}_C^{*T}\varvec{{\uppsi } }_C +\varepsilon _{\mathbf{C}_X } \end{aligned}$$

(12b)

$$\begin{aligned} \mathbf{g}_\mathbf{x}= & {} \mathbf{w}_g^{*T}\varvec{{\uppsi } }_g +\varepsilon _{\mathbf{g}_X } \end{aligned}$$

(12c)

where $\mathbf{w}_D^*\in \mathfrak {R}^{n^{2}R}$, $\mathbf{w}_C^*\in \mathfrak {R}^{n^{2}R}$, and $\mathbf{w}_g^*\in \mathfrak {R}^{nR}$ and $\varvec{{\uppsi } }_D \in \mathfrak {R}^{n^{2}R}$, $\varvec{{\uppsi } }_C \in \mathfrak {R}^{n^{2}R}$, $\varvec{{\uppsi } }_G \in \mathfrak {R}^{nR}$. R represents the rule number of FNN. Note that $\hat{\mathbf{D}}_\mathbf{x} \in \mathfrak {R}^{n\times n}$ has $n\times n$ functions, then we have $n\times n\times R$ adjustable parameters when each unknown function is approximated by an FNN having R rules.

As above, we have the following theorem to guarantee the stability of the closed-loop systems for tracking control problem.

Theorem 1

Consider the nonlinear system (2) with uncertainties and nonsingular property, i.e., $\mathbf{D}_{\mathbf{x}},\, \mathbf{C}_{\mathbf{x}}$, and $\mathbf{g}_{\mathbf{x}}$ are not exactly known, the adaptive controllers are designed as

$$\begin{aligned}&\varvec{{\uptau }}=\mathbf{J}^{T}\left( \mathbf{F}_\mathrm{ext} +\hat{\mathbf{g}}_\mathbf{x} +\quad \hat{\mathbf{D}}_\mathbf{x} \ddot{\mathbf{x}}_\mathbf{d} -\hat{\mathbf{D}}_\mathbf{x} \varvec{\Lambda }\dot{\mathbf{e}}+\hat{\mathbf{C}}_\mathbf{x} \dot{\mathbf{x}}_\mathbf{d} \right. \nonumber \\&\qquad \left. -\hat{\mathbf{C}}_\mathbf{x} \varvec{\Lambda } \mathbf{e}-\mathbf{K}_\mathrm{d} \mathbf{s}\right) \,+\varvec{{\uptau } }_\mathrm{robust} \end{aligned}$$

(13)

$$\begin{aligned}&\quad \varvec{{\uptau }}_\mathrm{robust} = -\delta [\mathrm{sgn}(s_1 ),\ldots ,\mathrm{sgn}(s_n )]^{T} \end{aligned}$$

(14)

where $\varvec{{\uptau } }_\mathrm{robust}$ is the robust controller which plays the role of compensator, $s_i$, $i=1,\ldots ,n$ is the ith element of $\mathbf{s},\, \delta$ is the selected amplitude of robust controller (robust control gain), and $\mathbf{K}_{d}$ is positive matrix in which is usually chosen as diagonal matrix, i.e., $\mathbf{K}_{d}= \hbox {diag}(k_{d1},\, k_{d2}, {\ldots },\, k_{dn})$. In addition, the update laws of FNNs are chosen as

$$\begin{aligned} \dot{\hat{{\mathbf{w}}}}_\mathbf{D}= & {} -\mathbf{Q}_\mathbf{D}^{-1} [\varvec{{\uppsi } }_\mathbf{D} (\ddot{\mathbf{x}}_\mathrm{d} -\varvec{\Lambda }\dot{\mathbf{e}})\mathbf{s}^{T}] \end{aligned}$$

(15a)

$$\begin{aligned} \dot{\hat{{\mathbf{w}}}}_\mathbf{C}= & {} -\mathbf{Q}_\mathbf{C}^{-1} [\varvec{{\uppsi } }_\mathbf{C} (\dot{\mathbf{x}}_\mathrm{d} -\varvec{\Lambda } \mathbf{e})\mathbf{s}^{T}] \end{aligned}$$

(15b)

$$\begin{aligned} \dot{\hat{{\mathbf{w}}}}_\mathbf{g}= & {} -\mathbf{Q}_\mathbf{g}^{-1} (\varvec{{\uppsi } }_\mathbf{g} \mathbf{s}^{T}) \end{aligned}$$

(15c)

where $\mathbf{Q}_\mathbf{D} \in \mathfrak {R}^{n^{2}R\times n^{2}R}$, $\mathbf{Q}_\mathbf{C} \in \mathfrak {R}^{n^{2}R\times n^{2}R}$, $\mathbf{Q}_\mathbf{g} \in \mathfrak {R}^{nR\times nR}$ are positive definite matrices. Then, the asymptotically convergence of tracking error is guaranteed, i.e., the state $\mathbf{x}$ will follow the desired trajectory $\mathbf{x}_{\mathbf{d}}$ when t approaches to infinity.

Proof

Substituting (11) into (2)

$$\begin{aligned}&\mathbf{D}_x \dot{\mathbf{s}}+\mathbf{C}_\mathbf{x} \mathbf{s}+\mathbf{K}_\mathbf{d} \mathbf{s}=\left( {\hat{\mathbf{D}}_\mathbf{x} -\mathbf{D}_\mathbf{x} } \right) \left( {\ddot{\mathbf{x}}_\mathbf{d} -\Lambda \dot{\mathbf{e}}} \right) \nonumber \\&\quad +\left( {\hat{\mathbf{C}}_\mathbf{x} -\mathbf{C}_\mathbf{x} } \right) \left( {\dot{\mathbf{x}}_\mathbf{d} -\Lambda \mathbf{e}} \right) +\left( {\hat{\mathbf{g}}_x -\mathbf{g}_x } \right) +\varvec{{\uptau } }_\mathrm{robust}.\nonumber \\ \end{aligned}$$

(16)

By the representation of (11) and (12), we have

$$\begin{aligned}&\mathbf{D}_\mathbf{x} \dot{\mathbf{s}}+\mathbf{C}_\mathbf{x} \mathbf{s}+\mathbf{K}_\mathbf{d} \mathbf{s}=\tilde{\mathbf{w}}_\mathbf{D}^T \varvec{{\uppsi } }_\mathbf{D} \left( {\ddot{\mathbf{x}}_\mathbf{d} -\varvec{\Lambda }\dot{\mathbf{e}}} \right) \nonumber \\&\quad +\tilde{\mathbf{w}}_\mathbf{C}^T \varvec{{\uppsi } }_\mathbf{C} \left( {\dot{\mathbf{x}}_\mathbf{d} -\varvec{\Lambda } \mathbf{e}} \right) +\tilde{\mathbf{w}}_\mathbf{g}^T \varvec{{\uppsi } }_\mathbf{g} \,+\varvec{{\upvarepsilon }}_1 +\varvec{{\uptau } }_\mathrm{robust} \, \end{aligned}$$

(17)

where $\tilde{\mathbf{w}}=\hat{{\mathbf{w}}}-\mathbf{w}^{*}$ and $\varvec{{\upvarepsilon }}_1 =\varvec{{\upvarepsilon }}_1 (\varvec{{\upvarepsilon }}_{{\mathbf{D}_X}} ,\varvec{{\upvarepsilon }}_{{\mathbf{C}_x}} ,\, \varvec{{\upvarepsilon }}_{\mathbf{g}_x} ,\mathbf{s},\ddot{\mathbf{x}})$ denotes the lumped bounded approximation error of $\mathbf{D}_{\mathbf{x}},\, \mathbf{C}_{\mathbf{x}}$, and $\mathbf{g}_{\mathbf{x}}$. Define the Lyapunov candidate function

$$\begin{aligned}&V(\mathbf{s},\tilde{\mathbf{w}}_\mathbf{D},\, \tilde{\mathbf{w}}_\mathbf{C} ,\, \tilde{\mathbf{w}}_\mathbf{g} )=\frac{1}{2}{} \mathbf{s}^{T}{} \mathbf{D}_x \mathbf{s} \nonumber \\&\quad +\frac{1}{2}\hbox {Trace}\left( \tilde{\mathbf{w}}_\mathbf{D}^T \mathbf{Q}_\mathbf{D} \tilde{\mathbf{w}}_\mathbf{D} +\tilde{\mathbf{w}}_\mathbf{C}^T \mathbf{Q}_\mathbf{C} \tilde{\mathbf{w}}_\mathbf{C} +\tilde{\mathbf{w}}_\mathbf{g}^T \mathbf{Q}_\mathbf{g} \tilde{\mathbf{w}}_\mathbf{g}\right) \nonumber \\ \end{aligned}$$

(18)

where $\mathbf{Q}_\mathbf{D} \in \mathfrak {R}^{n^{2}R\times n^{2}R}$, $\mathbf{Q}_\mathbf{C} \in \mathfrak {R}^{n^{2}R\times n^{2}R}$, $\mathbf{Q}_\mathbf{g} \in \mathfrak {R}^{nR\times nR}$ are positive definite matrices and Trace(.) is the trace operation. Hence

$$\begin{aligned} \dot{V}= & {} \mathbf{s}^{T}\left( -\mathbf{C}_\mathbf{x} \mathbf{s}-\mathbf{K}_\mathrm{d} \mathbf{s}+\tilde{\mathbf{w}}_\mathbf{D}^T \varvec{{\uppsi } }_\mathbf{D} \right. \nonumber \\&\left( {\ddot{\mathbf{x}}_\mathbf{d} -\varvec{\Lambda }\dot{\mathbf{e}}} \right) +\tilde{\mathbf{w}}_\mathbf{C}^T \varvec{{\uppsi } }_\mathbf{C} \left( {\dot{\mathbf{x}}_\mathbf{d} -\varvec{\Lambda }{} \mathbf{e}} \right) \nonumber \\&\left. +\,\tilde{\mathbf{w}}_\mathbf{g}^T \varvec{{\uppsi } }_\mathbf{g} +\varvec{{\upvarepsilon }}_1 +\varvec{{\uptau } }_\mathrm{robust} \right) \nonumber \\&+\,\frac{1}{2}{} \mathbf{s}^{T}\dot{\mathbf{D}}_\mathbf{x} \mathbf{s}+\hbox {Trace}(\tilde{\mathbf{w}}_\mathbf{D}^T \mathbf{Q}_\mathbf{D} \dot{\tilde{\mathbf{w}}}_\mathbf{D} +\tilde{\mathbf{w}}_\mathbf{C}^T \mathbf{Q}_\mathbf{C} \dot{\tilde{\mathbf{w}}}_\mathbf{C} \nonumber \\&+\,\tilde{\mathbf{w}}_\mathbf{g}^T \mathbf{Q}_\mathbf{g} \dot{\tilde{\mathbf{w}}}_\mathbf{g} ) \end{aligned}$$

(19)

then

$$\begin{aligned} \dot{V}= & {} -\mathbf{s}^{T}{} \mathbf{K}_\mathrm{d} \mathbf{s}+\frac{1}{2}\mathbf{s}^{T}[\dot{\mathbf{D}}_\mathbf{x} -2\mathbf{C}_\mathbf{x} ]\mathbf{s} \nonumber \\&+\,\hbox {Trace}\left[ \tilde{\mathbf{w}}_\mathbf{D}^T \left( \varvec{{\uppsi } }_\mathbf{D} \left( {\ddot{\mathbf{x}}_\mathbf{d} -\varvec{\Lambda }\dot{\mathbf{e}}} \right) \mathbf{s}^{T}+\mathbf{Q}_\mathbf{D} \dot{\hat{{\mathbf{w}}}}_\mathbf{D} \right) \right. \nonumber \\&+\,\tilde{\mathbf{w}}_\mathbf{C}^T \left( \varvec{{\uppsi } }_\mathbf{C} \left( {\dot{\mathbf{x}}_\mathbf{d} -\varvec{\Lambda } \mathbf{e}} \right) \mathbf{s}^{T}+\mathbf{Q}_\mathbf{C} \dot{\hat{{\mathbf{w}}}}_\mathbf{C}\right) \nonumber \\&\left. +\,\tilde{\mathbf{w}}_\mathbf{g}^T \left( \varvec{{\uppsi }}_\mathbf{g} \mathbf{s}^{T}+\mathbf{Q}_\mathbf{g} \dot{\hat{{\mathbf{w}}}}_\mathbf{g}\right) \right] +\mathbf{s}^{T}\varvec{{\upvarepsilon }}_1 +\mathbf{s}^{T}\varvec{{\uptau } }_\mathrm{robust}.\nonumber \\ \end{aligned}$$

(20)

Note that $\mathbf{s}^{T}[\dot{\mathbf{D}}_x (\mathbf{x})-2\mathbf{C}_x (\mathbf{x},\dot{\mathbf{x}})]\mathbf{s}=0$ for all $\mathbf{s}\in \mathfrak {R}^{n}$. We choose the FNNs’ update laws (15) and robust controller (14) such that

$$\begin{aligned}&\dot{V}\le -\mathbf{s}^{T}{} \mathbf{K}_\mathrm{d} \mathbf{s}+\mathbf{s}^{T}\varvec{{\upvarepsilon }}_1 -\delta \left| \mathbf{s} \right| \nonumber \\&\quad \le -\mathbf{s}^{T}{} \mathbf{K}_\mathrm{d} \mathbf{s}+\left| \mathbf{s} \right| \left| {\varvec{{\upvarepsilon }}_1 } \right| -\delta \left| \mathbf{s} \right| \nonumber \\&\quad \le -\mathbf{s}^{T}{} \mathbf{K}_\mathrm{d} \mathbf{s}-\left| \mathbf{s} \right| (\delta -\left| {\varvec{{\upvarepsilon }}_1 } \right| ) \nonumber \\&\quad \le 0. \end{aligned}$$

(21)

This concludes that the convergence of $\mathbf{s}$ is guaranteed if the proper value of $\delta$ is selected. This completes the proof. $\square$

Remark 1

To avoid the highly control gain of robust controller, we have the robust controller with adaptive boundary as follows

$$\begin{aligned} \varvec{{\uptau } }_\mathrm{robust}= & {} -\hat{{\delta }}[sgn(s_1 ),\ldots ,sgn(s_n )]^{T} \end{aligned}$$

(22)

$$\begin{aligned} \dot{\hat{{\delta }}}= & {} -\gamma _\delta \left| \mathbf{s} \right| . \end{aligned}$$

(23)

where $\varvec{{\uptau } }_\mathrm{robust}$ is the robust controller (or compensation controller) with adaptive boundary $\hat{{\delta }}$ and $\delta ^{*}$ denotes the existed optimal bound of robust controller. Thus, the corresponding Lyapunov function candidate of V is

$$\begin{aligned}&V(\mathbf{s},\tilde{\mathbf{w}}_\mathbf{D} ,\, \tilde{\mathbf{w}}_\mathbf{C} ,\, \tilde{\mathbf{w}}_\mathbf{g} ,\tilde{\delta })=\frac{1}{2}{} \mathbf{s}^{T}\mathbf{D}_x \mathbf{s}+\frac{1}{2\gamma _\delta }\tilde{\delta }^{2} \nonumber \\&\quad +\frac{1}{2}\hbox {Trace}\left( \tilde{\mathbf{w}}_\mathbf{D}^T \mathbf{Q}_\mathbf{D} \tilde{\mathbf{w}}_\mathbf{D} +\tilde{\mathbf{w}}_\mathbf{C}^T \mathbf{Q}_\mathbf{C} \tilde{\mathbf{w}}_\mathbf{C} +\tilde{\mathbf{w}}_\mathbf{g}^T \mathbf{Q}_\mathbf{g} \tilde{\mathbf{w}}_\mathbf{g}\right) \nonumber \\ \end{aligned}$$

(24)

where $\tilde{\delta }\equiv \hat{{\delta }}-\delta ^{*}$ denotes the estimated error of approximated error bound. According the above results, we can obtain

$$\begin{aligned}&\dot{V}\le -\mathbf{s}^{T}{} \mathbf{K}_\mathrm{d} \mathbf{s}+\left| \mathbf{s} \right| \left| {\varvec{{\upvarepsilon }}_1 } \right| +\frac{1}{\gamma _\delta }\tilde{\delta }\dot{\hat{{\delta }}}+\mathbf{s}^{T}\varvec{{\uptau }}_\mathrm{robust} \nonumber \\&\quad \le -\mathbf{s}^{T}{} \mathbf{K}_\mathrm{d} \mathbf{s}+\left| \mathbf{s} \right| \left| {\varvec{{\upvarepsilon }}_1 } \right| -\hat{{\delta }}\left| \mathbf{s} \right| +\frac{1}{\gamma _\delta }\tilde{\delta }\dot{\hat{{\delta }}} \nonumber \\&\quad \le -\mathbf{s}^{T}{} \mathbf{K}_\mathrm{d} \mathbf{s}+\left| \mathbf{s} \right| \left| {\varvec{{\upvarepsilon }}_1 } \right| -\hat{{\delta }}\left| \mathbf{s} \right| +(\hat{{\delta }}-\delta ^{*})\left| \mathbf{s} \right| \nonumber \\&\quad \le -\mathbf{s}^{T}{} \mathbf{K}_\mathrm{d} \mathbf{s}-\left| \mathbf{s} \right| (\delta ^{*}-\left| {\varvec{{\upvarepsilon }}_1 } \right| )\le 0. \end{aligned}$$

(25)

Therefore, substitute (23) into (25), we have $\dot{V}\le 0$ and asymptotic convergence of $\mathbf{s}$ can be concluded. This guarantees the stability of the closed-loop system.

The remaining work is to develop the adaptive force tracking control for contact space when the environment stiffness is unknown.

3.2 Adaptive force control scheme

As above description, our goal is to achieve $\mathbf{F}_\mathrm{ext}=\mathbf{F}_{d}$. In contact cases, the end-effector position of robot manipulator $\mathbf{x}$ satisfies the target impedance equation (10). The inertia and damping parameters only influence the transient response of the end-effector [14, 26]; thus, the steady-state contact force is

$$\begin{aligned} \mathbf{F}_\mathrm{ext} \cong \mathbf{K}_m (\mathbf{x}-\mathbf{x}_\mathrm{d} ). \end{aligned}$$

(26)

Considering for simplicity the environment modeled by a linear spring with stiffness $\mathbf{K}_\mathrm{e}$, the contact force is given by

$$\begin{aligned} \mathbf{F}_\mathrm{ext} \cong \mathbf{K}_\mathrm{e} (\mathbf{x}-\mathbf{x}_\mathrm{e} ) \end{aligned}$$

(27)

where $\mathbf{K}_\mathrm{e}$ is the stiffness coefficient of contact environment and $\mathbf{x}_\mathrm{e}$ is the position of environment. This leads to the following steady-state position and contact force [36]

$$\begin{aligned} \mathbf{x}_{ss} =(\mathbf{K}_m +\mathbf{K}_\mathrm{e} )^{-1}(\mathbf{K}_\mathrm{d} \mathbf{x}_\mathrm{d} +\mathbf{K}_\mathrm{e} \mathbf{x}_\mathrm{e}). \end{aligned}$$

(28)

As above description, the desired force $\mathbf{F}_{d}$ between robot and environment is obtained when $\mathbf{K}_\mathrm{e}$ is known

$$\begin{aligned} \mathbf{F}_\mathrm{d} \cong \mathbf{K}_\mathrm{e} (\mathbf{x}^{*}-\mathbf{x}_\mathrm{e} ) \end{aligned}$$

(29)

where $\mathbf{x}^*$ is ideal trajectory such that $\mathbf{F}_\mathrm{ext}=\mathbf{F}_{d}$ which is achieved by designing reference trajectory from (28)

$$\begin{aligned} \mathbf{x}_\mathrm{d}^*=\mathbf{K}_m^{-1} \left[ {(\mathbf{K}_m +\mathbf{K}_\mathrm{e} )\mathbf{x}^{*}-\mathbf{K}_\mathrm{e} \mathbf{x}_\mathrm{e} } \right] . \end{aligned}$$

(30)

However, the stiffness coefficient $\mathbf{K}_\mathrm{e}$ is usually unknown; therefore, $\mathbf{x}^{*}$ cannot be obtained directly. From (26) and (29), the tracking error of force can be represented as

$$\begin{aligned} \mathbf{F}_\mathrm{d} -\mathbf{F}_\mathrm{ext} \cong \mathbf{K}_\mathrm{e} (\mathbf{x}^{*}-\mathbf{x}). \end{aligned}$$

(31)

Since the stiffness should be estimated, thus we rewrite (29) as

$$\begin{aligned} \mathbf{F}_\mathrm{d} \cong \hat{{\mathbf{K}}}_\mathrm{e} (\mathbf{x}^{*}-\mathbf{x}_\mathrm{e} ) \end{aligned}$$

(32)

where $\hat{{\mathbf{K}}}_\mathrm{e}$ is the estimated stiffness coefficient. In this paper, the update law of $\hat{{\mathbf{K}}}_\mathrm{e}$ is derived by the gradient method and the convergence is guaranteed by Lyapunov approach. To obtain the adaptation of $\hat{{\mathbf{K}}}_\mathrm{e}$, we first define the force error and the corresponding objective function to be minimized as

$$\begin{aligned} \mathbf{e}_\mathrm{f} =\mathbf{F}_\mathrm{d} -\mathbf{F}_\mathrm{ext} \end{aligned}$$

(33)

and the Lyapunov candidate function is defined

$$\begin{aligned} V_\mathrm{f} =\frac{1}{2}{} \mathbf{e}_\mathrm{f}^T \mathbf{e}_\mathrm{f} . \end{aligned}$$

(34)

For simplicity, we consider that the force is applied to only one direction, therefore, $\mathbf{e}_\mathrm{f} ,\mathbf{F}_\mathrm{d}$, and $\mathbf{F}_\mathrm{ext}$ are scalar, i.e., $e_\mathrm{f} =f_\mathrm{d} -f_\mathrm{ext}$ where $f_{d}$ and $f_\mathrm{ext}$ denote the desired force and contact force for one direction. Then, let $\hat{{K}}_\mathrm{e}$ be an element of $\hat{{\mathbf{K}}}_\mathrm{e}$, thus, $V_F =\frac{1}{2}e_\mathrm{f}^2$ and the corresponding gradient of $V_F$ is

(35)

Thus, the update of $\hat{{K}}_\mathrm{e}$ is chosen as follows by the gradient method

$$\begin{aligned} \Delta \hat{{K}}_\mathrm{e} =-\eta _{K_\mathrm{e} } \frac{\partial V_F }{\partial \hat{{K}}_\mathrm{e} }=-\eta _{K_\mathrm{e} } \cdot e_\mathrm{f} \cdot \frac{\partial e_\mathrm{f} }{\partial \hat{{K}}_\mathrm{e} } \end{aligned}$$

(36)

where $\eta _{K_\mathrm{e}}$ is the learning rate. For the training process, the learning rate plays an important role for this case. A small value of $\eta _{K_\mathrm{e}}$ leads a slower convergence and a large value may have unstable result. Hence, the selection of $\eta _{K_\mathrm{e} }$ is important. Herein, the Lyapunov approach is adopted to guarantee the convergence of $\hat{{K}}_\mathrm{e}$. We then have the convergence theorem.

Theorem 2

Consider the force tracking control problem as above description and let $\eta _{K_\mathrm{e} }$ be the learning rate of the estimation of stiffness. The force tracking can be achieved if the learning rate $\eta _{K_\mathrm{e} }$is selected satisfies

$$\begin{aligned} 0<\frac{\eta _{K_\mathrm{e}}}{2}\left( {\frac{\partial e_\mathrm{f} }{\partial \hat{{K}}_\mathrm{e} }} \right) ^{2}<1. \end{aligned}$$

(37)

Proof

Rewrite (34) as

$$\begin{aligned} V_F (k)=\frac{1}{2}e_\mathrm{f}^2 (k)=\frac{1}{2}(f_\mathrm{d} (k)-f_\mathrm{ext} (k))^{2} \end{aligned}$$

(38)

where $e_\mathrm{f} (k)=f_\mathrm{d} (k)-f_\mathrm{ext} (k)$ and k is time-instant for parameter update. Let $\Delta e_\mathrm{f} (k)=e_\mathrm{f} (k+1)-e_\mathrm{f} (k)$ and then we have

$$\begin{aligned} \Delta V_F (k)= & {} V_F (k+1)-V_F (k) \nonumber \\= & {} \frac{1}{2}[e_\mathrm{f} (k+1)+e_\mathrm{f} (k)][e_\mathrm{f} (k+1)-e_\mathrm{f} (k)] \nonumber \\= & {} \frac{1}{2}[2e_\mathrm{f} (k)+\Delta e_\mathrm{f} (k)]\cdot \Delta e_\mathrm{f} (k) \nonumber \\= & {} \frac{\Delta e_\mathrm{f}^2 (k)}{2}+e_\mathrm{f} (k)\cdot \Delta e_\mathrm{f} (k). \end{aligned}$$

(39)

By the gradient result, $\Delta e_\mathrm{f} (k)\approx \frac{\partial e_\mathrm{f} }{\partial \hat{{K}}_\mathrm{e} }\Delta \hat{{K}}_\mathrm{e}$ and $\Delta \hat{{K}}_\mathrm{e} =-\eta _{K_\mathrm{e} } (\frac{\partial V_F }{\partial \hat{{K}}_\mathrm{e} })$, we obtain

$$\begin{aligned} \Delta e_\mathrm{f} (k)=\frac{\partial e_\mathrm{f} }{\partial \hat{{K}}_\mathrm{e} }\left( {-\eta _{K_\mathrm{e} } \frac{\partial V_F }{\partial \hat{{K}}_\mathrm{e} }} \right) =-\eta _{K_\mathrm{e} } e_\mathrm{f} \left( {\frac{\partial e_\mathrm{f} }{\partial \hat{{K}}_\mathrm{e} }} \right) ^{2}\nonumber \\ \end{aligned}$$

(40)

and

$$\begin{aligned} \Delta V(k)= & {} \frac{\eta _{K_\mathrm{e} }^2 e_\mathrm{f}^2 }{2}\left( {\frac{\partial e_\mathrm{f} }{\partial \hat{{K}}_\mathrm{e} }} \right) ^{4}-\eta _{K_\mathrm{e} } e_\mathrm{f}^2 \left( {\frac{\partial e_\mathrm{f} }{\partial \hat{{K}}_\mathrm{e} }} \right) ^{2} \nonumber \\= & {} -\eta _{K_\mathrm{e} } e_\mathrm{f}^2 \left( {\frac{\partial e_\mathrm{f} }{\partial \hat{{K}}_\mathrm{e} }} \right) ^{2} \nonumber \\&\cdot \left[ {1-\frac{1}{2}\eta _{K_\mathrm{e} } \left( {\frac{\partial e_\mathrm{f} }{\partial \hat{{K}}_\mathrm{e} }} \right) ^{2}} \right] . \end{aligned}$$

(41)

As above, we can obtain the stability condition for selection of learning rate $\eta _{K_\mathrm{e} }$, condition (37), this implies $\Delta V(k)<0, \quad \forall k>0$, this means that the force error will approach to zero. In addition, the convergence of stiffness coefficient can be guaranteed, i.e., actual value of $K_\mathrm{e}$ can be obtained. This completes the proof. $\square$

After estimating the coefficient $\mathbf{K}_\mathrm{e}$, we remain to find the desired trajectory $\mathbf{x}^*$ such that $\mathbf{F}_\mathrm{ext}=\mathbf{F}_{d}$. In addition, to accomplish force control, we should design the suitable $\mathbf{x}$ for contact space. From (28) and estimation of $\mathbf{K}_\mathrm{e}$, we have the variation of desired position

$$\begin{aligned} \Delta \mathbf{x}=\hat{{\mathbf{K}}}_\mathrm{e}^{-1} \Delta \mathbf{F} \end{aligned}$$

(42)

where $\Delta \mathbf{x}=\mathbf{x}_{ss} -\mathbf{x}$ and $\Delta \mathbf{F}=\mathbf{F}_\mathrm{d} -\mathbf{F}_\mathrm{ext}$, then we can design the ideal trajectory to achieve force control as follows iteratively

$$\begin{aligned} \mathbf{x}^{*}(k+1)=\mathbf{x}(k)+\Delta \mathbf{x}(k). \end{aligned}$$

(43)

According equation (30), in considering the steady state, we obtain the new desired trajectory for the contact case

(44)

As the results of Theorem 1, the end-effector of robot will follows the desired trajectory, thus, the above discussion guarantees the convergence of force tracking error even the stiffness gain $K_\mathrm{e}$ is unknown, i.e., $\mathbf{F}_\mathrm{ext}$ approaches to $\mathbf{F}_\mathrm{d}$.

4 Simulation results

Herein, the proposed control approach is applied on the impedance force tracking control of a robot manipulator system with two rigid links and two rigid revolute joints. For $i=1, 2,\, m_{i}$, $l_{i},\, l_{ci}$, and $I_{i}$ are mass, length, gravity center length and inertia of link i, respectively. The actual values of quantities are $m_{1}=2\,\hbox {kg},\, m_{2}=1\,\hbox {kg},\, l_{1}=l_{2}=0.75\,\hbox {m},\, l_{c1}=l_{c2}=0.375\,\hbox {m},\, I_{1}=0.09375\,\hbox {kg}\,\hbox {m}^{2},\, I_{2}=0.046975\,\hbox { kg}\,\hbox {m}^{2}$ [40]. The inertia matrix $\mathbf{D}(\mathbf{q})$ is defined as

$$\begin{aligned} \mathbf{D}(\mathbf{q})=\left[ {{\begin{array}{lll} {d_{11} }&{} {d_{12} } \\ {d_{21} }&{} {d_{22} } \\ \end{array} }} \right] \end{aligned}$$

(45)

where $d_{11}=m_1 l_{c1}^2 +m_2 l_1^2 +I_1 +m_2 l_{c2}^2 +I_2 +2m_2 l_1 l_{c2} \cos q_2 , \quad d_{12} =d_{21} =m_2 l_{c2}^2 +I_2 +m_2 l_1 l_{c2} \cos q_2$, and $d_{22} =m_2 l_{c2}^2 +I_2$. $\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})$ and $\mathbf{g(q)}$ are defined as

$$\begin{aligned} \mathbf{C}(\mathbf{q},\dot{\mathbf{q}})= & {} \left[ {{\begin{array}{llc} &{}-m_2 l_1 l_{c2} \dot{q}_2\sin q_2 &{} {-m_2 l_1 l_{c2} (\dot{q}_1 +\dot{q}_2 )\sin q_2 } \\ &{}{m_2 l_1 l_{c2} \dot{q}_1 \sin q_2}&{} 0 \end{array}}} \right] ,\nonumber \\ \end{aligned}$$

(46a)

$$\begin{aligned} \mathbf{g(q)}= & {} \left[ {{\begin{array}{ll} &{}\left( {m_1 l_{c2} +m_2 l_1 } \right) g\cos q_1 +m_2 l_{c2} g\cos (q_1 +q_2 ) \\ &{}{m_2 l_{c2} g\cos (q_1 +q_2 )} \\ \end{array}}} \right] .\nonumber \\ \end{aligned}$$

(46b)

The Jacobian matrix is

$$\begin{aligned} \mathbf{J(q)}{=}\left[ {{\begin{array}{cc} {{-}m_2 l_1 l_{c2} \dot{q}_2 \sin q_2 }&{} \quad {{-}m_2 l_1 l_{c2} (\dot{q}_1 {+}\dot{q}_2 )\sin q_2 } \\ {m_2 l_1 l_{c2} \dot{q}_1 \sin q_2 }&{} 0 \\ \end{array} }} \right] .\nonumber \\ \end{aligned}$$

(47)

The initial condition for the end-effector and reference state are $\mathbf{x}(0)=[0.75\,0.75\,0\,0]^{T}$ and $\mathbf{x}_m (0)=[0.8\,0.8\,0\,0]^{T}$. The desired trajectory $\mathbf{x}_{d}$ is a 0.2 m-radius circle centered at (0.8, 1.0 m) in 10 s as follows

$$\begin{aligned} x_\mathrm{d} (t)= & {} 0.8+0.2\sin \frac{2\pi }{10}t \nonumber \\ y_\mathrm{d} (t)= & {} -0.2\cos \frac{2\pi }{10}t. \end{aligned}$$

(48)

As above discussion, system parameter matrices $\mathbf{D},\, \mathbf{C}$, and $\mathbf{g}$ are assumed to be not exactly known and are approximated by the FNNs. Initial weighting vectors of FNN are chosen as to be zero to avoid initial larger control effort and the fuzzy rule number are chosen as seven for $\hat{\mathbf{D}}_\mathbf{x},\,\hat{\mathbf{C}}_\mathbf{x} ,$ and $\hat{\mathbf{g}}_\mathbf{x}$. The update laws gain matrices in (15) are chosen with

$$\begin{aligned} \mathbf{Q}_\mathbf{D}^{-\mathbf{1}}= & {} \mathbf{Q}_\mathbf{C}^{-\mathbf{1}} =\hbox {diag}(q_1 ,\ldots ,q_7 ), \nonumber \\ q_i= & {} 1, i=1,\,\ldots ,\,28 \end{aligned}$$

(49a)

$$\begin{aligned} \mathbf{Q}_\mathbf{g}^{-\mathbf{1}}= & {} \hbox {diag}(q_1 ,\ldots ,q_7 ), q_i =100, \nonumber \\ i= & {} 1,\,\ldots ,\,28. \end{aligned}$$

(49b)

According to the approximation theorem of FNNS, we assume $\varvec{{\upvarepsilon }}_1$ cannot be eliminated and there exists a positive constant $\delta$ such that $\left\| {\varvec{{\upvarepsilon }}_1} \right\| \le \delta$ for all $t\ge 0$. Herein, $\delta$ is selected to be one. The constraint surface is a flat wall with a triangle crack, and the environment can be modeled as linear spring $f_\mathrm{ext} =k_w (x-x_w )$. $f_\mathrm{ext}$ is the force acting on the surface, $k_w =5000~\hbox {N}/\hbox {m}$ is the environment stiffness, x is the coordinate of the end-effector in the x-direction, and $x_w =0.95m$ is the position of the surface. Therefore, the external force vector in equation (2) becomes $\mathbf{F}_\mathrm{ext} =[f_\mathrm{ext} \,0]^{T}$. The controller gains are selected as

$$\begin{aligned} K_\mathrm{d} =\left[ {{\begin{array}{ll} {100}&{} 0 \\ 0&{} {100} \\ \end{array} }} \right] , \quad \varvec{\Lambda }=\left[ {{\begin{array}{ll} {10}&{} 0 \\ 0&{} {10} \\ \end{array}}} \right] . \end{aligned}$$

(50)

Herein, the gain matrices in the target impedance are described in [5]. Several illustrated examples are introduced to demonstrate the performance and effectiveness of the proposed adaptive control approach.

Fig. 4

Position tracking performance result at $t =$ 0–5 s

Fig. 5

Force tracking performance with different learning rates

4.1 Adaptive tracking and force control

In this example, the desired force is selected as 3 Nt. Figure 4 shows the trajectory tracking performance in the Cartesian space (solid: robot position; dashed: environment trajectory; dash-dotted: estimated environment trajectory). We can find that the end point of robot contact the constraint surface is a flat wall with a triangle crack and track the reference trajectory in free space. For the force control, herein, we test the different learning rates $\eta =$10000, 30000 and 60000 to have the comparison results in Fig. 5. Obviously, the larger value of $\eta$ performs quickly. Figure 6 shows the estimated stiffness $\hat{{\mathbf{K}}}_\mathrm{e}$ and environment position. One can observe that the variations of the estimated $\hat{{\mathbf{K}}}_\mathrm{e}$ and $x^{*}$ are changed at 1.35 s, 2.1 s, 2.51 s, 2.9 s due to the end-effector touches the wall and triangle crack. From the observation of Fig. 6, we can find that the estimated stiffness coefficient is convergent and the estimated environment position is contained to achieve the adaptive force control. Figure 7 shows the control effort at $t =$ 1–10 s. We can observe that the impulse control torque is obtained due to the change of environment. In addition, the fast convergence of tracking error and control efforts also shows the performance and effectiveness of our approach.

Fig. 6

Stiffness and estimated environment position

Fig. 7

Control effort of example 1

4.2 Variation of tracking force

From the observation of Fig. 5, we can find that the estimated stiffness coefficient is convergent and the estimated environment position is obtained to achieve the adaptive force control. Herein, simulation results of variant tracking force example are introduced. Figure 8a introduces the force variation (dashed: desired force; solid: actual force). It can be observed that the contact force follows the desired force even the environment surface is changed. Figure 8b shows the estimated stiffness $\hat{{K}}_\mathrm{e}$ and environment position. One can find that the adaptive force tracking control is achieved by our proposed approach and the estimated $x^{*}$ is also obtained such that $f_\mathrm{ext}$ approaches to $f_{d}$. From this illustrated examples, we can observe that the proposed adaptive approach performs well (the estimated $\hat{{K}}_\mathrm{e}$ and $x^{*}$ can vary at the same time due to the change of environment and desired tracking force).

Fig. 8

Simulation results of variant tracking force, a force tracking performance with different force, b estimated stiffness and estimated environment position

Fig. 9

The controller performance with uncertainties as mass $=$ 5 kg of link 2 (dashed desired trajectory; dotted our proposed approach, and dash-dotted ideal controller)

4.3 Robustness illustration

Herein, we introduce the robustness of the proposed adaptive approach and the necessity of the estimation of robot model ($\mathbf{D}_{\mathbf{x}}$, $\mathbf{C}_{\mathbf{x}}$, $\mathbf{g}_{\mathbf{x}}$) for uncertain systems. In order to illustrate the effectiveness of our approach for system with uncertainties, we assumed the nominal and actual masses of link two are 1 and 5 kg, respectively. The comparison results between our approach and the ideal impedance controller are presented, where the ideal controller is derived by nominal model ($\mathbf{D}_{\mathbf{x}}$, $\mathbf{C}_{\mathbf{x}}$, $\mathbf{g}_{\mathbf{x}}$ are given), i.e., $\hat{\mathbf{D}}_\mathbf{x} ,\, \hat{\mathbf{C}}_\mathbf{x} ,\, \hat{\mathbf{g}}_\mathbf{x}$ in equation (15) are replaced by $\mathbf{D}_{\mathbf{x}}$, $\mathbf{C}_{\mathbf{x}}$, $\mathbf{g}_{\mathbf{x}}$. Figure 9 shows the tracking trajectories of (x, y) space, dashed: desired trajectory; dotted: our proposed approach, and dash-dotted: ideal controller. From Fig. 9, we can observe that the proposed approach perform well with smaller tracking error than the ideal controller. This illustrates the effectiveness of the proposed approach.

4.4 Discussion of selecting the learning rate $\eta _{K_\mathrm{e} }$

As above description, choosing the suitable learning rate is important for force tracking control. A small value of $\eta _{K_\mathrm{e}}$ results slower convergence and a large one leads higher amplitude of transient response or unstable result. Herein, the discussion of learning rate selection is introduced, in which these selections satisfy the convergent condition (37). Figure 10a, b show the comparison results of force tracking control, the estimated stiffness and desired position, respectively (solid-line: large $\eta _{K_\mathrm{e} }$; dotted-line: suggested $\eta _{K_\mathrm{e}}$; dash-dotted: small $\eta _{K_\mathrm{e} } )$. The adopted large $\eta _{K_\mathrm{e}}$, suggested $\eta _{K_\mathrm{e}}$, and small $\eta _{K_\mathrm{e}}$ are selected such that $\lambda =0.8;\lambda =0.45$; and $\lambda =0.001$, respectively, where $\lambda \equiv \frac{\eta }{2}\left( {\frac{\partial e_\mathrm{f} }{\partial \hat{{K}}_\mathrm{e} }} \right) ^{2}$. That is, the suggested learning rate is $\eta _{K_\mathrm{e} } =\frac{9}{10\left( {{\partial e_\mathrm{f} }/{\partial \hat{{K}}_\mathrm{e} }} \right) ^{2}}$ as our experience. From Fig. 10, large $\eta _{K_\mathrm{e} }$ results faster response in force tracking control, but higher transient amplitude of force and $\hat{{K}}_\mathrm{e}$ are obtained. In addition, this results the larger tracking error when the environment is changed (shown in Fig. 10b). On the other hand, small $\eta _{K_\mathrm{e} }$ has slow convergence. It can be found that the suggested learning rate $\eta _{K_\mathrm{e} } =\frac{9}{10\left( {{\partial e_\mathrm{f} }/{\partial \hat{{K}}_\mathrm{e} }} \right) ^{2}}$ preserves the stability and good performance in force tracking and estimation of stiffness and desired position.

Fig. 10

Discussion of selecting learning rate, a force tracking performance, b stiffness, estimated environment position

5 Conclusion

In this paper, we have proposed the adaptive tracking force control scheme using FNNs for an n-link robot manipulator under unknown task environment. The unknown system parameter matrices are estimated by the FNNs to develop the tracking control scheme, and the adaptive force control laws are established by gradient method. Based on the Lyapunov stability analysis, we guarantee the stability of the closed-loop system and the convergence of parameters. In addition, the update laws of FNNs and estimation coefficient are designed. Finally, simulation results of a two-link robot manipulator with environment constraint are introduced to illustrate the performance and effectiveness of our approach.