Abstract
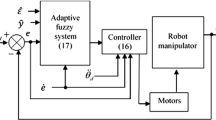
This paper presents a novel robust decentralized control of electrically driven robot manipulators by adaptive fuzzy estimation and compensation of uncertainty. The proposed control employs voltage control strategy, which is simpler and more efficient than the conventional strategy, the so-called torque control strategy, due to being free from manipulator dynamics. It is verified that the proposed adaptive fuzzy system can model the uncertainty as a nonlinear function of the joint position error and its time derivative. The adaptive fuzzy system has an advantage that does not employ all system states to estimate the uncertainty. The stability analysis, performance evaluation, and simulation results are presented to verify the effectiveness of the method. A comparison between the proposed Nonlinear Adaptive Fuzzy Control (NAFC) and a Robust Nonlinear Control (RNC) is presented. Both control approaches are robust with a very good tracking performance. The NAFC is superior to the RNC in the face of smooth uncertainty. In contrast, the RNC is superior to the NAFC in the face of sudden changes in uncertainty. The case study is an articulated manipulator driven by permanent magnet dc motors.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
A great attention has been focused on the robust control of robot manipulators to overcome uncertainty in the joint-space [1, 2] and in the task-space [3, 4]. The uncertainty may include unmodeled dynamics, parametric uncertainty, and external disturbances. The practical implementation of model-based control approaches requires consideration of various sources of uncertainties such as modeling errors, unknown loads, and computation errors. Uncertainty is a challenge for using feedback linearization as one of the popular techniques used in the control of robot manipulators for canceling nonlinearities and decoupling purposes [5]. A perfect model is required to apply the feedback linearization while a perfect model is not available. Instead, a nominal model can be used while it differs from the actual system. As a result, the model inaccuracy degrades the control system. Therefore, uncertainty should be compensated by the control laws to enhance performance of the control system. In fact, a considerable attention has been devoted to the robust control due to overcoming uncertainties [6, 7]. Robust control is an effective approach in the presence of a wide range of uncertainties. A proper uncertainty bound parameter has been proposed to simplify and improve robust control of robot manipulators [8]. Time delay control [9] and uncertainty estimation [10] can be used to control the robot manipulator by estimating current effects of unknown dynamics and disturbances. In this paper, we present a novel robust control of electrically driven robot manipulators using an adaptive fuzzy system to estimate and compensate uncertainties.
The majority of presented robust control approaches are based on the torque control strategy. The practical implementation of the torque control strategy is involved in some problems. The most important problem is that the torque command cannot be applied to the robot joints without the use of actuators whereas the dynamics of actuators are excluded. Another issue is the chattering problem caused by the switching control laws. We should also consider the additional sensing requirements, actuator saturation, and long processing time to implement the torque control strategy. To solve the aforementioned problems, voltage control strategy has been devoted to the electrically driven robot manipulators [11]. In this strategy, the electric motors of the robot are controlled while the robot manipulator behaves as a load on the motors. Thus, a nominal model of the motor is required to design the controller with an advantage that the used model is simpler than the robot model. As a result, robust voltage control is much faster and more efficient than the robust torque control [12]. Voltage control strategy has been successfully used to the robust control of flexible-joint electrically driven robots [13, 14]. To benefit from these advantages, we use voltage control strategy in this paper.
As an alternative to the conventional robust control, fuzzy control is a robust model-free control approach that can be simply designed [15]. To form fuzzy rules, an exact knowledge of model is not required. Fuzzy controller is an intelligent controller using linguistic fuzzy rules to include information from experts. Consequently, fuzzy control of robot manipulators has attracted a great deal of researches to overcome uncertainty, nonlinearity, and coupling [16–22]. The direct method of Lyapunov has been successfully used to design Adaptive Fuzzy Control (AFC) in the form of either direct or indirect adaptive control [23–26]. In indirect adaptive control, the fuzzy system estimates the robot’s model to use in the control law. In direct adaptive control, the parameters of fuzzy controller are updated to achieve a desired tracking performance.
In this paper, we design an adaptive fuzzy system to estimate and compensate the uncertainty in the nonlinear control system. The proposed fuzzy system enhances the feedback linearization performance. The proposed controller has a nonlinear structure equipped by a fuzzy uncertainty compensator and thus is called as Nonlinear Adaptive Fuzzy Control (NAFC) that differs from AFC. The proposed NAFC uses a nominal model of system, whereas the AFC requires the expert’s knowledge about the system model or about the system control. The usage of fuzzy system in the proposed controller is also completely different with the AFC for example in [23–26]. We employ a fuzzy system as an uncertainty estimator not as a controller. Unlike the AFC, the proposed NAFC has an advantage that does not require the all system states.
This paper is organized as follows. Section 2 explains modeling of the robotic system including the robot manipulator and the permanent magnet dc motors. Section 3 develops the proposed control law. Section 4 describes the adaptive fuzzy method to estimate and compensate the uncertainties. Section 5 presents the stability analysis. Section 6 describes performance evaluation of the control system. Section 7 illustrates the simulation results. Finally, Sect. 8 concludes the paper.
2 Modeling
Consider an electrical robot driven by geared permanent magnet dc motors [8]. The dynamics of robot manipulator can be expressed as
where q∈R n is the vector of joint positions, D(q) the n×n matrix of manipulator inertia, \(\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}} \in R^{n}\) the vector of centrifugal and Coriolis torques, g(q)∈R n the vector of gravitational torques, \(\boldsymbol{\tau}_{\mathbf{f}}(\dot{\mathbf{q}}) \in R^{n}\) the vector of frictional torques, and τ∈R n the vector of joint torques. The electric motors provide the joint torques τ by
where τ m ∈R n is the torque vector of motors, θ m ∈R n the position vector of motors, and J, B, and r the n×n diagonal matrices for inertia, damping, and reduction gear of motors, respectively. The vector of joint velocities \(\dot{\mathbf{q}}\) is obtained by the vector of motor velocities \(\dot{\boldsymbol{\theta}}_{\mathbf{m}}\) through the gears as
Note that vectors and matrices are represented in the bold form for clarity.
In order to obtain the motor voltages as the inputs of system, consider the electrical equation of geared permanent magnet dc motors in the matrix form as
where v∈R n is the vector of motor voltages, and I a ∈R n the vector of motor currents. R, L, and K b represent the n×n diagonal matrices for the armature resistance, inductance, and back-emf constant of the motors, respectively. The motor torque vector τ m as the input for the dynamic equation (2) is produced by the motor current vector
where K m is the diagonal matrix of the torque constants. A model for the electrically driven robot in the state space is introduced by the use of (1)–(5) as
where

The state space equation (6) shows a highly coupled nonlinear large multivariable system. Complexity of the model has opened a serious challenge in the literature of robot modeling and control. Voltages of motors denoted by v have been considered as the inputs of the robotic system in (6).
3 Proposed control law
The voltage equation of the permanent magnet dc motor is expressed by
where R, L, and k b denote the armature resistance, inductance, and back emf constant, respectively. v is the motor voltage, I a motor current, and θ m the rotor position. ϕ represents the external disturbance. The relation between the motor position θ m and the joint position q is given by
where r stands for the motor reduction gear. Substituting (9) into (8) yields the dynamics
The robot manipulator is expressed by the multi-input/multi-output system (1), whereas the electric motor is expressed by the single-input/single-output system (10). The proposed control approach is based on the voltage control strategy [11] using the model of motor (10) which is much simpler than the model of robot manipulator (1). Therefore, the control problem is taken from the control of the multi-input/multi-output system (1) used in the torque control strategy to the control of the n individual systems of the form single-input/single-output system (10) used in voltage control strategy.
In order to propose a control law, we choose a nominal model of the form
The nominal model is known and proposed based on the knowledge about the system such that the nominal parameters \(\hat{R}\), \(\hat{k}_{b}\), and \(\hat{r}\) are the estimations of R,k b , and r, respectively. The dynamics of the nominal model is simpler than the actual model. Compared with the actual model (10), the terms \(L\dot{I}_{a}\) and ϕ are not used in the nominal model (11). It is easy to write from (10)
Then, one can calculate F from (10) and (12) as
In fact, F is referred to as the uncertainty that includes external disturbance ϕ, unmodeled dynamics \(L\dot{I}_{a}\), and parametric uncertainty \((R - \hat{R})I_{a} + (k_{b}r^{ - 1} - \hat{k}_{b}\hat{r}^{- 1})\dot{q}\).
Using (12), a control law is proposed as
where sat(⋅) denotes the saturation function defined by
where u max is the maximum permitted voltage of motor and u is described as
where \(\hat{F}\) is the estimate of F using an adaptive fuzzy system presented in the next section, q d is the desired joint position, and k p is a control design parameter. We cannot use F in the control law since F is not known. Instead, \(\hat{F}\) is employed.
4 Adaptive fuzzy estimation of the uncertainty
4.1 Estimation of uncertainty if |u|<u max
We design an adaptive fuzzy system to calculate \(\hat{F}\) for the control law (14)–(16). Out of the area |u|<u max, we propose simple rules to calculate \(\hat{F}\) in the end of this section.
Control law (14)–(16) yields the closed-loop system
It is easy to show from (15), (16), and (17) for |u|<u max that

In other words, (18) can be written as
where e is the tracking error expressed by
Suppose that \(\hat{F}\) is the output of an adaptive fuzzy system in the normalized form with the inputs of x 1 and x 2. If three fuzzy sets are given to each fuzzy input, the whole control space will be covered by nine fuzzy rules. The linguistic fuzzy rules are proposed in the Mamdani type of the form
where FR l denotes the lth fuzzy rule for l=1,…,9. In the lth rule, A l , B l , and C l are fuzzy membership functions belonging to the fuzzy variables x 1, x 2, and \(\hat{F}\), respectively. Three Gaussian membership functions, \(\mu_{A_{l}}(x_{1})\), named as Positive (P), Zero (Z), and Negative (N) are defined for input x 1 in the operating range of manipulator as shown in Fig. 1. Three Gaussian membership functions, \(\mu_{B_{l}}(x_{2})\), named as P, Z, and N in the same shape as Fig. 1, are used for input x 2. Nine symmetric Gaussian membership functions, \(\mu_{C_{l}}(\hat{F})\), named as Very Positive High (VPH), Positive High (PH), Positive Medium (PM), Positive Small (PS), Zero (Z), Negative Small (NS), Negative Medium (NM), Negative High (NH), and Very Negative High (VNH) are defined for \(\hat{F}\) in the form of \(\mu_{l}(\hat{F}) = \exp( - ( (\hat{F} -\hat{p}_{l})/\sigma)^{2} )\) for l=1,…,9 in the operating range of output. The symmetric Gaussian function depends on two parameters \(\hat{p}_{l}\) and σ. In this work, \(\hat{p}_{l}\) is adjusted by an adaptive law, whereas σ is an arbitrary constant value.
The fuzzy rules should be defined such that the tracking control system goes to the equilibrium point. We may use an expert’s knowledge, the trial and error method, or an optimization algorithm such as PSO to design the fuzzy controller. The obtained fuzzy rules are given in Table 1. In this paper, the centers of Gaussian membership functions for \(\hat{F}\) are adapted to optimize performance of the control system.
If we use the product inference engine, singleton fuzzifier, center average defuzzifier, and Gaussian membership functions, the fuzzy system [15] is of the form
where \(\mu_{A_{l}}(x_{1}) \in [0,1]\) and \(\mu_{B_{l}}(x_{2}) \in [0,1]\) are the membership functions for the fuzzy sets A l and B l , respectively, and \(\hat{p}_{l}\) is the center of fuzzy set C l . An important contribution of fuzzy systems theory is to provide a systematic procedure for transforming a set of linguistic rules into a nonlinear mapping as stated by (22). One can easily manipulate this transformation by regulating \(\hat{p}_{l}\) in (22).
One can easily obtain from (22) that
where ζ=[ζ1 ⋯ ζ9]T, ζ l is a positive value expressed as
and
Using the input scaling factors k 1 and k 2 to scale x 1 and x 2, we have


Substituting (26) and (27) into (22) describes \(\hat{F}\) as a function of e and \(\dot{e}\) of the form
Substituting \(\hat{F}(e,\dot{e})\) into the closed-loop system (19) yields
Thus, F is a function of e and \(\dot{e}\) as described by (29). The fuzzy system \(\hat{F}(e,\dot{e})\) in (28) can approximate F in (29) based on the universal approximation theorem [15], which states that the fuzzy systems with product inference engine, singleton fuzzifier, center average defuzzifier, and Gaussian membership functions are universal approximators. Thus,
where ρ is a positive scalar. In the adaptive fuzzy system, we regulate \(\hat{p}\) in (23) so that \(\hat{F}(e,\dot{e}) \to F(e,\dot{e})\). Suppose that \(F(e,\dot{e})\) can be modeled by an adaptive fuzzy system as
where ε is the modeling error, and p T ζ is the goal of adaptive fuzzy estimation such that \(\hat{p}^{T}\boldsymbol{\zeta} \to p^{T}\boldsymbol{\zeta}\). Note that the vector p is constant, and \(\hat{p}\) moves toward p. Thus, based on the universal approximation theorem,
where ε is bounded as |ε|≤β and β is the upper bound of modeling error. We have \(\hat{F}(e,\dot{e}) = \hat{p}^{T}\boldsymbol{\zeta}\) , and p T ζ is the best value for \(\hat{p}^{T}\boldsymbol{\zeta}\) such that
It follows that β≤ρ.
Substituting (23) and (31) into (19) yields
Consider the closed-loop system expressed by (19). The estimation error \(F - \hat{F}\) is proportional with \(\dot{e} + k_{p}e\). Also, the estimation error depends on the difference in parameters given by \(p^{T}- \hat{p}^{T}\) in the closed-loop system (34). Regulating \(\hat{p}^{T}\) reduces \(\dot{e} + k_{p}e\). Therefore, we use (34) to suggest a positive definite function V of the form
where γ is a positive scalar. We differentiate V with respect to time to get
From (34) we have
Substituting (37) into (36) yields

It is easy to show that

\(\dot{V}\) in (39) includes two terms, where the first and second terms are \(( p^{T} - \hat{p}^{T} )( ( \dot{e} + k_{p}e )k_{p}\hat{k}_{b}^{ -1}\hat{r}\zeta - \frac{1}{\gamma} \dot{\hat{p}} )\) and \(( \dot{e} +k_{p}e )( \ddot{e} + k_{p}\hat{k}_{b}^{ - 1}\hat{r}\varepsilon -k_{p}^{2}e )\), respectively. We can control \(\dot{V}\) by regulating \(\hat{p}\) which is in the first term of \(\dot{V}\). This leads to propose an adaptive law which should be evaluated afterward as follows:
Therefore, the adaptation law is given by
in which α is given by
Thus, the parameters of the fuzzy system are calculated by
where \(\hat{p}(0)\) is the initial value.
In order to evaluate the adaptive law (43), we substitute (40) into (39) to obtain
We should consider (44) to evaluate performance of the uncertainty estimation method. Taking the derivative of \(\dot{e}\) in (37) with respect to time gives
where ϑ is
Substituting (45) into (44), to satisfy \(\dot{V} < 0\) in (44), it is required that
According to the Cauchy–Schwartz inequality, we can write
Suppose that
where Ψ is a positive scalar. Thus, to satisfy inequality (47), it is sufficient that
Then (50) results in
As a result of reasoning above, as long as \(\hat{k}_{b}^{ -1}\hat{r}\varPsi /k_{p} < | \dot{e} + k_{p}e |\), we have \(\dot{V} < 0\). Then, \(| \dot{e} + k_{p}e |\) reduces until
Note that \(| \dot{e} + k_{p}e |\) cannot reduce further to be \(\hat{k}_{b}^{ - 1}\hat{r}\varPsi /k_{p} > | \dot{e} + k_{p}e |\). If \(\hat{k}_{b}^{ - 1}\hat{r}\varPsi /k_{p} > | \dot{e} + k_{p}e |\), we have \(\dot{V} > 0\), which contradicts to the reduction of \(| \dot{e} + k_{p}e|\). Considering (52) verifies that the minimum value of error will be small if we use a large gain value k p . The error does not approach zero but is bounded to a small limit as described in (52). The tracking error is affected by the upper bound of uncertainty Ψ as stated by (52), as well.
The estimation error in the area of |u|<u max can be calculated from (19) as
From (52) and (53) we can write
The size of estimation error of the proposed adaptive fuzzy system, ρ, can be given by considering (30) and (54) as
4.2 Estimation of uncertainty out of the area |u|<u max
In order to estimate F out of the area |u|<u max, we use another rule. From (15) and (17) it follows that
Thus, we estimate F:
Similarly, we estimate F in the area of u≤−u max by
The estimation error in the areas of u>u max and u≤−u max is zero since \(\hat{F} = F\).
5 Stability analysis
Stability analysis of the control system is presented to verify the proposed control law (14)–(16). Since the proposed control law is a decentralized control, stability analysis is presented for every individual joint to verify stability of the robotic system.
It follows from (12) that the lumped uncertainty F enters the system the same channel as the control input v. Thus, the uncertainty is said to satisfy the matching condition [27] or equivalently is said to be matched.
To make the dynamics of the tracking error well defined such that the robot can track the desired trajectory, we make the following assumption.
Assumption 1
The desired trajectory q d must be smooth in the sense that q d and its derivatives up to a necessary order are available and all uniformly bounded.
As a necessary condition to design a robust control, the external disturbance must be bounded.
Assumption 2
The external disturbance ϕ is bounded as
where ϕ max is a positive constant.
Since the proposed control law (14)–(16) obtains a bounded input for every motor as
It is verified in [14] that the electrically driven robot under the bounded voltage input v and the bounded external disturbance ϕ provides, for each motor, the bounded joint velocity \(\dot{q}\), the motor current I a , and its derivative \(\dot{I}_{a}\).
Consider the closed-loop system (19). The term \(\hat{k}_{b}^{ -1}\hat{r}(F - \hat{F})\) can be seen as the input. We verified in (30) that \(| F(e,\dot{e}) - \hat{F}(e,\dot{e}) | \le\rho\). Thus, the input \(\hat{k}_{b}^{ - 1}\hat{r}(F - \hat{F})\) is bounded in the linear system (19). As a result, e is bounded. It follows that q is bounded since q=q d −e.
For each motor, the joint position q, the joint velocity \(\dot{q}\), and the motor current I a are bounded. Thus, in the robotic system, the joint position vector q, the joint velocity vector \(\dot{\mathbf{q}}\), and the motor current vector I a are bounded. Therefore, the state vector z in (7) is bounded.
6 Performance evaluation
We have evaluated performance of the control system in the area of |u|<u max in Sects. 4 and 5. \(| \dot{e} + k_{p}e |\) is reduced until it satisfies \(| \dot{e} + k_{p}e | = \hat{k}_{b}^{ - 1}\hat{r}\varPsi /k_{p}\) in (50). We evaluate the performance of the control system out of the area |u|<u max as follows: A positive definite function V is proposed as
where V(0)=0 and V(e)>0 for e≠0. The time derivative of V is calculated as
Substituting control law (14) into (12) forms the closed-loop system
Considering (15) for u<−u max and u>u max implies that
where \(\operatorname{sgn} (u)\) is the signum function defined as \(\operatorname{sgn} (u) = 1\) if u>1 and \(\operatorname{sgn} (u) = - 1\) if u<−1. Thus, the closed-loop system is described by
From (65) we have
Then we can write

Substituting for \(\dot{e} = \dot{q}_{d} - \dot{q}\) into (67), we obtain
Substituting (68) into (62) yields
Assume that there exits a positive scalar denoted by μ such that
We can ensure (70) since \(I_{a}, \dot{I}_{a}, \phi\), and \(\dot{q}_{d}\) are bounded. To establish the convergence, the condition \(\dot{V} < 0\) should be satisfied. For this purpose, it is sufficient that
Proof
Substituting (71) into (69) yields
By the triangle inequality and (70),

Hence,
Using \(e.{\operatorname{sgn}}(e) = | e |\) in (72) yields
Substituting (74) into (75) proves that \(\dot{V} < 0\). Thus, the tracking error is converged until the control system comes into the area |u|<u max. Equation (71) implies that
Therefore, the maximum voltage of motor should satisfy (76) for the convergence of the tracking error e. In other words, motor should be sufficiently strong to track \(\dot{q}_{d}\) when driving the robot.
Starting from an arbitrary e(0) under the condition u max=μ, the value of |e| is reduced. Then, motor moves to the area of u max>|u|. □
7 Simulation results
The proposed control law is applied to control an articulated robot manipulator with a symbolic representation in Fig. 2. The Denavit–Hartenberg (DH) parameters of the articulated robot are given in Table 2, where the parameters θ i ,d i ,a i , and α i are called the joint angle, link offset, link length, and link twist, respectively. Parameters of manipulator are given in Table 3, where for the ith link, m i is the mass, and r ci =[x ci y ci z ci ]T is the center of mass in the ith frame. The inertia tensor in the center of mass frame is expressed as
Motor parameters are given in Table 4. To consider the parametric uncertainties, \(\hat{k}_{b}\), \(\hat{r}\), and \(\hat{R}\) are assumed to be 80% of their real values. The maximum voltage of each motor is set to u max=40 V. The desired joint trajectory for the joints is shown in Fig. 3. The desired trajectory should be sufficiently smooth such that all its derivatives up to the required order are bounded. The desired trajectory starts from zero and goes to 2 rad in 5 sec. The control laws for all three motors are the same with k p =100.
Simulation 1
We set the adaptation law (43) with \(\hat{p}_{l}(0) = 0\) and γ=2000 in (42). The performance of the NAFC is shown in Fig. 4, while the external disturbance is zero by given ϕ=0 in system (8). The maximum error of 2.6×10−5 rad occurs in joint 2 when starting, and then the error goes under 6.5×10−6 rad. The mean value of absolute error for joint 2 is about 3.4×10−6 rad. The tracking errors confirm that the parameters are well adapted. The adaptation of parameters is shown in Fig. 5. Actually, three curves in Fig. 5 represent the adaptation of nine parameters. It seems that the output of fuzzy system can be set into three fuzzy sets in place of nine fuzzy sets. The uncertainty described by (13) is shown in Fig. 6. The performance of the estimation of uncertainty for joint 2 is shown in Fig. 7 with a maximum estimation error of 0.1 V when starting, then the estimation error goes under 0.03 V. Motors behave well under the permitted voltages as shown in Fig. 8. The simulation results confirm the effectiveness of the proposed NAFC.
Simulation 2
A comparison between the NAFC and a Robust Nonlinear Control (RNC) [14] is provided, while the external disturbance is zero by given ϕ=0 in system (8). The proposed RNC is given by


where sat(⋅) is the saturation function stated by (15), and δ is a small positive constant called as time delay. In this simulation, we use the RNC, while the control design parameters \(\hat{R}\), \(\hat{k}_{b}\), \(\hat{r}\), and k p are the same as ones used in the NAFC. We set the time delay δ=0.001. The RNC shows a very good performance shown in Fig. 9, and the maximum tracking error is about 2.25×10−5 rad occurred for the joint 2. The mean value of absolute error for the joint 2 in the RNC is calculated about 1.6×10−5 rad, whereas this value was calculated about 3.4×10−6 rad for NAFC. Although the RNC control shows a very good performance, the NAFC control is superior to RNC control by comparing their performances in Fig. 7 and Fig. 9.
Simulation 3
We compare the NAFC and the RNC in Fig. 10 subject to sudden changes in uncertainty by inserting the external disturbance given by
where s(t) is the unit step function. The function ϕ in (80) is an example for considering a bounded disturbance with sudden changes. The uncertainty F described in (13) is shown in Fig. 11. The RNC is superior to the NAFC in the face of uncertainty with sudden changes. The maximum tracking error in the RNC is about 1.2×10−4 rad, whereas the maximum tracking error in the NAFC is about 6.5×10−4 rad in Fig. 10. In contrast, the NAFC is superior to RNC subject to smooth changes in uncertainty.
According to the stability analysis, performance evaluation and simulation results for the RNC in [14] and for the NAFC in this paper, both control approaches are robust with a very good tracking performance. The reason is that both approaches are based on the voltage control strategy which obtains important advantages over the torque control strategy due to being free from manipulator dynamics. As a result, they are computationally simple, decoupled, and well behaved with fast response. The NAFC is superior to RNC subject to smooth changes in uncertainty, whereas the RNC is superior to NAFC subject to sudden changes in uncertainty. The reason is that the adaptive fuzzy system can approximate an uncertainty that is continuous and smooth or differentiable, while the RNC presented in [14] is free from this condition.
8 Conclusion
This paper has developed a novel robust decentralized NAFC control of electrically driven robot manipulators using the voltage control strategy. We have used a fuzzy system to estimate and compensate uncertainty. The uncertainty has been modeled as a nonlinear function of the joint position error and its time derivative in replace of employing all system states. The stability analysis verifies that the system states are bounded. The proposed NAFC has shown a very good performance such that the value of \(| \dot{e} + k_{p}e |\) is ultimately bounded to a small value. Simulation results have shown the effectiveness of the method. We have compared the NAFC with the RNC. Both control approaches are robust with a very good tracking performance. The RNC is superior to the NAFC in the face of sudden changes in uncertainty, whereas the NAFC is superior to the RNC in the face of an uncertainty without sudden changes.
References
Qu, Z., Dawson, D.M.: Robust Tracking Control of Robot Manipulators. IEEE Press, New York (1996)
Abdallah, C., Dawson, D., Dorato, P., Jamshidi, M.: Survey of robust control for rigid robots. IEEE Control Syst. Mag. 11, 24–30 (1991)
Cheah, C.C., Hirano, M., Kawamura, S., Arimoto, S.: Approximate Jacobian control for robots with uncertain kinematics and dynamics. IEEE J. Robot. Autom. 19(4), 692–702 (2003)
Fateh, M.M., Soltanpour, M.R.: Robust task-space control of robot manipulators under imperfect transformation of control space. Int. J. Innov. Comput. Inf. Control 5(11A), 3949–3960 (2009)
Fateh, M.M.: Robust control of electrical manipulators by joint acceleration. Int. J. Innov. Comput. Inf. Control 6(12), 5501–5510 (2010)
Corless, M.J.: Control of uncertain nonlinear systems. J. Dyn. Syst. Meas. Control 115(2B), 362–372 (1993)
Sage, H.G., De Mathelin, M.F., Ostertag, E.: Robust control of robot manipulators: a survey. Int. J. Control 72(16), 1498–1522 (1999)
Fateh, M.M.: Proper uncertainty bound parameter to robust control of electrical manipulators using nominal model. Nonlinear Dyn. 61(4), 655–666 (2010). doi:10.1007/s11071-010-9677-7
Youcef-Toumi, K., Shortlidge, C.: Control of robot manipulators using time delay. In: Proc. IEEE Int. Conf. on Robotics and Automation, Sacramento, CA, pp. 2391–2398 (1991)
Talole, S.E., Phadke, S.B.: Model following sliding mode control based on uncertainty and disturbance estimator. J. Dyn. Syst. Meas. Control 130, 1–5 (2008)
Fateh, M.M.: On the voltage-based control of robot manipulators. Int. J. Control. Autom. Syst. 6(5), 702–712 (2008)
Fateh, M.M.: Robust voltage control of electrical manipulators in task-space. Int. J. Innov. Comput. Inf. Control 6(6), 2691–2700 (2010)
Fateh, M.M.: Nonlinear control of electrical flexible-joint robots. Nonlinear Dyn. 67(4), 2549–2559 (2012). doi:10.1007/s11071-011-0167-3
Fateh, M.M.: Robust control of flexible-joint robots using voltage control strategy. Nonlinear Dyn. 67, 1525–1537 (2012). doi:10.1007/s11071-011-0086-3
Wang, L.X.: A Course in Fuzzy Systems and Control. Prentice-Hall, New York (1996)
Lim, C.M., Hiyama, T.: Application of fuzzy logic control to a manipulator. IEEE Trans. Robot. Autom. 1(5), 688–691 (1991)
Ham, C., Qu, Z., Johnson, R.: Robust fuzzy control for robot manipulators. IEE Proc., Control Theory Appl. 147(2), 212–216 (2000)
Kim, E.: Output feedback tracking control of robot manipulator with model uncertainty via adaptive fuzzy logic. IEEE Trans. Fuzzy Syst. 12(3), 368–376 (2004)
Hwang, J.P., Kim, E.: Robust tracking control of an electrically driven robot: adaptive fuzzy logic approach. IEEE Trans. Fuzzy Syst. 14(2), 232–247 (2006)
Fateh, M.M.: Robust fuzzy control of electrical manipulators. J. Intell. Robot. Syst. 60(3–4), 415–434 (2010). doi:10.1007/s10846-010-9430-y
Fateh, M.M.: Fuzzy task-space control of a welding robot. Int. J. Robot. Autom. 25(4), 372–378 (2010). doi:10.2316/Journal.206.2010.4.206-3437
Fateh, M.M., Shahrabi Frahani, S., Khatamianfar, A.: Task space control of a welding robot using a fuzzy coordinator. Int. J. Control. Autom. Syst. 8(3), 574–582 (2010). doi:10.1007/s12555-010-0310-9
Wang, L.X.: Adaptive Fuzzy Systems and Control: Design and Stability Analysis. Prentice-Hall, New York (1994)
Hsu, F.Y., Fu, L.C.: Adaptive robust fuzzy control for robot manipulators. In: Proc. IEEE Conf. on Robotics and Automation, San Diego, CA, pp. 649–654 (1994)
Sun, F.C., Sun, Z.Q., Feng, G.: An adaptive fuzzy controller based on sliding mode for robot manipulators. IEEE Trans. Syst. Man Cybern., Part B, Cybern. 29(4), 661–667 (1999)
Hwang, J.P., Kim, E.: Robust tracking control of an electrically driven robot: adaptive fuzzy logic approach. IEEE Trans. Fuzzy Syst. 14(2), 232–247 (2006)
Corless, M., Leitmann, G.: Continuous state feedback guaranteeing uniform ultimate boundedness for uncertain dynamics systems. IEEE Trans. Autom. Control 26, 1139–1144 (1981)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Fateh, M.M., Khorashadizadeh, S. Robust control of electrically driven robots by adaptive fuzzy estimation of uncertainty. Nonlinear Dyn 69, 1465–1477 (2012). https://doi.org/10.1007/s11071-012-0362-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-012-0362-x