Dynamic properties of a delayed predator–prey system with Ivlev-type functional response

Abstract

In this paper, the dynamical behavior of a modified predator–prey system with time delay is investigated. By regarding the time delay as the bifurcation parameter, we study the impact of the time delay on the dynamics of the system. The analysis shows that Hopf bifurcation can occur as the time delay passes some critical values. By employing the normal form theory and the center manifold reduction for functional differential equation, some sufficient conditions are derived for the direction and stability of the Hopf bifurcation. Finally, to verify our theoretical predictions, some numerical simulations are also included.

1 Introduction

A generalized predator–prey system [15] takes the form

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}(t)&{}=&{}x(t)f(x(t))-y(t)F(x(t),y(t)),\\ \dot{y}(t)&{}=&{}y(t)G(x(t),y(t)),\\ \end{array}\right. \end{aligned}$$

(1.1)

where x(t) and y(t) represent the prey density and predator density at time t, respectively. The function f(x) is the intrinsic growth rate or per capita growth rate; $F=F(x,y)$ describes the predator functional response; and $G=G(x,y)$ describes the predator numerical response.

To reflect that the dynamical behavior of the models depends on the past history of the system, it is often necessary to incorporate time delay into the models. Therefore, a more realistic predator–prey model should be described by delayed differential equations. In recent years, there has been a great and continuing interest especially on predator–prey systems with time delay [8, 10, 11, 14, 16, 17]. The inclusion of time delay in these systems has illustrated more complicated and richer dynamics in terms of stability, bifurcation, periodic solutions and so on. In Ref. [8], we find that the gestation delay $\tau$ of prey species is incorporated into a predator–prey system with non-selective harvesting. Inspired by Kar and Pahari [8], we introduce the gestation delay of prey species into the system (1.1), and then we get the following predator–prey system with time delay

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}(t)&{}=&{}x(t)f(x(t-\tau ))-y(t)F(x(t),y(t)),\\ \dot{y}(t)&{}=&{}y(t)G(x(t),y(t)).\\ \end{array}\right. \end{aligned}$$

(1.2)

In this paper, we choose the traditional logistic form for f(x(t)): $f(x(t))=a\left( 1-\frac{b}{a}x\right)$, where $a>0$ is the growth rate of the prey in the absence of predators, $b>0$ represents the self-regulation constant of the prey. The predator functional response F is chosen as the Ivlev-type functional response [1, 7], that is, $F=k\left( 1-e^{-cx}\right) ,$ where $k>0$ represents the maximum rate of predation and $c>0$ denotes the decrease in motivation to hunt. We can find that the Ivlev-type functional response is monotonically increasing as well as uniformly bounded. We choose the predator numerical response as the Lotka–Volterra predator–prey model [3, 12], that is, $G=-d+x,$ where $d>0$ stands for the intrinsic death rate of predator. Substituting f(x), F and G into Eq. (1.2), we have the following predator–prey system

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}(t)&{}=&{}x(t)\left( a-bx(t-\tau )-\dfrac{ky(t)}{x(t)} \left( 1-e^{-cx(t)}\right) \right) ,\\ \dot{y}(t)&{}=&{}y(t)\left( -d+x(t)\right) .\\ \end{array}\right. \nonumber \\ \end{aligned}$$

(1.3)

In Ref. [4], Gordon studied the effect of the harvest effort on the ecosystem from an economic perspective and proposed the following equation which investigates the economic interest of the yield of the harvesting effort

$$\begin{aligned}&\text{ Net } \text{ Economic } \text{ Revenue } \text{(NER) }\\&\quad =\text{ Total } \text{ Revenue } \text{(TR) }-\text{ Total } \text{ Cost } \text{(TC) }. \end{aligned}$$

Referring to the predator–prey system (1.3), an algebraic equation which considers the economic profit v of the harvest effort on prey can be established as follows

$$\begin{aligned} E(t)(px(t)-s)=v, \end{aligned}$$

(1.4)

where E(t) denotes the harvesting effort for prey, p and s represent harvesting reward per unit harvesting effort for unit weight of prey and harvesting cost per unit harvesting effort, respectively.

From (1.3) and (1.4), we obtain the following modified predator–prey system with time delay, which takes the form of differential algebraic equations

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}(t)&{}=&{}x(t)\left( a-bx(t-\tau )\right. \\ &{}&{}\quad \left. -\,\dfrac{ky(t)}{x(t)} \left( 1-e^{-cx(t)}\right) -E(t)\right) ,\\ \dot{y}(t)&{}=&{}y(t)\left( -d+x(t)\right) ,\\ 0&{}=&{}E(t)(px(t)-s)-v. \end{array}\right. \end{aligned}$$

(1.5)

We can see that the delayed predator–prey systems in Refs. [8, 10, 14] are governed by differential equations or difference equations. Compared with the delayed systems in Refs. [8, 10, 14], our system (1.5) is formulated by differential algebraic equations. By this way, we can study the effect of the harvest effort on the predator–prey system from an economic perspective. Some relevant modified predator–prey models can be found in Refs. [11, 16–18]. In the research of the dynamic behaviors of the modified predator–prey models, the authors [11, 16–18] have systematically studied the issues of local stability, flip bifurcation, Neimark–Sacker bifurcation, chaotic behavior, etc. Different from the previous work [11, 16–18], we aim to obtain the formulae for determining the properties of Hopf bifurcation of the modified predator–prey model with delay by using the local parameterization method [2] and center manifold theory introduced by Hassard et al. [6]. Our research enriches the dynamic behaviors of the modified predator–prey models. In this paper, by considering the time delay $\tau$ as a bifurcation parameter, we investigate the stability and direction of the Hopf bifurcation of system (1.5). We mainly discuss the effect of varying the time delay $\tau$ on the dynamics of the predator–prey system (1.5) in the region $\mathrm {R}_+^3=\{(x,y,E)|\ x>0,\,y>0,\,E>0\}$. In addition, when there is no danger of confusion, t is occasionally dropped from the related variables.

2 Local stability

In this section, we will investigate the local stability of system (1.5) according to the local parameterization method [2] and Hopf bifurcation theorem [5].

By computing, we can obtain that the system (1.5) has an equilibrium point $X_0=(x_0,y_0,E_0)^T=\left( d,\tfrac{d(a-bd-E_0)}{k\left( 1-e^{-cd}\right) },\tfrac{v}{pd-s}\right) ^T.$ In order to guarantee that the equilibrium point $X_0$ is positive, throughout this paper we assume that

$$\begin{aligned} a>bd+E_0,\ pd-s>0,\ v>0. \end{aligned}$$

(2.1)

In order to use the local parameterization method in Ref. [2], we need to make the transformation $X=Q\overline{X}$ for system (1.5), where $Q=\begin{pmatrix} 1 &{} 0 \quad &{} 0\\ 0 &{} 1 \quad &{} 0\\ -\frac{pE_0}{px_0-s} &{} 0 \quad &{} 1 \end{pmatrix},\ \,\overline{X}(t)=(x(t),y(t),\overline{E}(t))^T.$ Consequently, the system (1.5) becomes

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}(t)&{}=&{}x(t)\left( a-bx(t-\tau )-\dfrac{ky(t)}{x(t)} \left( 1-e^{-cx(t)}\right) \right. \\ &{}&{}\quad \left. +\,\dfrac{pE_0}{px_0-s}x(t)-\overline{E}(t)\right) ,\\ \dot{y}(t)&{}=&{}y(t)\left( -d+x(t)\right) ,\\ 0&{}=&{}\left( -\dfrac{pE_0}{px_0-s}x(t)+\overline{E}(t)\right) (px(t)-s)-v. \end{array}\right. \nonumber \\ \end{aligned}$$

(2.2)

We employ the following local parameterization in Ref. [2] for the third equation of system (2.2)

$$\begin{aligned} \overline{X}(t)=\psi (Y(t))=\overline{X}_0+U_0Y(t)+V_0h(Y(t)), \end{aligned}$$

where $U_0=\begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \\ 0 &{} 0 \end{pmatrix}$, $V_0=\begin{pmatrix} 0\\ 0\\ 1\\ \end{pmatrix}$, $Y(t)=(y_1(t), y_2(t))^{T}\in \mathrm {R}^2$, h(Y(t)) is a smooth mapping from $\mathrm {R}^2$ into $\mathrm {R}^3$, $h(Y(t))=(h_1(y_1(t), y_2(t)), h_2(y_1(t), y_2(t)), h_3(y_1(t), y_2(t)))^T$. That is,

$$\begin{aligned} x(t)= & {} x_0+y_1(t),\ \,y(t)=y_0+y_2(t),\\ \overline{E}(t)= & {} \overline{E}_0+h_3(y_1(t), y_2(t))), \end{aligned}$$

where $\overline{E}_0=E_0+\tfrac{px_0E_0}{px_0-c}$. Subsequently, the parametric system of system (2.2) takes the form

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{y}_1(t)&{}=&{}(x_0+y_1(t))\bigg (a-b(x_0+y_1(t-\tau ))\\ &{}&{}-\,\,\dfrac{k(y_0+y_2(t))}{(x_0+y_1(t))}\left( 1-e^{-c(x_0+y_1(t))}\right) \\ &{}&{}+\,\,\dfrac{pE_0}{px_0-s}(x_0+y_1(t))\\ &{}&{}-\,\,(\overline{E}_0+h_3(y_1(t), y_2(t)))\bigg ),\\ \dot{y}_2(t)&{}=&{}(y_0+y_2(t))\left( -d+x_0+y_1(t)\right) . \end{array}\right. \end{aligned}$$

(2.3)

Then we can get the following linearized system of the parametric system (2.3) at (0, 0),

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{y}_1(t)&{}=&{}\left( \dfrac{ky_0}{x_0} +\dfrac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}\right. \\ &{}&{}\left. -\, \dfrac{ky_0e^{-cx_0}}{x_0}\right) y_1(t)-bx_0y_1(t-\tau )\\ &{}&{}-\,k\left( 1-e^{-cx_0}\right) y_2(t),\\ \dot{y}_2(t)&{}=&{}y_0y_1(t). \end{array}\right. \end{aligned}$$

(2.4)

Hence, the characteristic equation of the linearized system (2.4) is

$$\begin{aligned}&\lambda ^2+\left[ bx_0e^{-\lambda \tau }+\dfrac{ky_0e^{-cx_0}}{x_0} +kcy_0e^{-cx_0}\right. \nonumber \\&\quad \left. -\left( \dfrac{ky_0}{x_0}+ \dfrac{px_0E_0}{px_0-s}\right) \right] \lambda +ky_0\left( 1-e^{-cx_0}\right) =0.\nonumber \\ \end{aligned}$$

(2.5)

If $\tau =0$, the characteristic Eq. (2.5) becomes

$$\begin{aligned}&\lambda ^2+\left[ bx_0+\dfrac{ky_0e^{-cx_0}}{x_0} +kcy_0e^{-cx_0}\right. \nonumber \\&\quad \left. -\,\left( \dfrac{ky_0}{x_0}+ \dfrac{px_0E_0}{px_0-s}\right) \right] \lambda +ky_0\left( 1-e^{-cx_0}\right) =0.\nonumber \\ \end{aligned}$$

(2.6)

By Routh–Hurwitz criterion [9], we have the following Lemma.

Lemma 2.1

For the system (2.2) with $\tau =0$,

• (i) if

  $$\begin{aligned} bx_0+\frac{ky_0e^{-cx_0}}{x_0}+kcy_0e^{-cx_0}>\frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s}, \end{aligned}$$

  then the positive equilibrium point $\overline{X}_0$ is locally asymptotically stable, i.e., $X_0$ is locally asymptotically stable;

• (ii) if

  $$\begin{aligned} bx_0+\frac{ky_0e^{-cx_0}}{x_0}+kcy_0e^{-cx_0}<\frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s}, \end{aligned}$$

  then the positive equilibrium point $\overline{X}_0$ is unstable, i.e., $X_0$ is unstable.

When $\tau \ne 0$, if $\lambda =i\omega \ (\omega >0)$ is a root of (2.5), then we can get

$$\begin{aligned}&-\,\omega ^2+i\omega \left( bx_0(\cos \omega \tau -i\sin \omega \tau )+\dfrac{ky_0e^{-cx_0}}{x_0}\right. \nonumber \\&\quad \left. +\,kcy_0e^{-cx_0}-\left( \dfrac{ky_0}{x_0}+ \dfrac{px_0E_0}{px_0-s}\right) \right) \\&\quad +ky_0\left( 1-e^{-cx_0}\right) =0. \end{aligned}$$

That is,

$$\begin{aligned}&-\,\omega ^2+ky_0\left( 1-e^{-cx_0}\right) +b\omega x_0\sin \omega \tau \\&+\,i\left( b\omega x_0\cos \omega \tau +kc\omega y_0e^{-cx_0}+\dfrac{k\omega y_0e^{-cx_0}}{x_0}\right. \nonumber \\&\quad \left. -\,\left( \dfrac{k\omega y_0}{x_0}+ \dfrac{p\omega x_0E_0}{px_0-s}\right) \right) =0. \end{aligned}$$

Hence,

$$\begin{aligned} b\omega x_0\sin \omega \tau= & {} \omega ^2-ky_0\left( 1-e^{-cx_0}\right) ,\end{aligned}$$

(2.7)

$$\begin{aligned} b\omega x_0\cos \omega \tau= & {} \dfrac{k\omega y_0}{x_0}+ \dfrac{p\omega x_0E_0}{px_0-s}\nonumber \\&-\,\,kc\omega y_0e^{-cx_0}-\dfrac{k\omega y_0e^{-cx_0}}{x_0}. \end{aligned}$$

(2.8)

It is known that $\sin ^2\omega \tau +\cos ^2 \omega \tau =1$, by Eqs. (2.7) and (2.8), we get

$$\begin{aligned}&\omega ^4+\bigg [\left( \dfrac{ky_0}{x_0}+ \dfrac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}- \dfrac{ky_0e^{-cx_0}}{x_0}\right) ^2\nonumber \\&\quad -b^2x_0^2-2ky_0\left( 1-e^{-cx_0}\right) \bigg ] \omega ^2\nonumber \\&\quad +k^2y_0^2\left( 1-e^{-cx_0}\right) ^2=0. \end{aligned}$$

(2.9)

Lemma 2.2

For the system (2.2),

• (i) if

  $$\begin{aligned}&\left( \frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}-\frac{ky_0e^{-cx_0}}{x_0} \right) ^{2}\\&\quad >b^2x_0^2+2ky_0\left( 1-e^{-cx_0}\right) \end{aligned}$$

  and

  $$\begin{aligned} bx_0+\frac{ky_0e^{-cx_0}}{x_0}+kcy_0e^{-cx_0}>\frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s}, \end{aligned}$$

  then all the roots of Eq. (2.5) have negative real parts for all $\tau >0$;

• (ii) if

  $$\begin{aligned}&\bigg [\left( \frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}-\frac{ky_0e^{-cx_0}}{x_0}\right) ^2\\&\quad -b^2x_0^2-2ky_0\left( 1-e^{-cx_0}\right) \bigg ]^2\\&>4k^2y_0^2\left( 1-e^{-cx_0}\right) ^2 \end{aligned}$$

  and

  $$\begin{aligned}&\left( \frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}-\frac{ky_0e^{-cx_0}}{x_0}\right) ^2\\&\quad <b^2x_0^2+2ky_0\left( 1-e^{-cx_0}\right) , \end{aligned}$$

  then Eq. (2.5) has two positive roots $\omega ^{+}$ and $\omega ^{-}$. Substituting $\omega ^{\pm }$ into Eq. (2.8), we derive

  $$\begin{aligned} \tau _k^{\pm }= & {} \dfrac{1}{\omega ^{\pm }}\arccos \left( \dfrac{ky_0}{bx_0^2} +\frac{pE_0}{b(px_0-s)}-\frac{kcy_0e^{-cx_0}}{bx_0}\right. \\&\left. -\frac{ky_0e^{-cx_0}}{bx_0^2}\right) +\dfrac{2k\pi }{\omega ^{\pm }},\ \,k=0, 1, 2, \ldots . \end{aligned}$$

Proof

It follows from (2.9) that if

$$\begin{aligned}&\left( \frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}-\frac{ky_0e^{-cx_0}}{x_0}\right) ^{2}\\&\quad >b^2x_0^2+2ky_0\left( 1-e^{-cx_0}\right) , \end{aligned}$$

then Eq. (2.9) does not have positive roots. Subsequently, Eq. (2.5) does not have purely imaginary roots. Besides, when

$$\begin{aligned} bx_0+\frac{ky_0e^{-cx_0}}{x_0}+kcy_0e^{-cx_0}>\frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s} \end{aligned}$$

holds, then all roots of Eq. (2.6) have negative real parts. By Rouche’s theorem [13], Eq. (2.5) also have negative real parts. $\square$

If

$$\begin{aligned}&\bigg [\left( \frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}-\frac{ky_0e^{-cx_0}}{x_0}\right) ^2\\&\quad -b^2x_0^2-2ky_0\left( 1-e^{-cx_0}\right) \bigg ]^2\\&\quad >4k^2y_0^2\left( 1-e^{-cx_0}\right) ^2 \end{aligned}$$

and

$$\begin{aligned}&\left( \frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}-\frac{ky_0e^{-cx_0}}{x_0}\right) ^2\\&\quad <b^2x_0^2+2ky_0\left( 1-e^{-cx_0}\right) , \end{aligned}$$

then Eq. (2.9) has two positive roots $\omega ^{+}$ and $\omega ^{-}$,

$$\begin{aligned} \omega ^{\pm }=\Bigg \{\frac{-B\pm \sqrt{B^2-4k^2y_0^2\left( 1-e^{-cx_0}\right) ^2}}{2}\Bigg \}^{1/2}, \end{aligned}$$

where

$$\begin{aligned} B= & {} \left( \dfrac{ky_0}{x_0}+ \dfrac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}-\dfrac{ky_0e^{-cx_0}}{x_0}\right) ^{2}\\&\quad -b^2x_0^2-2ky_0\left( 1-e^{-cx_0}\right) . \end{aligned}$$

Substituting $\omega ^{\pm }$ into Eq. (2.8), then we get $\tau _k^{\pm }$. The proof is completed.

Differentiating the characteristic Eq. (2.5) with respect to $\tau$, we have

$$\begin{aligned}&2\lambda \dfrac{\text {d}\lambda }{\text {d}\tau }+ \left( bx_0e^{-\lambda \tau }+\dfrac{ky_0e^{-cx_0}}{x_0} +kcy_0e^{-cx_0}-\dfrac{ky_0}{x_0}\right. \\&\quad \left. -\, \dfrac{px_0E_0}{px_0-s}\right) \dfrac{\text {d}\lambda }{\text {d}\tau } +bx_0\lambda e^{-\lambda \tau }\left( -\lambda -\tau \dfrac{\text {d}\lambda }{\text {d}\tau }\right) =0. \end{aligned}$$

Thus,

$$\begin{aligned} \left( \dfrac{\text {d}\lambda }{\text {d}\tau }\right) ^{-1}= \dfrac{2\lambda +bx_0e^{-\lambda \tau }+\dfrac{ky_0e^{-cx_0}}{x_0} +kcy_0e^{-cx_0}-\dfrac{ky_0}{x_0}- \dfrac{px_0E_0}{px_0-s}-bx_0\lambda \tau e^{-\lambda \tau }}{bx_0\lambda ^2 e^{-\lambda \tau }}. \end{aligned}$$

We can calculate that

$$\begin{aligned}&\left( \left. \dfrac{\text {d}\lambda }{\text {d} \tau }\right) ^{-1}\right| _{\lambda =i\omega } =\left( -\dfrac{1}{\omega ^2}+\dfrac{2\sin \lambda \tau }{bx_0\omega } -\dfrac{\cos \lambda \tau }{bx_0\omega ^2}\right. \nonumber \\&\left. \times \, \left( \dfrac{ky_0e^{-cx_0}}{x_0}+kcy_0e^{-cx_0}-\dfrac{ky_0}{x_0}- \dfrac{px_0E_0}{px_0-s}\right) \right) \nonumber \\&+\,i\left( \dfrac{\tau }{\omega }-\dfrac{2\cos \lambda \tau }{bx_0\omega } -\dfrac{\sin \lambda \tau }{bx_0\omega ^2}\left( \dfrac{ky_0e^{-cx_0}}{x_0}\right. \right. \nonumber \\&\left. \left. +\,kcy_0e^{-cx_0}-\dfrac{ky_0}{x_0}- \dfrac{px_0E_0}{px_0-s}\right) \right) . \end{aligned}$$

(2.10)

By Eqs. (2.7), (2.8) and (2.10), we have

$$\begin{aligned}&\left. \text {sign}\left\{ \text {Re}\left( \dfrac{\text {d}\lambda }{\text {d}\tau }\right) \right\} \right. _{\lambda =i\omega }= \left. \text {sign}\left\{ \text {Re}\left( \dfrac{\text {d}\lambda }{\text {d}\tau }\right) ^{-1}\right\} \right. _{\lambda =i\omega }\\ =&\text {sign}\bigg \{-\dfrac{1}{\omega ^2}+\dfrac{2}{bx_0\omega } \left( \dfrac{\omega }{bx_0}-\dfrac{ky_0\left( 1-e^{-cx_0}\right) }{bx_0\omega }\right) \\&\qquad \ \ -\dfrac{1}{bx_0\omega ^2}\left( \dfrac{ky_0e^{-cx_0}}{x_0} +kcy_0e^{-cx_0}-\dfrac{ky_0}{x_0}- \dfrac{px_0E_0}{px_0-s}\right) \\&\qquad \ \ \times \left( \dfrac{ky_0}{bx_0^2}+\frac{pE_0}{b(px_0-s)}-\frac{kcy_0e^{-cx_0}}{bx_0}-\frac{ky_0e^{-cx_0}}{bx_0^2}\right) \bigg \}\\ =&\text {sign}\Bigg \{\dfrac{1}{b^2x_0^2\omega ^2}\Bigg [2\omega ^2-2ky_0\left( 1-e^{-cx_0}\right) -b^2x_0^2\\&\qquad \ \ +\left( \dfrac{ky_0}{x_0}+ \dfrac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}-\dfrac{ky_0e^{-cx_0}}{x_0}\right) ^2 \Bigg ]\Bigg \}. \end{aligned}$$

Then the transversality conditions

$$\begin{aligned}&\left. \text {sign}\left\{ \text {Re}\left( \dfrac{\text {d}\lambda }{\text {d}\tau }\right) \right\} \right. _{\tau =\tau _k^+,\ \omega =\omega ^+}>0,\\&\quad \left. \text {sign}\left\{ \text {Re}\left( \dfrac{\text {d}\lambda }{\text {d}\tau }\right) \right\} \right. _{\tau =\tau _k^-,\ \omega =\omega ^-}<0 \end{aligned}$$

are satisfied. Hence, we have the following theorem in view of Refs. [5, 6].

Theorem 2.1

For the system (2.2), we assume that

$$\begin{aligned} bx_0+\frac{ky_0e^{-cx_0}}{x_0}+kcy_0e^{-cx_0}>\frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s} \end{aligned}$$

holds, then

• (i) if

  $$\begin{aligned}&\left( \frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}- \frac{ky_0e^{-cx_0}}{x_0}\right) ^{2}\\&\quad >b^2x_0^2+2ky_0\left( 1-e^{-cx_0}\right) , \end{aligned}$$

  all the roots of Eq. (2.5) have negative real parts for all $\tau >0$, and the equilibrium point $X_0$ of system (1.5) is asymptotically stable;

• (ii) if

  $$\begin{aligned}&\bigg [\left( \frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}-\frac{ky_0e^{-cx_0}}{x_0}\right) ^{2}\\&-\,b^2x_0^2-2ky_0\left( 1-e^{-cx_0}\right) \bigg ]^2\\&>4k^2y_0^2\left( 1-e^{-cx_0}\right) ^2 \end{aligned}$$

  and

  $$\begin{aligned}&\left( \frac{ky_0}{x_0}+ \frac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}-\frac{ky_0e^{-cx_0}}{x_0}\right) ^2\\&\quad <b^2x_0^2+2ky_0\left( 1-e^{-cx_0}\right) , \end{aligned}$$

  there is a positive integer N, such that the equilibrium point $X_0$ of system (1.5) switches N times from stability to instability and to stability. That is, the equilibrium point $X_0$ is asymptotically stable when $\tau \in [0,\tau _0^+)\bigcup \left( \bigcup \limits _{n=0}^{N-1}(\tau ^-_{n},\tau ^+_{n+1})\right) ,$ and $X_0$ is unstable when $\tau \in \left( \bigcup \limits _{n=0}^{N-1}(\tau ^+_{n},\tau ^-_{n})\right) \bigcup (\tau _N^+,+\infty ).$

Remark 2.1

It is clear that the system (1.5) undergoes Hopf bifurcations at the equilibrium point $X_0$ when $\tau =\tau _n^{\pm }$. Besides, when $\tau =0$ and the roots of Eq. (2.5) exist zero real parts, the system (1.5) also undergoes Hopf bifurcation.

3 Direction and stability of the Hopf bifurcation

As pointed out by Hassard et al. [6], it is interesting to determine the direction, stability and period of the bifurcating periodic solutions. In this section, we aim to establish the formulae for determining these factors at the critical value $\tau =\tau _n$ using the normal form [5] and the center manifold theory [6].

Throughout this section, we assume that the system (1.5) undergoes Hopf bifurcations at the positive equilibrium $X_0$ for $\tau =\tau _n$, and $i\omega _0$ is the corresponding purely imaginary root of the characteristic equation at the positive equilibrium $X_0$. For the sake of simplicity, throughout this section we use the notation $i\omega$ for $i\omega _0$.

Let $y_1(t)=x(\tau t)-x_0$, $y_2(t)=y(\tau t)-y_0$, $\tau =\mu +\tau _n$, then the parametric system (2.3) can be transformed into a FDE in $C=C([-1,0],\mathrm {R}^2)$:

$$\begin{aligned} \dot{Y}(t)=L_{\mu }(Y_t)+F(\mu , Y_t), \end{aligned}$$

(3.1)

where $Y(t)=(y_1(t), y_2(t))^{T}$, $Y_t=Y(t+\theta )=(y_1(t+\theta ), y_2(t+\theta ))$, $\theta \in [-1,0]$, for $\Phi =(\Phi _1, \Phi _2)\in C$,

$$\begin{aligned} L_\mu \Phi =&\,(\tau _n+\mu )\begin{pmatrix} \dfrac{ky_0}{x_0} +\dfrac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}- \dfrac{ky_0e^{-cx_0}}{x_0} &{} -k\left( 1-e^{-cx_0}\right) \\ y_0 &{} 0\\ \end{pmatrix}\Phi ^T(0)\\&\,+(\tau _n+\mu )\begin{pmatrix} -bx_0 &{} 0\\ 0 &{} 0\\ \end{pmatrix}\Phi ^T(-1), \end{aligned}$$

and

$$\begin{aligned} F(\mu , \Phi )=(\tau _n+\mu )\begin{pmatrix} F_{11}\\ F_{22}\\ \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} F_{11}&=\left( \dfrac{1}{2} kc^2y_0e^{-cx_0} -\dfrac{psE_0}{(px_0-s)^2}\right) \\&\quad \Phi _1^2(0)-b \Phi _1^2(-1)-kce^{-cx_0}\Phi _1(0)\Phi _2(0)+\cdots ,\\ F_{22}&=\Phi _1(0)\Phi _2(0)+\cdots . \end{aligned}$$

By Riesz representation theorem, there exists a function $\eta (\theta , \mu )$ of bounded variation for $\theta \in [-1,0]$, such that

$$\begin{aligned} L_\mu \Phi =\int _{-1}^0 \mathrm {d}\eta (\theta ,\mu )\Phi (\theta ),\ \,\Phi \in C. \end{aligned}$$

In fact, we can choose

$$\begin{aligned} \eta (\theta ,\mu )=&\,(\tau _n+\mu )\begin{pmatrix} \dfrac{ky_0}{x_0} +\dfrac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}-\dfrac{ky_0e^{-cx_0}}{x_0} &{} -k\left( 1-e^{-cx_0}\right) \\ y_0 &{} 0\\ \end{pmatrix}\delta (\theta )\\&\,+(\tau _n+\mu )\begin{pmatrix} bx_0 &{} 0\\ 0 &{} 0\\ \end{pmatrix}\delta (\theta +1), \end{aligned}$$

where $\delta (\theta )=\left\{ \begin{array}{lll} 0,\ \ \theta \ne 0,\\ 1,\ \ \theta =0.\\ \end{array}\right.$

For $\Phi \in C^1([-1,0],\mathrm {R}^2)$, define

$$\begin{aligned} A(\mu )\Phi =\left\{ \begin{array}{l@{\quad }l} \dfrac{\text {d}\Phi (\theta )}{\text {d}\theta }, &{} -1\le \theta <0, \\ \int _{-1}^0 \mathrm {d}\eta (\theta ,\mu )\Phi (\theta ), &{} \theta =0, \\ \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} R(\mu )\Phi =\left\{ \begin{array}{l@{\quad }l} 0, &{} -1\le \theta <0, \\ F(\mu , \Phi ), &{} \theta =0.\\ \end{array} \right. \end{aligned}$$

Then the system (3.1) can be written as

$$\begin{aligned} \dot{Y}(t)=A(\mu )Y_t+R(\mu )Y_t. \end{aligned}$$

(3.2)

For $\Psi \in C^1([-1,0],(\mathrm {R}^2)^*)$, where $(\mathrm {R}^2)^*$ is the 2-dimensional space of row vectors, the adjoint operator $A^*$ of A(0) is defined as

$$\begin{aligned} A^*\Psi (s)=\left\{ \begin{array}{l@{\quad }l} -\dfrac{\text {d}\Psi (s)}{\text {d}s}, &{} 0<s\le 1, \\ \int _{-1}^0 \mathrm {d}\eta ^T(s,0)\Psi (-s), &{} s=0. \\ \end{array} \right. \end{aligned}$$

For $\Phi \in C^1([-1,0],\mathrm {R}^2)$, $\Psi \in C^1([-1,0],(\mathrm {R}^2)^*)$, we define the bilinear form

$$\begin{aligned}&<\Psi (s),\Phi (\theta )>=\bar{\Psi }(0)\Phi (0)\\&\quad - \int ^0_{\theta =-1}\int ^\theta _{\xi =0}\bar{\Psi }(\xi -\theta ) \mathrm {d}\eta (\theta )\Phi (\xi )\mathrm {d}\xi , \end{aligned}$$

where $\eta (\theta )=\eta (\theta ,0)$. By the discussion in Sect.  2, we know that $\pm i\omega \tau _n$ are eigenvalues of A(0) and $A^*$. We need to calculate the eigenvector of A(0) and $A^*$ corresponding to $i\omega \tau _n$ and $- i\omega \tau _n$, respectively. Suppose that $q(\theta )=(1,q_2)^T e^{i\omega \tau _n\theta }$ is the eigenvector of A(0) corresponding to $i\omega \tau _n$, then $A(0)q(\theta )=i\omega \tau _nq(\theta )$. Let $q^*(s)=\frac{1}{D}(q_2^*, 1) e^{i\omega \tau _ns}$ be the eigenvector of $A^*$ corresponding to $-i\omega \tau _n$, then $A^*q^*(s)=-i\omega \tau _nq^*(s)$. Some computations can show that

$$\begin{aligned}&q_2=\dfrac{\dfrac{ky_0}{x_0} +\dfrac{px_0E_0}{px_0-s}-kcy_0e^{-cx_0}-\dfrac{ky_0e^{-cx_0}}{x_0} -i\omega -bx_0e^{-i\omega \tau _n}}{k\left( 1-e^{-cx_0}\right) },\\&q_2^*=\dfrac{i\omega }{k\left( 1-e^{-cx_0}\right) },\ \,\bar{D}=q_2+\bar{q_2^*}+bx_0\bar{q_2^*}\tau _ne^{-i\omega \tau _n}. \end{aligned}$$

Clearly, $<q^*,q>=1$ and $<q^*,\bar{q}>=0$.

At first, we construct the coordinates to describe the center manifold $C_0$ at $\mu =0$ (i.e., $\tau =\tau _n$). Define

$$\begin{aligned} \dot{z}(t)=<q^*, Y_t>,\ \,W(t,\theta )=Y_t-2\mathrm {Re}\{z(t)q(\theta )\}. \end{aligned}$$

On the center manifold $C_0$, we have $W(t,\theta )=W(z(t),\bar{z}(t),\theta )$, where

$$\begin{aligned} W(z,\bar{z},\theta )= & {} W_{20}(\theta )\dfrac{z^2}{2} +W_{11}(\theta )z\bar{z}\nonumber \\&+\,W_{02}(\theta )\dfrac{\bar{z}^2}{2}+\cdots . \end{aligned}$$

(3.3)

z and $\bar{z}$ are local coordinates for $C_0$ in the direction of q and $\bar{q}^*$. Note that W is real if $Y_t$ is real. We only consider real solutions. For the solution $Y_t\in C_0$, since $\mu =0$, from (3.2), we have

$$\begin{aligned} \dot{z}=i\omega \tau _nz+\bar{q}^*(0)F_0(z,\bar{z}) :=i\omega \tau _nz+g(z,\bar{z}), \end{aligned}$$

(3.4)

where

$$\begin{aligned} g(z,\bar{z})=g_{20}(\theta )\dfrac{z^2}{2}+g_{11} (\theta )z\bar{z}+g_{02}(\theta )\dfrac{\bar{z}^2}{2}+\cdots .\nonumber \\ \end{aligned}$$

(3.5)

By Eq. (3.4), we have

$$\begin{aligned} g(z,\bar{z})=\bar{q}^*(0)F_0(z,\bar{z})= \dfrac{1}{\bar{D}}\tau _n(\bar{q^*_2},1)\begin{pmatrix} F_{11}^0\\ F_{22}^0\\ \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned}&F_{11}^0=\left( \dfrac{1}{2} kc^2y_0e^{-cx_0}-\dfrac{psE_0}{(px_0-s)^2}\right) y_{1t}^2(0)\\&\quad -by_{1t}^2(-1)-kce^{-cx_0}y_{1t} (0)y_{2t}(0)+\cdots ,\\&F_{22}^0=y_{1t}(0)y_{2t}(0)+\cdots . \end{aligned}$$

In view of Eq. (3.3), we get

$$\begin{aligned}&g(z,\bar{z})=\dfrac{\tau _n}{\bar{D}}\Bigg \{\bar{q_2^*}\bigg [\dfrac{1}{2} kc^2y_0e^{-cx_0}-\dfrac{psE_0}{(px_0-s)^2}\bigg ]\\&\quad \times \bigg [z+\bar{z}+W_{20}^{(1)}(0)\dfrac{z^2}{2}+W_{11}^{(1)}(0)z\bar{z}+W_{02}^{(1)}(0)\dfrac{\bar{z}^2}{2}\bigg ]^2\\&\quad -b\bar{q_2^*}\bigg [ze^{-i\omega \tau _n\theta }+\bar{z}e^{i\omega \tau _n\theta }+W_{20}^{(1)}(-1)\dfrac{z^2}{2}\\&\quad +W_{11}^{(1)}(-1)z\bar{z}+W_{02}^{(1)}(-1)\dfrac{\bar{z}^2}{2}\bigg ]^2\\&\quad -kce^{-cx_0}\bar{q_2^*}\bigg [z+\bar{z}+W_{20}^{(1)}(0)\dfrac{z^2}{2}+W_{11}^{(1)}(0)z\bar{z} +W_{02}^{(1)}(0)\dfrac{\bar{z}^2}{2}\bigg ]\\&\quad \times \bigg [q_2z+\bar{q}_2\bar{z}+W_{20}^{(2)}(0)\dfrac{z^2}{2}+W_{11}^{(2)}(0)z\bar{z} +W_{02}^{(2)}(0)\dfrac{\bar{z}^2}{2}\bigg ]\\&\quad +\bigg [z+\bar{z}+W_{20}^{(1)}(0)\dfrac{z^2}{2}+W_{11}^{(1)}(0)z\bar{z}+W_{02}^{(1)}(0)\dfrac{\bar{z}^2}{2}\bigg ]\\&\quad \times \bigg [q_2z+\bar{q}_2\bar{z}+W_{20}^{(2)}(0)\dfrac{z^2}{2}+W_{11}^{(2)}(0)z\bar{z}\\&\quad +W_{02}^{(2)}(0)\dfrac{\bar{z}^2}{2}\bigg ]+\cdots \Bigg \}. \end{aligned}$$

That is,

$$\begin{aligned}&g(z,\bar{z})=\dfrac{\tau _n}{\bar{D}}\Bigg \{z^2\bigg [\dfrac{1}{2} kc^2\bar{q_2^*}y_0e^{-cx_0}-\dfrac{ps\bar{q_2^*}E_0}{(px_0-s)^2}\\&\quad -b\bar{q_2^*}e^{-2i\omega \tau _n\theta }-kcq_2\bar{q_2^*}e^{-cx_0}+q_2\bigg ]\\&\quad +z\bar{z}\bigg [kc^2\bar{q_2^*}y_0e^{-cx_0}-\dfrac{2ps\bar{q_2^*}E_0}{(px_0-s)^2}\\&\quad -2b\bar{q_2^*}-2kc\bar{q_2^*}e^{-cx_0}\mathrm {Re}(q_2)+2\mathrm {Re}(q_2)\bigg ]\\&\quad +\bar{z}^2\bigg [\dfrac{1}{2} kc^2\bar{q_2^*}y_0e^{-cx_0}-\dfrac{ps\bar{q_2^*}E_0}{(px_0-s)^2}\\&\quad -b\bar{q_2^*}e^{2i\omega \tau _n\theta }-kc\bar{q}_2\bar{q_2^*}e^{-cx_0}+\bar{q}_2\bigg ]\\&\quad +z^2\bar{z}\bigg [\bigg (kc^2\bar{q_2^*}y_0e^{-cx_0}-\dfrac{2ps\bar{q_2^*}E_0}{(px_0-s)^2}\\&\quad -kcq_2\bar{q_2^*}e^{-cx_0}+q_2\bigg )W_{11}^{(1)}(0) +\bigg (1-kc\bar{q_2^*}e^{-cx_0}\bigg )W_{11}^{(2)}(0)\\&\quad +\bigg (\dfrac{1}{2} kc^2\bar{q_2^*}y_0e^{-cx_0}-\dfrac{ps\bar{q_2^*}E_0}{(px_0-s)^2}-\dfrac{1}{2}kc\bar{q}_2\bar{q_2^*}e^{-cx_0}\\&\quad +\dfrac{1}{2}\bar{q}_2\bigg )W_{20}^{(1)}(0)\\&\quad +\bigg (\dfrac{1}{2}-\dfrac{1}{2}kc\bar{q_2^*}e^{-cx_0}\bigg )W_{20}^{(2)}(0)-2b\bar{q_2^*}e^{-i\omega \tau _n\theta }W_{11}^{(1)}(-1)\\&\quad -b\bar{q_2^*}e^{i\omega \tau _n\theta }W_{20}^{(1)}(-1)\bigg ]+\cdots \Bigg \}. \end{aligned}$$

Comparing the coefficients with (3.5), we have

$$\begin{aligned} g_{20}&=\dfrac{2\tau _n}{\bar{D}}\bigg [\dfrac{1}{2} kc^2\bar{q_2^*}y_0e^{-cx_0}-\dfrac{ps\bar{q_2^*}E_0}{(px_0-s)^2}\\&\quad -b\bar{q_2^*}e^{-2i\omega \tau _n\theta }-kcq_2\bar{q_2^*}e^{-cx_0}+q_2\bigg ],\\ g_{11}&=\dfrac{\tau _n}{\bar{D}}\bigg [kc^2\bar{q_2^*}y_0e^{-cx_0}\\&\quad -\dfrac{2ps\bar{q_2^*}E_0}{(px_0-s)^2}-2b\bar{q_2^*}-2kc\bar{q_2^*}e^{-cx_0}\mathrm {Re}(q_2)+2\mathrm {Re}(q_2)\bigg ],\\ g_{02}&=\dfrac{2\tau _n}{\bar{D}}\bigg [\dfrac{1}{2} kc^2\bar{q_2^*}y_0e^{-cx_0}\\&\quad -\dfrac{ps\bar{q_2^*}E_0}{(px_0-s)^2}-b\bar{q_2^*}e^{2i\omega \tau _n\theta }-kc\bar{q}_2\bar{q_2^*}e^{-cx_0}+\bar{q}_2\bigg ],\\ g_{21}&=\bigg (kc^2\bar{q_2^*}y_0e^{-cx_0}-\dfrac{2ps\bar{q_2^*}E_0}{(px_0-s)^2}-kcq_2\bar{q_2^*}e^{-cx_0}+q_2\bigg )\\&\quad \times W_{11}^{(1)}(0)+\bigg (1-kc\bar{q_2^*}e^{-cx_0}\bigg )W_{11}^{(2)}(0)\\&\quad +\bigg (\dfrac{1}{2} kc^2\bar{q_2^*}y_0e^{-cx_0}-\dfrac{ps\bar{q_2^*}E_0}{(px_0-s)^2}\\&\quad -\dfrac{1}{2}kc\bar{q}_2\bar{q_2^*}e^{-cx_0}+\dfrac{1}{2}\bar{q}_2\bigg )W_{20}^{(1)}(0)\\&\quad +\bigg (\dfrac{1}{2}-\dfrac{1}{2}kc\bar{q_2^*}e^{-cx_0}\bigg )W_{20}^{(2)}(0)\\&\quad -2b\bar{q_2^*}e^{-i\omega \tau _n\theta }W_{11}^{(1)}(-1)-b\bar{q_2^*}e^{i\omega \tau _n\theta }W_{20}^{(1)}(-1). \end{aligned}$$

Now we have known the expressions of $g_{20}$, $g_{11}$, $g_{02}$. In order to obtain the expression of $g_{21}$, we need to calculate $W_{20}(\theta )$ and $W_{11}(\theta )$. According to the method in Ref. [6], one can obtain

$$\begin{aligned}&W_{20}(\theta )=\dfrac{ig_{20}}{\omega \tau _n}q(0)e^{i\omega \tau _n\theta } +\dfrac{i\bar{g}_{02}}{3\omega \tau _n}\bar{q}(0)e^{-i\omega \tau _n\theta }+M_1e^{2i\omega \tau _n\theta },\\&W_{11}(\theta )=-\dfrac{ig_{11}}{\omega \tau _n}q(0)e^{i\omega \tau _n\theta } +\dfrac{i\bar{g}_{11}}{\omega \tau _n}\bar{q}(0)e^{-i\omega \tau _n\theta }+M_2, \end{aligned}$$

where

$$\begin{aligned}&M_1=\left( \begin{array}{l@{\quad }l} 2i\omega -\dfrac{ky_0}{x_0} -\dfrac{px_0E_0}{px_0-s}+kcy_0e^{-cx_0}+\dfrac{ky_0e^{-cx_0}}{x_0} +bx_0e^{-2i\omega \tau _n} &{} k\left( 1-e^{-cx_0}\right) \\ -y_0 &{} 2i\omega \\ \end{array} \right) ^{-1}\times 2\left( \begin{array}{c} G_{11} \\ G_{21} \\ \end{array} \right) ,\\&M_2=\left( \begin{array}{l@{\quad }l} bx_0+kcy_0e^{-cx_0}+\dfrac{ky_0e^{-cx_0}}{x_0}-\dfrac{ky_0}{x_0} -\dfrac{px_0E_0}{px_0-s} &{} k\left( 1-e^{-cx_0}\right) \\ -y_0 &{} 0 \\ \end{array} \right) ^{-1}\times 2\left( \begin{array}{c} H_{11} \\ H_{21} \\ \end{array} \right) , \end{aligned}$$

with

$$\begin{aligned}&G_{11}=\dfrac{1}{2} kc^2y_0e^{-cx_0}-\dfrac{psE_0}{(px_0-s)^2}-be^{-2i\omega \tau _n\theta }\\&\quad -kcq_2e^{-cx_0},\\&G_{21}=q_2,\\&H_{11}=\dfrac{1}{2}kc^2y_0e^{-cx_0}-\dfrac{psE_0}{(px_0-s)^2} -b\\ {}&\quad -kce^{-cx_0}\mathrm {Re}(q_2),\\&H_{21}=\mathrm {Re}(q_2). \end{aligned}$$

Consequently, we have

$$\begin{aligned}&M_1=\left( \begin{array}{c} \dfrac{4G_{11}i\omega -2k\left( 1-e^{-cx_0}\right) G_{21}}{\Omega } \\ \dfrac{\Lambda }{\Omega } \\ \end{array} \right) ,\\&M_2=\left( \begin{array}{c} -\dfrac{2H_{21}}{y_0}\\ \dfrac{2y_0H_{11}-\left( \dfrac{2ky_0}{x_0} +\dfrac{2px_0E_0}{px_0-s}-2kcy_0e^{-cx_0}-\dfrac{2ky_0e^{-cx_0}}{x_0} -2bx_0\right) H_{21}}{ky_0\left( 1-e^{-cx_0}\right) }\\ \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned}&\Omega =ky_0\left( 1-e^{-cx_0}\right) +2bx_0i\omega e^{-2i\omega \tau _n}-4\omega ^2\\&\qquad -\left( \dfrac{2ky_0}{x_0} +\dfrac{2px_0E_0}{px_0-s}-2kcy_0e^{-cx_0}-\dfrac{2ky_0e^{-cx_0}}{x_0}\right) i\omega ,\\&\Lambda =2y_0G_{11}+\left( 4i\omega -\dfrac{2ky_0}{x_0}-\dfrac{2px_0E_0}{px_0-s}\right. \\&\left. \qquad +\,2kcy_0e^{-cx_0}+\dfrac{2ky_0e^{-cx_0}}{x_0}+2bx_0 e^{-2i\omega \tau _n}\right) G_{21}. \end{aligned}$$

And then we can evaluate the following values:

$$\begin{aligned}&c_1(0)=\dfrac{i}{2\omega \tau _n}\left( g_{11}g_{20}-2\left| g_{11}\right| ^{2}\right. \\&\left. \quad -\dfrac{\left| g_{02}\right| ^2}{3}\right) +\dfrac{g_{21}}{2}, \mu _2=-\dfrac{\mathrm {Re}\{c_1(0)\}}{\mathrm {Re}\{\lambda '(\tau _n)\}},\\&\beta _2=2\mathrm {Re}\{c_1(0)\},\ \, T_2=-\dfrac{\mathrm {Im}\{c_1(0)\}+\mu _2\mathrm {Im} \{\lambda '(\tau _n)\}}{\omega \tau _n}, \end{aligned}$$

which determine the properties of bifurcating periodic solutions at the critical value $\tau _n$. $\mu _2$ determines the direction of Hopf bifurcation, $\beta _2$ determines the stability of bifurcating periodic solutions and $T_2$ determines the period of the bifurcating periodic solutions. In view of Ref. [6], we have the following Theorem.

Theorem 3.1

For the system (1.5),

• (i) if $\mu _2>0$ ($\mu _2<0$), then the Hopf bifurcation is supercritical (subcritical);

• (ii) if $\beta _2<0$ ($\beta _2>0$), then the bifurcating periodic solutions are stable (unstable);

• (iii) if $T_2>0$ ($T_2<0$), then the bifurcating periodic solutions increase (decrease).

4 Numerical simulations

In this section, we will present some numerical simulations to verify the theoretical results in Sects. 2 and 3. With the sole purpose of illustrating the results that we have established in the previous sections, in view of (2.1) and the conditions in Theorem 2.1, we choose the parameters of the modified predator–prey system (1.5) as  $a=5.5-1.5e^{-1},\ \,b=2-0.5e^{-1},\ \,k=1,\ \,c=0.5,\ \,d=2,\ \,p=1,\ \,s=1,\ \,v=1,$ then we have the following system

(4.1)

The system (4.1) has a positive equilibrium point $X_0=(2,1,1)$. In view of the discussion in Sect. 2, we can obtain that $\omega ^+=3.1417$ and $\omega ^-=0.2012$. And then, the critical values of the time delay corresponding to $\omega ^\pm$ are $\tau ^+_0=0.3003$ and $\tau ^-_0=4.6890$. By Theorem 2.1, $X_0=(2,1,1)$ is asymptotically stable when $\tau \in [0, 0.3003)$ and unstable when $\tau \in (0.3003, 4.6890)$. Thus the system (4.1) undergoes a Hopf bifurcation at $\tau =0.3003$.

Besides, according to the algorithms used in Sect. 3, we can obtain the following values with the help of Matlab 7.0 : $c_1(0)=1.7529-8.7556i,\ \,\lambda '(\tau _0^+)=10.2460-5.5445i,$  $\mu _2=-0.1711<0,\ \,\beta _2=3.5058>0,\ \,T_2=8.2749>0.$ By the discussion in Sect. 3, we know that the system (4.1) undergoes a subcritical Hopf bifurcation at the positive equilibrium $X_0$, the bifurcating periodic solutions occur when $\tau$ crosses $\tau _0^+$ to the left, and the bifurcating periodic solutions are unstable and increase.

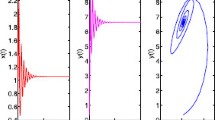
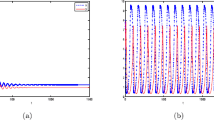
According to Theorem 2.1 and Theorem 3.1, the equilibrium point $X_0=(2,1,1)$ is locally asymptotically stable when $\tau =0.295<\tau _0^+$ as it is illustrated by computer simulations in Fig. 1. The periodic solutions occur from $X_0$ when $\tau =0.3001<\tau _0^+$ as it is illustrated by computer simulations in Fig. 2. The bifurcating periodic solutions are unstable and increase when $\tau =0.3004>\tau _0^+$ as it is illustrated by computer simulations in Fig. 3. The equilibrium point $X_0$ is unstable when $\tau =0.303>\tau _0^+$ as it is illustrated by computer simulations in Fig. 4.

Fig. 1

The equilibrium point $X_0$ of system (4.1) is asymptotically stable when $\tau =0.295<\tau _0^+$ and the initial conditions $x_{0}=1.999,\,y_{0}=1.0062,\,E_{0}=0.999$

Fig. 2

Periodic solutions bifurcating from the equilibrium point $X_0$ of system (4.1) when $\tau =0.3001<\tau _0^+$ and the initial conditions $x_{0}=1.999,\,y_{0}=1.0062,\,E_{0}=0.999$

Fig. 3

The bifurcating periodic solutions are unstable and increase when $\tau =0.3004>\tau _0^+$ and the initial conditions $x_{0}=1.999,\,y_{0}=1.0062,\,E_{0}=0.999$

Fig. 4

The equilibrium point $X_0$ of system (4.1) is unstable when $\tau =0.303>\tau _0^+$ and the initial conditions $x_{0}=1.999,\,y_{0}=1.0062,\,E_{0}=0.999$

5 Discussion

As we known, time delay plays an important role in the dynamic behavior of predator–prey systems. From the stability analysis of the system in Sect. 2, we can see that the time delay switches the stability of the proposed system. When there is no time delay or the time delay is less than the critical value $\tau _0^+$, the positive equilibrium $X_0$ is asymptotically stable. That is, the prey population, the predator population and the harvest effort will stay at steady states. And then, the sustainable development of the biological resources can be ensured. As the time delay increases beyond the critical value $\tau _0^+$, the time delay can cause a stable equilibrium to become unstable and a Hopf bifurcation occurs, which would induce ecosystem unbalance and even biological disaster. In Sect. 3, the formulae for determining the direction of the bifurcations and the stability of the bifurcating periodic solutions are given by using the normal form theory and center manifold theorem. The biological meaning implies that both the species may coexist in an oscillatory mode when the bifurcating periodic solutions are stable.

In this paper, the harvest reward p and the cost s are constants. However, from real-world view, they are not always constants and may vary with numerous factors, such as seasonality, market supply, market demand and so on. Hence, it is more reasonable that the reward p and the cost s should be variables. Besides, the existence of the periodic solutions remain valid only in a small neighborhood of the critical values here, we may investigate the global continuation of the local Hopf bifurcation. Furthermore, the feedback delay of predator species, or more time delays may be introduced into the model system and consider the combined effect of multiple delays for the dynamical behavior of biological populations.

We leave these issues for future consideration.