Strange attractors generated by a fractional order switching system and its topological horseshoe

Abstract

Chaos generation in a new fractional order unstable dissipative system with only two equilibrium points is reported. Based on the integer version of an unstable dissipative system (UDS) and using the same system’s parameters, chaos behavior is observed with an order less than three, i.e., 2.85. The fractional order can be decreased as low as 2.4 varying the eigenvalues of the fractional UDS in accordance with a switching law that fulfills the asymptotic stability theorem for fractional systems. The largest Lyapunov exponent is computed from the numerical time series in order to prove the chaotic regime. Besides, the presence of chaos is also verified obtaining the topological horseshoe. That topological proof guarantees the chaos generation in the proposed fractional order switching system avoiding the possible numerical bias of Lyapunov exponents. Finally, an electronic circuit is designed to synthesize this fractional order chaotic system.

1 Introduction

During the last years, fractional calculus starts to attract attention of physicists and engineers due to the fractional order models give more accuracy results than the corresponding integer-order models [1–11]. There are two main features for that claim; the fractional order parameter improves the system performance by increasing one degree of freedom, and the other one is related to fractional derivative that provides a valuable tool for the description of memory and hereditary properties in various processes [1–5]. Therefore, the fractional derivatives have been used to describe elegantly interdisciplinary applications; for instance, in control theory a fractional order controller has a unique isodamping property that improves robustness via reducing the sensitivity of the system stability margins with respect to the system uncertainties [6, 7]; in viscoelastic materials, the fractional order damping element provides a superior model because it is modeled as a force proportional to the fractional order derivative of the displacement [8]; also in dielectric polarization, a fractional model is better to study the relation between the dynamic polarization, and frequency and electric field amplitude [9]; and so on [10, 11].

One of the main objectives in the literature about fractional calculus is to find chaotic behavior in fractional order systems. Usually chaotic attractors cannot be observed in nonlinear systems whose order is less than three, so it is highly interesting to analyze the routes to get chaos of fractional systems with low orders. Recently there has been a trend to transform integer-order chaotic systems in fractional versions because the integer-order versions preserve chaotic dynamics when their models become fractional [5], such as the fractional Lorenz system [12], the fractional Chen system [13], the fractional Chua’s circuit [14], the fractional Rössler system [15], the fractional jerk system [16], the fractional Lü system [17], and many others [18]. Compared to integer-order, the fractional chaotic systems have the following advantages; the fractional derivatives have complex geometrical interpretation because of their nonlocal character and high nonlinearity; the power spectrum of fractional order chaotic systems fluctuates complexly increasing the chaoticity in frequency domain; and the computational complexity goal is also achieved. More specifically, the security in cryptosystems based on chaos can be increased using the derivative orders of fractional chaotic systems as secret keys in addition to the system’s parameters [19, 20]; so, the complexity of the verification of each key is strengthened causing the traditional cracking algorithms of chaotic masking to be unusable. Therefore, new fractional chaotic systems are crucial to enhance the performance of several integer-order chaos-based applications. Recently, engineering applications using fractional order chaotic systems have been demonstrated, such as a digital cryptography approach, an image encryption method, a cipher and an authenticated encryption scheme [21–24].

In this work, a fractional order unstable dissipative system (FOUDS) is proposed and analyzed, considering the dynamical characteristics of the integer-order UDS that have been previously reported [25]. In a first case, we are interested in finding an effective minimum order using the same system’s parameters as integer-order version while chaos behavior is preserved. The chaotic attractor of the fractional system appears as a result of the combination of several unstable one-spiral trajectories around a saddle hyperbolic equilibrium point. As second case, we study the trade-off between the eigenvalues of equilibrium points and the reduction in effective dimension, which is the sum of all orders concerned to derivatives, in the proposed fractional order chaotic system. The resulting chaotic attractor has the same number of equilibria as scrolls as shown herein.

The presence of chaos in FOUDS has been validated by using the time series analysis of the numerical temporal data. Additionally, we also demonstrate that chaotic behavior obtaining the topological horseshoe of FOUDS in both cases because it not only provides much information that Lyapunov exponents, but also shows detailed dynamics of chaos. Therefore, a fractional order system should be chaotic if a horseshoe can be found to exist in it [26–31]. The reason to find a horseshoe is that Lyapunov exponents seem insufficient to reveal chaotic characteristics of the fractional order systems because the numerical error may make them uncertain, especially when the computed largest Lyapunov exponent is close to zero. Finally, an electronic circuit is designed to obtain circuit simulations of FOUDS with two different fractional orders.

2 Basic definitions in fractional calculus

In literature, there are different definitions for fractional derivatives [2–5]. The Riemann–Liouville and the Caputo definitions are more reported than others [3]. The Caputo definition of the fractional derivative is,

$$\begin{aligned} {}_{0}D_t^{\alpha }f(t)=\frac{1}{\varGamma (n-\alpha )}\int _0^t\frac{f^{(n)}(\tau )}{(t-\tau )^{\alpha +1-n}}\mathrm{{d}}\tau , \end{aligned}$$

(1)

and the Riemann–Liouville definition can be described as

$$\begin{aligned} {}_{a}D_t^{\alpha }f(t)=\frac{1}{\varGamma (n-\alpha )}\frac{d^n}{\mathrm{{d}}t^n}\int _a^t(t-\tau )^{n-\alpha -1}f(\tau )\mathrm{{d}}\tau , \end{aligned}$$

(2)

where $n=\lceil \alpha \rceil$, and $\varGamma$ is the Gamma function,

$$\begin{aligned} \varGamma (z)=\int _0^{\infty }t^{z-1}e^{-t}\mathrm{{d}}t, \end{aligned}$$

(3)

in both definitions.

Fig. 1

Stability region of a fractional order linear time invariant system with order $0<\alpha <1$

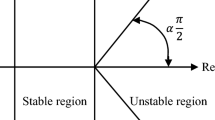
Besides, for fractional order systems the stability region depends on the fractional order $\alpha$ as shown in Fig. 1. Note that a saddle hyperbolic stationary point of a fractional order linear system can be transformed in a stable stationary point by just changing the derivative order $\alpha$ of the system. This is an important consideration for the design of chaotic attractors based on the proposed FOUDS.

2.1 Numerical method for solving fractional differential equations

Similar to integer-order systems, the solution of the fractional systems is computed using a numerical integration algorithm. The Adams–Bashforth–Moulton (ABM) method, a predictor–corrector scheme, reported in [32] is used herein to obtain the time evolution of fractional derivatives of the proposed FOUDS. That algorithm is a generalization of the classical Adams–Bashforth–Moulton integrator that is well known for the numerical solution of first-order problems [33, 34]. We select the ABM as numerical solver because it is based on the Caputo derivatives which allows us to specify both homogeneous and inhomogeneous initial conditions contrary to Riemann–Liouville-based methods. Additionally, recent literature has shown that using a frequency domain approximation in the numerical simulations of fractional systems may result in wrong consequences [35].

Consider the following fractional differential equation:

$$\begin{aligned} \begin{array}{l} D^{\alpha }y(t) =f(t,y(t)), \quad 0\le t\le T; \\ y^{(k)}(0) =y_0^{(k)}, \quad k=0,1,\ldots , n-1. \end{array} \end{aligned}$$

(4)

The solution of (4) is given by an integral equation of Volterra type as

$$\begin{aligned} y(t)=\sum _{k=0}^{ \lceil \alpha \rceil -1}y_{0}^{k}\frac{t^{k}}{k!}+\frac{1}{\varGamma (\alpha )}\int _0^t(t-z)^{\alpha -1}f(z,y(z))\mathrm{{d}}z. \end{aligned}$$

(5)

As it is showed in [3], there is a unique solution of (4) on some interval [0, T], thence we are interested in a numerical solution on the uniform grid $\{t_n=nh |n=0,1,\ldots ,N\}$ with some integer N and step size $h=T/N$, then (5) can be replaced by a discrete form to get the corrector as follows

$$\begin{aligned} y_h\left( t_{n+1}\right)= & {} \sum _{k=0}^{ \lceil \alpha \rceil -1}y_{0}^{k}\frac{t^{k}}{k!}+\frac{h^{\alpha }}{\varGamma (\alpha +2)}f\left( t_{n+1},y_h^p(t_{n+1})\right) \nonumber \\&+\frac{h^{\alpha }}{\varGamma (\alpha +2)}\sum _{j=0}^{n}a_{j,n+1}f\left( t_j,y_h\left( t_j\right) \right) , \end{aligned}$$

(6)

where

$$\begin{aligned} a_{j,n+1} = \left\{ \begin{array}{l} n^{\alpha +1}-(n-\alpha )(n+1)^{\alpha }, \quad j=0,\\ (n-j+2)^{\alpha +1}+(n-j)^{\alpha +1}\\ \quad -2(n-j+1)^{\alpha +1} , \quad 1\le j \le n,\\ 1, \quad j=n+1, \end{array} \right. \end{aligned}$$

(7)

Moreover, the predictor has the following structure

$$\begin{aligned} y_{h}^p(t_{n+1})=\sum _{k=0}^{ \lceil \alpha \rceil -1}y_{0}^{k}\frac{t^{k}}{k!}+\frac{1}{\varGamma (\alpha )} \sum _{j=0}^{n}b_{j,n+1}f\left( t_j,y_h\left( t_j\right) \right) , \end{aligned}$$

(8)

with $b_{j,n+1}$ defined by

$$\begin{aligned} b_{j,n+1}=\frac{h^{\alpha }}{\alpha }\left( \left( n+1-j\right) ^\alpha -\left( n-j^\alpha \right) \right) . \end{aligned}$$

(9)

The error of this approximation is given by

$$\begin{aligned} \max _{j=0,1,\ldots N}\left| y\left( t_{j}\right) -y_{h}\left( t_{j}\right) \right| =\mathcal {O}\left( h^{P}\right) , \end{aligned}$$

(10)

where $P=\min (2,1+\alpha )$.

2.2 Stability conditions of fractional order systems

A general fractional order linear time invariant system is described by

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }x}{\mathrm{{d}}t^{\alpha }}=Ax+ Bu, \end{aligned}$$

(11)

where $x\in R^n$ is the state vector, $u\in R$ is a scalar signal, $A\in R^{n\times n}$ is a linear operator, $B\in R^{n}$ is a constant vector and $\alpha$ is the fractional commensurate order. The linear part of the system given by (11) can be rewritten as

$$\begin{aligned} \frac{\mathrm{{d}}^{\alpha }x}{\mathrm{{d}}t^{\alpha }}=Ax, \quad x(0)=x_0, \end{aligned}$$

(12)

with $0 < \alpha < 1$. The stability analysis of that system can be divided in two conditions as follows [5]:

• Asymptotically stable The system (12) is asymptotically stable if and only if $|\arg (\lambda )|> \frac{\alpha \pi }{2}$ for all eigenvalues ($\lambda$) of matrix A. In this case, the solution x(t) tends to 0 like $t^{-\alpha }$.

• Stable The system (12) is stable if and only if $|\arg (\lambda )|\ge \frac{\alpha \pi }{2}$ for all eigenvalues ($\lambda$) of matrix A obeying that the critical eigenvalues must satisfy $|\arg (\lambda )|=\frac{\alpha \pi }{2}$ and have geometric multiplicity of one.

Accordingly, the equilibrium points $p\equiv (x_1^*,x_2^*,x_3^*)$ of a general commensurate fractional order system, $\frac{\mathrm{{d}}^{\alpha }x}{\mathrm{{d}}t}=f(x)$ with fractional order $0 < \alpha <1$, are locally asymptotically stable if all the eigenvalues ($\lambda$) of its Jacobian matrix evaluated at the equilibrium point fulfill the following condition

$$\begin{aligned} \min _i\left| \arg \left( \lambda _i\right) \right| >\frac{\alpha \pi }{2}. \end{aligned}$$

(13)

Hence, the fractional order $\alpha$ is the key parameter to change the stability of an equilibrium point as a function of the stable and unstable regions which are shown in Fig. 1.

Fig. 2

Projections of the attractors onto the xy-plane for parameters given in Table 2

3 Fractional order unstable dissipative system (FOUDS)

3.1 Unstable dissipative system

A dynamical system is called unstable dissipative system (UDS) because it is dissipative in one of its components while unstable in the other two. The UDS is built with a switching law to obtain a strange attractor. The strange attractor appears as a result of the combination of several unstable one-spiral trajectories. Each of these trajectories lies around a saddle hyperbolic equilibrium point. [25] proposed the following multiscroll chaotic system by switching linear systems

$$\begin{aligned} \begin{array}{l} \dot{x}=y,\\ \dot{y}=z,\\ \dot{z}=-ax-by-cz +g(x), \end{array} \end{aligned}$$

(14)

with

$$\begin{aligned} g(x)= \left\{ \begin{array}{l} \beta , \quad \text {if} \quad x\ge 0.35,\\ 0, \quad \text {otherwise,} \\ \end{array} \right. \end{aligned}$$

(15)

being $a=1.5$, $b=1$, $c=1$ and $\beta =1$ the system’s parameters. The system in (14) is dissipative if the sum of its eigenvalues is negative, additionally this system has three eigenvalues; one eigenvalue is a negative real number and two eigenvalues are complex numbers with positive real part.

3.2 Chaos generation in FOUDS

In this section, the corresponding fractional order system of (14), considering (15) as the switched function, is introduced and analyzed. The main idea is to find the minimum fractional order where the system exhibits chaotic behavior using the same value for the system’s parameters as the integer-order case. The resulting FOUDS is given by

$$\begin{aligned} \begin{array}{l} D^{\alpha }x=y,\\ D^{\alpha } y=z,\\ D^{\alpha } z=-ax-by-cz +g(x), \end{array} \end{aligned}$$

(16)

where $\alpha \in (0,1)$. The equilibrium points of the system in (14) and its eigenvalues are given in Table 1. The system has only two equilibrium points O and $E_1$ which are saddle points of instability index two; therefore, there is a double-scroll attractor given by the system (16) as its equilibrium points are the same as the integer-order version.

Table 1 Equilibrium points and corresponding eigenvalues

Table 2 Parameters for which FOUDS generates chaotic behavior

In order to obtain fractional chaos from FOUDS, the stability general theorem given in (13) must be satisfied. As a result, the system (16) displays regular and stable behavior if

$$\begin{aligned} \alpha <\frac{2}{\pi }\min _i\left| \arg \left( \lambda _i\right) \right| \approx 0.9417 \end{aligned}$$

(17)

Accordingly, the system does not show chaotic behavior for $\alpha <0.9417$ as demonstrated in Fig. 2a where the projection of the attractor onto the xy-plane for $\alpha =0.94$ is displayed.

Table 3 Parameters for which FOUDS generates regular oscillations and chaotic behavior with low orders

Fig. 3

Projections of the attractors onto the xy-plane for parameters given in Table 3

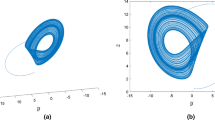
Hence, in order to show that FOUDS can generate chaotic behavior we consider $\alpha \ge 0.95$. Figure 2b shows the projection of the chaotic attractor onto the xy-plane for $\alpha =0.95$. Figure 2c–f shows the projections of the attractors onto the xy-plane for $\alpha =0.96, 0.97, 0.98, 0.99$, respectively. This set of chaotic attractors has the same number of equilibria as scrolls. By using the same parameters as integer-order case, we observe that FOUDS generates chaotic behavior with an effective minimum dimension as low as 2.85. Table 2 summarizes the results.

Figure 4a shows the largest Lyapunov exponent $\lambda _{\max }$ for the attractors of FOUDS in Fig. 2 as a function of the fractional order $\alpha$. The largest Lyapunov exponent is computed from the numerical time series of the state variable x using TISEAN package software as it has been appointed as a proved tool to investigate the presence of chaos in several numerical and experimental systems [36]. As a result, FOUDS shows chaotic behavior because it has an attractor with a positive Lyapunov exponent at least. We observe this behavior in the approximate range of $\alpha \in [0.95, 0.99]$ by considering the system’s parameters $a=1.5,b=1, c=1, \beta =1$. Table 2 shows that the magnitude of the largest Lyapunov exponent depends on the fractional order $\alpha$, as reported in [12–18].

3.3 Chaos in lowest orders of FOUDS

As mentioned in the introduction, a viable application of the fractional chaotic systems consists on using the fractional derivative order as the key for secure communications schemes. So smaller the value of the fractional order, the greater the number of possible combinations for the secret key.

As second case, other values for system’s parameters a, b, c, and function g(x) are proposed in order to find chaos behavior with lower fractional orders. By means of considering the strange attractor that appears as a result of the combination of several unstable one-spiral trajectories around a saddle hyperbolic stationary point, the corresponding eigenvalues are scaled in a proper form to preserve the chaotic regime and the asymptotic stability in (13). Notice that the equilibrium points (Table 1) together with commutation plane are identical as integer-order case. It means a and $\beta$ must be chosen in a convenient way to preserve the relation $\beta /a=$ 0.66.

Chaotic attractors of FOUDS are observed for two different sets of parameters, given in Table 3, as shown in Fig. 3d–f. Compared to previous case, chaos can be obtained with lower effective dimensions of 2.49, 2.46 and 2.4, respectively. Similarly, the largest Lyapunov exponent of these attractors is plotted versus $\alpha$ in Fig. 4b. Again, the fractional system in (16) presents chaotic behavior in the approximate interval of $\alpha \in [0.815, 0.84]$ with $a=4.75,b=0.9, c=0.9, \beta =3.16$. In addition, regular oscillations are found when the system’s parameters do not fulfill the stability condition, as displayed in Fig. 3a–c.

Fig. 4

Largest Lyapunov exponent of the proposed fractional system in (16) for cases in Tables 2 and 3, respectively. The horizontal axis represents fractional order $\alpha$ with dimensionless, the vertical axis represents the magnitude of $\lambda _{\max }$

4 Topological horseshoe analysis in FOUDS

A common analysis to verify the chaotic behavior of a dynamical system is carried out by computing its Lyapunov exponents as they are a good tool to characterize the high sensitivity to the initial conditions. Nevertheless, when dealing with chaotic systems, sometimes it is difficult to get Lyapunov exponents with high computation accuracy because it may also depend on the length of time computed as well as the step size used to numerical integration algorithms [30, 31]. Therefore, the largest Lyapunov exponent seems insufficient to validate absolutely the chaotic behavior of fractional order systems, especially when the computed value of this exponent is close to zero, and the numerical error may cause a bias.

On the other hand, the topological horseshoe theory, which is based on the notion of symbolic dynamics [26–31], provides a rigorous proof to estimate topological entropy, verifies existence of chaos and reveals invariant sets of chaotic attractors in chaotic systems. The topological horseshoe depends on the geometry of continuous maps on some subsets of interest in state space based on the second return Poincaré map; for continuous-time systems, the topological horseshoe theorem cannot be directly applied [27]. Therefore, one needs to find an appropriate Poincaré section to obtain a Poincaré map.

In this work, the topological horseshoe of FOUDS is determined for the cases shown in previous section in order to double check its chaotic regime and because not only provides much information that Lyapunov exponents, but also shows detailed dynamics of chaos, that is to say, the attractor of a fractional order system should be chaotic if a horseshoe can be found to exist in it [26].

The basic procedure is to propose an appropriate Poincaré section and define a second return Poincaré map, which implies that the entropy of the attractors of FOUDS is not less than $\log 2$, giving a compelling signature of chaos.

4.1 Aspects of symbolic dynamics

Let $S_m=\{0,1,\ldots ,m-1\}$ and $\sum _m$ be the collection of all bi-infinite sequences with their elements $s\in \sum _m$:

$$\begin{aligned} s= & {} \{\ldots ,s_{-n},\ldots ,s_{-1},s_{0},s_{1},\ldots ,s_{n},\dots \},\\&\quad s_i\in S_m, \forall i. \end{aligned}$$

If we consider another sequence $\bar{s}\in \sum _m$, with

$$\begin{aligned} \bar{s}= & {} \{\ldots ,\bar{s}_{-n},\ldots ,\bar{s}_{-1},\bar{s}_{0},\bar{s}_{1},\ldots ,\bar{s}_{n},\dots \},\\&\quad \bar{s}_i\in S_m, \forall i. \end{aligned}$$

Then the distance between s and $\bar{s}$ is defined as

$$\begin{aligned} d\left( s,\bar{s}\right) =\sum \limits _{-\infty }^{\infty } \frac{1}{2^{|i|}}\frac{\left| s_i-\bar{s}_i\right| }{1+\left| s_i-\bar{s}_i\right| }. \end{aligned}$$

(18)

4.2 Metric space and the m-shift

With the distance defined in (18), $\sum _m$, is a metric space and with the following three properties whereby a set is called a Cantor set.

Theorem 1

[28] The metric space $\sum _m$ is

• (i) compact;

• (ii) totally disconnected;

• (iii) perfect.

Now define a map of $\sum _m$ into itself, denoted by $\gamma$, as follows:

$$\begin{aligned} \gamma (s_i)=s_{i+1}, \quad \forall i. \end{aligned}$$

(19)

The map $\gamma$ is called an m-shift map, which has the following properties.

Theorem 2

[26] (a) $\gamma (\sum _m) = \sum _m$, and $\gamma$ is continuous; (b) The shift map $\gamma$ as a dynamical system defined on $\sum _m$ has:

• (i) a countable infinity of periodic orbits consisting of orbits of all periods;

• (ii) an uncountable infinity of nonperiodic orbits;

• (iii) a dense orbit.

In this manner, the dynamics generated by the shift map $\gamma$ displays sensitive dependence on initial conditions on a closed invariant set and transitivity; therefore, it is chaotic. (See [26–31] for proofs of the theorems.)

Let X be a metric space, D be a compact subset of X and $f : D \rightarrow X$ be a map satisfying the assumption that there exist m mutually disjoint subsets $D_1,\ldots , D_{m-1}$ and $D_m$ of D, so that the restriction of f to each $D_i$, f|Di, is continuous, for all $i=1,\ldots , m-1.$

Definition 1

[28, 29] Let $\xi$ be a compact subset of D,  such that for every $1\le i\le m,$ $\xi _i=\xi \bigcap D_i$ is nonempty and compact. Then $\xi$ is called a connection with respect to $D_1,\ldots ,D_{m-1}$ and $D_m$. Let F be a family of connections with respect to $D_1,\ldots ,D_{m-1}$ and $D_m,$ satisfying the property:

$$\begin{aligned} \xi \in F \Rightarrow f\left( \xi _i\right) \in F. \end{aligned}$$

Then F is said to be an f-connected family with respect to $D_1,\ldots ,D_{m-1}$ and $D_m$.

Definition 2

[26] If there is a continuous and onto map

$$\begin{aligned} h:K\rightarrow \sum _m \end{aligned}$$

such that $h \circ f=\gamma \circ h,$ then f is said to be a semi-conjugate to $\gamma .$

Theorem 3

[26–29] If there is an f-connection family with respect to $D_1,D_2,\ldots ,D_m,$ then there is a compact invariant set $K \subset D,$ such that f|K is semi-conjugate to an m-shift map.

Theorem 4

[17] For two dynamical systems (X, f) and (Y, g), if (X, f) is semi-conjugate to (Y, g),  then the topology entropy of f is not less than that of g.

The topological entropy is a nonnegative real number. Then, the system is chaotic if its topological entropy is not zero. Furthermore, if g is an m-shift map, then $ent(f ) \ge ent(g) = \log m$, that is, f is chaotic when $m > 1$.

4.3 Finding the topological horseshoe in the proposed FOUDS

In this subsection, we prove the existence of the horseshoe in the fractional order system in (16) based on the review of the section above.

Fig. 5

Chaotic attractor of the FOUDS with parameters $a=4.75, b=0.9, c=0.9, \beta =3.16$

First, the plane $\varOmega =\{(x,y,z)\in R^3:x=0\}$ which is shown in Fig. 5 is proposed considering FOUDS in (16) with $a=4.75,b=0.9, c=0.9, \beta =3.16$. On this plane, we choose a Poincaré section with its four vertices being

$$\begin{aligned}&A(0,0.45,0.48), \quad B(0,0.53,0.538),\\&C(0,0.54,0.498), \quad D(0,0.46,0.44). \end{aligned}$$

The Poincaré map

$$\begin{aligned} P:|ABCD|\rightarrow \varOmega , \end{aligned}$$

is defined as follows. For each point $x\in |ABCD|, P(x)$ is chosen to be the second return intersection point with $\varOmega$ under the flow of the system (16) with initial condition x. Under this Poincaré map P, P(x) is very thin hook-like strip which is wholly across |ABCD| as shown in Fig. 6, where

$$\begin{aligned} A^{\prime }=P(A),\; B^{\prime }=P(B),\;C^{\prime }=P(C),\;D^{\prime }=P(D), \end{aligned}$$

are the images of points, respectively.

Theorem 5

The Poincaré map P corresponding to the Poincaré section |ABCD| has the property that there is a closed invariant set $\varLambda \subset |ABCD|$ for which $P|\varLambda$ is semi-conjugate to the 2-shift map. Hence, $ent(P)\ge \log 2>0.$ This implies that attractor generated by the proposed FOUDS in (16) with $a=4.75, b=0.9, c=0.9, \beta =3.16,$ has a positive topological entropy.

Proof

In order to prove the assertion, one must find two mutually disjointed subsets of |ABCD|,  such that a P-connected family with respect to them exists. $\square$

The subsets are denoted by $Q_1$ and $Q_2$ as shown in Fig. 6, the first subset $Q_1$ with the quadrangle |ADEF| . Under the first return Poincaré map P, the subset $Q_1$ is mapped to $|A^{\prime }D^{\prime }E^{\prime }F^{\prime }|$ with AD mapped to $A^{\prime }D^{\prime }$ and EF mapped to $E^{\prime }F^{\prime }$. We can make the conclusion that the image $P(Q_1)$ lies wholly across the quadrangle |ABCD| with respect to AD and BC as shown in the Fig. 7.

Fig. 6

Two mutually disjoint subsets |AEFD| and |GBCH| of the quadrangle |ABCD|

Fig. 7

The image $|A^{\prime }E^{\prime }F^{\prime }D^{\prime }|$ of the quadrangle |AEFD| under the map P

Fig. 8

The image $|G^{\prime }B^{\prime }C^{\prime }H^{\prime }|$ of the quadrangle |GBCH| under the map P

The second subset $Q_2$, namely quadrangle |GBCH|, with GH and BC being its bottom and top edges, respectively. Like $Q_1$, the subset $Q_2$ is mapped to $|G^{\prime }B^{\prime }C^{\prime }H^{\prime }|$ under the Poincaré map P with GH mapped to $G^{\prime }H^{\prime }$ and BC mapped to $B^{\prime }C^{\prime }$. Thus, the image $P(Q_2)$ lies wholly across the quadrangle |ABCD| with respect to AD and BC as shown in the Fig. 8.

Evidently, the subsets $Q_1$ and $Q_2$ are mutually disjointed. Therefore, it follows that for every connection of |ABCD| respect $Q_1$ and $Q_2$, for instance, $Q_5$, the images $P(Q_5 \cap Q_1 )$ and $P(Q_5 \cap Q_2 )$ also lie wholly across the quadrangle |ABCD|. Thus the images of $P(Q_5 \cap Q_1 )$ and $P(Q_5 \cap Q_2 )$ are still connected with respect to $Q_1$ and $Q_2$. According to Definition 1 and Theorem 3, there is a P-connected family, so that the Poincaré map P is semi-conjugate to the 2-shift map. Based on Theorem 4, it is concluded that the entropy of P is not less than $\log 2$, which implies that the attractors in Fig. 3e, f have a positive entropy. The proof is completed.

Similarly, we apply the same proof to demonstrate the topological horseshoe when $a=3.75,b=0.7, c=0.7, \beta =2.5$, are selected as system’s parameters of FOUDS in (16), the corresponding attractor is shown in Fig. 3d. In this plane, i.e., $x=0$, we set a Poincaré section with its four vertexes being

$$\begin{aligned}&\hat{A}(0,0.4,0.45),\quad \hat{B}(0,0.45,0.475),\\&\hat{C}(0,0.5,0.45), \quad \hat{D}(0,0.45,0.4). \end{aligned}$$

The Poincaré map

$$\begin{aligned} \hat{P}:|\hat{A}\hat{B}\hat{C}\hat{D}|\rightarrow \hat{\varOmega }, \end{aligned}$$

is defined as follows. For each point $x\in |\hat{A}\hat{B}\hat{C}\hat{D}|, \hat{P}(x)$ is chosen to be the first return intersection point with $\hat{\varOmega }$ under the flow of the system (16) with initial condition x. Under this Poincaré map $\hat{P}$, $\hat{P}(x)$ is a very thin hook-like strip which is wholly across $|\hat{A}\hat{B}\hat{C}\hat{D}|$ as shown in Fig. 9, where

$$\begin{aligned} \hat{A}^{\prime }= & {} \hat{P}\left( \hat{A}\right) ,\; \hat{B}^{\prime }=\hat{P}\left( \hat{B}\right) ,\\\hat{C}^{\prime }= & {} \hat{P}\left( \hat{C}\right) ,\;\hat{D}^{\prime }=\hat{P}\left( \hat{D}\right) , \end{aligned}$$

are the images of points, respectively.

Theorem 6

The Poincaré map P corresponding to the Poincaré section $|\hat{A}\hat{B}\hat{C}\hat{D}|$ has the property that there is a closed invariant set $\hat{\varLambda } \subset |\hat{A}\hat{B}\hat{C}\hat{D}|$ for which $\hat{P}|\hat{\varLambda }$ is semi-conjugate to the 2-shift map, Hence, $ent(\hat{P})\ge \log 2>0.$ This implies that attractor generated by system (16) with $a=3.75,b=0.7, c=0.7, \beta =2.5,$ has a positive topological entropy.

Proof

In order to demonstrate the Theorem 6, two mutually disjointed subsets of $|\hat{A}\hat{B}\hat{C}\hat{D}|$ must be found, such that a $\hat{P}$-connected family with respect to them exists. $\square$

The subsets are denoted by $Q_3$ and $Q_4$ as shown in Fig. 9, the first subset $Q_3$ with the quadrangle $|\hat{A}\hat{D}\hat{E}\hat{F}|$. Under the first return Poincaré map $\hat{P}$, the subset $Q_3$ is mapped to $|\hat{A}^{\prime }\hat{D}^{\prime }\hat{E}^{\prime }\hat{F}^{\prime }|$ with $\hat{A}\hat{D}$ mapped to $\hat{A}^{\prime }\hat{D}^{\prime }$ and $\hat{E}\hat{F}$ mapped to $\hat{E}^{\prime }\hat{F}^{\prime }$. Again, the conclusion is the image $\hat{P}(Q_3)$ lies wholly across the quadrangle $|\hat{A}\hat{B}\hat{C}\hat{D}|$ with respect to $\hat{A}\hat{D}$ and $\hat{B}\hat{C}$ as shown in the Fig. 9.

Fig. 9

The image $|\hat{A}^{\prime }\hat{E}^{\prime }\hat{F}^{\prime }\hat{D}^{\prime }|$ of the quadrangle $|\hat{A}\hat{E}\hat{F}\hat{D}|$ under the map $\hat{P}$

The second subset $Q_4$ shown is, namely quadrangle $|\hat{G}\hat{B}\hat{C}\hat{H}|$, with $\hat{G}\hat{H}$ and $\hat{B}\hat{C}$ being its bottom and top edges, respectively. Like $Q_3$, the subset $Q_4$ is mapped to $|\hat{G}^{\prime }\hat{B}^{\prime }\hat{C}^{\prime }\hat{H}^{\prime }|$ under the Poincaré map $\hat{P}$ with $\hat{G}\hat{H}$ mapped to $\hat{G}^{\prime }\hat{H}^{\prime }$ and $\hat{B}\hat{C}$ mapped to $\hat{B}^{\prime }\hat{C}^{\prime }$. Thus, the image $\hat{P}(Q_4)$ lies wholly across the quadrangle $|\hat{A}\hat{B}\hat{C}\hat{D}|$ with respect to $\hat{A}\hat{D}$ and $\hat{B}\hat{C}$ as shown in the Fig. 10.

Fig. 10

The image $|\hat{G}^{\prime }\hat{B}^{\prime }\hat{C}^{\prime }\hat{H}^{\prime }|$ of the quadrangle $|\hat{G}\hat{B}\hat{C}\hat{H}|$ under the map $\hat{P}$

Fig. 11

a Circuit diagram to realize the fractional order unstable dissipative system (16) for $\alpha =0.95$. b Fractance element to get a fractional order, $\alpha =0.8$

Fig. 12

Circuit simulations of the chaotic attractors of FOUDS with fractional orders a $\alpha =0.95$ and, b $\alpha =0.8$

Evidently, the subsets $Q_3$ and $Q_4$ are mutually disjointed. Therefore, it follows that for every connection of $|\hat{A}\hat{B}\hat{C}\hat{D}|$ respect $Q_3$ and $Q_4$, for instance, $Q_6$, the images $\hat{P}(Q_6 \cap Q_3 )$ and $\hat{P}(Q_6 \cap Q_4 )$ also lie wholly across the quadrangle $|\hat{A}\hat{B}\hat{C}\hat{D}|$. Thus, the images of $\hat{P}(Q_6 \cap Q_3 )$ and $\hat{P}(Q_6 \cap Q_4 )$ are still connections with respect to $Q_3$ and $Q_4.$ According to Definition 1 and Theorem 3, there is a $\hat{P}$-connected family, so that the Poincaré map $\hat{P}$ is semi-conjugate to the 2-shift map. Based on Theorem 4, it is concluded that the entropy of $\hat{P}$ is not less than $\log 2$, which implies that the attractor in Fig. 3d has a positive entropy. The proof is completed.

All these facts prove that the attractors of FOUDS with fractional orders 0.83, 0.82 and 0.8 are chaotic.

5 Circuit simulation of FOUDS

This section describes the design and simulation of an analog electronic circuit that realizes the fractional order system in (16) using three integration channels to implement the state variables x, y, z and an only circuit that models the nonlinearity (15). These integration channels are designed by general analog computation approaches incorporated with a fractional order impedance called fractance, as shown in Fig. 11. Up to now, there are many papers about the guidelines to design circuits for fractances [2, 15, 16, 37]. By considering the design procedure in Refs. [15, 16], the fractances to approximate two different fractional orders, $\alpha =0.95$ and $\alpha =0.8$, are obtained as sketched by the blue dotted box and red dot–dash box, respectively, in Fig. 11.

For the nonlinearity (15), the electronic implementation uses a high-gain amplifier configuration based on operational amplifiers (opamps), and two diodes to generate a vertical voltage shift. The area remarked by the green solid line in Fig. 11 represents the nonlinearity where resistors Rs1, Rs2 and voltage E control its breakpoint whereas the resistor Rs3 and saturation voltage of opamps set $\beta$.

Figure 12a shows the circuit simulation of the chaotic attractor of FOUDS with a fractional order $\alpha =0.95$. The circuit parameters are chosen to $R=Rg1=Rg2=Ry=Rz=10\,k\varOmega , Rx=7.78\,k\varOmega , Rs1=1\,k\varOmega , Rs2=1\,M\varOmega , Rs3=68\,k\varOmega , E=0.35\,V, R1=694.6\,M\varOmega , R2=32.82\,M\varOmega , R3=0.3260\,M\varOmega , C1=0.7794\,\mu F, C2=0.2699\,\mu F, C3=0.3260\,\mu F, D1=D2=1n4001$, and TL081 opamps. By connecting the fractance marked with a red dot–dash box as shown in Fig. 11a, the circuit simulation of the chaotic attractor of FOUDS with a fractional order $\alpha =0.8$ is given in Fig. 12b. The updated parameters are $Rx=2.9\,k\varOmega , Ry=Rz=13.8\,k\varOmega , Rs3=25.37\,k\varOmega , R1=39.80\,M\varOmega , R2=9.839\,M\varOmega , R3=0.9330\,M\varOmega , R4=0.09319\,M\varOmega , R5=0.009555\,M\varOmega , C1=0.1884\,\mu F, C2=0.7619\,\mu F, C3=0.4520\,\mu F, C4=0.2545\,\mu F, C5=0.1396\,\mu F$.

By comparing the chaotic attractors in Fig. 12 with those in Figs. 2b and 3d, it can be concluded that the circuit simulations are consistent with the numerical simulations.

6 Conclusion

A fractional order unstable dissipative system has been introduced and analyzed. Chaotic behavior was observed with different fractional orders as a function of the system’s parameters. The minimum fractional order, $\alpha =0.8$, was obtained by modifying the eigenvalues of the fractional system but preserving the same equilibrium points as interger-order case. All fractional chaotic attractors analyzed have same scrolls than equilibria. The largest Lyapunov exponent was computed to give a first validation of chaotic behavior for all fractional chaotic attractors. Furthermore, the topological horseshoe for the lower fractional orders was found in order to confirm that the entropy of P is not less than $\log 2$. This gave a rigorous proof to guarantee that the proposed fractional order unstable dissipative system (FOUDS) can generate chaotic behavior. Finally, an electronic circuit to realize the fractional order chaotic system has been also introduced.