Nonlinear analysis on purely mechanical stabilization of a wheeled inverted pendulum on a slope

Abstract

This paper investigates the potential for stabilizing an inverted pendulum without electric devices, using gravitational potential energy. We propose a wheeled mechanism on a slope, specifically, a wheeled double pendulum, whose second pendulum transforms gravity force into braking force that acts on the wheel. In this paper, we derive steady-state equations of this system and conduct nonlinear analysis to obtain parameter conditions under which the standing position of the first pendulum becomes asymptotically stable. In this asymptotically stable condition, the proposed mechanism descends the slope in a stable standing position, while dissipating gravitational potential energy via the brake mechanism. By numerically continuing the stability limits in the parameter space, we find that the stable parameter region is simply connected. This implies that the proposed mechanism can be robust against errors in parameter setting.

1 Introduction

Electric and electronic control devices are indispensable for a variety of modern technologies. However, these technologies typically become useless during massive power outages such as those caused by natural or other disasters. In this paper, we consider a non-electrified alternative control method to stabilize an inverted pendulum using gravitational potential. Our proposed mechanism is a wheeled inverted pendulum that descends a slope. The brake mechanism of our proposed mechanism transforms gravity force into friction force between the pendulum and the wheel. This friction produces a restoring force by which the pendulum is asymptotically stabilized in a standing position.

Approaches similar to ours can be found in the field of passive dynamic walking, pioneered by McGeer [1], in which two-legged mechanisms are designed to stably walk down a slope that consume only gravitational potential energy. Extensive studies have been reported on the passive dynamic walking, including experimental development of passive walkers [1–3] and nonlinear analyses of passive dynamic walking based on simplified models [4–6]. Early insights into the use of such passivity can also be found in the study of passive gravity-gradient attitude stabilization [7–10], wherein the alignment of one axis of a satellite along the earth’s local vertical direction was achieved without the use of active control elements.

On the other hand, the wheeled inverted pendulum has attracted significant attention in the fields of control engineering and robotics. Because of the applications of wheeled inverted pendulums in personal mobility devices, including the Segway$^{\circledR }$ [11], methods for controlling wheeled inverted pendulums have been developed via approaches such as partial feedback linearization [12], inclined surface control [13], sliding-mode velocity control [14], neuro-fuzzy-based control [15], and robust control based on a quasi-linear parameter-varying model [16]. Not surprisingly, these studies implied the use of electric devices.

In this paper, we merge concepts from passive dynamic walking and studies of the wheeled inverted pendulum to derive our new mechanical design for the non-electrified stabilization of a wheeled inverted pendulum. As stated above, we propose a wheeled double pendulum mechanism, whose second pendulum transforms gravity force into braking force that acts on the wheel. To investigate the dynamic stabilities of this newly proposed mechanism, we start with deriving a nonlinear analytical model of the mechanism to examine the stabilities of its steady states. Three types of critical points arise in the analytical model. These critical points are analytically characterized and numerically continued in the parameter space to obtain stability limits for the steady-standing motions. It is found that the stability of the proposed mechanism is limited by Hopf bifurcation and vanishing external resistance on the wheel.

Fig. 1

Friction-controlled wheeled inverted pendulum (FCWIP)

2 Wheeled inverted pendulum with friction control

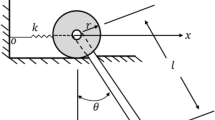
We propose a wheeled inverted pendulum with friction control, as shown in Fig. 1, that comprises (1) a wheel placed on a slope without slipping, (2) a double pendulum suspended on the wheel axis, and (3) a friction control mechanism that generates a braking force on the wheel proportional to the angle between the first and second pendulums. Hereinafter, we refer to this model as a friction-controlled wheeled inverted pendulum (FCWIP).

Configuration of the FCWIP can be described by a three-dimensional generalized coordinate: ($^T$denotes transpose)

$$\begin{aligned} \varvec{\theta }=(\theta _1,\theta _2,\theta _3)^T, \end{aligned}$$

(1)

where $\theta _1$ is the rotational angle of the wheel, $\theta _2$ is the absolute slant angle of the first pendulum, and $\theta _3$ is the relative angle of the second pendulum from the first pendulum. In addition, we consider the corresponding generalized force:

$$\begin{aligned} \varvec{T}=(T_1,T_2,T_3)^T, \end{aligned}$$

(2)

where $T_i$ is a torque acting on $\theta _i$.

2.1 Wheeled double pendulum

Unless the friction control mechanism (or ${\varvec{T}}$) is specified, the FCWIP in Fig. 1 is simply a wheeled double pendulum whose Lagrangian is given by

$$\begin{aligned} L:= & {} T - U: \end{aligned}$$

(3)

$$\begin{aligned} T:= & {} \frac{1}{2} {\dot{\theta }}_1^2 (Q_1 r+I_1) +\frac{1}{2} {\dot{\theta }}_2^2 \left\{ -2 Q_3 l \cos (\theta _3)+Q_2+I_2\right\} \nonumber \\&+\, \frac{1}{2} {\dot{\theta }}_3^2 (Q_3 w_G+I_3) +{\dot{\theta }}_2 {\dot{\theta }}_3 Q_3 \left\{ w_G-l \cos (\theta _3)\right\} \nonumber \\&+\, {\dot{\theta }}_1 {\dot{\theta }}_2 \left\{ -Q_3 r \cos (\alpha -\theta _2-\theta _3) +Q_4 r \cos (\alpha -\theta _2) \right\} \nonumber \\&-\, {\dot{\theta }}_1 {\dot{\theta }}_3 Q_3 r \cos (\alpha -\theta _2-\theta _3),\end{aligned}$$

(4)

$$\begin{aligned} U:= & {} -g \left\{ Q_3 \cos (\theta _2+\theta _3)-Q_4 \cos (\theta _2) +\theta _1 Q_1 \sin (\alpha )\right\} ,\nonumber \\ \end{aligned}$$

(5)

with

$$\begin{aligned} Q_1&= (m_1+m_2+m_3)r,\nonumber \\ Q_2&= m_2 l_G^2 + m_3 (w_G^2+l^2),\nonumber \\ Q_3&= m_3 w_G, \quad Q_4 = m_2 l_G+ m_3l, \end{aligned}$$

(6)

where the physical parameters are listed in Table 1.

Table 1 Mechanical parameters of the wheeled double pendulum

On substituting L into Lagrange’s equations with the generalized force ${\varvec{T}}$, we obtain the equations of the motion of the wheeled double pendulum as

$$\begin{aligned} M\ddot{\varvec{\theta }} = \varvec{F} + \varvec{T}, \end{aligned}$$

(7)

with

$$\begin{aligned}&M^T=M,\; M_{11} = Q_1 r+I_1 ,\nonumber \\&M_{12} = -Q_3 r \cos (\alpha -\theta _2-\theta _3) + Q_4 r \cos (\alpha -\theta _2),\nonumber \\&M_{13} = -Q_3r \cos (\alpha -\theta _2-\theta _3) ,\nonumber \\&M_{22} = -2 Q_3 l \cos (\theta _3) +Q_2 + I_2 ,\nonumber \\&M_{23} = Q_3 \{w_G-l \cos (\theta _3)\} ,\quad M_{33} = Q_3 w_G + I_3, \end{aligned}$$

(8)

and

$$\begin{aligned} F_1=&Q_3 r ({\dot{\theta }}_2+{\dot{\theta }}_3){}^2 \sin (\alpha -\theta _2-\theta _3) \nonumber \\&\quad -\,Q_4 r {\dot{\theta }}_2^2 \sin (\alpha -\theta _2)+g Q_1 \sin (\alpha ), \nonumber \\ F_2=&- Q_3l {\dot{\theta }}_3 (2 {\dot{\theta }}_2+{\dot{\theta }}_3) \sin (\theta _3) \nonumber \\&\quad -\,g\left\{ Q_3 \sin (\theta _2+\theta _3)- Q_4 \sin (\theta _2)\right\} , \nonumber \\ F_3=&Q_3l {\dot{\theta }}_2^2 \sin (\theta _3)-g Q_3 \sin (\theta _2+\theta _3) , \end{aligned}$$

(9)

where $M_{ij}$ represents the (i, j) component of the matrix M and $F_i$ is the ith component of the vector ${\varvec{F}}$.

2.2 Friction control mechanism

Next, we introduce a friction control mechanism (FCM) into the wheeled double pendulum by specifying ${\varvec{T}}$ as follows.

Let z be a displacement of the brake rod outputted from the cam mechanism, as shown in Fig. 1, and suppose that the cam function $z(\theta _3)$ is given as a linear function:

$$\begin{aligned} z=z(\theta _3):= \rho \,(\theta _3-\eta ) ,\quad \dot{z} = \rho \,\dot{\theta }_3 \end{aligned}$$

(10)

where $\rho$ is a cam ratio and $\eta >0$ is an offset angle. Accordingly, the follower is expected to follow both the positive and negative rotation of the cam.

Fig. 2

Example of the structure of the brake mechanism

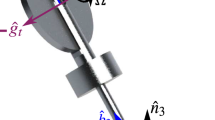
Then, we consider a brake mechanism, as shown in Fig. 2. In this mechanism, a pad (in light gray) is bonded on a brake rod (in dark gray) and sandwiched between the fixed base on the first pendulum and the brake disk without clearance at $z=0$. We refer to the lower half of the pad as a brake pad and the upper half as a dummy. The dummy pad has no function in terms of braking but is assumed to have the same mechanical property as the brake pad.

Thus, the brake pad touches the brake disk when $z\ge 0$ but is separated from the disk when $z<0$. We assume that the brake rod receives a continuous reaction force from the pads in the following form:

$$\begin{aligned} R = R(z,\dot{z}) :=&-(k_b z + c_b \dot{z}) \nonumber \\ =&-\rho \left\{ k_b (\theta _3-\eta ) + c_b \dot{\theta }_3\right\} , \end{aligned}$$

(11)

where $c_b$ and $k_b$ are viscoelastic coefficients of the pad.

The reaction force R produces a torque on $\theta _3$ as a generalized force $F_{\theta _3}$ on $\theta _3$, given by

$$\begin{aligned} F_{\theta _3} = \frac{\partial z}{\partial \theta _3}R(z,\dot{z}) = \rho R(z,\dot{z}). \end{aligned}$$

(12)

At the same time, we assume that R causes a Coulomb friction force between the brake pad and the brake disk. This force can be modeled by a tangential force on the contact surface as

$$\begin{aligned} F_R = \mu R(z,\dot{z})\,\text {sgn}(\dot{\theta }_1-\dot{\theta }_2)\chi (z) \end{aligned}$$

(13)

where $\mu$ is the Coulomb friction coefficient, $\text {sgn}(\cdot )$ is the unit signum function, and $\chi (\cdot )$ is the unit step function representing the separation of the brake pad from the brake disk. We have the torques $T_i$ on $\theta _i$ ($i=1,2,3$) as

$$\begin{aligned} {\left\{ \begin{array}{ll} T_1 = r_b F_R - c_1|\dot{\theta }_1|\dot{\theta }_1,\\ T_2 = -r_bF_R,\\ T_3 = F_{\theta _3} = \rho R(z,\dot{z}), \end{array}\right. } \end{aligned}$$

(14)

where $c_1$ is the coefficient of the quadratic resistance including aerodynamic force on the wheel (or $\theta _1$). Table 2 summarizes the parameters of the FCM and quadratic resistance. Note that the value of the spring coefficient listed in Table 2 can be obtained approximately from a medium-carbon steel rod (Young’s modulus 205 GPa) of $5\times 10^{-4}$m diameter and 0.5 m length.

Table 2 Parameters of the FCM

Therefore, we derive the dynamic model of the FCWIP as the wheeled double pendulum in (7) with the braking torque in (14).

Fig. 3

Time responses of the FCWIP for the condition listed in Tables 1 and 2

Fig. 4

Attraction basin of the stable steady state in Fig. 3

2.3 Numerical examples

Figure 3 shows a numerical solution of the FCWIP model obtained by solving (2), (7), and (14) from the trivial initial state $\theta _1(0)=\theta _2(0)=0$, $\theta _3(0)=\eta$ (or $z(0)=0$), and $\dot{\theta }_i(0)=0$ ($i=1,2,3$). The parameter values are listed in Tables 1 and 2 that are empirically chosen to achieve a stable standing motion. For numerical integration, a fourth-order Runge–Kutta–Gill method is employed with a time step of $10^{-3}$.

As shown in Fig. 3, the FCWIP model becomes asymptotically stable under the suitable parameter condition. In this example, the angle of the first pendulum $\theta _2(t)$ converges to a small negative value representing a standing position that is slightly slanted toward the upside of the slope. Consequently, the angle of the second pendulum $\theta _3(t)$ converges to a small positive value that represents it hanging from the first pendulum to produce the brake force $F_R$ in (13). Moreover, the descent velocity of the wheel $\dot{\theta }_1(t)$ converges to 9.46 rad/s (6.81 km/h in translational velocity).

Figure 4 shows the sets of initial angles $\theta _2(0), \theta _3(0)$ of the first and second pendulums, respectively. The other initial values are set as $\theta _1(0)=\dot{\theta }_i(0)=0$ $(i=1,2,3)$. The area hatched in gray is the set of initial angles from which the state converges to fallen positions of the FCWIP model, and the white area surrounded by the hatched area is the set that converges to the steady-standing state, as shown in Fig. 3. From Fig. 4, it appears that the set of the initial angles that belongs to the standing position forms a mostly connected area. Therefore, it can be expected that the proposed FCWIP model exhibits some robustness against disturbance of the initial angles.

Considering potential real-life applications of the proposed system, dependencies of the parameters on the size of the attraction basin that belongs to the standing position could be a crucial problem. This will be addressed in a future study.

3 Steady-state analysis

3.1 State-space representation

For a simple expression, we perform a timescale transformation $t:=qt^*$, where q is a timescale and $t^*$ is non-dimensional time. Taking a state vector:

$$\begin{aligned} {\varvec{x}}:= \left( \theta _1,\theta _2,\theta _3-\eta , q\dot{\theta }_1,q\dot{\theta }_2,q\dot{\theta }_3\right) ^T,\quad \dot{\theta }_i := d\theta _i/dt, \end{aligned}$$

(15)

we transform the dynamic model (7) and (14) to a state-space form:

$$\begin{aligned} {\dot{\varvec{x}}}= {\mathcal M}({\varvec{x}})^{-1}\Big \{{\varvec{f}}({\varvec{x}}) + {\varvec{\tau }}({\varvec{x}})\Big \}, \quad {\dot{\varvec{x}}}:= \mathrm{d}{\varvec{x}}/\mathrm{d}t^*, \end{aligned}$$

(16)

with

$$\begin{aligned} {\mathcal M}({\varvec{x}}):= & {} \text {diag}\Big (E_3,M({\varvec{x}})\Big ) ,\; \end{aligned}$$

(17)

$$\begin{aligned} {\varvec{f}}({\varvec{x}}):= & {} \begin{pmatrix} x_4\\ x_5\\ x_6\\ q^2{\varvec{F}}({\varvec{x}}) \end{pmatrix} ,\quad {\varvec{\tau }}({\varvec{x}}) := \begin{pmatrix} 0\\ 0\\ 0\\ q^2{\varvec{T}}({\varvec{x}}) \end{pmatrix} , \end{aligned}$$

(18)

where $M({\varvec{x}})$, ${\varvec{F}}({\varvec{x}})$, and ${\varvec{T}}({\varvec{x}})$ are the matrix and vectors in the dynamic model (7) and (14) via (15), and $E_3$ is a $3\times 3$ identity matrix.

We choose $q:=(k_b\rho ^2)^{-1/2}$ to normalize the spring coefficient $k_b$ and introduce non-dimensional parameters listed in Table 3. In this case, the components of the vectors in (18) are obtained as

$$\begin{aligned} {\left\{ \begin{array}{ll} q^2F_1= -Q_3 r (x_5+x_6)^2 \sin (\eta +x _2+x _3 -\alpha ) \\ \qquad \qquad +\,Q_4 r x_5^2 \sin (x_2 -\alpha )+g^*Q_1 \sin (\alpha ), \\ q^2F_2= -\,Q_3l x_6 (2 x_5+x_6) \sin (\eta +x_3) \\ \qquad \qquad -g^*\left\{ Q_3 \sin (\eta +x_2+x_3)- Q_4 \sin (x_2)\right\} , \\ q^2F_3= Q_3l x_5^2 \sin (\eta +x_3)-g^*Q_3 \sin (\eta +x_2+x_3) , \end{array}\right. } \end{aligned}$$

(19)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} q^2T_1 = - \,\mu ^*\text {sgn}(x_4-x_5)\chi (x_3) \left\{ x_3+c_b^*x_6\right\} \\ \qquad \qquad - \,c_1|x_4|x_4 ,\\ q^2T_2 = \mu ^*\text {sgn}(x_4-x_5)\chi (x_3) \left\{ x_3+c_b^*x_6\right\} ,\\ q^2T_3 = -\left\{ x_3+c_b^*x_6\right\} . \end{array}\right. } \end{aligned}$$

(20)

Table 3 Non-dimensional parameters

3.2 Assumption of steady state

In view of the numerical example presented in Fig. 3, we consider a steady state ${\varvec{x}}^*$ of the FCWIP model (16) that satisfies

$$\begin{aligned} {\dot{\varvec{x}}}= {\dot{\varvec{x}}}^*:=\left( \omega ,0,0,0,0,0\right) ^T ,\quad \omega >0\;(\text {constant}). \end{aligned}$$

(21)

The steady state ${\varvec{x}}^*$ mentioned above describes the rotation of the wheel down the slope with a constant angular velocity $x_4^*= \omega >0$, while the first and second pendulum maintain certain steady angles $x_2^*$ and $x_3^*$, respectively, with $x_5^*=x_6^*=0$. The angles $x_2^*$ and $x_3^*$ are assumed to satisfy the following conditions:

• (A) $x_2^*< 0$: the first pendulum reaches a standing position (slightly) slanted to the upside of the slope.

• (B) $x_3^*> 0$ (or $z^*>0$): due to (A), the second pendulum hangs from the first pendulum (due to gravity and while maintaining $x_2^*<0$) to produce the brake force $F_R$ in (13).

These conditions are required to stabilize the first pendulum in a standing position. Because, they guarantee existence of the braking force $F_R$ caused by a negative clearance between the brake pad and disk, $x_3^*>0$ (or $z^*>0$), and that is mechanically caused by $x_2^*<0$. Otherwise, the braking force vanishes, and the FCWIP becomes nothing more than an uncontrolled wheeled double pendulum that can never be stabilized around the standing position.

In addition, note that the FCWIP model, in absence of the floor model of the slope, can theoretically have another stable steady state, a static equilibrium where the second pendulum is hanging down at rest at $x_2^*=\pi +\epsilon _2$ and $x_3^*=\epsilon _3$ for small $\epsilon _2,\epsilon _3>0$.

3.3 Steady-state equation

The steady-state equation is given by

$$\begin{aligned} {\dot{\varvec{x}}}^*= {\mathcal M}({\varvec{x}}^*)^{-1}\Big \{{\varvec{f}}({\varvec{x}}^*) + {\varvec{\tau }}({\varvec{x}}^*)\Big \}, \end{aligned}$$

(22)

where the derivative ${\dot{\varvec{x}}}^*$ is the constant vector already defined in (21) and ${\varvec{x}}^*$ is an unknown vector representing the steady state. Multiplying both the sides by ${\mathcal M}({\varvec{x}}^*)$, we obtain

$$\begin{aligned} {\varvec{f}}({\varvec{x}}^*) + {\varvec{\tau }}({\varvec{x}}^*)= & {} {\mathcal M}({\varvec{x}}^*){\dot{\varvec{x}}}^*\nonumber \\= & {} \text {diag}\big (E_3,M({\varvec{x}}^*)\big ) {\dot{\varvec{x}}}^*= {\dot{\varvec{x}}}^* \end{aligned}$$

(23)

where the last equality is due to the zero components of ${\dot{\varvec{x}}}^*:=(\omega ,0,0,0,0,0)$. Therefore, the steady-state condition is obtained as follows:

$$\begin{aligned} x_4^*=\omega ,\quad x_5^*=x_6^*= 0, \end{aligned}$$

(24)

$$\begin{aligned} 0 = q^2F_1+q^2T_1 = g^*Q_1 \sin (\alpha ) - c_1\omega ^2 - \mu ^*x_3^*, \end{aligned}$$

(25)

$$\begin{aligned} 0 = q^2F_2+q^2T_2&=-g^*\left\{ Q_3 \sin (\eta +x_2^*+x_3^*)\right. \nonumber \\&\quad \left. -\,Q_4 \sin (x_2^*)\right\} +\mu ^*x_3^*, \end{aligned}$$

(26)

$$\begin{aligned} 0 = q^2F_3+q^2T_3 = -g^*Q_3 \sin (\eta +x_2^*+x_3^*) - x_3^*, \end{aligned}$$

(27)

where $|x_4^*|x_4^*= \omega ^2$ and $\text {sgn}(x_4^*-x_5^*)\chi (x_3^*)=1$ are substituted according to the assumption: $x_4^*-x_5^*=x_4^*=\omega >0$ and $x_3^*>0$ in Sect. 3.2.

Note that the Eqs. (25), (26), and (27) represent the balance of the torque from the brake force and the gravity force at about $\theta _1$, $\theta _2$, and $\theta _3$, respectively. In particular, (25) can also be derived from the balance of the energy supply from the gravitational potential and the energy consumption via Coulomb friction and quadratic resistance.

The steady-state equations in (24), (25), (26), and (27) can be reduced to the following form:

$$\begin{aligned} \left\{ \begin{aligned}&x_5^*=x_6^*= 0, \\&{c_1} (x_4^*)^2 = {g^*Q_1 \sin (\alpha )- \mu ^*x_3^*} > 0, \\&\sin (x_2^*) = -\frac{(1+\mu ^*)x_3^*}{g^*Q_4}, \\&\sin (x_2^*+x_3^*+\eta ) = -\frac{x_3^*}{g^*Q_3 }. \end{aligned} \right. \end{aligned}$$

(28)

Thus, we have derived the steady-state equations of the FCWIP model with three unknowns $x_2^*$, $x_3^*$, and $x_4^*$ ($=\omega$). Note that the angle of the wheel in the steady state $x_1^*(t)\propto \omega t$ never appears explicitly in these steady-state equations.

It is clear from (28) that under the given mechanical structure and environment, the non-trivial components of steady state $(x_2^*,$ $x_3^*,$ $x_4^*)$ depend on three parameters, namely $\mu ^*$, $\eta$, and $c_1$. More precisely, $x_2^*$ and $x_3^*$ can be solved independently of $x_4^*$, and they depend on the non-dimensional friction $\mu ^*$ and the offset $\eta$ of the FCM. After that, $x_4^*$ is obtained as a function of $x_3^*$ depending on $c_1$.

3.4 Jacobian matrix at steady state

We consider a variation $\delta {\varvec{x}}$ of ${\varvec{x}}$ around ${\varvec{x}}^*$ as ${\varvec{x}}:= {\varvec{x}}^*+ \delta {\varvec{x}}$ and substitute it into the state-space model (16) as ${\mathcal M}({\varvec{x}}^*+ \delta {\varvec{x}})\{{\dot{\varvec{x}}}^*+\delta {\dot{\varvec{x}}}\} = ({\varvec{f}}+{\varvec{\tau }})({\varvec{x}}^*+ \delta {\varvec{x}}).$ The ith component of the left side can be written by the Einstein notation as

$$\begin{aligned} L_i&={\mathcal M}_{ij}({\varvec{x}}^*+\delta {\varvec{x}}) \Big \{\dot{x}_j^*+ \delta \dot{x}_j\Big \} \nonumber \\&=\Big \{{\mathcal M}_{ij}({\varvec{x}}^*)+\frac{\partial {\mathcal M}_{ij}}{\partial x_k}\delta x_k\Big \} \Big \{\dot{x}_j^*+ \delta \dot{x}_j\Big \}\nonumber \\ {}&\quad +O(\delta {\varvec{x}},\delta \dot{x}_j)^2 \nonumber \\&= {\mathcal M}_{ij}({\varvec{x}}^*)\dot{x}_j^*+{\mathcal M}_{ij}({\varvec{x}}^*)\delta \dot{x}_j \nonumber \\&\quad +\,\frac{\partial {\mathcal M}_{ij}}{\partial x_k}\delta x_k\dot{x}_j^*+O(\delta {\varvec{x}},\delta {\dot{\varvec{x}}})^2. \end{aligned}$$

(29)

Due to the structures of ${\mathcal M}=\text {diag}(E_3,M)$ and ${\dot{\varvec{x}}}^*=(\omega ,0,0,0,0,0)^T$, we have

$$\begin{aligned} \frac{\partial {\mathcal M}_{ij}}{\partial x_k}\delta x_k\dot{x}_j^*= 0 = {\left\{ \begin{array}{ll} 0\cdot \delta x_k\omega &{}\quad (j=1)\\ \frac{\partial {\mathcal M}_{ij}}{\partial x_k}\delta x_k\cdot 0&{}\quad (j>1) \end{array}\right. } \end{aligned}$$

(30)

for all i and j. Therefore, neglecting the second- and higher-order term of $\delta {\varvec{x}}$ and $\delta {\dot{\varvec{x}}}$, we arrive at a variation equation of (16) as

$$\begin{aligned} \delta {\dot{\varvec{x}}}= {\mathcal M}({\varvec{x}}^*)^{-1}\Big \{ D{\varvec{f}}({\varvec{x}}^*) + D{\varvec{\tau }}({\varvec{x}}^*) \Big \} \delta {\varvec{x}}=: J({\varvec{x}}^*) \delta {\varvec{x}}, \end{aligned}$$

(31)

where $D{\varvec{f}}({\varvec{x}}^*)$ denotes the Jacobian matrix of ${\varvec{f}}({\varvec{x}})$ around ${\varvec{x}}^*$, and $J({\varvec{x}}^*)$ provides a closed-loop state matrix whose eigenvalues represent the stabilities of the FCWIP model. The components of $J({\varvec{x}}^*)$ are given by

$$\begin{aligned} D{\varvec{f}}({\varvec{x}}^*) = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} g^*Q_4C_1^*-g^*Q_3C_2^*&{} -g^*Q_3C_2^*&{} 0 &{} 0 &{} 0 \\ 0 &{} -g^*Q_3C_2^*&{} -g^*Q_3C_2^*&{} 0 &{} 0 &{} 0 \\ \end{pmatrix}, \end{aligned}$$

(32)

where $C_1^*:= \cos (x_2^*)$, $C_2^*:= \cos (x_2^*+x_3^*+\eta )$, and

$$\begin{aligned} D{\varvec{\tau }}({\varvec{x}}^*) = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -\mu ^*&{} -2c_1x_4^*&{} 0 &{} -c_b^*\mu ^*\\ 0 &{} 0 &{} \mu ^*&{} 0 &{} 0 &{} c_b^*\mu ^*\\ 0 &{} 0 &{} -1 &{} 0 &{} 0 &{} -c_b^*\\ \end{pmatrix}. \end{aligned}$$

(33)

To obtain (32) and (33), $|x_4|x_4 = x_4^2$ and $\text {sgn}(x_4-x_5)\chi (x_3)=1$ are assumed, because $x_3(t) >0$, $x_4(t) >0$, and $x_4(t)-x_5(t) >0$ hold for $x_i(t) = x_i^*+ \delta x_i(t)$, $|\delta x_i(t)|\ll 1$ $(i=1,\ldots ,6)$.

The results in (32) and (33) imply that the stability of the FCWIP model depends on the non-dimensional viscous coefficient $c_b^*$ in addition to the parameters $\mu ^*$, $\eta$, and $c_1$ that determine the steady states $(x_2^*,x_3^*,x_4^*)$.

In summary, we have found that under a given mechanical structure and environment,

• the steady angles $(x_2^*,x_3^*)$ depend on $(\mu ^*, \eta )$,

• the steady descent velocity $x_4^*$ depends on $(\mu ^*, \eta , c_1)$, and

• the stability depends on $(\mu ^*, \eta , c_1, c_b^*)$.

3.5 Eigenvalue equation

It can be proved that $\text {rank}\,[J({\varvec{x}}^*)] = 5<6=\dim {\varvec{x}}$, which follows from the assumption of the uniform motion $\dot{x}_1(t)=\omega$. Thus, the characteristic equation of $J({\varvec{x}}^*)$ is given in the following form:

$$\begin{aligned}&\det \left( J({\varvec{x}}^*)-\lambda E_6\right) = \lambda \,h(\lambda ) = 0, \end{aligned}$$

(34)

$$\begin{aligned}&h(\lambda )=\lambda ^5+a_1\lambda ^4+a_2\lambda ^3+a_3\lambda ^2+a_4\lambda +a_5, \end{aligned}$$

(35)

where $\det (\cdot )$ denotes a determinant and $E_6$ is a $6\times 6$ identity matrix. For simplicity, we refer to $h(\lambda )=0$ as an eigenvalue equation of the FCWIP model.

Therefore, the steady state ${\varvec{x}}^*$ becomes stable if the maximal real part of the eigenvalues is negative, that is

$$\begin{aligned} \varLambda :=\text {Re}\,\lambda _{\max }<0,\quad \lambda _{\max }:=\mathop {\text {arg max}}_{\lambda } \text {Re}\,(\lambda ), \end{aligned}$$

(36)

where $\lambda _i$ ($i=1,\ldots ,5$) are the roots of $h(\lambda )=0$.

4 Critical points of steady state

As mentioned in Sect. 3.4, the stabilities of the steady state $\varvec{x}^*$ depend on $\mu ^*$, $\eta$, $c_1$, and $c_b^*$. Here, we provide some numerical examples of that dependency. Thus, the parameter values are set to those listed in Tables 1, 2, and 3 by default unless otherwise noted.

4.1 Dependency on $\mu ^*$ and $\eta$

We first examine the dependency on the non-dimensional friction $\mu ^*$ and the offset $\eta$, which determine the steady angles $x_2^*$ and $x_3^*$ via (28).

Figure 5 shows the maximal real part of the eigenvalue $\varLambda$ and the non-trivial components $x_i^*$ $(i=2,3,4)$ of the steady state $\varvec{x}^*$ as functions of the non-dimensional friction $\mu ^*$. $\varLambda$ and $x_i^*$ are obtained from numerical solutions of (28) by Newton’s method and (36), respectively. The solid line in the top graph represents $\varLambda$, and the solid and dotted lines in the bottom graph represent stable and unstable $x_i^*$, respectively. The values of $x_i^*$ $(i=2,3)$ are scaled to share a common vertical axis.

Fig. 5

Maximal real part of eigenvalue $\varLambda$ and steady state $x_i^*$ as functions of the non-dimensional friction $\mu ^*$

It is clear from Fig. 5 that three types of critical points $P_0$, $P_1$, and $P_2$ appear, which are denoted as open circles, filled circles, and a triangle, respectively. $P_0$ gives an infimum $\inf _{\mu ^*} (x_4^*)=0$ of the descent velocity $x_4^*>0$, $P_1$ gives a stability boundary, and $P_2$ gives a folded (non-smooth) minimum of $\varLambda (\mu ^*)$.

Fig. 6

Root loci along the steady states in Fig. 5

To characterize these points, Fig. 6 plots the root loci of $h(\lambda )=0$ in (35) along the steady states $\varvec{x}^*$ in Fig. 5. It can be numerically proven that under the considered condition, the eigenvalue equation $h(\lambda )=0$ has three real roots and a pair of complex conjugate roots as

$$\begin{aligned} \lambda _0= & {} s_0,\; \lambda _{1\pm }=s_1\pm j\varOmega ,\; \lambda _2=s_2,\; \lambda _3 = s_3, \nonumber \\&s_0, s_1 \gg s_2,s_3<0, \end{aligned}$$

(37)

where $s_i$, $\varOmega$ are real numbers and $j:=\sqrt{-1}$. Among the five roots, only the first three roots $\lambda _0$, $\lambda _{1+}$, and $\lambda _{1-}$ affect the stability change, and only these three roots appear in the range of Fig. 6.

On the basis of the root loci obtained in Fig. 6, we can characterize the critical points in terms of eigenvalue types as follows:

• (P0): $P_0$ is a point such that $\lambda _{\max }=0$.

• (P1): $P_1$ is a Hopf bifurcation point, for which the loci cross the imaginary axis at $\lambda _{\max }=\pm j\varOmega$, where $\varOmega$ is an angular frequency of a limit cycle.

• (P2): $P_2$ is a point such that maximal real root $s_0$ and the real part of the complex conjugate roots $s_1$ coincide, at which point they switch roles to produce the maximal real part.

Physically speaking, $P_0$ and $P_1$ provide stability limits, and $P_2$ maximizes the total stability or minimizes the time constant of the FCWIP model. The descent velocity vanishes ($x_4^*=0$) at $P_0$ in this case, and a self-excited oscillation (limit cycle) emerges for $\varLambda (\mu ^*)>0$ near $P_1$.

Fig. 7

Limit cycle for $\mu ^*=1.01$ (just after Hopf bifurcation)

Figure 7a shows the limit cycle for $\mu ^*=1.01$ immediately after the Hopf bifurcation point $P_1$. Under this condition, the FCWIP model descends the slope in a standing position while the angles of the pendulums oscillate slightly and periodically. As this limit cycle is stable, $P_1$ is identified as a Hopf bifurcation point. In general, a limit cycle occurs because of the temporal presence of negative resistance (i.e., negative energy consumption per unit time). In our problem, this is given by the braking torque $T_2$ in (20) multiplied by the friction velocity $(x_4-x_5)$, specifically as

$$\begin{aligned} {\mathcal D}&= T_2\cdot (x_4 - x_5) \nonumber \\&= q^{-2} \mu ^*\text {sgn}(x_4 - x_5)\chi (x_3)(x_3+c_b^*x_6) \cdot (x_4 - x_5) \nonumber \\&= q^{-2} \mu ^*|x_4 - x_5|\chi (x_3)(x_3+c_b^*x_6) \nonumber \\&=: C\chi (x_3)(x_3+c_b^*x_6)\quad (C>0), \end{aligned}$$

(38)

where $\text {sgn}(x)x=|x|$ is applied. As $\chi (x_3)$ is a step function, ${\mathcal D}<0$ occurs when $x_3\ge 0$ and $x_3+c_b^*x_6<0$. This implies that when ${\mathcal D}<0$, the brake pad (see Fig. 2 recalling $z=\rho x_3,\dot{z}=(\rho /q)x_6$) will be released with a velocity less than $x_6<-x_3/c_b^*\le 0$ while the pad is still pressed against the disk ($x_3\ge 0$). Figure 7b shows the energy consumption ${\mathcal D}$ along the limit cycle as a function of $x_3$, which numerically confirms the presence of ${\mathcal D}<0$. During this negative energy consumption, the cycle comes across the deadband border $x_3 = z = 0$. At this point, the step function $\chi (x_3)$ jumps from 1 to 0. This causes the ${\mathcal D}$ to jump from a negative to a positive value, similar to $x_6$.

Figure 8a shows the result as functions of the offset $\eta$ for $\mu ^*=0.97$. In this case, a Hopf bifurcation point $P_1$ does not appear in the plotted range $\eta >0$. Outside this range, $x_2^*$ and $x_3^*$ vanish at $\eta =0$ and violate the physical assumptions $x_2^*<0$ and $x_3^*>0$ for $\eta <0$.

Fig. 8

Maximal real part of eigenvalue $\varLambda$ and steady states $x_i^*$ for $\mu ^*=0.97$ as functions of a the offset $\eta$, b the quadratic resistance $c_1$, and c the viscous coefficient $c_b^*$

4.2 Dependency on $c_1$ and $c_b^*$

Figure 8b shows the results as functions of the quadratic resistance $c_1$. It is clear that all the critical points $P_0$, $P_1$, and $P_2$ appear, although $x_2^*$ and $x_3^*$ become constant here because $c_1$ only affects $x_4^*$, as already discussed in (28).

However, the physical results of $P_0$ are different. That is, $P_0$ (or $\lambda _{\max }=0$) on $\varLambda (\mu ^*)$ in Fig. 5 corresponds to the descent velocity at rest $x_4^*=0$. In contrast, $P_0$ on $\varLambda (c_1)$ in Fig. 8b corresponds to the infinite descent velocity $x_4^*\rightarrow \infty$ ($c_1\rightarrow 0$). This can be explained by the second equation in (28), which is hyperbolic with respect to $c_1$ and $x_4^*$:

$$\begin{aligned} {c_1} (x_4^*)^2 = {g^*Q_1 \sin (\alpha )- \mu ^*x_3^*} \quad =:\bar{C}>0. \end{aligned}$$

(39)

This equation exhibits the following features:

• The right side of (39) (e.g., $\bar{C}$) is expected to be constant because $x_3^*$ is determined independently of (39).

• The left side ${c_1}(x_4^*)^2$ vanishes at $P_0$ (or $\lambda _{\max }=0$), as will be discussed in Sect. 5.1.1.

The second feature ${c_1}(x_4^*)^2=0$ holds when $c_1=0$ and/or $x_4^*=0$. The latter condition $x_4^*=0$ directly explains $P_0$ in Fig. 5 for a constant $c_1>0$. On the other hand, $P_0$ in Fig. 8b can be explained by the limit $c_1\rightarrow 0$ that causes $x_4^*= \sqrt{\bar{C}/c_1}\rightarrow \infty$ for the constant $\bar{C}$. In addition, these different $P_0$ can also be explained physically. That is, the condition ${c_1} (x_4^*)^2=0$ results in vanishing of the quadratic resistance force $c_1|x_4^*|x_4^*=0$. This can be caused by the mechanism at rest $x_4^*=0$ as well as by the absence of the effect of the quadratic resistance $c_1=0$.

Figure 8c plots the result for the non-dimensional viscous coefficient $c_b^*$ of the FCM. It is found that only the Hopf bifurcation point $P_1$ appears. Moreover, it appears that $x_i^*$ ($i=1,2,3$) are all constant because the steady-state equation in (28) is independent of $c_b^*$, which only affects the components of the Jacobian matrix as $\mp c_b^*\mu ^*$ and $-c_b^*$ in (33).

5 Stability limits

Finally, we numerically continue the critical points in two-parameter planes to characterize the stability limits of the FCWIP model.

5.1 Conditions of the critical points

5.1.1 Zero quadratic resistance

The condition of $P_0$ (or $\lambda _{\max }=0$) is mathematically equivalent to $a_5=0$ in the eigenvalue Eq. (35). It follows that

$$\begin{aligned} 0&=a_5 =\det {\mathcal M}^{-1} \cdot 2 c_1 x_4^*g^*\nonumber \\&\quad \times \Big \{-C_1^*Q_4 -C_2^*Q_3 \left\{ C_1^*g^*Q_4 -(1+\mu ^*)\right\} \Big \} \nonumber \\&\Longleftrightarrow 0 = c_1 x_4^*\Big \{C_1^*Q_4 + C_2^*Q_3 \left\{ C_1^*g^*Q_4 - (1+\mu ^*)\right\} \Big \} \nonumber \\&\Longleftarrow c_1 x_4^*=0 \nonumber \\&\Longleftrightarrow c_1=0\;\quad \text {or}\quad \;x_4^*=0 \;\Longleftrightarrow \; c_1 (x_4^*)^2 =0. \end{aligned}$$

(40)

Therefore, it is mathematically shown that the sufficient condition for $P_0$ (or $\lambda _{\max }=0$) is given by the zero quadratic resistance $c_1(x_4^*)^2 = 0$.

As discussed in Sect. 4.2, the condition $P_0$ (or $c_1(x_4^*)^2 = 0$) causes two distinct descent velocities: $x_4^*=0$ for $c_1>0$ and $x_4^*=\infty$ for $c_1=0$. Therefore, we denote them as $P_0^0$ and $P_0^\infty$, respectively, in the following sections.

The condition of $P_0^0$ is given by (39) with $c_1(x_4^*)^2 = 0$, from which we can eliminate $x_2^*$ and $x_3^*$ to obtain

$$\begin{aligned} \varPhi _0:= & {} \eta + \arcsin \left( \frac{Q_1\sin \alpha }{Q_3\mu ^*}\right) +\frac{g^*Q_1\sin \alpha }{\mu ^*} \nonumber \\&-\arcsin \left( \frac{Q_1(1+\mu ^*)\sin \alpha }{Q_4\mu ^*}\right) =0. \end{aligned}$$

(41)

On the other hand, $P_0^\infty$ is simply given by $c_1=0$. Because the condition (41) does not contain $x_2^*$ and $x_3^*$, the zero quadratic resistance points $P_0^0$ and $P_0^\infty$ are determined independently of the pendulum angles $x_2^*$ and $x_3^*$.

5.1.2 Hopf bifurcation

The condition $P_1$ (or $\lambda _{\max }=\pm j\varOmega$) for a Hopf bifurcation point is given by $\text {Re}\,h(j\varOmega ) = \text {Im}\,h(j\varOmega ) = 0$. On eliminating $\varOmega$ from them, we obtain

$$\begin{aligned} \varPhi _1:= & {} a_5 \Big \{a_4 (-a_1 a_2 a_3 + a_3^2 + a_1^2 a_4) \nonumber \\&+ \big (-a_2 a_3 + a_1 (a_2^2 - 2 a_4)\big ) a_5 + a_5^2\Big \} = 0\nonumber \\ \end{aligned}$$

(42)

for the Hopf bifurcation point. It is implied from (42) that $P_1$ coincides with $P_0^0$ (or $P_0^\infty$) because $a_5=0$ for $P_0^0$ (or $P_0^\infty$) leads to $\varPhi _1=0$.

Note that, rigorously speaking, the above condition provides only a necessary condition of a Hopf bifurcation point; however, it leads to satisfactory results in the present analysis.

5.1.3 Minimal time constant

We numerically detect the condition of $P_2$ for the minimal time constant that satisfies

$$\begin{aligned} |s_0 - s_1| < 10^{-9} \end{aligned}$$

(43)

where $s_0$ is the maximal real eigenvalue and $s_1$ is the real part of the complex conjugate eigenvalues, as defined in (37). In numerical calculations, the parameter values considered are swept to detect a point that satisfies (43), where the point in the first detection is taken as the point detected.

Note that we attempted to derive an equation for the minimal time constant in a closed form of $a_1,\ldots ,a_5$ based on a given form of eigenvalue equation: $h(\lambda ) = (\lambda - \lambda _{\max }) (\lambda - \lambda _{\max }- jv) (\lambda - \lambda _{\max }+ jv)(\lambda ^2 + p \lambda + q)$, however, the result was very weak to detect $P_2$ precisely. Therefore, in this paper, we employ the numerical method mentioned above, although another approach would be possible for an analytical expression of $P_2$.

5.2 Numerical continuation of the critical points

Figure 9 plots the sets of the critical points $P_0^0$, $P_1$, and $P_2$ on two-parameter planes obtained from the numerical solutions of (41), (42), and (43) under (28). The results on the $(\mu ^*,\eta )$, $(\mu ^*,c_1)$, and $(\mu ^*,c_b^*)$ planes are labeled (a), (b), and (c), respectively, in Fig. 9. The solid line denotes the set of the zero quadratic resistance point $P_0^0$ for $x_4^*=0$, the dotted line denotes the set of the Hopf bifurcation point $P_1$, and the chained line denotes the set of the minimal time constant point $P_2$. The plots of $P_0^\infty$ for $c_1=0$ do not appear in the ranges of these plots. The hatched areas represent the stable regions of the steady state satisfying $\varLambda < 0$ in (36).

Fig. 9

Continuation of the critical points $P_0^0$, $P_1$, and $P_2$ on the two-parameter planes: a for the $(\mu ^*,\eta )$ plane, b for the $(\mu ^*,c_1)$ plane, and c for the $(\mu ^*,c_b^*)$ plane. The hatched areas represent asymptotically stable conditions of the steady states

It is clearly seen in Fig. 9 that the stable regions are bounded by $P_0^0$ and $P_1$ and that the minimal time constant point $P_2$ is sandwiched between them. Note that in Fig. 9a, the plots are bounded by the assumption $\eta >0$ and that in Fig. 9b, c, $P_0^0$ lies along the vertical line at $\mu ^*=\bar{\mu }^*\approx$0.89474. This is because $P_0^0$ is determined independently of $c_1$ and $c_b^*$ in (41). Moreover, it appears that the critical points $P_0^0$, $P_1$, and $P_2$ tend to coincide as $\mu ^*$ increases on the $(\mu ^*,\eta )$ plane, as $c_b^*$ increases and decreases on the $(\mu ^*,c_b^*)$ plane, and as $c_1$ increases on the $(\mu ^*,c_1)$ plane. In contrast, as $c_1$ decreases on the $(\mu ^*,c_1)$ plane, $P_1$ and $P_2$ also tend to coincide but they approach $c_1=0$ or $P_0^\infty$ instead of $P_0^0$. As discussed in Sect. 5.1.2, the convergence between $P_0^0$ (or $P_0^\infty$) and $P_1$ can be explained by (42), in which the condition $\varPhi _1=0$ for the Hopf bifurcation point $P_1$ contains $a_5=0$ for the zero quadratic resistance point $P_0^0$ (or $P_0^\infty$). As shown in Fig. 10, however, it can be numerically proven that a purely imaginary eigenvalue $\lambda _{\max }=j\varOmega$ along $P_1$ does not vanish even when $P_1$ coincides with $P_0^0$ (or $P_0^\infty$) in the parameter planes. Therefore, the Hopf bifurcation point $P_1$ does not degenerate and double-zero eigenvalues never arise at that point.

From an engineering viewpoint, the results obtained above imply that the FCWIP model allows a certain amount of tolerance in parameter settings because the stable conditions are obtained as simply connected finite areas. This suggests the possibility that the proposed mechanism can work even if there are some manufacturing errors. Furthermore, the stable area on the $(\mu ^*,\eta )$ plane in Fig. 9a forms a monotonically increasing shape, which implies that the offset $\eta$ can be designed to shift the stable range of the friction coefficient $\mu ^*$.

Fig. 10

Imaginary part of complex conjugate eigenvalues along $P_1$ in Fig. 9a

Fig. 11

Angular velocities of the wheel $x_4^*$ within the stable areas on the two-parameter planes: a for the $(\mu ^*,\eta )$ plane; b for the $(\mu ^*,c_1)$ plane; and c for the $(\mu ^*,c_b^*)$ plane

5.3 Numerical evaluation of the descent velocity

In view of engineering applications, the descent velocity (or angular velocity of the wheel) $x_4^*$ must be adjusted to a value suitable for the intended use. Figure 11 shows the values of $x_4^*$ mapped into a gray scale within the stable areas on the parameter planes in Fig. 9. $x_4^*$ values are numerically obtained by solving (28).

It is clear from Fig. 11 that $x_4^*$ tends toward zero as the parameter conditions approach $P_0^0$ (solid lines), which is in agreement with the definition of $P_0^0$. Particularly, in Fig. 11b, it is also clarified that $x_4^*$ is diverging as the condition approaches $P_0^\infty$ or $c_1=0$. Moreover, it appears that $x_4^*$ changes smoothly and monotonically with the variations of the parameters. This suggests that one can adjust the descent velocity $x_4^*$ by continuously shifting the parameters. However, it is also observed in Fig. 11b that a sufficiently large value of the quadratic resistance $c_1$ is required to stabilize the mechanism because although a range of $\mu ^*$ exists for small $x_4^*$ near $\mu ^*=\bar{\mu }^*\approx 0.89474$, it narrows significantly as $c_1$ decreases. In addition, it appears in Fig. 11c that $x_4^*$ does not depend on $c_b^*$, as discussed in the last paragraph in Sect. 3.4.

6 Conclusion

For a non-electrified method to stabilize a wheeled inverted pendulum descending a slope, we proposed the FCWIP mechanism, a wheeled double pendulum, whose second pendulum transforms gravity force into brake force acting on the wheel. We conducted steady-state analysis of the proposed model and obtained the following results:

• The steady angles $(x_2^*,x_3^*)$ depend on $(\mu ^*, \eta )$.

• The steady descent velocity $x_4^*$ depends on $(\mu ^*, \eta , c_1)$.

• The stability depends on $(\mu ^*, \eta , c_1, c_b^*)$.

Then, we found three types of critical points in the steady states, as

• $P_0$: the point for zero quadratic resistance on the wheel. ($P_0^0$ for $x_4^*=0$ and $P_0^\infty$ for $x_4^*=\infty$ in detail)

• $P_1$: the Hopf bifurcation point.

• $P_2$: the point for the minimal time constant.

Finally, we conducted numerical continuations of these points on the two-parameter planes and evaluated the descent velocity to obtain the following results:

• The stable conditions are obtained as simply connected finite areas on the parameter planes, bounded by $P_0^0$ and $P_1$.

• The minimal time constant point $P_2$ is sandwiched between $P_0^0$ and $P_1$.

• The descent velocity $x_4^*$ changes smoothly and monotonically with the parameter variations.

The abovementioned results lead to the conclusion that the parameter selection to design the FCWIP mechanism stabilized on a slope will not be highly sensitive, at least in theory.

In future work, we plan to develop a physical FCWIP mechanism. For this purpose, we will introduce stick-slip effects into the friction term in our model and investigate the effect on the stabilities. We also plan to conduct stochastic analysis on the FCWIP model to consider robustness against random disturbances and random parameter fluctuations.