1 Introduction

The last few decades witness a significant interest on developing the attitude control approaches for rigid spacecrafts. This is motivated by its wide range of applications, such as oil, mineral and gas exploration, communication, risk management and weather forecasting [15, pp. 3–4]. Since spacecrafts have become now often integrated with electric actuators such as reaction wheels and control moment gyroscopes, they are constrained ever more tightly by high accurate slewing and pointing maneuvers of large-angle amplitude specifications [36]. The increased emphasis placed on efficient plant operation dictates the need for the nonlinear dynamics of spacecraft model for control system synthesis and effective control to guarantee the satisfaction of operational objectives.

Further complications arise from the fact that the control system needs satisfactory performance in the presence of external disturbances, model uncertainties, measurement errors, actuators constraints and actuators misalignments. Various nonlinear control algorithms have been purposed to improve the closed-loop system performance in these unwanted situations (see, for instance [8, 9, 11, 14, 17–19, 30, 46–48]). Time delay is one of the other salient features whose frequently encountered co-presences in many practical systems can lead to severe performance limitations, or even causes the instability of closed-loop systems. Generally speaking, time delay may arise in the measurements as a consequence of inherent operational limitations of sensors, or communication delays, or such time lag may be occurred in the actuators due to the time takes to create control decisions and to execute these decisions [36, 41]. The latter case is the subject of this article. More precisely, we study the nonlinear control of spacecraft attitude dynamics with parametric uncertainties and constant unknown delayed inputs.

Whereas the case of delay-free attitude control of spacecraft, as mentioned before, has been well studied and documented in the literature, the control of spacecraft in the presence of time delay has received relatively little attention from the control community. The problem of attitude regulation of a rigid spacecraft in the presence of delayed input signals has been studied for the first time in [1]. By adapting Rodrigues parameters (RPs) to represent the orientation of the spacecraft and employing a velocity-free controller, the sufficient conditions for exponential stability of the system inside a region of attraction have been obtained, whereas the results reported therein are valid only for sufficiently small time delays. Moreover, the delay must be precisely known in order to design the controller, which is a restrictive condition.

In [12], by using modified RPs (MRPs) to represent attitude oration and modifying the original complete-type Lyapunov–Krasovskii (L–K) functional, a control law has been obtained. This method can relax the restriction of requiring precise knowledge of time delay; also, the authors of [12] attempted to maximize the estimation of region of attraction by utilizing a systematic numerical optimization. Although the adopted strategy in [12] can improve some drawbacks of [1], since the controller is obtained based on the linearization of the plant (more precisely, the plant is divided into a nominal linear part and an additive nonlinear perturbation satisfying the linear growth constrain), the results obtained therein are still local, similar to [1, 49]; i.e., the results are only valid for a small of operation range. As the range of operation increases or system is exposed to disturbances, the performance of the overall system decreases or even instability may be occurred due to the contribution of the nonlinear terms.

Using MRPs for attitude representation, based on inverse dynamics approach, and assuming that known constant time delay exists in only one of the actuators, the authors of [36] developed a proportional-integral-derivative (PID)-type control law where the Hsu–Bhatt–Vyshnegradskii stability chart is used to select the gains of the controller. Since in derivation of the controller, it is assumed that the norm of MRPs and its time derivation are small enough, the closed-loop system is not globally stable. Attitude control in the presence of time delay has also been investigated in [38] and [4]. However, in contrast to the present research, the delay is presented in measurements and not in inputs.

Undoubtedly, global stabilization of nonlinear systems is one of the most imperative issues in nonlinear control theory. Roughly speaking, instead of requiring stability condition to hold in a neighborhood of the equilibrium, we require that the plant is stable over a wide range of conditions due to large process upsets or large initial values.

The difficulty associated with the stabilization of a spacecraft in the presence of delayed inputs is largely due to the fact that the spacecraft system is inherently nonlinear. Thus, stability analysis of such system is a difficult problem, and its combination with delayed inputs introduces extra challenge, especially if delay itself is unknown. Moreover, the few existing control frameworks for nonlinear systems are devoted to the case in which the delay is involved in the input signals. In last two decades, some efficient but yet restrictive studies have appeared to deal with the control of nonlinear systems with retarded inputs. Generally speaking, these works can be divided into three categories. The first class of the control algorithms is utilized predictor-based feedback control law to compensate delay effects (see, for example [5, 6, 13, 24–26]). This method is essentially a nonlinear version of the Smith predictor [25] which was extended to nonlinear systems in [25] by Krstic. In the second group of control algorithms, the controller is firstly designed by neglecting delay. Then, conditions that guarantee stability for the closed-loop system based on Lyapunov, Razumikhin or small-gain theorems are obtained (see [33, 44]). Finally, the third class of control methodologies exploits certain characteristics of the system to obtain a feedback law which guarantees stability for the corresponding closed-loop system (see, for instance [2, 10, 20, 21, 29, 32, 35]). However, these insightful approaches are capable to interact with delay, but their scope is restricted to either known or small delays, and to the best of our knowledge, the stabilization of nonlinear systems in the presence of arbitrarily long delay in which the delay value is unknown has been remained open so far.

In this paper, we adopt the third-class line approach for developing a control law, and since the representation of orientation by MRPs has notable advantages, including characterizing by a set of three parameters (i.e., a minimal set), wide range of singularity-free behavior and being free of ambiguity, then the attitude of spacecraft is represented by MRPs in the present paper.

We use the backstepping technique as the control design approach to regulate the spacecraft attitude with delayed inputs where delay is an unknown constant. This control scheme allows the systematic design of controllers for cascade-structured nonlinear systems. The basic idea of backstepping is to design a controller by following recursive procedure which interlaces at each sequence the proper change of coordinates, and then, the intermediate stabilizing feedback control laws are developed by considering some of the state variables as virtual controls.

The contributions of this paper are stated as follows.

  1. 1.

    The backstepping method in [20, 23, 32, 35] is extended to uncertain nonlinear systems with unknown delayed inputs; then, this strategy is applied to the attitude stabilizing control problem. By means of the Sepulchre–Janković–Kokotović approach [40] and an operator of a new type which is introduced in [34], the L–K functional is constructed and it is utilized to prove the stability of the closed-loop system.

  2. 2.

    In comparison with the works of [1, 12, 36], for the zero-disturbance case, the proposed backstepping controller achieves global asymptotical attitude stabilization. Furthermore, the controller also ensures a shorter path stabilizing, i.e., the unwinding phenomenon is avoided. This is due to the fact that the virtual control law (control law for the kinematics subsystem) is obtained by minimizing a performance index which includes quadratic penalty in oration parameters and angular velocity.

  3. 3.

    While considering the influence of disturbances (internal or external), the closed-loop attitude system under the proposed controller is input-to-state stable (ISS), namely, the trajectories of the attitude control system remain bounded in the presence of bounded disturbances.

The remaining parts of the paper are organized as follows. Section 2 describes system modeling, the problem formulation and some definitions. The controller development and the closed-loop system stability analysis are given in Sec. 3. In Sec. 4, extensive numerical simulation results are reported, in which the robustness to variations in time delay is demonstrated and the controller performance is examined under the influence of disturbances. Conclusions and directions for future work are given in Sec. 5.

1.1 Notation

\(\bullet \) For a vector \(x=\left[ x_1, x_2, x_3\right] ^T \in \mathfrak {R}^3\), the Euclidean norm of x is expressed as \(\Vert x\Vert \). \(\Vert x\Vert _\infty \) denotes the infinity norm of x. The operator \(S_x\) denotes a skew-symmetric matrix acting on vector x and has the form

$$\begin{aligned} S_x =\left[ {\begin{matrix} 0 &{}\quad -x_3 &{}\quad x_2 \\ x_3 &{}\quad 0 &{}\quad -x_1 \\ -x_2 &{}\quad x_1 &{}\quad 0 \end{matrix}}\right] . \end{aligned}$$

\(\bullet \) For a matrix \(M \in \mathfrak {R}^{n\times n}\), the induced 2-norm, expressed as \(\Vert M\Vert \), is defined as \(\Vert M\Vert =\sqrt{\lambda _{\mathrm {max}}\left( M^TM\right) }\) where \(\lambda _{\mathrm {max}}\left( M^TM\right) \) denotes the maximal eigenvalue of \(M^TM\).

\(\bullet \) A continues function \(f : \mathfrak {R}_+ \rightarrow \mathfrak {R}_+\) belongs to a class \(\mathcal {K}_\infty \) if it is strictly increasing, \(f(0)=0\) and \(f(t) \rightarrow \infty \) as \(t \rightarrow \infty \). A continues function \(g:\mathfrak {R}_+ \times \mathfrak {R}_+ \rightarrow \mathfrak {R}_+ \) is said to be a \(\mathcal {KL}\) if for each fixed \(\ell \), the mapping \(g\left( t,\ell \right) \) is \(\mathcal {K}_\infty \) class function with respect to t, and for each fixed \(\ell \), the mapping \(g\left( t, \ell \right) \) is decreasing in \(\ell \) and \(g\left( t, \ell \right) \rightarrow 0\) as \(\ell \rightarrow 0\).

\(\bullet \) Throughout this paper, the argument of the functions (functionals) will be omitted whenever no confusion arises from the context.

2 Background and problem statement

2.1 Spacecraft attitude kinematics and dynamics

Let the unit vector e be the principal (right-hand) axis of rotation associated with Euler’s theorem and \(\varPhi \) be principle angle of such rotation. The MRP vector \(\sigma \in \mathfrak {R}^{3}\) can be defined in terms of principal rotation elements as [39, p. 117]

(1)

From Eq. (1), it is clear that the MRP representation has a singularity at \(360^\circ \); i.e., MRPs can be used for describing eigenaxis rotations upto \(360^\circ \), which is wide enough and can be encountered in whole attitude maneuvers that considered in this study.

By employing MRPs to represent the attitude oration of the rigid body, the kinematics equation can be expressed as [39, p. 122]

$$\begin{aligned} \dot{\sigma }\left( t\right) = B\left( \sigma \right) \omega (t) \end{aligned}$$
(2)

where \(\omega \in \mathfrak {R}^3\) is the angular velocity prescribed in the body-fixed frame and \(B \in \mathfrak {R}^{3\times 3}\) is Jacobin matrix defined as

$$\begin{aligned} B\left( \sigma \right) = \frac{1}{4}\left( \left( 1-\Vert \sigma \Vert ^2 \right) I + 2 S_\sigma + 2 \sigma \sigma ^T\right) . \end{aligned}$$
(3)

Remark 1

The principal rotation angle \(\varPhi \) is not unique. Suppose that \(\varPhi \) is the shortest rotation about the principle axis will be performed to move from one reference frame to another. It is obvious that this is not necessary, since one can found the second rotation angle \(\varPhi ^S=\varPhi -2\pi \) such that the exact same orientation is achieved by rotation through the angle \(\varPhi ^S\) [39, p. 96]. It is often the case and also in this paper, the magnitude of the principal rotation angle is simply chosen to be \(|\varPhi | \le \pi \). Hence, while one MRP set is chosen corresponding to the shortest rotation, there is another set, referred to as the shadow set, corresponding to a principal rotation \(\varPhi ^S\), defined as [39, p. 119]. As discussed in [39, p. 120], switching between original and shadow MRP sets and choosing the switching surface as \(\sigma ^T \sigma =1\) provide a singularity-free unique attitude description.

Next, let \(J \in \mathfrak {R}^{3\times 3}\) be the spacecraft inertial matrix consisting of principal moment of inertia. Let \(T\left( t \right) \) and \(T_\mathrm{d} \left( t \right) \) denote control (actuator) torque and disturbance torque, respectively. From Euler’s moment equation, the dynamics model of rigid spacecraft motion with delayed inputs can be founded as [39, p. 153]

$$\begin{aligned} \dot{\omega }\left( t \right) = -J^{-1}S_\omega J \omega \left( t \right) + J^{-1} T \left( t-\tau \right) + J^{-1} T_\mathrm{d} \left( t \right) \end{aligned}$$
(4)

where \(\tau \in \mathfrak {R}_+\) is the time delay.

Another issue that must be considered in the mathematical description of the spacecraft is a disturbance model. A satellite orbiting the Earth is influenced by various disturbances including internal torques (for example, momentums caused by inner moving parts of the spacecraft) or external torques (such as gravitational torque, radiation torque, aerodynamic torque). Since the satellites in all altitudes are highly affected by the gravitational perturbation [15, p. 105], all external disturbance torques are neglected, except the gravity gradient torque \(T_\mathrm{g}\in \mathfrak {R}^3\), which can be expressed as [28, p. 121]

$$\begin{aligned} T_\mathrm{g} = 3\omega _o^2 S_{c_3}Jc_3 \end{aligned}$$
(5)

with \(c_3 = C \exp \left( -\omega _o t S_{e_2}\right) e_3\), where \(\omega _o = \sqrt{\mu _\mathrm{g}/r_\mathrm{c}^3}\) is the orbital rate, \(\mu _\mathrm{g}\) denotes geocentric gravitational constant, \(r_\mathrm{c}\) represents the distance of the satellite center of mass from the Earth’s center, \( e_2=[0, 1, 0]^T,\) \(e_3 = [0, 0, 1]^T\) and \(C\in \mathfrak {R}^{3\times 3}\) denotes the direction cosine matrix in terms of MRPs which is given by [39, p. 120]:

$$\begin{aligned} C\left( \sigma \right) = I-4\frac{1-\Vert \sigma \Vert ^2}{\left( 1+\Vert \sigma \Vert ^2 \right) ^2}S_\sigma +\frac{8}{\left( 1+\Vert \sigma \Vert ^2 \right) ^2}S_\sigma ^2. \end{aligned}$$
(6)

Also, the disturbance \(T_\mathrm{d}\) may be seen as an internal disturbance. Since the mass properties of the spacecraft may be difficult to approximate with high enough precision, \(T_\mathrm{d}\) can be interpreted as torque caused by mismatch between the nominal inertial J and real one.

Two properties related to the described spacecraft mathematical model are given next. These properties will be used to develop the controller.

Property 1

The matrix B has the following properties for all \(\sigma \), \(\omega \in \mathfrak {R}^3\) [39, p. 120]:

$$\begin{aligned} \sigma ^T B\left( \sigma \right) \omega = \frac{1+\Vert \sigma \Vert ^2}{4} \sigma ^T \omega \end{aligned}$$
(7)

and

$$\begin{aligned} B^T\left( \sigma \right) ~ B\left( \sigma \right) =\left( \frac{1+\Vert \sigma \Vert ^2}{4} \right) ^2 I. \end{aligned}$$
(8)

Property 2

For the inertial matrix of the spacecraft J, we have [15, p. 76]:

  • \(J=J^T>0\).

  • The inertia matrix J, by definition, must respect precise constraints among its elements. Namely, there are constraints on the admissible values of inertia moments. Suppose that J is expressed as

    $$\begin{aligned} J = \mathrm {diag} \left[ J_1, J_2, J_3\right] , J_i\in \mathfrak {R}_+, i=1, 2, 3. \end{aligned}$$

    It is possible to define 6 triangular inequalities that relate the inertia moments, for example: \(J_1+J_2 \ge J_3\), \(J_3 \ge J_1-J_2\).

For the development of the control system, the following assumptions are made.

Assumption 1

The size of the unknown time delay \(\tau \) is bounded by a known constants \(\bar{\tau }\in \mathfrak {R}_+\), that is, \(0\le \tau \le \bar{\tau }\).

It should be emphasized that only the upper bound of \(\tau \) is required for analytical purposes, and its true value is not necessary to be known, since it is not used for controller design. As will be shown in next section, a restriction on the delay size guaranties that the stabilizing problem of aforementioned system always has a solution.

Assumption 2

Both angular velocity (inertial measurement) and attitude (noninertial measurement) are assumed to be accessible for feedback control law. Furthermore, we assume that these measurements are perfect, i.e., without bias, without noise and without delay.

2.2 Problem statement

The main objective of this paper is to design an attitude stabilizing control law for a spacecraft system described by Eqs. (2) and (4). Having an unknown delay in inputs (actuators), the attitude must be asymptotically stabilized for any given initial values in the absence of disturbances, namely, \(\sigma (t) \rightarrow 0\) and \(\omega (t) \rightarrow 0\) as \(t \rightarrow \infty \). Furthermore, under the proposed control law, the attitude oration and angular velocity should be driven to a small set containing the origin in the presence of external disturbances and dynamic model uncertainty in the spacecraft inertia matrix.

2.3 Technical preliminaries

Theorem 1

(Inverse Optimal Problem) Let dynamic system which is affine in the control input be

$$\begin{aligned} \dot{x} = f(x) + g(x) u \end{aligned}$$

where \(x \in \mathfrak {R}^n\) denotes the system state, \(u \in \mathfrak {R}^m\) is the control input, and f and g are smooth functions.

Consider the cost functional given as

$$\begin{aligned} \mathcal {J} = \int _0^\infty \mathcal {C}\left( x,u\right) \, \mathrm {d}t \end{aligned}$$
(9)

where \(\mathcal {C} = Q(x) + u^T R(x) u\), Q(x) and R(x) are symmetric positive definite matrices for all x.

Given a control law u(x) and an associated Lyapunov function V(x) for the controlled system, Q(x) and R(x) can be obtained by solving

$$\begin{aligned} u =&-\frac{1}{2}R^{-1}\left( \frac{\partial V}{\partial x}g \right) ^T \end{aligned}$$
(10)
$$\begin{aligned} Q =&- \left( \frac{\partial V }{\partial x}\right) f-\frac{1}{2} \left( \frac{\partial V}{\partial x}\right) g u. \end{aligned}$$
(11)

Moreover, the minimum value of the cost functional is \(\mathcal {J}^* = V\left( x\left( 0\right) \right) \).

Proof

It is a straightforward extension of [27, Proposition1] for the cost functional described by (9). The proof is omitted here. \(\square \)

Definition 1

(Input-to-State Stability Concept) Consider a general delayed system

$$\begin{aligned} \dot{x}=f\left( x(t+\eta ),d(t),t\right) \end{aligned}$$
(12)

where \(f:\mathfrak {R}^n\times \mathfrak {R}^m \times \mathfrak {R}_+ \rightarrow \mathfrak {R}^n\), \(\eta \in [-\bar{\tau }, 0]\) and \(\bar{\tau }\) is the maximum involved delay. This system is said to be input-to-state stable (ISS) with respect to d if there is a function \(\beta \) of class \(\mathcal {KL}\) and function \(\kappa \) of class \(\mathcal {K}_\infty \) such that for any bounded input d and any initial condition \(x_0\), the corresponding solution x(t) exists for all \(t \ge 0\), and satisfies

$$\begin{aligned} \Vert x(t)\Vert \le \beta \left( \Vert x_0\Vert _\infty , t\right) + \kappa \left( \Vert d\Vert _\infty \right) . \end{aligned}$$

Furthermore, if the system (12) is ISS with respect to d, there exist a functional \(v_{\ell }\left( x(t+\eta )\right) \in \mathfrak {R}^+\), and functions \(\kappa _{\ell _i} \in \mathcal {K}_\infty ,\, i=1,2, \ldots , 4\), such that for all \(\eta \in \left[ -\bar{\tau }, 0\right] \) and all trajectories x(t), we have

(i):

\(\kappa _{\ell _1}(\Vert x(t)\Vert ) \le v_{\ell } \le \kappa _{\ell _2}\left( \sup _{\eta \in [-\bar{\tau }, 0]}\Vert x(t+\eta )\Vert \right) \);

(ii):

\(\dot{v}_{\ell } \le -\kappa _{\ell _3}(\Vert x\Vert ) + \kappa _{\ell _4} (\Vert d\Vert )\). The functional \(v_{\ell }\) is called an ISS Lyapunov–Krasovskii functional (ISS-LKF see [31, p. 56] or [37]).

3 Control design

The control design and closed-loop stability analysis that follows are divided into two parts. First, we consider the zero-disturbance case, in which the global asymptotic convergence is guaranteed. Next, we study the effect of disturbances on the nominal system.

By considering the fact that the attitude system in (2) and (4) has a nonlinear cascade interconnected structure, stabilizing control law for such system can be efficiently investigated by employing the backstepping method which consists of two steps. In the first step, the angular velocity \(\omega \) in (2) is regarded as a virtual control input and then a state feedback control is designed to stabilize the kinematics subsystem. In the second step, with in mind that the kinematics subsystem must remain stable, the actual control T is designed to stabilize the dynamics subsystem (4).

3.1 Disturbance-free case

Step one: Control of the Kinematics Subsystem

Consider the subsystem (2) with \(\omega \) promoted to the virtual control input. Let the control law be

$$\begin{aligned} \omega _{\mathrm {desire}} (t) = -P\sigma (t) \end{aligned}$$
(13)

where \(P=P^T \in \mathfrak {R}^{3\times 3}\) is a positive definite matrix. We have the following lemma on the convergence of \(\sigma \).

Lemma 1

Given the kinematics subsystem in (2), the controller in (13) ensures that the MRP vector \(\sigma \) exponentially converges to zero for all initial conditions \(\sigma (0)\).

Proof

Following Tsiotras [45], a Lyapunov function is defined as

$$\begin{aligned} v_0(t)= 2 \ln \left( 1+\Vert \sigma \Vert ^2\right) . \end{aligned}$$
(14)

Differentiation of \(v_0\) with respect to time and substitution of the attitude kinematics from Eq. (2) yield \(\dot{v}_0 = \frac{4}{1+\Vert \sigma \Vert ^2} \sigma ^T B \omega \). Applying the virtual control law (13) and using identity (7) in the Property 1, we have \(\dot{v}_0=\sigma ^T\omega = -\sigma ^T P \sigma \). This proves that the control law makes \(\sigma = 0\) a global exponential stable equilibrium in the sense of Lyapunov. \(\square \)

The proposed control law (13) not only has a simple structure (linear in the attitude vector \(\sigma \)), but also has a certain optimality property which is illustrated below.

Property 3

Considering the kinematics subsystem (2), the control law (13) is optimal with respect to the cost

$$\begin{aligned} \mathcal {J} = \frac{1}{2} \int _0^\infty \left( \sigma ^T(t)P\sigma (t)+ \omega ^T(t) P^{-1} \omega (t)\right) \, \mathrm {d}t. \end{aligned}$$
(15)

Proof

The optimality property of the proposed kinematics control law was derived in [45] when the control gain P is a scalar positive constant. We present an alternative way to show its optimality.

Since the control law and the Lyapunov function are available, instead of solving the Hamilton–Jacobi–Bellman (HJB) equation for finding the optimal control law, we seek a meaningful cost functional that is minimized by available controller. This route is known as inverse optimal control approach which is easier than the direct one.

To this end, with combination of Theorem 1 and identity (7) in Property 1, we are able to rewrite control law \(\omega _{\mathrm {desire}}\) as

$$\begin{aligned} \omega _{\mathrm {desire}}=&-\frac{1}{2} R^{-1} \left[ \left( \frac{\partial }{\partial \sigma } 2\ln \left( 1+\Vert \sigma \Vert ^2\right) \right) B\right] ^T \nonumber \\ =&-\frac{1}{2}R^{-1} \frac{4}{1+\Vert \sigma \Vert ^2} \left( \sigma ^TB\right) ^T \nonumber \\ =&-\frac{1}{2}R^{-1} \sigma \end{aligned}$$
(16)

which immediately results \(R = 1/2 P^{-1}\). An analogous approach can be presented to calculate weighting matrix Q. Definition of Q in Theorem 1 implies that we have \(Q=-1/2 \left( \frac{\partial V_0}{\partial \sigma }\right) B \omega _{\mathrm {desire}} = 1/2 \sigma ^T P \sigma \). This completes the proof. \(\square \)

It should be emphasized that since the control law for kinematics subsystem is obtained by minimizing a linear quadratic regulator (LQR)-type cost functional, it possesses certain robustness properties (see [27] for more details), and it ensures a shorter path stabilizing, i.e., the trajectories of the closed-loop system travels a shorter path in the state space to return to the desired attitude [7]. This means that we overcome the unwinding problem which can waste control effort by causing the spacecraft to rotate through large angles, while a small angle of the opposite rotational direction is adequate to bring the system to rest [7]. Therefore, by using control law (13), the principle angle \(\varPhi \) remains in \(0\le |\varPhi | \le 180^\circ \), i.e., we do not need to switch the shadow set; consequently, form Eq. (1), the corresponding MRP vector \(\sigma \) is bounded to unit magnitude or less, that is \(\Vert \sigma \Vert \le 1\). In what follows, this property aids the control design and analysis.

Step two: Control of the full rigid body model

Let the auxiliary variable \(\alpha \in \mathfrak {R}^3\) be defined as

$$\begin{aligned} \alpha = \omega - \omega _{\mathrm {desire}}. \end{aligned}$$
(17)

The dynamics equation (4) in term of \(\alpha \) is transformed to

$$\begin{aligned} \dot{\alpha }(t) = \varXi (\sigma , \alpha ) + J^{-1} T\left( t-\tau \right) \end{aligned}$$
(18)

where

$$\begin{aligned} \varXi= & {} -J^{-1}S_{\alpha -P\sigma }J (\alpha -P\sigma ) + PB [\alpha -P\sigma ],\, \varXi \in \mathfrak {R}^3.\nonumber \\ \end{aligned}$$
(19)

We use the actual control input T to drive \(\alpha \) to zero. If \(\alpha \) goes to zero, \(\omega \) will tend to the desired value \(\omega _{\mathrm {desire}}\) and then the kinematics subsystem (2) is asymptotically stable as shown in Lemma 1, namely, \(\sigma \rightarrow 0\) and eventually \(\omega \rightarrow 0\); hence, the entire system will be stabilized.

To aid the subsequent control design and analysis, we show that the function \(\varXi \) is bounded under the condition of bounded state. For the sake of simplicity, assume that the feedback gain P is a diagonal matrix, that is \(P = \mathrm {dig} [P_1, P_2, P_3\)]. Furthermore, \(\bar{P}\) and \(\underline{P}\) denote maximal and minimal eigenvalues of P, respectively.

The application of Euclidean norm together with the triangular inequality and Properties 1 and 2 yields (see Appendix 2 for more details):

$$\begin{aligned} \Vert \varXi \Vert \le \gamma _1\Vert \sigma \Vert + \gamma _2\Vert \alpha \Vert , \qquad \forall \sigma , \alpha \in \mathfrak {R}^3 \end{aligned}$$
(20)

where \(\gamma _1 = 1.5 \bar{P}^2\) and \(\gamma _2 = 2.5 \bar{P} + \Vert \alpha \Vert _\infty \).

Next theorem presents a state feedback controller that achieves the global asymptotic attitude regulation.

Theorem 2

Consider the rigid spacecraft described by Eqs. (2) and (4) with the virtual law (13). Suppose there is no disturbance i.e., \(T_\mathrm{d}(t)=0\), and Assumptions 1 and 2 are satisfied. Let the control law be

$$\begin{aligned} T(t) = J e^{\varrho \bar{\tau }} \left( \varrho \alpha + \dot{\omega }_{\mathrm {desire}}+J^{-1}S_\omega J \omega \right) . \end{aligned}$$
(21)

If a negative scalar constant \(\varrho \) and a symmetric positive definite matrix P are selected such that the following conditions hold

$$\begin{aligned}&\varrho > 2.5 \bar{P} +\Vert \alpha (0)\Vert _\infty -\frac{1}{2.1\bar{\tau }} \end{aligned}$$
(22)
$$\begin{aligned}&\bar{P} < \frac{4}{21\bar{\tau }}-0.4 \Vert \alpha (0)\Vert _\infty \end{aligned}$$
(23)
$$\begin{aligned}&\frac{\bar{P}^2}{\underline{P}}< \frac{1}{1.5\sqrt{5.01}\bar{\tau }} \end{aligned}$$
(24)

then, the closed-loop system is uniformly globally asymptotically stable (UGAS).

Proof

See Appendix 3.

Remark 2

The dependency of \( \varrho \) on \(\bar{\tau }\) is illustrated in condition (22). As it is expected, the admissible value for \(\varrho \) shrinks as the time delay increases. From conditions (22) and (23), it is observed that as \(\tau \rightarrow \infty \), there are no such values for \(\varrho \) and P which meet our goal. Therefore, the necessity of Assumption 1 is clarified.

Remark 3

It is convenient to simply choose the matrix \(P = pI\) in the virtual controller, where p is a positive constant.

3.2 With disturbances

In Theorem 2, we have presented the state feedback control law that solves the regulating problem for the spacecraft attitude system (2) and (4) without external disturbances. One may come to a quick conclusion that since the zero-disturbance system is UGAS, when disturbance impacts are taken into account, the system is ISS. But as shown in [43], this is not true for nonlinear systems in general, and the disturbance \(T_\mathrm{d}\) may destabilize the system.

In the next theorem, we consider the case where there is additive disturbance in the input T of Eq. (4).

Theorem 3

Suppose that Assumptions 1 and 2 are satisfied. The spacecraft attitude system described by Eqs. (2) and (4) in closed-loop with the control law described by Eqs. (13) and (21) is ISS.

Proof

See Appendix 4.

4 Simulation and comparison results

In order to evaluate the performance of the proposed attitude stabilization control strategy, a set of numerical simulation scenarios have been carried out using the rigid spacecraft system, where the physical parameters of the system are taken from [1, 12]; that is, the inertia matrix of the satellite is \(J=\mathrm {diag}\left[ 1000, 500, 700\right] \,\mathrm {Kgm}^2\), the satellite is moving in a circular orbit with inclination \(40^\circ \) and altitude of \(400\,\mathrm {km}\), which yields an orbital angular velocity of \(\omega _o = 0.0649^\circ /\mathrm {s}\).

4.1 Nominal performance

At first, the effectiveness of the proposed control scheme is examined in disturbance-free scenario. Using the rotation sequence 1–2–3 for direction cosine matrix [39, p. 759], the initial Euler angles of the satellite are taken to be \(\left( \phi , \theta , \psi \right) = \left( 125^\circ , 65^\circ , 55^\circ \right) \), yielding the initial MRP vector \(\sigma (0) = [0.3507, 0.3612, -0.1552]^T\). It is noteworthy to mention that for stabilizing the spacecraft with the specified initial value, we need \(111.1262^\circ \) eigenaxis rotation angle about principal axis . Such angle of rotation illustrates the capability of the controller to achieve large-angle attitude maneuvers of the spacecraft. The initial angular velocity of the satellite is taken to be \(\omega (0) = [0.01,\) \(-0.02, 0.01]^T\, \mathrm {rad/s}\). We assume that the maximum time delay \(\bar{\tau }\) is \(750\, \mathrm {ms}\). So, according to Theorem 2, the gain parameters must be chosen such that \(p<0.254\) and \(\varrho > -0.334\).

From the proof of Lemma 1, the role of the gain parameter p becomes clear in the controller operation. It can be accounted as the decay rate of exponential stable subsystem, so its value determines the time required for \(\sigma \) to converge to the origin. If p increases, the system states tend to zero faster, but \(\omega \) and subsequently T take higher values. The same statement is also true for \(|\varrho |\). The gain \(\varrho \) appears as a scaling factor on the input control T, so higher \(|\varrho |\) values serve to much larger control magnitudes. However, this implies a faster response. Thus, a trade-off between the system speed response and magnitude of the control action can be realized. Hence, for an acceptable performance, we must properly select these parameters to tune the controller. By several trials an observing the simulation responses, these parameters are chosen to be \(p=0.11\) and \(\varrho = -0.1\).

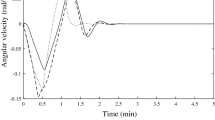
Figure 1 shows the time histories of MRPs, angular velocity, auxiliary variable \(\alpha \) and actuator effort T when the actual time delay is \(\tau = 500\, \mathrm {ms}\). In addition, since the MRPs bear no physical meaning from the practical viewpoint, we also show the spacecraft attitude responses using associated Euler angles in Fig. 2. As it is observed, after approximately \(200\, \mathrm {s}\), the satellite settles.

Fig. 1
figure 1

Simulation results for \(\tau = 500 \, \mathrm {ms}\) and \(\bar{\tau }=750\, \mathrm {ms}\)

Full size image
Fig. 2
figure 2

The time responses of the Euler angles for \(\tau = 500 \, \mathrm {ms}\) and \(\bar{\tau }=750\, \mathrm {ms}\)

Full size image

To illustrate the conservatism in the selection of the upper bound for the delay time, a simulation is performed under the given conditions using various time delays. Figure 3 depicts the results of such simulation.

Fig. 3
figure 3

Norm of MRP vector \(\Vert \sigma \Vert \), angular velocity \(\Vert \omega \Vert \) and control torque \(\Vert T\Vert \) for different \(\tau \) and \(\bar{\tau } = 750\, \mathrm {ms}\)

Full size image

Hereafter, we observe that for actual delay \(\tau \ge 10.2\,\mathrm {s}\), the closed-loop system is not stable anymore. The first \(250\,\mathrm {s}\) of simulation results for \(\tau =10.2\, \mathrm {s}\) are plotted in Fig. 4.

Fig. 4
figure 4

Norm of MRP vector \(\Vert \sigma \Vert \), and angular velocity \(\Vert \omega \Vert \) for \(\tau = 10.2\,\mathrm {s}\) and \(\bar{\tau }=0.75\, \mathrm {s}\)

Full size image

Some points can be extracted from Figs. 1, 2, 3, 4: (1) since \(\Vert \sigma \Vert <1\) for all situations, it is confirmed that the MRP vector travel a minimum path to reach the origin, i.e., the unwinding phenomenon is avoided; (2) because the controller of the kinematics subsystem is optimal, MRPs are robust against the variation of system condition; (3) when the length of delay increases, the controller torque also increases; this is due to the fact that the amount of errors build over delay interval increase as time delay \(\tau \) increases. This leads to large control torque demands; (4) as expected, the simulation results also confirm that the auxiliary variable \(\alpha \) takes maximum value in the starting point; (5) we observe that the actual delay length \(\tau \) that causes instability is relatively large compared to \(\bar{\tau }\); indeed, we find our results very conservative. This is in part caused by the nature of the L–K functional methods, but it is also due to the conservativeness introduced in the procedures that are performed to obtain the inequality (20). So, this issue needs further investigations to reduce the conservativeness.

4.2 Uncertainty scenario

In order to clearly demonstrate the robustness of the resulted closed-loop system with respect to external disturbance and uncertainties in the spacecraft parameters, a simulation is conducted by considering gravity gradient torque \(T_\mathrm{g}\) which is introduced in Eq. (5) and the constant mismatch in the inertia matrix of the spacecraft, simultaneously. All simulation parameters are selected the same as the first simulation except the actual time delay, which is assumed here to be \(\tau = 634 \,\mathrm {ms}\).

As we previously alluded, the mismatch in the inertial matrix can be caused by a variety of circumstances, e.g., fuel consumption, instruments/structure deployment and pre-launch imprecision. Hence, without going into the details of possible nature of this mismatch, we assume that the real inertial matrix \(J_\mathrm{r}\) is given by

$$\begin{aligned} J_\mathrm{r} =\left[ \begin{array}{rrr} 939.1205 &{} \,-160.6458 &{} \,-26.5661 \\ -160.6458 &{} \,573.6174 &{} \,-42.7836 \\ -26.5661 &{} \,-42.7836 &{} \,687.2621 \end{array} \right] . \end{aligned}$$
(25)

Note that the real inertia matrix \(J_\mathrm{r}\) has been used in the place of the nominal one in the spacecraft dynamics (4). Meanwhile, the inertia matrix used by the controllers remains the nominal one. Now, we apply the proposed controller. The simulation results are illustrated in Fig. 5, from which we conclude that the spacecraft reaches the demanded oration with high accuracy less than \(2.0394\mathrm {e-}4\) and \({2.2053\mathrm {e-}5} \, \mathrm {rad/s}\) for MRPs and velocity, respectively. Also, the discrepancy between the nominal plant variables and their perturbed ones is presented in Fig. 6, where \(\delta \) denotes the mismatch between the same variables in two different conditions. For example, \(\delta \sigma \) equals to \(\sigma \) in nominal case minus \(\sigma \) in perturbed situation, etc. The results illustrate that all \(\sigma _i\) and \(\omega _i,\, i=1, 2, 3\) evaluations are close to their nominal values. So the suggested controller is capable of rejecting the disturbances.

Fig. 5
figure 5

Simulation results in the presence of disturbances: MRP vector \(\sigma \), angular velocity \(\omega \), gravity gradient torque \(T_\mathrm{g}\) and control input T for \(\tau = 634\,\mathrm {ms}\) and \(\bar{\tau }=750\, \mathrm {ms}\)

Full size image
Fig. 6
figure 6

The discrepancy between related parameters in two different conditions: nominal case and perturbed situation for \(\tau = 634\, \mathrm {ms}\) and \(\bar{\tau } = 750\, \mathrm {ms}\)

Full size image

4.3 Comparison with other controllers

Finally, the proposed algorithm is compared to the controller presented in [12]. Toward this end, the system parameters are taken from [12] as

$$\begin{aligned} \begin{array}{lcc} \sigma (0) = [0, 0.0014, -0.0014]^T \quad &{} \bar{\tau } = 0.0125\, \mathrm {s} \quad &{} {T_\mathrm{d}(t)=0} \\ \omega (0) = [0.001, 0, 0]^T \quad &{} \tau = 0.012\, \mathrm {s}. \quad &{} \end{array} \nonumber \end{aligned}$$

Note that since in this scenario, the value of \(\bar{\tau }\) is changed and it takes a different value from the first and the second simulations, again we tune the proposed control parameters to satisfy the conditions (22)–(24) of Theorem 2. Adopting an analogous approach presented in the first scenario, the controller gains are changed to \(p = 4.5\) and \(\varrho = -1.25\) (note that however, the controller with previous gains is still able to stabilize the system, but to have a fair performance comparison between our approach and the control law extracted in [12], the controller parameters are changed).

The results of such comparison are reported in Fig. 7. It can be observed that the plant behavior under the proposed control strategy is comparable with the controller presented in [12] and there is no considerable difference between both schemes in the convergence rate, the magnitude of control effort and the accuracy.

Fig. 7
figure 7

Performance comparison of our approach (solid line) and the controller presented in [12] (dashed line) for \(\tau = 0.012\,\mathrm {s}\) and \(\bar{\tau }=0.0125\, \mathrm {s}\)

Full size image

For the sake of completeness, we also compare our control approach with the controller proposed in [1] where therein the time delay is considered as a known constant and RP is used to represent the attitude oration. The major difference between our proposed strategy and the works done in [1, 12] is the allowed maximum rotation angle. For same delay, in [1] and [12], the maximum principle rotation angles are restricted to \(0.0036\, \mathrm {rad}\) and \(0.0274\, \mathrm {rad}\), respectively. This implies that these strategies are only able to stabilize the spacecraft in a small neighborhood of the origin. However, in our approach, there is not such a restriction, and the introduced controller can stabilize the spacecraft for any arbitrary rotation; i.e., according to Theorem 2, our approach is global. Furthermore, we prove that our approach possesses robustness properties; however, neither the controller [1] nor the approach [12] owns such features. The performance comparison of three different controllers is summarized in Table 1.

Table 1 The performance comparison of different controllers
Full size table

5 Conclusions

In this paper, a backstepping method for stabilizing the rigid spacecraft attitude with unknown constant delayed inputs has been investigated. The adopted scheme has the advantages in not only uniformly globally asymptotically stabilizing the system but also achieving an ISS property to the closed-loop system. Furthermore, it is shown that the intermediate (virtual) control law is inverse optimal with respect to a meaningful cost functional that consists of penalties on the system states. The benefits of the inverse optimal approach are that it implies robustness properties against model uncertainties and external disturbances, while avoiding unwinding phenomenon. Numerical simulation results show that the proposed strategy can efficiently stabilize the system even in the presence of disturbances. Reducing conservatism and extending our results for unknown time-varying delays, while the angular velocity is unmeasurable are the topics for future research.