1 Introduction

Chaos can occur in third- or higher-order continuous-time nonlinear systems, second- or higher-order non-autonomous continuous-time nonlinear systems, and first-order invertible discrete maps. Recently, it has been shown that chaos can also occur in time-delayed nonlinear dynamical systems [1–12]. Delay systems take place in a wide variety of engineering, physical, chemical, economic, and biological systems, and their networks and play important roles.

It is well known that the delay term in a dynamical system results in infinite dimensional ordinary differential equations and may yield limit cycles, bifurcations, chaos, hyperchaos, multistability, and instabilities. Therefore, delay systems have been getting a great deal of attention of researchers in different fields, for getting the mathematical models of naturally occurring phenomena and high-dimensional chaotic behaviors for various applications. Some natural events modeled by delay systems include population dynamics [13, 14], El-Nino oscillations [15], the electrodynamics of interacting charged particles [16], dynamics of optical systems [17], neural networks [18], circulating-fuel fission reactor [19], and blood production in patients with leukemia [20]. The most recent studies have been devoted to the design of simple and well-characterized delay systems to produce chaos for secure communications [21–26], random number generators [27], and various other applications [28–35].

The main aim of this work is to introduce some chaotic delay systems that can occur in electronic circuits and a practical electronic design approach to realize chaotic delay differential equations. A first-order delay system can consist of infinite dimensional ordinary systems and can model a phenomenon or can be utilized for practical applications including communications and high-performance circuit designs. The delay systems to be seen in this study are the simplest chaotic delay systems consisted of a single constant delay and a nonlinear term. All delay systems are realized with simple electronic circuits by utilizing all-pass filters as delay elements, while the delay unit designs available in the literature are based on the inductor–capacitor–inductor (LCL) filters [1, 29, 31, 35], and inbuilt delay lines [36, 37]. The main advantage of the all-pass filters over other delay elements is its non-attenuating output. These novel circuit realizations of the novel chaotic delay systems pose high potentials for various applications in scientific, engineering, and industrial fields.

The following sections present the novel chaotic delay systems, their electronic implementations, and a conclusion to the paper.

2 Novel chaotic delay systems and electronic solutions

Delay (or retarded) systems arise in many practical models of problems in engineering, science, and medicine, where there is a time lag or after effect [38]. A delay system with a constant delay may be described by

$$\begin{aligned} \dot{x}=f(t,x,x_\tau ) \end{aligned}$$
(1)

where \(x_\tau =x(t-\tau )\) is the time-delayed term with a positive delay constant \(\tau \). System (1) is a closed form of many practical dynamical systems, including optics [17, 39], biology [20, 40], and economics [41]. Some specific delay system examples are the business model [42], population dynamics [43], tumor growth [44], immune systems [45], and lossless electrical transmission lines [46, 47]. For example, a model for blood production in patients with leukemia [20] is given by \(\dot{x}=-bx+(ax_\tau )/(1+x_\tau ^c)\), the dynamics of an optical bistable resonator [17] is given by \(\dot{x}=-ax-b\sin (x_\tau )\), a chaos–hyperchaos generator [3] is given by \(\dot{x}=\sin (x_\tau )\), and the self-oscillation model of shipbuilding industry [2] is described by \(\dot{x}=\alpha x_\tau -\varepsilon x_\tau ^3 \). There are also some non-chaotic delay systems occurring in nature, including \(\dot{x}=x-xx_\tau \) for modeling single-species population growth [48], \(\dot{x}=x-x^{3}-\alpha x_\tau \) for explaining El-Nino temperature oscillations [15], and \(\dot{x}=-\alpha x_\tau (x+1)\) for modeling a circulating-fuel fission reactor [19]. For these reasons, several novel delay systems to be introduced in this work are going to be in the form of the system (1).

Practical applications and experimental realizations of the chaotic delay systems can be performed with electronic circuit designs. Electronic implementation of delay systems available in the literature is based on the T-type LCL filter with matching resistors at the input and output of the delay unit [1, 29, 31, 35], and the inbuilt delay lines (bucket brigade line) [36, 37]. Most of the delay units used in the literature are based on LCL filters. Figure 1 illustrates the delay unit constructed with LCL filters. The LCL filters provide a lossless filter configuration, but they require matching circuits which result in signal attenuation, and inductances need a large space. In addition, integrated circuit (IC) realizations of such filters are not possible (or very difficult).

Fig. 1
figure 1

Delay unit constructed with T-type LCL filters

Full size image

These attenuation, space, and matching issues can simply be solved with the use of all-pass filters. An all-pass filter requires only one op-amp, one capacitor, and one resistor to add delay to the response of the circuit [49]. The amplitude of the all-pass filter is unity for all frequencies. Figure 2 shows first-order and second-order all-pass filter configurations. The delay function can be obtained from a RC low-pass function (Fig. 2a), a RC high-pass function (Fig. 2b), and a second-order all-pass structure (Fig. 2c). Both first-order all-pass filter structures hold the same delay equations, but the signal is inverted in the low-pass configuration; on the other hand, the second-order all-pass filter needs only one op-amp. The transfer function of the first-order all-pass filters is given by

$$\begin{aligned} {v_{\hbox {o}} }/{v_{\hbox {in}} }={({\textit{sRC}}-1)}\big /{({\textit{sRC}}+1)} \end{aligned}$$
(2)

where time constant of the filter is \(\tau ={\textit{RC}}\). Similarly, Eq. (2) becomes second order for a second-order all-pass filter.

Fig. 2
figure 2

All-pass filter configurations. a RC low-pass function, b RC high-pass function, and c second-order all-pass filters

Full size image

An all-pass filter passes all frequency components of the input signal without attenuation, but provides predictable phase shifts for different frequencies of the input signals. If input is \(\sin (\omega t)\), then the output is \(\sin (\omega t+\phi )\). The phase shift, \(\phi \), of the first-order all-pass filters is given by

$$\begin{aligned} \phi =\pi -2\tan ^{-1}(2\pi {\textit{FRC}}),\quad 0<\phi <\pi \end{aligned}$$
(3)

where \(F\) (in Hz) is the frequency and the phase shift is frequency dependent. The dynamic behavior of a first-order all-pass filter with the output lagging behind the input is illustrated in Fig. 3 for \(R=40\,\hbox {k}\Omega \), \(C=10\,\hbox {nF}\) and \(F=80\,\hbox {Hz}\). It is seen that a given phase shift corresponds to a larger time difference for lower frequencies. The phase shift varies from \(\pi \) (or 180) at \(F=0\) to \(\hbox {0}\) at \(F=\infty \), and \(\phi =\pi /2\) when \(2\pi {\textit{FRC}}=1\). However, since the bandwidth of the practical operational amplifiers is limited, an infinite frequency is not possible. It should be noted that the phase shift of the cascaded all-pass filters varies from \(n\pi \) to \(\hbox {0}\) where \(n\) represents the number of cascades. The all-pass filters can be used for time-delayed feedback control [50, 51] and chaotic circuit designs. For chaotic delay systems, the delay term will be realized with the phase shift.

Fig. 3
figure 3

Dynamic response of an all-pass filter. a Phase diagram, b input-output waveforms

Full size image

System (1) with various simple nonlinear terms and all-pass filters given in Fig. 2 will serve as reference structures in the following subsections for developing novel chaotic delay systems and electronic circuit realizations.

2.1 A chaotic delay system with exponential nonlinearity

Consider a delay system in the form of (1) described by

$$\begin{aligned} \dot{x}=-\delta x_\tau +(e^{x_\tau }-1) \end{aligned}$$
(4)

where the parameters are \(\tau =1\) and \(\delta =3.29\). The saturated exponential function is the well-known diode’s characteristic equation, which will facilitate electronic implementations directly. System (4) has two fixed points at \(x_e =(0,\gamma )\) in which origin is stable (note that \(\gamma \) is the solution of \(e^{\gamma }-\delta \gamma -1=0\), and \(\gamma >0\) when \(\delta >1\) and \(\gamma <0\) when \(\delta <1)\) when the system delay is neglected. If we consider the effects of the delay term, for an eigenvalue \(\lambda =\alpha +\beta i\) where \(\alpha \) and \(\beta \) are real, by using the linear stability analysis at the origin, the following characteristic equation is obtained

$$\begin{aligned} \lambda +(\delta -1)e^{-\lambda \tau }=0 \end{aligned}$$
(5)

In (5), for \(\tau =0\), we have \(\lambda =1-\delta \), and thus the origin is stable for \(\delta >1\). If \(\tau \ne 0\), then Eq. (5) is a transcendental equation with infinite number of roots. To figure out conditions on \(\delta \) and \(\tau \) for stability of the fixed point at the origin, substituting \(\lambda =\alpha +\beta i\) into Eq. (5), one can get the following relations

$$\begin{aligned} \alpha +(\delta -1)e^{-\alpha \tau }\cos (\beta \tau )= & {} 0 \nonumber \\ \beta -(\delta -1)e^{-\alpha \tau }\sin (\beta \tau )= & {} 0 \end{aligned}$$
(6)

Following the procedure given in [52], it is obvious that the fixed point at the origin is stable if \(1<\delta <1\,+\,\pi /{2\tau }\), and a Hopf bifurcation occurs at \(\delta =1\,+\,\pi /{2\tau }\) for initial conditions selected around the origin. The existence of the bifurcations and chaos can be shown with bifurcation diagrams and phase plane analysis via numerical simulations.

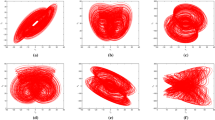
Bifurcation diagrams exhibiting a period-doubling route to chaos for the new chaotic system (4) are shown in Fig. 4 for the parameter \(\delta \) versus maximum \(x\) (Fig. 4a) and for \(\tau \) versus maximum \(x \)(Fig. 4b). All numerical results are obtained by using MATLAB/Simulink programs. There exists a quite complicated and atypical bifurcation scenario. There is an interleaving of chaos and order for \(3.26\le \delta \le 3.3\). The bifurcation diagrams show that the chaotic structure is non-symmetric in the phase plane, and the bifurcation diagram for small delay variations when \(\delta =10\) is quite different than the one obtained for \(\delta \) variations. Figure 5 shows the ring-shaped attractor of the chaotic system (4) for its nominal values \(\delta =3.29\) and \(\tau =1\).

Fig. 4
figure 4

Bifurcation diagrams of the chaotic delay system (4), a for \(\delta \) versus maximum \(x\), b for \(\tau \) versus maximum \(x (\delta =10)\)

Full size image
Fig. 5
figure 5

Chaotic attractor of the chaotic delay system (4) for \(\delta =3.29\) and \(\tau =1\)

Full size image

A simple electronic circuit implementation of the novel chaotic system (4) is provided in Fig. 6. Electronic elements of the circuit include a single quad TL08\(\times \) JFET-input op-amp and 10BQ015 Schottky diode as the nonlinear element of the circuit. The circuit is composed of four parts: integrator, cascaded first-order all-pass filters, sign inverter, and a nonlinear feedback element. By assuming that a first-order all-pass filter has a linear phase response, each filter block can provide a delay around \(\tau ={\textit{RC}}\) at a phase shift \(\phi =\pi /2\). Therefore, if \(n\) blocks are cascaded, we should get a total time delay of \(\tau ={\textit{nRC}}\). However, the phase shift (or delay) is frequency dependent, and the resistors of the all-pass filters, together with the feedback resistor of the nonlinear element, should be adjusted to getting a desired chaotic behavior. In the following circuit realizations, the amplitude of the signal from the nonlinear feedback element, i.e., diode, is controlled by a resistance for bifurcations and chaos.

Fig. 6
figure 6

An electronic circuit implementation of the chaotic delay system (4) with diode nonlinearity

Full size image
Fig. 7
figure 7

Phase-portrait analysis of the electronic circuit of the system (4) in the phase-space \(x-x_{\tau }\).

Full size image

Figure 7 displays the ring-shaped attractor of the system (4) which is generated by the electronic circuit given in Fig. 6. It is clear that both numerical and experimental results are compatible with each other (as seen in Figs. 5, 7) and prove the existence of the chaotic dynamics.

2.2 A chaotic delay system with absolute value nonlinearity

The effectiveness of the absolute value nonlinearity was shown in non-autonomous chaotic systems [53]. It is also possible to obtain a chaotic delay system by

$$\begin{aligned} \dot{x}=\delta x_\tau -x_\tau \left| {x_\tau } \right| \end{aligned}$$
(7)

where the system parameters are \(\delta =3\) and \(\tau =1\). The system (7) has three fixed points at \(x_e =(-\delta ,0,\delta )\) with stable nonzero fixed points, if the delay is neglected. By considering the effects of the delay term, the following characteristic equation is obtained for an eigenvalue \(\lambda \) as

$$\begin{aligned} \lambda +\delta e^{-\lambda \tau }=0 \end{aligned}$$
(8)

Similar to the analysis given in Sect. 2.1, the fixed points \(x_e =\pm \delta \) are stable if \(0<\delta <\pi /{2\tau }\), and a Hopf bifurcation occurs at \(\delta =\pi /{2\tau }\).

Bifurcation diagrams exhibiting a period-doubling route to chaos for the chaotic delay system (7) are shown in Fig. 8 for the parameter \(\delta \) versus \(x_{\hbox {max}}\) (Fig. 8a), and \(\tau \) versus \(x_{\hbox {max}}\) (Fig. 8b). There is an interleaving of chaos and order for \(\delta \ge 2.9\). Figure 9 illustrates the chaotic attractor of this new chaotic system for its nominal values \(\delta =3\) and \(\tau =1\).

Fig. 8
figure 8

Bifurcation diagram of the delayed chaotic system (7), a for \(\delta \) versus maximum \(x\), b for \(\tau \) versus maximum \(x (\delta =10)\)

Full size image
Fig. 9
figure 9

Chaotic attractor of the chaotic delay system (7) for \(\delta =3, \tau =1\) and \(x_{0}=0.1\)

Full size image

Figure 10 shows an electronic circuit implementation of the chaotic system (7). The circuit includes two quad TL08\(\times \) JFET-input op-amps, a multiplier, and a 1N4002 diode. In this electronic circuit realization, the number of the circuit elements is increased compared to the Fig. 6 due to the complexity of the nonlinear element. The chaotic attractor of this electronic circuit seen in Fig. 11 carries the features obtained in numerical simulations (e.g., for \(\delta =3.28\)).

Fig. 10
figure 10

An electronic circuit implementation of the chaotic delay system (7) with all-pass filters and a diode

Full size image

2.3 A chaotic delay system with hyperbolic nonlinearity

Trigonometric (sinusoidal) nonlinearity-based simple chaotic delay systems [3, 39] exist in literature. This section will show that chaotic delay systems can also be obtained with simple hyperbolic functions. Let a delay system be defined by the following equation

$$\begin{aligned} \dot{x}=\delta x_\tau -\sinh (x_\tau ) \end{aligned}$$
(9)

where \(\delta =2.27\) and \(\tau =1\). The system (9) has three fixed points at \(x_e =(0,\pm \eta )\) (\(\eta \) is the solution of \(\delta \eta -\sinh (\eta )=0\) for \(\delta >1\)) with stable nonzero fixed points without any delay.

Fig. 11
figure 11

Phase-portrait analysis of the electronic circuit of the system (7) in the phase-space \(x-x_{\tau }\)

Full size image

By considering effects of the delay term, the following characteristic equation is obtained for an eigenvalue \(\lambda \) as

$$\begin{aligned} \lambda +\left( {\cosh (\eta )-\delta } \right) e^{-\lambda \tau }=0 \end{aligned}$$
(10)

With numerical evaluation of the function \(\cosh (\eta )-\delta =\pi /2\), one can find that the fixed points \(x_e =\pm \eta \) are stable if \(1<\delta <1.67\), and Hopf bifurcation occurs at around \(\delta \approx 1.67\).

Bifurcation diagrams of the system (9) are shown in Fig. 12 for the parameter \(\delta \) versus \(x_{\hbox {max}}\), and \(\tau \) versus \(x_{\hbox {max}}\). A periodic doubling route to chaos is seen in Fig. 12 and there is an interleaving of chaos and order for \(2.22<\delta <2.31\). Figure 13 shows the attractor of the novel chaotic delay system for \(\delta =2.27\) and \(\tau =1\).

Fig. 12
figure 12

Bifurcation diagram of the chaotic delay system (9), a for \(\delta \) versus maximum \(x\), b for \(\tau \) versus maximum \(x (\delta =5)\)

Full size image

It is interesting to see that the bifurcation diagrams of the chaotic delay systems (7) and (9) have very similar characteristics. While both systems have completely different nonlinear structures, for small \(x\) values, i.e., \(-3\le x\le 3\), their nonlinearities produce very close values to each other. This resemblance results in similar chaotic dynamics. Therefore, the electronic implementation of the system (9) should be the same as the circuit diagram of the system (7) and will not be repeated in this subsection.

Fig. 13
figure 13

Chaotic attractor of the chaotic delay system (9) for \(\delta =2.27\) and \(\tau =1\)

Full size image

2.4 A chaotic delay system with signum nonlinearity

A chaotic delay system can be defined by

$$\begin{aligned} \dot{x}=-\delta x_\tau +\hbox {sgn}(x_\tau ) \end{aligned}$$
(11)

where \(\delta =1.8\), \(\tau =1\), and the sgn\((\cdot )\) is the signum function. If \(x_\tau \ne 0\), then \(\hbox {sgn}(x_\tau )=x_\tau /\left| {x_\tau } \right| \). The sgn\((\cdot )\) function can also be approximated to \(\hbox {sgn}(x_\tau )\approx \tanh (kx_\tau )\) for \(k{>>}1\) (e.g., \(k=100\)) for smooth results. Note that Eq. (11) is studied by Lakshmanan and Senthilkumar [52] for large delay constant values, but in this work it is shown that the chaotic dynamics can also be obtained for small delay constants and that its existence can be verified with an electronic circuit.

The system (11) has three fixed points \(x_e =(-1/\delta , 0, 1/\delta )\) where the nonzero fixed points are stable when the system delay is ignored. On the other hand, to analyze the effects of the delay term, the following characteristic equation is obtained for an eigenvalue \(\lambda \) as

$$\begin{aligned} \lambda +\delta e^{-\lambda \tau }=0 \end{aligned}$$
(12)

From (12), the fixed points \(x_e =\pm 1/\delta \) are stable if \(0<\delta <\pi /{2\tau }\), and a Hopf bifurcation occurs at \(\delta =\pi /{2\tau }\). Bifurcation diagrams of the chaotic delay system (11) are shown in Fig. 14 for the parameter \(\delta \) versus \(x_{\hbox {max}}\), and \(\tau \) versus \(x_{\hbox {max}}\). There is an interleaving of chaos and order for \(\delta >1.55\).

Fig. 14
figure 14

Bifurcation diagram of the chaotic delay system (11), a for \(\delta \) versus maximum \(x\), b for \(\tau \) versus maximum \(x (\delta =5)\)

Full size image

Electronic circuit implementation of the chaotic system (11) is shown in Fig. 15, which includes a single quad TL08\(\times \) JFET-input op-amp and 1N4002 diodes to get the nonlinear element of the circuit. Similar to Fig. 6, the electronic circuit is composed of an integrator, cascaded first-order all-pass filters, and a nonlinear element. The chaotic attractor of this electronic circuit is seen in Fig. 16b, which is compatible with the numerical simulations given in Fig. 16a.

Fig. 15
figure 15

An electronic circuit implementation of the chaotic delay system (11) with signum nonlinearity

Full size image
Fig. 16
figure 16

Phase-portrait of the system (11) in the phase-space \(x-x_{\tau }\): a numerical results and b the electronic circuit implementation results

Full size image

It should be noted that for quantitative measure of the system dynamics, the first five Lyapunov exponents (LEs) of the above chaotic delay systems are computed using the Wolf algorithm [54]. For example, LEs of the system (4) are found as \(\lambda _1 =0.2736\), \(\lambda _2 =-0.3081\), \(\lambda _3 =-1.2203\), \(\lambda _4 =-1.303\), and \(\lambda _5 =-1.815\). For small delay values, \(\tau \le 1\), all systems provided in this work have only one positive LE in the chaotic region, so hyperchaos indication is not found. On the other hand, multiple positive LEs are found for large delay values, but the related results are not illustrated since one of the goals of this work is to show the existence of chaos for small delays in simple nonlinear delay systems.

3 Conclusion

This study presents novel first-order chaotic delay systems and their electronic circuit realizations. The chaotic delay systems include the simplest nonlinearities that can be seen in nature, medicine, and engineering systems, e.g., electronic circuit elements. Electronic circuit implementation of the chaotic delay systems is achieved with simple all-pass filters and diode nonlinearities. The all-pass filters eliminate the matching, space, and signal attenuation issues of LCL type filters in practical applications, and the use of diodes simplifies the circuits. Chaotic delay systems introduced in this paper have high potentials in many applications including secure communications, circuit designs, and random number generations and can also be used to model natural, scientific, electronic, medical, and engineering systems.