Coordinated path following control of multi-unicycle formation motion around closed curves in a time-invariant flow

Abstract

This paper utilizes a dynamic model of unicycles to address the stabilization of formation motion around closed curves in the presence of a time-invariant flow field. It is shown that our previous concentric compression design can be extended to deal with robust coordinated path following control for fighting against the external flow field. Linear acceleration control for each unicycle is used and combined with the rotation control to achieve both temporal and spatial formations in the case of a spatially variable flow, which breaks the restriction of temporally balanced formation relied solely on the angle control in the literature. A potential function is introduced to force each unicycle’s speed greater than the magnitude of flow. The theoretical result is proved by two numerical examples.

1 Introduction

Recent advances in control techniques for autonomous vehicles and agile sensor networks bring researchers the dawn to apply a family of sensor-equipped vehicles to execute surveillance [1], environmental fields measurement [2, 3] and persistent survey of biological system [4]. In almost any environment, the sensory performance has been severely affected by an external flow field (e.g., ocean current or atmospheric wind). For example, the atmospheric wind can push each unicycle away from its given path and disrupt the relative position of each pair of unicycles (that is formation), which leads to reducing the accuracy of data sampling. Nowadays, most existing coordinated path following control protocols [5–13] are derived based on flow-free motion models, and thus, they often fail to account for the degradation of control performance caused by flow fields. Therefore, it is urgently needed to design a robust coordinated path following control when vehicles suffer an external flow field.

Although robust consensus control with disturbances of the external environment are well discussed in the literature [14–16], prior works on robust coordinated path following control for fighting against an external flow field are still few due to the geometric constraints on the vehicles’ movements (that is, each vehicle must follow its given orbit). In [17], an angular velocity algorithm is provided for each constant-speed particle to stabilize the temporally balanced formation around a circle in a steady, uniform flow field and then extended to deal with double integrators by the backstepping technology [18]. A similar idea is used to give a solution to coordinate UAVs flying around a convex loop in a spatially invariant wind [19]. Furthermore, all the above results [17–19] are based on the assumption that the magnitude of the flow is weaker than the vehicle’s speed. It must be emphasized that one relying solely on the angle control cannot maintain the spatial formation (that is the uniform separation around orbits) even in the simplest case of a steady, uniform flow field. This is due to the fact that the external flow leads to the various actual linear speed of the vehicle at different locations even though the vehicle satisfies constant speed. Since the exact spatial formation is important to the accuracy of data measurements and the (near) optimal sampling trajectory for each vehicle is often planned to be a simple and closed curve (not limited in a circle or a convex loop) [2–4], we discuss coordinated path following control for the temporal and spatial formation motions around a set of closed orbits in an external flow field.

This paper builds upon our prior research on the geometric extension design. The key idea of this approach is to extend the given curve to be a set of level curves of the orbit function for path following and then incorporate the orbit function into the arc-length function to give the solution to formation motion around the given orbits. In the absence of a flow field, coordinated Newtonian particle formation motion around closed curves is solved based on the geometric extension along each curve’s normal vector [9, 10]. To maintain the same geometric topology among the extended curves and the given curve, Chen and Tian propose the concentric compression design to deal with cooperative motion along convex loops at first [11, 12] and then a kind of general non-convex and closed curves [13]. However, the result of using the geometric extension design for coordinated path following control in the presence of a time-invariant flow field is not established yet.

The main contribution of this paper is that we show that the concentric compression design can be extended to deal with the temporal and spatial formation motions around a family of given closed curves in the presence of a flow field, which breaks the restriction of temporally balanced formation on a circle or a convex loop when vehicles suffer an external flow in the literature [17–19]. The external flow field under consideration is known, non-uniform and time-invariant, which covers the types of the flow field discussed in [17–19]. We deal with the control of the unicycle’s dynamics which is the difference from the constant-speed particle on the additional linear acceleration control. In this paper, the inertial velocity of the flow is first converted to the linear speed and the orientation of the unicycle. Then, the component where the linear acceleration and the angular acceleration are projected onto the actual orientation of each unicycle is used to accomplish both temporal and spatial formations, and at the same time, the component where the linear acceleration and the angular acceleration are projected onto the normal vector perpendicular to the actual orientation of each unicycle is applied to achieve the orbit tracking. For the purpose of ensuring that each unicycle’s speed is greater than the magnitude of flow, a potential function often used in collision avoidance [21] is introduced into the controller design.

This paper is organized as follows. Section 2 summarizes the unicycle’s model in an external flow field and formulates the coordinated control problem based on concentric compression. In Sect. 3, the control design scheme is designed based on the backstepping technology. Simulation results are given in Sect. 4. Section 5 provides conclusion.

2 Problem statement

2.1 Unicycle’s model in a time-invariant flow field

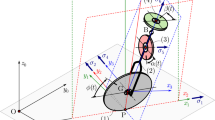
In this subsection, we will show the dynamic model of a unicycle in a time-invariant flow field. Each unicycle is subject to two independent control inputs $\{u_i,\tau _i\}$ in order to provide the linear acceleration force and the angular moment in the flow field. Let $\mathbf {z}_i = \left[ {z_{i}^{x} ,z_{i}^{y} } \right] ^T\in {\mathbb {R}}^{2}$ indicate the position of the wheel axis center defined in an inertia coordinate frame ${\fancyscript{W}}$. Also let $\theta _i$ be the $i$th unicycle’s orientation with respect to the $x$-axis of ${\fancyscript{W}}$. $\upsilon _i$ and $\omega _i$ are its linear and angular velocities, respectively. In this paper, the flow field is known and time-invariant. Its inertial velocity at $\mathbf {z}_i$ is represented as $\mathbf {f}(\mathbf {z}_i)=\left[ f^x(\mathbf {z}_i),f^y(\mathbf {z}_i)\right] ^T$ such that $\left\| {\mathbf {f} } \right\| \le f_M$ where $f_M$ is a bounded constant. With loss of generality, the flow field is permitted to be spatially variable (non-uniform) as long as it is $C^2$ smooth where $\mathbf {f}' = \partial \mathbf {f} /\partial \mathbf {z}_i = \left[ {\nabla f^x ,\nabla f^y } \right] ^T = \left[ {\begin{array}{cc} {\partial f^x /\partial z_i^x } &{} {\partial f^x /\partial z_i^y } \\ {\partial f^y /\partial z_i^x } &{} {\partial f^y /\partial z_i^y } \\ \end{array}} \right]$. The dynamics of a unicycle in the presence of a time-invariant flow field (see Fig. 1) is

$$\begin{aligned} \left\{ {\begin{array}{ll} {\dot{z}_i^x = {\upsilon _i}\cos {\theta _i} \!+\! {f^x}}\\ {\dot{z}_i^y = {\upsilon _i}\sin {\theta _i} \!+\! {f^y}}\\ {{{\dot{\theta }}_i} = {\omega _i}}\\ {{{\dot{\upsilon }}_i} = {u_i}}\\ {{{\dot{\omega }}_i} = {\tau _i}} \end{array}} \right. \end{aligned}$$

(1)

Fig. 1

Unicycle’s model in a time-invariant flow field

Remark 1

In [18, 19], only a uniform, time-invariant flow so that $\mathbf {f}=[\beta ,0]^T$ is considered where constant $\beta$ satisfies that $|\beta |<1$ due to the unit speed of each particle. A simple non-uniform time-invariant flow $\mathbf {f} =\left[ f^x({z}_i^x),f^y({z}_i^y)\right] ^T$ is discussed in [17]. Compared with the flow field considered in this paper, each above-mentioned flow field can be regarded as a special case of this paper.

Let $\gamma _i=\arctan 2(\dot{z}_{i}^{x},\dot{z}_{i}^{y})$ be the orientation of the actual inertial velocity of the $i$th unicycle and $\upsilon _{f_i } = \left\| {\dot{\mathbf {z}}_i + \mathbf {f} } \right\|$ denote its magnitude. Also let $\mathbf {x}_i = \left[ {\cos \gamma _i ,\sin \gamma _i } \right] ^T$ be the unit vector tangent to the trajectory of the $i$th unicycle at the current location and the normal vector $\mathbf {y}_i$ is perpendicular to $\mathbf {x}_i$. The dynamics of the position of the $i$th unicycle can be written as $\dot{\mathbf {z}}_{i } = \upsilon _{f_i } \mathbf {x}_i$. In the following, we first show the dynamics of $\gamma _i$. From the first two equations of (1), we have

$$\begin{aligned} \tan \gamma _i = \frac{{\upsilon _i \sin \theta _i + f^y }}{{\upsilon _i \cos \theta _i + f^x }}. \end{aligned}$$

(2)

Differentiating (2) with respect to time along the solution of (1) for $\dot{\gamma }_i$, we obtain

$$\begin{aligned} \dot{\gamma }_i = \kappa _{\gamma _i }^u u_i + \kappa _{\gamma _i }^\omega \omega _i + d_{\gamma _i } \end{aligned}$$

(3)

where

$$\begin{aligned} \kappa _{\gamma _i}^u= & {} - \upsilon _i^{ - 1} \upsilon _{f_i }^{ - 1} f_i^y \cos \gamma _i + \upsilon _i^{ - 1} \upsilon _{f_i }^{ - 1} f_i^x \sin \gamma _i\\= & {} - \upsilon _i^{ - 1} \upsilon _{f_i }^{ - 1} \left( {\mathbf {f}_i \cdot \mathbf {y}_i } \right) ,\\ \kappa _{\gamma _{i}}^{\omega }= & {} 1 - \upsilon _{f_i }^{ - 1} \left( {f_i^x \cos \gamma _i + f_i^y \sin \gamma _i } \right) \\= & {} 1 - \upsilon _{f_i }^{ - 1} \left( {\mathbf {f}_i \cdot \mathbf {x}_i } \right) ,\\ d_{\gamma _{i}}= & {} \left( {\nabla f^x \cdot \mathbf {x}_i } \right) \cos \gamma _i - \left( {\nabla f^y \cdot \mathbf {x}_i } \right) \sin \gamma _i. \end{aligned}$$

It is obvious that Eq. (3) is suitable when $\upsilon _i>\Vert \mathbf {f}\Vert$ or $\upsilon _i<\Vert \mathbf {f}\Vert$. In this paper, we only consider the situation that $\upsilon _i>\Vert \mathbf {f}\Vert$. Next we will express $\upsilon _{f_i}$ as a function of $(\upsilon _i,\mathbf {f},\gamma _i)$. Also from the first two equations of (1), one gets

$$\begin{aligned} \upsilon _{f_i } = \sqrt{\upsilon _i^2 - \left\| {\mathbf {f} } \right\| ^2 + 2\left( {\mathbf {f} \cdot \mathbf {x}_i } \right) \upsilon _{f_i } } \end{aligned}$$

(4)

which implies

$$\begin{aligned} \upsilon _{f_i }^2 - 2\left( {\mathbf {f} \cdot \mathbf {x}_i } \right) \upsilon _{f_i } + \left\| {\mathbf {f} } \right\| ^2 - \upsilon _i^2 = 0. \end{aligned}$$

(5)

When $\upsilon _i>\Vert \mathbf {f}\Vert$, the quadratic Eq. (5) has the solution

$$\begin{aligned} \upsilon _{f_i } = \mathbf {f} \cdot \mathbf {x}_i + \sqrt{\upsilon _i^2 - \left( {\mathbf {f} \cdot \mathbf {y} } \right) ^2 }. \end{aligned}$$

(6)

Differentiating (6) with respect to time along the solution of (1) and solving for $\dot{\upsilon } _{f_i }$ using (3), we obtain

$$\begin{aligned} \dot{\upsilon } _{f_i } = \kappa _{\upsilon _{f_i} }^u u_i + \kappa _{\upsilon _{f_i} }^\omega \omega _i + d_{\upsilon _{f_i} } \end{aligned}$$

(7)

where

$$\begin{aligned} \kappa _{\upsilon _{f_i} }^u= & {} \kappa _{\gamma _i }^u \left[ \left( {\mathbf {f}_i \cdot \mathbf {y}_i } \right) - \left( \upsilon _i^2 - \left( {\mathbf {f}_i \cdot \mathbf {y}_i } \right) ^2 \right) ^{ - \frac{1}{2}} \right. \\&\times \left. \left( {\mathbf {f}_i \cdot \mathbf {y}_i } \right) \left( {\mathbf {f}_i \cdot x_i } \right) \right] \\&+ \left( {\upsilon _i^2 - \left( {\mathbf {f}_i \cdot \mathbf {y}_i } \right) ^2 } \right) ^{ - \frac{1}{2}} \upsilon _i,\\ \kappa _{\upsilon _{f_i} }^\omega= & {} \kappa _{\gamma _i }^\omega \left[ {\left( {\mathbf {f} \cdot \mathbf {y}_i } \right) -\left( {\upsilon _{f_i} - \mathbf {f} \cdot \mathbf {x}_i} \right) ^{ -1}\left( {\mathbf {f} \cdot \mathbf {y}_i } \right) \left( {\mathbf {f} \cdot \mathbf {x}_i } \right) } \right] ,\\ d_{\upsilon _{f_i } }= & {} \upsilon _{f_i } \left( {\mathbf {f}' \mathbf {x}_i } \right) \cdot \mathbf {x}_i\\&- \upsilon _{{f}_i } \left( {\upsilon _{f_i} - \mathbf {f} \cdot \mathbf {x}_i} \right) ^{ -1} \left( {\mathbf {f} \cdot \mathbf {y}_i } \right) \left( {\mathbf {f}' \mathbf {x}_i } \right) \cdot \mathbf {y}_i. \end{aligned}$$

Furthermore, one gets $\upsilon _i{=}\sqrt{\upsilon _{f_i }^2 {-} 2( \mathbf {f} {\cdot } \mathbf {x}_i )\upsilon _{f_i } {+} \Vert {\mathbf {f} } \Vert ^2 }$ from (5) and then $\kappa _{\gamma _i }^u$ can be rewritten as

$$\begin{aligned} \kappa _{\gamma _i }^u=\upsilon _{f_i }^{ - 1}(\upsilon _{f_i }^2 - 2( {\mathbf {f} \cdot \mathbf {x}_i } )\upsilon _{f_i } + \left\| {\mathbf {f} } \right\| ^2)^{-\frac{1}{2}} ( \mathbf {f} \cdot \mathbf {y}_i ). \end{aligned}$$

In the Sect. 3, we first regard $\omega _i$ as a virtual control and then apply the backstepping technology to design $\tau _i$. By using (3) and (7) to calculate $(\omega _i,u_i)$ , it is required

$$\begin{aligned} \left\| {\begin{array}{cc} {\kappa _{\gamma _i }^u } &{} {\kappa _{\gamma _i }^\omega } \\ {\kappa _{\upsilon _{f_i} }^u } &{} {\kappa _{\upsilon _{f_i} }^\omega } \\ \end{array}} \right\| \ne 0 \end{aligned}$$

(8)

which implies

$$\begin{aligned} g_{\kappa _i }= & {} \sqrt{\upsilon _{f_i }^2 - 2\left( {\mathbf {f} \cdot \mathbf {x}_i } \right) \upsilon _{f_i } + \left\| {\mathbf {f} } \right\| ^2 } \left( {\upsilon _{f_i} - \mathbf {f} \cdot \mathbf {x}_i} \right) ^{ -1}\nonumber \\&\times \left( {1 - \upsilon _{f_i }^{ - 1} \left( {\mathbf {f} \cdot \mathbf {x}_i } \right) } \right) \ne 0. \end{aligned}$$

(9)

(9) is true when $\upsilon _i>\Vert \mathbf {f}\Vert$ and the proof is similar to the procedure described in [17].

From the above discussion, the dynamics of unicycle with a time-invariant flow becomes

$$\begin{aligned} \left\{ {\begin{array}{ll} \dot{\mathbf {z}}_{i } = \upsilon _{f_i } \mathbf {x}_i \\ \dot{\mathbf {x}}_i = ( {\kappa _{\gamma _i }^u u_i + \kappa _{\gamma _i }^\omega \omega _i + d_{\gamma _i } })\mathbf {y}_i \\ \dot{\mathbf {y}}_i = - ( {\kappa _{\gamma _i }^u u_i + \kappa _{\gamma _i }^\omega \omega _i + d_{\gamma _i } })\mathbf {x}_i \\ \dot{\upsilon }_{f_i } = \kappa _{\upsilon _{f_i} }^u u_i + \kappa _{\upsilon _{f_i} }^\omega \omega _i + d_{\upsilon _{f_i } } \\ \dot{\omega }_i = \tau _i \end{array}} \right. \end{aligned}$$

(10)

Remark 2

As compared with the model of unit-speed particle in a time-invariant flow field [17–19], the dynamic model (10) with the acceleration control is more complex. $\kappa _{\upsilon _{f_i} }^u u_i + \kappa _{\upsilon _{f_i} }^\omega \omega _i$ is the term where the linear acceleration and the angular acceleration are projected onto $\mathbf {x}_i$, and we use it to accomplish the temporal and spatial formations. $\kappa _{\gamma _i }^u u_i + \kappa _{\gamma _i }^\omega \omega _i$ is the component where the linear acceleration and the angular acceleration are projected onto $\mathbf {y}_i$, and it is used to achieve the orbit tracking. In Subsect. 3.2, these two components are designed at first and then used to solve $u_i$ and $\omega _i$. At last, $\tau _i$ is obtained by using the backstepping technology.

2.2 Concentric-compressing-based design

Consider that the given orbit $\varGamma _{i0}$ associated with the $i$th unicycle is a simple and closed curve with nonzero curvature. Suppose that $\varGamma _{i0}$ can be parameterized by using a smooth map $\varGamma _{i0}:[0,2\pi )\rightarrow {\mathbb {R}}^{2}$, $\phi _{i}\mapsto \varGamma _{i0}(\phi _{i})$ with $\Vert \varGamma _{i0}(\phi _{i})\Vert >0$ and $\Vert \text {d}\varGamma _{i0}(\phi _{i})/\text {d}\phi _{i}\Vert >0$, where $\phi _{i}$ is the phase angle that describes the direction of the vector from the origin of the orbit to the point on the orbit with respect to the positive axis of ${\fancyscript{W}}$. Also assume that the vector from the origin of the orbit to each point $\mathbf {z}_{i,k}$ on the orbit and the tangent vector to the orbit on $\mathbf {z}_{i,k}$ are linearly independent, that is $\left| \varGamma _{i0}(\phi _{i}),\frac{\text {d}\varGamma _{i0}(\phi _{i})}{\text {d}\phi _{i}}\right| \ne 0$ for all $\phi _{i}$. Referring to Lemma 1 in [13], a set of orbits can be obtained by concentric compressing, that is

$$\begin{aligned} \varGamma _{i\lambda } \left( {\phi _i ,\lambda } \right) = \left( {1- \lambda } \right) \varGamma _{i0} \left( {\phi _i } \right) \end{aligned}$$

(11)

and each one corresponds to a special constant value of the orbit function $\lambda _i(\mathbf {z}_{i})$, where $\lambda _i(\mathbf {z}_{i})$ satisfies $\nabla \lambda _i(\mathbf {z}_{i} ) \ne 0$ and $\left| {\lambda _i (\mathbf {z}_{i})} \right| < \varepsilon _i, (\varepsilon _i> 0)$. The orbit value associated with the given orbit $\varGamma _{i0}$ is $0$ (see Fig. 2). Some corresponding proofs and examples can be found in [11, 13].

Fig. 2

Concentric compression: a A family of convex and closed curves, b A family of non-convex and closed curves

In order to follow the given orbit, the path following control should drive the orbit value $\lambda _i \left( {\mathbf {z}_{i} } \right)$ and the direction error $\alpha _i \in \left( { - \pi ,\pi } \right]$ between the unicycle’s motion and the tangent vector to the orbit to $0$ asymptotically (see Fig. 3), i.e.,

$$\begin{aligned}&\lim _{t \rightarrow \infty } \lambda _i\left( \mathbf {z}_{i}(t)\right) = 0,\end{aligned}$$

(12)

$$\begin{aligned}&\lim _{t \rightarrow \infty } \alpha _i ( t ) = 0, \end{aligned}$$

(13)

Due to the domain of the orbit function, the trajectory of each unicycle should be limited in the set $\varOmega _{i}$, i.e.,

$$\begin{aligned} \left| \lambda _i(\mathbf {z}_{i}(t)) \right| < \varepsilon _i. \end{aligned}$$

(14)

Fig. 3

Path following control design method

When each unicycle moves along its given orbit, the control object is to achieve the desired formation with the given orbits adopted. To this end, communication among the unicycles is essential. Let ${\fancyscript{G}}=\{{\fancyscript{V}},{\fancyscript{E}}\}$ be the bidirectional graph induced by the inter-unicycle communication topology, where ${\fancyscript{V}}$ denotes the set of $n$ unicycles and ${\fancyscript{E}}$ is a set of data links. Also let ${\fancyscript{N}}_{i}$ denote the neighbor set of the $i$th unicycle and we assume that ${\fancyscript{N}}_{i}$ is time-invariant. Two matrices such as the adjacency matrix $A=[a_{ij}]$ and the Laplacian matrix $L=[l_{ij}]$ are used to represent the graph. The key idea of the formation description on given orbits is based on the consensus design (see Fig. 4), which is widely applied in recent works. Some corresponding explanations can be found in [7, 10–13]. It is said that the formation is maintained when the generalized arc-lengths $\xi _{i}(t)$ defined in Assumption 1 reach consensus, i.e.,

$$\begin{aligned} \lim _{t\rightarrow \infty }\left( \xi _{i}(t)-\xi _{j}(t)\right) =0. \end{aligned}$$

(15)

Assumption 1

Each generalized arc-length $\xi _{i}(s_i(t))$ is a $C^2$ smooth function of arc-length $s_i$ that ${\partial \xi _i } \big / \partial s_i$ satisfies $+\infty >\bar{\varepsilon }_M \ge \frac{{\partial \xi _i }}{{\partial s_i }} \ge \bar{\varepsilon }_m >0$ and that is uniformly bounded.

Remark 3

Let us consider a rigid formation on a set of ellipses as shown in Fig. 4a. Each ellipse is obtained by translating the desired trajectory of the group center along the formation vector $\mathbf {h}_{i}, i=1,2,3$. Also let $\mathbf {z}_{i}^{*}$ denote the starting point associated with $\varGamma _{i0}$ for computing the arc-length $s_i$ and each pair satisfies $\mathbf {z}_{i}^{*}-\mathbf {z}_{j}^{*}=\mathbf {h}_{i}-\mathbf {h}_{j}$. The rigid formation $\mathbf {z}_{i}(t)-\mathbf {z}_{j}(t)=\mathbf {h}_{i}-\mathbf {h}_{j}$ is maintained if $s_{i}(t)=s_{j}(t)$. To form an in-line formation and move along the concentric orbits with different parameters $a_i\in {\mathbb {R}}$, it is required that $\xi _{i}=s_{i}/a_i$ reach to consensus where the starting point for each orbit is selected as the intersection of the orbit with the horizontal axis (see Fig. 4b).

Fig. 4

Formation description on orbits: a Rigid formation, b In-linear formation

In some practical situations, multiple unicycles are required for the formation motion at a specified orbital speed. Note that the deviation of the generalized arc-length $\eta _{i}(t)=\text {d}\xi _{i}(t)/\text {d}t$ on the given orbit reflects the orbital speed of the unicycle. This is due to the fact that $\eta _{i}(t)$ defined in (25) is a product obtained by multiplying the actual linear speed of a unicycle and a parameter with respect to the desired formation pattern. Therefore, $\eta _{i}(t)$ is regarded as the generalized orbital speed. To accomplish formation motion in accordance with the desired orbital speed, it is required that the generalized orbital speed $\eta _{i}(t)$ converges to the reference $\eta _*(t)$, i.e.,

$$\begin{aligned} \lim _{t\rightarrow \infty }\eta _{i}(t)=\eta _* (t). \end{aligned}$$

(16)

It must be emphasized that condition $\upsilon _i>\Vert \mathbf {f}\Vert$ is important to deduce the dynamics of unicycle in the flow field. Differing from the assumption that $\upsilon _i>\Vert \mathbf {f}\Vert$ in [17–19], we design the controller to ensure it in this paper. Because of the relationships between $\upsilon _i$ and the definition of $\eta _i$, here we use

$$\begin{aligned} \eta _{i} > \eta ^{m} = 2\bar{\varepsilon }_M f_M \end{aligned}$$

(17)

to replace $\upsilon _i>\Vert \mathbf {f}\Vert$. From (16), (25) and Assumption 1, one gets

$$\begin{aligned} \upsilon _{f_i}= \left( \frac{\partial \xi _i}{\partial s_i}\right) ^{-1}\eta _{i} > 2\left( \frac{\partial \xi _i}{\partial s_i}\right) ^{-1}\bar{\varepsilon }_M f_M \ge 2 f_M \end{aligned}$$

(18)

and then

$$\begin{aligned} \upsilon _i^2= & {} \upsilon _{f_i }^2 - 2\left( {\mathbf {f} \cdot x_i } \right) \upsilon _{f_i } + \left\| {\mathbf {f} } \right\| ^2\nonumber \\\ge & {} \left( {\upsilon _{f_i } - \left\| {\mathbf {f} } \right\| } \right) ^2 >\left\| {\mathbf {f} } \right\| ^2. \end{aligned}$$

(19)

To move on, we make an assumption as follow:

Assumption 2

The reference $\eta _{*}(t)$ is uniformly bounded and greater than $2\bar{\varepsilon }_M f_M$. Also $\dot{\eta }_{*}(t)$ is uniformly bounded.

From the above discussion, we define the coordinated path following control problem in a time-invariant flow field as follows:

Problem 1

Design a coordinated path following controller

$$\begin{aligned} \tau _i= & {} g_i ( \mathbf {z}_{i} ,\upsilon _{f_i},\gamma _i,\omega _i,u_i,\mathbf {f},\lambda _i, \alpha _i ,\mathbf {x}_i ,\mathbf {y}_i, s_{i}, \xi _i ,\xi _j,\\&\eta _{*},\dot{\eta }_{*})\\ u_i= & {} \tilde{g}_i \left( {\mathbf {z}_{i},\upsilon _{f_i}, \gamma _i, \omega _i,\mathbf {f}, \lambda _i, s_{i}, \xi _i ,\eta _{i} ,\xi _j ,\eta _j },{\eta }_{*},\dot{\eta }_{*} \right) \end{aligned}$$

for the $i$th unicycle who suffers a time-invariant flow field $\mathbf {f}$ by using its neighbors’ communication information such that requirements (12)-(17) are satisfied, where $i\in {\fancyscript{V}},j\in {\fancyscript{N}}_{i}$.

Remark 4

The information required in the control consists of two parts. On the one hand, the states $\{\mathbf {z}_i,u_i,\upsilon _i,\theta _i,\omega _i,\mathbf {f}\}$ are measured in the inertial reference frame. Then, we use them to calculate the states $\{\upsilon _{f_i},\gamma _i, \mathbf {x}_i ,\mathbf {y}_i,d_{\gamma _i },d_{\upsilon _i}$, $\alpha _{i}\}$ and the values of $\left\{ \lambda _i,\,\nabla \lambda _i,\,\nabla ^2\lambda _i,\,\nabla ^3 \lambda _i,s_i,\,\frac{\partial s_i}{\partial \lambda _i},\frac{\partial ^2 s_i}{\partial \lambda _i^2},\xi _i,\frac{\partial \xi _i}{\partial s_i},\frac{\partial ^2 \xi _i}{\partial s_i^2},\eta _i\right\}$ according to the functional forms of $\{\lambda _i,s_i,\xi _i,\eta _i\}$. The definition of each function can be found in Subsects. 2.1 and 3.1. On the other hand, information $\left\{ \xi _i,\eta _i\right\}$ should be transferred to its neighbors for the cooperation. The details can be found in Subsect. 3.2.

3 Main results

3.1 Coordinated control system

Let $\mathbf {N}_i = - \frac{{\nabla \lambda _i }}{{\left\| {\nabla \lambda _i } \right\| }}$ and $\mathbf {T}_i = \left[ {\begin{array}{cc} 0 &{} 1 \\ { -1} &{} 0 \\ \end{array} } \right] \mathbf {N}_i$ be the normal vector and the tangent vector to each level orbit, respectively. The direction error $\alpha _i$ between $\mathbf {x}_i$ and $\mathbf {T}_i$ can be defined as

$$\begin{aligned}&\cos \alpha _i = \mathbf {x}_i \cdot \mathbf {T}_i = \mathbf {y}_i \cdot \mathbf {N}_i,\end{aligned}$$

(20a)

$$\begin{aligned}&\sin \alpha _i = \mathbf {y}_i \cdot \mathbf {T}_i ~ = - \mathbf {x}_i \cdot \mathbf { N}_i. \end{aligned}$$

(20b)

The time derivative of (20b) yields

$$\begin{aligned} \dot{\alpha }_i= & {} \upsilon _{f_i } \left( {\kappa _{i }^a \cos \alpha _i + \kappa _{i }^b \sin \alpha _i } \right) \nonumber \\&- \left( \kappa _{\gamma _i }^u u_i + \kappa _{\gamma _i }^\omega \omega _i + d_{\gamma _i } \right) \end{aligned}$$

(21)

where

$$\begin{aligned} \kappa _{i}^a= & {} \frac{1}{{\left\| {\nabla \lambda _i } \right\| }} \mathbf {T}_i \cdot \nabla ^2 \lambda _i \mathbf {T}_i,\\ \kappa _{i}^b= & {} - \frac{1}{{\left\| {\nabla \lambda _i } \right\| }} \mathbf {T}_i \cdot \nabla ^2 \lambda _i \mathbf {N}_i \end{aligned}$$

and $\nabla ^2 \lambda _i$ is the Hessian matrix of $\lambda _{i}\left( \mathbf {z}_{f_i}\right)$. Since the orbit value with respect to $\varGamma _{i0}$ is $0$, the position error of path following can be represented as $\lambda _{i}\left( \mathbf {z}_{f_i}\right)$, and then, the dynamics of position error of path following can be written as

$$\begin{aligned} \dot{\lambda }_i = \nabla \lambda _i \cdot \dot{\mathbf {z}}_{i} =\upsilon _{f_i}\left\| {\nabla \lambda _i } \right\| \sin \alpha _i. \end{aligned}$$

(22)

Since the movement of the $i$th unicycle projected to $\mathbf {T}_i$ leads to the variation in arc-length $s_{i}$ while the motion along the direction of concentric compression causes the orbit change which also induces the changes of the arc-length, the arc-length $s_{i}$ measured from the starting point can be written as

$$\begin{aligned} s_i \left( {\lambda _i ,\phi _i } \right) \triangleq \int _{\phi _{i}^{*} }^{\phi _i } {\frac{{\partial s_i \left( {\lambda _i ,\tau } \right) }}{{\partial \tau }}} \mathrm {d}\tau . \end{aligned}$$

(23)

where the starting points for computing $s_i$ around each level orbit in $\varOmega _{i}$ are chosen based on the same value of arc-length parameter $\phi _{i}^{*}$ corresponding to the starting point selected on the given orbit $\varGamma _{i0}$. When the unicycle moves, the variation of generalized arc-length is

$$\begin{aligned} \dot{\xi }_i= & {} \frac{{\partial \xi _i }}{{\partial s_i }}\left( \frac{{\partial s_i }}{{\partial \phi _i }}\dot{\phi }_i + \frac{{\partial s_i }}{{\partial \lambda _i }}\dot{\lambda }_i\right) \nonumber \\= & {} \frac{{\partial \xi _i }}{{\partial s_i }}\left( \frac{{\mathrm {d}s_i }}{{\mathrm {d}t}}\left| {_{\lambda _i = const} } \right. + \frac{{\partial s_i }}{{\partial \lambda _i }}\left\| {\nabla \lambda _i } \right\| \upsilon _{f_i} \sin \alpha _i\right) \nonumber \\= & {} \frac{{\partial \xi _i }}{{\partial s_i }}\upsilon _{f_i} \left( {\cos \alpha _i + \frac{{\partial s_i }}{{\partial \lambda _i }}\left\| {\nabla \lambda _i } \right\| \sin \alpha _i } \right) . \end{aligned}$$

(24)

In the next subsection, each unicycle is driven to arrive at its given orbit, which implies $\alpha _{i}(t)=0$ and then $\dot{\xi }_i(t)=\frac{{\partial \xi _i }}{{\partial s_i }}\upsilon _{f_i}$. In order to reduce the amount of calculation and simplify the design of the control laws, $\eta _{i}$ is defined as

$$\begin{aligned} \eta _{i} = \frac{{\partial \xi _i }}{{\partial s_i }}\upsilon _{f_i}. \end{aligned}$$

(25)

Then, the variation of the generalized arc-length can be written as

$$\begin{aligned} \dot{\xi }_i = \eta _{i}+d_{\eta _i} \end{aligned}$$

(26)

where $d_{\eta _i}= \eta _{i} \left( { - 2\sin ^2 \frac{{\alpha _i }}{2} + \frac{{\partial s_i }}{{\partial \lambda _i }}\left\| {\nabla \lambda _i } \right\| \sin \alpha _i } \right)$. Differentiating $\eta _{i}$, we have

$$\begin{aligned} \dot{\eta }_{i}= & {} \frac{{\partial \xi _i }}{{\partial s_i }}\left( {\kappa _{\upsilon _{f_i} }^u u_i + \kappa _{\upsilon _{fi} }^\omega \omega _i + d_{\upsilon _{f_{_i } } } } \right) \nonumber \\&+\,\frac{{\partial ^2 \xi _i }}{{\partial s_i^2 }}\upsilon _{f_i } \left( {\eta _{i} + d_{\eta _{i} } } \right) . \end{aligned}$$

(27)

3.2 Backstepping design

Step 1. Convergence of $\lambda _{i},\alpha _{i},\xi _{i}-\xi _{j},\eta _{i}-\eta _*$: The control Lyapunov function is selected as follows:

$$\begin{aligned} V_I= & {} \sum _{i = 1}^n {h_i \left( {\lambda _i } \right) } - \sum _{i = 1}^n {\ln \left( {\cos ^{2} \frac{{\alpha _i }}{2}} \right) }\nonumber \\&+\,\frac{{k_0 }}{4}\sum _{i = 1}^n {\sum _{j = 1}^n {a_{ij} \left( {\xi _i - \xi _j } \right) ^2 } } \nonumber \\&+ \sum _{i = 1}^n {\left( {\ln \left( {\frac{{\eta _{i} - \eta ^m }}{{\eta _{*} - \eta ^m }}} \right) + \frac{{\eta _{*} - \eta ^m }}{{\eta _{i} - \eta ^m }} - 1} \right) } \end{aligned}$$

(28)

where $k_0 >0$ and $h_i \left( {\lambda _i } \right)$ is a $C^2$ smooth, nonnegative function on $\left( { - \varepsilon _i ,\varepsilon _i }\right)$. Let $h_i \left( { \lambda _i } \right)$ and satisfy the following conditions:

(C1) :

$h_i \left( { \lambda _i } \right) \rightarrow + \infty$ and $\nabla h_i \rightarrow - \infty$ as $\lambda _i \rightarrow - \varepsilon _i$.

(C2) :

$h_i \left( { \lambda _i } \right) \rightarrow + \infty$ and $\nabla h_i \rightarrow +\infty$ as $\lambda _i \rightarrow \varepsilon _i$.

(C3) :

$h_i \left( { \lambda _i } \right) =0$ if and only if $\lambda _i=0$.

There are many functions that satisfy all the above properties of $h_i \left( {f_i } \right)$. An example is

$$\begin{aligned} h_i \left( f_i\right)= & {} \int _{f_{i}^{*}}^{f_i}\left[ c_1\left( \frac{1}{{\varepsilon _i - \tau }} - \frac{1}{{\varepsilon _i + \tau }}\right) \right. \\&\left. +\,c_2\left( \ln \left( {\varepsilon _i + \tau } \right) - \ln \left( {\varepsilon _i - \tau } \right) \right) \right] \text {d}\tau , \end{aligned}$$

where $f_{i}^{*}=f_i( \mathbf {z}_i(0))\in \varOmega _i$ and $c_1,c_2>0$.

In the function (28), the first term contributes to forcing the trajectory of each unicycle to its given orbit and stays in $\varOmega _i$ when it start from $\varOmega _i$. It vanishes when $\lambda _i=0$. The second term aligns the direction of each unicycle’s motion and the tangent vector to the orbit. It vanishes when $\alpha _{i}=0$. The next term ensures the consensus of the generalized arc-lengths. It vanishes when $\xi _{i}=\xi _{j}$. The fourth term guarantees that $\eta _i$ converge to the reference and $\upsilon _i>\Vert \mathbf {f}\Vert$ for all time. It vanishes when $\eta _{i}=\eta _{*}$.

The time derivation of $V_I$ is

$$\begin{aligned} \dot{V}_I= & {} \sum _{i = 1}^n {\tan \frac{{\alpha _i }}{2}\left( {\varDelta _{\alpha _i } - \left( {\kappa _{\gamma _i }^u u_i + \kappa _{\gamma _i }^\omega \omega _i + d_{\gamma _i } } \right) } \right) } \nonumber \\&+ \sum _{i = 1}^n \left( {\eta _{i} - \eta _{*} } \right) \left( \left( {\eta _{i} - \eta ^m } \right) ^{ - 2} \frac{{\partial \xi _i }}{{\partial s_i }}\right. \nonumber \\&\times \left. \left( {\kappa _{\upsilon _{f_i} }^u u_i + \kappa _{\upsilon _{f_i} }^\omega \omega _i + d_{\upsilon _{f_i} } } \right) + \varDelta _{\eta _{i} } \right) \end{aligned}$$

(29)

where

$$\begin{aligned} \varDelta _{\alpha _i }&= \upsilon _{f_i } \left( {\kappa _{i }^a \cos \alpha _i + \kappa _{i }^b \sin \alpha _i } \right) \\&\quad + 2\upsilon _{f_i } \nabla h_i \left\| {\nabla \lambda _i } \right\| \cos ^2 \frac{{\alpha _i }}{2} \\&\quad + k_0 \eta _{i} \left( { - \sin \alpha _i + 2\frac{{\partial s_i }}{{\partial \lambda _i }}\left\| {\nabla \lambda _i } \right\| \cos ^2 \frac{{\alpha _i }}{2}} \right) \\&\quad \times \sum \limits _{j = 1}^n {a_{ij} \left( {\xi _i - \xi _j } \right) }, \end{aligned}$$

$$\begin{aligned}&\varDelta _{\eta _{i} } = \left( {\eta _{*} - \eta ^m } \right) ^{ - 2} \frac{{\partial ^2 \xi _i }}{{\partial s_i^2 }}\upsilon _{f_i } \left( {\eta _{i} + d_{\eta _{i} } } \right) \\&\quad + \,k_0 \sum _{j = 1}^n {a_{ij} \left( {\xi _i \! - \!\xi _j } \right) }\!-\! \left( {\eta _{i} \!-\! \eta ^m } \right) ^{ - 1} \left( {\eta _* - \eta ^m } \right) ^{ - 1} \dot{\eta }_* . \end{aligned}$$

Here, we first use the unicycle’s angular velocity $\omega _i$ as the virtual control $\bar{\omega }_i$ and the acceleration input $u_i$ to fulfill the coordinated path following control problem. The choices are

$$\begin{aligned} \left[ {\begin{array}{cc} {\kappa _{\gamma _i }^u } &{} {\kappa _{\gamma _i }^\omega } \\ {\kappa _{\upsilon _{f_i} }^u } &{} {\kappa _{\upsilon _{f_i} }^\omega } \\ \end{array}} \right] \left[ {\begin{array}{cc} {u_i } \\ {\bar{\omega }_i } \\ \end{array}} \right] = \left[ {\begin{array}{cc} {g_{\alpha _i } } \\ {g_{\eta _{i} } } \\ \end{array}} \right] \end{aligned}$$

(30)

where

$$\begin{aligned}&g_{\alpha _i } = \varDelta _{\alpha _i } + k_1 \sin \frac{{\alpha _i }}{2} - d_{\gamma _i },\\&g_{\eta _{i} } = - \left( {\eta _{i} - \eta ^m } \right) ^2 \left( {\frac{{\partial \xi _i }}{{\partial s_i }}} \right) ^{ - 1} \\&\times \left( {\varDelta _{\eta _{i} } \!+\! k_2 \left( {\eta _{i} \!-\! \eta _{*} } \right) } \!+\! {k_3 \sum _{j = 1}^n {a_{ij} \left( {\eta _{i} - \eta _j } \right) } }\right) - d_{\upsilon _{f_i} }. \end{aligned}$$

Obviously, Eq. (30) has a unique solution

$$\begin{aligned} u_i= & {} g_{\kappa _i }^{ - 1} \left( {\kappa _{\gamma _i }^u g_{\alpha _i } - \kappa _{\upsilon _{fi} }^u g_{\eta _{i} } } \right) ,\end{aligned}$$

(31)

$$\begin{aligned} \bar{\omega }_i= & {} g_{\kappa _i }^{ - 1} \left( {\kappa _{\upsilon _{fi} }^\omega g_{\alpha _i } - \kappa _{\gamma _i }^\omega g_{\eta _{i} } } \right) . \end{aligned}$$

(32)

Remark 5

Since the speed of particle in [17–19] is fixed (that is, unit-speed), the authors just assume that the flow field satisfies $\Vert \mathbf {f}\Vert <1$. In this paper, the speed is controllable and serves two targets. On the one hand, the linear acceleration contributes to accomplishing the temporal and spatial formation motions along given orbits. On the other hand, the goal such that the speed is greater than $\Vert \mathbf {f}\Vert$ and converges to the reference is guaranteed by using the speed control. For the latter object, a potential function used in collision avoidance [21] is introduced in this paper, which can be found in the last term in (28).

Remark 6

In the flow field, the virtual control $\bar{\omega }_i$ and the acceleration input $u_i$ work together to achieve path following and formation motion, while they are separately responsible for path following and formation motion in [11]. All these changes are due to the effect of the external flow field.

Now, substituting (31) and (32) into (29) results in

$$\begin{aligned} \dot{V}_I= & {} - k_1 \sum _{i = 1}^n {\frac{{\sin ^2 \frac{{\alpha _i }}{2}}}{{\cos \frac{{\alpha _i }}{2}}}} - k_2 \sum _{i = 1}^n {\left( {\eta _{i} - \eta _{*} } \right) ^2 }\nonumber \\&-\,k_3 \left( {\mathbf {\eta } - \eta _* \mathbf {1}_n } \right) ^T L\left( {\mathbf {\eta } - \eta _* \mathbf {1}_n } \right) \le 0 \end{aligned}$$

(33)

where $\mathbf {\eta }=[\eta _1,\ldots ,\eta _n]^T$ and $\mathbf {1}_n=[1,\ldots ,1]^T$.

To accomplish the control input $\tau _i$, the error variable is introduced such as

$$\begin{aligned} \omega _{e_i } = \omega _i - \bar{\omega }_i \end{aligned}$$

(34)

which should be driven to zero, and re-write $\dot{V}_I$ as

$$\begin{aligned} \dot{V}_I= & {} - k_1 \sum _{i = 1}^n {\frac{{\sin ^2 \frac{{\alpha _i }}{2}}}{{\cos \frac{{\alpha _i }}{2}}}} - k_2 \sum _{i = 1}^n {\left( {\eta _{i} - \eta _{*} } \right) ^2 }\nonumber \\&- k_3 \left( {\mathbf {\eta } - \eta _* \mathbf {1}_n } \right) ^T L\left( {\mathbf {\eta } - \eta _* \mathbf {1}_n } \right) +\sum _{i = 1}^n \omega _{e_i }\varDelta _{e_i }\nonumber \\ \end{aligned}$$

(35)

where

$$\begin{aligned} \varDelta _{e_i } = - \kappa _{\gamma _i }^\omega \tan \frac{{\alpha _i }}{2} + \kappa _{\upsilon _{f_i} }^\omega \frac{{\partial \xi _i }}{{\partial s_i }}\left( {\eta _{i} - \eta ^m } \right) ^{ - 2} \left( {\eta _{i} - \eta _{*} } \right) . \end{aligned}$$

Step 2. Backstepping for $\omega _{e_{i}}$: The second control Lyapunov function is given by

$$\begin{aligned} V_{ {II}} = V_I + \sum \limits _{i = 1}^n {\omega _{e_i }^2 }. \end{aligned}$$

(36)

Taking the time derivative of both sides of Eq. (36) along the solution of (31), one gets

$$\begin{aligned} \dot{V}_{ {II}}= & {} -\,k_1 \sum _{i = 1}^n {\frac{{\sin ^2 \frac{{\alpha _i }}{2}}}{{\cos \frac{{\alpha _i }}{2}}}} - k_2 \sum \limits _{i = 1}^n {\left( {\eta _{i} - \eta _* } \right) ^2 } \nonumber \\&- \, k_3 \left( {\mathbf {\eta } - \eta _{*} \mathbf {1}_n } \right) ^T L\left( {\mathbf {\eta } - \eta _{*} \mathbf {1}_n } \right) \nonumber \\&+ \sum _{i = 1}^n {\omega _{e_i } \left( {\tau _i - \dot{\bar{\omega }}_i - \varDelta _{e_i } } \right) }. \end{aligned}$$

(37)

We design the yaw force $\tau _i$ as follows:

$$\begin{aligned} \tau _{r_i } = \dot{\bar{\omega }} _i + \varDelta _{e_i } - k_4 \omega _{e_i } \end{aligned}$$

(38)

where $k_4>0$, which yields

$$\begin{aligned} \dot{V}_{ {II}}= & {} - k_1 \sum _{i = 1}^n {\frac{{\sin ^2 \frac{{\alpha _i }}{2}}}{{\cos \frac{{\alpha _i }}{2}}}} - k_2 \sum _{i = 1}^n {\left( {\eta _{i} - \eta _* } \right) ^2 } \nonumber \\&-\,k_3 \left( {\mathbf {\eta } - \eta _{*} \mathbf {1}_n } \right) ^T L\left( {\mathbf {\eta } - \eta _{*} \mathbf {1}_n } \right) \nonumber \\&-\,k_4 \sum _{i = 1}^n \omega _{e_i }^{2}\le 0. \end{aligned}$$

(39)

3.3 Stability analysis

Under the control laws (31) and (38), the equation of the closed-loop system for $\lambda _{i}$ is denoted as (22), the equation of the closed-loop system for $\alpha _{i}$ is (21) where $\dot{\omega } _{i}$ satisfies (32) , and the equation of the closed-loop system for the relative generalized arc-length is

$$\begin{aligned} \dot{\xi }_i - \dot{\xi }_j = \eta _i+d_{\eta _i}- \eta _j-d_{\eta _j}, \end{aligned}$$

(40)

the equation of the closed-loop system for $\eta _i-\eta _*$ satisfies

$$\begin{aligned} \dot{\eta }_{i} - \dot{\eta }_{*}= & {} \left( {\frac{{\eta _{i} - \eta ^m }}{{\eta _{*} - \eta ^m }} - 1} \right) \dot{\eta }_{*} - \left( {\eta _{i} - \eta ^m } \right) ^2 \nonumber \\&\times \left( k_0 \sum _{j = 1}^n {a_{ij} \left( {\xi _i - \xi _j } \right) } +\, k_2 \left( {\eta _{i} - \eta _{*} } \right) \right. \nonumber \\&\left. + \,k_3 \sum _{j = 1}^n a_{ij} \left( {\eta _{i} - \eta _j } \right) \right) . \end{aligned}$$

(41)

Theorem 1

Consider a family of level closed curves of the orbit function constructed by concentric compression. Suppose the generalized arc-lengths and the reference $\eta _{*}(t)$ satisfy Assumption 1 and Assumption 2, respectively. Assume the initial conditions of unicycles make the initial value of $V_{II}$ given in (36) finite. Then, Problem 1 is solved via the linear acceleration force (31) and the angular acceleration force (38) if the communication topology is connected.

Proof

The set $\varPhi = \left\{ \left( \lambda _i, \alpha _i ,\xi _i - \xi _j,\eta _{i}-{\eta }_*, \omega _{e_{i}}\right) | {V_{II} \leqslant c } \right\}$ such that $V_{II}\le c$, for $c>0$, is closed by continuity. Since $\left| {\lambda _i } \right| <\varepsilon _i$ due to the boundedness of $V_{II}$, $\alpha _i$ is defined in $\left( -\pi ,\pi \right]$, $\left| {\xi _i - \xi _j } \right| \le \sqrt{4c }$, and $\left| \eta _{i} \right| \le h_{\eta _{i} } ^{ - 1} (c )+{\eta }_*+{\eta } ^{m}$ where $h_{\eta _{i}}=\ln \left( \left( \eta _{i}-{\eta }^m\right) /\left( {\eta }_{*}-{\eta }^{m} \right) \right) + \left( \eta _{i}-{\eta }^{m}\right. /\left( {\eta }_{*}-{\eta }^{m} \right) -1$, the set $\varPhi$ is compact. On the compact set $\varPhi$, and $\left| \partial ^2 s_i \left( {\lambda _i ,\phi _i } \right) / \partial \lambda _i^2 \right|$ are bounded because $\phi _i \in \left[ {0,2\pi } \right)$. $\left\| {\nabla \lambda _i } \right\|$ is bounded by continuity. Since is bounded away from $0$, $\upsilon _{f_i} = \left( {\frac{{\partial \xi _i }}{{\partial s_i }}} \right) ^{ - 1} \eta _{i}$ is also bounded on $\varPhi$. Thus, the closed-loop system is Lipschitz continuous on the set $\varPhi$ and a solution exists and is unique.

Because the value of $V_{II}$ is time independent and non-increasing, we conclude that the entire solution stays in $\varPhi$ and then $\eta _i>\eta ^m$ when the initial value of $V_{II}$ is finite. At the same time, $\left| {\lambda _i \left( {\mathbf {z}_{i} \left( t \right) } \right) }\right| < \varepsilon _i$ is satisfied by (C1) and (C2). Applying the invariance-like theorem, it follows that the trajectories of the closed-loop system will converge to the set inside the region $E = \{\left( \lambda _i, \alpha _i ,\xi _i - \xi _j,\eta _{i}-\eta _*, \omega _{e_{i}} \right) \left| {\dot{V}_{II} = 0} \right. \}$ as $t\rightarrow \infty$, that is

$$\begin{aligned}&\alpha _i=0,~\eta _i=\eta _*,~\omega _{e_{i}}=0,\end{aligned}$$

(42a)

$$\begin{aligned}&\left( {\mathbf {\eta } - \eta _{*} \mathbf {1}_n } \right) ^T L\left( {\mathbf {\eta } - \eta _{*} \mathbf {1}_n } \right) = 0 \Rightarrow \eta _{i} = \eta _j. \end{aligned}$$

(42b)

On the set $E$, the equations of the whole closed-loop system become

$$\begin{aligned}&\dot{\lambda }_i =0,\end{aligned}$$

(43a)

$$\begin{aligned}&\dot{\alpha }_i = - 2\upsilon _{f_i } \nabla h_i \left\| {\nabla \lambda _i } \right\| \nonumber \\&\quad - 2k_0 \eta _{i} \frac{{\partial s_i }}{{\partial \lambda _i }}\left\| {\nabla \lambda _i } \right\| \sum _{j = 1}^n {a_{ij} \left( {\xi _i - \xi _j } \right) }, \end{aligned}$$

(43b)

$$\begin{aligned}&\dot{\xi }_i- \dot{\xi }_j = 0,\end{aligned}$$

(43c)

$$\begin{aligned}&\dot{\eta }_{i} - \dot{\eta }_{*} = - k_0 \left( {\eta _{i} - \eta ^m } \right) ^2 \sum _{j = 1}^n {a_{ij} \left( {\xi _i - \xi _j } \right) }. \end{aligned}$$

(43d)

In the following, we will show $\xi _i-\xi _j \rightarrow 0$ as $t\rightarrow \infty$. On the set $E$, from (43c) one gets that $\xi _i-\xi _j$ is constant. Applying the extension of the Barbalat lemma in [22], from (43d) and Assumption 2, $\dot{\eta }_{i} - \dot{\eta }_{*} = - k_0 \left( \eta _{i} - \eta ^m \right) ^2 \sum _{j = 1}^n a_{ij} ( \xi _i - \xi _j ) \rightarrow 0$. Since $\eta _{i} - \eta ^m\rightarrow \eta _* - \eta ^m\ne 0$ as $t\rightarrow \infty$, one gets $L\mathbf {\xi }=0$ where $\mathbf {\xi }=\left[ \xi _1,\ldots ,\xi _n\right] ^T$, which implies that $\xi _i-\xi _j \rightarrow 0$ as $t\rightarrow \infty$ when the communication topology is connected.

Because $\xi _i-\xi _j \rightarrow 0$ as $t\rightarrow \infty$, the equation of the closed-loop system for $\alpha _i$ on the set $E$ is changed to

$$\begin{aligned} \dot{\alpha }_i = - 2\upsilon _{f_i } \nabla h_i \left\| {\nabla \lambda _i } \right\| . \end{aligned}$$

(44)

It is easy to check that $\lim _{t\rightarrow \infty }\upsilon _{f_i}=(\partial \xi /\partial s_i)\eta _*> 0$ is uniformly continuous and bounded from Assumption 1 and 2. The details can be found in [11]. From (43a), $\lambda _i$ approaches to a constant and thus $\nabla h_{i}$ approaches to a constant. Therefore, $- 2\nabla h_i \upsilon _{f_i} \left\| {\nabla \lambda _i } \right\|$ is uniformly continuous. Applying the extension of the Barbalat lemma [22], from (44) we have $\dot{\alpha _{i}} \rightarrow 0$ as $t\rightarrow \infty$. Because ${\lim }_{t \rightarrow \infty } \upsilon _{f_i} \left\| {\nabla \lambda _i } \right\| \ne 0$, one gets $\nabla h_i\rightarrow 0$ as $t\rightarrow \infty$. By (C3), $\lambda _i$ approaches to $0$. $\square$

4 Simulation results

In this section, the proposed control law is applied to coordinate four unicycles moving along the given closed curves. The communication topology is shown in Fig. 5. The control gains are selected as $k_{0}=20, k_j=10, j=1,\ldots ,5$. The non-uniform flow field is $\mathbf {f}_i=[-0.25*\sin (2*\pi *5/360*(z_{i}^x+z^y_i)),0.25*\cos (2*\pi *5/360*(z_{i}^x+z^y_i))]^T$.

Fig. 5

Communication topology

Case 1

The given orbits are a set of concentric ellipses with different semi-major axis and semi-minor axis, that is

$$\begin{aligned} {\left( {\frac{{z_i^{x }}}{3l_i}} \right) ^2 + \left( {\frac{{z_i^{y } }}{2l_i}} \right) ^2 = 1 } \end{aligned}$$

where $l_i = 1+0.5\left( {i - 1} \right)$, $i=1,\ldots ,4$. In this case, four unicycles are required to form the in-line formation with $\eta _*(t)=2+0.2\sin (t)$. The starting points are defined as the intersection of the orbits with the positive horizontal axis of ${\fancyscript{W}}$, and we choose the general arc-lengths as $\xi _j=s_i/l_i$. The movement of unicycles is shown in Fig. 6a. From this figure, we can see that four unicycles finally move along the set of given orbits and form the desired formation. The path following errors $f_{i}$ and $\alpha _{i}$ tend to zero and are plotted in Fig. 6b, c, respectively. Figure 6d demonstrates that $\xi _{i}$ reaches consensus and Fig. 6e shows $\eta _{i}$ converges to the reference. According to these pictures, we conclude that our control law is suitable to deal with formation motion around convex curves.

Fig. 6

In-linear formation motion along convex orbits: a Plot of movements, b Plot of $\lambda _{i}$, c Plot of $\alpha _{i}$, d Plot of $\xi _{i}-\xi _{j}$, e Plot of $\eta _{i}$

Case 2

The given orbits are a set of concentric superellipses (non-convex orbits) such as

$$\begin{aligned} \frac{1}{a_i}\left[ {\left( {2z_i^x z_i^y } \right) ^4 + \left( {\left( {z_i^x } \right) ^2 - \left( {z_i^y } \right) ^2 } \right) ^4 } \right] ^{\frac{1}{8}}=1 \end{aligned}$$

where $a_i = 3 + 0.5\left( {i - 1} \right) , i=1,\ldots ,4$. In this case, the desired pattern is that forming a trapezoidal formation with $\eta _*=0.5$. The starting points are defined as the intersection of the orbits with the positive horizontal axis of ${\fancyscript{W}}$, and we choose $\xi _j=s_j/a_j;(j=1,4)$, $\xi _2=s_2/a_2+\pi /6$ and $\xi _3=s_3/a_3+\pi /8$. The movement of unicycles is shown in Fig. 7a. From this figure, we can see that four unicycles finally move along the set of given orbits and form the desired formation. The path following errors $f_{i}$ and $\alpha _{i}$ tend to zero and are plotted in Fig. 7b, c, respectively. Figure 7d demonstrates that $\xi _{i}$ reaches consensus, and Fig. 7e shows $\eta _{i}$ converges to the reference. According to these pictures, coordinated non-convex curve path following control problem is also solved via our proposed controller.

Fig. 7

Trapezoidal formation motion along non-convex orbits: a Plot of movements, b Plot of $\lambda _{i}$, c Plot of $\alpha _{i}$, d Plot of $\xi _{i}-\xi _{j}$, e Plot of $\eta _{i}$

5 Conclusion

In this paper, our previous geometric extension design [11] is developed to deal with coordinated path following control of unicycles in an external time-invariant flow field. Both temporal and spatial formations is achieved by introducing the acceleration control. The potential function is used to force each unicycle’s speed greater than the magnitude of flow. The validity of the proposed approach is confirmed by theoretical analysis and numerical simulation.