Effect of driver’s anticipation in a new two-lane lattice model with the consideration of optimal current difference

Abstract

In this paper, a new lattice hydrodynamic traffic flow model is proposed by considering the driver’s anticipation effect (DAE) in sensing optimal current difference (OCD) for two-lane system. The effect of anticipation parameter on the stability of traffic flow is examined through linear stability analysis and shown that it can significantly enlarge the stability region on the phase diagram. Nonlinear analysis is conducted, and mKdV equation is derived to describe propagation behavior of a density wave near the critical point. The driver’s physical delay in sensing optimal current difference effect is also investigated and found that it has different effect on two-lane traffic based on whether lane changing is allowed or not. Simulation results are found in good agreement with the theoretical findings, which confirms that traffic jam can be suppressed efficiently by considering the DAEOCD effect in a two-lane traffic system.

1 Introduction

Due to the rapid increase in automobile on roads, the traffic problems became more and more serious and attracted much attention of scientists and researchers because of its complex mechanism, recently. Therefore, to understand the dynamics of traffic flow and investigate the properties of traffic jams, a considerable variety of traffic models have been developed and discussed by physicists, mathematicians, and so on [1–23] in past few decades. To explain the dynamical phase transitions on freeway, Nagatani [11] firstly in 1998 proposed a simple lattice hydrodynamic model and derived modified Korteweg–de Vries (mKdV) equation to describe the traffic congestion in terms of kink density wave near the critical point. Thereafter, this modeling approach was widely referred and extended to study various nonlinear phenomenon present in real traffic flow like backward effect [12], lateral effect of the lane width [13] and anticipation effect of potential lane changing [14]. Recently, Peng [15] incorporated the effect of anticipation individual driving behavior and proposed a new lattice model. Kang and Sun [16] introduced a lattice hydrodynamic model by taking into account driver’s delay effect in sensing relative flux (DDSRF) and found that this effect has an important influence on the traffic jams.

Most of the aforementioned models focus mainly on some traffic phenomena only on a single lane. These models cannot fully describe the real traffic on roadways consists of two or more lanes since they do not consider the lane-changing behavior. In view of the above mentioned facts, Nagatani [24] further extended his model to two-lane system, two-dimensional traffic system [25] and also to high-dimensional [26] traffic dynamics. Later, some modifications have been made in two-lane lattice model by incorporating different factors like optimal current difference [27] and flow difference effect [28]. Peng [29] analyzed the effect of driver anticipation in two-lane system. Very recently, Gupta and Redhu [30] developed a new model to investigate the effect of driver’s anticipation in sensing relative flux (DAESRF) for two-lane system.

In real traffic, the driver always adjusts his/her velocity according to observed traffic situation in the surroundings and estimates his/her driving individual behavior. Most of highways comprise of multi-lanes, so it will be more adequate to investigate this effect on a two-lane system with the consideration of potential lane changing. However, in the existing lattice models, driver’s anticipation effect in sensing optimal current difference effect (DAEOCD) in two-lane system has not been studied. This motivates us to develop a two-lane lattice model by incorporating the effect of driver’s anticipation individual behavior in sensing OCD effect.

In this paper, a more realistic lattice model with DAE in sensing OCD effect for two-lane traffic system is presented. In Sect. 3, the stability condition of traffic flow is investigated by means of linear stability theory. To describe the propagation behavior of traffic jams, Sect. 4 is devoted to the nonlinear analysis in which mKdV equation is derived near the critical point. Numerical simulations are carried out to validate the theoretical findings in Sect. 5, and finally, conclusions are drawn in Sect. 6.

2 A new model

To describe the traffic phenomena on single lane, the simplest lattice hydrodynamic model was, firstly, proposed by Nagatani [11] in 1998 and is given as

$$\begin{aligned}&\partial _t{\rho _j} +\rho _0 (\rho _j v_j-\rho _{j-1} v_{j-1})=0, \end{aligned}$$

(1)

$$\begin{aligned}&\partial _t (\rho _j v_j)=a[\rho _0 V(\rho _{j+1})-\rho _j v_j]. \end{aligned}$$

(2)

where $\rho _0$ is the average density; $\rho _j$ and $v_j$, respectively, represent the local density and velocity at site $j$ at time $t$. $V(.)$ is the optimal velocity function, which is a monotonically decreasing function having an upper bound and an inflection point at critical density. The idea is that the variation in traffic flow $\rho v$ at site $j$ is determined by the difference between the actual flow at site $j$ and the optimal flow $\rho _0 V(\rho _{j+1})$ at the next site.

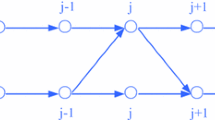
While describing the traffic flow on road networks, multi-lane models are found to be more appropriate as most of the road networks are made up of more than one lane. In this regard, Nagatani [11] further extended single-lane lattice model to describe traffic phenomenon on two lanes by incorporating lane change effect in the lattice version of continuity equation. The lane changing on a two-lane highway occurs only in the following two cases.

Case (a): If $\rho _ {2,j-1}(t)>\rho _ {1,j}(t)$, i.e., the density at site $j-1$ on the second lane is higher than that at site $j$ on the first lane, the lane changing occurs from the second lane to the first lane and the lane-changing rate will be proportional to their density difference as follows: $\gamma |\rho _0^2 V'(\rho _0)|\left( \rho _ {2,j-1}(t)-\rho _{1,j}(t)\right)$.

Case (b): If $\rho _ {1,j}(t)>\rho _ {2,j+1}(t)$, i.e., the density at site $j$ on the first lane is higher than that at site $j+1$ on the second lane, the lane changing occurs from the first lane to the second lane and the lane-changing rate will be proportional to their density difference as follows: $\gamma |\rho _0^2 V'(\rho _0)|\left( \rho _ {1,j}(t)-\rho _{2,j+1}(t)\right)$.

Here, $\rho _{1,j}(t)$ and $\rho _{2,j}(t)$ are the densities on the first and second lane, respectively, and $\gamma$ is a fixed dimensionless coefficient. The proportionality constant $\left( \gamma |\rho _0^2 V'(\rho _0)|\right)$ is chosen in such a way that it becomes dimensionless. Based on the above lane-changing rules, the continuity equation for two-lane traffic can be obtained in the same fashion as in Ref. [24] and is given by

$$\begin{aligned}&\partial _t \rho _j +\rho _0 (\rho _j v_j-\rho _{j-1}v_{j-1}) \nonumber \\&\quad =\gamma |\rho _0^2 V'(\rho _0)| (\rho _{j+1}-2\rho _j+\rho _{j-1}), \end{aligned}$$

(3)

where $\rho _j=\frac{\rho _{1,j} +\rho _{2,j}}{2}$ represents the local density at site $j$ and $\rho _j v_j=\frac{\rho _{1,j} v_{1,j}+\rho _{2,j} v_{2,j}}{2}$ represents the local flow at site $j$ for the two-lane system.

In addition, the evolution equation of traffic current on each lane will not be affected by lane changing. Hence, the evolution equation for two-lane traffic [24] was incorporated as

$$\begin{aligned} \partial _t (\rho _j v_j)=a[\rho _0 V(\rho _{j+1})-\rho _j v_j]. \end{aligned}$$

(4)

Further, Peng [27] extended the Nagatani’s two-lane lattice model by considering the optimal current difference effect and found that it has an important influence on multi-lane traffic flow system. The continuity equation remains preserved, while the evolution equation is modified by looking at the difference of optimal traffic currents on site—$j+2$ and $j+1$. This effect plays a significant role in stabilizing the traffic flow and suppresses effectively the traffic jams. Then, the modified evolution equation is given by

$$\begin{aligned} \partial _t{(\rho _j v_j)}&= a\rho _0 V(\rho _{j+1})-a\rho _j v_j \nonumber \\&\quad +~a\lambda [\rho _0 V(\rho _{j+2})-\rho _0 V(\rho _{j{+}1})]. \end{aligned}$$

(5)

Here, $\lambda$ is the reaction coefficient of optimal current difference. However, the important aspect of driver’s anticipation effect (DAE) was not incorporated in this lattice traffic flow model. As observed in real traffic flow, drivers always adjust their vehicles based on the available dynamic estimation information. In this dynamic process, drivers sense the traffic relative information from surroundings at time $t$ and make a decision to adjust velocity of their vehicles at a later time $t+\tau _1$, where $\tau _1$ is the delay of driver’s response in sensing headway. Once the decision has been taken, vehicle actually moves at some later time $t+\tau _1+\tau _2$ due to the delay of car motion, where $\tau _2$ represents the delay time of car motion. So, the total delay time is the sum of two different delay times $\tau _1$ and $\tau _2$. Without lose of generality, a linear relationship between driver’s response delay $\tau _1$ and the total delay time $\tau$ is chosen as $\tau _1=\alpha \tau$, where the $\alpha$ is the anticipation coefficient that corresponds to driver’s behavior and $\tau =1/a$ denote the delay time, which allows for the time lag, that it takes the traffic current to reach the optimal current when the traffic is varying. However, driver’s anticipation effect was not explicitly considered in two-lane Peng’s model [27]. Therefore, we propose a new evolution equation with consideration of anticipation driving effect in sensing optimal current difference effect (DAEOCD) on a two-lane system as follows:

$$\begin{aligned} \partial _t(\rho _j(t)v_j(t))&=a\rho _0V[\rho _{j+1}(t+\alpha \tau )]-a\rho _j (t)v_j(t)\nonumber \\&\quad + a\lambda [Q_{j{+}2}(t{+}\alpha \tau )-Q_{j{+}1}(t{+}\alpha \tau )]. \end{aligned}$$

(6)

where $Q_{j}(t)=\rho _0V[\rho _{j}(t)]$ and the last term in the above evolution equation denote the optimal current difference on site $j+1$. In the proposed model, the sign of anticipation coefficient $\alpha$ explores different characteristics of driver’s behavior on two-lane highway. The positive value of $\alpha$ represents anticipation driving behavior or the drivers forecast effect in a traffic system with intelligent transportation system (ITS). Here, driver adjusts his driving individual speed to the anticipation optimal speed at time $t+\alpha \tau$ after delay time $\tau$ in advance. So, the bigger value of $\alpha$ corresponds to more skillful drivers in the model.

For $\alpha <0$, i.e., negative anticipation coefficient corresponds to the explicit driver’s physical delay in sensing optimal current difference effect. The effect of driver’s delay in sensing relative flux is also analyzed in single-lane model by Kang and Sun [16] and for two-lane traffic system by Zhang et al. [31], recently. When $\alpha =0$, the new model reduces to Peng’s [27]. For simplicity, using the Taylor series expansion and neglecting the nonlinear terms, the new evolution equation can be obtained as:

$$\begin{aligned}&\partial _t(\rho _j(t)v_j(t)) = a\rho _0[V(\rho _{j+1}(t)) \nonumber \\&\quad +~\alpha \tau V'(\rho _{j+1}(t))\partial _t\rho _{j+1}(t)]-a\rho _j (t) v_j(t) \nonumber \\&\quad +~a \lambda \rho _0[V(\rho _{j+2}(t))-V(\rho _{j+1}(t))] \nonumber \\&\quad +~a\lambda \alpha \tau \rho _0[V'(\rho _{j+2}(t))\partial _t\rho _{j+2}(t) \nonumber \\&\quad -~V'(\rho _{j+1}(t))\partial _t\rho _{j+1}(t)]. \end{aligned}$$

(7)

By taking the difference form of Eqs. (3) and (7) and eliminating speed $v_j$, the density equation is obtained as

$$\begin{aligned}&\rho _j(t+2\tau )-\rho _j(t+\tau )+\tau \rho ^2_0[V(\rho _{j+1}(t)) \nonumber \\&\quad -~V(\rho _{j}(t))] \nonumber \\&\quad +~\alpha \rho ^2_0 \tau [V'(\rho _{j+1}(t))\tilde{{\varDelta }}\rho _{j+1}(t)-V'(\rho _{j}(t))\tilde{{\varDelta }}\rho _{j}(t)] \nonumber \\&\quad +~\lambda \tau \rho ^2_0 [V(\rho _{j+2}(t))-2V(\rho _{j+1}(t))+V(\rho _{j}(t))]\nonumber \\&\quad +~\alpha \tau \lambda \rho ^2_0 [V'(\rho _{j+2}(t))\tilde{{\varDelta }}\rho _{j+2}(t) \nonumber \\&\quad -~2V'(\rho _{j+1}(t))\tilde{{\varDelta }}\rho _{j+1}(t)+V'(\rho _{j}(t))\tilde{{\varDelta }}\rho _{j}(t)]\nonumber \\&\quad -~\tau \gamma |\rho ^2_0 V'(\rho _0)|[\rho _{j+1}(t+\tau ) \nonumber \\&\quad -~2\rho _{j}(t+\tau )+\rho _{j-1}(t+\tau )]=0, \end{aligned}$$

(8)

where $\tilde{{\varDelta }}{\rho _j(t)}=\rho _j(t+\tau )-\rho _j(t)$.

3 Linear stability analysis

To investigate the influence of driver anticipation effect on jamming transition of traffic flow, linear stability analysis is conducted on the extended model in this section. For this, under the condition of homogeneous traffic flow, the state of uniform traffic is defined by constant density $\rho _0$ and optimal velocity $V(\rho _0)$. Hence, the steady-state solution of the homogeneous traffic flow is given as

$$\begin{aligned} \rho _j(t)=\rho _0,\quad v_j(t)=V(\rho _0). \end{aligned}$$

(9)

Let $y_j(t)$ be a small deviation to the steady-state density on site $j$. Then,

$$\begin{aligned} \rho _j(t)=\rho _0+y_j(t). \end{aligned}$$

(10)

Putting this perturbed density profile into Eq. (8) and linearizing it, we obtain

$$\begin{aligned}&y_j(t+2\tau ){-}y_j(t+\tau )+\tau \rho ^2_0V'(\rho _0)[y_{j{+}1}(t)-y_{j}(t)] \nonumber \\&\quad +~\alpha \tau \rho ^2_0V'(\rho _0)\tilde{{\varDelta }}[y_{j+1}(t)-y_{j}(t)] \nonumber \\&\quad +~\lambda \rho _0\tau V'(\rho _0)[y_{j+2}(t)-2y_{j+1}(t)+y_{j}(t)] \nonumber \\&\quad +~\alpha \tau \lambda \rho ^2_0V'(\rho _0)\tilde{{\varDelta }}[y_{j+2}(t)-2y_{j+1}(t)+y_{j}(t)] \nonumber \\&\quad -~\tau \gamma |\rho ^2_0 V'(\rho _0)|[y_{j+1}(t+\tau )-2y_{j}(t+\tau ) \nonumber \\&\quad +~y_{j-1}(t+\tau )]=0. \end{aligned}$$

(11)

Substituting $y_j (t)=exp(ikj+zt)$ in Eq. (11), we get

$$\begin{aligned}&e^{2\tau z}-e^{\tau z}+\tau \rho ^2_0 V'(\rho _0)[e^{ik}-1] \nonumber \\&\quad +~\alpha \tau \rho ^2_0 V' [e^{\tau z}-1][e^{ik}-1]\nonumber \\&\quad +~\lambda \rho _0^2 \tau V'(\rho _0)[e^{ik}-1]^2 \nonumber \\&\quad +~\lambda \tau \rho ^2_0\alpha V'(\rho _0)[e^{\tau z}-1][e^{ik}-1]^2 \nonumber \\&\quad -~\tau \gamma |\rho ^2_0 V'(\rho _0)|[e^{ik}-2+e^{-ik}]e^{\tau z}=0. \end{aligned}$$

(12)

Inserting $z=z_1(ik)+z_2(ik)^2\ldots$ into Eq. (12), we obtained the first-order and second-order terms of the coefficient $ik$ and $(ik)^2$, respectively, as

$$\begin{aligned} z_1= & {} -\rho ^2_0 V'(\rho _0), \end{aligned}$$

(13)

$$\begin{aligned} z_2= & {} -\frac{3\tau z^2_1}{2}-\frac{\rho ^2_0 V'(\rho _0)}{2}-\tau \alpha \rho ^2_0 V'(\rho _0)z_1 \nonumber \\&-~\lambda \rho ^2_0V'(\rho _0)+\gamma |\rho ^2_0 V'(\rho _0)|. \end{aligned}$$

(14)

When $z_2<0$, the uniform steady-state flow becomes unstable for long-wavelength waves. For $z_2>0$, the uniform flow becomes stable. Thus, the stability condition for the steady state is

$$\begin{aligned} \tau =-\frac{1+2\gamma +2\lambda }{\rho ^2_0 V'(\rho _0)(3-2\alpha )}. \end{aligned}$$

(15)

The instability condition for the homogeneous traffic flow can be described as

$$\begin{aligned} \tau >-\frac{1+2\gamma +2\lambda }{\rho ^2_0 V'(\rho _0)(3-2\alpha )}. \end{aligned}$$

(16)

As $\alpha =0$, the above unstability criteria (Eq. 16) will become same as that of Peng’s model [27].

Eq. (16) clearly shows that lane-changing parameter $\gamma$, anticipation coefficient $\alpha$ and reaction coefficient $\lambda$ play a significant role on the stability of traffic flow. The neutral stability curves in the phase space $(\rho , a)$ are shown by solid curves in Fig. 1 for different values of $\alpha$. Figure 1a corresponds to without lane changing, i.e., $\gamma =0$ and Fig. 1b corresponds the lane-changing case for $\gamma =0.1$. It can be observed from the figures that the apex of these curves $(\rho _c, a_c)$ decreases with an increase in $\alpha$ in both the cases, which means that larger value of $\alpha$ leads to enlargement of stability region, and hence, the traffic jam is suppressed efficiently. For negative values of $\alpha$, when explicit driver’s physical delay is present, the instability region increases, which is in accordance with the result of Gupta and Redhu [30] for two-lane and Kang and Sun [16] for single-lane traffic models. On comparing Fig. 1a, b, it can also be concluded that under the same conditions, the traffic flow has been strengthen with the increase in the value of $\gamma$, which means that lane changing reduces traffic jams significantly. This is similar to the real traffic phenomenon as under the jam situation, vehicles try to accommodate themselves in a less denser lane by changing their lane quite frequently to overcome the congestion.

Fig. 1

Phase diagram in parameter space $(\rho ,a), \lambda =0.1$ for a $\gamma =0$, and b $\gamma =0.1$, respectively

4 Nonlinear stability analysis

In this section, we investigate the evolution characteristic of traffic jam around the critical point $(\rho _c,a_c)$ on coarse-grained scales using reduction perturbation technique. Long-wavelength expansion method is used to understand the slowly varying behavior near the critical point. For that, the slow variables $X$ and $T$ for a small positive scaling parameter $\epsilon (0<\epsilon \ll 1)$ are defined as follows:

$$\begin{aligned} X=\epsilon (j+bt), \quad T=\epsilon ^3{t}, \end{aligned}$$

(17)

where $b$ is a constant to be determined. Let $\rho _j$ satisfy the following equation:

$$\begin{aligned} \rho _j(t) =\rho _c +\epsilon R(X,T). \end{aligned}$$

(18)

By expanding Eq. (8) using Taylor expansion up to fifth order (see Appendix 1) of $\epsilon$ with the help of Eqs. (17) and (18), the following nonlinear equation is obtained.

$$\begin{aligned}&\epsilon ^2 k_1\partial _X R+\epsilon ^3 k_2\partial ^2_X R \nonumber \\&\quad +~ \epsilon ^4(\partial _T R+k_3\partial ^3_X R+k_4\partial _X R^3)\nonumber \\&\quad +~\epsilon ^5(k_5\partial _T\partial _X R+k_6\partial ^4_X R+k_7 \partial ^2_X R^3)=0. \end{aligned}$$

(19)

The coefficients $k_i\, (i=1,2,\cdots ,7)$ are given in Table 1, where $V'=\frac{dV(\rho )}{d\rho }|_{\rho =\rho _c},\, V'''=\frac{dV^3(\rho )}{d\rho ^3}|_{\rho =\rho _c}$. Near the critical point ($\rho _c, a_c$), the value of $\tau$ is set as

$$\begin{aligned} \tau =\tau _c(\epsilon ^2+1). \end{aligned}$$

(20)

By taking $b=-\rho ^2_c V'$ and eliminating the second-order and third-order terms of $\epsilon$, we obtain

$$\begin{aligned}&\epsilon ^4(\partial _T R-g_1\partial ^3_X R+g_2\partial _X R^3) \nonumber \\&\quad +~\epsilon ^5(g_3\partial ^2_X R+g_4\partial ^4_X R+g_5 \partial ^2_X R^3)=0, \end{aligned}$$

(21)

where the coefficients $g_i\,(1,2,\cdots ,5)$ are shown in Table 2.

Table 1 The coefficients $k_i$ of the model

Table 2 The coefficients $g_i$ of the model

In order to determine the value of propagation velocity for the kink–antikink solution, it is necessary to satisfy the following condition:

$$\begin{aligned} (R'_0,M[R'_0])\equiv \int _{-\infty }^{\infty } dXR'_0 M[R'_0]=0, \end{aligned}$$

(22)

with $M[R'_0]=M[R']$. By solving Eq. (22), the selected value of $c$ is

$$\begin{aligned} c=\frac{5g_2 g_3}{2g_2 g_4-3g_1g_5}. \end{aligned}$$

(23)

Hence, the kink–antikink solution is given by

$$\begin{aligned} \rho _j=\rho _c+\epsilon \sqrt{\frac{g_1 c}{g_2}} \tanh \left( \sqrt{\frac{c}{2}}(X-cg_1 T)\right) , \end{aligned}$$

(24)

with $\epsilon ^2=\frac{a_c}{a}-1$ and the amplitude $A$ of the solution is

$$\begin{aligned} A=\sqrt{\frac{g_1 }{g_2}\epsilon ^2 c}. \end{aligned}$$

(25)

The kink–antikink soliton solution represents the coexisting phase including both freely moving phase (within low density) and congested phase (within high density), which can be described by $\rho _j=\rho _c\pm A$, respectively, in the phase space $(\rho ,a)$. For a particular case, when $\alpha =0$, the results become similar to those found by Peng [27]. The dashed lines in Fig. 1 represent the coexisting curves, which divide the phase plane into three regions: the stable region, the metastable region and the unstable region. In the stable region, the traffic flow will remain stable under a disturbance, while in metastable and unstable region, a small disturbance will lead to the congested traffic. Moreover, with the consideration of DAE when lane changing is allowed, the corresponding neutral and coexisting curves both lower down, which means that the stability of uniform traffic flow has been further strengthen, while the negative value of $\alpha$ produces the opposite effect and the amplitude of these curves increases, which leads to reduction in the stability region of traffic flow.

5 Numerical simulation

In this section, we carry out numerical simulation of the new model to investigate the effect of drivers anticipation on traffic flow dynamic as well as to validate linear and nonlinear analysis. Periodic boundary conditions are chosen, and the initial conditions are taken as follows:

$$\begin{aligned} \rho _j(1)=\rho _j(0)=\left\{ \begin{array} {ll} \rho _0 ; &{}\quad j\ne \frac{M}{2} , \frac{M}{2}+1 \\ \rho _0-\sigma ; &{}\quad j=\frac{M}{2} \\ \rho _0+\sigma ; &{}\quad j=\frac{M}{2}+1 \end{array}\right. \end{aligned}$$

where $\sigma$ is the initial disturbance, $M$ is the total number of sites taken as $100$, and other parameters are set as follows: $\sigma =0.1, a=2.3, \tau =\frac{1}{a}$.

The optimal velocity function given by Nagatani [24] is adopted.

$$\begin{aligned} V(\rho ){=}\frac{V_\mathrm{{max}}}{2}\left[ \tanh \left( \frac{1}{\rho }{-}\frac{1}{\rho _\mathrm{{c}}}\right) {+}\tanh \left( \frac{1}{\rho _c}\right) \right] , \end{aligned}$$

(26)

where $V_\mathrm{{max}}$ and $\rho _c$ denote the maximal velocity and the safety critical density, respectively. The optimal velocity function is monotonically decreasing and has an upper bound and a turning point at $\rho =\rho _{c}=\rho _0$. For computation, maximal velocity and critical density are set at $2.0$ and $0.25$, respectively.

Figure 2 depicts the simulation results of spatiotemporal evolution of density after $2\times 10^4$ time steps for different values of $\alpha$ under no lane-changing situation $(\gamma = 0)$ and $\lambda = 0.1$. It is clear from the Fig. 2a–d that initial disturbance leads to the kink–antikink soliton, which propagates in the backward direction. Due to this, initial uniform flow under a small amplitude disturbance evolves into congested flow as the stability condition is not satisfied. Figure 2d shows that as soon as $\alpha =0.4$, i.e., we entered into the stable region, a small amplitude perturbation to the homogeneous density dies out and stop-and-go wave disappears. It is also clear from Fig. 2a–d that anticipation driving behavior has efficiently suppressed the traffic jam and also validate the theoretical findings when lane changing is not allowed.

Fig. 2

Spatiotemporal evolutions of density when $\gamma =0,\lambda =0.1$ for a $\alpha =0$, b $\alpha =0.1$, c $\alpha =0.3$, and d $\alpha =0.5$, respectively

Figure 3 describes the density profile at time $t=20,300$ s corresponding to panel of Fig. 2. It can be easily depicted from Fig. 3a–d that the number of stop-and-go waves gradually decreases with an increase in anticipation coefficient. This validates the fact that in real traffic, more skillful drivers help in removing the traffic congestion. The region of free flow turns wide, and the amplitude of density waves is weakened with the increase in anticipation coefficient, which means that anticipation effect enhances the stability of the traffic flow. The traffic jam disappears, and flow becomes homogeneous at $\alpha =0.5$. Therefore, it is worth to conclude that driver’s anticipation effect significantly enhances the stability of system.

Fig. 3

Density profile at time $t=20300$ when $\gamma =0, \lambda =0.1$ for a $\alpha =0$, b $\alpha =0.1$, c $\alpha =0.3$, and d $\alpha =0.5$, respectively

Now, we examined the effect of anticipation coefficient $\alpha$ on traffic flow dynamics when lane changing is allowed $(\gamma = 0.1)$. Figures 4 and 5 display the simulation results under the different values of anticipation coefficient $\alpha$ for $\lambda = 0.1$. The results corresponding to $\gamma =0.1$ are found qualitatively similar to those obtained for $\gamma =0$. Parallel to no lane-changing case, initial small amplitude disturbance is amplified in patterns (a, c), while the disturbance will dissolve quickly and the traffic flow becomes uniform over the whole space for an appropriate value of the parameter $\alpha$ as shown in pattern (d). It is also clear from the density profile (Fig. 5d) that the traffic flow becomes stable for small value of anticipation coefficient for lane changing in comparison with without lane-changing situation. This verifies that more skillful drivers play a crucial role in avoiding jams when lane changing is permitted in two-lane system. It indicates that the stability of the new two-lane lattice model is better than that of Nagatani’s lattice model by taking the DAE’s effect into consideration.

Fig. 4

Spatiotemporal evolutions of density when $\gamma =0.1,\lambda =0.1$ for a $\alpha =0$, b $\alpha =0.1$, c $\alpha =0.2$, and d $\alpha =0.3$, respectively

Fig. 5

Density profile at time $t=20300$ when $\gamma =0.1,\lambda =0.1$ for a $\alpha =0$, b $\alpha =0.1$, c $\alpha =0.2$, and d $\alpha =0.3$, respectively

We further investigate the effect of negative anticipation coefficient representing the explicit drier’s physical delay in sensing optimal current difference effect. Figures 6 and 7 show the simulation results when $\alpha <0$ and lane changing are not allowed $(\gamma = 0.0)$. It is clear from the Fig. 6a, b that driver’s delay in sensing optimal current difference effect plays an important role in traffic congestion. The amplitude of the density waves increases with an increase in the explicit drier’s physical delay, which means that jam can easily appear as the driver has large delay of response.

Fig. 6

Spatiotemporal evolutions of density when $\gamma =0, \lambda =0.1$ for a $\alpha =-0.1$, and b $\alpha =-0.2$, respectively

Fig. 7

Density profile at time $t=10300$ when $\gamma =0,\lambda =0.1$ for a $\alpha =-0.1$, and b $\alpha =-0.2$, respectively

Figures 8 and 9 show the simulation results when the anticipation coefficient takes the negative values and lane changing is permitted $(\gamma = 0.1)$. The results corresponding to $\gamma =0.1$ are quite different from those obtained for $\gamma =0$. On comparing Fig. 7 with Fig. 9, it is observed that the density profiles of congested flow in passing case are no longer periodic. This jam pattern exhibits irregular complex structure and propagates in the opposite direction to the vehicle’s movement that is a characteristic of chaos. In chaotic flow, density waves band with one another, break up, and propagates in the backward direction. From these results, we can conclude that kink–antikink as well as chaotic region can exist in the instable region on the phase plane for different values of $\alpha$ when passing is allowed in two-lane traffic system.

Fig. 8

Spatiotemporal evolutions of density when $\gamma =0.1,\lambda =0.1$ for a $\alpha =-0.1$, and b $\alpha =-0.2$, respectively

Fig. 9

Density profile at time $t=10300$ when $\gamma =0.1, \lambda =0.1$ for a $\alpha =-0.1$, and b $\alpha =-0.2$, respectively

Figures 10 and 11 represent the phase space plot of density difference $\rho (t)-\rho (t-1)$ against $\rho (t)$ for $t=10000-20000$ corresponding to the traffic flows in Figs. 7 and 9, respectively. Figure 10 of kink jam exhibit the limit cycle, which corresponds to the periodic traffic behavior. The points on the right and left ends represent, respectively, the states within the traffic jams and within the freely moving phase. The pattern in Fig. 11 represents the set of dispersed points around a closed loop in the phase space plot. It corresponds to the irregular traffic behavior, which exhibits the behavior characteristic of chaos. It is also clear from the figure that the chaotic jam becomes more stronger by decreasing the vale of $\alpha$, which validates the fact that as the driver’s delay increases, the traffic becomes more and more irregular on a two-lane highway when lane changing is allowed. Therefore, from theoretical and simulation results, it is reasonable to conclude that traffic jam can efficiently be suppressed by incorporating the driver’s anticipation effect on a two-lane traffic system.

Fig. 10

Plot of density difference against density corresponds to the panels in Fig. 8, respectively

Fig. 11

Plot of density difference against density corresponds to the panels in Fig. 9, respectively

6 Conclusion

In this paper, we presented a new lattice hydrodynamic model for two-lane traffic flow by considering anticipation driving individual behavior in sensing optimal current difference effect (DAEOCD). Linear and nonlinear analyses are performed to investigate the traffic behavior analytically. We derived the mKdV equation to describe the traffic jam near the critical point and obtained kink–antikink soliton solution related to the traffic flow density. In addition, phase diagrams in the density-sensitivity space with the neutral stability curves and the coexisting curves are presented, showing the phase transition among the freely moving phase to uniform congested phase through coexisting phase in two-lane system. It is concluded that anticipation coefficient corresponds to driver’s behavior in sensing that optimal current difference increases the stability of traffic flow significantly in two-lane system, while the negative value of anticipation coefficient corresponds to driver’s delay response in sensing that optimal current difference effect reduces the stable region and increases congestion. The simulation results are in good accordance with the theoretical findings. Therefore, it is reasonable to conclude that driver’s anticipation effect plays an important role in stabilizing/destabilizing the traffic flow on two-lane highway. Though the results discussed in this paper are complete, yet the proposed two-lane model will be analyzed in our future work to incorporate many important factors discussed in Refs. [1–10] .

Appendix 1

In this appendix, we give the expansion of each terms in Eq. (8) using Eqs. (17) and (18) to the fifth order of $\epsilon$.

$$\begin{aligned} \rho _j(t+\tau )= & {} \rho _c +\epsilon R+\epsilon ^2 (b\tau )\partial _X R \nonumber \\&\quad +~\frac{\epsilon ^3}{2}(b\tau )^2 \partial ^{2}_X R+\frac{\epsilon ^4}{6}(b\tau )^3 \partial ^{3}_X R+\epsilon ^4\tau \partial _T R \nonumber \\&\quad +~ \frac{\epsilon ^5}{24}(b\tau )^4 \partial ^{4}_X R +\epsilon ^{5}b\tau ^2 \partial _T \partial _X R. \end{aligned}$$

(27)

$$\begin{aligned} \rho _j(t+2\tau )= & {} \rho _c +\epsilon R+\epsilon ^2 (2b\tau )\partial _X R \nonumber \\&\quad +~\frac{\epsilon ^3}{2}(2b\tau )^2 \partial ^{2}_X R \nonumber \\&\quad +~\frac{\epsilon ^4}{6}(2b\tau )^3 \partial ^{3}_X R+\epsilon ^4(2\tau ) \partial _T R\nonumber \\&\quad + \,\frac{\epsilon ^5}{24}(2b\tau )^4 \partial ^{4}_X R +\epsilon ^{5}(4b\tau ^2) \partial _T \partial _X R. \end{aligned}$$

(28)

$$\begin{aligned} \rho _{j+1}(t)= & {} \rho _c+\epsilon R+\epsilon ^2 \partial _X R \nonumber \\&\quad +~\frac{\epsilon ^3}{2} \partial ^2_X R+\frac{\epsilon ^4}{6}\partial ^3_X R+\frac{\epsilon ^5}{24}\partial ^4_X R. \end{aligned}$$

(29)

$$\begin{aligned}&\rho _{j+1}(t+\tau )-2\rho _{j}(t+\tau )+\rho _{j-1}(t+\tau ) \nonumber \\= & {} \epsilon ^3\partial ^2_X R +~\epsilon ^4(b\tau )\partial ^3_X R\nonumber \\&\qquad +~\frac{\epsilon ^5}{12}(1+6b^2\tau ^2)\partial ^4_X R. \end{aligned}$$

(30)

The expansion of optimal velocity function at the turning point is

$$\begin{aligned} V(\rho _j)= & {} V(\rho _c)+V'(\rho _c)(\rho _j-\rho _c) \nonumber \\&\quad +~\frac{V'''(\rho _c)}{6}(\rho _j-\rho _c)^3. \end{aligned}$$

(31)

$$\begin{aligned} V(\rho _{j+1})= & {} V(\rho _c)+V'(\rho _c)(\rho _{j+1}-\rho _c) \nonumber \\&\quad +~\frac{V'''(\rho _c)}{6}(\rho _{j+1}-\rho _c)^3. \end{aligned}$$

(32)

Using Eqs. (31) and (32), we get

$$\begin{aligned}&V(\rho _{j+1})-V(\rho _j)\nonumber \\&\quad = V'(\rho _c)\left[ \epsilon ^2\partial _XR +\frac{\epsilon ^3}{2}\partial _X^2R+\frac{\epsilon ^4}{6}\partial _X^3R+\frac{\epsilon ^5}{24}\partial _X^4R\right] \nonumber \\&\qquad \quad +\frac{V'''(\rho _c)}{6}\left[ \epsilon ^4\partial _XR^3+\frac{\epsilon ^5}{2}\partial ^2_XR^3\right] . \end{aligned}$$

(33)

Some other important expansions are also computed using Eqs. (27)–(33) and are given as

$$\begin{aligned}&V'(\rho _{j+2}(t))\tilde{{\varDelta }}\rho _{j+2}(t)-2V'(\rho _{j+1}(t))\tilde{{\varDelta }}\rho _{j+1}(t) \nonumber \\&\quad \quad +~V'(\rho _{j}(t))\tilde{{\varDelta }}\rho _{j}(t)=\epsilon ^3 (b\tau )V'(\rho _c)\partial ^2_X R \nonumber \\&\quad \quad +~\epsilon ^4 (b\tau )V'(\rho _c)\partial ^3_X R \nonumber \\&\quad \quad +~\frac{\epsilon ^5 }{2} (b^2\tau ^2+2b\tau )V'(\rho _c)\partial ^4_X R. \end{aligned}$$

(34)

$$\begin{aligned}&V(\rho _{j+2})-2V(\rho _{j+1})+V(\rho _j)\nonumber \\&\quad =\epsilon ^3 V'(\rho _c) \partial ^2_X R +\epsilon ^4 V'(\rho _c)\partial ^3_X R \nonumber \\&\quad \quad +~\frac{7\epsilon ^5 }{12}V'(\rho _c)\partial ^4_X R. \end{aligned}$$

(35)

$$\begin{aligned}&V'(\rho _{j+1}(t))\tilde{{\varDelta }}\rho _{j+1}(t) -V'(\rho _{j}(t))\tilde{{\varDelta }}\rho _{j}(t)\nonumber \\&\quad =\frac{\epsilon ^3}{2} (b\tau )V'(\rho _c)\partial ^2_X R\nonumber \\&\quad \quad +~\frac{\epsilon ^4}{2} (B^2\tau ^2+b\tau )V'(\rho _c)\partial ^3_X R+\epsilon ^5 V'(\rho _c)\nonumber \\&\quad \quad \times ~\left[ \tau \partial _T \partial _X R +\frac{(4b\tau +6b^2\tau ^2+4b^3\tau ^3)}{24}\partial ^4_X R\right] .\nonumber \\ \end{aligned}$$

(36)

By inserting (27), (28), (30), (33), (34), (35) and (36) into Eq. (8), we obtain Eq. (19).