1 Introduction

The possibility of realizing synchronization in coupled or forced chaotic systems came as a major breakthrough in nonlinear science. Until 1990, it had appeared impossible, due to the well-known divergence of trajectories caused by the sensitivity of chaotic systems to initial conditions, but the pioneering work of Pecora and Carroll [1] showed that this negative expectation was wrong. Since then, the synchronization of chaotic systems has attracted much attention. In addition to its own intrinsic interest, and its rich variety of intriguing features, chaos synchronization has acquired a wide range of important interdisciplinary applications, including time series analysis, secure communication systems, modeling cardiac rhythm and brain activity, and earthquake dynamics [2–6]. These have provided the motivation and driving force for the huge effort currently being devoted to ways of achieving chaos synchronization.

In general, for coupled or interacting chaotic systems with state space variables \(x_1(t)\) and \(x_2(t)\), a complete /identical synchronization manifold \(x_1(t)=x_2(t)\) exists if the condition, \(\lim _{ t\rightarrow \infty }\Vert x_1(t)-x_2(t)\Vert =0\), \(\forall t \ge 0\), is satisfied [1]. However, as proposed by Mainieri and Rehacek [7], two chaotic systems can synchronize up to a scaling factor, \(\phi \) such that \(\lim _{ t\rightarrow \infty }\Vert x_1(t)-\phi x_2(t)\Vert =0\), \(\forall t \ge 0\). In this case, they achieve projective synchronization (PS). Projective synchronization has been investigated with increasing interest in recent years due to the possibility of achieving faster communication with its scaling feature, and a wide variety of PS schemes have been proposed (See Refs. [8–19] and references therein); all of them are concerned with a single driving—single-response configuration.

Very recently, however, a novel form of projective synchronization was proposed by Luo et al. [20], in which three classic chaotic systems were made to synchronize simultaneously via systematically designed nonlinear controls; two of which were driving a single-response system, in a kind of double-driving/ single-response arrangement. The implication of combination synchronization proposed in [20] for communication is such that a signal can be split into two, each loaded and transmitted between two drive systems or at different intervals. Further developments in this direction are reported in Refs. [21–27]; in particular, compound synchronization [28, 29], double compound synchronization [30], combination-combination synchronization [23, 24, 26], finite-time combination–combination synchronization [24–27], finite-time stochastic combination synchronization [22], hybrid and reduced-order hybrid combination synchronization [31, 32] have been proposed and investigated. It is noteworthy that in all these previous works, the goals were to achieve synchronization between state variables of the driver systems and that of identical response system. This constrained the coupled systems to evolve in predetermined and predictable directions simultaneously.

In order to improve the security of information transmission via synchronization, it may be required that in master–slave synchronization, different states of the slave system are synchronized with desired state of the master system in a multi-switching manner. This form of synchronization was proposed by Ucar et al. [33] based on active control formalism. Despite its clear relevance to information security, only a few studies of this kind of synchronization have been reported [34–40]. To the best of our knowledge, all the work on multi-switching synchronization of this kind reported in the literature have related to single-driver/single-response systems.

In this paper, we propose a multi-switching combination synchronization scheme, wherein two driver chaotic systems are multi-switched in diverse ways with a single-response chaotic system. The possibility of realizing such a form of synchronization would present varieties of synchronization directions between the driver systems’ and response system’s variables, thereby ensuring better security when employed in communication applications.

The rest of the paper is organized as follows: In Sect. 2, the definitions and basic formulation of multi-switching combination synchronization (MSCS) are presented. In Sect. 3, an example of the MSCS of three classic chaotic systems is formulated. The corresponding numerical simulation results are presented in Sect. 4. The paper is summarized and concluded in Sect. 5.

2 Definition and formulation of MSCS

Consider the following master–slave \(n\)-dimensional chaotic systems, where the master systems are given by

$$\begin{aligned} \dot{x}_{1m}&= f_{1x}(x_{1m},\dots ), \dot{x}_{2m} = f_{2x}(x_{1m},\dots ), \dots , \nonumber \\ \dot{x}_{nm}&= f_{nx}(x_{1m},\dots ) \end{aligned}$$
(1)

and

$$\begin{aligned} \dot{y}_{1m}&= f_{1y}(y_{1m},\dots ), \dot{y}_{2m} = f_{2y}(y_{1m},\dots ), \dots , \nonumber \\ \dot{y}_{nm}&= f_{ny}(y_{1m},\dots ) \end{aligned}$$
(2)

and the controlled slave system is given by

$$\begin{aligned} \dot{z}_{1s}&= g_{1z}(z_{1s},\dots )+U_{1}, \dot{z}_{2s}= g_{2z}(z_{1s},\dots )+U_{2}, \dots , \nonumber \\ \dot{z}_{ns}&= g_{nz}(z_{1s},\dots )+U_{n}; \end{aligned}$$
(3)

where \(x_{jm},y_{km},z_{is}(i,j,k=1,2,\dots n)\in R^n\) are state space vectors of the systems, \(f_{jx},f_{ky},g_{iz}:R^n \rightarrow R^n\) are three continuous vector functions composed of linear and nonlinear components, and \(U_i(i=1,2,\dots , n):R^n \rightarrow R^n\) is a nonlinear control function. The indices \(m\) and \(s\) stand for master and slave systems, respectively.

Definition 1

[20] If there exists three constant matrices \(A,B,C \in R^n\) and \(C \ne 0\), such that

$$\begin{aligned} \lim _{t \rightarrow \infty } ||Cz_{is}-Ax_{jm}-By_{km}|| = 0, \end{aligned}$$

where \(||.||\) is the matrix norm and \(A,B,C\) are scaling matrices, then, systems (1), (2) and (3) are said to be in combination synchronization.

Comment 1

The error states in relation to the definition 1 are strictly chosen to satisfy the definition, \(e_{ijk}(i=j=k)\), where \(i, j\) and \(k\) are the indices of the error.

Definition 2

If the error states in relation to Definition 1 are redefined such that \(i=j\ne {k}\) or \(i=k\ne {j}\), or \(j=k\ne {i}\) or \(i\ne {j}\ne {k}\), \(i\ne {j}=k\) or \(j\ne {i} = k\) and

$$\begin{aligned} \lim _{t \rightarrow \infty } ||Cz_{is}-Ax_{jm}-By_{km}|| = 0, \end{aligned}$$

then systems (1), (2) and (3) are said to be in multi-switching combination synchronization.

Comment 2

We refer to the conditions, \(i=j\ne {k}\) or \(i=k\ne {j}\), \(j=k\ne {i}\) or \(i\ne {j}\ne {k}\), as generic conditions that must be met. In addition, there are several non-generic cases where the above possible generic cases are combined in a mixed mode.

To formulate the active backstepping procedure, we define a typical multi-switching synchronization error for a 3-dimensional system, as

$$\begin{aligned} e_{123}&= \gamma _1{z}_{1s}-\alpha _2x_{2m}- \beta _3y_{3m},\nonumber \\ e_{231}&= \gamma _2{z}_{2s}-\alpha _3x_{3m}- \beta _1y_{1m},\\ e_{312}&= \gamma _3{z}_{3s}-\alpha _1x_{1m}-\beta _2y_{2m},\nonumber \end{aligned}$$
(4)

and obtain the following error dynamical system

$$\begin{aligned} \dot{e}_{123}&= \gamma _1{g}_{1z}+\gamma _1{U}_{1}-\alpha _2f_{2x}-\beta _3f_{3y},\nonumber \\ \dot{e}_{231}&= \gamma _2{g}_{2z}+\gamma _2{U}_{2}-\alpha _3f_{3x}-\beta _1f_{1y},\\ \dot{e}_{312}&= \gamma _3{g}_{3z}+\gamma _3{U}_{3}-\alpha _1f_{1x}-\beta _2f_{2y},\nonumber \end{aligned}$$
(5)

where \(\alpha _j, \gamma _i, \beta _k (i,j,k=1,2,3)\) are scaling factors. In principle and by some algebraic manipulations, the error dynamical system (5) can be expressed in terms of the synchronization error, \({e}_{123}, {e}_{231}\) and \({e}_{312}\), because \({g}_{iz}\), \({f}_{jx}\), and \({f}_{ky}\) consist of linear and nonlinear parts. Thus, the synchronization problem reduces to that of asymptotic stabilization of Eq. (5) with appropriate control inputs. Here, we use the active backstepping technique, because it provides a systematic design approach for both control and synchronization and guarantees global stability of the closed loop system. The main feature of this approach is that it allows for flexibility in the construction of control laws, so that the control strategy can be extended very easily to higher-dimensional systems. We now provide a description of a simple design procedure for active backstepping-based multi-switching combination synchronization.

Let \(\nu _{1}=e_{123}\), so that we obtain the \(\nu _1\)-subsystem

$$\begin{aligned} \dot{\nu }_{1}&= F_1(\nu _1,f_{xyz},U_{1}); \end{aligned}$$
(6)

where \(f_{xyz}\) is a nonlinear function derived from \({g}_{iz}(z_{is})\), \({f}_{jx}(x_{jm})\), and \({f}_{ky}(y_{km})\). Considering the error variable \(e_{231}\) as a virtual control input via a classical Lyapunov function \(V_{1}\), if \(V_{1}\) satisfies the conditions

$$\begin{aligned} \left\{ \begin{array}{ll} V_{1}(e_{231})>0&{} \quad \text{ if } \ e_{231}\ne 0,\\ V_{1}(e_{231})=0&{} \quad \text{ if } \ e_{231}=0, \end{array} \right. \end{aligned}$$
(7)

and

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{V}_{1}(e_{231}) < 0 &{} \quad \text{ if } \ e_{231}\ne 0,\\ \dot{V}_{1}(e_{231}) = 0 &{} \quad \text{ if } \ e_{231}=0, \end{array} \right. \end{aligned}$$
(8)

then the \(\nu _1\)-subsystem of Eq. (6) is asymptotically stable. When \(e_{231}\) has been designed, we can obtain the following \((\nu _{1},\nu _{2})\)-subsystem

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{\nu }_{1}= &{} F_{1}(\nu _{1},f_{xyz},U_{1}),\\ \dot{\nu }_{2}= &{} F_{2}(\nu _{1},\nu _{2},e_{123},g_{xyz},U_{2}), \end{array} \right. \end{aligned}$$
(9)

by setting \(\nu _{2}=e_{231}-\alpha _{1}(\nu _{1})\), where \(\alpha _{1}(\nu _{1})\) is a virtual control and \(g_{xyz}\) is a nonlinear function derived from \({g}_{iz}(z_{is})\), \({f}_{jx}(x_{jm})\) and \({f}_{ky}(y_{km})\).

In other to stabilize the \((\nu _{1},\nu _{2})\)-subsystem, a second positive Lyapunov function \(V_{2}\) is chosen. The process continues by consideration of the variable \(e_{312}=\alpha _{2}(\nu _{1},\nu _{2})\) as the virtual control input for the \((\nu _{1},\nu _{2})\)-subsystem, and so on. Then, if \(\dot{V}_{2}\) is negative definite, we can conclude that \((\nu _{1}, \nu _{2})\)-subsystem is asymptotically stable. Finally, the full \((\nu _{1},\nu _{2},\nu _{3})\)-system can be constructed and stabilized in the same manner.

3 MSCS of three chaotic systems

In order to generalize the concept, we examine multi-switching combination synchronization of three strictly different chaotic systems, namely, Rössler, Newton-Leipnik, and Lorenz systems. The Rössler and Newton-Leipnik systems provide the driving and are represented by the state variables \(x,y\) as

$$\begin{aligned} \dot{x_1}&= -x_2-x_3,\nonumber \\ \dot{x_2}&= x_1+a_1x_2,\\ \dot{x_3}&= b_1+x_3(x_2-c_1),\nonumber \end{aligned}$$
(10)

and

$$\begin{aligned} \dot{y_1}&= -a_2y_1+y_2+10y_2y_3,\nonumber \\ \dot{y_2}&= -y_1-0.4y_2+5y_1y_3,\\ \dot{y_3}&= b_2y_3-5y_1y_2;\nonumber \end{aligned}$$
(11)

while the response of the Lorenz system represented by the state variable \(z\) is given by

$$\begin{aligned} \dot{z_1}&= a_3(z_2-z_1)+U_1,\nonumber \\ \dot{z_2}&= b_3z_1-z_2-z_1z_3+U_2,\\ \dot{z_3}&= z_1z_2-c_3z_3+U_3,\nonumber \end{aligned}$$
(12)

where \(U_1\), \(U_2\) and \(U_3\) are controllers to be designed.

There are several possible generic switching combinations that could exist for the drive-response system (10), (11) and (12), some of which are given below.

  • For \(i=j\ne {k}\), we have: \(e_{112},e_{221},e_{331}\) and \(e_{113},e_{223},e_{332}\).

  • For \(i=k\ne {j}\), we have: \(e_{121},e_{212},e_{313}\) and \(e_{131},e_{232},e_{323}\).

  • For \(j=k\ne {i}\), we have: \(e_{122},e_{211},e_{311}\) and \(e_{133},e_{233},e_{322}\).

  • For \(i\ne {j}\ne {k}\), we have: \(e_{123},e_{213},e_{312}\) and \(e_{132},e_{231},e_{321}\).

  • For \(i\ne {j}=k\), we have \(e_{122},e_{233},e_{311}\) and \(e_{133},e_{211},e_{322}\).

  • For \(j\ne {i}=k\), we have \(e_{121},e_{212},e_{313}\).

In this paper, we present results for some particular switching combinations, randomly selected from the combinations given above. They are:

$$\begin{aligned} e_{112}&= \gamma _{1}z_{1}-\alpha _{1}x_{1}-\beta _{2}y_{2}, \nonumber \\ e_{213}&= \gamma _{2}z_{2}-\alpha _{1}x_{1}-\beta _{3}y_{3}, \qquad \quad \mathrm{Switch~1}\end{aligned}$$
(13)
$$\begin{aligned} e_{311}&= \gamma _{3}z_{3}-\alpha _{1}x_{1}-\beta _{1}y_{1};\nonumber \\ e_{123}&= \gamma _{1}z_{1}-\alpha _{2}x_{2}-\beta _{3}y_{3}, \nonumber \\ e_{213}&= \gamma _{2}x_{2}-\alpha _{1}x_{1}-\beta _{3}y_{3}, \qquad \quad \mathrm{Switch~2}\end{aligned}$$
(14)
$$\begin{aligned} e_{323}&= \gamma _{3}z_{3}-\alpha _{2}x_{2}-\beta _{3}y_{3};\nonumber \\ e_{112}&= \gamma _{1}z_{1}-\alpha _{1}x_{1}-\beta _{2}y_{2}, \nonumber \\ e_{223}&= \gamma _{2}z_{2}-\alpha _{2}x_{2}-\beta _{3}y_{3}, \qquad \quad \mathrm{Switch~3}\end{aligned}$$
(15)
$$\begin{aligned} e_{321}&= \gamma _{3}z_{3}-\alpha _{2}x_{2}-\beta _{1}y_{1};\nonumber \\ e_{113}&= \gamma _{1}z_{1}-\alpha _{1}x_{1}-\beta _{3}y_{3}, \nonumber \\ e_{221}&= \gamma _{2}z_{2}-\alpha _{2}x_{2}-\beta _{1}y_{1}, \qquad \quad \mathrm{Switch~4}\\ e_{312}&= \gamma _{3}z_{3}-\alpha _{1}x_{1}-\beta _{2}y_{2}.\nonumber \end{aligned}$$
(16)

The notations for the scaling factors \(\alpha _i, \gamma _j, \beta _k (i,j,k=1,2,3)\) are set for convenient and may assume different or same values in applications. For simplicity and reference, we refer to the error dynamics Eq. (13) as Switch 1, Eq. (14) as Switch 2, Eq. (15) as Switch 3, and Eq. (16) as Switch 4.

3.1 Switch 1

For Switch 1 Eq. (13), the time derivative of the errors is given by

$$\begin{aligned} \dot{e}_{112}&= \gamma _{1}\dot{z_1}-\alpha _{1}\dot{x_1}-\beta _{2}\dot{y_2}, \nonumber \\ \dot{e}_{213}&= \gamma _{2}\dot{z_2}-\alpha _{1}\dot{x_1}-\beta _{3}\dot{y_3},\\ \dot{e}_{311}&= \gamma _{3}\dot{z_3}-\alpha _{1}\dot{x_1}-\beta _{1}\dot{y_1}.\nonumber \end{aligned}$$
(17)

Substituting for \(\dot{z_1}\), \(\dot{x_1}\), \(\dot{y_2}\), \(\dot{z_2}\), \(\dot{y_3}\), \(\dot{z_3}\) and \(\dot{y_1}\) from Eqs. (10),(11) and (12), the error dynamical system for Switch \(1\) can be written as:

$$\begin{aligned} \dot{e}_{112}&= \frac{\gamma _{1}a_3}{\gamma _{2}}e_{213}-a_3e_{112}+f+\gamma _{1}U_1\nonumber \\ \dot{e}_{213}&= \frac{\gamma _{2}b_3}{\gamma _{1}}e_{112}\!-\!\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}e_{112}e_{311}\!-\!\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}[\alpha _{1}x_1\!+\!\beta _{1}y_1]e_{112}\nonumber \\&-\,e_{213}-\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}[\alpha _{1}x_1+\beta _{2}y_2]e_{311}+g+\gamma _{2}U_2 \\ \dot{e}_{311}&= \frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}[\alpha _{1}x_1+\beta _{3}y_3]e_{112}+\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}e_{112}e_{213}\nonumber \\&+\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}[\alpha _{1}x_1+\beta _{2}y_2]e_{213}-c_3e_{311}+h+\gamma _{3}U_3\nonumber \end{aligned}$$
(18)

where,

$$\begin{aligned} f&= \left( \frac{\gamma _{1}a_3}{\gamma _{2}}-a_3\right) \alpha _{1}x_1+\frac{\gamma _{1}a_3\beta _{3}}{\gamma _{2}}y_3-a_3\beta _{2}y_2+\alpha _{1}x_2\\&+\,\alpha _{1}x_3+\beta _{2}y_1+0.4\beta _{2}y_2-5\beta _{2}y_1y_3\nonumber \\ g&= \frac{\gamma _{2}b_3}{\gamma _{1}}\left( \alpha _{1}x_1+\beta _{2}y_2\right) +\alpha _{1}(x_2+x_3)-\beta _{3}[b_2y_3-5y_1y_2]\nonumber \\&-\,[\alpha _{1}x_1+\beta _{3}y_3]-\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}[(\alpha _{1}x_1+\beta _{2}y_2)(\alpha _{1}x_1+\beta _{1}y_1)]\\ h&= \frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}(\alpha _{1}x_1+\beta _{2}y_2)(\alpha _{1}x_1+\beta _{3}y_3)+\alpha _{1}(x_2+x_3)\\&-\,c_3(\alpha _{1}x_1+\beta _{1}y_1)+\beta _{1}(+a_2y_1-y_2-10y_2y_3)]\nonumber \end{aligned}$$

Theorem 1

If the control functions \(U_1\), \(U_2\) and \(U_3\) are chosen such that

$$\begin{aligned} \begin{array}{lll} U_1&{}=-\frac{1}{\gamma _{1}}f,\\ U_2&{}=-\frac{1}{\gamma _{2}}\left[ \left( \frac{\gamma _{2}b_3}{\gamma _{1}}-\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}(\alpha _{1}x_1+\beta _{1}y_1)\right) \nu _{1}+g\right] , \\ U_3&{}=-\frac{1}{\gamma _{3}}\Big [\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}(\alpha _{1}x_1+\beta _{3}y_3)\nu _{1}+\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}\\ &{}\qquad (\alpha _{1}x_1+\beta _{2}y_2)\nu _{2}+\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}\nu _{1}\nu _{2}+h\Big ], \end{array} \end{aligned}$$
(19)

where \(\nu _{1}=e_{112}, \nu _{2}=e_{213}\), then the drive systems (10) and (11) will achieve multi-switching combination synchronization with the response system (12).

Proof 1

We use the active backstepping technique to prove the above theorem.

Let \(\nu _{1}=e_{112}\); its derivative is given by

$$\begin{aligned} \dot{\nu }_{1}&=\dot{e}_{112}=&\frac{\gamma _{1}a_3}{\gamma _{2}}e_{213}-a_3e_{112} \end{aligned}$$
(20)

where \(e_{213}\equiv \alpha _{1}(\nu _{1})\) can be regarded as a virtual controller. For the design of \(\alpha _{1}(\nu _{1})\) to stabilize the \(\nu _{1}\)-subsystem defined by Equ. (20), we consider the following Lyapunov function

$$\begin{aligned} V_1=\frac{1}{2}\nu _{1}^2. \end{aligned}$$
(21)

Its time derivative is given by

$$\begin{aligned} \dot{V_1}=\nu _{1}\dot{\nu }_{1}=\nu _{1}\left( \frac{\gamma _{1}a_3}{\gamma _{2}}\alpha _{1}(\nu _{1})-a_3\nu _{1}\right) . \end{aligned}$$
(22)

The virtual control \(\alpha _{1}(\nu _{1})\) is an estimated control input, and it can take any convenient values that yields the desired control function. In practice, and for the purpose of applications, \(\alpha _{1}(\nu _{1})\) should be chosen such that the overall controller complexity is reduced as much as possible. Suppose \(\alpha _{1}(\nu _{1})\equiv 0\), then \(\dot{V_1}=-a_3\nu _{1}^2 \le 0\) is negative definite, and according to Lyapunov stability theorem, the \(\nu _{1}\)-subsystem is asymptotically stable.

If we denote the error between \(e_{213}\) and \(\alpha _{1}(\nu _{1})\) by \(\nu _{2}\), i.e., \(\nu _{2}=e_{213}-\alpha _{1}(\nu _{1})\), then we have the \((\nu _1,\nu _2)\)-subsystem

$$\begin{aligned} \dot{\nu }_{1}&= \frac{\gamma _{1}a_3}{\gamma _{2}}\nu _{2}-a_3\nu _{1},\nonumber \\ \dot{\nu }_{2}&= \left( \frac{\gamma _{2}b_3}{\gamma _{1}}-\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}\left[ \alpha _{1}x_1+\beta _{1}y_1\right] \right) \nu _{1}-\nu _{2},\nonumber \\&-\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}\nu _{1}e_{311}-\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}\left[ \alpha _{1}x_1+\beta _{2}y_2\right] e_{311}\nonumber \\&+g+\gamma _{2}U_2. \end{aligned}$$
(23)

To stabilize the \((\nu _{1},\nu _{2})\)-subsystem, \(e_{311}\equiv \alpha _{2}(\nu _{1}, \nu _{2})\) can be regarded as a virtual controller. Assuming the Lyapunov function

$$\begin{aligned} V_2=V_1+\frac{1}{2}\nu _{2}^2, \end{aligned}$$

and its time derivative given by

$$\begin{aligned}&\dot{V_2}=-a_3\nu _{1}^2-\nu _{2}^2+\nu _{2}\Big [\left( \frac{\gamma _{2}b_3}{\gamma _{1}}-\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}[\alpha _{1}x_1+\beta _{1}y_1]\right) \nu _{1}\nonumber \\&\quad -\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}\left( \nu _{1}+\alpha _{1}x_1+\beta _{2}y_2\right) \alpha _{2}(\nu _{1},\nu _{2})+g+\gamma _{2}U_2\Big ].\nonumber \\ \end{aligned}$$
(24)

Similarly, if we let \(\alpha _{2}(\nu _{1}, \nu _{2})=0\) and the control function \(U_2\) is chosen as in Theorem 1, then \(\dot{V_2}=-a_3\nu _{1}^2-\nu _{2}^2<0\), implying that the \((\nu _{1},\nu _{2})\) - subsystem is asymptotically stable.

Finally, suppose \(\nu _{3}\equiv e_{311}-\alpha _{2}(\nu _{1}, \nu _{2})\). We then obtain

$$\begin{aligned} \dot{\nu }_{3}&= \frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}[\alpha _{1}x_1+\beta _{3}y_3]\nu _{1}+\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}\nu _{1}\nu _{2}\nonumber \\&+\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}[\alpha _{1}x_1+\beta _{2}y_2]\nu _{2}-c_3\nu _{3}+h+\gamma _{3}U_3.\nonumber \\ \end{aligned}$$
(25)

This allows us to stabilize the full dimensional system \((\nu _{1}, \nu _{2}, \nu _{3})\), by taking the Lyapunov function as

$$\begin{aligned} V_3=V_2+\frac{1}{2}\nu _{3}^2. \end{aligned}$$
(26)

Using Theorem 1, its time derivative is given by

$$\begin{aligned} \dot{V_3}=-a_3\nu _{1}^2-\nu _{2}^2-c_3\nu _{3}^2<0. \end{aligned}$$
(27)

Since \(\dot{V_3}=-a_3\nu _{1}^2-\nu _{2}^2-c_3\nu _{3}^2<0\), we can conclude, based on the Lyapunov stability theorem, that the equilibrium \((0,0,0)\) of the full dimensional system \((\nu _{1}, \nu _{2}, \nu _{3})\) given by

$$\begin{aligned} \dot{\nu }_{1}&= \frac{\gamma _{1}a_3}{\gamma _{2}}\nu _{2}-a_3\nu _{1}\nonumber \\ \dot{\nu }_{2}&= -\nu _{2}-\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}\nu _{1}\nu _{3}-\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}[\alpha _{1}x_1+\beta _{2}y_2]\nu _3\\ \dot{\nu }_{3}&= -c_3\nu _{3} \nonumber \end{aligned}$$
(28)

is asymptotically stable and that global multi-switching combination synchronization has been achieved. This ends the proof. \(\square \)

Comment 3

The following corollaries can be easily obtained from Theorem 1, but their proofs are omitted here for brevity.

If we let \(\beta _{1}=\beta _{2}=\beta _{3}=0\), \(\gamma _{1}=\gamma _{2}=\gamma _{3}=1\), then we have Corollary 1.

Corollary 1

If the controllers are chosen as

$$\begin{aligned} U_{1}&= -\alpha _{1}x_{2}-\alpha _{1}x_{3},\nonumber \\ U_{2}&= -(b_{3}-\alpha _{1}x_{1})\nu _{1}-(b_{3}-1)\alpha _{1}x_{1}+\alpha _{1}^2x_{1}^2 \nonumber \\&+\,\alpha _{1}(x_{2}+x_{3}),\\ U_{3}&= -(\nu _{1}\!+\!\nu _{2}-c_3)\alpha _{1}x_{1}-\nu _{1}\nu _{2}\!-\!\alpha _{1}^2x_{1}^2-\alpha _{1}(x_{2}+x_{3}),\nonumber \end{aligned}$$
(29)

then the drive system (10) will achieve multi-switching projective synchronization with the response system (12), with \(\alpha _{1}\), \(\alpha _{2}\) and \(\alpha _{3}\) being the scaling factors.

If we let \(\alpha _{1}=\alpha _{2}=\alpha _{3}=0\), \(\gamma _{1}=\gamma _{2}=\gamma _{3}=1\), then we obtain Corollary 2.

Corollary 2

If the controllers are designed as

$$\begin{aligned} U_{1}&= -a_{3}(\beta _{3}y_{3}-\beta _{2}y_{2})-\beta _{2}y_{1}-0.4\beta _{2}y_{2}+5\beta _{2}y_{1}y_{3},\nonumber \\ U_{2}&= -(b_{3}-\beta _{1}y_{1})\nu _{1}-b_{3}\beta _{2}y_{2}+\beta _{3}y_{3}+\beta _{2}y_{2}\beta _{1}y_{1}\nonumber \\&+\beta _{3}(b_{2}y_{3}-5y_{1}y_{2}),\\ U_{3}&= -\beta _{3}y_{3}\nu _{1}-\beta _{2}y_{2}\nu _{2}-\nu _{1}\nu _{2}-\beta _{2}y_{2}\beta _{3}y_{3}-c_{3}\beta _{1}y_{1}\nonumber \\&+\beta _{1}(a_{2}y_{1}-y_{2}-10y_{2}y_{3}),\nonumber \end{aligned}$$
(30)

then the drive system (11) and the response system (12) will reach multi-switching projective synchronization, with \(\beta _{1}\), \(\beta _{2}\) and \(\beta _{3}\) being the scaling factors.

Suppose \(\alpha _{1}=\alpha _{2}=\alpha _{3}=0\), \(\beta _{1}=\beta _{2}=\beta _{3}=0\), \(\gamma _{1}=\gamma _{2}=\gamma _{3}=1\), then one gets Corollary 3.

Corollary 3

If the controllers are chosen as

$$\begin{aligned} U_{1}&= 0\nonumber \\ U_{2}&= -b_{3}\nu _{1}\\ U_{3}&= -\nu _{1}\nu _{2}\nonumber \end{aligned}$$
(31)

then the equilibrium point \((0,0,0)\) of the response system (12) will be asymptotically stable, and stabilization of the system (12) is achieved.

3.2 Switch 2, Switch 3, and Switch 4

Following the same procedure presented in Sect. 3.1, and considering Switch 2 given by Eq. (14), we can give the following Theorem 2.

Theorem 2

If the control functions \(U_1\), \(U_2\) and \(U_3\) are chosen such that

$$\begin{aligned} U_1&= -\frac{1}{\gamma _{1}}f\nonumber \\ U_2&= -\frac{1}{\gamma _{2}}\left[ \left( \frac{\gamma _{2}b_3}{\gamma _{1}}-\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}(\alpha _{2}x_2+\beta _{3}y_3)\right) \nu _{1}+g\right] \\ U_3&= -\frac{1}{\gamma _{3}}\Big [\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}(\alpha _{1}x_1+\beta _{3}y_3)\nu _{1}+\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}\\&\times \,(\alpha _{2}x_2+\beta _{3}y_3)\nu _{2}+\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}\nu _{1}\nu _{2}+h\Big ]\nonumber \end{aligned}$$

where \(\nu _{1}=e_{123}\), \(\nu _{2}=e_{213}\), then the drive systems (10) and (11) will achieve multi-switching combination synchronization with the response system (12).

Comment 4

The following corollaries are easily obtained from Theorem 2, but their proofs are omitted for brevity.

If we let \(\beta _{1}=\beta _{2}=\beta _{3}=0\), \(\gamma _{1}=\gamma _{2}=\gamma _{3}=1\), then we have Corollary 4.

Corollary 4

If the controllers are chosen as

$$\begin{aligned} U_1&= (a_3+a_1)\alpha _{2}x_2-a_3\alpha _{1}x_1+\alpha _{2}x_1, \nonumber \\ U_2&= \alpha _{2}^2x_{2}^2-(b_3-\alpha _{2}x_2)\nu _{1}+\alpha _{1}(-x_2-x_3)\nonumber \\&-b_3\alpha _{2}x_2-\alpha _{1}x_1,\\ U_3&= \alpha _{2}(x_1+a_1x_2)-\nu _{1}\nu _{2}-(\nu _{2}+\alpha _{1}x_1-c_3)\alpha _{2}x_2,\nonumber \end{aligned}$$
(32)

then, the driven system (10) will achieve multi-switching projective synchronization with the response system (12), with \(\alpha _{1}\), \(\alpha _{2}\) and \(\alpha _{3}\) being the scaling factors.

If we let \(\alpha _{1}=\alpha _{2}=\alpha _{3}=0\), \(\gamma _{1}=\gamma _{2}=\gamma _{3}=1\), then we obtain Corollary 5.

Corollary 5

If the controllers are designed as

$$\begin{aligned} U_1&= -(a_3-b_2)\beta _{3}y_3-5\beta _{3}y_1y_2,\end{aligned}$$
(33)
$$\begin{aligned} U_2&= -(b_3-\beta _{3}y_3)\nu _{1}-(b_3-1-\beta _{3}y_3)\beta _{3}y_3\nonumber \\&+\beta _{3}(b_2y_3-5y_1y_2),\\ U_3&= -[\nu _{1}\nu _{2}+(\nu _{2}+\nu _{1}-c_3)\beta _{3}y_3+\beta _{3}^2y_{3}^2\nonumber \\&-\beta _{3}(b_2y_3-5y_1y_2)],\nonumber \end{aligned}$$
(34)

then the drive system (10) and the response system (12) will reach multi-switching projective synchronization, with \(\beta _{1}\), \(\beta _{2}\) and \(\beta _{3}\) being the scaling factor.

Suppose \(\alpha _{1}=\alpha _{2}=\alpha _{3}=0\), \(\beta _{1}=\beta _{2}=\beta _{3}=0\), \(\gamma _{1}=\gamma _{2}=\gamma _{3}=1\), then one gets Corollary 6.

Corollary 6

If the controllers are chosen as

$$\begin{aligned} U_1&= 0, \nonumber \\ U_2&= -b_3\nu _{1},\\ U_3&= -\nu _{1}\nu _{2},\nonumber \end{aligned}$$
(35)

then the equilibrium point \((0,0,0)\) of response system (12) will be asymptotically stable.

Similarly for Switch 3, given by Eq. (15), we give the following theorem.

Theorem 3

If the control functions \(U_1\), \(U_2\) and \(U_3\) are chosen such that

$$\begin{aligned} U_1&= -\frac{1}{\gamma _{1}}f\nonumber \\ U_2&= -\frac{1}{\gamma _{2}}\left[ \left( \frac{\gamma _{2}b_3}{\gamma _{1}}-\frac{\gamma _{2}}{\gamma _{1}\gamma _{3}}(\alpha _{2}x_2+\beta _{1}y_1)\right) \nu _{1}+g\right] \\ U_3&= -\frac{1}{\gamma _{3}}\Big [\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}(\alpha _{2}x_2+\beta _{3}y_3)\nu _{1}+\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}\\&(\alpha _{1}x_1+\beta _{2}y_2)\nu _{2}+\frac{\gamma _{3}}{\gamma _{1}\gamma _{2}}\nu _{1}\nu _{2}+h\Big ]\nonumber \end{aligned}$$

where \(\nu _{1}=e_{112}\), \(\nu _{2}=e_{223}\), then the drive systems (10) and (11) will achieve multi-switching combination synchronization with the response system (12).

Comment 5

The following corollaries are easily obtained from Theorem 3, but their proofs are omitted.

If we let \(\beta _{1}=\beta _{2}=\beta _{3}=0\), \(\gamma _{1}=\gamma _{2}=\gamma _{3}=1\), then we have corollary 7.

Corollary 7

If the controllers are chosen as

$$\begin{aligned} U_1&= a_3\alpha _{1}x_1-(\alpha _{1}+a_3\alpha _{2})x_2-\alpha _{1}x_3, \nonumber \\ U_2&= (\alpha _{1}+x_1\alpha _{2}x_2)-(b_3-\alpha _{2}x_2)\nu _{1}+b_3\alpha _{1}x_1\nonumber \\&+\alpha _{2}(x_1+a_1x_2)-\alpha _{2}x_2,\\ U_3&= -\nu _{1}\nu _{2}-\alpha _{1}x_1\nu _{2}-(\nu _{1}+\alpha _{1}x_1-c_3)\alpha _{2}x_2\nonumber \\&+\alpha _{2}(x_1+a_1x_2),\nonumber \end{aligned}$$
(36)

then the drive system (10) will achieve multi-switching projective synchronization with the response system (12), with \(\alpha _{1}\), \(\alpha _{2}\) and \(\alpha _{3}\) being the scaling factors.

If we let \(\alpha _{1}=\alpha _{2}=\alpha _{3}=0\), \(\gamma _{1}=\gamma _{2}=\gamma _{3}=1\), then we obtain corollary 8.

Corollary 8

: If the controllers are chosen as

$$\begin{aligned} U_1&= a_3\beta _{2}y_2-a_3\beta _{3}y_3-\beta _{2}y_1-0.4\beta _{2}y_2+5\beta _{2}y_1y_3,\nonumber \\ U_2&= -(b_3-\beta _{1}y_1)\nu _{1}-(b_3-\beta _{1}y_1)\beta _{2}y_2+\beta _{3}y_3\nonumber \\&+\beta _{3}(b_2y_3-5y_1y_2),\\ U_3&= -\nu _{1}\nu _{2}-\beta _{2}y_2\nu _{2}-(\nu _{1}+\beta _{2}y_2)\beta _{3}y_3+c_3\beta _{1}y_1 \nonumber \\&-\beta _{1}(a_2y_1-y_2-10y_2y_3),\nonumber \end{aligned}$$
(37)

then the drive system (11) will achieve multi-switching projective synchronization with the response system (12), with \(\beta _{1}\), \(\beta _{2}\) and \(\beta _{3}\) being the scaling factor.

Suppose \(\alpha _{1}=\alpha _{2}=\alpha _{3}=0\), \(\beta _{1}=\beta _{2}=\beta _{3}=0\), \(\gamma _{1}=\gamma _{2}=\gamma _{3}=1\), then one gets corollary 9.

Corollary 9

If the controllers are chosen as

$$\begin{aligned} U_1&= 0, \nonumber \\ U_2&= -b_3\nu _{1},\\ U_3&= -\nu _{1}\nu _{2},\nonumber \end{aligned}$$
(38)

then the equilibrium point \((0,0,0)\) of response system (12) will be asymptotically stable.

4 Numerical results

We now present the results of numerical simulations. These were done using a fourth-order Runge-Kutta method with variable time-step. As stated earlier, the main interest is to achieve multi-switching combination synchronization of the Rössler system, Newton-Leipnik system, and Lorenz system. The systems’ parameters were chosen as \(a_1=0.2\), \(b_1=0.2\), \(c_1=5.7\), \(a_2=0.4\), \(b_2=0.175\), \(a_3=10.0\), \(b_3=23.0\) and \(c_3=8.0/3\), in order to ensure the existence of chaotic attractors, with the initial states for the master system and for the slave system taken arbitrarily to be \((x_1,x_2,x_3)\) = \((0.0,1.0,-2.0)\), \((y_1,y_2,y_3)\) = \((0.349,0.0,-0.16)\) and \((z_1,z_2,z_3)\) = \((1.0,0.40,0.80)\), respectively. Although the system parameters may be chosen so that the systems are non-chaotic, we emphasize that the chaotic synchronized state is a special case: It is of tremendous importance in the field of secure communications, and the achievement of a synchronization state is independent of the choice of initial conditions or of the parameters of the system since the control inputs are dependent on the system parameters. Thus, any set of initial conditions leading to either a chaotic or a periodic orbit would give synchronization. For the control parameters, we assume that the master systems scaling factors \(\alpha _{1}\) = \(\alpha _{2}\) = \(\alpha _{3}=1\), \(\beta _{1}=\beta _{2}=\beta _{3}=-2\). Note that \(\gamma _i\) is the scaling factor for the slave system, and that its value should be set to unity to ensure that only the master systems are projected onto the slave [7]. Thus, \(\gamma _{1}=\gamma _{2}=\gamma _{3}=1\), while \(\alpha _j\) and \(\beta _k\) may take on some convenient values according to the required projections, ensuring bounded solutions. Boundedness of the chaotic attractors should be preserved to ensure that the orbits stay within the basins of attraction. From our numerical experiments using different values of \(\alpha _j\) and \(\beta _k\), we found that, in general, a regime of \(\alpha _j\) and \(\beta _k\) exists for which the solution is bounded and synchronization is reachable. Typically, this lies approximately in the control parameter range \(-8 < \alpha _j,\beta _k < 8\); otherwise, the solutions are unbounded, because the orbits tends to exit the basins of attraction. It is interesting to note that this regime encloses a variety of possible synchronization phenomena. For instance, when \(\alpha _j,\beta _k < 0\), we have projective multi-switching combination anti-synchronization, \(\alpha _j,\beta _k = 1\) yields complete multi-switching combination synchronization, and when \(0<\alpha _j,\beta _k > 1\), projective multi-switching combination anti-synchronization is achieved.

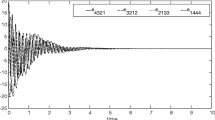
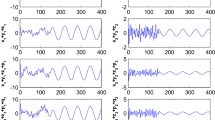
For switch 1, the control inputs given in Theorem 1 were programmed to turn on at time, \(t \ge 1\), simultaneously. The result is shown in Fig. 1, where we can see that multi-switching combination synchronization has clearly been achieved. Similar results were obtained using corollaries 1–3. In addition, Fig. 2 illustrates the temporal behavior of the synchronizing variables \(z_1,x_1+y_2\), \(z_2,x_1+y_3\), and \(z_3,x_1+y_1\) in the multi-switching compound synchronization state, with simultaneous activation of the controls at \(t \ge 25\). In Fig. 3, we illustrate the stabilization of the response system 12 to the equilibrium point \((0,0,0)\) on the application of Corollary 3.

Fig. 1
figure 1

Synchronization error for switch 1 with error states \(e_{112}\), \(e_{213}\), and \(e_{311}\). Control was activated at time, \(t \ge 1\). The parameters of the systems were chosen as \(a_1=0.2\), \(b_1=0.2\), \(c_1=5.7\), \(a_2=0.4\), \(b_2=0.175\), \(a_3=10.0\), \(b_3=23.0\) and \(c_3=8.0/3\)

Full size image
Fig. 2
figure 2

Temporal behavior of the synchronizing variables (a) \(z_1,(x_1+y_2)\), (b) \(z_2,(x_1+y_3)\), and (c) \(z_3,(x_1+y_1)\) in the multi-switching compound synchronization state, with simultaneous activation of the controls at \(t \ge 25\). The parameters of the systems were chosen as \(a_1=0.2\), \(b_1=0.2\), \(c_1=5.7\), \(a_2=0.4\), \(b_2=0.175\), \(a_3=10.0\), \(b_3=23.0\) and \(c_3=8.0/3\)

Full size image
Fig. 3
figure 3

Stabilization of state variables \(z_1,z_2,z_2\) of the Lorenz system, when the controllers in Corollary 3 were activated at time, \(t \ge 25\)

Full size image

For the other cases, namely switches 2,3 and 4, the control functions \(U_i(i=1,2,3)\) were programmed to turn on at different times, namely: \(t \ge 1.5\), for switch 2; \(t \ge 2\), for switch 3 and \(t \ge 1\), for switch 4, respectively. The numerical results corresponding to these cases are shown in Fig. 4. In all these cases, synchronization have been achieved.

Fig. 4
figure 4

Multi-switching synchronization error for switches 2, 3 and 4. The controllers were activated at different times, switch 2 at time \(t \ge 1.5\), Switch 3 at \(t \ge 2\) and Switch 4 at \(t \ge 1\). The error states are \(e_{112}\), \(e_{223}\), \(e_{321}\), \(e_{123}\), \(e_{213}\), \(e_{323}\), \(e_{113}\), \(e_{221}\), and \(e_{312}\)

Full size image

5 Conclusions

In summary, we have introduced, analyzed, and validated a novel form of chaotic synchronization that can involve three or more dynamical systems, namely multi-switching combination synchronization (MSCS) of three chaotic systems, based on the backstepping nonlinear control approach. In this new synchronization scheme, the state space variables of the three systems are multi-switched in different ways, such that their mutual synchronization takes place between different state variables. When synchronization is achieved in this manner in the communications context, it would be difficult or even impossible for an intruder to predetermine the vector space in which synchronization would occur, thereby enhancing information security. Numerical simulations using there the Lorenz, Newton-Leipnik and Rössler systems have verified the theories presented. This synchronization scheme is applicable to all chaotic systems, including those of higher order that exhibits hyperchaotic behavior. Higher-dimensional systems are attractive in this context because they present more switching options for constructing the error space vector due to the larger number of variables that are then available for this purpose. Finally, the present results pave way for new directions in the study of various kinds of chaotic synchronization. For instance, considering the uncertainties in system parameters, the possibilities of function scaling factors, parameter uncertainty and the effect of noise on such synchronization schemes would be interesting directions for future work.