Analysis of the effects of nonlinear viscous damping on vibration isolator

Abstract

In this paper, vibration isolator of single degree of freedom systems having a nonlinear viscous damping is studied under force excitation. Stability of the steady state periodic response has been discussed. The influence of damping coefficients on the force transmissibility and displacement transmissibility is investigated. The relationship between amplitude and frequency is derived by using the averaging method. Results reveal that the performance of the nonlinear isolator has some beneficial effects compared with linear isolator in a certain range. Numerical simulations are presented to illustrate the results.

1 Introduction

Vibration isolator is often inserted between the vibration source and the vibration receiver to reduce the unwanted vibrations so that the adverse effects are controlled within a specified range. Viscous damping is one of the most commonly used damping in a vibration isolator device. For linear viscous damping, increasing the linear viscous damping coefficient can reduce transmissibility in the resonant region, but this leads to the deterioration of isolation performance at high frequencies. This is a basically well-known dilemma associated with linear viscous damping systems. In order to resolve this problem, isolators with nonlinear damping have deserved more attention from researchers for years [2–9]. This is because all isolators in vibration systems are inherently nonlinear [1, 2], and the nonlinear damping has the potential in proving the isolator performance at both the resonance and the higher frequencies.

Milovanovic et al. [4] compared vibration isolators with linear and cubic nonlinearities in damping and stiffness terms under base excitation, it was shown that pure cubic damping has better performance if the damping parameter is smaller than a certain value. Lang [5, 6] proposed the concept of Output Frequency Response Function and theoretically discussed the effects of nonlinear viscous damping on vibration isolation of single degree of freedom systems. The results reveal that the cubic nonlinear viscous damping can produce an ideal vibration isolation such that only the resonant region is modified and the non-resonant regions remain unaffected. Peng et al. [7] investigated the performance of passive vibration isolators with cubic nonlinear damping using Harmonic Balance Method. They presented that either linear damping or cubic nonlinear damping could reduce the transmissibility over the resonance region and that the influence of the cubic nonlinear damping is dependent on the type of the disturbing force.

The present study is concerned with nonlinear damping which is a function of the displacement and velocity [10–14]. The vibration isolators with cubic nonlinear damping under both force and base excitations have been analyzed by Xiao et al. [13]. They pointed out that the cubic-order nonlinear damping can improve the transmissibility. Sun et al. [14] investigated the vibration isolators with geometric nonlinear damping, and the results show that this kind of damping has advantages in improving isolation performance at both resonance and higher frequencies when the velocity exponent is limited to a certain range.

Stability is a very important aspect in the vibration system, it has a significant impact on the performance of the system. Jazar et al. [15] analyzed the stability of frequency response of a nonlinear passive vibration isolator system by using perturbation method. Zhang et al. [16, 17] obtained the uniform stabilization of wave equation with dissipative term and boundary damping by using multiplier technique.

In the engineering applications, both displacement exponent and velocity exponent are not always fixed constants, they may be arbitrary positive values. Therefore, it is necessary to discuss the general case of viscous damping. In this article, a single degree of freedom (SDOF) vibration isolation system with $n\hbox {th}$ power viscous damping is investigated. Stability of the steady state periodic response has been discussed. The influence of damping coefficients on the transmissibility is studied, and the equation described amplitude and frequency is obtained. Simulation results are provided to illustrate the results.

2 Theoretical analysis

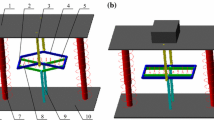
A nonlinear SDOF system, as shown in Fig. 1, is investigated, where $M$ and $m$ are the mass of the base and the body. The harmonic force

$$\begin{aligned} f(t)=Y\omega ^{2}\sin \omega t \end{aligned}$$

(1)

is directly exerted on the base $M$ with excitation amplitude $Y$ and frequency $\omega$. The isolator is modeled as a parallel combination of a linear spring with stiffness $k$ and a damper. The damping force with cubic damping can be written that it is proportional to the product of the square of the displacement and the velocity [11]. Using this transformation, general case can be investigated. In this paper, The damping is given using the viscous damping laws expressed as [9]

$$\begin{aligned} f_{d}(t)=c\left( {1+z}\right) ^{n}\dot{z} \end{aligned}$$

(2)

where $c$ is the damping coefficient, $z=y-x$ is the relative displacement, and $n$ is a nonnegative coefficient representing different damping laws. A linear damping law is introduced when $n=0$, and in other cases, the damping is nonlinear.

Fig. 1

A vibration isolator system subjected to force excitation

The equation of motion of the isolation system with respect to the relative displacement $z$ is given by

$$\begin{aligned}&{M\ddot{y} +kz+c(1+z)^{n}\dot{z} =Y\omega ^{2}\sin \omega t} \nonumber \\&m{\ddot{x} -kz-c(1+z)^{n}\dot{z} =0} \end{aligned}$$

(3)

where overdots denote derivatives with respect to time $t$. Eliminate the variable $x$ and $y$ in Eq. (3). We have

$$\begin{aligned} \ddot{z} +\frac{M+m}{Mm}[c(1+z)^{n}\dot{z} +kz]=\frac{Y}{M}\omega ^{2}\sin \omega t \end{aligned}$$

(4)

Introducing the following dimensionless parameters:

$$\begin{aligned} u&= z,\quad \omega _{0}=\sqrt{\frac{k}{\mu }},\quad \varOmega =\frac{\omega }{\omega _{0}},\quad \tau =\omega _{0}t \nonumber \\ \xi&= \frac{c}{2\omega _{0}\mu },\quad \mu =\frac{Mm}{M+m},\quad A=\frac{Y}{M} \end{aligned}$$

(5)

Equation (4) becomes

$$\begin{aligned} u^{{\prime }{\prime }}+2\xi (1+u)^{n}u^{{\prime }}+u=A\varOmega ^{2}\sin (\varOmega \tau ) \end{aligned}$$

(6)

In order to obtain an approximate solution of Eq. (6), the averaging method is used [4]. The solution is assumed to be of the form

$$\begin{aligned} u(\tau )=\alpha (\tau )\sin \left( {\varphi (\tau )}\right) \end{aligned}$$

(7)

with

$$\begin{aligned} \varphi (\tau )=\varOmega \tau +\psi (\tau ) \end{aligned}$$

(8)

where $\alpha$ is the amplitude of the relative motion, and $\psi$ is the phase.

The first derivative of Eq. (8) with respect to the time has the form

$$\begin{aligned} u^{{\prime }}=\alpha (\tau )\varOmega \cos (\varphi \left( \tau \right) ) \end{aligned}$$

(9)

differentiating Eq. (7) with respect to time, and comparing with Eq. (9), the constraint can be obtained as follows

$$\begin{aligned} \alpha ^{{\prime }}\sin \varphi +\alpha \psi ^{{\prime }}\cos \varphi =0 \end{aligned}$$

(10)

The derivative of Eq. (9) is

$$\begin{aligned} u^{{\prime }{\prime }}=\varOmega \alpha ^{{\prime }}\cos \varphi -\varOmega \alpha \left( {\varOmega +\psi ^{{\prime }}}\right) \sin \varphi \end{aligned}$$

(11)

Substituting for Eqs. (7), (9) and (11) in Eq. (6) yields

$$\begin{aligned}&\varOmega \alpha ^{{\prime }}\cos \varphi +2\xi \varOmega \alpha \left( {1+\alpha \sin \varphi }\right) ^{n}\cos \varphi \nonumber \\&\qquad -\,\varOmega \alpha \left( {\varOmega +\psi ^{{\prime }}}\right) \sin \varphi +\alpha \sin \varphi =A\varOmega ^{2}\sin (\varOmega \tau )\nonumber \\ \end{aligned}$$

(12)

Using Eq. (10) to eliminate $\psi ^{{\prime }}$ in Eq. (12) and simplify it to the following equations:

$$\begin{aligned} \varOmega \alpha ^{{\prime }}&= -\left[ \alpha \left( {1-\varOmega ^{2}}\right) \sin \varphi \right. \nonumber \\&\quad +\,2\xi \varOmega \alpha \left( {1+\alpha \sin \varphi }\right) ^{n}\cos \varphi \nonumber \\&\quad \left. -\,A\varOmega ^{2}\sin \left( {\varOmega \tau }\right) \right] \cos \varphi \end{aligned}$$

(13)

$$\begin{aligned} \varOmega \alpha \psi ^{{\prime }}&= \left[ \alpha \left( {1-\varOmega ^{2}}\right) \sin \varphi -A\varOmega ^{2}\sin \left( {\varOmega \tau }\right) \right. \nonumber \\&\quad \left. +\,2\xi \varOmega \alpha \left( {1+\alpha \sin \varphi }\right) ^{n}\cos \varphi \right] \sin \varphi \end{aligned}$$

(14)

Averaging the right-hand sides of Eqs. (13) and (14) over a period of $2\pi$:

$$\begin{aligned} \varOmega \alpha ^{{\prime }}&= -\frac{1}{2\pi }\int _{0}^{2\pi } \left[ \alpha \left( {1-\varOmega ^{2}}\right) \sin \varphi \right. \nonumber \\&\quad +\,2\xi \varOmega \alpha \left( {1+\alpha \sin \varphi }\right) ^{n}\cos \varphi \nonumber \\&\quad \left. -\,A\varOmega ^{2}\sin \left( {\varOmega \tau }\right) \right] \cos \varphi d\varphi \end{aligned}$$

(15)

$$\begin{aligned} \varOmega \alpha \psi ^{{\prime }}&= \frac{1}{2\pi }\int _{0}^{2\pi } \left[ \alpha \left( {1-\varOmega ^{2}}\right) \sin \varphi \right. \nonumber \\&\quad -\,A\varOmega ^{2}\sin \left( {\varOmega \tau }\right) \nonumber \\&\quad \left. +\,2\xi \varOmega \alpha \left( {1+\alpha \sin \varphi }\right) ^{n}\cos \varphi \right] \sin \varphi d\varphi \end{aligned}$$

(16)

For the purpose of reducing calculation amount, $n$ is constrained to a positive integer. Then, Eqs. (15) and (16) can be rewritten as the following form:

$$\begin{aligned}&\varOmega \alpha ^{{\prime }}=-\frac{1}{2\pi }\left[ {A\pi \varOmega ^{2}\sin \psi +2\xi \varOmega \alpha S_{n}}\right] \end{aligned}$$

(17)

$$\begin{aligned}&\varOmega \alpha \psi ^{{\prime }}=\frac{1}{2\pi }\left[ {\alpha \left( {1-\varOmega ^{2}}\right) \pi -A\pi \varOmega ^{2}\cos \psi }\right] \end{aligned}$$

(18)

where

$$\begin{aligned} S_{n}=\sum _{k=0}^{n}{C_{n}^{k}\alpha ^{k}B\left( {\frac{k+1}{2}, \frac{3}{2}}\right) } \left[ {1+\left( {-1}\right) ^{k}}\right] \end{aligned}$$

(19)

and $B$ stands for Bata function.

The steady state response, defined by $\alpha ^{{\prime }}=\varphi ^{{\prime }}=0$, is found to satisfy

$$\begin{aligned}&A\pi \varOmega ^{2}\sin \psi +2\xi \varOmega \alpha S_{n}=0 \end{aligned}$$

(20)

$$\begin{aligned}&\alpha \left( {1-\varOmega ^{2}}\right) \pi -A\pi \varOmega ^{2}\cos \psi =0 \end{aligned}$$

(21)

Combining Eqs. (20) and (21) gets the implicit amplitude–frequency equation

$$\begin{aligned} 4\xi ^{2}\varOmega ^{2}\alpha ^{2}S_{n}^{2}+\alpha ^{2}\pi ^{2} \left( {1-\varOmega ^{2}}\right) ^{2}=A^{2}\pi ^{2}\varOmega ^{4} \end{aligned}$$

(22)

3 Stability of periodic response

Stability of stationary oscillations plays an important role in the vibration system, especially for high-frequency oscillatory processes. Using the approach [15], the stability of frequency response is discussed. A very small displacement $e(\tau )$ is used to the steady state solution. The form is

$$\begin{aligned} u\left( \tau \right) =u_{0}\left( \tau \right) +e\left( \tau \right) \end{aligned}$$

(23)

where $u_{0}$ is the periodic solution of the dimensionless equation of system. Inserting Eqs. (23) into (6) yields

$$\begin{aligned}&\left( {u_{0}+e}\right) ^{{\prime }{\prime }}+2\xi \left[ {1+\left( {u_{0}+e}\right) }\right] ^{n}\left( {u_{0}^{\prime } +e^{{\prime }}}\right) \nonumber \\&\quad +\,u_{0}+e=A\varOmega ^{2}\sin \left( {\varOmega \tau }\right) \end{aligned}$$

(24)

Since $e$ and $e^{{\prime }}$ are assumed to be very small, the nonlinearities can be neglected. The simplified equation can be produced as follows

$$\begin{aligned}&e^{{\prime }{\prime }}+2\xi \left( {1+\alpha \sin \varphi }\right) ^{n}e^{{\prime }}\nonumber \\&\quad +\left[ {1+2\xi n\alpha \varOmega \cos \varphi \left( {1+\alpha \sin \varphi }\right) ^{n-1}}\right] e=0 \end{aligned}$$

(25)

Time is shifted by $\psi /\varOmega$, and the form of $e$ can be assumed as follows

$$\begin{aligned} e\left( \tau \right) =D\sin \left( {\varOmega \tau }\right) +B\cos \left( {\varOmega \tau }\right) \end{aligned}$$

(26)

Substituting Eqs. (26) in (25) produces

$$\begin{aligned}&-D\varOmega ^{2}\sin \left( {\varOmega \tau }\right) -B\varOmega ^{2}\cos \left( {\varOmega \tau }\right) \nonumber \\&\quad +\,2\xi \left( {\sum _{k=0}^{n}{C_{n}^{k}\alpha ^{k}\sin ^{k} \left( {\varOmega \tau }\right) } }\right) \left( D\varOmega \cos \left( {\varOmega \tau }\right) \right. \nonumber \\&\left. \quad -B\varOmega \sin \left( {\varOmega \tau }\right) \right) \nonumber \\&\quad +\left[ {2\xi n\alpha \varOmega \cos \left( {\varOmega \tau }\right) \left( {\sum _{k=0}^{n-1} {C_{n-1}^{k}\alpha ^{k}\sin ^{k}\left( {\varOmega \tau }\right) } }\right) +1}\right] \nonumber \\&\quad \times \left( D\sin \left( {\varOmega \tau }\right) \right. \nonumber \\&\left. \quad +\,B\cos \left( {\varOmega \tau }\right) \right) =0 \end{aligned}$$

(27)

Neglecting the coefficients of $\sin k\varOmega \tau$ and $\cos k\varOmega \tau$ when $k\ge 2$, Eq. (27) is rewritten as

$$\begin{aligned}&\left[ D-D\varOmega ^{2}+2B\xi \varOmega \left( {1+\sum _{j=1}^{\left[ {\frac{n}{2}}\right] } {C_{n}^{2j} \alpha ^{2j}\frac{1}{2^{2j}}\left( {C_{2j}^{j}+C_{2j}^{j-1} }\right) }}\right) \right. \nonumber \\&\quad \left. +B\xi n\alpha \varOmega \sum _{j=0}^{\left[ {\frac{n-2}{2}}\right] } {C_{n-1}^{2j+1} \alpha ^{2j+1}\frac{1}{2^{2j+1}}\left( {C_{2j+1}^{j}-C_{2j+1}^{j-1}} \right) } \right] \sin (\varOmega \tau ) \nonumber \\&\quad +\left[ B-B\varOmega ^{2}+2D\xi \varOmega \left( {1+\sum _{j=1}^{\left[ {\frac{n}{2}}\right] } {C_{n}^{2j} \alpha ^{2j}\frac{1}{2^{2j}}\left( {C_{2j}^{j}-C_{2j}^{j-1} }\right) }} \right) \right. \nonumber \\&\quad \left. +\,D\xi n\alpha \varOmega \sum _{j=0}^{\left[ {\frac{n-2}{2}}\right] } {C_{n-1}^{2j+1} \alpha ^{2j+1}\frac{1}{2^{2j+1}}\left( {C_{2j+1}^{j}-C_{2j+1}^{j-1}} \right) } \right] \cos (\varOmega \tau ) \nonumber \\&\quad +\,2B\xi \varOmega \sum _{j=0}^{\left[ {\frac{n-1}{2}}\right] } C_{n}^{2j+1} U^{2j+1}\frac{1}{2^{2j+1}}\nonumber \\&\quad +\, B\xi n\alpha \varOmega \left[ {1+\sum _{j=1}^{\left[ {\frac{n-1}{2}}\right] } {C_{n-1}^{2j} \alpha ^{2j}\frac{1}{2^{2j}}\left( {C_{2j}^{j}-C_{2j}^{j-1}}\right) }} \right] \nonumber \\&\quad =0 \end{aligned}$$

(28)

This will produce the following algebraic equations from the above equation

$$\begin{aligned}&\left( {1-\varOmega ^{2}}\right) D\nonumber \\&\quad +\left[ 2\xi \varOmega \left( {1+\sum _{j=1}^{\left[ {\frac{n}{2}}\right] } {C_{n}^{2j} \alpha ^{2j}\frac{1}{2^{2j}}\left( {C_{2j}^{j}+C_{2j}^{j-1} }\right) } }\right) \right. \nonumber \\&\quad \left. +\,\xi n\alpha \varOmega \sum _{j=0}^{\left[ {\frac{n-2}{2}}\right] } {C_{n-1}^{2j+1} \alpha ^{2j+1}\frac{1}{2^{2j+1}}\left( {C_{2j+1}^{j}-C_{2j+1}^{j-1}} \right) }\right] B \nonumber \\&\quad =0\nonumber \\&\quad \left[ 2\xi \varOmega \left( {1+\sum _{j=1}^{\left[ {\frac{n}{2}}\right] } {C_{n}^{2j} \alpha ^{2j}\frac{1}{2^{2j}}\left( {C_{2j}^{j}-C_{2j}^{j-1} }\right) }} \right) \right. \nonumber \\&\quad \left. +\,\xi n\alpha \varOmega \sum _{j=0}^{\left[ {\frac{n-2}{2}}\right] } {C_{n-1}^{2j+1} \alpha ^{2j+1}\frac{1}{2^{2j+1}}\left( {C_{2j+1}^{j}-C_{2j+1}^{j-1} }\right) } \right] D\nonumber \\&\quad +\,\left( {1-\varOmega ^{2}}\right) B=0 \nonumber \\&\quad \left[ 2\xi \varOmega \sum _{j=0}^{\left[ {\frac{n-1}{2}}\right] } C_{n}^{2j+1} \alpha ^{2j+1}\frac{1}{2^{2j+1}}\right. \nonumber \\&\quad \left. +\, \xi n\alpha \varOmega \left[ {1+\sum _{j=1}^{\left[ {\frac{n-1}{2}}\right] } {C_{n-1}^{2j} \alpha ^{2j}\frac{1}{2^{2j}}\left( {C_{2j}^{j}-C_{2j}^{j-1} }\right) }} \right] \right] B=0\nonumber \\ \end{aligned}$$

(29)

where $[n]$ represents the largest positive integer less than $n$.

Since $C_{2j}^{j}-C_{2j}^{j-1} >0$, it can be got $B=0$ from the third equation of Eq. (29). Substituting the result of $B=0$ into rest equations of Eq. (29), $D=0$ is obtained.

Through the above analysis, the conclusion can be drawn that the periodic solution of the dimensionless equation of motion is stable.

4 The force and displacement transmissibility

In order to understand the effects of different nonlinear viscous damping characteristics on the transmissibility of SDOF vibration isolation system, in this section, the force transmissibility and force-displacement transmissibility will be developed.

From Eqs. (3) and (7), variables $\frac{d^{2}x}{d\tau ^{2}}$ and $x(\tau )$ can be got. Assuming that initial conditions are $x(0)=0$ and $x^{{\prime }}(0)=0$, then

$$\begin{aligned} \frac{\hbox {d}^{2}x}{\hbox {d}\tau ^{2}}&= \frac{M}{M+m}\left( {A\varOmega ^{2}\sin (\varOmega \tau )-\frac{\hbox {d}^{2}u}{\hbox {d}\tau ^{2}}}\right) \end{aligned}$$

(30)

$$\begin{aligned} x(\tau )&= -\frac{M}{M+m}\left( {A\sin \left( {\varOmega \tau }\right) +\alpha \sin \left( {\varOmega \tau +\psi }\right) }\right) \end{aligned}$$

(31)

The force transmissibility $T_{ff}$ can be expressed as

$$\begin{aligned} T_{ff}&= \frac{\max \left| {m\omega _{0}^{2} \frac{\hbox {d}^{2}x}{\hbox {d}\tau ^{2}}} \right| }{Y\omega ^{2}} \nonumber \\&= \frac{m}{A(M+m)}\sqrt{\alpha ^{2}+A^{2}+2\alpha ^{2} \varOmega ^{-2}(1-\varOmega ^{2})}\nonumber \\ \end{aligned}$$

(32)

The force-displacement transmissibility $T_{fd}$ can be defined as follows

$$\begin{aligned} T_{fd}&= \frac{\max \left| {x(\tau )} \right| }{Y\omega ^{2}} \nonumber \\&= \frac{1}{A\varOmega ^{2}\omega _{0}^{2}(M+m)} \sqrt{\alpha ^{2}+A^{2}+2\alpha ^{2}\varOmega ^{-2}(1-\varOmega ^{2})} \nonumber \\ \end{aligned}$$

(33)

The relationship between force transmissibility $T_{ff}$ and force-displacement transmissibility $T_{fd}$ can be derived from Eqs. (32) and (33), and $T_{fd} =\frac{m}{\varOmega ^{2}\omega _{0}^{2}}T_{ff}$. It is obviously that once characteristics of $T_{ff}$ have been obtained, it is unnecessary to pay much attention to discuss $T_{fd}$. In the following part, $T_{ff}$ will be focused on.

5 Simulation results and discussions

In this section, we present the effects of nonlinear viscous damping on vibration isolation, which have been theoretically analyzed above. Numerical simulation studies are conducted for the dimensionless; the figures will reveal how the transmissibility $T_{ff}$ changes with the linear and nonlinear viscous damping characteristic parameters $\xi$, $n$ and $\varOmega$.

Figure 2a shows the force transmissibility in four linear viscous damping cases of $\xi =0.1,0.4,0.7,1.0$. This is a well-known result that the peaks of transmissibility appear near the $\varOmega =1$. An increase of the linear viscous damping characteristic parameter $\xi$ can decrease transmissibility and suppress the vibration at the resonant frequency; however, the results are poor for vibration isolation at high-frequency region with the increase of $\xi$.

Fig. 2

a Force transmissibility $T_{ff}$ and b force-displacement transmissibility $T_{fd}$ with $n=0$ and $m=M=A=1$. In figures: solid line, $\xi =0.1$; plus, $\xi =0.4$; asterisk, $\xi =0.7$; dashed-dashed line $\xi =1.0$

Figure 3a represents the force transmissibility for the isolator subjected to the force excitation under different nonlinear damping coefficients when $n=2$. It is shown that the force transmissibility has been significantly suppressed over the resonant frequency when viscous damping characteristic parameter $\xi$ increases, but the force transmissibility at high frequency is dramatically deteriorated compared with that the damping coefficient $\xi =0.1$. The performance deteriorated at high frequency illustrates that value of $\xi$ selected should not be too large.

Fig. 3

a Force transmissibility $T_{ff}$ and b force-displacement transmissibility $T_{fd}$ with $n=2$ and $m=M=A=1$. In figures: solid line, $\xi =0.1$; plus, $\xi =0.4$; asterisk, $\xi =0.7$; dashed-dashed line, $\xi =1.0$

In Fig. 4a, the force transmissibility is plotted for different values of $n$ when $\xi =0.1$. It can be seen that as $n$ increases, the force transmissibility has been significantly suppressed over the resonant frequency. But the performance at high frequencies becomes worse. To compare the performance of the viscous nonlinear damping and the linear damping $(n=0)$, it can be observed when the frequency exceeds a threshold, linear damping has better performance than nonlinear, the transmissibility of the nonlinear damping is larger than the linear as $\varOmega$ increases. From the figure, it can be observed that when $n=2$, the difference between linear and nonlinear is very small at high frequency, Therefore, if the frequency range is wide, the case $n\le 2$ can be considered in vibration isolation, it may perform better than linear damping.

Fig. 4

a Force transmissibility $T_{ff}$ and b force-displacement transmissibility $T_{fd}$ with $\xi =0.1$ and $m=M=A=1$. In figures: solid line, $n=0$; plus, $n=2$; asterisk, $n=4$; dashed-dashed line, $n=6$

Figure 5a shows how the force transmissibility changes with respect to $\xi$ and $n$, when $\varOmega =10$. Force transmissibility increases with $\xi$ and $n$ in positive correlation. Hence, in order to obtain a better performance at high frequencies, $\xi$ and $n$ should be selected as small as possible. 5(b) plots the case that $\varOmega =50$, the relationship between transmissibility and $\xi$, and $n$ is similar to Fig. 5a.

Fig. 5

a Force transmissibility $T_{ff}$ at $\varOmega =10$ and b $T_{ff}$ at $\varOmega =50$ varying with damping coefficient $\xi$ (from 0.1 to 3.1, step 0.2) and nonnegative coefficient $n$ (from 0 to 6, step 1)

Based on Eqs. (17) and (18), for specific parameters $n$, $\varOmega$ and $\xi$, the relationship between force transmissibility and non-dimensional variable $\tau$ can be derived. In Fig. 6a, b, the effects of the nonlinear damping force on the time history response curves of the force transmissibility at two different excitation frequencies are evident. Initially, force transmissibility fluctuates greatly, but it tends to be a constant value as time $\tau$ increases. Compared with low frequency $(\varOmega =0.5)$, high frequency $(\varOmega =3)$ takes less time to be stable values. Under the two differently frequencies, force transmissibility changes different with $\xi$. When $\varOmega =0.5$, as time $\tau$ goes on, force transmissibility increases with $\xi$ in negative correlation, that is the opposite of $\varOmega =3$.

Fig. 6

Time history response curves for the force transmissibility of the nonlinear isolator at a $\varOmega =0.5$, b $\varOmega =3$ with $n=2$ and $m=M=A=1$. In figures: solid line, $\xi =0.1$; plus, $\xi =0.4$; asterisk, $\xi =0.7$; dashed-dashed line, $\xi =1.0$

6 Conclusion

In this article, stability of the frequency response has been investigated. The force and displacement transmissibility of nonlinear damping vibration isolation system have been considered. Through theoretical analysis and numerical simulations, it is found that compared with linear damping in the resonance region, nonlinear damping has a beneficial response, but the performance becomes very poor at high frequencies when exponent $n$ and damping coefficient $\xi$ increase. It can be concluded that in order to achieve efficient performance for force excitation, it is better to choose a relatively small number of combinations of the damping parameter and exponent, i.e., if the frequency range is wide, the value of $n$ should be selected less than 2, otherwise, it has detrimental effect on the transmissibility in the high-frequency region.