Fast projective synchronization of fractional order chaotic and reverse chaotic systems with its application to an affine cipher using date of birth (DOB)

Abstract

In this paper, a fractional order dynamical system is constructed that exhibits chaotic and reverse chaotic attractors by changing the sign of the one parameter which involves in the existence of the phase reversal function. A new method of fast projective synchronization of fractional order dynamical systems is introduced. An affine cipher is proposed for secure communication based on the solutions of the synchronized fractional order chaotic systems with the support of the sender’s and receiver’s date of birth. The efficiency and security of an affine cipher are analyzed. Numerical simulations are demonstrated to show the feasibility of the presented theory.

1 Introduction

Fractional calculus is a mathematical issue with more than 300-year-old history, and it has been known since the work of Leibniz and L’Hopital in 1695. Recently, the study of fractional order differential systems has greatly attracted the interest of many researchers due to the applications in science and engineering. It has been proven that many systems in different disciplines could be described by fractional differential equations such as viscoelastic [1], diffusion [2], dynamo theory [3], dengue fever [4], and chemical processing [5]. Chaotic phenomena in fractional order dynamical systems become an important theme of study in nonlinear dynamics. Chaotic behaviors have been found in certain long familiar fractional order dynamical systems such as Lorenz system [6], Rössler system [7] and Lü system [8].

In the fractional field, to find a minimum effective dimension for retaining chaos in a fractional order dynamical system is an important problem. Another challenge that to analyze stability theory, the method of constructing chaos control and synchronization are also equally important. Synchronization of chaotic systems means two or more chaotic systems share a mutual dynamical behavior. A method of synchronization between two identical chaotic systems with different initial conditions has been introduced by Pecora and Carroll [9]. Recently, fractional order chaotic and synchronization of fractional order chaotic systems have been started to attract increasing attention among researchers due to its potential applications in secure communication, circuit theory, and control processing see [3, 10–13]. Some investigations have been dedicated in [14, 15] for achieving stability and stabilization of fractional order systems.

Lately, several techniques have been applied for synchronizing fractional order chaotic systems such as adaptive method [16], phase synchronization [17], nonlinear control technique [18], impulsive [19], sliding mode approach [20], and projective synchronization [21–24]. Among the various types of chaos synchronization, projective synchronization (PS) has received much attention due to its faster communication with proportional feature. PS is qualified that the master system and the slave system could be synchronized up to a scaling factor. The unpredictability of the scaling function in PS can additionally strengthen the security of communication, so this feature could be utilized to get more secure communication in practical application, see [24, 25].

Inspired by the above discussions, in this paper, a fractional order dynamical system is modified. The dynamical behaviors of the modified fractional order system are investigated analytically and numerically. It has phase reversed by changing the sign of the one parameter, and the system exhibits reverse chaotic attractor. A new fast projective synchronization (FPS) method is described for synchronizing fractional order dynamical systems and applied for fractional order chaotic and reverse chaotic systems. It is shown that there is no synchronization error that exists between the fractional order dynamical systems by using the proposed FPS. That is, the synchronization error is zero for every time $t\ge 0$. These synchronized systems are utilized into a novel secured affine cipher for sharing text and image secretly. At the first time, the affine cipher key can be consider as a combination of date of birth (DOB) and the solutions of the derived synchronized fractional order chaotic systems in the proposed affine cipher. Also, the level of security and efficiency of the proposed affine cipher are discussed. Finally, the higher-level security is obtained for the proposed affine cipher due to the hardness of fractional order system and DOB keys.

The outline of this paper is organized as follows: Some basic preliminaries of fractional calculus are presented in Sect. 2. In Sect. 3, a fractional order dynamical system is constructed and their particular cases are discussed. Basic dynamical properties of the modified fractional order system are analyzed in Sect. 4. The FPS of fractional order dynamical systems is investigated by analytically and numerically in Sect. 5. Section 6 is devoted to the application of the synchronized fractional order chaotic systems. The conclusions are finally drawn in Sect. 7.

2 Preliminaries

In this section, a mathematical definition of fractional derivative, some important theorems, and definitions will be presented.

Even though several definitions for fractional derivatives exist such as Riemann–Liouville definition, Caputo definition, and Grunwald–Letnikov definition, we use the following Caputo’s derivative since it has the traditional initial conditions.

Definition 1

([28]) The Caputo fractional derivative is defined as

$$\begin{aligned} D^{q}f(t)=\frac{1}{\varGamma (n-q)}\int \limits _a^t (t-\tau )^{-q+n-1}f^{(n)}(\tau )\hbox {d}\tau , \end{aligned}$$

(1)

where $n=[q]+1,\,[q]$ is the integer part of $q,\,\varGamma (\cdot )$ is the gamma function and $D^q$ is called the $q$-order Caputo differential operator.

Theorem 1

([29]) For a given fractional order autonomous system

$$\begin{aligned} D^qx(t)=Ax(t),\quad x(0)=x_0, \end{aligned}$$

(2)

where $0<q<1,\,x\in \mathbb {R}^n$ and $A\in \mathbb {R}^{n\times n}$. Then the fractional order system (2) is asymptotically stable if and only if

$$\begin{aligned} |\arg (\mathrm{eig}(A))|>\frac{q\pi }{2}. \end{aligned}$$

(3)

In this case, the component of the state decay toward 0 like $t^{-q}$.

Definition 2

([30]) An equilibrium point $E$ of the system (2) is called a saddle point of index 1 (index 2) if the Jacobian matrix $J$ at $E$ has one (two) unstable eigenvalue(s).

Theorem 2

([30]) A necessary condition for the system (2) to remain chaotic is keeping at least one eigenvalue $\lambda$ in the unstable region. This means that

$$\begin{aligned} q>\frac{2}{\pi }\ \arctan \left( \frac{|Im(\lambda )|}{Re(\lambda )}\right) . \end{aligned}$$

(4)

3 Description of a 3D modified fractional order chaotic system

Recently, a new chaotic attractor has been introduced and their dynamical behaviors have been studied in [26] for the following

$$\begin{aligned} \dot{x}(t)&= -ax+fyz,\nonumber \\ \dot{y}(t)&= cy-dxz,\nonumber \\ \dot{z}(t)&= -bz+ey^2, \end{aligned}$$

(5)

where $(x,y,z)\in \mathbb {R}^3, a,b,c,d,e,f$ are the parameters of the system (5). It has found that, the system (5) exhibits chaos when $a=16,b=5,c=10,d=6,e=18$ and $f=0.5$.

The following fractional order form of the system (5) has been introduced in [27], and its dynamical behaviors have been investigated for the above parameter values

$$\begin{aligned} D^{q}x(t)&= -ax+fyz, \nonumber \\ D^{q}y(t)&= cy-dxz,\nonumber \\ D^{q}z(t)&= -bz+ey^2. \end{aligned}$$

(6)

Further, the authors in [27] found that the fractional order system (6) exhibits chaos when a fractional order $q\ge 0.95$ and has been synchronized via adaptive sliding mode control.

Remark 1

For the system (6), replacing the nonlinear term $y^2$ by $xy$ and fixing the parameters $f=-1,d=-1,e=1,$ we found the following simulations hold for $q=1$.

• 1. If $a=-5,b=3.83$and $c=-10$, then the attractor is similar to the Lorenz attractor [32], which is depicted in Fig. 1.

• 2. If $a=-5,b=3.4$ and $c=-10$, then the attractor is similar to the Chen’s attractor [33], which is depicted in Fig. 2.

Remark 2

The Euler equations for motion of a 3D rigid body with principle axes at the center of mass is described by [34]

$$\begin{aligned}&I_{xx}\dot{w}_x =(I_{yy}-I_{zz})w_yw_z+M_x,\nonumber \\&I_{yy}\dot{w}_y =(I_{zz}-I_{xx})w_zw_x+M_y,\nonumber \\&I_{zz}\dot{w}_z =(I_{xx}-I_{yy})w_xw_y+M_z, \end{aligned}$$

(7)

where $w_x,w_y,w_z$ are the angular velocities of the spindle, $I_{xx},I_{yy},I_{zz}$ are the main moments of inertia, and $M_x,M_y,M_z$ are applied moments. We take the applied moments are the linear feedback of the angular velocities, let it be $M_x=l_{11}w_x,M_y=l_{22}w_y$ and $M_z=l_{33}w_z$.

Define $w_x=x,w_y=y$ and $w_z=z$, then the system (7) can be written as

$$\begin{aligned} \dot{x}&= \frac{I_{yy}-I_{zz}}{I_{xx}}yz+\frac{l_{11}}{I_{xx}}x,\nonumber \\ \dot{y}&= \frac{I_{zz}-I_{xx}}{I_{yy}}xz+\frac{l_{22}}{I_{yy}}y,\nonumber \\ \dot{z}&= \frac{I_{xx}-I_{yy}}{I_{zz}}xy+\frac{l_{33}}{I_{zz}}z, \end{aligned}$$

(8)

If $I_{zz}=3I,I_{yy}=I,I_{xx}=2I,\frac{l_{11}}{I_{xx}}=5,\frac{l_{22}}{I_{yy}}=-10$ and $\frac{l_{33}}{I_{zz}}=-3.8$, then the system (8) behave chaos, which is represented in Fig. 3.

Substitute $\frac{I_{yy}-I_{zz}}{I_{xx}}=f, \frac{I_{zz}-I_{xx}}{I_{yy}}=-d,\frac{I_{xx}-I_{yy}}{I_{zz}}=e,\frac{l_{11}}{I_{xx}}=-a, \frac{l_{22}}{I_{yy}}=c, \frac{l_{33}}{I_{zz}}=b$ and replace $xy$ by $y^2$ in (8), then the Euler equation of motion (8) is equivalent to the system (6) with fractional order $q$. Hence, the fractional order system (6) is more generalization of the integer order Lorenz, Chen’s and the Euler equations for motion.

Fig. 1

Lorenz-like attractor

Fig. 2

Chen’s-like attractor

Fig. 3

Strange attractor

In order to reduce the minimum effective dimension and the synchronization error, a parameter $f$ should be replaced by a parameter $a$ of an existing fractional order system (6). Now, the modified fractional order system (6) is described by

$$\begin{aligned} D^{q}x(t)&=-a(x-yz),\nonumber \\ D^{q}y(t)&=cy-dxz,\nonumber \\ D^{q}z(t)&=-bz+ey^2, \end{aligned}$$

(9)

where $D^{q}$ denotes the Caputo fractional operator defined in [28], $0<q<1, (x,y,z)\in \mathbb {R}^3$ are state variables and $a,b,c,d,e$ are the parameters of the modified system (9).

Now, we have fixed the parameters $a=18,b=5,c=10,d=6$ and $e=18$. For these fixed parameter values, the integer order ($q=1$) of the modified system (9) exhibits chaos with the Lyapunov exponents $L_1=1.3424 >0, L_2=0$ and $L_3=-14.3447<0$. The chaotic attractor corresponding to the integer order system (9) is depicted in Fig. 4. The basic dynamical properties of the proposed system (9) will be analyzed in the following section.

Fig. 4

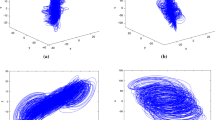
Different phase portraits of the modified system (9) with $q=1$

4 Analysis of dynamical properties

In this section, some basic dynamical properties of the system (9) are analyzed. Throughout this manuscript, we consider the value of the parameters of the system (9) are $a=18,b=5,c=10,d=6$ and $e=\pm 18$. We will start with equilibria of the system (9).

The equilibrium points of the system (9) can be obtained by solving the equations

$$\begin{aligned} -a(x-yz)=0\nonumber \\ cy-dxz=0\nonumber \\ -bz+ey^2=0 \end{aligned}$$

(10)

The system of equations (10) has three equilibrium points for the above parameter values. If $e=18$, then the three equilibrium points are $O=(0,0,0)$, $E_+=(0.7731,0.5988,1.2910)$ and $E_-=(-0.7731,-0.5988,1.2910)$. If $e=-18$, then the three equilibrium points are $O=(0,0,0), F_+=(0.7731,0.5988,-1.2910)$ and $F_-=(-0.7731, -0.5988,-1.2910)$.

4.1 Symmetry, invariance, and phase reversal

The system (9) has a natural symmetry under the transformation $(x,y,z)\rightarrow (-x,-y,z)$ based on equilibria. But the invariance of the system (9) under the coordinate transformation is $(x,y,z,a,b,c,d,e)\rightarrow (-x,y,-z,a,b,c,d,-e)$. Hence, the phase reversal function exists for parameter $e$. That is, the polarity of signals $x,z$ changes only with parameter e. It is displayed in Fig. 5.

Fig. 5

The time series for $x(t),y(t),z(t)$ for $e=18$ and $e=-18$

4.2 Dissipation

The dynamical system is called dissipative if

$$\begin{aligned} \nabla \cdot V=\frac{\partial \dot{x}}{\partial x}+\frac{\partial \dot{y}}{\partial y}+\frac{\partial \dot{z}}{\partial z} <0. \end{aligned}$$

(11)

In that case of system (9), $\nabla \cdot V = -a+c-b=-13<0$. Therefore, the dissipative condition holds for the system (9). Further, the exponential contraction rate of the system (9) is

$$\begin{aligned} \frac{\hbox {d}V}{\hbox {d}t}=e^{(-a+c-b)t}=e^{-13t}. \end{aligned}$$

(12)

4.3 Stability and chaos

The stability of the system based on the eigenvalues, which are determined through the evaluation of the Jacobian matrix of the system (9).

For equilibrium $O(0,0,0)$, the system (9) are linearized. The Jacobian matrix at $O$ is defined as

$$\begin{aligned} J(0,0,0)&= \left( \begin{array} {c@{\quad }c@{\quad }c} -a &{} 0 &{} 0 \\ 0 &{} c &{} 0 \\ 0 &{} 0 &{} -b \end{array} \right) . \end{aligned}$$

(13)

The eigenvalues of (13) are $\lambda _1=-a=-18,\lambda _2=c=10$ and $\lambda _3=-b=-5$. Here $\lambda _2$ is a positive real number, $\lambda _1$ and $\lambda _3$ are negative real numbers.

According to Theorem 1 and Definition 2, the equilibrium point $O$ is unstable and it is a saddle point with index 1.

For equilibria $E_{\pm }$ or $F_{\pm }$, the system (9) are linearized. The Jacobian matrix at $E_{\pm }$ or $F_{\pm }$ is defined by

$$\begin{aligned} J(x,y,z)&= \left( \begin{array} {c@{\quad }c@{\quad }c} -a &{} az &{} ay \\ -dz &{} c &{} -dx\\ 0 &{} 2ey &{} -b \end{array} \right) . \end{aligned}$$

(14)

The eigenvalues of (14) are $\lambda _1=-17.1124,\lambda _2=2.0562+14.3578i$ and $\lambda _3=2.0562-14.3578i$.

Here $\lambda _2$ and $\lambda _3$ become a pair of complex conjugate eigenvalue with positive real part, $\lambda _1$ is a negative real number. Therefore, the equilibrium points $E_{\pm }$ or $F_{\pm }$ are unstable and they are saddle points with index 2 according to Theorem 1 and Definition 2.

According to Theorem 2, the necessary condition for the system (9) to remain chaos is

$$\begin{aligned} q>\frac{2}{\pi } \arctan \left( \frac{14.3578}{2.0562}\right) = 0.9094. \end{aligned}$$

(15)

Therefore, the system (9) exhibits chaos when the fractional order $q>0.9094$. Consequently, the system (9) is stable and doesn’t exhibit chaos when $q\le 0.9094$. The corresponding iconography is visualized in Fig. 6 when $q=0.90$. Further, the chaotic attractor corresponding to the system (9) are depicted in Figs. 7 and 8 when $q=0.91$ and $q=0.99$ respectively.

Fig. 6

System (9) at $q=0.90$: A 3D view, B time series of $x(t),y(t),z(t)$ for $e=18$ and $e=-18$

Fig. 7

Different phase portraits of system (9) when $q=0.91$

Fig. 8

Different phase portraits of the system (9) when $q=0.99$

Result 1

The proposed system (9) exhibits chaos when $q>0.9094$. But an existing fractional order system (6) exhibits chaos when $q\ge 0.95$. Hence, the minimum effective dimension is obtained for the modified system (9).

5 Novel method of FPS of fractional order dynamical systems

In this section, we describe the FPS between two fractional order dynamical systems.

Consider the $n$-dimensional fractional order drive system

$$\begin{aligned} D^qX(t)=G(X), \end{aligned}$$

(16)

where $X=(x_1,x_2,\ldots ,x_n)^T\in \mathbb {R}^n$ and $G(X)$ is a nonlinear function of $X$.

Construct the $n$-dimensional fractional order response system

$$\begin{aligned} D^qY(t)=G(Y)+U(Y,X), \end{aligned}$$

(17)

where $Y=(y_1,y_2,\ldots ,y_n)^T\in \mathbb {R}^n$ and $G(Y)$ is a nonlinear function of $Y$ and $U(Y,X)$ is the controller to be designed.

Define the error function $e=Y-\beta X$ where $\beta$ is the scaling factor and $e=(e_1,e_2,\ldots ,e_n)^T$. The ultimate aim is to design the controller $U(Y,X)$ such that

$$\begin{aligned} \lim _{t\rightarrow \infty }\Vert e(t)\Vert =\lim _{t\rightarrow \infty }\Vert Y(t)-\beta X(t)\Vert =0, \end{aligned}$$

(18)

where $\Vert \cdot \Vert$ is the Euclidean norm.

The error dynamical system can be written as

$$\begin{aligned} D^qe(t)&= G(Y)+U(Y,X)-\beta G(X) \nonumber \\&= G(Y)-\beta G(X)+U(Y,X). \end{aligned}$$

(19)

Since $e=Y-\beta X$,

$$\begin{aligned} G(Y)-\beta G(X)&= G(\beta X+e)-\beta G(X),\nonumber \\ U(Y,X)&= U(\beta X+e,X). \end{aligned}$$

Define

$$\begin{aligned} \phi (X,e)&= G(\beta X+e)-\beta G(X).\nonumber \\ \psi (X,e)&= U(\beta X+e,X). \end{aligned}$$

(20)

Using (20) in (19), the error dynamical system becomes

$$\begin{aligned} D^qe(t)=\phi (X,e)+\psi (X,e). \end{aligned}$$

(21)

Construct

$$\begin{aligned} \phi (X,e)=Ae+\left( \begin{array} {c} F_1(X,e) \\ F_2(X,e) \\ \vdots \\ F_n(X,e) \end{array} \right) , \end{aligned}$$

where $A=\left( \begin{array} {c@{\quad }c@{\quad }c@{\quad }c} a_1 &{} 0 &{} \ldots &{} 0 \\ 0 &{} a_2 &{} \ldots &{} 0 \\ \vdots \\ 0 &{} 0 &{} \ldots &{} a_n \end{array} \right) , \ \forall \ a_i\in \mathbb {R}, \ i=1,2,\ldots ,n$

and

$$\begin{aligned} \psi (X,e)=\left( \begin{array} {c} \psi _1(X,e) \\ \psi _2(X,e) \\ \vdots \\ \psi _n(X,e). \end{array} \right) . \end{aligned}$$

Then the error dynamical system (21) can be written as

$$\begin{aligned} D^qe(t)=Ae+\left( \begin{array} {c} F_1(X,e) \\ F_2(X,e) \\ \vdots \\ F_n(X,e) \end{array} \right) +\left( \begin{array} {c} \psi _1(X,e) \\ \psi _2(X,e) \\ \vdots \\ \psi _n(X,e) \end{array} \right) \!.\quad \quad \end{aligned}$$

(22)

Theorem 3

In general, if

$$\begin{aligned} \left( \begin{array}{c} \psi _1(X,e) \\ \psi _2(X,e) \\ \vdots \\ \psi _n(X,e) \end{array} \right) =Be-\left( \begin{array} {c} F_1(X,e) \\ F_2(X,e) \\ \vdots \\ F_n(X,e) \end{array} \right) , \end{aligned}$$

where $B=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} b_1 &{} 0 &{} \ldots &{} 0 \\ 0 &{} b_2 &{} \ldots &{} 0 \\ \vdots \\ 0 &{} 0 &{} \ldots &{} b_n \end{array} \right) ,\ \forall \ b_i\in \mathbb {R},\ i=1,2,\ldots ,n$ then $(i)$ if $(A+B)<0$, then the PS between the drive system (16) and the response system (17) can be achieved. $(ii)$ if $(A+B)=0$, then the fractional order error dynamical system (22) makes the fastest potential PS between the drive system (16) and the response system (17). That is, the necessary condition for the existence of FPS between the drive system (16) and the response system (17) is $(A+B)=0$ in the corresponding error dynamical system.

Proof

Substituting given hypothesis in (22), we get

$$\begin{aligned}&D^qe(t)=Ae+\left( \begin{array} {c} F_1(X,e) \\ F_2(X,e) \\ \vdots \\ F_n(X,e) \end{array} \right) +Be-\left( \begin{array} {c} F_1(X,e) \\ F_2(X,e) \\ \vdots \\ F_n(X,e) \end{array} \right) \nonumber \\&\quad =(A+B)e.\nonumber \\&D^q\left( \begin{array} {c} e_1 \\ e_2 \\ \vdots \\ e_n \end{array} \right) (t)=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} a_1+b_1 &{} 0 &{} \ldots &{} 0 \\ 0 &{} a_2+b_2 &{} \ldots &{} 0 \\ \vdots \\ 0 &{} 0 &{} \ldots &{} a_n+b_n \end{array} \right) \nonumber \\&\qquad \times \left( \begin{array} {c} e_1 \\ e_2 \\ \vdots \\ e_n \end{array} \right) . \end{aligned}$$

(23)

The Jacobian matrix of (23) is

$$\begin{aligned}&J(e_1,e_2,\ldots ,e_n)\nonumber \\&\quad =\left( \begin{array} {c@{\quad }c@{\quad }c@{\quad }c} a_1+b_1 &{} 0 &{} \ldots &{} 0 \\ 0 &{} a_2+b_2 &{} \ldots &{} 0 \\ \vdots \\ 0 &{} 0 &{} \ldots &{} a_n+b_n \end{array} \right) . \end{aligned}$$

(24)

The eigenvalues of (24) are $\lambda _i=a_i+b_i$, where $i=1,2,\ldots ,n$ and $(a_i+b_i)\in \mathbb {R}$.

• (i) If $(A+B)<0$, then $(a_i+b_i)<0$. Hence the stability condition $|\arg (\lambda _i)|>\frac{q\pi }{2}$ is satisfied for all $0<q<1$ and the error states $e_i(t),\ i=1,2,\ldots ,n$ are tend to zero as $t\rightarrow \infty$. Therefore the fractional order error dynamical system (23) is asymptotically stable and hence the PS is achieved between the systems (16) and (17).

• (ii) If $(A+B)=0$, then the zero error fractional order dynamical system is obtained for the system described by

  $$\begin{aligned} D^qe(t)=0. \end{aligned}$$

  (25)

Thus the error states are $e_i(t)=0$ for every $t\ge 0, i=1,2,\ldots ,n$. Therefore, the FPS is achieved between the systems (16) and (17) because the convergence rate of error states in case $(ii)$ is faster than the convergence rate of error states in case $(i)$ for the system (23). Therefore, this PS with the condition $(A+B)=0$ is called as FPS.

Remark 3

In the proposed method of FPS, if $\beta =-1$ then anti-synchronization between the fractional order dynamical systems (16) and (17) could be achieved. Therefore, the proposed FPS is fully suitable for synchronization and anti-synchronization of fractional order dynamical systems.

Remark 4

From the case $(ii)$ of Theorem 3, the convergence rate of synchronization error of the proposed PS method is very faster than the convergence rate of all exiting PS methods with a small or large quantity of synchronization errors, for example see [21–24] because the states of fractional order error dynamical system (25) are tend to zero for every $t\ge 0$. That is, there is no synchronization error exists between the fractional order dynamical systems (16) and (17).

5.1 Numerical example

Let $e=18$ be $\hat{e_1}$ and let $e=-18$ be $\hat{e_2}$ for the system (9). Consider the fractional order chaotic system (9) with $\hat{e_1}$ as a drive system and the system (9) with $\hat{e_2}$ as a response system. Here, the drive system is a fractional order chaotic system and the response is a fractional order reverse chaotic system.

The drive system is described by

$$\begin{aligned} D^{q}x_1(t)&=-a(x_1-y_1z_1), \nonumber \\ D^{q}y_1(t)&=cy_1-dx_1z_1,\nonumber \\ D^{q}z_1(t)&=-bz_1+\hat{e_1}y_1^2. \end{aligned}$$

(26)

and the response system is described by

$$\begin{aligned} D^{q}x_2(t)&=-a(x_2-y_2z_2)+u_1,\nonumber \\ D^{q}y_2(t)&=cy_2-dx_2z_2+u_2,\nonumber \\ D^{q}z_2(t)&=-bz_2+\hat{e_2}y_2^2+u_3. \end{aligned}$$

(27)

Here $X=(x_1,y_1,z_1)^T, Y=(x_2,y_2,z_2)^T$ and $U=(u_1,u_2,u_3)^T$. The fractional order $q$ is set arbitrarily as $q=0.93$ since the fractional order drive system (26) and the fractional response system (27) are chaotic for every $q>0.9094$. The scaling factor $\beta$ is chosen as $\beta =3$.

The fractional order error dynamical system is

$$\begin{aligned} D^qe(t)=\phi (X,e)+\psi (X,e). \end{aligned}$$

(28)

Then $\phi (X,e)$

$$\begin{aligned} =\left( \begin{array} {c@{\quad }c@{\quad }c} -a(e_1-e_2e_3)+a\beta z_1(y_1\beta +\frac{y_1}{z_1}e_3+e_2-y_1)\\ ce_2-de_1e_3-d\beta x_1(z_1\beta +e_3+e_1\frac{z_1}{x_1}-z_1) \\ -be_3+\hat{e_1}\beta y_1(y_1\beta +2e_2-y_1)+\hat{e_1}e_2^2 \end{array} \right) . \end{aligned}$$

(29)

Here

$$\begin{aligned}&\left( \begin{array} {c} F_1(X,e) \\ F_2(X,e) \\ F_3(X,e) \end{array} \right) \\&\quad =\left( \begin{array} {c} a\beta z_1(y_1\beta +\frac{y_1}{z_1}e_3+e_2-y_1) \\ -de_1e_3-d\beta x_1(z_1\beta +e_3+e_1\frac{z_1}{x_1}-z_1) \\ \hat{e_1}\beta y_1(y_1\beta +2e_2-y_1)+\hat{e_1}e_2^2 \end{array} \right) \end{aligned}$$

and $A=\left( \begin{array} {c@{\quad }c@{\quad }c} -a &{} 0 &{} 0 \\ 0 &{} c &{} 0 \\ 0 &{} 0 &{} -b \end{array} \right) .$

Construct

$$\begin{aligned} U(Y,X)&= U(\beta X\!+\!e,X)\!=\!\psi (X,e)\!=\!\left( \begin{array}{c} \psi _1(X,e) \\ \psi _2(X,e) \\ \psi _3(X,e) \end{array} \right) . \end{aligned}$$

According to Theorem 3,

$$\begin{aligned} \left( \begin{array}{c} \psi _1(X,e) \\ \psi _2(X,e) \\ \psi _3(X,e) \end{array} \right)&= Be-\left( \begin{array} {c} F_1(X,e) \\ F_2(X,e) \\ F_3(X,e) \end{array} \right) . \end{aligned}$$

Case (i): Assume that $(A+B)<0.$

Choose $B=\left( \begin{array} {c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 \\ 0 &{} -2c &{} 0 \\ 0 &{} 0 &{} 0 \end{array} \right)$. Then the error dynamical system (28) can be written as

$$\begin{aligned} D^{q}e_1(t)&=-ae_1,\nonumber \\ D^{q}e_2(t)&=-ce_2,\nonumber \\ D^{q}e_3(t)&=-be_3. \end{aligned}$$

(30)

The Jacobian matrix of (30) is

$$\begin{aligned} J(e_1,e_2,e_3)&= \left( \begin{array}{c@{\quad }c@{\quad }c} -a &{} 0 &{} 0 \\ 0 &{} -c &{} 0 \\ 0 &{} 0 &{} -b \end{array} \right) . \end{aligned}$$

(31)

The eigenvalues of (31) are $\lambda _1=-a, \lambda _2=-c$ and $\lambda _3=-b$. Then, the fractional order error dynamical system (30) is asymptotically stable according to Theorem 1.

Since by Theorem 3, the systems (26) and (27) are achievable PS.

The time response of the states of the PS of fractional order chaotic (drive) system and reverse chaotic (response) system is exposed in Fig. 9 and the projections of the synchronized chaotic attractors of the drive system (26) and the response system (27) are shown in Fig. 10. Further, the PS errors between the systems (26) and (27) are depicted in Fig. 11.

Fig. 9

The time response of the states of the drive system (26) and response system (27) when $q=0.93$

Fig. 10

Projection of the synchronized attractors of the drive system (26) and response system (27) onto the corresponding plane when $q=0.93$

Fig. 11

The PS error states $e_1, e_2,e_3$ when $q=0.93$

Case (ii): Assume that $(A+B)=0.$

Choose $B=\left( \begin{array} {c@{\quad }c@{\quad }c} a &{} 0 &{} 0 \\ 0 &{} -c &{} 0 \\ 0 &{} 0 &{} b \end{array} \right)$. Then the error system (28) can be written as

$$\begin{aligned} D^qe_i(t)=0,\ i=1,2,3. \end{aligned}$$

Therefore, the state trajectories of the fractional order error dynamical system (28) attains zero for every time $t\ge 0$.

Since by Theorem 3, the systems (26) and (27) are achievable FPS. The FPS errors between the systems (26) and (27) are depicted in Fig. 12. It is evident that from Figs. 11 and 12 that the convergence rate of the error states $e_i,\ i=1,2,\ldots ,n$ in (28) with the condition $(A+B)=0$ is very faster than the error states $e_i,\ i=1,2,\ldots ,n$ in (28) with the condition $(A+B)<0$.

Fig. 12

The FPS error states $e_1, e_2,e_3$ when $q=0.93$

6 Application of synchronized systems

In this section, we propose an affine cipher based on the synchronized fractional order chaotic and reverse chaotic systems with the support of the DOB keys. DOB key means, a key consist of birth day, month, and year of the sender (receiver).

Cryptography is split into two ways of changing the message systematically to confuse anyone who intercepts it: these are codes and ciphers. A code is a way of changing the message by replacing each word with another word that has a different meaning. Ciphers convert the message by a rule, known only to the sender and the recipient, which change each individual letter.

An affine cipher is a combination of the shift cipher and the multiplication cipher. The key for an affine cipher consists of two integers $k=(l,m)$. The encryption $E(\cdot )$ and decryption $D(\cdot )$ processes of affine cipher for given message $\mathbf {M}$ are defined by [31] as

$$\begin{aligned} E(\mathbf {M})&= (l*\mathbf {M})+m\ (\text {mod}\ p),\\ D(\mathbf {M})&= l'*(E(\mathbf {M})-m)\ (\text {mod}\ p), \end{aligned}$$

where $l'$ is the inverse of $l$ modulo $p$ and $p$ is a positive integer.

Note that, if $l=1$ then $E(\cdot )$ and $D(\cdot )$ process is called shift cipher. If $m=0$ then the $E(\cdot )$ and $D(\cdot )$ process is called multiplicative cipher. In the proposed affine cipher, we generate the affine cipher key pair as a combination of the solutions of fractional order chaotic system and date of birth of sender (receiver). At the first time, an affine will be utilized for image encryption and decryption technique based on synchronized fractional order chaotic systems.

6.1 Proposed affine cipher

Before going to propose an affine cipher, some basic assumptions are needed. Consider $\mathcal {S}$ as a sender and $\mathcal {R}$ as a receiver in the cryptosystem. Also consider the drive system (26) as a sender’s system and the response system (27) as a receiver’s system. $\mathcal {S}$ and $\mathcal {R}$ are agree on a time $t\ge t_0$ ( synchronization errors between the systems (26) and (27) are tend to zero from time $t_0$ onwards), a scaling factor $\beta$, fractional order $q\ge 0.91$ and a positive integer $p$. Let $D=(D_1,D_2)$ be a pair of date of birth of $\mathcal {S}$ and $\mathcal {R}$. Here, $D_1$ is DOB of $\mathcal {S}$ and $D_2$ is the DOB of $\mathcal {R}$ and they can be represented as $D_1=DD\text {-}MM\text {-}YYYY$, $D_2=dd\text {-}mm\text {-}yyyy$ in the day, month, and year format. Then $D$ is only shared by $\mathcal {S}$ and $\mathcal {R}$. The details of key generation, encryption, and decryption processes between $\mathcal {S}$ and $\mathcal {R}$ are described as follows.

Key generation:

In the key generation phase, both $\mathcal {S}$ and $\mathcal {R}$ generate their own secret key pair.

• 1. $\mathcal {S}$ solves a fractional order chaotic system (26) at time $t$ when fractional order $q\ge 0.91$ and generates $K_1=DD*x_1(t)+MM*y_1(t)+YYYY*z_1(t)$ (mod $p$) and $K_2=dd*x_1(t)+mm*y_1(t)+yyyy*z_1(t)$ (mod $p$).

• 2. $\mathcal {S}$ kept secret on his/him key pair $(K_1,K_2)$.

• 3. $\mathcal {R}$ solves a fractional order reverse chaotic system (27) at time $t$ when fractional order $q\ge 0.91$ and generates $L_1=DD*x_2(t)+MM*y_2(t)+YYYY*z_2(t)$ (mod $p$) and $L_2=dd*x_2(t)+mm*y_2(t)+yyyy*z_2(t)$ (mod $p$).

• 4. $\mathcal {R}$ kept secret on his/him key pair $(L_1,L_2)$.

Encryption:

In the encryption phase, $\mathcal {S}$ wants to share a message $\mathbf {M}$ with $\mathcal {R}$ secretly. So, $\mathcal {S}$ encrypted a message $\mathbf {M}$ by using the function $E(\cdot )$.

• 1. $\mathcal {S}$ computes, $E(\mathbf {M})=(\mathbf {M}*K_1)+K_2$ (mod $p$).

• 2. $\mathcal {S}$ sends $E(\mathbf {M})$ to the receiver $\mathcal {R}$.

Decryption:

In the decryption phase, $\mathcal {R}$ receives $E(\mathbf {M})$ from $\mathcal {S}$ and recovers an original message $\mathbf {M}$ by the following computation.

• 1. $\mathcal {R}$ computes $D(\mathbf {M})=(E(\mathbf {M})-L_2)*L_1^{-1}$ (mod $p$).

• 2. Finally, $\mathcal {R}$ recovers an original message $D(\mathbf {M})=\mathbf {M}$ (mod $p$).

For, $D(\mathbf {M})$

$$\begin{aligned}&= (E(\mathbf {M})-L_2)*L_1^{-1}\ (\mathrm{mod}\ p)\\&= (\mathbf {M}*K_1+K_2 (\mathrm{mod}\ p)-L_2)*L_1^{-1}\ (\mathrm{mod}\ p)\\&= (\mathbf {M}*K_1+K_2-L_2)*L_1^{-1}\ (\mathrm{mod}\ p) \\&= (\mathbf {M}*K_1+dd*x_1(t)+mm*y_1(t)+yyyy*z_1(t)\\&\ \ -dd*x_2(t)-mm*y_2(t)-yyyy*z_2(t))*L_1^{-1}\ (\mathrm{mod}\ p) \\&= (\mathbf {M}*K_1+dd(x_1(t)-x_2(t))+mm(y_1(t)-y_2(t)) \\&\ \ +yyyy(z_1(t)-z_2(t)))*L_1^{-1}\ (\mathrm{mod}\ p) \\&= (\mathbf {M}*K_1+dd(x_1(t)-x_2(t))+mm(y_1(t)-y_2(t)) \\&\ \ +yyyy(z_1(t)-z_2(t)))*L_1^{-1}\ (\mathrm{mod}\ p) \\&= (\mathbf {M}*K_1)*L_1^{-1}\ (\mathrm{mod}\ p) \\&= \mathbf {M}*(DD*x_1(t)+MM*y_1(t)+YYYY*z_1(t))\\&\ \ *(DD*x_2(t)+MM*y_2(t)+YYYY*z_2(t))^{-1}\ (\mathrm{mod}\ p) \\&= \mathbf {M}\ (\text {mod}\ p) \\&\ \ (\mathrm{since}\ x_1(t)=x_2(t),y_1(t)=y_2(t),z_1(t)=z_2(t)\ \forall \ t\ge t_0) \end{aligned}$$

Note that, a message $\mathbf {M}$ has two types. One is text and another one is an image. The proposed affine cipher is fully suitable for both text and image encryption–decryption. The detailed procedure is given in the following remarks.

Remark 5

Suppose $\mathcal {S}$ and $\mathcal {R}$ want to share a text message $\mathbf {M}$. In that case, $\mathcal {S}$ and $\mathcal {R}$ are assigning the numerical value 0–25 for alphabets $A-Z$ and 26 for blank space (gap between two words). Then, find the number of characters including the blank space of $M$, let it be ${{\varvec{c}}}$. Finally, assign a suitable $M_{m\times n}$ matrix ( that is, ${{\varvec{c}}}$ is equal to $m\times n$) for numerical message $M$. If ${{\varvec{c}}}$ is not equal to $m\times n$, then add the necessary blank spaces at the end of the message to complete the $\mathbf {M}_{m\times n}$.

Remark 6

Any image of size $m\times n$ can be easily encrypted with high security through the proposed affine cipher because an image can be easily represented by matrices of size $m\times n$. Each element of the matrix determines the intensity of the corresponding pixel value. Every digital image has intensity between 0 and 255. Therefore, we assume that the value of $p$ as 256 in the proposed affine cipher only for image encryption and decryption. Hence the proposed affine cipher is well supported to encrypt and decrypt a text message and an image.

In the following subsection, the proposed affine cipher will be demonstrated numerically.

6.2 Demonstration of the proposed affine cipher

Assume that, $\mathcal {S}$ and $\mathcal {R}$ agree on the fractional order $q=0.93$. For $q=0.93$, the PS (FPS) errors between the systems (26) and (27) are tend to zero after a time $t\ge t_0=0.8$ ($t\ge t_0=0$) with a scaling factor $\beta =3$ since by Figs. 11 and 12 respectively. For every $\beta \ne 0, q\ge 0.91$, the FPS errors between the systems (26) and (27) are tend to zero after a time $t\ge t_0=0$. Therefore, both $\mathcal {S}$ and $\mathcal {R}$ agree on a time $t=5.001$ with a scaling factor $\beta =1$ and set $p=29$. Further, $\mathcal {S}$ and $\mathcal {R}$ shared their DOBs, $D_1=\,DD\text {-}MM\text {-}YYYY=27\text {-}06\text {-}1986$ and $D_2=\,dd\text {-}mm\text {-}yyyy=11\text {-}06\text {-}1986$.

$\mathcal {S}$ wants to send a message $\mathbf {M}=\mathbf{PASSWORD}$. Here, $\mathbf {M}$ has eight elements then $\mathcal {S}$ choose a $3\times 3$ matrix. Note that, $3\times 3$ matrix has nine elements. So, $\mathcal {S}$ insert a blank space at the end of the message $\mathbf {M}$ and assign the numerical value of each character of the message $\mathbf {M}$. According to Remark 5, the numerical assignment of $\mathbf {M}$ as 15 0 18 18 22 14 17 3 26. Then, the matrix form of the message $\mathbf {M}$ as $\mathbf {M}=\left( \begin{array} {ccc} 15 &{} 0 &{} 18 \\ 18 &{} 22 &{} 14 \\ 17 &{} 3 &{} 26 \end{array} \right)$.

For encryption, $\mathcal {S}$ solves a system (26) at $t$ when $q=0.93$ and finds $x_1(t)=0.5615,y_1(t)=1.017,z_1(t)=1.098$.

Thus, $\mathcal {S}$ generates a secret key pair $(K_1,K_2)$ as

$$\begin{aligned} K_1&=27*0.5615+06*1.017+1986*1.098\\&=21 \ (\text {mod}\ 29),\\ K_2&=11*0.5615+06*1.017+1986*1.098\\&=6 \ (\text {mod}\ 29). \end{aligned}$$

Then, $\mathcal {S}$ computes

$$\begin{aligned} E(\mathbf {M})&=\left( \begin{array} {c@{\quad }c@{\quad }c} 15 &{} 0 &{} 18 \\ 18 &{} 22 &{} 14 \\ 17 &{} 3 &{} 26 \end{array} \right) *K_1+K_2\nonumber \\&=\left( \begin{array} {c@{\quad }c@{\quad }c} 2 &{} 6 &{} 7 \\ 7 &{} 4 &{} 10\\ 15 &{} 11 &{}1 \end{array} \right) (\text {mod}\ 29). \end{aligned}$$

$\mathcal {S}$ assigns an alphabet for each numerical value of $E(\mathbf {M})$, $E(\mathbf {M})=\mathbf{CGHHEKPLA}$ and sends to $\mathcal {R}$. $\mathcal {R}$ receives $E(\mathbf {M})$ from $\mathcal {S}$.

For decryption, $\mathcal {R}$ solves a system (27) at $t$ when $q=0.93$ and finds $x_2(t)=0.5615,y_2(t)=1.017,z_2(t)=1.098$.

Then, $\mathcal {R}$ generates a secret pair $(L_1,L_2)$ as

$$\begin{aligned} L_1&=27*0.5615+06*1.017+1986*1.098\\&=21 \ (\mathrm{mod}\ 29), \\ L_2&=11*0.5615+06*1.017+1986*1.098\\&=6 \ (\mathrm{mod}\ 29). \end{aligned}$$

Further, $\mathcal {R}$ computes $D(\mathbf {M})$

$$\begin{aligned}&= \left[ \left( \begin{array} {c@{\quad }c@{\quad }c} 2 &{} 6 &{} 7 \\ 7 &{} 4 &{} 10\\ 15 &{} 11 &{} 1 \end{array} \right) -L_2\right] *L_1^{-1}\nonumber \\&= \left( \begin{array} {c@{\quad }c@{\quad }c} -4 &{} 0 &{} 1 \\ 1 &{} -2 &{} 4 \\ 9 &{} 5 &{} -5 \end{array} \right) *21^{-1} \\&= \left( \begin{array} {c@{\quad }c@{\quad }c} 15 &{} 0 &{} 18 \\ 18 &{} 22 &{} 14 \\ 17 &{} 3 &{} 26 \end{array} \right) \ (\text {mod}\ 29). \end{aligned}$$

Finally, $\mathcal {R}$ assigns an alphabet for each numerical value of $D(\mathbf {M}),\,D(\mathbf {M})=\mathbf{PASSWORD }$. Hence, the original message $\mathbf {M}$ has been recovered.

Suppose $\mathcal {S}$ wants to send an image $I$ with size $596\times 411\ (I_{596\times 411})$, which is visualized in Fig. 13. Assume that, $t,q,\beta$ values and the solutions of (26) and (27) are given above. Further, set $p=256, \mathbf {M}=I_{596\times 411}$, $D_1=DD\text {-}MM\text {-}YYYY\,=\,02\text {-}02\text {-}1986$ and $D_2=\,dd\text {-}mm\text {-}yyyy=11\text {-}06\text {-}1986$. Then, $\mathcal {S}$ generates a secret key pair $(K_1,K_2)$ as

$$\begin{aligned} K_1&=02*0.5615+02*1.017+1986*1.098\\&=131 \ (\mathrm{mod}\ 256), \\ K_2&=11*0.5615+06*1.017+1986*1.098\\&=202 \ (\mathrm{mod}\ 256). \end{aligned}$$

For encryption, $\mathcal {S}$ computes

$$\begin{aligned} E(\mathbf {M})=(\mathbf {M}*K_1)+K_2 \ (\mathrm{mod}\ 256). \end{aligned}$$

The encrypted image is depicted in Fig. 14. $\mathcal {S}$ sends $E(\mathbf {M})$ to $\mathcal {R}$.

Fig. 13

Original image

Fig. 14

Encrypted image

$\mathcal {R}$ receives an encrypted message $E(\mathbf {M})$ and generates a secret pair $(L_1,L_2)$ as

$$\begin{aligned} L_1&=02*0.5615+02*1.017+1986*1.098\\&=131 \ (\mathrm{mod}\ 256),\\ L_2&=11*0.5615+06*1.017+1986*1.098\\&=202 \ (\mathrm{mod}\ 256). \end{aligned}$$

For decryption, $\mathcal {R}$ computes

$$\begin{aligned} D(\mathbf {M})=(E(\mathbf {M})-L_2)L_1^{-1} \ (\mathrm{mod}\ 256). \end{aligned}$$

The decrypted image is depicted in Fig. 15.

Fig. 15

Decrypted image

Finally, $\mathcal {R}$ recovers an original image $D(\mathbf {M})=\mathbf {M}=I_{596\times 411}$.

6.3 Security analysis of proposed affine cipher

The proposed affine cipher consists of two pairs of keys $(K_1,K_2)$ and $(L_1,L_2)$, which are computed by the sender and receiver separately. Which is entirely different from the existing affine ciphers. The receiver cannot recover an original text or image without the knowledge of the receivers private key $(K_1,K_2)$. Further, the proposed scheme only allows a designated receiver to recover the original text or image from the encrypted message because the private key $(K_1,K_2)$ is used for message encryption and it is generated by the public key $(D_1,D_2)$. Hence, the proposed cipher is fully authenticated.

Only the sender’s private key is used for encryption and that cannot be used anywhere in the proposed ciphers. Therefore, it has non-repudiation. Moreover, only the receiver recovers the message $\mathbf {M}$ by computing $D(\mathbf {M})=(E(\mathbf {M)}-L_2)L_1^{-1}$ (mod $p$) using the private key $(L_1,L_2)$ with the knowledge of $(L_1,L_2)$ and the solutions of the response system (27). Hence, the communication must be observable only by the sender and the receiver, but not anyone else. Hence, it has confidentiality. Therefore, the proposed affine cipher is more efficient than the ordinary affine cipher method due to the existence of message authentication, non-repudiation, and confidentiality.

Suppose an adversary (ADV) trying to recover an original message, she/he should be computed the $(E(\mathbf {M})-L_2)L_1^{-1}$ (mod $p$). It is impossible because $L_1$ and $L_2$ are the private keys of the receiver. On the other hand, ADV would try to obtain $L_1$ and $L_2$ with the knowledge of $D_1$ and $D_2$. It is also impossible because $L_1$ and $L_2$ are a combination of the solutions of the response system (27) and the public key $(D_1,D_2)$. Moreover, finding the solutions of the fractional order chaotic system at time $t$ is impossible. So, ADV would fail to recover the private keys of the receiver. Hence, ADV would fail to recover an original message.

Suppose ADV only has $(L_1,L_2)$ and try to recover an original message from $(E(\mathbf {M})-L_2)L_1^{-1}$ (mod $p$), which is also impossible because the computational part of the $L_1^{-1}$ (mod $p$) is not possible without the knowledge of modulo $p$ and the computation of integer factorization problem is very hard. Note that, $p$ is only shared by the receiver and sender not by else. This attempt is also failed for ADV. Hence, the proposed affine cipher is more secure and efficient than the ordinary affine cipher.

7 Conclusions

In this paper, the stability and chaotic behaviors of an altered fractional order dynamical system have been investigated. We found that, the modified fractional order dynamical system has phase reversal and exhibits reverse chaotic attractor. Further, the minimum effective dimension of the modified fractional order system is 2.73. The FPS of fractional order dynamical systems has been presented analytically and numerically. The different phase projections have been displayed. An efficient and secured affine cipher has been proposed based on these synchronized fractional chaotic systems with the support of the sender’s and receiver’s DOB. The efficiency and security of the proposed affine cipher have been assured. Numerical simulations have been confronted to validate the efficacy of the proposed fractional order chaotic system and an affine cipher.