1 Introduction

The discrete dynamic behavior and its applications have been paid much attention in various applied areas, such as synchronization control [1–3], secure communication [4, 5], biomolecular network evolution [6, 7], and so on.

The DFC is one of recent topics and some results were already reported in the discrete fractional dynamics. In 1989, Miller and Ross [8] began the theory of the fractional difference, and the fractional integral was given as a fractional summation. After that, several authors developed the theory of the fractional difference equations on time scales [9], such as the initial value problems [10], the discrete calculus of variations [11], the Laplace transform [12, 13], the properties of the Caputo and the Riemann-Liouville difference [14], and so on (see, for example, Refs. [15–21] and the references therein). Very recently, the DFC tool was applied to the chaotic aspects of the discrete systems in [22, 23]. The logistic map of fractional order is proposed as

$$\begin{aligned} x(n)&= x({0})+\frac{\mu }{\varGamma (\nu )} \sum ^{n}_{j=1}\frac{\varGamma (n-j+\nu )}{\varGamma (n-j+1)}\nonumber \\&\,\times \, x(j-1)(1-x(j-1)). \end{aligned}$$
(1)

It holds discrete memory effects and can describe the long interaction of the systems. Besides, the parameter \(\nu \) can be varied and the more general chaos can shrink to the results of integer maps for the \(\nu =1\). These merits help us understand the discrete chaotic behaviors more deeply.

This study considers the general results in a two-dimensional case and it is organized as follows: Sect. 2 introduces some of the basic definitions and the preliminaries of the DFC. In Sect. 3 we applied the tool of the DFC to the two-dimensional logistic equation and a discrete fractional map is obtained. Then the chaotic behaviors are reported and the bifurcation diagrams are given for various difference orders.

2 Basic definitions and preliminaries

In the following we recall some definitions and preliminaries of the DFC. The following notation \(\mathbb {N}_a\) denotes the isolated time scale and \(\mathbb {N}_a=\{a,a+1,a+2,\ldots \}, \) (\(a \in \mathbb {R}\) fixed). For the function \(x(n)\), the difference operator \(\Delta \) is defined as \(\Delta x(n)=x(n+1)-x(n)\).

Definition 2.1

([10]) Let \(x:\) \(\mathbb {N}_a\rightarrow \mathbb {R}\) and \(0<\nu \) be given. Then the fractional sum of order \(\nu \) is defined by

$$\begin{aligned} \Delta ^{-\nu }_{a}x(t):=\frac{1}{\varGamma (\nu )}\sum ^{t-\nu }_{s=a} (t-\sigma (s))^{(\nu -1)}x(s), \,\, t \in \mathbb {N}_{a+\nu }\nonumber \\ \end{aligned}$$
(2)

where \(a\) is the starting point, \(\sigma (s)=s+1\), and \(t^{(\nu )}\)is the falling function defined as

$$\begin{aligned} t^{(\nu )}=\frac{\varGamma (t+1)}{\varGamma (t+1-\nu )}. \end{aligned}$$
(3)

Definition 2.2

([14]) For \(0<\nu < 1\), and \(x(t)\) defined on \(\mathbb {N}_{a}\), the Caputo-like delta difference is defined by

$$\begin{aligned}&\!\!\!^{C}\Delta ^{\nu }_{a} x(t):=\frac{1}{\varGamma (1-\nu )}\nonumber \\&\quad \times \sum ^{t-(1-\nu )}_{s=a}(t -\sigma (s))^{(-\nu )}\Delta x(s), \quad t \in \mathbb {N}_{a+1 -\nu }. \end{aligned}$$
(4)

Theorem 2.3

The delta fractional difference equation

$$\begin{aligned}&\!\!\!{^{C}\Delta ^{\nu }_{a}} x(t)=f(t+\nu -1,x(t+\nu -2)),\nonumber \\&\!\!\!\quad \,0 <\nu <1, \quad t \in \mathbb {N}_{a+1-v} \end{aligned}$$
(5)

has an equivalent discrete integral equation

$$\begin{aligned} x(t)&= x(a)+\frac{1}{\varGamma (\nu )}\sum ^{t-\nu }_{s=a+1-\nu } (t-\sigma (s))^{(\nu -1)}\nonumber \\&\times f(s +\nu -1,x(s+\nu -2)), \quad t \in \mathbb {N}_{a+1}. \end{aligned}$$
(6)

Proof

Suppose that \(x(t)\) is a solution of (5), then according to the discrete Taylor expansion [16]

$$\begin{aligned} x(t)&{=} x(a){+}\frac{1}{\varGamma (\nu )}\sum ^{t{-}\nu }_{s{=}a+1{-}\nu }\!\! (t{-}\sigma (s))^{{(\nu {-}1)}}{\times }{}^{C}\Delta ^{\nu }_{a} x(s),\!\!\!\!\nonumber \\&0 <\nu <1, \quad t \in \mathbb {N}_{a+{1}} \end{aligned}$$
(7)

and substituting Eq. (5) into Eq. (7), we can prove (6).

Conversely, if \(x(t)\) is a solution of (6), from the right hand sides of (6) and (7), we can obtain

$$\begin{aligned}&\!\!\!\frac{1}{\varGamma (\nu )}\sum ^{t-\nu }_{s=a+1-\nu }(t-\sigma (s))^{(\nu -1)} ( {^{C}\Delta ^{\nu }_{a}} x(s) \nonumber \\&\!\!\!\!\quad -f(s+\nu -1,x(s+\nu -2)))=0. \end{aligned}$$
(8)

As a result, we get that

$$\begin{aligned} ^{C}\Delta ^{\nu }_{a} x(t)=f(t+\nu -1,x(t+\nu -2)) \end{aligned}$$

which implies that \(x(t)\) is a solution of (6). \(\square \)

3 Discrete chaos in fractional delayed logistic maps

3.1 Fractional discretization of the delayed logistic equation

The logistic equation

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=r x(t)(1-x(t)) \end{aligned}$$
(9)

is originally proposed by Verhulst [24] in 1845 and has numerous applications. Particularly in the biology and ecology, the model depicts the ratio of the population’s growth.

As it was already pointed out by Hutchinson [25], the events from nature are not continuous, therefore, we have seasonal cycle which generates oscillations due to the internal demographic factors. In view of this point, the discrete maps can better depict the evolution of the population.

Several modified logistic equations and their discrete versions have been suggested in [25–33]. One of them is the delayed logistic map [29], namely

$$\begin{aligned} x(n+1)=K x(n)(1-x(n-1)). \end{aligned}$$
(10)

It is derived by the discretization of the delayed Eq. [25]

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=\mu x(t)(1-x(t-\tau )), \end{aligned}$$
(11)

where \(\tau \) is the delay time and \(\mu \) denotes the rate of the maximum population growth. We assume that the amount of resources available at time \(t\) will depend on the density of the species at an earlier time by a delay of \(\tau \).

At this point we recall that some discretization techniques were reported in the literature [10–14, 34–38]. We introduce the following fractional difference equation by the DFC [10–14]

$$\begin{aligned}&\!\!\!\!{}^{C}\Delta ^{\nu }_{a} x(t)=\mu x(t+\nu -1)(1-x(t+\nu -2)),\nonumber \\&\quad t \in \mathbb {N}_{a+1-\nu }. \end{aligned}$$
(12)

By using the Theorem 2.3 we obtain the fractional delayed logistic maps as

$$\begin{aligned} \left\{ \begin{array}{l} \!\!x(n)=x(0)+\frac{\mu }{\varGamma (\nu )} \sum ^{n}_{j=1}\frac{\varGamma (n-j+\nu )}{\varGamma (n-j+1)}\\ \quad x(j-1)(1-y(j-1)), \\ \!\!y(n)=x(n-1).\\ \end{array} \right. \end{aligned}$$
(13)

The initial iterations are assumed as \(x(0)=y(0)=0.001\).

We notice that for \(\nu =1\), the system reduces to the following delayed logistic map

$$\begin{aligned} x(n+1)= (\mu +1) x(n)-\mu x(n)x(n-1) \end{aligned}$$
(14)

and \(x(0)=x(-1)=0.001\).

Since there is a discrete weighted or kernel function \(\frac{\varGamma (n-j+\nu )}{\varGamma (n-j+1)}\) in (13), the present statue \(x(n)\) depends on the past information \(x(0),\ldots ,x(n-1)\) which is called the discrete memory effect. This is one of crucial differences between the fractional map and the classical one.

3.2 Discrete chaos in fractional delayed logistic maps

We recall that the system (14) generates a chaotic series for \(\mu =1.25\) and comes across the Hopf bifurcation. With the mathematic software Maple, we plot the numerical solution and the discrete attractor in Fig. 1a, b, respectively. Figure 2 represents the bifurcation diagram.

Fig. 1
figure 1

The chaotic behaviors of the delayed logistic maps of integer order. a Numerical solution for \(\mu =1.25\). b Discrete strange attractor

Full size image
Fig. 2
figure 2

The bifurcation diagram of the classical delayed logistic maps

Full size image

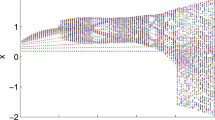
Now we consider the fractional case for \(\nu =0.8\). Figures 3, 4 and 5 illustrate the dynamic behaviors of the system when the coefficient \(\mu \) is varied. Figure 6 is the bifurcation diagram. It is found that quasiperiodic behavior persists over most of the range of \(1.096<\mu <1.412\) and some for \(1.412<\mu \). In order to distinguish the chaos, we discard the first 70 values of \(x(i)\) and adopt the Jacobian matrix algorithm to plot the distribution of the maximal Lyapunov exponents in Fig. 7. Through the analysis of the positive Lyapunov exponents, we can note that the system meets chaotic statues when \(\mu \) increases through 1.096. We enlarge the interval [1.3, 1.412] in Fig. 8. It can be more clearly observed that the chaotic zone is non-continuous from Figs. 7 and 8.

Fig. 3
figure 3

Damped oscillation phenomenon for \(\mu = \)1.05 and \(\nu =\) 0.8

Full size image
Fig. 4
figure 4

Sustained oscillation phenomenon for \(\mu = \)1.08 and \(\nu =\) 0.8

Full size image
Fig. 5
figure 5

Chaos in the maps for \(\mu =\) 1.42 and \(\nu =\) 0.8

Full size image
Fig. 6
figure 6

The bifurcation diagram of the fractional delayed logistic maps for \(\nu =0.8\)

Full size image
Fig. 7
figure 7

The maximal Lyapunov exponent \(\lambda _{max}\) for \(\nu =0.8\)

Full size image
Fig. 8
figure 8

A piece of the bifurcation diagram (6) and its enlargement

Full size image

Similarly, for \(\nu =0.6\) and \(\nu =0.4\), we can give the bifurcation diagrams in Figs. 9 and 10, respectively. For the varied difference order, the chaotic zones are different and new chaotic behaviors are observed.

Fig. 9
figure 9

The bifurcation diagram of the fractional delayed logistic maps for \(\nu =0.6\)

Full size image
Fig. 10
figure 10

The bifurcation diagram of the fractional delayed logistic maps for \(\nu =0.4\)

Full size image

4 Conclusions

This study applies the DFC to the two-dimensional delayed logistic equation and as a result a novel delayed logistic map of fractional difference order is given in a form of an iteration formula. Then the dynamic behaviors are discussed by varying the coefficient \(\mu \) and the difference order \(\nu \). The Lyapunov exponents are plotted to identify the chaos. The reported results show that the discrete fractional maps hold some new degrees of freedom which can be used in catching the hidden aspects for real world phenomena encountered in ecology.