1 Introduction

The phenomenon of chaos is very common in nature, the fundamental characteristic of a chaotic system is its sensitive dependence on initial conditions, that is, a small shift in the initial states can lead to extraordinary perturbation in the system states [1]. Over the past two decades, many chaotic systems have been found, such as the Lorenz system [2], the Lur’e system [3], the Duffing-Holmes system [4], the Genesio system [5], the Rössler system [6], Chua’s circuit [7], and so on.

Since the discovery of chaos synchronization [8], chaos synchronization has received increasing attention in nonlinear science. One of the reasons is that chaotic behaviors have been discovered in many engineering systems such as information processing, chemical reactions, power converters, biological systems, secure communication, and so on. For chaos synchronization there are two chaotic systems called the master (or drive) and the slave (or response) system, the objective of the designed controller for synchronization is to make the output of the master system follow the output of the slave system asymptotically. Diverse methods have been proposed to achieve chaos synchronization, for instance, backstepping control [9, 10], adaptive backstepping control [11], active control [12, 13], PI observe design [14], dynamic surface control [15], variable structure control [16, 17], robust control [18], and impulsive control [19] et al. In [19], a novel dual-stage impulsive control was proposed for the robust exponential synchronization problem of a class of chaotic delayed neural networks with different parametric uncertainties, which provides a more practical framework for the synchronization of multi-perturbation delayed chaotic systems. In the past few years, synchronization in complex networks has been discussed extensively [20]. In [21], the synchronization in an inter-neuronal networks was studied and the effects of long inhibitory synaptic delays were specifically considered. Additionally, synchronization transition has been reported in some neuronal networks [22]. In [23–25], Wang et al. studied synchronization transitions on neuronal networks for the information transmission delays. Recently, Wang and Szolnoki et al. studied the evolution games on inter-dependent networks which are connected by means of a utility function [26, 27]. It is shown that the stronger the bias in the utility function is, the higher the level of the public cooperation.

On the other hand, anti-synchronization is a noticeable phenomenon in periodic oscillators [28, 29], which is defined as vanishing of the sum of relevant variables, and has important application significance. Using anti-synchronization for lasers [30] and particle separation [31], some control methods, for instance, adaptive backstepping control [32], linear feedback control [33], active control [34], linear sliding mode control (LSMC) [35], have been applied to anti-synchronization chaotic systems. However, in real physical systems, due to the existence of external disturbances and model uncertainties, the anti-synchronization errors cannot often converge to zero in a finite time.

As is well known, variable structure control (VSC) with sliding mode control was first proposed and elaborated in the early 1950s in the Soviet Union by Emelyanov [35] and Utkin [36]. Since then, VSC has developed into a general design method being examined for a wide spectrum of system types including single-input and single-output (SISO) nonlinear systems [37–39], multi-input and multi-output (MIMO) nonlinear systems [40], discrete-time systems [41], stochastic systems [42], large-scale systems [43], and so forth. Sliding mode control has become one of the most important approaches to handle systems with large uncertainties, nonlinearities, and bounded external disturbances.

Over the past decades, in order to design sliding mode control systems, a linear sliding mode (LSM) switching surface was first defined [44], and a LSM controller was then designed to drive the system state variables to reach the sliding mode surface, and asymptotically converge to zero. However, the system states in the sliding mode surface cannot converge to zero in a finite time. In order to get fast convergence on the sliding mode surface, terminal sliding mode control (TSMC) was first proposed in [45] and [46]. The terminal sliding mode switching surface is formed by inserting a nonlinear term of the system states in the linear sliding mode switching surface. It is shown that a TSMC robust controller can drive the system state variables to reach the sliding mode surface and converge to zero in a finite time [45, 46]. TSMC was further investigated for SISO linear systems [47], MIMO linear systems [48], and nonlinear systems [46, 49–51]. However, the terminal sliding mode control has a singularity problem in [46] (see [52]). Soon after, [50] and [51] proposed a non-singular terminal sliding manifold and avoided the singularity problem. Then another approach was proposed to avoid the singularity by switching from the terminal to the linear sliding manifold [48].

In this paper, we will adopt adaptive terminal sliding mode control for anti-synchronization of uncertain chaotic system. A non-singular terminal sliding mode controller is designed to drive the track error to reach the terminal sliding mode surface and converge to zero in a finite time. The main contributions of this paper are listed as follows.

  1. (1)

    Combining terminal sliding mode control and adaptive control, a robust controller is designed for the investigated system.

  2. (2)

    By selecting the control law in the different case, the singularity problem on terminal sliding mode can be avoided.

  3. (3)

    The boundary layer control law was used to eliminate the effect of chattering.

  4. (4)

    The anti-synchronization errors can converge to zero in a finite time.

The rest of this paper is organized as follows. Section 2 presents problem formulation and preliminaries. In Sect. 3, the adaptive terminal sliding mode controller for Duffing-Holmes chaotic system is designed. In Sect. 4, the design of the controller for anti-synchronization of different chaotic system is given. Simulation results are included in Sect. 5. Section 6 gives the conclusions.

2 Problem formulation and preliminaries

Consider a chaotic system formulated by the following equations:

$$ \begin{aligned} & \dot{x}_{i} = x_{i + 1},\quad i = 1, \ldots,n - 1 \\ &\dot{x}_{n} = f ( x ) \end{aligned} $$
(1)

where x=[x 1,…,x n ]T is the states variable of the system, f: is a continuous function including nonlinear terms. We take system (1) as the master system. On the other hand, the slave system is given by

$$ \begin{aligned} &\dot{y}_{i} = y_{i + 1},\quad i = 1, \ldots,n - 1 \\ &\dot{y}_{n} = g ( y ) + z ( y )u + \Delta ( t ) \end{aligned} $$
(2)

where y=[y 1,…,y n ]T is the state variable of the system, g is a continuous function including nonlinear terms, function z(y)≠0, u∈R is the control input, Δ(t) is the uncertainty of the parameter disturbances and external noise perturbations applied to the chaotic system.

Assumption 1

Without loss of generality, we assume Δ(t) is bound and satisfies |Δ(t)|≤ξ.

The anti-synchronization of the master-slave system is achieved for any initial condition x i (0) and y i (0) if the following equation holds:

$$ \lim_{t \to \infty} \bigl \Vert e_{i} ( t ) \bigr \Vert = \lim_{t \to \infty} \bigl \Vert y_{i} ( t ) + x_{i} ( t ) \bigr \Vert = 0 $$
(3)

Hence the error system becomes

$$ \begin{aligned} & \dot{e}_{i} = e_{i + 1} \\ & \dot{e}_{n} = f ( x ) + g ( y ) + z ( y )u + \Delta ( t ) \end{aligned} $$
(4)

To design a control system with the error converging in a finite time, the following hierarchical terminal sliding mode structure is defined [47]:

$$ \begin{aligned} & s_{1} = e_{1} \\ & s_{i + 1} = \dot{s}_{i} + \beta_{i}s_{i}^{q_{i} / p_{i}}, \quad i = 1, \ldots,n - 1 \end{aligned} $$
(5)

where β i >0,p i >q i and p i ,q i are positive odd integers [47, 52].

Remark 1

If a terminal sliding mode controller is designed such that \(s_{n}\dot{s}_{n} < 0\) is satisfied, namely s n can reach to zero in a finite time, then s n−1,…,s 1 can converge to zero in finite time sequentially and errors variable can reach zero in a finite time. The time for the error system state e 1 to reach zero is

$$ t = t_{1} + \sum_{i = 1}^{n - 1} \frac{1}{\beta_{i}} \frac{p_{i}}{p_{i} - q_{i}}s_{i} ( t_{n - i} )^{p_{i} - q_{i} / p_{i}} $$
(6)

where t i is the reaching time of the terminal sliding mode s n−i+1 for i=1,…,n.

Remark 2

Firstly, by choosing p i >q i , then 1−q i /p i >0. Secondly, in order to make \(s_{i} ( t_{n - i} )^{p_{i} - q_{i} / p_{i}} > 0\), then, p i and q i are selected as positive odd integers [52].

One uses a sliding mode controller

$$ u = \begin{cases} - \frac{1}{z ( y )}\operatorname{sign} ( s_{n} ) ( \vert f ( x ) + g ( y ) + \sum_{i = 1}^{n - 1} \beta_{i} \frac{d^{n - i}}{dt^{n - i}} ( s_{i}^{q_{i} / p_{i}} ) \vert + \xi + \hat{k} ) & \mbox{for }s_{n} \ne 0\mbox{ and }s_{i} \ne 0 \\ 0& \mbox{for }s_{n} = 0\mbox{ or } ( s_{n} \ne 0\mbox{ and }s_{i} = 0 ) \end{cases} $$
(7)

Remark 3

It is easy to see that, at the point e 1≠0 with s i =0, the control signal \(\sum_{i = 1}^{n - 1} \beta_{i} \frac{d^{n - i}}{dt^{n - i}} ( s_{i}^{q_{i} / p_{i}} )\) can generate an unbounded value. To deal with this problem, by choosing u=0, thus, the singularity problem can also be overcome [46].

Proof

Define a Lyapunov function

$$ V = \frac{1}{2}s_{n}^{2} + \frac{1}{2\gamma} \tilde{k}^{2} $$
(8)

where k represent the control input gain, since k is unknown, so we need to estimate k, and we will use the notation \(\hat{k}\) to denote the estimation of k, \(\tilde{k} = k - \hat{k}\), \(\dot{\tilde{k}} = - \dot{\hat{k}}\).

Differentiating V with respect to time, we have

$$\begin{aligned} \dot{V} = & s_{n}\dot{s}_{n} - \frac{1}{\gamma} \tilde{k}\dot{\hat{k}} \\ =& s_{n} \Biggl( \dot{e}_{n} + \sum_{i = 1}^{n - 1} \beta_{i}\frac{d^{n - i}}{dt^{n - i}} \bigl( s_{i}^{q_{i} / p_{i}} \bigr) \Biggr) - \frac{1}{\gamma} \tilde{k}\dot{\hat{k}} \end{aligned}$$
(9)

Using (7) in (9), we get

$$\begin{aligned} \dot{V} \le& - \hat{k}\vert s_{n} \vert - \frac{1}{\gamma} \tilde{k}\dot{\hat{k}} = - \hat{k}\vert s_{n} \vert - \tilde{k}\vert s_{n} \vert + \tilde{k}\vert s_{n} \vert - \frac{1}{\gamma} \tilde{k}\dot{\hat{k}} \\ =& - k\vert s_{n} \vert + \tilde{k} \biggl( \vert s_{n} \vert - \frac{1}{\gamma} \dot{\hat{k}} \biggr) \end{aligned}$$
(10)

by choosing \(\dot{\hat{k}} = \gamma \vert s_{n} \vert \), we get

$$ \dot{V} = - k\vert s_{n} \vert < 0 $$
(11)

where k>0. □

3 Anti-synchronization of two-dimensional Duffing–Holmes systems

Firstly, we consider the following Duffing–Holmes equation as the master (or drive) system:

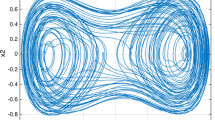
$$ \begin{cases} \dot{x}_{1} = x_{2} \\ \dot{x}_{2} = - p_{1}x_{1} - p_{2}x_{2} - x_{1}^{3} + q_{1}\cos ( w_{1}t ) \end{cases} $$
(12)

in the case that p 1=−1, p 2=0.25, q 1=0.3, w 1=1 system (1) exhibits a chaotic behavior [38], as shown in Fig. 1.

Fig. 1
figure 1

Duffing–Holmes system state space trajectory

Full size image

By using a controller input u(t) and considering Δf(x,y) as uncertainty term on the Duffing–Holmes system (12) as slave (or response) system:

$$ \begin{cases} \dot{y}_{1} = y_{2} \\ \dot{y}_{2} = - p_{1}y_{1} - p_{2}y_{2} - y_{1}^{3} + q_{1}\cos ( w_{1}t )\\ \phantom{\dot{y}_{2} ={}} + \Delta f ( y_{1},y_{2} ) + u \end{cases} $$
(13)

where x i (i=1,2) and y i (i=1,2) are states variable on the master and slave systems, respectively, the u(t)∈R is the control input, Δf(y 1,y 2) is the uncertainty of parameter disturbances and external noise perturbations applied to the chaotic system. In general it is assumed that Δf(y 1,y 2) is bounded by

$$ \Delta f ( y_{1},y_{2} ) \le \sigma = 0.3 + 0.8 \bigl \Vert ( y_{1},y_{2} ) \bigr \Vert $$
(14)

The synchronization error system between system (12) and system (13) is defined as

$$ \begin{aligned} &\dot{e}_{1} = e_{2} \\ &\dot{e}_{2} = \dot{x}_{2} + \dot{y}_{2} \end{aligned} $$
(15)

The following first-order terminal sliding variable is defined:

$$ s = e_{2} + \beta e_{1}^{q/p} $$
(16)

where β>0,p and q are positive odd integers and p>q.

Using a sliding mode controller

$$ u = \left\{\begin{array}{@{}l@{}} - ( \hat{k}_{1} + \eta )\operatorname{sign} ( s ),\quad s \ne 0\mbox{ and }e_{1} \ne 0 \\ 0, \quad ( s \ne 0\mbox{ and }e_{1} = 0 )\mbox{ or }s = 0 \end{array}\right. $$
(17)

where

$$\begin{aligned} \eta = &\biggl \vert - p_{1} e_{1} - p_{2}e_{2} - \bigl(x_{1}^{3} + y_{1}^{3} \bigr) \\ &{}+ 2q_{1}\cos ( w_{1}t ) + \beta \frac{q}{p}e_{1}^{q / p - 1} e_{2} \biggr \vert + \sigma \end{aligned}$$
(18)

and the control input gain estimate \(\hat{k}_{1}\) is

$$ \dot{\hat{k}}_{1} = \frac{1}{\gamma} \vert s \vert $$
(19)

Proof

Define a Lyapunov function

$$ V = \frac{1}{2}s^{2} + \frac{\gamma}{2}\tilde{k}_{1}^{2} $$
(20)

Differentiating V with respect to time, we have

$$\begin{aligned} \dot{V} = &s\dot{s} + \gamma \tilde{k}_{1}\dot{k}_{1} \\ =& s \biggl(\dot{e}_{2} + \beta \frac{q}{p}e_{1}^{q / p - 1} \dot{e}_{1} \biggr) - \gamma \tilde{k}_{1}\dot{ \hat{k}}_{1} \\ =& s\biggl( - p_{1}e_{1} - p_{2}e_{2} - \bigl(x_{1}^{3} + y_{1}^{3}\bigr) + 2q_{1}\cos (w_{1}t) \\ &{} + \Delta f + u + \beta \frac{q}{p}e_{1}^{q / p - 1}e_{2} \biggr) - \gamma \tilde{k}_{1}\dot{\hat{k}}_{1} \\ \le& \vert s \vert \eta + su - \gamma \tilde{k}_{1}\dot{ \hat{k}}_{1} = - \vert s \vert \hat{k}_{1} - \gamma \tilde{k}_{1}\dot{\hat{k}}_{1} \\ =& - \vert s \vert \hat{k}_{1} - \vert s \vert \tilde{k}_{1} + \vert s \vert \tilde{k}_{1} - \gamma \tilde{k}_{1}\dot{\hat{k}}_{1} \\ =& - \vert s \vert k_{1} + \tilde{k}_{1}\bigl(\vert s \vert - \gamma \dot{\hat{k}}_{1}\bigr) = - \vert s \vert k_{1} < 0 \end{aligned}$$
(21)

 □

Remark 4

Because the control input u is discontinuous across the sliding mode surfaces, it may excite undesired high frequency dynamics. To eliminate the effects of the chattering, we use the following boundary layer control law in place of the discontinuous control law in expression (17) [46]:

(22)

where ε 1>0.

4 Anti-synchronization of three-dimensional Lur’e and Genesio systems

In this section, we consider anti-synchronization of the three-dimensional chaotic system.

Firstly, the Lur’e dynamic system has been selected as the master system:

$$\begin{aligned} &{ \left\{\begin{array}{@{}l@{}} \dot{x}_{1} = x_{2} \\ \dot{x}_{2} = x_{3} \\ \dot{x}_{3} = a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3} + 12\varphi ( x_{1} ) + c\sin ( t )v ( t ) \end{array} \right.} \\ &{ \varphi ( x_{1} ) = \begin{cases} kx_{1}, & \vert x_{1} \vert < \frac{1}{k} \\ \operatorname{sign} ( x_{1} ),& \mbox{otherwise} \end{cases} } \end{aligned}$$
(23)

for a 1=−7.4, a 2=−4.1, a 3=−1, k=3.6, c=0, the behavior of the system is chaotic [53], as shown in Fig. 2.

Fig. 2
figure 2

Lur’e system state space trajectory

Full size image

Secondly, the Genesio chaotic system is chosen as the slave (or response) response system. The dynamic equation of the Genesio system is

$$ \left\{\begin{array}{l} \dot{y}_{1} = y_{2} \\ \dot{y}_{2} = y_{3} \\ \dot{y}_{3} = b_{1}y_{1} + b_{2}y_{2} + b_{3}y_{3} + y_{1}^{2} + ( 0.5 + \vert y_{1} \vert )u \end{array} \right. $$
(24)

for b 1=−5.6, b 2=−2.74, b 3=−1.1, u=0, the dynamic behavior of the Genesio system is chaotic [9], as shown in Fig. 3.

Fig. 3
figure 3

Genesio system state space trajectory where x i (i=1,2,3) and y i (i=1,2,3) are state variables on the master and slave systems, respectively. u(t)∈R is the control input, v(t) is a bounded continuous random process and |v|<N

Full size image

The anti-synchronization error system between systems (23) and (24) is defined as

$$ \begin{array}{@{}l@{}} \dot{e}_{1} = e_{2} \\ \dot{e}_{2} = e_{3} \\ \dot{e}_{3} = \dot{x}_{3} + \dot{y}_{3} \end{array} $$
(25)

To design control system with the error converging in a finite time, the following hierarchical terminal sliding mode structure is defined:

$$\begin{aligned} \begin{aligned} &s_{1} = e_{1} \\ & s_{2} = \dot{s}_{1} + \beta_{1}s_{1}^{q_{1}/p_{1}} \\ & s_{3} = \dot{s}_{2} + \beta_{2}s_{2}^{q_{2}/p_{2}} \end{aligned} \end{aligned}$$
(26)

The control input is designed such that

$$\begin{aligned} &{u = \left \{ \begin{array} {@{}l@{}} \frac{ - 1}{0.5 + \vert y_{1} \vert } ( \eta_{1} + \hat{k}_{2} )\operatorname{sign} ( s_{3} ) \\ \quad \mbox{for }s_{3} \ne 0\mbox{ and }s_{2} \ne 0\mbox{ and }e_{1} \ne 0 \\ 0 \quad \mbox{for } s_{3} = 0\mbox{ or } ( s_{3} \ne 0 \mbox{ and }( e_{1} = 0\mbox{ or }s_{2} = 0 ) ) \end{array} \right .} \\ \end{aligned}$$
(27)
$$\begin{aligned} &{ \begin{aligned}[b] \eta_{1} &= \biggl \vert a_{1} x_{1} + a_{2}x_{2} + a_{3}x_{3} + 12\varphi ( x_{1} ) + b_{1}y_{1} \\ &\quad + b_{2}y_{2} + b_{3}y_{3} + y_{1}^{2} \\ &\quad + \beta_{1}\frac{q_{1}}{p_{1}} \biggl( \frac{q_{1}}{p_{1}} - 1 \biggr)e_{1}^{q_{1} / p_{1} - 2}e_{2}^{2} + \beta_{1}\frac{q_{1}}{p_{1}}e_{1}^{q_{1} / p_{1} - 1}e_{3} \\ & \quad + \beta_{2}\frac{q_{2}}{p_{2}} \bigl( e_{2} + \beta_{1}e_{1}^{q_{1} / p_{1}} \bigr)^{q_{2} / p_{2} - 1} \\ &\quad\times\biggl( e_{3} + \beta_{1}\frac{q_{1}}{p_{1}}e_{1}^{q_{1} / p_{1} - 1}e_{2} \biggr) \biggr \vert \\ &\quad + \bigl \vert c\sin ( t )N \bigr \vert \end{aligned}} \end{aligned}$$
(28)

and we have the adaptive law \(\dot{\hat{k}}_{2} = \gamma_{2}\vert s_{3} \vert \).

Proof

Define a Lyapunov function

$$ V = \frac{1}{2}s_{3}^{2} + \frac{1}{2\gamma_{2}} \tilde{k}_{2}^{2} $$
(29)

Differentiating V with respect to time, we have

$$\begin{aligned} \dot{V} =& s_{3}\dot{s}_{3} + \frac{1}{\gamma_{2}} \tilde{k}_{2}\dot{\tilde{k}}_{2} \\ =& s_{3}\biggl(\dot{e}_{3} + \beta_{1} \frac{q_{1}}{p_{1}}\biggl(\frac{q_{1}}{p_{1}} - 1\biggr)e_{1}^{q_{1} / p_{1} - 2}e_{2}^{2} \\ &{}+ \beta_{1}\frac{q_{1}}{p_{1}}e_{1}^{q_{1} / p_{1} - 1}e_{3} \\ &{} + \beta_{2}\frac{q_{2}}{p_{2}}\bigl(e_{2} + \beta_{1}e_{1}^{q_{1} / p_{1}}\bigr)^{q_{2} / p_{2} - 1} \\ &{}\times \biggl(e_{3} + \beta_{1}\frac{q_{1}}{p_{1}}e_{1}^{q_{1} / p_{1} - 1}e_{2} \biggr)\biggr) \,{+}\, \frac{1}{\gamma_{2}}\tilde{k}_{2}\dot{\tilde{k}}_{2} \\ =& s_{3}\biggl(a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3} + 12\varphi (x_{1}) \\ &{} + c\sin (t)v(t) + b_{1}y_{1} + b_{2}y_{2} + b_{3}y_{3} + y_{1}^{2} \\ &{}+ \bigl(0.5 + \vert y_{1} \vert \bigr)u \\ &{} + \beta_{1}\frac{q_{1}}{p_{1}}\biggl(\frac{q_{1}}{p_{1}} - 1 \biggr)e_{1}^{q_{1} / p_{1} - 2}e_{2}^{2} + \beta_{1}\frac{q_{1}}{p_{1}}e_{1}^{q_{1} / p_{1} - 1}e_{3} \\ &{} + \beta_{2}\frac{q_{2}}{p_{2}}\bigl(e_{2} + \beta_{1}e_{1}^{q_{1} / p_{1}}\bigr)^{q_{2} / p_{2} - 1} \\ &{}\times \biggl(e_{3} + \beta_{1}\frac{q_{1}}{p_{1}}e_{1}^{q_{1} / p_{1} - 1}e_{2} \biggr)\biggr) \,{-}\, \frac{1}{\gamma_{2}}\tilde{k}_{2}\dot{\hat{k}}_{2} \\ \le& \vert s_{3} \vert \eta_{1} + s_{3}\bigl(0.5 + \vert y_{1} \vert \bigr)u - \frac{1}{\gamma_{2}}\tilde{k}_{2} \dot{\hat{k}}_{2} \\ =& - k\vert s_{3} \vert + \tilde{k}\biggl(\vert s_{3} \vert - \frac{1}{\gamma_{2}}\dot{\hat{k}}_{2}\biggr) = - k\vert s_{3} \vert < 0 \end{aligned}$$
(30)

 □

Remark 5

Likewise, we use the boundary layer control law in place of the discontinuous control law in expression (27),

$$ u = \left\{ \begin{array}{@{}l@{}} \frac{ - 1}{0.5 + \vert y_{1} \vert } (\eta_{1} + k_{2} )\operatorname{sign} ( s_{3} ) \\ \quad \mbox{for }\vert s_{3} \vert \ge \varepsilon_{2}\mbox{ and }e_{1} \ne 0\mbox{ and }s_{2} \ne 0 \\ \frac{ - 1}{0.5 + \vert y_{1} \vert } ( \eta_{1} + k_{2} )\frac{s_{3}}{\varepsilon_{2}} \\ \quad \mbox{for }\vert s_{3} \vert < \varepsilon_{2}\mbox{ and }e_{1} \ne 0\mbox{ and }s_{2} \ne 0 \\ 0 \quad \mbox{for }s_{3} = 0\mbox{ or } ( s_{3} \ne 0\mbox{ and } ( e_{1} \,{=}\, 0\mbox{ or }s_{2} \,{=}\, 0 ) ) \end{array} \right. $$
(31)

where we have ε 2>0.

Remark 6

The objective of this paper is to design a non-singular robustness controller for an uncertain chaotic system, finite time convergence and stability of the closed loop system can be guaranteed.

Remark 7

The proposed method is different from the impulsive control method in [19], where an efficient impulsive control method was presented to deal with the dynamical systems which cannot be controlled by continuous control methods. In this paper, an adaptive terminal sliding mode control method is proposed for anti-synchronization of two-dimensional identical chaotic systems and three-dimensional different chaotic systems.

5 Simulation

The numerical simulation is presented in this section. The following two methods are compared.

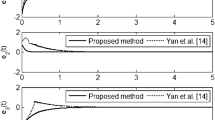
Firstly, we consider anti-synchronization of the Duffing–Holmes chaotic system (12)–(13) as shown in Figs. 4 and 5.

Fig. 4
figure 4

TSMC: the parameter values are p 1=−1, p 2=0.25, q 1=0.3, w 1=1, p=5, q=3, β=1, γ 1=0.35, ε 1=0.01, x 0=[0.1;0.2], and y 0=[−0.5;0.5]. (a) The control input. (b) The system states. (c) Anti-synchronization errors

Full size image
Fig. 5
figure 5

LSMC: the parameter values are p 1=−1, p 2=0.25, q 1=0.3, w 1=1, p=5, q=3, β=1, γ 1=0.35, ε 1=0.01, x 0=[0.1;0.2], y 0=[−0.5;0.5]. (d) The control input. (e) The system states. (f) Anti-synchronization errors

Full size image

Next, we consider anti-synchronization of the Lur’e and Genesio systems as shown in Figs. 6 and 7.

Fig. 6
figure 6

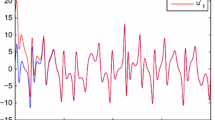
TSMC: the parameter values are a 1=−7.4, a 2=−4.1, a 3=−1, k 1=3.6, c=0.2, v=10, b 1=−5.6, b 2=−2.74, b 3=−1.1, q 1=3, p 1=5, q 2=3, p 2=5, β 1=0.5, β 2=0.57, γ 2=1.4, ε 2=0.01, we pick up the initial values of x 0=[2.25;4;2.5] and y 0=[−3;−5;20]. (g) The control input. (h) The system states. (i) Anti-synchronization errors

Full size image
Fig. 7
figure 7

LSMC: the parameter values are a 1=−7.4, a 2=−4.1, a 3=−1, k 1=3.6, c=0.2, v=10, b 1=−5.6, b 2=−2.74, b 3=−1.1, q 1=3, p 1=5, q 2=3, p 2=5, β 1=0.5, β 2=0.57, ε 2=0.01, x 0=[2.25;4;2.5], y 0=[−3;−5;20]. (j) The control input. (k) The system states. (l) Anti-synchronization errors

Full size image

The simulation examples show that TSMC is superior to LSMC. TSMC can converge to zero in a finite time, however, LSMC cannot converge to zero in a finite time and the control input performs a high frequency chattering.

6 Conclusions

In this paper, a new adaptive terminal sliding mode control for anti-synchronization of uncertain chaotic system has been proposed. Based on Lyapunov stability theory, a robust controller is designed to drive the track error to reach terminal sliding mode surface and converge to zero in a finite time.

The future research will focus on the investigation of the terminal sliding control of the synchronization of chaotic systems with delay, as well as the limitations and the relevant solutions in the terminal sliding control.