1 Introduction

Financial markets are complex dynamical systems [1–5], which consist of a large number of interacting units that can be clustered into two major groups: one is the traders (e.g., private investors, common funds, brokers, insurers, and banks), and the other is the assets (e.g., stocks, bonds, warrants, options, and futures) [6]. These heterogeneous units interact nonlinearly over time with each other and lead to transactions mediated by the trading platform (e.g., the stock exchange) [6, 7]. The dynamics of a financial market are typically vague and hard to understand and describe [8]: not only because of the complexity of its inside units, but also because of many intractable outside parts working on the financial market [6].

The cross-correlations between financial variables are the important characteristics of market dynamics in financial markets [9–19]. The study of cross-correlations of a set of financial entities is very significant for understanding and describing the mechanisms and natures of financial markets [18]. Besides, the study of cross-correlations between financial variables can improve the financial forecasting and modeling of composed financial entities (e.g., stock portfolios) [20]. That is to say, the nature and dynamical properties of cross-correlations between financial entities are conducive to avoiding the risk of an investment in financial markets. Therefore, it is an important and interesting study to quantify the cross-correlation features between financial variables.

In previous works, there are many different approaches to study the cross-correlations between the financial entities, such as the correlation networks method [21–24] and the random matrix theory [25–28], which assume that both of analyzed time series are stationary [15]. However, in the real-world, the financial time series are usually nonstationary and characterized by a high level of heterogeneity [29]. Thus, the above mentioned methods to investigate the cross-correlations between the financial time series may be not very accurate. To overcome the limitation in previous studies, many methods based on the mono and multifractal theory are proposed to study the autocorrelation and cross-correlations in financial markets [11–18, 20]. For a nonstationary time series, the detrended fluctuation analysis (DFA) method was proposed by Peng et al. [30], which can be adopted to determine its long-range dependence and autocorrelation. The detrending moving-average (DMA) method [31] is an alternative approach of DFA, which was also used to quantify the long-range correlations of nonstationary time series. However, for multifractal time series, the multifractal detrending moving average (MF-DMA) [32] is more robust than the multifractal detrended fluctuation analysis (MF-DFA) [33]. Podobnik and Stanley [34] proposed detrended cross-correlation analysis (DCCA) to quantify power-law cross-correlations between simultaneously recorded nonstationary time series, which is widely applied in various fields [13, 18, 35–38]. Then, both the MF-DFA and MF-DMA were combined with DCCA to investigate the long-range cross-correlations between two nonstationary time series, which are called as multifractal detrended cross-correlation analysis (MF-DCCA, or MF-XDFA) [39] and multifractal detrending moving-average cross-correlation analysis (MF-XDMA) [40], respectively. The results of empirical analysis in [40] indicated that, for the financial return time series, the centered MF-XDMA performs better than the MF-XDFA.

In the complex and dynamic financial markets, the futures markets play important roles in avoiding the systemic risk for investors and practitioners, and discovering the price mechanism. On April 16, 2010, China Financial Futures Exchange (CFFEX) launched its decade-long awaited index futures—China Securities Index 300 (CSI 300) futures, which is a milestone event in the China’s efforts to push the reform of the capital market, and shows that the China’s capital market is entering a new period. However, the study of cross-correlations between index spot and futures markets is rare, especially between CSI 300 spot and futures markets. Therefore, in this study, we employ the MF-XDMA method to investigate the cross-correlations between CSI 300 spot and futures markets. Moreover, by using the method of rolling windows, we examine the evolution of cross-correlations.

The rest of this paper is organized as follows. In the next section, we provide the methodology of MF-XDMA. In Sect. 3, we present the data set and make the preliminary analysis. We show the main empirical results and some relevant discussions in Sect. 4. Finally, in Sect. 5, we draw some conclusions.

2 Methodology

MF-XDMA is used to investigate the cross-correlations between two nonstationary time series, which can be described as follows [40]:

Step 1

Consider two time series {x(t)} and {y(t)} of the same length N, where t=1,2,…,N. We calculate two sequences of cumulative sums

$$ \begin{aligned} &X(t) = \sum _{i = 1}^t {x(i)},\\ &Y(t) = \sum _{i = 1}^t y(i),\quad t = 1,2, \ldots,N. \end{aligned} $$
(1)

Step 2

For a wind of size n, the moving average function \(\tilde{Z}(t)\) of Z∈{X,Y} is defined by

$$ \tilde{Z}(t) = \frac{1}{n}\sum _{k = - \lfloor{(n - 1)\theta} \rfloor}^{ \lceil{(n - 1)(1 - \theta)} \rceil} {Z(t - k)} , $$
(2)

where θ is the position parameter ranging from 0 to 1, ⌊g⌋ and ⌈g⌉ are the largest integer not greater than g and the smallest integer not smaller than g, respectively. In [32, 40], the authors implied that “the moving average function considers ⌈(n−1)(1−θ)⌉ data points in the past and ⌊(n−1)θ⌋ points in the future.” In particular, [32, 40] considered three special cases about θ: (i) θ=0 corresponds to the backward moving average [41], where \(\tilde{Z}(t)\) is calculated over all the past n−1 data points. (ii) θ=0.5 refers to the centered moving average [41], where \(\tilde{Z}(t)\) is calculated from half-past data points and half-future data points. (iii) θ=1 corresponds to the forward moving average [41], where \(\tilde{Z}(t)\) is calculated over all the future n−1 data points. In this study, as suggested by Jiang et al. [40], we only consider the case of the centered moving average, i.e., θ=0.5.

Step 3

By subtracting the moving average function \(\tilde {Z}(i)\) from Z(i), we can remove the possible trends of the time series and obtain the cross-correlation residual series ε(i) by

$$ \varepsilon(i) = \bigl[X(i) - \tilde{X}(i)\bigr] \bigl [Y(i) - \tilde{Y}(i)\bigr], $$
(3)

where n−⌊(n−1)θ⌋≤i≤N−⌊(n−1)θ⌋.

Step 4

The residual sequence ε(i) is subdivided into N n =⌊N/n−1⌋ nonoverlapping segments of equal length n. For each nonoverlapping segment v, ε v (i) is such that ε v (i)=ε v (l+i) for 1≤i≤n, where l=(v−1)n and 1≤v≤N n . The cross-correlation fluctuation variance for each segment can be calculated by

$$ F(n,v) = \frac{1}{n}\sum _{i = 1}^n {\varepsilon_v (i)} . $$
(4)

Step 5

The qth-order fluctuation function can be obtained by averaging over all segments

$$ F_{xy} (q,n) = \Biggl\{ {\frac{1}{N_n }\sum _{v = 1}^{N_n } {\bigl\vert F(n,v)\bigr\vert^{q / 2}} } \Biggr \}^{1 / q}, $$
(5)

for any real value q≠0 and

$$ F_{xy} (0,n) = \exp\Biggl\{ {\frac{1}{2N_n }\sum _{v = 1}^{N_n } {\ln\bigl\vert F(n,v)\bigr\vert} } \Biggr\}. $$
(6)

Step 6

By observing the log-log plots F xy (q,n) versus n, we can determine the scaling behavior of the fluctuation function. If the two time series are long-range power-law cross-correlated, the fluctuation function F xy (q,n) will increase as a power-law [33]

$$ F_{xy} (q,n)\sim n^{h_{xy} (q)}, $$
(7)

for large values of n. The scaling exponent h xy (q) can be obtained by observing the slope of the log-log plot of F xy (q,n) versus n via the method of ordinary least squares (OLS) [14–17]. In general, the scaling exponent h xy (q) depends on q, and there are three cases of h xy (q): (i) If h xy (q)<0.5, the cross-correlations between the two time series are antipersistent (negative). This implies that if there is an increase of the spot (futures) price, then the futures (spot) price is likely to be followed by a decrease [17], and vice versa. (ii) If h xy (q)>0.5, the cross-correlations between the two time series are persistent (positive). This means that if the spot (futures) price has been an increase or decrease, then the futures (spot) price is likely to be increased or decreased, respectively [17]. (iii) If h xy (q)=0.5, there are no cross-correlations between the two time series, and the change of one price cannot affect the behavior of the other price [16–18].

Especially, if the time series {x(i)} is the same as {y(i)}, the MF-XDMA method reduces to the MF-DMA; and when q=2, the scaling exponent h xy (q) is equivalent to the well-known Hurst exponent H (or denotes as h xy (2)), and the MF-DMA method is just the DMA [15]. According to the multifractal theory, we can use the multifractal scaling (or Rényi) exponent τ(q) to characterize the multifractal nature by

$$ \tau_{xy} (q) = qh_{xy} (q) - D_f , $$
(8)

where D f is the fractal dimension of a geometric object [32]. In our study, D f =1 for the time series analysis. If the multifractal scaling exponent τ xy (q) increases nonlinearly with q, then cross-correlation of the two correlated series has multifractal nature [32]. Via a Legendre transform of τ xy (q), the multifractal spectrum f xy (α) is defined by

$$ f_{xy} (\alpha) = \alpha q - \tau_{xy} (q), \quad \alpha= \mbox{d}\tau_{xy} (q) / \mbox{d}q, $$
(9)

where α is the singularity strength which can characterize the singularities in a time series [16].

3 Data and preliminary analysis

The underlying asset of CSI 300 futures is CSI 300 index (spot), and CSI 300 futures are traded on the CFFEX. The underlying index is composed with 300 largest A-shares listed on the Shanghai Stock Exchange and the Shenzhen Stock Exchange, which covers about 60 % of the China stock markets’ value [42]. The empirical data employed in this study consists of high-frequency transaction prices (every 5 min) of CSI 300 spot and futures from 9:35 a.m. April 16, 2010, to 3:00 p.m. February 17, 2012, which includes 22 dominant futures and 21408 high-frequency data (i.e., 446 trading days in total, and every trading day contains 48 high-frequency data). The transaction information and empirical data of CSI 300 spot and futures are provided by the CFFEX (http://www.cffex.com.cn/) and Tinysoft (http://www.tinysoft.com.cn/).

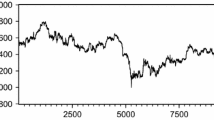
Under the high-frequency data environment, the return is calculated by a log-difference. That is, the return r(t) at time t is defined by

$$ r(t) = \ln P(t) - \ln P(t - \Delta t), $$
(10)

where P(t) and P(t−Δt) are the prices at time t and t−Δt, respectively. Δt is the time interval. At this point, Δt is 5 min. The volatility is defined by the absolute return |r(t)|. Figure 1 provides the graphical representation of prices and returns of CSI 300 spot and futures. Descriptive statistics of returns of CSI 300 spot and futures are described in Table 1. The mean values of the two return series are close to zero, while the standard deviations are very large. The Jarque–Bera statistics reject the null hypothesis of the Gaussian distribution at 1 % significance level, also evidenced by nonzero skewness and kurtosis larger than 3, which imply that the two return series are fat-tailed. The statistics of the ADF unit root tests reject the null hypothesis of a unit root at the 1 % significance level.

Fig. 1
figure 1

Prices and returns of CSI 300 spot and futures

Full size image
Table 1 Descriptive statistics of CSI 300 spot and futures returns
Full size table

In order to investigate the fat-tailed distribution of the two return series, we use a novel approach of power-law estimation proposed by Podobnik et al. [12], which can be briefly defined as follows. Podobnik et al. [12] implied that, on average, there is one volatility above threshold q after each time interval τ ave(q), then

(11)

For the CSI 300 spot and futures markets, we can calculate the average time interval \(\tau_{\rm{ave}}(q)\) for varying q, and acquire the estimates for β by the relationship

$$ \tau_{\rm{ave}} (q) \propto q^\beta. $$
(12)

Figure 2 presents the log-log plots of the average time interval \(\tau_{\rm{ave}}(q)\) versus threshold q. We set the different thresholds q, ranging from 2σ to 8σ with a fixed step of 0.25σ, where σ is the standard deviation of the absolute return. There is a power-law relationship with Podobnik’s tail exponent β=2.9963 for the CSI 300 spot market and with β=2.9021 for the CSI 300 futures market. We can find that the two Podobnik’s tail exponents are close to 3, which are similar to the results of [12] and confirmed the conclusion of “inverse cubic law (β≈3) [12, 43].”

Fig. 2
figure 2

Log-log plots of the average time interval \(\tau_{\rm{ave}}(q)\) vs. threshold q (in units of σ)

Full size image

4 Empirical results

4.1 Cross-correlations test

To quantify the cross-correlations between CSI 300 spot and futures markets, we use a new cross-correlations test proposed by Podobnik et al. [44], which is in analogy to the Ljung-Box test [45] and widely used in the financial markets [14, 16, 17, 46–48]. For two time series, {x(t)|t=1,2,…,N} and {y(t)|t=1,2,…,N}, the cross-correlation statistic is defined by

$$ Q_{cc} (m) = N^2\sum _{t = 1}^m {\frac{C^2(t)}{N - t}} , $$
(13)

where the cross-correlation function C(t) is defined as

$$ C(t) = \frac{\sum_{k = t + 1}^N {x(k)y(k - t)} }{\sqrt {\sum_{k = 1}^N {x^2(k)} \sum_{k = 1}^N {y^2(k)} } }. $$
(14)

Podobnik et al. [44] indicated that, the cross-correlation statistic Q cc (m) is approximately χ 2(m) distributed with m degrees of freedom. It can be used to test the null hypothesis of none of the first m cross-correlation coefficients is different from zero [44].

Figure 3 shows the log-log plots of cross-correlation statistics Q cc (m) versus degrees of freedom m for spot and futures return series of CSI 300, where the degrees of freedom range from 100 to 103. In order to make a comparison, as plotted in Fig. 3, we also provide the critical values for the χ 2(m) distribution at the 1 % level of significance. We can find that all the cross-correlation test statistics are lager than the critical values at the 1 % significance level. Hence, we can reject the null hypothesis of no cross-correlations between spot and futures return series of CSI 300. That is to say, cross-correlations significantly exist between CSI 300 spot and futures markets.

Fig. 3
figure 3

Log-log plots of test statistics Q cc (m) vs. degrees of freedom m

Full size image

4.2 Multifractal detrending moving-average cross-correlation analysis

Podobnik et al. [44] suggested that, the cross-correlations test of Eq. (13) can only be used to qualitatively test the presence of cross-correlations; while MF-XDMA can test the presence of cross-correlations quantitatively by estimating the cross-correlation exponent. Therefore, we use the MF-XDMA to investigate the cross-correlations quantitatively between CSI 300 spot and futures markets. We set the wind size (or time scale) n varying from 10 to N/10, where N is the equal length of the two return series of CSI 300, and q ranges from −4 to 4 with a step of 1/4. We present the log-log plots of the cross-correlation fluctuation function F xy (q,n) versus time scale n in Fig. 4. As shown in Fig. 4, it can be found that, for different q, all the curves are linear, which indicates that there exist power-law cross-correlations between the two return series of CSI 300. This finding implies that, a large price change in the CSI 300 futures market is possible to be followed by a large price change in the CSI 300 spot market, and vice versa.

Fig. 4
figure 4

Log-log plots of fluctuation functions F xy (q,n) vs. time scale n for cross-correlations between CSI 300 spot and futures markets

Full size image

Figure 5 illustrates the relationship of cross-correlation exponent h xy (q) and q between CSI 300 spot and futures markets (the curve with delta symbols). For a comparison, we calculate the scaling exponents h xx (q) and h yy (q) of CSI 300 spot and futures markets by MF-DMA, respectively. In Fig. 5, the curve with circle symbols represents CSI 300 spot market, and the curve with square symbols stands for CSI 300 futures market. If the scaling exponent varies with different q, the market is multifractal; otherwise, it is monofractal [15]. From Fig. 5, we can find that the h xy (q) decreases from larger than 0.61 to smaller than 0.50 for varying q, i.e., for different q, there is a different exponent. This implies that the cross-correlations between the CSI 300 spot and futures markets have obvious multifractal features. The multifractal features can also be found in CSI 300 spot and futures markets by observing the changes of h xx (q) and h yy (q), respectively. According to the previous studies by Podobnik and Stanley [34] and Zhou [39], in general, there exists the following relationship among h xy (q), h xx (q), and h yy (q):

$$ h_{xy} (q) = \bigl(h_{xx} (q) + h_{yy} (q)\bigr) / 2. $$
(15)

Therefore, we also calculate the average scaling exponents between the CSI 300 spot and futures markets by Eq. (15), and show the graphical representations in Fig. 5 (the curve with diamond symbols). From Fig. 5, however, we can find that the cross-correlation exponent is larger than the average scaling exponent for different q, which suggests that cross-correlations between CSI 300 spot and futures markets are stronger than the individual market’s long range auto-correlations (or long-term memories). This unexpected finding may be due to the influence of some unknown external events that simultaneously affect the behavior of the two markets of CSI 300. In other words, a large price change in one market is accompanied by a large price change in the other market more often than governed by the individual market’s behavior (e.g., autocorrelations).

Fig. 5
figure 5

The nonlinear relationship of h(q) and q between the CSI 300 spot and futures markets

Full size image

Figure 6 plots the Rényi exponent spectra τ xy (q) between the CSI 300 spot and futures markets estimated by the MF-XDMA (the curve with delta symbols). In Fig. 6, the curves with circle and square symbols stand for the Rényi exponent spectra of CSI 300 spot and futures return series estimated by the MF-DMA, respectively. The solid line with diamond symbols shows the monofractal region for Gaussian noise. According to the fractal theory, the monofractal time series generate a linear Rényi exponent spectrum while multifractal time sequences produce nonlinear spectrum [49]. As shown in Fig. 6, it can be seen that the τ xy (q) is nonlinearly dependent on q, and deviates from the linear monofractal region, which is another piece of evidence that multifractality exists in the cross-correlations between CSI 300 spot and futures markets.

Fig. 6
figure 6

The nonlinear relationship of τ(q) and q between the CSI 300 spot and futures markets

Full size image

We estimate the multifractal spectra between the two markets and the CSI 300 spot and futures markets, respectively, and plot the results in Fig. 7. It is widely known that if multifractal spectrum appears as a point, it is monofractal [15]. In Fig. 7, we can see that the multifractal spectra in the two markets are not a point, which implies that multifractality exists separately in the CSI 300 spot and futures markets and in the cross-correlated markets. To quantify the strength of multifractality, we introduce two measures [50]:

(16)
(17)
Fig. 7
figure 7

Multifractal spectra f(α) between the CSI 300 spot and futures markets

Full size image

The numerical results of multifractality degrees are organized in Table 2. By comparing the results in Table 2, we can find that the multifractality strength of cross-correlations between the two markets is greater than that of th CSI 300 spot but smaller than that of the CSI 300 futures. The results show once again that the cross-correlated markets have prominent multifractal features. One can find that the CSI 300 futures market has the strongest multifractality degree in Table 2. The reason may be that the CSI 300 futures market includes more noise than the CSI 300 spot market, such as speculations.

Table 2 Multifractality degrees Δh and Δα
Full size table

4.3 Rolling windows analysis

To capture the dynamics of cross-correlations, we use the method of rolling windows to investigate the evolution of cross-correlations varying time. The method of rolling windows is used to investigate the temporal evolution of the Hurst (scaling) exponent h xy (2) (when q=2) at different scales, which is also called as the local Hurst (scaling) exponent [51], or a rolling test [17]. The detailed introduction of the rolling windows method can be explained as follows: Suppose we have two high-frequency (5-min by 5-min) return time series with the same length of N (i.e., the returns series of the CSI 300 spot and futures), we use the first L (L<N) observations of the two pairs of return series to estimate scaling exponent h xy (2) (i.e., the time window width is L). After that, we calculate the second exponent from the ΔLth to (m+ΔL)th observations of the two pairs of return series (i.e., the window step length is ΔL). We proceed the above steps until both of the last ΔL observation(s) are used and we can obtain the time varying scaling exponents [52].

We calculate that the number of the average business days of the 22 dominant futures is approximately equal to 20 (about one trading month). Hence, we set the time window width L to be 20 trading days (i.e., 960 high-frequency data). Figure 8 presents the time-varying scaling exponents h xy (2) for two pairs of return series of the CSI 300 when the window step length ΔL is 5 min (i.e., one high-frequency data). As illustrated in Fig. 8, most of the scaling exponents are larger than 0.5 but are very near to 0.5, which indicates that the CSI 300 spot and futures markets are positively cross-correlated at present.

Fig. 8
figure 8

Dynamics of scaling exponents for q=2 between the CSI 300 spot and futures markets with window moving. The time window width is 20 trading days (i.e., 960 high-frequency data), and the window step length is 5 min (i.e., one high-frequency data)

Full size image

For robustness, we adjust the length of the window step to be one trading day (i.e., 48 high-frequency data) and present the results in Fig. 9. From Fig. 9, we can get similar results with Fig. 8. That is, the cross-correlations between the CSI 300 spot and futures returns are positive over time. The reason may be that the variations of futures prices partly determine the long-term trend of spot prices in the futures. The cross-correlated behaviors between the CSI 300 spot and futures markets are nonlinear (multifractal), which suggests that traditional linear models (e.g., vector auto-regression models (VAR)) could not be applied to describe the dynamics of the cross-correlations between the two markets. A similar conclusion was drawn by Wang and Xie [47] who investigated the cross-correlations between the WTI crude oil market and US stock market. As a whole, China’s stock markets are not mature and efficient markets and easily effected by market external factors, such as some irregular factors imposed by the governmental authorities, financial crisis, war, and politics, which need to improve the market efficiency and weaken the cross-correlations between spot and futures markets.

Fig. 9
figure 9

Dynamics of scaling exponents for q=2 between the CSI 300 spot and futures markets with window moving. The time window width is 20 trading days (i.e., 960 high-frequency data), and the window step length is one trading day (i.e., 48 high-frequency data)

Full size image

5 Conclusions

In summary, we investigate the cross-correlations between the return series of the CSI 300 spot and futures markets. By using a statistical test [44] in analogy to the Ljung–Box test, which can qualitatively test the presence of cross-correlations, we find that the cross-correlations are significant at the 1 % level. Through employing the MF-XDMA method, which can quantitatively test the presence of cross-correlations, we find that the cross-correlations are strongly multifractal. We also find that cross-correlation exponents are larger than the averaged generalized scaling exponents. Via using the method of rolling windows, which can capture the dynamics of cross-correlations, we find that most of the scaling exponents of cross-correlations between the two return series are larger than 0.5. This finding indicates that the CSI 300 spot and futures markets are positively cross-correlated at present. Finally, we also make some discussion on the cross-correlated behaviors of the two markets.