1 Introduction

The double pendulum has been widely studied in literature from different points of view [1–7], and it would appear that its scope has been exhausted. In a large number of the investigations carried out, the important parameter that has been singled out is the total energy E of the system, which is a conserved quantity, and hence extremely useful. While the really low energy dynamics where linearization holds would lead to motion on a torus, complications will set in as the amplitude is increased. This can lead to persistence of the torus (KAM) or breaking of torus according to the Poincare–Birkhoff scenario. The outcome should be sensitive to initial conditions and has not been explored for the double pendulum in the low energy regime. Calculations generally use canonical perturbation theory in action-angle variables and is difficult to implement for the double pendulum. Consequently, we decided to use a more easily implementable approach (Lindstedt–Poincare method and harmonic balance) for this system to see if initial conditions do make a difference. Having found that they do, we numerically integrated the full system to carry out a systematic analysis.

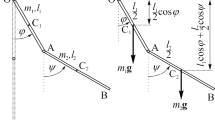
We would like to focus here on the two normal modes of the double oscillator when it undergoes small amplitude motion. These two modes are shown in Fig. 1. These two modes, which can be designated as “in-phase” and “out-of-phase,” will be the backbone of our work. We will concentrate on initial conditions, which are these normal modes even when the angular amplitude becomes large and will see in numerical integration that these two classes of initial conditions have strikingly different behaviors. This is also reflected in an analytic calculation of the amplitude dependence of the normal modes which are done by both harmonic balance and the Lindstedt–Poincare technique.

Fig. 1
figure 1

The “in-phase” and “out-of-phase” motions of a double pendulum

Full size image

In Sect. 2, we recall the salient features of the double pendulum and in Sect. 3 explain the harmonic balance and the Lindstedt–Poincare technique. This is necessary because we will adopt these techniques for the two degree-of-freedom case that we have here. While Sect. 4 describes our harmonic balance approach, Sect. 5 describes the Lindstedt–Poincare technique. Numerical results are presented in Sect. 6, and a short conclusion is in Sect. 7.

2 Double pendulum recalled

In this section, we recall briefly the equations of motion of the double pendulum, which will be of constant use in the subsequent sections. The double pendulum consists of two masses (m 1 and m 2 in general) attached to two massless rigid rods of length l 1 and l 2, respectively. The rod of length l 2 is attached to the mass m 1 and the rod of length l 1 is attached to a fixed support as shown in Fig. 2.

Fig. 2
figure 2

A standard double pendulum

Full size image

The Lagrangian of the system is found to be

(2.1)

As is often the case, one simplifies the subsequent algebraic complications by setting m 1=m 2=m and l 1=l 2=l. The Lagrangian now becomes

(2.2)

The equations of motion are

$$ 2\ddot{\theta}_1+\ddot{\theta}_2\cos( \theta_1-\theta_2)=-2\varOmega^2\sin \theta_1 -\dot{\theta}_2^2\sin( \theta_1-\theta_2) $$
(2.3)

and

$$ \ddot{\theta}_1\cos(\theta_1- \theta_2)+\ddot{\theta}_2=-\varOmega^2\sin \theta_2 -\dot{\theta}_1^2\sin( \theta_1-\theta_2) $$
(2.4)

where \(\varOmega^{2}=\frac{g}{l}\) is the basic frequency unit in the problem. We can cast (2.3) and (2.4) in the form

(2.5)
(2.6)

For small amplitude motion, we get the linearized equations of motion from (2.3) and (2.4) as

$$ 2\ddot{\theta}_1+\ddot{\theta}_2+2 \varOmega^2\theta_1=0 $$
(2.7)
$$ \ddot{\theta}_1+\ddot{\theta}_2+ \varOmega^2\theta_2=0 $$
(2.8)

Trying the solution,

$$ \theta_1=A\cos\omega t $$
(2.9)
$$ \theta_2=B\cos\omega t $$
(2.10)

leads to

$$ \bigl(2\varOmega^2-2\omega^2\bigr)A- \omega^2B=0 $$
(2.11)
$$ -\omega^2A+\bigl(\varOmega^2- \omega^2\bigr)B=0 $$
(2.12)

The consistency condition yields,

$$ \bigl(\varOmega^2-\omega^2\bigr)-\frac{\omega^4}{2}=0 $$

and thus we get the two roots

$$ \omega_1^2=(2-\sqrt{2}) \varOmega^2 $$
(2.13)
$$ \omega_2^2=(2+\sqrt{2}) \varOmega^2 $$
(2.14)

corresponding to the two normal modes of motion. For the mode whose frequency is \(\omega_{1}^{2}\), we see from (2.11) that

$$ A=\frac{B}{\sqrt{2}} $$
(2.15)

while for the mode with frequency \(\omega_{2}^{2}\), we see

$$ A=-\frac{B}{\sqrt{2}} $$
(2.16)

The lower frequency mode is such that the two pendulums oscillate in phase while for the higher frequency mode the oscillations are out of phase.

At this point, it is worth pointing out that the other fixed points of the system (±π,0),(0,±π),(π,π) are all unstable. The fixed point (0,π) correspond to an energy of E=2mgl. Straightforward calculation reveals that it is the out of phase mode, which is unstable. This leads us to assume that the out of phase mode will be sensitive to increasing amplitude of oscillation and with this in mind we address the issue of what happens to these two fundamental frequencies at higher amplitudes of motion. This will be the subject of Sects. 4 and 5 where we use both harmonic balance and the Lindstedt–Poincare perturbation theory to look at the issue.

For completeness, we give the results in the Hamiltonian formalism as well. From the Lagrangian of (2.2), we get the two momenta as

$$ p_1=2ml^2\dot{\theta}_1+ml^2 \cos(\theta_1-\theta_2)\dot{\theta}_2 $$
(2.17)
$$ p_2=ml^2\dot{\theta}_2+ml^2 \cos(\theta_1-\theta_2)\dot{\theta}_1 $$
(2.18)

This allows us to solve for \(\dot{\theta}_{1}\) and \(\dot{\theta}_{2}\) in terms of p 1 and p 2, and hence using \(H=p_{1}\dot{\theta}_{1}+p_{2}\dot {\theta}_{2}-L\) we get,

(2.19)

In writing down the total energy of the system, one very often adds a constant to the Hamiltonian and writes

(2.20)

We note that if the lower(outer) pendulum has to go around completely, then one need a minimum energy of 2mgl, if the upper(inner) pendulum has to go around completely then a minimum energy of 4mgl is required and a total energy of 6mgl is required to make both the pendulums go around.

We note that if we pass to the limit g→0, then the Hamiltonian depends on θ 1−θ 2 instead of the two angles θ 1 and θ 2. Consequently there is another “angular momentum” like conservation law and with two conserved quantities the problem is integrable in this limit. Obviously, as shown before, it is also integrable in the low amplitude situation. The intermediate region is where interesting dynamics can occur. Our point in this paper is that in the unsuspecting low energy region there will be initial conditions, which make the dynamics nontrivial.

3 Harmonic balance and Lindstedt–Poincare recalled

For a single degree-of-freedom systems, harmonic balance [8], and the Lindstedt–Poincare [9] technique yield the same answer provided the harmonic balance is also being used in the perturbative limit. To illustrate our point, we consider the anharmonic oscillator

$$ \ddot{x}+\omega^2 x=-\lambda x^3 $$
(3.1)

To examine the problem in the harmonic balance method, we expand

$$ x=A_1\cos\varOmega t+A_3\cos3\varOmega t+ \cdots $$
(3.2)

where Ω is the unknown frequency, which needs to be found along with the unknown coefficients A 1 and A 3. In the above, cos2Ωt is absent because of the form of nonlinearity. Inserting the expansion in (3.1), we get

(3.3)

Equating separately the coefficient of cosΩt and cos3Ωt from either side of the equation, we get

$$ \bigl(\omega^2-\varOmega^2 \bigr)A_1=-\frac{3}{4}\lambda A_1^3- \frac{3}{4}\lambda A_1^2A_3- \frac{3}{2}\lambda A_1A_3^2 $$
(3.4)
$$ \bigl(\omega^2-9\varOmega^2 \bigr)A_3=-\frac{\lambda}{4}A_1^3- \frac{3}{2}\lambda A_1^2A_3- \frac{3}{4}\lambda A_3^3 $$
(3.5)

From (3.4), we have

$$ \varOmega^2=\omega^2+\frac{3}{4} \lambda A_1^2+\frac{3}{4}\lambda A_3A_1+\frac{3}{2}\lambda A_3^2 $$
(3.6)

and using this in (3.5), we get

(3.7)

To make further progress, we need to write the expression for energy. This is seen to be

$$ E=\frac{1}{2}m\dot{x}^2+\frac{1}{2}m \omega^2 x^2+\frac{1}{4}m\lambda x^4 $$
(3.8)

Since E is a constant of motion, it can be evaluated by averaging over a time period, and thus

$$ E=\frac{1}{2}m\bigl\langle \dot{x}^2\bigr\rangle +\frac{1}{2}m\omega^2 \bigl\langle x^2\bigr\rangle +\frac {1}{4}m\lambda\bigl\langle x^4\bigr\rangle $$
(3.9)

We can evaluate the average with the solutions given in (3.2) and it follows that

(3.10)

In principle now, we have three Eqs. (3.6), (3.7), and (3.10) in A 1 and A 3 expressing them in terms of E and Ω. We eliminate A 1 and A 3 from these three equations and then obtain Ω as a function of ω,λ and E. We can keep an arbitrary number of harmonics and follow this procedure. It should immediately be clear that for systems with two degrees-of-freedom written as

where f(x 1,x 2) and g(x 1,x 2) are nonlinear functions, we are going to have flexibility of approach in harmonic balance since the energy E is going to be some function of x 1,x 2 which is not related to f and g. The frequencies are now no longer functions of the energy but the individual amplitudes.

We give explicit answers for just one harmonic, i.e., we set A 3=0 in (3.2). Now (3.6) becomes

$$ \varOmega^2=\omega^2+\frac{3}{4} \lambda A_1^2 $$
(3.11)

and (3.10) becomes

$$ E=\frac{1}{4}mA_1^2\bigl( \varOmega^2+\omega^2\bigr) $$
(3.12)

This leads to

$$ \varOmega^2=\omega^2+\frac{3\lambda E}{m(\varOmega^2+\omega^2)} $$
(3.13)

We notice immediately that harmonic balance is capable of yielding a nonperturbative answer (albeit approximate). If we stick to the perturbative answer (i.e., λ≪1), then we notice that A 3 is O(λ) from (3.7) and correct to O(λ) obtained from (3.6)

$$ \varOmega^2=\omega^2+\frac{3}{4} \lambda A_1^2 $$
(3.14)

This is independent of the existence of higher harmonics and is an exact perturbation theory result.

We now recall the Lindstedt–Poincare technique, which is by construction a perturbation theory. The correct frequency Ω will have an expansion of the form

$$ \varOmega^2=\omega^2+\lambda \omega_1^2+\lambda^2\omega_2^2+ \cdots $$
(3.15)

and in terms of Ω, (3.1) reads

$$ \ddot{x}+\varOmega^2 x=-\lambda x^3+ \lambda\omega_1^2x+\lambda^2\omega _2^2x+\cdots $$
(3.16)

We now expand

$$ x=x_0+\lambda x_1+\lambda^2 x_2+\cdots $$
(3.17)

and inserting this in (3.16) at different order of λ obtain

(3.18)
(3.19)
(3.20)

and so on. Solving for x 0, we get

$$ x_0=A\cos\varOmega t $$
(3.21)

and inserting this in (3.19), we get

(3.22)

The cosΩt term on the right-hand side of (3.22) introduces a spurious resonance. To keep the theory finite this resonance needs to be suppressed and this can be done by the choice

$$ \omega_1^2=\frac{3}{4}A^2 $$
(3.23)

leading to

$$ \varOmega^2=\omega^2+\frac{3}{4} \lambda A^2+O\bigl(\lambda^2\bigr) $$
(3.24)

If we are dealing with a system with more than one degree-of-freedom [10, 11], a normal mode decomposition would have to be done before implementing this step. This is in exact agreement with the perturbation theory answer of (3.14) obtained from harmonic balance. In the next section, we will apply harmonic balance to the two degree-of-freedom system [12–17]. It should be noted that for the two degree-of-freedom system, the harmonic balance method and the Lindstedt–Poincare procedure will give the same answer only if the harmonic balance is done after expressing the equations of motion in terms of the normal modes. A good feature of the harmonic balance procedure is that it can be applied without going through the exercise of shifting to normal modes.

4 Harmonic balance for the double pendulum

This section and the next will deal with perturbation theory and for that we will restrict our discussion to angular amplitudes θ 1 and θ 2, which are much smaller than π. Noting that

$$ \sin\theta\approx\theta-\frac{\theta^3}{6} $$

gives a 7 % error at \(\theta=\frac{\pi}{2}\), we proceed to work to this order to get the first correction to the linear motion. Clearly, what we get from this procedure should be reliable for angles up to about \(\frac{\pi}{2}\). With this in mind, we expand the trigonometric function to write (2.3) and (2.4) as

(4.1)

and

(4.2)

A harmonic balance analysis at this point would require the expansion

$$ \theta_1 =A_1\cos\omega t+A_2 \cos3\omega t+\cdots $$
(4.3)
$$ \theta_2 =B_1\cos\omega t+B_2 \cos3\omega t+\cdots $$
(4.4)

The second harmonic is absent because of the cubic nonlinearity. To get the first reasonable answer, we will set A 2=B 2=0 and work with the lowest harmonic. We insert the assumed form of θ 1 and θ 2 in (4.1) and obtain

(4.5)

As done earlier, we expand cos3 ωt in power of cosωt and cos3ωt and equate the coefficient of cosωt on either side of Eq. (4.5) to obtain after some algebra

(4.6)

We now treat (4.2) identically and obtain

(4.7)

At this point, we define our scheme for implementing harmonic balance in this system with two degrees-of- freedom. This is a variation of a technique described in [10]. We look at the terms in the square brackets in Eqs. (4.6) and (4.7) and decide to treat the amplitudes appearing there as initial conditions which can be taken to be parameters, which modify the frequency of oscillation. Accordingly, we still treat Eqs. (4.6) and (4.7) as two linear conditions on the amplitude of oscillation A and B and for consistency demand that

(4.8)

In opening the determinant, we pay heed to the fact that terms quartic in A and B have not been included at the outset (two term expansion for sines and cosines), and hence cannot be included now. Thus,

(4.9)

We treat the right-hand side of (4.9) as small, i.e., we want to introduce it as a first correction to the frequency of the linearized motion. Writing this term as ϵ, we have two possible values of ϵ — ϵ 1 corresponding to the linearized frequency \(\omega_{1}^{2}=2-\sqrt{2}\) and ϵ 2 corresponding to the linearized \(\omega_{2}^{2}=2+\sqrt{2}\). The frequencies ω 1 and ω 2 with the effect of amplitude included become

$$ \omega_1^2=(2-\sqrt{2}) \varOmega^2-\frac{\epsilon_1}{\sqrt{2}\varOmega^2} $$
(4.10)
$$ \omega_2^2=(2+\sqrt{2}) \varOmega^2+\frac{\epsilon_2}{\sqrt{2}\varOmega^2} $$
(4.11)

and

(4.12)
(4.13)

Thus, we find

$$ \omega_1^2=(2-\sqrt{2})-0.04 A^2-0.017 B^2 $$
(4.14)
$$ \omega_2^2=(2+\sqrt{2})-5.187 A^2-3.8 B^2 $$
(4.15)

We note two important things:

  1. 1.

    The frequencies are determined by the initial condition and not the energy. For the same energy, we can alter the initial condition and get different frequencies.

  2. 2.

    While the frequency of the first mode (in-phase vibration) is virtually unchanged with amplitude, the frequency of the second mode actually goes down to zero suggesting an instability for a set of initial conditions.

This is the picture that we get from the method of harmonic balance. In the next section, we will look at the problem from the point of view of the Lindstedt–Poincare perturbation theory.

5 Lindstedt–Poincare for the double pendulum

In order to apply the Lindstedt–Poincare, it is essential to expand the trigonometric functions in powers of the arguments and also to use the normal coordinates. As a first step, we will expand (2.5) and (2.6) and write up to cubic nonlinearity.

(5.1)

and

(5.2)

The normal modes as explained in Sect. 2 are given by

(5.3)
(5.4)

from which it follows that

$$ \theta_1=\frac{1}{2}(x_1+x_2) $$
(5.5)

and

$$ \theta_2=\frac{1}{\sqrt{2}}(x_1-x_2) $$
(5.6)

After long and tedious algebra using (5.1), (5.2), and (5.5), (5.6) we arrive at

(5.7)

and

(5.8)

To implement the Lindstedt–Poincare technique on this two degree-of-freedom system, we expand

$$ x_1=x_{10}+x_{11}+x_{12}+ \cdots $$
(5.9)
$$ x_2=x_{20}+x_{21}+x_{22}+ \cdots $$
(5.10)
$$ \omega_1^2=(2-\sqrt{2})+ \omega_{11}^2+\cdots $$
(5.11)
$$ \omega_2^2=(2+\sqrt{2})+ \omega_{21}^2+\cdots $$
(5.12)

where we have not shown in explicit expansion parameter, but it is implied that x 11,x 21 are determined by the third power of the amplitudes, while x 12,x 22 are determined by the fifth power with the amplitudes A and B set by

(5.13)
(5.14)

The equations of motion (5.7) and (5.8) can be written as

(5.15)
(5.16)

With the expansion of Eq. (5.9) and (5.10) introduced in the above equations and terms separated by order, we have to the first nontrivial order

$$ \ddot{x}_{10}+\omega_1^2x_{10}=0 $$
(5.17)
$$ \ddot{x}_{11}+\omega_1^2x_{11}=f_1(x_{10},x_{20})+ \omega_{11}^2x_{10} $$
(5.18)
$$ \ddot{x}_{20}+\omega_2^2x_{20}=0 $$
(5.19)
$$ \ddot{x}_{21}+\omega_2^2x_{21}=f_2(x_{10},x_{20})+ \omega_{21}^2x_{20} $$
(5.20)

From (5.17) and (5.19), we obtain (5.13) and (5.14), where we have imposed the initial conditions x 1(t=0)=A, \(\dot{x}_{1}(t=0)=0\), x 2(t=0)=B and \(\dot{x}_{2}(t=0)\!=\!0\). We now turn to (5.18) and (5.20). If we evaluate f 1(x 10,x 20) and f 2(x 10,x 20), we will find terms like cosω 1 t, cosω 2 t, cos3ω 1 t, cos3ω 2 t, cos(2ω 1±ω 2)t, cos(ω 1±2ω 2)t. If we are looking at (5.18), then the terms on the right-hand side, which contain cosω 1 t are resonance inducing, and hence dangerous, while for (5.20), it is the terms of the form cosω 2 t, which are dangerous. In order to solve for x 11 and x 21, we need to remove these terms and this is done by the appropriate choice of \(\omega_{11}^{2}\) and \(\omega_{21}^{2}\). We find, after straightforward algebra,

(5.21)
(5.22)

In this case of two degree-of-freedom system [18], we see that the result of the harmonic balance and the Lindstedt-Poincare technique are not identical. However, their content are similar in that for the first mode there is no visible effect of amplitude on the frequency while there is a strong effect in the case of the second mode. The primary difference between (5.22) and (4.15) is in the coefficient of A 2 term. The primary point of Sects. 4 and 5 is that the out of phase mode suffers an instability at a finite amplitude. The perturbation theory can only be indicative. So, in the next section, we carry out a numerical investigation to see if this indication is true or not.

6 Numerical results

The two equations of motions (2.5) and (2.6) can be converted into four first-order differential equations and then solved numerically using the fourth-order Runge–Kutta method [19]. The differential equation is given by

(6.1)

where the parameters g and l have been taken to be 1 implying Ω=1.

For initial condition \(\theta_{1}=0.01, \theta_{2}=0.01\sqrt{2}, \dot{\theta }_{1}= \dot{\theta}_{2} = 0, E \approx0.02\), we have Figs. 3 and 4.

Fig. 3
figure 3

Time series of θ 2

Full size image
Fig. 4
figure 4

Frequency spectrum of θ 2

Full size image

For initial condition \(\theta_{1}=0.01, \theta_{2}=-0.01\sqrt{2}\), \(\dot {\theta}_{1}=\dot{\theta}_{2}=0, E \approx0.02\), we have Figs. 5 and 6.

Fig. 5
figure 5

Time series of θ 2

Full size image
Fig. 6
figure 6

Frequency spectrum of θ 2

Full size image

For initial condition \(\theta_{1}=0.8, \theta_{2}=0.8\sqrt{2}, \dot{\theta }_{1}=\dot{\theta}_{2}=0\), we have Figs. 7 and 8, while for \(\theta_{1}=0.8, \theta_{2}=-0.8\sqrt{2}, \dot{\theta}_{1}=\dot {\theta}_{2}=0\) Figs. 9 and 10 both having energy E=1.18.

Fig. 7
figure 7

Phase plot of θ 2 vs. θ 1

Full size image
Fig. 8
figure 8

Frequency spectrum of θ 2

Full size image
Fig. 9
figure 9

Phase plot of θ 2 vs. θ 1

Full size image
Fig. 10
figure 10

Frequency spectrum of θ 2

Full size image

From the above set of figures, the following facts emerge:

  1. 1.

    For very low amplitudes, the motion is linearized in the sense that a pure in-phase or out-of-phase initial condition remains in-phase or out-of-phase giving a periodic trace as the phase portrait. The angular frequencies are found to be \(\sqrt{2-\sqrt{2}}\) and \(\sqrt {2+\sqrt{2}}\) as expected.

  2. 2.

    As the amplitude increases, the motion even for a “pure” initial conditions lie on a torus because the other mode is excited through the nonlinearity. The existence of two frequencies is seen in the spectrum.

  3. 3.

    At finite amplitudes, we see that the “in-phase” mode frequency hardly changes with amplitude while frequency of the “out-of-phase” mode decrease in agreement with the results obtained from the perturbative calculations. For example, the primary angular frequency for the former in Fig. 8 is 0.722 as opposed to 0.765, which is the angular frequency for the linearized motion while for the latter in Fig. 10 it is 1.099 as opposed to 1.848, which is for the linearized motion.

For a further increase in amplitude corresponding to an energy exceeding 2mgl, the dynamics changes drastically and that is shown in Figs. 11 and 12, which correspond to initial conditions \(\theta_{1} = 1.16,\theta_{2} = 1.16\sqrt{2},\dot{\theta_{1}} = \dot{\theta_{2}} = 0\), and Figs. 13 and 14, which correspond to initial conditions \(\theta_{1} = 1.16,\theta_{2} =-1.16\sqrt {2}\), \(\dot{\theta_{1}} = \dot{\theta_{2}} = 0\) with E≈2.27.

Fig. 11
figure 11

Phase plot of θ 2 vs. θ 1

Full size image
Fig. 12
figure 12

Frequency spectrum of θ 2

Full size image
Fig. 13
figure 13

Phase plot of θ 2 vs. θ 1

Full size image
Fig. 14
figure 14

Frequency spectrum of θ 2

Full size image

The characteristics of this energy region is that different initial conditions with same energy show different dynamic behavior. The “in-phase” initial conditions remain to be quasiperiodic while the “out-of-phase” show chaotic behavior, which is evident from the phase plot and the frequency spectrum. The Lyapunov exponent has been found out to be almost zero for the former initial conditions while positive (>0) for the latter.

However, it is possible for a pure initial condition to produce a mixed state at those amplitudes, and hence it is possible that an “in-phase” initial condition can lead to chaotic behavior and this is shown in Figs. 15 and 16, which corresponds to initial conditions \(\theta_{1} = 1.1,\theta_{2} = 1.1\sqrt{2},\dot{\theta _{1}} = \dot{\theta_{2}} = 0\), and in Figs. 17 and 18, which correspond to initial conditions \(\theta_{1} = 1.1,\theta_{2} =-1.1\sqrt{2},\dot{\theta_{1}} = \dot{\theta_{2}} = 0\) both having E≈2.08

Fig. 15
figure 15

Phase plot of θ 2 vs. θ 1

Full size image
Fig. 16
figure 16

Frequency spectrum of θ 2

Full size image
Fig. 17
figure 17

Phase plot of θ 2 vs. θ 1

Full size image
Fig. 18
figure 18

Frequency spectrum of θ 2

Full size image

7 Conclusion

For the low energy oscillations, both harmonic balance and the Lindstedt–Poincare techniques reveal the importance of initial conditions in the dynamics of a double pendulum. For large amplitude, the frequency of the oscillator has amplitude dependence, which is different for the two modes. The frequency for the “out-of-phase” mode has been seen to be strongly initial condition dependent than that of the “in-phase” mode. With the increase in amplitude the “out-of-phase” rapidly develops small frequencies oscillations, which makes the motion chaotic while the “in-phase” mode is able to sustain quasiperiodic behavior for the same energy other than some initial conditions where the mixing of the modes have an appreciable effect on the dynamics causing it to behave chaotically. Numerical investigation gives an estimate of the energy domain to be between 2mgl and 2.5mgl for which the above dynamics hold.