1 Introduction

Hyperchaotic systems, exhibiting more than one positive Lyapunov exponent, have been extensively studied in recent years in systems such as Chua’s circuit and the Rössler system. In [1], a variety of such recent chaotic systems were studied, primarily using Shilnikov’s theorems to establish horseshoe chaos, and also employing numerical simulations. The general quadratic system in [1] is given by

(1.1)

Shilnikov’s theorems have also been applied to a multitude of dynamical systems recently (see, for instance, [2–19]). In this approach, one analytically constructs the homoclinic or heteroclinic orbits present for parameter sets for which there is Smale horseshoe chaos emergent in a dynamical system.

One objective in this paper is to examine the chaotic regimes of (1.1) from a different point of view. Toward that end, we employ the technique of Competitive Modes analysis (see [20–24]) to identify “possible chaotic regimes” for this large, multiparameter system.

Many of the dynamical systems giving chaotic or hyperchaotic behavior are expressed as quadratic dynamics on ℝn. Hence, in Sect. 2, we outline the general problem of quadratic dynamics on ℝn. Then, in Sect. 3, we discuss how one goes about obtaining the mode frequencies for such systems, which involves recasting the dynamical system as a system of n second-order equations, some of which take the form of oscillators. Regarding the use of competitive modes, it is those equations which describe nonlinear oscillators that will permit a competitive modes analysis. From here, we then apply the method of competitive modes to a general quadratic vector field on ℝ3, namely (1.1), which has been shown to exhibit chaotic behavior.

We apply the theory of competitive modes as necessary conditions, or predictors, to determine parameter regimes for which our multiparameter system may exhibit chaotic behavior. Indeed, we find that if two of the three frequency components of the modes for (1.1) become competitive (or, nearly competitive), then chaotic behavior is observed in the solutions. We delineate parameter regimes for which the frequency components are nearly competitive, thereby demonstrating the utility of the method in determining parameter regimes resulting in random solution behaviors, and which would be extremely hard to pinpoint otherwise in a system with so many parameters. In particular, the competitive modes conjecture is validated for several chaotic parameter sets identified in [1] by Shilnikov analysis and numerical simulations.

Later, in Sect. 4, we recast the Competitive Modes analysis in a totally novel way as simple geometric criteria to map out the location, spatial extent, and approximate outline of the system attractor for any parameter sets corresponding to chaos. The surprising accuracy of these mappings further strengthens the growing body of evidence on the usefulness of the Competitive Modes procedure, and in fact may be taken as strong “a posteriori” evidence of the validity of the conjectures on which it based.

In Sect. 5, we consider multiple well-known hyperchaotic systems of dimension 4, in an attempt to discern between chaos and hyperchaos with a competitive modes analysis. We find that in many of the hyperchaotic modes, three mode frequencies become competitive at a discrete collection of points in time, as opposed to the standard competitive modes requirement of two mode frequencies being competitive in order to have chaos.

In Sect. 6, we make some observations on the relation between competitiveness of modes and the actual appearance of chaos in dynamical systems. Section 7 briefly reviews the results and discusses directions for further research.

2 Quadratic dynamics on ℝn

Many chaotic systems are modeled by quadratic dynamics. Indeed, quadratic terms are the simplest types of nonlinearity present in dynamical systems. Here we shall define some notation, which will be useful in the following sections.

Let x∈C 2(ℝn), F∈C 2(ℝn), and consider the n-dimensional dynamical system with general quadratic dynamics

(2.1)

Define the matrix \(A(k)=[\alpha^{[k]}_{i,j}]_{j\geq i} + [\alpha^{[k]}_{i,j}]_{j\geq i}^{\dagger}+ \text{diag}(\alpha_{1,1}^{[k]}, \alpha_{2,2}^{[k]}, \dots, \alpha_{n,n}^{[k]})\), where † denotes transposition. We then see that

$$ \frac{\partial F_k}{\partial x_\ell} = \sum_{i=1}^n \alpha_{\ell,i} x_i + \beta^{[k]}_{\ell}. $$
(2.2)

Then,

$$ \Delta V = \frac{\partial \dot{x}_i}{\partial x_i} = \nabla\cdot\mathbf{F} = \sum _{i=1}^n \nu_i x_i + \nu_0, $$
(2.3)

where \(\nu_{i} = \sum_{j=1}^{n} \alpha_{j,i}^{[j]}\) and \(\nu_{0} = \sum_{i=1}^{n} \beta_{i}^{[i]}\). Define \(\mathbf{\nu} = (\nu_{1}, \nu_{2}, \dots,\nu_{n})\). Then, \(\Delta V = \mathbb{\nu} \cdot \mathbf{x} + \nu_{0}\). The hypersurface \(\mathbb{\nu} \cdot\mathbf {x} + \nu_{0} =0\) partitions ℝn. Now, if system (2.1) is strictly dissipative (ΔV<0), the system falls on the \(\mathbb{\nu} \cdot\mathbf{x} + \nu_{0} <0\) partition of ℝn. If system (2.1) is weakly dissipative, then there exists ϵ>0 such that \(- \epsilon< \mathbb{\nu} \cdot\mathbf{x} + \nu_{0} <0\).

3 Classification of chaotic regimes by use of competitive modes

In recent literature, the idea of analyzing chaotic behavior through the study of “competitive modes” has begun to show promise in establishing parameter regions for the onset of chaos. The notion of a “mode” in mathematics and physics varies depending on the field. The idea is to break the system under consideration into “model” systems and consider the solution of the model system as a “mode.” A particular system may have several appropriate modes. Consider the general nonlinear autonomous system given by

$$ \dot{x_{i}}=f_i(x_1,x_2, \ldots,x_n). $$
(3.1)

Differentiation of (3.1) once gives

(3.2)

We will consider the competitive modes to be solutions x i of the model system given by (3.1), and, in analogy with systems of coupled parametric oscillators, we shall term the g i in (3.2) as the squared frequency corresponding to the oscillations of the mode x i . Like these squared frequencies, the h i (the forcing terms) can also depend on the other mode amplitudes (but not on the ith).

In order to apply the theory of competitive modes to determine parameter regimes for which (1.1) may exhibit chaotic behavior, recall that the following conjecture is posed in [20] (p. 95):

Conjecture 3.1

The conditions for dynamical systems to be chaotic are given by:

  1. (1)

    there exist at least two modes, labeled g i ’s in the system;

  2. (2)

    at least two g’s are competitive or nearly competitive, that is, for some i and j, g i ≈g j >0 at some t;

  3. (3)

    at least one of the g’s is a function of evolution variables such as t; and

  4. (4)

    at least on of the h’s is a function of system variables.

To obtain the mode frequencies for the general quadratic vector field on ℝn, we need to differentiate the vector field F with respect to t. From the quadratic form of system (2.1) we find that

$$ \ddot{x}_k = \frac{d}{dt} F_k(\mathbf{x}) = \bigl(\nabla F_k(\mathbf {x})\bigr) \cdot\mathbf{F}(\mathbf{x}) = - p_k(\mathbf{x}), $$
(3.3)

where p k (x) is in general a degree 3 polynomial in the x i ’s. We can always write \(p_{k}(\mathbf{x}) = g_{k}(\mathbf{x}) - h_{k}(\hat{\mathbf{x}}_{k})\), where \(\hat{\mathbf{x}}_{k} = (x_{1},\dots, x_{k-1}, x_{k+1}, \dots,x_{n})\), deg(g k )≤2 in x k , and deg(h k )=0 in x k . Then, we obtain the system

$$ \ddot{x}_k + g_k(\mathbf{x}) x_k = h_k(\hat{\mathbf{x}}_k) \quad \text{for } k=1,2,\dots, n. $$
(3.4)

If 1≤κ≤n of the g k ’s are positive over a subset \(\mathcal{U} \subset\mathbb{R}^{n}\), then we effectively have a system of κ nonlinear oscillators with frequencies given by the g k ’s. Suppose κ≥2, and let i and j be two indices corresponding to mode frequencies g i (x) and g j (x) which are positive on \(\mathcal{U}\). Then, if on a subset \(\mathcal{U}^{\prime}\subset\mathcal{U}\) it holds g i (x)=g j (x), we say that the modes x i and x j are competitive on \(\mathcal{U}^{\prime}\).

In the case of quadratic dynamics, the restriction g i (x)=g j (x) defines a relation of degree less than or equal to three in the x k ’s. At the hypersurface corresponding to g i (x)=g j (x), we obtain values of x for which x i and x j are competitive.

4 Competitive modes for the 3D quadratic system (1.1)

Here we consider the competitive modes analysis of the 3D quadratic system (1.1).

4.1 The squared mode frequencies

First, we compute the modes along the lines of [20]. In Sect. 4.2, we then consider conditions under which modes become competitive in finite time, or as t→∞ (on a chaotic attractor). We find that if two of the three frequency components of the modes for (1.1) become competitive (or, nearly competitive), then chaotic behavior is observed in the solutions. We delineate parameter regimes for which the frequency components are nearly competitive, thereby demonstrating the utility of the method in determining parameter regimes resulting in random solution behaviors, and which would be extremely hard to pinpoint otherwise in a system with so many parameters. The competitive modes conjecture is validated for several chaotic parameter sets identified in [1] by Shilnikov analysis and numerical simulations. In Sect. 4.3, we recast the Competitive Modes analysis as simple geometric criteria to map out the location, spatial extent, and approximate outline of the system attractor for any parameter sets corresponding to chaos.

Taking time derivatives of (1.1) and comparing to (3.2), the squared frequencies for the modes x 1, x 2, and x 3 in are explicitly given by

(4.1)
(4.2)
(4.3)

4.2 Competitive g functions

Clearly, one may obtain three conditions for competitive modes from enforcing the competitiveness condition g i ≈g j ,i,j=1,2,3.

It is now straightforward to test these conditions as good indicators or predictors for parameter sets where one should encounter chaos, subject of course to the squared mode frequencies remaining positive and comparable as the system evolves in time on the chaotic attractor. We first consider the parameter set [1]

(4.4)

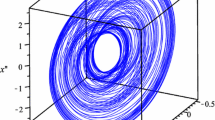
For these parameters, choosing initial conditions for (x 1,x 2,x 3) which make the squared mode frequencies all large positive, with two of them being initially competitive, and integrating (1.1), we indeed observe chaos. The resulting attractor is shown in Fig. 1, and the squared mode frequency g 1 as the orbits evolve on it in time is shown in Fig. 2.

Fig. 1
figure 1

The wafer-thin attractor in (x 1,x 2,x 3) phase (state) space for the parameters (4.4)

Full size image
Fig. 2
figure 2

Squared mode frequency g 1 for the parameters (4.4)

Full size image

While we have clearly found a chaotic regime, there is one feature that appears to contravene one of the Competitive Modes conjectures. The squared mode frequencies g i , i=1,2,3, all oscillate around zero, taking on both positive and negative values.

In fact, this feature is already present in earlier work using Competitive Modes [20–24]. The mystery is resolved, and the Competitive Modes hypothesis salvaged, when one plots the ratios of pairs of squared mode frequencies. As seen in Fig. 3, the ratio g 1/g 2 locks to values of O(1), with very rare deviations to larger values at isolated instants of time, apparently of measure zero in the whole time interval. At these isolated instants, the other two ratios of the squared mode frequencies however have values of O(1), thus ensuring competitivity of at least one pair of mode frequencies at all times, as required by the conjecture [20]. We have also examined the forcing terms (the h i ’s in (3.2)) graphically. There is no apparent correlation between their signs and amplitudes and those of the g i ’s.

Fig. 3
figure 3

Ratio g 1/g 2 of squared mode frequencies for the parameters (4.4). Note that the modes stay strongly competitive at all times, except at isolated instants where the other frequency ratios are of O(1)

Full size image

Hence, the Competitive Modes conjectures should perhaps be weakened to allow the squared mode frequencies to take on both positive and negative values in the chaotic regime, or on the attractor. This also raises an interesting similarity to another ubiquitous feature of chaotic attractors. This new feature allows for the system variables to grow exponentially in time intervals when the mode frequencies are imaginary and comparable (g i ’s negative and competitive), while oscillating at instants when the frequencies are real and matched or locked in. This is reminiscent of, but of course not directly correlated to, “stretching (along unstable manifolds) and folding (due to local volume dissipation)” on chaotic attractors. The repeated stretching and folding is thought to lead to sensitivity to initial conditions, and the fractal structure, of chaotic attractors. Different solution behaviors in time intervals corresponding to opposite signs of the squared mode frequencies would of course not correlate to either of these features.

We test the above by next considering the squared mode frequencies for another parameter set corresponding to the famous Lorenz butterfly attractor

(4.5)

For this case, g 1=1, g 2<0, g 3>0 for all times. The ratios g 3/g 1 and g 2/g 3 corresponding to (4.5) are shown in Figs. 4 and 5, respectively. As noted for our first parameter set (4.4), both ratios lock into values whose magnitudes remain bounded by values of order one, except for excursions to large values at isolated time instants. Once again, in agreement with our earlier observations, the ratio of the squares of one of the pairs of mode frequencies remains of O(1) at each instant of time.

Fig. 4
figure 4

Ratio g 3/g 1 of squared mode frequencies for the parameters (4.5). Note that, as before, the squared mode frequencies stay strongly competitive at all times, except at isolated instants where the other frequency ratios are of O(1)

Full size image
Fig. 5
figure 5

Ratio g 2/g 3 of squared mode frequencies for the parameters (4.5). As in Fig. 3, the modes stay strongly competitive at all times, except at isolated instants where the other frequency ratios are of O(1)

Full size image

4.3 Geometrically mapping the attractor

Next we shall consider the components of the Competitive Modes conjecture from a completely different point of view. In particular, we shall employ a geometric, rather than an algebraic, standpoint.

Having reviewed the basic features of the squared mode frequencies, we note that, both in the Competitive Modes conjecture, as well as in the plots in Figs. 2 to 4, the squared frequencies or the g i ’s have the following features:

  1. a.

    they take on both signs, but oscillate around zero, and

  2. b.

    a pair remains competitive with g i ≈g j at each instant of time in the chaotic regime.

Now, after the system orbits settle to the chaotic regime after a possible initial transient, they are ON the attractor. Since the attractor is an invariant set, this also implies that the trajectories remain there forever after. Hence, the two above-mentioned features of the squared mode frequencies or g i ’s in the chaotic regime may be taken as characteristics of the strange attractor of the chaotic system. We rewrite them in mathematical terms as

(4.6)

We will consider these conditions, essentially part of the Competitive Modes conjecture, not as algebraic conditions, which is the way they have previously been used [20–24]. Instead, for any given set of parameters where there are chaotic solutions, we shall turn them around and interpret them as geometric conditions to map out the location, extent, and rough outlines of the attractor.

For our system (1.1), with parameters (4.4), the region of (x 1,x 2,x 3) space mapped out by the geometric conditions (4.6) is shown in Fig. 6. Clearly, both the location and spatial extent of the attractor plotted in Fig. 1 for the same parameters are well delineated using these geometric conditions. Although a bit hard to see visually, superposing Figs. 1 and 6 reveals how tightly the location, extent and rough outline of the actual wafer-thin chaotic attractor (shown in Fig. 11) for these parameters is delineated by (4.6). The actual attractor surface, usually of very irregular shape and outline, can of course only be roughly approximated here by the conditions g i ≈g j ,i,j=1,2,3.

Fig. 6
figure 6

Region of (x 1,x 2,x 3) phase (state) space mapped out by the geometric conditions (4.6) for the parameters (4.5). Note how tightly the location, extent and rough outline of the actual wafer-thin chaotic attractor (shown in Fig. 1) for these parameters is delineated by (4.6)

Full size image

To further strengthen the case for the usefulness of inequalities (4.6) in delimiting chaotic attractors, we also consider this geometric mapping for our other parameter set (4.5) corresponding to the Lorenz equations. The pair of Figs. 7 and 8 juxtaposes the actual attractor with the region mapped out by the geometric conditions (4.6) for the parameter set (4.5). Note that the geometric conditions (4.6) delimit the attractor location and spatial extent in this example accurately too, while delineating its rough general outline or surface far worse than Fig. 6 did for the attractor in Fig. 1. However, having said that, we should add a caveat. Although hard to see visually, parts of the attractor in Fig. 7 do still directly lie on the outer surfaces in Fig. 8, with the remainder of the attractor being located in between the other surfaces shown in that figure.

Fig. 7
figure 7

The famous Lorenz attractor in (x 1,x 2,x 3) phase (state) space for the parameters (4.5)

Full size image
Fig. 8
figure 8

Region of (x 1,x 2,x 3) phase (state) space mapped out by the geometric conditions (4.6) for the parameters (4.5). Note that the geometric conditions (4.6) delimit the attractor location and spatial extent in this example accurately, while delineating its rough general outline or surface far worse than Fig. 6 did for the attractor in Fig. 1. However, although hard to see visually, superposing Figs. 7 and 8 reveals that parts of the attractor in Fig. 7 directly lie on the outer surfaces shown in Fig. 8, with the remainder being located in between the other surfaces shown here

Full size image

To test the usefulness of inequalities (4.6) in delimiting chaotic attractors, let us treat a third parameter set [1]

(4.7)

The pair of Figs. 9 and 10 juxtaposes the actual attractor with the region mapped out by the geometric conditions (4.6) for this parameter set (4.7). Note that the geometric conditions (4.6) accurately delimit the location and spatial extent of the tendrils of the ribbon-like attractor in this example far better than for the Lorenz system discussed above, while also delineating its rough general outline or surface.

Fig. 9
figure 9

The attractor in (x 1,x 2,x 3) phase (state) space for the parameters (4.7)

Full size image
Fig. 10
figure 10

Region of (x 1,x 2,x 3) phase (state) space mapped out by the geometric conditions (4.6) for the parameters (4.7). Note the close overlap in location, extent, and general shape with the actual chaotic attractor for these parameters shown in Fig. 9. In fact, although hard to see visually, superposing the figures reveals that the outermost tendrils of the attractor in Fig. 9 lie directly in the outer surfaces of Fig. 10, with the remainder of the attractor tendrils being located in between the other surfaces shown here

Full size image

Of particular interest in Fig. 10 is the close overlap in location, extent, and general shape with the actual chaotic attractor (shown in Fig. 9) for these parameters. In fact, although hard to see visually, superposing the figures reveals that the outermost tendrils of the attractor in Fig. 9 lie directly in the outer surfaces of Fig. 10, with the remainder of the attractor tendrils being located in between the other surfaces shown in Fig. 10.

As noted before, the actual attractor surface can only be roughly approximated in these figures by the mode competitiveness conditions g i ≈g j , i,j=1,2,3, in (4.6).

5 Competitive modes for hyperchaotic systems

In the present section, we shall extend our competitive modes analysis for four-dimensional quadratic vector fields which give hyperchaos. We only briefly highlight aspects for each system and use this later in order to draw some conclusions about the behavior of the mode frequencies in hyperchaotic regimes.

5.1 4D Rössler flow

The first known hyperchaotic system was found in 1979. The 4D Rössler flow [25] reads

(5.1)

For the chosen parameter values, this system exhibits hyperchaos. In Fig. 11, we take x 1(0)=−10, x 2(0)=−6, x 3(0)=0, x 4(0)=10 and plot the mode frequencies

(5.2)

for the 4D Rössler flow (5.1). We see that two mode frequencies are equal at many points in the time domain. However, the constant mode frequency g 2 is nearly equal to the mode frequencies g 1 and g 3 when g 1=g 3, so three modes are “nearly” competitive for the 4D Rössler model. Note that the 4D Rössler system is one of the simpler continuous-time models giving hyperchaos; for more complicated models, there might be three or more modes which are exactly competitive throughout a subset of the time domain. We shall see this in the following examples.

Fig. 11
figure 11

Plots of the nontrivial mode frequencies for the 4D Rossler system (5.1)

Full size image

5.2 Hyperchaotic Chen system

The hyperchaotic Chen system [26, 27] reads

(5.3)

Taking k=0, [27] found the following parameter sets which give hyperchaos:

$$ a=36,\quad b=3,\quad c=26,\quad d=16; $$
(5.4)
$$ a=36,\quad b=2,\quad c=28,\quad d=16; $$
(5.5)
$$ a=36,\quad b=3,\quad c=28,\quad d=18. $$
(5.6)

The mode frequencies for the hyperchaotic Chen system (5.3) read

(5.7)

In Figs. 12, 13, 14, we plot the mode frequencies for each of the parameter sets (5.4)–(5.6). We see that, although all three parameter sets give hyperchaos, the structure of the mode frequencies differs for each. For the first parameter set, two mode frequencies are often competitive (with a third being “nearly competitive”), whereas for the latter two parameter sets, three modes are often competitive (with the third mode frequency now being equal to the other two mode frequencies).

Fig. 12
figure 12

Plots of the nontrivial mode frequencies for the hyperchaotic Chen system (5.3), given parameter values (5.4)

Full size image
Fig. 13
figure 13

Plots of the nontrivial mode frequencies for the hyperchaotic Chen system (5.3), given parameter values (5.5)

Full size image
Fig. 14
figure 14

Plots of the nontrivial mode frequencies for the hyperchaotic Chen system (5.3), given parameter values (5.6)

Full size image

5.3 Hyperchaotic Lü system

The hyperchaotic Lü system reads

(5.8)

[28] found the following parameter set which gives hyperchaos:

$$ a=36,\quad b=3,\quad c=20,\quad d=1.3. $$
(5.9)

The mode frequencies for the hyperchaotic Lü system (5.8) read

(5.10)

In Fig. 15, we plot the mode frequencies for the hyperchaotic Lü system. Over a discrete subset of the time domain, three mode frequencies are equal, and, hence, three modes are competitive. Hence, not only are the conditions for the Lü system to have competitive modes satisfied, but we have one extra mode competitive with the two others simultaneously.

Fig. 15
figure 15

Plots of the nontrivial mode frequencies for the hyperchaotic Lü system (5.8)

Full size image

5.4 Modified hyperchaotic Lü system

The modified hyperchaotic Lü system reads

(5.11)

[29] found the following parameter sets which give hyperchaos:

$$ a=35,\quad b=14,\quad c=3,\quad d=5. $$
(5.12)

The mode frequencies for the modified hyperchaotic Lü system (5.11) read

(5.13)

In Fig. 16, we plot the mode frequencies for the modified hyperchaotic Lü system. As we have seen in other cases listed above, three of the modes are competitive.

Fig. 16
figure 16

Plots of the nontrivial mode frequencies for the modified hyperchaotic Lü system (5.11)

Full size image

5.5 Comparisons among the hyperchaotic systems

We now compare what we see in the plots of the squared mode frequencies for each of the hyperchaotic systems mentioned here. For the 4D Rössler model, two of the four modes are constant. The two nonconstant modes, g 1 and g 3, become competitive for a discrete collection of points. A similar situation is seen in Fig. 12 for parameter values (5.4) for the hyperchaotic Chen system, where only two positive mode frequencies are competitive. Such parameter values correspond to a hyperchaotic regime between two regimes for which periodic solutions exist [27].

Meanwhile, for parameter sets (5.5) and (5.6) for the hyperchaotic Chen system, there exist a discrete collection of points at which three modes are competitive and the mode frequencies are positive. These parameter values correspond to parameter regimes giving hyperchaos which are adjacent to parameter regimes leading to chaotic attractors [27]. Similar comments hold for the hyperchaotic Lü and modified Lü systems; for these systems, two modes are frequently competitive, and, less frequently, three modes become competitive. Hence, it seems that for hyperchaotic regimes adjoining chaotic regimes, one can expect to find three or more modes which are competitive over some countably infinite subset of the time domain. By contrast, for chaotic regimes, or hyperchaotic regimes located between regimes giving more stable dynamics, we might expect two modes to be competitive on such an infinite yet countable subset of the time domain.

6 Intermittence of mode competitiveness

In all of the plots of the mode frequencies which correspond to chaotic or even hyperchaotic behaviors, we find that two or more modes become competitive at a discrete collection of points in the time domain. While we have only numerical evidence for finite values of time, it seems reasonable to expect such patterns to continue as t→+∞ (otherwise, from what we have seen here, if the modes all became noncompetitive, then the chaotic attractor would dissipate).

However, as has been demonstrated in other cases, competitive modes are not sufficient for chaos, as a number of cases have been demonstrated where competitive modes occur for nonchaotic dynamics. Meanwhile, if the modes are either always competitive (see [24] for competitive modes “at equilibrium”) or never competitive, we do not detect chaos. Hence, we can view the competitive modes as a sort of “necessary condition” for chaos, when we observe modes which are competitive for intermittent values of time.

As shown by Van Gorder [30] in the case of the generalized Lorenz model, of which many three-dimensional quadratic dynamics are a special case, competitiveness of modes at a discrete set of points (which do not appear to occur with any regular or periodic behavior) can indicate the presence of chaotic behavior. Thus, it seems as though the existence of two competitive modes may be necessary for chaos. Beyond this, the greatest utility of a competitive modes analysis lies in any relations we can draw to the behavior of the modes and the intermittent manner in which they are competitive.

While many hyperchaotic systems exhibit more than two competitive modes at a discrete collection of points in the time domain, sometimes only two of the modes are competitive. As we removed hyperchaotic behavior (take a parameter set that gives chaos but not hyperchaos) from the 4D models discussed here, we observed that two of the three modes remained competitive, while the mode frequency for the third mode either become constant (and out of competition with one of the two aforementioned modes) or gradually become negative. Hence, there appears to be a strong correlation between the behavior of this third mode and the onset of hyperchaos.

7 Conclusions

In this paper we have considered the chaotic regimes of a variety of recently discovered hyperchaotic systems [1] from an alternative perspective. Toward that end, we employed the technique of Competitive Modes analysis to identify “all possible chaotic parameter regimes” for a multiparameter system as per the Competitive Modes conjecture. We find that the competitive modes conjectures [20] may in fact be interpreted and employed slightly more generally than has usually been done in recent investigations, with negative values of the squared mode frequencies in fact being admissible in chaotic regimes, provided that the competition among them persists. This is somewhat reminiscent of, but of course not directly correlated to, “stretching (along unstable manifolds) and folding (due to local volume dissipation)” on chaotic attractors. This new feature allows for the system variables to grow exponentially during time intervals when mode frequencies are imaginary and comparable, while oscillating at instants when the frequencies are real and matched.

Also, in a novel twist, we reinterpreted the competitive modes analysis as simple geometric criteria to map out the spatial location and extent, as well as the rough general shape, of the system attractor for any parameter sets corresponding to chaos. The general accuracy of this mapping for the various examples adds further evidence to the growing body of recent work on the correctness and usefulness of the Competitive Modes conjectures. In fact, it provides strong “a posteriori” validation of them and the entire procedure based on them.

In the case of hyperchaotic systems, we find that very often three modes are competitive or nearly competitive. It appears as if understanding the transition from two mode frequencies being equal to three mode frequencies being equal can shed some light on the onset of hyperchaos, at least in models with polynomial vector fields, such as the general quadratic vector fields considered here. We should also remark that, for any polynomial nonlinearities in the vector field, like the ones we considered here, competitive modes can be calculated (in the sense that g k ’s can be explicitly found). However, for more complicated systems involving different types of nonlinearities, the competitive modes cannot be easily applied. For such cases, perhaps approximate competitive modes can be developed in order to approximate the original system in terms of coupled oscillators. This would be one area of future interest.

Finally, we reiterate the point that competitive modes appear to be a necessary condition for chaos (or, hyperchaos, as the case may be). As there are cases where two mode frequencies agree over a time domain, yet nonchaotic dynamics are observed, it sees reasonable to restrict the requirement that two modes be competitive to a requirement that “two modes must be intermittently competitive on some discrete subset of the time domain.” The intuition here is that the oscillators representing each mode compete for dominance at every such discrete point. If the two oscillators lock (i.e., the modes remain competitive), only restrictive dynamics might be expected. However, if the two oscillators have approximately the same frequency at a discrete set of points, only to have one oscillator “win” and direct the system until the next time when the two frequencies are approximately equal, then complicated dynamics (such as chaos) could result.

There is no general way to measure the strength or weakness of any chaotic or hyperchaotic behavior via competitive modes. The reason for this is because competitive modes are used primarily for diagnostic purposes. However, it appears that the most chaotic and hyperchaotic systems exhibit strong intermittent behaviors, as we have seen in Sect. 5 and discussed in Sect. 6. The degree to which a system exhibits intermittent behavior described in Sect. 6 seems to be linked to the frequency at which the modes become competitive.