1 Introduction

It is well known that microelectromechanical systems (MEMS) are small integrated devices or systems, which combine both electrical and mechanical components.

MEMS, are a new technology, which exploits existing databases to create complex machines, with sizes of micrometers; these machines have many functions, including sensing and actuation.

Currently, a great deal of research has been performed to report nonlinear dynamic phenomena in MEMS resonators [1–3].

We remarked that nonlinearities, in MEMS, including nonlinear springs and damping mechanisms [4], nonlinear resistive, inductive and capacitive circuit elements [5] and nonlinear surface, fluid, electric, and magnetic forces [6].

Nonlinearities also may lead to chaotic behaviors [7].

The work done by [8], predicted the existence of chaotic motion in electrostatic MEMS. The appearance of chaotic motion, was also reported in [9, 10]. To reduce the chaotic movement to a stable orbit, an optimal linear feedback control was used in [11], robust adaptive fuzzy control in [12], and fuzzy sliding mode control design in [13].

In this paper, we characterized the chaotic behavior of a MEMS system, and also consider the fractional order approach.

The main goal of this work was to control the chaotic behavior of the considered system, into a stable orbit, which was obtained by the method of multiple scales, and consider three nonlinear control techniques: the State Dependent Riccati Equation (SDRE) Control, Optimal Linear Feedback Control, and Fuzzy Sliding Mode Control.

Fractional calculus, although it has a long history, its applications to physics and engineering, are just a recent focus of interesting.

More recently, many investigations are devoted to dynamics of fractional order dynamical systems [14–18]. In [14]; it is shown that the fractional order in Chua’s circuit can produce a chaotic attractor. In [15], it is shown that non-autonomous Duffing systems of fractional order can still behave in a chaotic regime. In [16], the chaotic dynamics of the fractional Lorenz system was shown. In [17], it was shown that modified Duffing systems of fractional order also has chaotic behavior.

The SDRE strategy has become very popular within the control community over the last decade. This method, first proposed by [19] and later expanded by [20], was independently studied by [21] and also used by [22]. The method, entails factorization (that is, parameterization) of the nonlinear dynamics, into the state vector and the product of a matrix valued function, which depends on the state itself. The SDRE strategy is an effective algorithm for synthesizing nonlinear feedback controls, by allowing nonlinearities, in the system states while additionally offering great design flexibility through state-dependent weighting matrices [23].

The Optimal Linear Feedback Control was proposed by [24]. In [24], the nonquadratic nonlinear Lyapunov function was proposed to solve the optimal nonlinear control design problem for a nonlinear system. Being formulated, the linear feedback control strategies for nonlinear systems, asymptotic stability of the closed-loop nonlinear system guaranteeing both stability and optimality. The theorem formulated by [24], expresses explicitly the form of minimized functional and gives the sufficient conditions that allow using the linear feedback control for nonlinear systems. Recent works, published using the Optimal Linear Feedback Control has shown interest in using the control in MEMS [11], synchronization of chaotic systems [25, 26], control of vehicle suspension [27] and control in a nonlinear oscillator [28, 29].

This paper also develops a fuzzy sliding mode control [13, 30–32] as a methodology to control chaos in MEMS. Firstly, the switching surface, which is required to achieve chaos control, is specified, and then a switching control law based on fuzzy linguistic rules is developed to generate a suitable chatter-free control signal for driving the error dynamic system such that the error state trajectories converge asymptotically to zero [13].

This paper was organized as follows. In Sect. 2, we obtained the mathematical model of the MEMS system and then we carried out numerical simulations to show its dynamical behavior. In Sect. 3, the chaotic behaviors, in the fractional order model, were studied, by using phase portraits, time history, and the Lyapunov exponent evaluation. In Sect. 4, an approximate analytical solution is obtained of the mathematical model, obtained in Sect. 2. In Sect. 5, the Optimal Linear Feedback Control is applied. In Sect. 6, it is applied to the SDRE control. In Sect. 7, the Fuzzy Sliding Mode Control is applied. In Sect. 8, we analyzed the robustness of the three controls, according to their sensitivities to parametric errors. The paper is concluded in Sect. 9. Finally, we list the bibliographic references.

2 Modelling of micro electromechanical systems

The microelectromechanical system studied in this work is represented by an electrostatic generator of energy and can be seen in Fig. 1 (as an example, undeserved others).

Fig. 1
figure 1

In-plane gap closing [33]

Full size image

It may be observed that the work done, against the electrostatic force between the plates, provides energy harvested [33]. According to [34], the physical system represented by Fig. 1, may be considered as a set of micro-beams. Microbeams have a wide range of applications, due to their simple geometries, easy productions, durabilities, and compact area of movements. Microbeams are also widely used in acceleration sensors, inertial navigation units, signal processing, electro, microturbines, weapon fusion, and mass storage devices motion detectors, and mechanical filters for telecommunications [2].

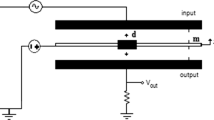
Considering a part of the device of Fig. 1, as consisting of two fixed plates and a movable plate between them (see Fig. 2), which it is applied a voltage V(t) composed of a polarization voltage (DC)V p , and an alternating voltage (AC)V i sin(ωt) [34]. The (DC) voltage applies an electrostatic force on the beam and usually changes the equilibrium position. The plates have the function of providing electrodes to form a capacitor or storage of electrical energy, and provide elasticity or mechanical strength.

Fig. 2
figure 2

Micro electromechanical system [34]

Full size image

Although the flexible structure has many vibration modes, this work will be considered the model, with one degree of freedom, denoted by x(t), the lateral movement of the front panel mass (m).

It is important to analyze the possible nonlinearities of the system, described in Fig. 2. It is also important to find both chaotic and periodic oscillations [11] and it is necessary, in many cases eliminate the chaotic behavior and control the system into to a periodic orbit.

2.1 Mathematical model of micro electromechanical systems

The governing equations of motion of the plates is given by

$$ m\ddot{x} = - F_{k} - F_{c} + F_{e}$$
(1)

where F k is the conservative force of the spring, F c the damping force of the elastic term, and F e the electric force.

We note in Fig. 2 that the distance d between the fixed and movable plates depends on the position of both x and d 0 (initial distance between the plates). Whereas the fixed plates have the same characteristics, the amount of total electric energy stored, in the system, can be obtained from:

(2)

where ε 0 is the permittivity of vacuum, A is the plate area, and V=(V p +V i sin(ωt)).

Thus, the electric force F e is a nonlinear function of displacement in x and a quadratic function of voltage:

$$F_{e} = \frac{\partial W^{*}}{\partial x} = 2\varepsilon_{0}{d}_{0}{AV}^{2}\frac{x}{( d_{0}^{2} - x^{2} )^{2}} $$
(3)

The spring stiffness is also a parameter that can be affected by elastic term phenomena and nonlinearities, considering these variations Force (F k ) conservative spring can be represented by:

$$ F_{k} = k_{1}x + k_{3}x^{3}$$
(4)

The force dissipation F c can be obtained from:

$$ F_{c} = c\dot{x}$$
(5)

Substituting (3), (4), and (5) in (1), we obtain the equation of motion:

$$ m\ddot{x} + k_{1}x + k_{3}x^{3} + c\dot{x} = 2\varepsilon_{0}d_{0}{AV}^{2}\frac{x}{ ( d_{0}^{2} - x^{2})^{2}}$$
(6)

Considering x(0)=x 0, \(\dot{x}(0) = \dot{x}_{0}\), and defining the new variables: \(T = \omega_{0}t, u = \frac{x}{x_{0}}\). Equation (10) can be represented in dimensionless form:

$$ \ddot{u} + \alpha_{1}u + \alpha_{3}u^{3}+ b\dot{u} = \beta{V}^{2}\frac{u}{ ( d^{2} - u^{2} )^{2}}$$
(7)

where

Rewriting (7) in state space:

(8)

Considering the parameters: α 1=1, α 3=0.4, β=69141.6, b=0.5, d=25, w=6.28, V p =2, V i =10, u 0=10, and \(\dot{u}_{0} = 5\). The displacement and velocity can be observed in Fig. 3, the phase portrait and Poincare map in Fig. 4, and Lyapunov exponent in Fig. 5.

Fig. 3
figure 3

(a) Displacement, (b) velocity

Full size image
Fig. 4
figure 4

(a) Phase portrait, (b) Poincare map

Full size image
Fig. 5
figure 5

Lyapunov exponent

Full size image

As can be observed in Fig. 5, the considered system, has a positive Lyapunov exponent. Evaluating the these exponents, for T=104, we obtain: λ 1=0.985693 and λ 2=−1.485693. The chaotic behavior also can be observed in the phase portrait, in Fig. 4a and Poincare map, in Fig. 4b.

3 Dynamic analysis of a fractional-order system

Differential equations may involve Riemann–Liouville differential operators of fractional-order q>0, which generally take the form below [35]:

$$ D^{q}x(t) = \frac{1}{\Gamma ( \eta - q )}\int_{t_{0}}^{t}\frac{x^{(\eta )}(u)}{ ( t - u )^{q - \eta + 1}}\, du$$
(9)

where η is the first integer not less than q. It is easily proved that the definition is the usual derivatives definition when q=1. The case 0<q<1 seems to be particularly important. For simplicity and without loss of generality, in the following, we assume that: t 0=0, 0<q<1.

3.1 Chaos in system with a fractional

In this section, we use the techniques of fractional calculus, to analyze the behavior of the system (5) with a fractional order. The system (8) is described as follows:

(10)

where 0<q 1, q 2≤1, its order is denoted by q=(q 1,q 2) here.

The dynamical behavior of the system, in the fractional order approach, is studied numerically, by using time history and phase portraits, considering the algorithm proposed by [36].

In Fig. 6, we may observe the results of numerical simulations, those carried out, considering of q 1=1 and 0.4≤q 2≤0.9.

Fig. 6
figure 6figure 6figure 6figure 6figure 6figure 6

Time history and phase portrait for q 1=1 and 0.4≤q 2≤0.9

Full size image

In Fig. 7, we can observe the results of numerical simulations, considering that 0.4≤q 1≤0.9 and q 2=1.

Fig. 7
figure 7figure 7figure 7figure 7figure 7figure 7

Time history and phase portrait for 0.4≤q 1≤0.9 and q 2=1

Full size image

In Fig. 8, we can observe the results considering that 0.4≤q 1, q 2≤0.9.

Fig. 8
figure 8figure 8figure 8figure 8figure 8figure 8

Time history and phase portrait for 0.4≤q 1,q 2≤0.9

Full size image

Using the numerical algorithms for the determination of the largest Lyapunov exponent (λ) of fractional-order [37], we found that chaos exists in the fractional-order for the model of MEMS (11).

Analyzing the numerical results, we find chaotic behavior for: Fig. 6a, q 1=1, q 2=0.9, λ=0.0015; Fig. 6c, q 1=1, q 2=0.7, λ=0.0016; Fig. 7a, q 1=0.9, q 2=1, λ=0.0022; Fig. 7c, q 1=0.7, q 2=1, λ=0.0018; Fig. 7d, q 1=0.6, q 2=1, λ=0.0018, and Fig. 8b, q 1=q 2=0.8, λ=0.0015.

4 Analytical approximate solutions obtained through the perturbation method

The basic idea is to use power series for a small parameter, which represents the greatness of a perturbation. This is a procedure used to obtain analytical solutions in time. These methods are used to generate an analytical solution to the problem, that is, an approximate solution [38].

The approximate solution of (7) can be obtained by using the methods of perturbation. Considering first the rational substitution of the term of (7): \(\frac{u}{( d^{2} - u^{2} )^{2}}\), by a polynomial function P 4(u)=δ 0+δ 1 u+δ 2 u 2+δ 3 u 3+δ 4 u 4, for −12≤u≤12.

According to [36], one can approximate the two functions by the least squares method minimizing the error:

$$\int_{ - 9}^{9} \biggl[ \biggl( \frac{u}{( d^{2} - u^{2} )^{2}}\biggr) - \bigl( P_{4}(u) \bigr) \biggr]^{2}\,du $$
(11)

Resulting in the following approximation:

$$\frac{u}{ ( d^{2} - u^{2} )^{2}} = 2.41\bigl(10^{ - 6}\bigr)u + 1.26\bigl(10^{ - 8}\bigr)u^{3} $$
(12)

Substituting (12) in (7), we obtain the following differential equation:

(13)

where a=0.3335, b=0.5, c=0.3965, ρ 1=13.3305, ρ 2=16.6631, ρ 3=0.0697, and ρ 4=0.0871.

Now, we will use the method of multiple scales to find analytically an approximate analytical solution to the above governing equation; this is done for a balance of order as follows. Therefore, the equation is

(14)

where ε is the parameter responsible for this balance [38]. Introducing the scales T 0=T and T 1=εT. Seeking solutions, in the following way:

$$ u = u_{0}(T_{0},T_{1}) + \varepsilon u_{1}(T_{0},T_{1}) + O \bigl(\varepsilon^{2} \bigr)$$
(15)

As the original independent variable (time scale T) was substituted by independent scales T 0 and T 1, derivatives with respect to T should be expressed in terms of partial derivatives in respect of T n such that

(16)

Substituting (15) in (14) and considering the derivatives (16), (14) is represented in the perturbed form:

(17)

Separating the terms in relation with the potential for ε 0 and ε 1, we have

(18)
(19)

one possible solution for (18) is

$$ u_{0} = a_{0}\cos ( \sqrt{a} T_{0} + \beta_{0} )$$
(20)

Or in polar form: \(u_{0} = Ae^{i\sqrt{a} T_{0}} + \bar{A}e^{ - i\sqrt{a}T_{0}}\), where \(A = \frac{1}{2}a_{k}e^{i\beta _{k}}\) and \(\bar{A}\) is the complex conjugate of A, for k=0,1,…,n. Substituting (20) in (19), we obtain

(21)

Eliminating the secular terms, (21) is as follows:

$$D_{0}^{2}u_{1} + au_{1}= - \frac{c}{4}a_{0}^{3}\cos ( 3\beta_{0}+ 3\sqrt{a} T_{0} ) $$
(22)

Solving (22) considering the homogeneous solution and private solution:

(23)

Substituting (23) and (20) in (15), we obtain:

(24)

where a 0,a 1,β 0, and β 1 are constant and can be obtained considering the initial conditions. Considering that u(0)=u 0 and \(\dot{u}(0) = \dot{u}_{0}\), (24) is in the following way:

(25)

where \(a_{0} = \sqrt{u^{2}_{0} + \dot{u}^{2}_{0}}\).

The phase portrait for the approximate analytical solution for ε=10−2 can be observed in Fig. 9a. In Fig. 9b, it can be observed comparing the phase portrait of (7), and the approximate analytical solution (25).

Fig. 9
figure 9

(a) Phase portrait for solution with MMS (25), (b) Phase portrait for (7) and analytical solution (25)

Full size image

5 Control design, using the optimal linear feedback control

The objective is to find the optimal control, such that the response of the controlled system (8) results in a periodic orbit u ∗(t) asymptotically stable.

Considering of the introduction of the control signal U in the system (8):

(26)

where \(U = u_{r} + \tilde{u}, u_{r}\) is the state feedback control and \(\tilde{u}\) is the feedforward control and is the control that maintains the system in the desired trajectory is given by

$$\tilde{u} = \dot{u}_{2}^{*} +\alpha_{1}u_{1}^{*} + \alpha_{3}u_{1}^{*3}+ bu_{2}^{*} - \beta V^{2}\frac{u_{1}^{*}}{ ( d^{2} - u_{1}^{*2} )^{2}} $$
(27)

Substituting (27) in (26) and defining the desired trajectory errors as

$$e = \left[\begin{array}{@{}c@{}}u_{1} - u_{1}^{*} \\u_{2} - u_{2}^{*}\end{array}\right] $$
(28)

The system (26) can be represented as deviations in the following way:

(29)

The system (29) can be represented in deviation as

$$\dot{e} = Ae + G\bigl(e,u^{*}\bigr) + Bu_{r} $$
(30)

Or in matrix form:

$$\left [\begin{array}{@{}c@{}}\dot{e}_{1} \\\dot{e}_{2}\end{array} \right ] =\left [\begin{array}{@{}c@{\quad}c@{}}0 & 1 \\- \alpha_{1} & - b\end{array}\right ]\left [\begin{array}{@{}c@{}}e_{1} \\e_{2}\end{array} \right ]+G\bigl(e,u^{*}\bigr) +\left [\begin{array}{@{}c@{}}0 \\1\end{array} \right ]u_{r} $$
(31)

where

$$ G\bigl(e,u^{*}\bigr) =\left [\begin{array}{@{}c@{}}0 \\ - \alpha_{3} [ (e_{1} + u_{1}^{*})^{3} - u_{1}^{*3} ] + \beta V^{2} \{ \frac{(e_{1}+ u_{1}^{*})}{ [ d^{2} - (e_{1} + u_{1}^{*})^{2} ]^{2}} -\frac{u_{1}^{*}}{ ( d^{2} - u_{1}^{*2} )^{2}} \}\\\end{array} \right ]$$
(32)

According to [27], if there exist matrices Q and R, with a positive definite symmetric matrix, such that the matrix:

$$ \tilde{Q} = Q - G^{T}\bigl(e,u^{*}\bigr)P - PG\bigl(e,u^{*}\bigr)$$
(33)

is positive definite for the limited matrix G(e,u ∗) then the control u r is optimal and transfers the nonlinear systems (29) from any initial state to final state e(∞)=0.

Minimizing the functional:

$$ J = \int_{0}^{\infty} \bigl(e^{T}\tilde{Q}e + u_{r}^{T}Ru_{r} \bigr)\,dt$$
(34)

The control u r can be found by solving the equation:

$$u_{r} = - R^{ - 1}B^{T}Pe = - Ke $$
(35)

Being the symmetric matrix P and can be found from the algebraic Riccati equation:

$$PA + A^{T}P - PBR^{ - 1}B^{T}P + Q =0 $$
(36)

In addition, with the feedback control (35), there exists a neighborhood Γ0⊂Γ, Γ⊂ℜn, of the origin such that if e 0∈Γ0, the solution e(T)=0, T≥0, of the controlled system (30) is locally asymptotically stable, and \(J_{\min} =e_{0}^{T}Pe_{0}\). Finally, if Γ=ℜn, then the solution e(T)=0, T>0, of the controlled system (30) is globally asymptotically stable [25].

What can be demonstrated considering to the dynamic programming rules one knows that if the minimum of functional (35) exists and if V is a smooth function of the initial conditions, then it satisfies the Hamilton–Jacobi–Bellman equation [25]:

$$ \mathop{\min} \limits _{u} \biggl( \frac{dV}{dT} +e^{T}\tilde{Q}e + u_{r}^{T}Ru_{r}\biggr) = 0$$
(37)

Considering a function,

$$ V = e^{T}Pe$$
(38)

Substituting \(\dot{V}\) in the Hamilton–Jacobi–Bellman equation (37), one obtains

(39)

Then: \(\tilde{Q} = Q - G^{T}(e,u^{*})P - PG(e,u^{*})\). Note that for positive definite matrices \(\tilde{Q}\) and R, the derivative of the function (38) is given by \(\dot{V} = - e\tilde{Q}e - u_{r}^{T}Ru_{r}\), is negative definite. Then the function (38) is Lyapunov function, and the controlled system (30) is locally asymptotically stable. Integrating the derivative of the Lyapunov function (39) given by \(\dot{V} = -e\tilde{Q}e - u_{r}^{T}Ru_{r}\) along the optimal trajectory, we obtain \(J_{\min} = e_{0}^{T}Pe_{o}\). Finally, if Γ=ℜn, global asymptotic stability follows as a direct consequence of the radial unbondedness condition for the Lyapunov function (38) V(e)→∞ as ∥e∥→∞ [25].

According to [27] to analyze the cases in which the matrix \(\tilde{Q}\) is analytically very difficult, it is possible to analyze numerically considering the function:

$$L(T) = e^{T}(T)\tilde{Q}(T)e(T) $$
(40)

Calculated on the optimal debt trajectory, L(T) is positive definite for any time interval, then the matrix \(\tilde{Q}\) is defined positive.

5.1 Application of the optimal linear feedback control

The matrix A and matrix B of the system (29) are represented by:

$$A = \left[ \begin{array}{@{}c@{\quad}c@{}}0 & 1 \\- 1 & - 0.5\end{array} \right], \quad B = \left[ \begin{array}{@{}c@{}}0 \\1\end{array} \right] $$
(41)

and defining

$$Q = \left[ \begin{array}{@{}c@{\quad}c@{}}2000 & 0 \\0 & 2\end{array} \right],\quad R = [ 0.0001 ] $$
(42)

using the Matlab function “LQR,” we obtain

(43)

Substituting K in (35), we obtain the control:

$$ u = - 4471.1360e_{1} - 169.6250e_{2}$$
(44)

Defining desired u ∗(t) trajectory with the solution obtained in (25). The displacement can be observed in Fig. 10a, and the phase portrait shown in Fig. 10b, considering the application of the control U in (26), and the following substitution: .

Fig. 10
figure 10

(a) Displacement of u 1. (b) Phase portrait

Full size image

How it can be observed in Fig. 10, control U carried the system (26) for the desired orbit (25). In Fig. 11, it can be observed the value of L(t) calculated numerically [39].

Fig. 11
figure 11

Function L(T) numerically calculated

Full size image

In Fig. 11, it can be observed that L(T) remained positive until the moment e→0, demonstrating that the control (44) is optimal and that the matrix \(\tilde{Q}\) is positive definite.

6 Control project, using of SDRE control

The SDRE method is used to determine the control signal being applied to the control system in the desired orbit. The dynamic system defined by (8) can be parameterized in first-order equations and written in the state-dependent coefficient (SDC) form [40]:

(45)

where the vector u=[u 1 u 2]T represents the system state-dependent time, \(\dot{u} \in R^{2}\) is the vector of first order time derivatives of the state, u s ∈U s ∈R is the control function, and U s is the control constraint set. This system represents the constraints from the nonlinear regulator problem, together with u(T 0)=u 0 and u(∞)=0, respectively, the initial and final conditions.

The state u and the control u s is given by f(u)=A(u)u and d(u)=S(u)u [33]. It is assumed that f(0)=0, which implies that the origin is an equilibrium point.

A state feedback rather that output feedback is adopted to enhance the control performance. The nonquadratic cost function for the regulator problem is given by

$$ J = \int_{0}^{\infty} \bigl(u^{T}Q(u)u + u_{s}^{T}R(u)u_{s}\bigr)\,dt$$
(46)

where Q(u) is semipositive-definite matrix and R(u) positive definite. There are weighting matrices on the outputs and control inputs, respectively. For a pointwise linear fashion, there matrices are assumed with constant coefficients.

Assuming full state feedback, the control law is given by

$$ u_{s} = - R^{ - 1}(u)B^{T}(u)P(u) = - K(u)u$$
(47)

The estate-dependent Riccati equation to obtain P(u) is given by

(48)

In the neighborhood Ω about the origin the SDRE method guarantees a closed-loop solution, local asymptotic stability. In the scalar case, the SDRE method reaches the optimal solution of the feedback regulator problem performance index (46), even when Q and R are functions of u [16].

The SDRE nonlinear feedback controller satisfies the first and the second necessaries conditions for optimality, H=0 (H is the Hamiltonian from the problem (45), (46) and \(\dot{\lambda} = - H_{u}\)). λ=P(u)u are the co-state trajectories, and P(u) is the solution of the Riccati equation (48).

The Hamiltonian for the optimal control problem is given by

(49)

From the Hamiltonian, the necessary conditions for the optimal control are found to be [41]

(50)

Since

$$u_{s} = - R^{ - 1}( u )B^{T}( u )\lambda $$
(51)

From the costate assumption, we know that

$$\lambda = P( u )u $$
(52)

Substituting (51) into (52) yields the SDRE controller (47). The system (45) is pointwise controllable and observable, for a region in neighborhood Ω about the origin. For controllability, this mean [B⋮A n B] from the static problem: \(\dot{u} = Au + Bu_{s}\), in this neighborhood. The SDRE method considers a solution for this static pointwise problem, for a small time interval, and obtains a suboptimal solution for dynamic control problem [41].

6.1 Application of the state-dependent Riccati equation (SDRE) control

Writing (8) in form (45):

$$ \dot{u} = \left [ \begin{array}{@{}c@{\quad}c@{}} 0 & 1 \\- \alpha_{1} -\alpha_{3}u_{1}^{2} + \frac{\beta V^{2}}{ ( d^{2} - u_{1}^{2})^{2}} & - b \\\end{array} \right ]\left [ \begin{array}{@{}c@{}} u_{1} \\u_{2} \\\end{array}\right ] + \left [ \begin{array}{@{}c@{}} 0 \\1\\\end{array} \right ]u_{s}$$
(53)

The matrix A and matrix Bare represented by

$$A = \left[ \begin{array}{@{}c@{\quad}c@{}}0 & 1 \\ - \alpha_{1} - \alpha_{3}u_{1}^{2} +\frac{\beta V^{2}}{( d^{2} - u_{1}^{2} )^{2}} & - b \end{array} \right],\quad B =\left[\begin{array}{@{}c@{}}0 \\ 1\end{array} \right] $$
(54)

The Riccati equation was solved using the Matlab function “LQR,” defining desired u ∗(t) trajectory with the solution obtained in (25).

The displacement can be seen in Fig. 12a, and the phase portrait shown in Fig. 12b, considering the application of the control (47) in (53), using the matrices A and B (54), the matrices Q and R (42), and the following substitution: .

Fig. 12
figure 12

System (10) with control (47). (a) Displacement. (b) Phase portrait

Full size image

How it can be observed in Fig. 12, control u s carried the system (53) for the desired orbit (25).

7 Fuzzy sliding mode control technique

Consider (26) of the form:

(55)

where U fs =u fr +u fs ,u fr is the feedforward control and u fs fuzzy sliding mode control.

Then the dynamic equations of these errors (28) can be obtained as

(56)

The sliding mode control field, the sliding surface is generally taken to be [13, 42]:

$$s = e_{2} + \lambda e_{1} $$
(57)

The existence of the sliding mode requires the following conditions to be satisfied [13, 42]:

(58)

Therefore, the u fr control law is given by

(59)

where λ represents a real number.

Equation (57) defines the output of the sliding mode control controller, while the reaching law is given by

$$ u_{fs} = k_{f}u_{f}$$
(60)

where k f is a normalization factor of the output variable and u f is the fuzzy control, and is determined in accordance with the normalized outputs of the sliding mode control, s and \(\dot{s}\).

Figure 13 shows the membership functions of the input linguistic variables (s and \(\dot{s})\) and the output linguistic variable (u f ), respectively.

Fig. 13
figure 13

Membership functions of the input–output variables for fuzzy sliding mode control [13]

Full size image

The fuzzy control rules are represented by the mapping of the input linguistic variables s and \(\dot{s}\), to an output linguistic variable u f .

Table 1 shows the corresponding fuzzy rule table.

Table 1 The corresponding fuzzy rule [13, 30]
Full size table

Considering the controls (59) and (60), we have

(61)

Let the Lyapunov function of the system, be defined as \(V =\frac{1}{2}s^{2}\).

The first derivative of this system with respect to time can be expressed as

(62)

If k f >0 is selected, then the reaching condition \((s\dot{s} < 0)\) is always satisfied. Therefore, the system (10) can be stabilized to a desired trajectory u ∗(t) [13, 30].

Defining desired u ∗(t) trajectory with the solution obtained in (23), λ=4, k f =4, considering the application of the control (61) and the following substitution: . The displacement can be seen in Fig. 14a, and the phase portrait shown in Fig. 14b.

Fig. 14
figure 14

System (10) with control (59). (a) Displacement. (b) Phase portrait

Full size image

8 The effect of parameter uncertainties on the control strategies

To consider the effect of the parameter uncertainties on the performance of the controller they are added to the state. The nominal values of parameters are stated above.

The real unknown parameters of system are supposed to be as follows: \(\bar{\alpha}_{1} = 0.8 + 0.4r(t)\), \(\bar{\alpha}_{3} = 0.32 + 0.16r(t)\), \(\bar{\beta} = 55313.4 + 27656.64r(t)\), \(\bar{b} = 0.4 + 0.2r(t)\), \(\bar{d} =20 + 10r(t)\), \(\bar{w} = 5.024 + 2.496r(t)\), \(\bar{V}_{p} = 1.6 + 0.8r(t)\), and \(\bar{V}_{i} = 8 + 4r(t)\), where r(t) are normally distributed random functions.

Numerical simulation results are shown in Fig. 15.

Fig. 15
figure 15

Error for uncertainty in parameters. (a) Optimal linear feedback control, (b) SDRE control, (c) Fuzzy sliding mode control

Full size image

This figure shows the robustness of the used methods when the systems parameters have random uncertainties.

9 Conclusions

By analysis of the MEMS vibrating system, which is studied here, has chaotic behavior, includes the case of fractional order. The total orders of the system for the existence of chaos are: q 1=1, q 2=1, q 1=1, q 2=0.9, q 1=1, q 2=0.7, q 1=0.9, q 2=1, q 1=0.7, q 2=1, q 1=0.6, q 2=1, and q 1=q 2=0.8.

The two control strategies (Optimal Linear Feedback, SDRE, and Fuzzy Sliding Mode controls) were used, controlling of the chaotic trajectory to a desired orbits, obtained from the application of the method of multiple scales. A comparison of the obtained results showed that both controls were efficient. The controls presented may be used for different physical models. An interesting contribution of these controls is that they do not need linearization or lose the nonlinearity of the considered systems and show the robustness of the controls when the systems parameters have random uncertainties.