1 Introduction

Drought as a complex and multifaceted event provokes considerable damage to agriculture, natural resources, and society (Li et al. 2015; Yu et al. 2016; An and Hao 2017; Byakatonda et al. 2018; Rahmani and Fattahi 2021). Climate change has induced massive alterations in temperature and precipitation behavior patterns, which has resulted in an increment in the occurrence of extreme phenomena (Li et al. 2020; Zhao et al. 2018; Ahmed et al. 2018). Therefore, drought forecasting and monitoring are significant and relevant; various studies have been conducted to monitor and predict drought in diverse catchments (Hao et al. 2017a, b; Tian et al. 2018; Aghelpour et al. 2020; Hao et al. 2018; Xu et al. 2018; Malik et al. 2019; Agana et al. 2017). On average, UK experiences a meteorological or hydrological drought every 5 to 10 years. From 1900 to 2015, twelve and three significant meteorological and hydrological droughts occurred in the UK, respectively. Details concerning recorded droughts are provided in Table 1.

Table 1 Droughts recorded from 1900 to 2015 in the UK (see www.metoffice.gov.uk)
Full size table

There are numerous definitions of meteorological and hydrological droughts varying based on the spatial and temporal of droughts. More limited than typical precipitation leading to alterations in climate patterns in a basin is a traditional interpretation of meteorological drought suggested by meteorological experts. A more accurate definition of meteorological and hydrological drought is that if precipitation or runoff of each year reduces by more than 35% compared to the long-term average leading up to that year, it is called meteorological and hydrological drought, respectively. It has been proved that hydrological and meteorological droughts are directly associated with the hydrological basin characteristics and climate of the study catchment (Van Loon and Laaha 2015; Yang et al. 2017); and recently, the relationship between meteorological and hydrological droughts has been investigated (Liu et al. 2019a, b; Bhardwaj et al. 2020; Peña-Gallardo et al. 2019a, b). However, the multifractal variations’ impact of temperature and precipitation on the multifractality of meteorological and hydrological drought hitherto has not been studied. The aforementioned will reveal the extent to which meteorological and hydrological droughts are sensitive (dependent) to pattern variations in temperature and precipitation. Moreover, it is of great significance for better understanding the drought mechanism, drought prediction, and its severity, to assess and manage the risk and consequences of drought, as well as hydrological studies.

Multifractality is the essence of natural phenomena, and studies have designated that hydrological parameters such as precipitation (Zhang et al. 2021; Morales Martinez et al. 2021), temperature (Santos da Silva et al. 2020; Toluwalope Ogunjo et al. 2021), and drought (Adarsh et al. 2019; Tatli and Dalfes 2020; Adarsh and Priya 2021; Toluwalope Ogunjo et al. 2021; Hou et al. 2018) have multifractal properties. The multifractal theory, associated with chaos theory, was advanced by Mandelbrot in the early 1970s.

The cross-correlation technique is a valuable tool for finding the hidden connection between two time series, by which the underlying association reveals between two phenomena or two simultaneously recorded signals. Several studies have been conducted on droughts that used the cross-correlation technique for prediction and studying agricultural, meteorological, and hydrological droughts (Crow et al. 2012; Stefan et al. 2004; Zarei et al. 2021; Uddin et al. 2020; Nabipour et al. 2020; Ullah et al. 2021). Multifractal detrended cross-correlation analysis (MF-DXA) is known as a practical technique for detecting the multifractal properties of two cross-correlated time series. This method is used for cross-correlated nonstationary series, applying polynomial fitting to eliminate the trends in time series. This theory has been employed to study on future market of energy (Wang et al. 2019), global methane and temperature (Tzanis et al. 2020), air pollutants (Manimaran and Narayana 2018), Bitcoin market (Zhang et al.2018), carbon market future in Europe (Zou and Zhang 2020), RMB exchange rates (Xie et al. 2017), streamflow and sediment fluctuation (Wu et al. 2018), river level records (Wu et al. 2020), the temperature anomalies and the SENSEX fluctuations (Chatterjee and Ghosh 2021), North Atlantic oscillation and precipitation (Tatli and Menteş 2019).

Met Office (the Met Office is the national meteorological service for the UK providing weather services and world-leading climate science) provides UK State of the Climate report annually. This governmental institution has recently published a report (Kendon et al. 2020) providing information on climate trends and observational data concerning climate quality in the UK. This report ignored the invisible mechanism between climatic parameters (precipitation, temperature, meteorological and hydrological droughts) and failed to examine the impact (sensitivity) of precipitation and temperature on droughts. In addition, this report paid scant attention to the nonlinear dynamic patterns of precipitation and temperature and their influence on the behavioral patterns of meteorological and hydrological droughts. In conclusion, the report delivered a superficial understanding of the climate parameters in the region (to be specific, precipitation, temperature, meteorological and hydrological droughts), whereas this study provided a profound perception of the underlying mechanisms governing the relationship between precipitation and temperature and meteorological and hydrological droughts. This study investigated the sensitivity (dependency) of meteorological and hydrological droughts to temperature and precipitation, as well as meteorological and hydrological droughts multifractality dependence on the multifractal variations in precipitation and temperature. It was conducted to reveal 1—the nonlinear dynamic patterns governing the climate of the study area; 2—the variation in the nonlinear dynamic behavior of precipitation and temperature after how long brings about a difference in the patterns of hydrological and meteorological droughts in the study area; 3—how strongly alterations in precipitation and temperature patterns affect droughts patterns (in other words, the severity of meteorological and hydrological droughts can be estimated by observing anomalies magnitude in the precipitation and temperature patterns); 4—the hidden correlation between precipitation and temperature and meteorological and hydrological droughts, and the latent effects of nonlinear dynamic behavioral patterns governing precipitation and temperature on meteorological and hydrological droughts patterns. Accordingly, this study serves to predict meteorological and hydrological droughts more efficiently and develop drought prediction methods by expanding our understanding of the underlying mechanisms governing the relationship between precipitation and temperature meteorological and hydrological droughts.

Standard Precipitation Index (SPI) and Streamflow Drought Index (SDI) were employed to estimate meteorological and hydrological droughts, respectively. To examine multifractal strength variations in precipitation and temperature time series, correlation analysis of meteorological and hydrological droughts with precipitation and temperature, multifractal detrended fluctuations analysis (MF-DFA), Pearson correlation coefficient (PCC), and Spearman rank correlation coefficient were employed, respectively. Additionally, to estimate droughts’ multifractal strength variations dependence on multifractal strength variations in precipitation and temperature, and cross-correlation among time series, cross-correlation, and multifractal detrended cross-correlation analysis (MF-DXA) techniques were applied, respectively.

The study is separated into five main segments. Chapter 2 discusses details concerning the study area, data sources, and theoretical and analytical details regarding cross-correlation, MF-DFA, MF-DXA, SPI, and SDI. In part 3, the results and discussions are presented, and finally, a summary and conclusion are delivered in chapter 4.

2 Materials and methods

The employed precipitation, temperature, and river flow data were associated with the Midlands in the UK (Fig. 1). The data were monthly and considered between 1921 and 2019 (99 years), and precipitation and temperature datasets and river flow data were collected from www.metoffice.gov.uk and www.nrfa.ceh.ac.uk websites, respectively. The Midlands area embraces the Peak District, the Cotswold Hills, and the Northamptonshire, toward the north, south, and east, respectively. The Midlands area is bounded by the Welsh border to the west. Mean annual temperatures over the study area vary from 8 °C to over 10 °C. The wettest and the driest areas in the Midlands experience, on average, 800- and 600-mm precipitation per year, respectively (for further details, see www.metoffice.gov.uk). Gauged daily flow data (m3/s) related to station Severn at Bewdley (ID 54,001, see www.nrfa.ceh.ac.uk), and daily data were converted to monthly to fit the drought estimation.

Fig. 1
figure 1

Selected region in the UK, marked with a green area (see www.metoffice.gov.uk)

Full size image

Since the long-term correlations and the multifractal spectrum width (for multifractal strength estimation) are strongly susceptible to the periodicities in hydrological time series, the Seasonal and Trend decomposition using Loess (STL) technique suggested by Cleveland et al. (1990) was employed to eliminate the periodic seasonal trends in temperature and precipitation time series. Following, hydrological and meteorological droughts were estimated using SDI and SPI, respectively. To evaluate the multifractal strength variations in temperature, precipitation, and drought indices, multifractal detrended fluctuation analysis (MF-DFA) was employed. Pearson correlation coefficient (PCC), Spearman rank correlation coefficient (SRCC), and cross-correlation technique, and multifractal detrended cross-correlation analysis (MF-DXA) were applied for correlation and cross-correlation evaluation between time series and persistency determination of cross-correlation between time series, respectively. The PCC method examines the correlation based on the linear relationship and linear trend between time series. PCC values are ranged between -1 and 1. PCC equal to zero indicates the absence of correlation between the two time series. Values close to 1 and -1 indicate a strong dependency and correlation between the two time series, in which negative and positive values represent the negative and positive correlation between the two series, respectively.

SRCC suggests a nonparametric method, evaluating the statistical rank correlation between two sets of rankings. SRCC assesses linear or nonlinear monotonic relationships between two time series. SRCC values and their interpretation are the same as the PCC method, with the difference that it describes the monotonic relationship between time series.

The cross-correlation function can be applied to assess the similarity between a time series and lagged versions of another time series as a function of the lag. Suppose the time series \(y_{{1a}}\) and \(y_{{2a}}\) and lags l  where l=  0, ± 1, ± 2, …. For data pairs \(\left( {y_{{11}} ,y_{{21}} } \right)\),\(\left( {y_{{12}} ,y_{{22}} } \right), \ldots ,\left( {y_{{1N}} ,y_{{2N}} } \right)\), cross-correlation can be computed based on the sample standard deviations and the lag l cross-covariance (Eqs. (1–2)):

$$\begin{array}{*{20}c} {S_{{y_{1} }} = \sqrt {C_{{y_{1} y_{2} }} \left( 0 \right)} ,~{\text{where}}~C_{{y_{1} y_{2} }} \left( 0 \right) = Var\left( {y_{1} } \right)} \\ {S_{{y_{2} }} = \sqrt {C_{{y_{2} y_{2} }} \left( 0 \right)} ,~{\text{where}}~C_{{y_{2} y_{2} }} \left( 0 \right) = Var\left( {y_{2} } \right)} \\ \end{array}$$
(1)
$$r_{{y_{1} y_{2} }} \left( l \right) = \frac{{C_{{y_{1} y_{2} }} \left( l \right)}}{{S_{{y_{1} }} S_{{y_{2} }} }}~;~~~~l = 0,~ \pm 1, \pm 2, \ldots$$
(2)

where \(C_{{y_{m} y_{n} }}\), \(S_{{y_{m} }}\), and \(r_{{y_{m} y_{n} }}\) are the lag l cross-covariance, the sample standard deviations, and cross-correlation, respectively.

In the following, the utilized drought indices and multifractal techniques will be introduced.

2.1 Standard precipitation index (SPI) and Streamflow drought index (SDI)

Standard Precipitation Index (SPI) and Streamflow Drought Index (SDI) were introduced by McKee (1993) and Nalbantis (2009), respectively, to determine duration, severity, and intensity of meteorological and hydrological drought in a catchment at multi-timescales. SPI is based on the probability density function and the gamma distribution. The transformed probability density function and the gamma distribution to the standard normal distribution are represented by Z, addressing the SPI (Harisuseno 2020). Z is characterized as Eq. (3):

$$Z = SPI = - \left( {t - \frac{{c_{0} + c_{1} + c_{2} t^{2} }}{{1 + d_{1} t + d_{2} t^{2} + d_{3} t^{3} }}} \right)$$
(3)

where c and d are constant and t is calculated based on the probability density function and the gamma distribution.

The computational process difference between SPI and SDI is that in SPI, the values of precipitation are applied, while in SDI, the values of river flow are applied. SDI can be estimated by Eq. (4) (Ozkaya and Zerberh 2019):

$$SDI_{{i,k}} = \frac{{V_{{i,k}} - \bar{V}_{k} }}{{S_{k} }}~~\;i = 1,~2,~ \ldots ~~~~k = 1,~2,~ \ldots$$
(4)

\(k\) and \(i\) show the months and years, respectively, and \(V_{{i,k}}\), \(\bar{V}_{k}\), and \(S_{k}\) are the cumulative streamflow volumes, mean, and standard deviation of cumulative streamflow volumes, respectively.

Drought can be classified as follows based on SPI and SDI values (Table 2).

Table 2 Drought’s classifications based on SPI and SDI values (Tigkas 2008)
Full size table

In this study, to scrutinize the meteorological and hydrological droughts, the values of SPI and SDI were calculated and applied monthly. To evaluate SPI and SDI, DrinC software (Tigkas et al. 2015) was employed, which is available at https://drought-software.com/download/.

2.2 Multifractal detrended fluctuation analysis (MF-DFA)

Detrended fluctuation analysis (DFA) method is widely used for the determination of monofractal scaling features and discovering long-range correlations in noisy, nonstationary time series (Kantelhardt et al. 2002). In geo-physical phenomenon including hydrologic processes which are expressing in time series formation, the complexity of multitude scaling behaviors makes it necessary to employ a multifractal approach to fully describe these interwoven connections. The multifractal detrended fluctuation analysis (MF-DFA) method is regularly exercised for estimation of the multifractality in the time series. MF-DFA method is acknowledged as the most effective technique for multifractality determination of time series and its appropriate function for nonstationary time series analysis (Adarsh et al. 2020; Miloş et al. 2020), making this technique proper for multifractal analysis of hydrological time series. Consequently, we employed the MF-DFA method to examine multifractal strength in time series. The singularity spectrum \(f\left( \alpha \right)\) is a mechanism for representing the multifractality of a time series. The singularity spectrum is assessed based on the scaling exponent \(\tau \left( q \right),\) and first-order Legendre transforms (Eq. (5)) and registers the time series segment dimensions distinguished by α (see Eq. (6)). Moreover, the width of \(f\left( \alpha \right)\) denotes the strength of the multifractality in a time series. Essentially, if \(f\left( \alpha \right)\) is a single point, then the time series is monofractal.

$$\tau \left( q \right) = q \times H\left( q \right) - 1$$
(5)
$$\alpha = \frac{{\partial \tau \left( q \right)}}{{\partial q}}\,,\,f\left( \alpha \right) = \alpha q - \tau \left( q \right)$$
(6)

where \(\alpha\) is perceived to be the Hölder exponent (singularity index) and q is the order weighting the local variations. \(H\left( q \right)\) represents the generalized Hurst exponent and is defined by Eq. (7).

$$F_{q} \left( s \right) \propto s^{{H\left( q \right)}}$$
(7)

Equation 7 is the power-law relationship between fluctuation segment \(F_{q} \left( s \right)\) and timescale s. The slope of the fitted \(F_{q} \left( s \right)\) and \(s\) estimates \(H\left( q \right)\).

The singularity index is utilized extensively to mark the degrees of the singularity of the time series. The width of \(f\left( \alpha \right)\) is exposed by \(\Delta \alpha\) and details related to the distribution evenness of the prospect of the fractal formation. The higher the value of \(\Delta \alpha \left( {\left( {\alpha _{{max}} - \alpha _{{min}} } \right)} \right)\), the more substantial the multifractality and complexity of the time series. It involves an asymmetrical time series with more severe fluctuations. \(\Delta \alpha\) was measured to estimate the multifractality of each window.

The graphs of the \(H\left( q \right)\sim q\) depict monofractal or multifractal behavior of the time series. A time series is multifractal when \(H\left( q \right)\) is dependent on the q values. Despite this, \(H\left( q \right)\) independency on the q values shows monofractality of the time series. The positive q for \(H\left( q \right)\) is granted to interpret the scaling behavior of fragments, which comprises considerable fluctuations. However, negative q is accepted to elucidate the scaling behavior of sections holding miniature fluctuations (Livina et al. 2007; Sun et al. 2001). To assess the multifractal strength variations in the time series, a fixed-size window was considered (for illustration, a window with 6-month long or lag = 6). This window was then moved from the beginning to the end of the time series and the multifractal strength was estimated in each window.

2.3 Multifractal detrended cross-correlation analysis (MF-DXA)

In 2008, the multifractal detrended cross-correlation analysis (MF-DXA) theory was introduced by Zhou. This method was suggested to assess the multifractal behaviors in the power-law cross-correlations between two signals, which is suitable for analyzing complex systems, including finance, ecology, physiology, geohydrology, and hydrology.

Suppose two time series \(x\left( i \right)\) and \(y\left( i \right)\) with the same length. The profile for calculation MF-DXA is shown in Eq. (8) (see (Zhou 2008)):

$$X\left( i \right) = \mathop \sum \limits_{{t = 1}}^{i} \left( {x\left( t \right) - \bar{x}} \right),~Y\left( i \right) = \mathop \sum \limits_{{t = 1}}^{i} \left( {y\left( t \right) - \bar{y}} \right),~i = 1,2, \ldots ,N$$
(8)

\(\bar{x}\) and \(\bar{y}\) represent the sample means, and N represents the time series length. In the next step, \(X\left( i \right)\) and \(Y\left( i \right)\) subsequences are divided into cell of length \(s\), while the cells should not have any overlap. The similar process is repeated starting from the other end of the time series due to timescale \(s\) that may not be a multiple of N (Cao and Shi 2017). To obtain the q-order fluctuation function, averaging should be applied through all segments (Eq. (9)).

$$\begin{array}{*{20}c} {F_{q} \left( s \right) = \left\{ {\frac{1}{{2N_{s} }}\mathop \sum \nolimits_{{\nu = 1}}^{{2N_{s} }} \left[ {F^{2} \left( {s,\nu } \right)} \right]^{{{\raise0.7ex\hbox{$q$} \!\mathord{\left/ {\vphantom {q 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} } \right\}^{{\frac{1}{q}}} ~~~~~~~~~~~~q \ne 0} \\ {F_{0} \left( s \right) = exp\left\{ {\frac{1}{{4N_{s} }}\mathop \sum \nolimits_{{\nu = 1}}^{{2N_{s} }} \ln \left[ {F^{2} \left( {s,\nu } \right)} \right]} \right\}~~~~~~~~~~~~~~q = 0} \\ \end{array}$$
(9)

where \(F^{2} \left( {s,\nu } \right)\) is the variance of each segment \(\nu\).

For two long-range cross-correlated time series, according to the power-law, \(F_{q} \left( s \right)\) values augment for large \(s\) values (Eq. (10)).

$$F_{q} \left( s \right)\sim S^{{H_{{xy}} \left( q \right)}} \to ~\log F_{q} \left( s \right) = H_{{xy}} \left( q \right)\log \left( s \right) + \log A$$
(10)

The power-law connection between two recorded signals (time series) is described by the generalized Hurst cross-correlation exponent, which is shown in Eq. (10) by \(H_{{xy}} \left( q \right)\). The interpretation of \(H_{{xy}} \left( q \right)\) values and \(H\left( q \right)\) values in the MF-DFA method is similar, with the difference that \(H_{{xy}} \left( q \right)\) determines the multifractality and persistency properties of cross-correlation between two time series.

MATLAB software was utilized to estimate cross-correlation, PCC, SRCC, MF-DFA, and MF-DXA.

3 Results and discussion

First, meteorological and hydrological droughts (SPI and SDI, respectively) were analyzed in the study area. Then, correlation, cross-correlation, and cross-correlation persistency were evaluated between hydrological parameters (precipitation, maximum temperature, and minimum temperature) and meteorological and hydrological droughts (SPI and SDI, respectively) to investigate the susceptibility of meteorological and hydrological droughts (SPI and SDI, respectively) to precipitation, maximum temperature, and minimum temperature. Subsequently, the identical process was applied to multifractal strength variations in the aforementioned data. Table 3 exposes the abbreviations adopted in this study, which from now on the results are presented based on these abbreviations. The analysis steps are illustrated in Fig. 2.

Table 3 Utilized abbreviations and the meanings
Full size table
Fig. 2
figure 2

Analysis steps for evaluation of meteorological and hydrological drought sensitivity to precipitation, \(T_{{max}}\), \(T_{{min}}\), and multifractal strength variations in the time series

Full size image

First, the drought analysis results are presented, and then the sensitivity analysis results will be reviewed. According to the Met Office data, the average annual precipitation, maximum temperature, and minimum annual temperature in the UK from 1961 to 2010 were 1126.9 mm, 12.6 °C, and 5.07 °C, respectively. However, the computed average annual precipitation, maximum temperature, and minimum temperature for the Midlands were 780.86 mm, 13.07 °C, and 5.38 °C, respectively. It indicated that the study area was drier and warmer (lower average precipitation and higher average temperature) than the entire UK.

As shown in Fig. 3a, the study area experienced five severe or extreme dry months and two very wet months between 1921 and 1923. By examining the fluctuations trend of SPI and SDI, it was revealed that the impact of meteorological dry or wet months affected the hydrology of the region with a delay of one to three months. A similar examination was conducted for subsequent years and confirmed the mentioned results. The general trend of SPI and SDI fluctuations registered that the fluctuations had an upward trend and a slope equal to \(3 \times 10^{{ - 6}}\). The fluctuations of SPI were much more severe than the SDI fluctuations (Fig. 3b).

Fig. 3
figure 3

SPI and SDI values for short- (1921–1923) (a) and long-term (1921 to 2019) (b) concerning Midlands in the UK

Full size image

Examination of anomalies in the monthly precipitation time series revealed that the number of anomalies (significant precipitation in a month; total precipitation above 150 mm in one month was considered an anomaly) in one year decreased over time. On the other hand, the number of anomalies in the minimum and maximum temperature time series (extremely high or notably low temperature in a month; concerning maximum temperature, temperatures above 23 °C and temperatures below 3 °C were considered anomalies, and concerning minimum temperature, temperatures above 12 °C and temperatures below − 2 °C were considered anomalies) increased. These anomalies can be seen in Fig. 4.

Fig. 4
figure 4

Monthly precipitation graphs, average monthly maximum temperature, and average monthly minimum temperature for Midlands in the UK between 1921 and 2019

Full size image

3.1 Results of Pearson, Spearman, Cross-Correlation, and Hurst’s values concerning precipitation and temperature time series

To investigate the dependency and sensitivity of meteorological and hydrological droughts to precipitation and temperature, Hurst exponent, Pearson correlation coefficient (PCC) (see Benesty et al. 2009), Spearman rank correlation coefficient (SRCC) (see Lyerly 1952), and cross-correlation were estimated for hydrological datasets (precipitation, \(T_{{\max }} \;{\text{and}}\;T_{{\min }}\)) and drought indices (SPI and SDI) time series, the results of which are sorted in Table 4 and Fig. 5.

Table 4 Generalized Hurst exponent, PCC, and SRCC’s values concerning precipitation and temperature time series and drought indices
Full size table
Fig. 5
figure 5

The cross-correlation graphs concerning precipitation and temperature time series and drought indices (the blue horizontal lines are confidence bounds consisting of 2 standard errors)

Full size image

To describe Spearman and Pearson’s values, the word Pre is used instead of precipitation. The values of \(P_{{Pre,~SPI}}\), \(P_{{Pre,~SDI}}\), \(P_{{Tmax,~SPI}}\), and \(P_{{Tmax,~SDI}}\) were negative (Table 4), indicating the presence of a negative (reverse connection) linear relationship between the two time series. The values of \(P_{{Tmin,~SPI}}\) and \(P_{{Tmin,~SDI}}\) were positive, suggesting a level of positive (direct connection) linear correlation between the two time series. The correlation between precipitation time series and drought indices was higher than temperature time series. This was indicative of a stronger linear relationship between precipitation and droughts. In other words, in the study area, meteorological and hydrological droughts were more susceptible to precipitation fluctuations than temperature fluctuations. Precipitation and \(T_{{{\text{min}}}}\) had a stronger linear correlation (negative and positive, respectively) with meteorological drought than hydrological drought. Moreover, hydrological drought exposes more correlation (a negative linear correlation) to \(T_{{{\text{max}}}}\) than meteorological drought.

Table 4 illustrates that the values of \(S_{{Pre,~SPI}}\), \(S_{{Tmax,~SDI}}\), and \(S_{{Tmin,~SDI}}\) were negative. It provided evidence for a negative monotonic relationship between precipitation and meteorological drought and temperature and hydrological drought. On the contrary, the values of \(S_{{Pre,~SDI}}\), \(S_{{Tmax,~SPI}}\), and \(S_{{Tmin,~SPI}}\) were positive, implying that temperature and meteorological drought and precipitation and hydrological drought are monotonically related. Besides, the values of \(S_{{Pre,~SPI}}\) and \(S_{{Tmin,~SPI}}\) were higher than \(S_{{Pre,~SDI}}\) and \(S_{{Tmin,~SDI}}\). It would suggest that, in the study area, meteorological drought exhibited a potent monotonical relation with precipitation and \(T_{{{\text{min}}}}\). However, the value of \(S_{{Tmax,~SPI}}\) was less than \(S_{{Tmax,~SDI}}\), drawing a conclusion of an effective monotonical relation between \(T_{{{\text{max}}}}\) and hydrological drought.

Figure 5 illustrates the cross-correlation values between precipitation and temperature time series and drought indices. It was obvious from Fig. 5 that the cross-correlation between precipitation and drought indices was higher than temperature and drought indices. Besides, the cross-correlation between precipitation and SPI was more substantial than precipitation and SDI (the maximum cross-correlation value and red lines crossed confidence bounds). It implied that meteorological drought showed more sensitivity to precipitation in comparison with hydrological drought. The maximum cross-correlation between precipitation and SPI was at lag 3, while between precipitation and SDI was at lag 19. The former supported the notion that precipitation fluctuations affected meteorological drought (first) and hydrological drought (subsequently) with a delay of 16 months.

More sensitivity of hydrological drought to temperature than meteorological drought to temperature was inferred from stronger cross-correlation between temperature and SDI than temperature and SPI. The cross-correlation between \(T_{{{\text{max}}}}\) and SDI was more solid (more values bigger than confidence bounds) than \(T_{{{\text{min}}}}\) and SDI, indicating more sensitivity of hydrological drought to \(T_{{{\text{max}}}}\) than \(T_{{{\text{min}}}}\). The cross-correlation between temperature and SPI was negligible, and the maximum cross-correlation between temperature and SDI was at lag 498 (maximum cross-correlation values concerning \(T_{{{\text{max}}}}\) and \(T_{{{\text{min}}}}\) were -0.0645 and -0.0656, respectively.)

The time series persistency was investigated by application of the Hurst exponent, and the results are provided in Table 4. As shown in Table 4, \(H_{{SPI}}\) values were higher than \(H_{{SDI}}\) values. It supported that precipitation and temperature registered cross-correlation with a stronger long-range persistency with meteorological than hydrological drought. Besides, \(H_{{Pre,SPI}}\) and \(H_{{Pre,SDI}}\) held the highest values, corroborating a cross-correlation with long-range persistency between precipitation time series and drought indices.

A long-range persistent cross-correlation between \(T_{{max}}\) and drought indices was inferred from greater values of \(H_{{Tmax,SPI}}\) and \(H_{{Tmax,SDI}}\) than \(H_{{Tmin,SPI}}\) and \(H_{{Tmin,SDI}}\). The cross-correlation between meteorological drought and precipitation exhibited more long-range memory than hydrologic drought and precipitation, concluded from the higher value of \(H_{{Pre,SPI}}\) than \(H_{{Pre,SDI}}\). The Hurst values confirmed linear, monotonic, and sensitivity analysis results concerning relationship between precipitation and temperature and drought indices. It was verified that there was an influential association between meteorological drought and precipitation.

To evaluate the timescale influences on Hurst’s values and time series multifractality, four timescales were considered (6–24 months (2 years), 6–60 months (5 years), 6–120 months (10 years), and 6–228 months (19 years)) (Table 5). The results proved that the cross-correlation long-range persistency intensified between hydrological series and drought indices owing to the reduction in scale length. However, the multifractal strength declined as a cutback in scale length except for the 6–24 months scale. At the 6–24 months scale, \(\Delta \alpha _{{Tmax,SPI}}\), \(\Delta \alpha _{{Tmin,SPI}}\), \(\Delta \alpha _{{Tmax,SDI}}\), and \(\Delta \alpha _{{Tmin,SDI}}\) experienced increments. The \(\Delta \alpha\) positive values for all scale-lengths provided evidence for more probability of large local fluctuations than small local fluctuations in the time series.

Table 5 Generalized Hurst exponent and multifractal strength’s values concerning hydrological time series and drought indices
Full size table

3.2 Results of Pearson, Spearman, Cross-Correlation, and Hurst’s values concerning multifractal strength variations in precipitation, temperature, and drought indices time series

The variations in multifractal strength in the time series were estimated (by MF-DFA) and analyzed by PCC, SRCC, cross-correlation, and MF-DXA; the results are sorted in Table 6 and Fig. 6. To analyze the multifractal strength variations in the time series (Precipitation, \(T_{{{\text{max}}}}\), \(T_{{{\text{min}}}}\), SPI, and SDI), the multifractality of each window was arranged sequentially to form a series (see Sect. 2.2) representing the multifractal strength fluctuations in each dataset.

Table 6 Hurst, PCC, and SRCC’s values concerning multifractal strength variations in the time series
Full size table
Fig. 6
figure 6

The cross-correlation graphs concerning multifractal strength variations in precipitation and temperature time series and drought indices (the blue horizontal lines are confidence bounds consisting of 2 standard errors)

Full size image

The values of \(P_{{Pre,~SPI}}\), \(P_{{temp,~SPI}}\), and \(P_{{Tmin,SDI}}\) were positive (Table 6). It was a proof of positive linear correlation between time series’ multifractal variations. The negative values of \(P_{{Pre,~SDI}}\) and \(P_{{Tmax,~SDI}}\) supported the notion that multifractal strength variations in precipitation and SDI, and \(T_{{{\text{max}}}}\) with SDI had negative (reverse) linear relationship. The results confirmed that as multifractal strength augments in precipitation and temperature time series, multifractal strength increases in meteorological drought. Likewise, augmentation of the multifractal strength in \(T_{{{\text{min}}}}\) increases the multifractality in hydrological drought. Conversely, multifractal strength augmentation in precipitation and \(T_{{{\text{max}}}}\) brings about a reduction in the multifractality of hydrological drought. Multifractal strength of meteorological drought exhibited more correlation with multifractal strength variations in precipitation and \(T_{{{\text{max}}}}\), whereas hydrological drought multifractality displayed more correlation with multifractal strength variations in \(T_{{{\text{min}}}}\). SPI and SDI presented the weakest linear relationship to \(T_{{{\text{min}}}}\) and \(T_{{{\text{max}}}}\), respectively.

As shown in Table 5, the values of \(S_{{Pre,SPI}}\), \(S_{{Tmax,SPI}}\), \(S_{{Tmin,SDI}}\), and \(S_{{Tmax,SDI}}\) were positive while \(S_{{Tmin,SPI}}\) and \(S_{{Pre,SDI}}\) were negative, verifying a positive (direct) and a negative (reverse) monotonical relation between time series, respectively. \(S_{{Tmax,SPI}}\) was higher than \(S_{{Tmax,SDI}}\), indicating that the multifractal strength variations in the \(T_{{{\text{max}}}}\) time series and the SPI were more monotonically related than \(T_{{{\text{max}}}}\) and SDI. Higher values of \(S_{{Pre,SDI}}\) and \(S_{{Tmin,SDI}}\) in comparison with \(S_{{Pre,SPI}}\) and \(S_{{Tmin,SPI}}\) suggested the existence of a more substantial relationship between multifractality in precipitation and \(T_{{{\text{min}}}}\) with hydrological drought multifractality than meteorological drought. The results made clear that multifractality variations in meteorological and hydrological droughts exhibited noticeable monotonic relation with \(T_{{{\text{max}}}}\) and \(T_{{{\text{min}}}}\), respectively. On the contrary, multifractality variations in meteorological and hydrological drought displayed negligible monotonic relationship with precipitation and \(T_{{{\text{min}}}}\) multifractal strength variations, respectively.

According to Fig. 6, the highest cross-correlation was recorded between multifractal variations in precipitation and drought indices. Besides, the cross-correlation between multifractal variations in precipitation and SPI was more effective than precipitation and SDI. It implied that multifractal variations in meteorological and hydrological droughts were more sensitive to multifractal changes in precipitation than temperature. Moreover, multifractal fluctuations in precipitation more influenced multifractal variations in meteorological drought than hydrological drought.

A higher level of cross-correlation was recorded between multifractal variations of \(T_{{{\text{max}}}}\) and drought indices than \(T_{{{\text{min}}}}\) and drought indices. It proved that multifractal variations in drought indices were more sensitive to multifractal fluctuations in \(T_{{{\text{max}}}}\) than \(T_{{{\text{min}}}}\). The maximum recorded cross-correlation value related to multifractal variations in temperature and SDI, providing evidence for high sensitivity of multifractal variations in hydrology drought (compared with meteorological drought) to multifractality in temperature.

The existence of the long-range persistence cross-correlation between multifractal strength variations in all time series was illustrated by the generalized Hurst exponent values greater than 0.5 (Table 6). The highest value of generalized Hurst exponent was associated with precipitation, confirming the highest long-range persistent cross-correlation between precipitation and drought indices. The generalized Hurst exponent values confirmed the linear and sensitivity analysis results concerning the relationship between multifractal strength variations in the time series. It verified that there was a substantial connection between meteorological drought and precipitation.

The q-order Hurst exponent diagram (\(H\left( q \right)\sim q\)) was used to investigate the fractality of cross-correlation between time series (Figs. 7 and 8).

Fig. 7
figure 7

The q-order Hurst exponent diagram (\(H\left( q \right)\sim q\)) concerning precipitation, \(T_{{max}}\), and \(T_{{min}}\) and SPI (left) and SDI (right) time series

Full size image
Fig. 8
figure 8

The q-order Hurst exponent diagram (\(H\left( q \right)\sim q\)) concerning multifractal strength variations in precipitation, \(T_{{max}}\), and \(T_{{min}}\) and SPI (left) and SDI (right) time series

Full size image

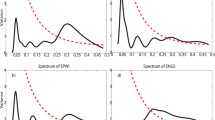
It is clear from Figs. 7 and 8 that cross-correlation between the time series exhibited multifractal properties due to the nonlinear dependence of \(H\left( q \right)\) on \(q\). The more nonlinear relationship between \(H\left( q \right)\) and \(q\), the greater the multifractal strength. Therefore, the cross-correlation between precipitation and drought indices (for original time series and multifractal strength variations in the time series) was more multifractal than temperature and drought indices. The multifractal analysis confirmed PCC, SRCC, and cross-correlation results concerning the quality of the relationship between precipitation and drought indices. The multifractal, PCC, SRCC, and cross-correlation results indicated that drought indices were highly sensitive to precipitation than temperature. Moreover, variations in droughts multifractality were more influenced by precipitation multifractality than temperature multifractality. Furthermore, meteorological drought and its multifractality were significantly impacted (sensitive and dependent) by precipitation and its multifractality, whereas hydrological drought and its multifractality were considerably affected by temperature and its multifractality.

According to mentioned results, we are able to draw a number of conclusions:

The linear correlation between precipitation and drought indices was stronger than temperature and drought indices. Meteorological drought had a significant linear and monotonic relationship with precipitation and \(T_{{{\text{min}}}}\), whereas hydrological drought had a considerable linear and monotonic relationship with \(T_{{{\text{max}}}}\). It was verified that cross-correlation between precipitation and drought indices was more long-range persistent than temperature and drought indices. Moreover, the cross-correlation between precipitation and meteorological drought had more long-term memory than precipitation and hydrological drought. Additionally, the cross-correlation between \(T_{{{\text{max}}}}\) and drought indices exhibited more long-range persistency than \(T_{{{\text{min}}}}\) and drought indices. The multifractal analysis confirmed correlation, monotonic, and sensitivity analysis results so that meteorological drought was sensitive to precipitation fluctuations and hydrological drought presented sensitivity to temperature variations.

The analysis results of multifractal strength variations demonstrated that meteorological drought multifractality had a strong linear correlation with multifractal strength variations in precipitation and \(T_{{{\text{max}}}}\), whereas hydrological drought multifractality had a substantial linear relationship with \(T_{{{\text{min}}}}\). The multifractal strength variations in \(T_{{{\text{max}}}}\) and meteorological drought (SPI) were monotonically related. Likewise, the multifractal strength variations in hydrological drought (SDI) and precipitation and \(T_{{{\text{min}}}}\) exhibited an influential monotonical relationship. The generalized Hurst exponent indicated that the cross-correlation between multifractal strength variations in all time series was long-range persistent. It was verified that as meteorological drought depended on precipitation and hydrological drought depended on temperature from linear correlation, monotonic relation, and cross-correlation points of view, multifractality in meteorological and hydrological droughts was dependent on multifractal variations in precipitation and temperature, respectively.

The analysis results of timescale changing proved augmentation of the long-range persistency of cross-correlation owing to the reduction in scale length. However, the multifractal strength declined as a cutback in scale length except for the 6–24 months scale. At the 6–24 months scale, \(\Delta \alpha _{{Tmax,SPI}}\), \(\Delta \alpha _{{Tmin,SPI}}\), \(\Delta \alpha _{{Tmax,SDI}}\), and \(\Delta \alpha _{{Tmin,SDI}}\) experienced increments. The \(\Delta \alpha\) positive values for all scale-lengths provided evidence for more probability of large local fluctuations than small local fluctuations in the time series.

The q-order Hurst exponent graph (\(H\left( q \right)\sim q\)) verified that cross-correlation between the time series exhibited multifractal properties, and the cross-correlation between precipitation and drought indices was more multifractal than temperature and drought indices. Since the multifractal strength of the cross-correlation between precipitation and droughts (meteorological and hydrological) was stronger than the multifractal strength of the cross-correlation between temperature and droughts, droughts’ sensitivity to precipitation is less than temperature. In other words, it demonstrates the leading role of temperature on drought events. Multifractal analysis indicated that as there was a more substantial linear relation, monotonical correlation, and long-range persistency between precipitation and droughts than temperature and droughts, the cross-correlation between droughts and precipitation was more multifractal than droughts and temperature. The cross-correlation of multifractal strength variations between precipitation and droughts (meteorological and hydrological) was multifractal than temperature and droughts. This proved that multifractal strength variations in droughts are more affected by temperature than precipitation.

Several studies hitherto have been conducted on meteorological and hydrological drought association (Li et al. 2020, 2018; Liu et al. 2019a, b; Zhu et al. 2019; Yao et al. 2020), cross-correlation analysis of hydro-meteorological time series (Wei et al. 2020), and multifractal characterization of drought (Adarsh et al. 2019; Hou et al. 2018; Toluwalope Ogunjo 2021; Adarsh and Priya 2021); however, no research has been performed on the sensitivity of meteorological and hydrological drought to precipitation and temperature, besides meteorological and hydrological droughts’ multifractality dependence on precipitation and temperature multifractality. Therefore, this issue was addressed in the present study to broader our understanding of droughts mechanism.

4 Conclusion

It was attempted to evaluate meteorological and hydrological droughts’ susceptibility to precipitation and temperature, besides meteorological and hydrological droughts’ multifractality dependence on precipitation and temperature multifractality. The nonlinear dynamic and cross-correlation results indicated that precipitation had a greater effect on droughts (meteorological and hydrological) than temperature. In other words, droughts were more sensitive to precipitation fluctuations than temperature fluctuations. Concerning temperature, meteorological and hydrological droughts were dependent on the minimum and maximum temperatures, respectively. The relationship between precipitation and meteorological drought was more long-range persistence than precipitation and hydrologic drought. Besides, the correlation between maximum temperature and droughts was more long-range persistence than minimum temperature and droughts. Analysis of nonlinear dynamic patterns governing the systems proved that the multifractal strength of meteorological drought depended on the multifractal strength of precipitation and maximum temperature, whereas the multifractal strength of hydrological drought depended on the multifractal strength of the minimum temperature. The analysis results of timescale changing proved augmentation of the long-range persistency of cross-correlation owing to the reduction in scale length. However, the multifractal strength declined as a cutback in scale length except for the 6–24 months scale. At the 6–24 months scale, \(\Delta \alpha _{{Tmax,SPI}}\), \(\Delta \alpha _{{Tmin,SPI}}\), \(\Delta \alpha _{{Tmax,SDI}}\), and \(\Delta \alpha _{{Tmin,SDI}}\) experienced increments. The \(\Delta \alpha\) positive values for all scale-lengths provided evidence for more probability of large local fluctuations than small local fluctuations in the time series. The q-order Hurst exponent graph (\(H\left( q \right)\sim q\)) verified that cross-correlation between the time series exhibited multifractal properties, and the cross-correlation between precipitation and drought indices was more multifractal than temperature and drought indices, demonstrating the leading role of temperature on drought events.

This study had a few limitations, including it did not consider the underlying relationship between other parameters (such as wind speed, sunshine, and evapotranspiration) and droughts (meteorological and hydrological). Moreover, it did not examine the impact of other non-climatic (or human factors) elements such as land-use or -cover change on nonlinear dynamic patterns governing meteorological and hydrological droughts. However, this study suggested a novel approach for those interested in studying the nonlinear dynamic mechanisms governing droughts (meteorological and hydrological) and hydrological elements.