1 Introduction

Due to the remarkable benefits of fractional calculus in delineating the dynamical properties of nonlinear systems, it has been broadly used in numerous areas such as disease treatment [1], fluid mechanics [2], formation control [3], etc. Fractional-order derivatives possess the infinite memory and hereditary properties compared with integer-order ones, and these superior aspects make differential equations with fractional calculus are capable of describing precisely the dynamical behaviors of complex systems and further reinforce the potentiality of representation, formulation and control [4, 5]. Fractional calculus has been currently emerged into neural networks (NNs) and formed fractional-order neural networks (FONNs) to research the intricate features of NNs [6]. Some delightful results and essential applications have been detected of FONNs, such as network approximation [7], parameter estimation [8], system identification [9]. Therefore, it is imperative to explore the dynamics of FONNs. Nowadays, FONNs have shown strong interest and concern, and some essential results were obtained [10,11,12].

After the distinguished work of merging a single time delay into NNs in [13], some researchers detected that multiple delays can be introduced into NNs to reflect more real, color and complex behaviors of dynamical systems [14,15,16]. In [17], the authors further highlighted that time delay may be inconsistent for the communication among different adjacent neurons as a result of finite signal propagation speeds and finite processing times in synapses. Therefore it is more realistic and meaningful to introduce different time delays between the connected neurons in NNs. Recently, some remarkable results on the dynamics of FONNs with multiple delays have been researched [18,19,20].

Bifurcation methodologies can be viewed as wonderful candidates to acquire some beneficial information of intricate systems [21,22,23]. Compared with the literatures available on bifurcations of traditional integer-order systems, the bifurcations of fractional-order systems are promising topics [24,25,26]. The bifurcations of FONNs with a single delay have received intensive surveys, and a number of eminent bifurcation attainments have been currently attained [27, 28]. For vanquishing the imperfection in depicting real systems with unique delay, some results on bifurcations of FONNs with multiple delays have been reported [29,30,31]. In [30], the issue of bifurcation for a FONN with two leakage delays was considered, and the stability performance of the proposed FONN can be undermined once leakage delays occur. It should be pointed out that the bifurcations of multiple-delayed FONNs were considered with relatively low-order dimension. As a matter of fact, low-order NNs possess numerous ingenerate imperfections in convergence rate, storage capacity, and fault tolerance. On the contrary, high-order NNs can satisfactorily vanquish these shortcomings and exhibit bigger storage capacity, stronger approximation property, faster convergence rate, and higher fault tolerance [32,33,34]. This motivates numerous scholars to make use of NNs with high order connections. Thus, it is essential to explore high-order interactions of NNs for vanquishing the deficiency of low-order NNs. Remarkably, most of existing results discussing the bifurcation of FONNs by using communication delay as a bifurcation parameter, few efforts can be found to investigate this issue by taking connection delay as a bifurcation parameter [27]. It is noteworthy that the discussions with respect to bifurcation of delayed high-order FONNs involving multiple delays are extremely inadequate as a result of experiencing theoretically the difficulty of discussing characteristic equation [35].

Motivated by the previous discussions, we are committed to presenting a theoretical research of bifurcation for high-order FONNs with multiple delays in this paper. The highlights of this paper can be protruded as follows: (1) The bifurcation results of a conventional integer-order NN with three neurons are generalized to high-order FONNs version in [36]. The obtained results are more accurate, and this reduces the conservatism of the previous ones. (2) By breaking through the difficulty of analyzing the characteristic equation, the exact bifurcation conditions-induced by two different delays are derived. (3) The effects of fractional order on the bifurcation points are explored in high-order FONNs with multiple delays. It discovers that fractional order has an important influence in affecting the stability and bifurcation for the developed NNs.

The framework of the paper is constructed in the following: In Sect. 2 presents the fractional Caputo derivative definition. In Sect. 3 addresses the fundamental mathematical model. Section 4 achieves the outcomes of bifurcations by making use of different delays as bifurcation parameters. Section 5 affirms the efficaciousness of the developed results by adopting simulation examples. Section 6 comes to the essential conclusion.

2 Preliminaries

This section addresses the Caputo definition with respect to fractional calculus for the next theoretical analysis and simulations.

Definition 1

[37] The fractional-order integral of non-integer order q for a function f(t) is defined as

$$\begin{aligned} I^{q}f(t)=\frac{1}{\varGamma (q)}\int _{t_0}^t(t-\tau )^{q-1}f(\tau )d\tau , \end{aligned}$$

where \(q>0\), \(\varGamma (\cdot )\) is the Gamma function, \(\varGamma (s)=\int _0^\infty t^{s-1}e^{-t}ds\).

Definition 2

[37] The Caputo fractional-order derivative is defined by

$$\begin{aligned} D^{q}f(t)=\frac{1}{\varGamma (\iota -q)}\int _{t_0}^t(t-s)^{\iota -q-1}f^{(\iota )}(s)ds, \end{aligned}$$

where \(\iota -1<q\le \iota \in Z^+\), \(t=t_0\) is the initial time.

Based on the Laplace transform, we can express as

$$\begin{aligned} L\{D^{q}f(t);s\}=s^q F(s)-\sum _{k=0}^{\iota -1}s^{q-k-1}f^{(k)}(0),\quad \iota -1<q\le \iota \in Z^+. \end{aligned}$$

If \(f^{(k)}(0)=0\), \(k=1,2,\ldots ,n\), then \(L\{D^{q}f(t);s\}=s^q F(s).\)

3 Mathematical Modeling

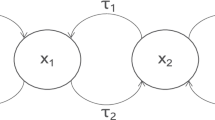
On the basis of the conventional NN model in [36], the following FONNs with n neurons and self-connection delay is formulated in this paper.

$$\begin{aligned} \left\{ \begin{aligned}&D^{q}x_{1}(t)=-kx_1(t)+pf(x_1(t-\eta ))+c_1g(x_n(t-\tau _1)),\\&D^{q}x_{i}(t)=-kx_i(t)+pf(x_i(t-\eta ))+c_ig(x_{i-1}(t-\tau _i)), \quad i=2,3,\ldots ,n, \end{aligned} \right. \end{aligned}$$
(1)

where \(q\in (0,1]\), \(x_1(t)\), \(x_i(t)\) \((i=2,3,\ldots ,n)\) denotes state variables, \(k>0\) denotes adjustable parameter of neurons, \(p>0\), \(c_i>0\) represents connection weights, and \(c_i>0\), \(f(\cdot )\), \(g(\cdot )\) denote activation functions, \(\eta \) is self-connection delay, \(\tau _i\) is communication delay.

Throughout this paper, the following assumption on the activation functions in FONNs (1) are addressed:

\((\mathbf{H1} )\) \(f,g\in C^3(R,R)\), \(f(0)=g(0)=0\), \(f'(0)\ne 0\), \(g'(0)\ne 0\).

Based on the analytic technique used in [38], we intend to establish the bifurcation point in FONNs (1) by selecting self-connection delay as a bifurcation parameter.

4 Main Results

In this section, the major stability results and the bifurcation points shall be established by selecting self-connection delay as a bifurcation parameter. Applying \((\mathbf{H1} )\), it can be observed that the origin is an equilibrium of FONNs (1). Adopting Taylor expansion, the following linear form of FONNs (1) can be derived as

$$\begin{aligned} \left\{ \begin{aligned}&D^{q}x_{1}(t)=-kx_1(t)+ax_1(t-\eta )+b_1x_n(t-\tau _1),\\&D^{q}x_{i}(t)=-kx_i(t)+ax_i(t-\eta )+b_ix_{i-1}(t-\tau _i),\quad i=2,3,\ldots ,n, \end{aligned} \right. \end{aligned}$$
(2)

where \(a=pf'(0)\), \(b_i=c_ig'(0)\).

The characteristic equation of FONNs (2) takes the following form

$$\begin{aligned} \det \mathrm {}\left[ \begin{array}{ccccc} s^{q}+k-ae^{-s\eta } &{} 0&{} \cdots &{}-b_1e^{-s\tau _1}\\ -b_2e^{-s\tau _2} &{} s^{q}+k-ae^{-s\eta } &{} \cdots &{}0\\ 0 &{} -b_3e^{-s\tau _3} &{} \cdots &{}0 \\ \vdots &{} \vdots &{} \ddots &{} 0\\ 0 &{} \cdots &{} \cdots &{} s^{q}+k-ae^{-s\eta } \end{array} \right] =0. \end{aligned}$$
(3)

Equation (3) can be simplified as

$$\begin{aligned} \big (s^{q}+k-ae^{-s\eta }\big )^n=\prod _{i=1}^nb_ie^{-ns\tau }, \end{aligned}$$
(4)

where \(\tau =\frac{\sum _{i=1}^n\tau _i}{n}\).

Equation (4) is equal to

$$\begin{aligned} s^{q}+k-ae^{-s\eta }=be^{-s\tau +\frac{2l\pi i}{n}},\quad l=0,1,\ldots ,n-1, \end{aligned}$$
(5)

where \(b=\root n \of {\prod _{i=1}^nb_i}\).

Let \(s=w(\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})(w>0)\) be a purely imaginary root of Eq. (5), then we arrive at

$$\begin{aligned} \left\{ \begin{aligned}&w^q\cos \frac{q\pi }{2}+k-a\cos w\eta =b\cos \Big (w\tau -\frac{2l\pi }{n}\Big ),\\&w^q\sin \frac{q\pi }{2}+a\sin w\eta =-b\sin \Big (w\tau -\frac{2l\pi }{n}\Big ). \end{aligned} \right. \end{aligned}$$
(6)

By employing Eq. (6), it derives

$$\begin{aligned} \left\{ \begin{aligned}&\cos w\eta =\ell _1(w),\\&\sin w\eta =\ell _2(w), \end{aligned} \right. \end{aligned}$$
(7)

where

$$\begin{aligned}&\ell _1(w)=\frac{w^q\cos \frac{q\pi }{2}+k-b\cos \big (w\tau -\frac{2l\pi }{n}\big )}{a},\\&\ell _2(w)=\frac{-w^q\sin \frac{q\pi }{2}-b\sin \big (w\tau -\frac{2l\pi }{n}\big )}{a}. \end{aligned}$$

It is clear from Eq. (7) that

$$\begin{aligned} \ell ^2_1(w)+\ell ^2_2(w)=1. \end{aligned}$$
(8)

To establish our main results, we assume

\((\mathbf{H2} )\) Assumed that Eq. (8) has positive real roots \(w_k(k=0,1,2,\ldots )\).

According to the first equation of Eq. (7), we get

$$\begin{aligned} \eta _{j}^{(k)}=\frac{1}{w_k}\big [\arccos \ell _1(w_k)+2j\pi \big ],\quad j=0,1,2,\ldots . \end{aligned}$$
(9)

Define the bifurcation point

$$\begin{aligned} \eta _{0}=\eta _{j}^{(0)}=\min \{\eta _{j}^{(k)}\},\quad w=w_{k_0},\quad k=0,1,2,\ldots . \end{aligned}$$

Let \(\eta =0\), then Eq. (5) can be transformed into

$$\begin{aligned} s^{q}+k-a=be^{-s\tau +\frac{2l\pi i}{n}},\quad l=0,1,\ldots ,n-1. \end{aligned}$$
(10)

Assume that \(s=\varpi (\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})(\varpi >0)\) is a purely imaginary root of Eq. (10), we have

$$\begin{aligned} \left\{ \begin{aligned}&\cos \frac{2l\pi }{n}\cos \varpi \tau +\sin \frac{2l\pi }{n}\sin \varpi \tau = \frac{\varpi ^q\cos \frac{q\pi }{2}+k-a}{b},\\&\sin \frac{2l\pi }{n}\cos \varpi \tau -\cos \frac{2l\pi }{n}\sin \varpi \tau = \frac{\varpi ^q\sin \frac{q\pi }{2}}{b}. \end{aligned} \right. \end{aligned}$$
(11)

By employing Eq. (11), it obtains as

$$\begin{aligned} \left\{ \begin{aligned}&\cos \varpi \tau =\hbar _1(\varpi ),\\&\sin \varpi \tau =\hbar _2(\varpi ), \end{aligned} \right. \end{aligned}$$
(12)

where

$$\begin{aligned}&{\hbar _1(\varpi )=\frac{\cos \frac{2l\pi }{n}(\varpi ^q\cos \frac{q\pi }{2}+k-a\big ) +\sin \frac{2l\pi }{n}(\varpi ^q\sin \frac{q\pi }{2}\big )}{b}},\\&{\hbar _2(\varpi )=\frac{-\cos \frac{2l\pi }{n}(\varpi ^q\sin \frac{q\pi }{2}\big ) +\sin \frac{2l\pi }{n}(\varpi ^q\cos \frac{q\pi }{2}+k-a\big )}{b}}. \end{aligned}$$

It follows from Eq. (12) that

$$\begin{aligned} \hbar ^2_1(\varpi )+\hbar ^2_2(\varpi )=1. \end{aligned}$$
(13)

If Eq. (13) has positive root, then the values of \(\varpi _k(k=0,1,2,\ldots )\) can be determined. In terms of Eq. (12), we get

$$\begin{aligned} \tau _{j}^{(k)}=\frac{1}{\varpi _k}\big [\arccos \hbar _1(\varpi _k)+2j\pi \big ],\quad j=0,1,2,\ldots . \end{aligned}$$
(14)

It defines as

$$\begin{aligned} \tau _0=\tau _{j}^{(0)}=\min \left\{ \tau _j^{(k)}\right\} ,\quad \varpi =\varpi _{k_0}, \quad k=0,1,2,\ldots . \end{aligned}$$

To establish the conditions of Hopf bifurcation, the following assumption is useful:

\((\mathbf{H3} )\) \(\varLambda >0\), where \(\varLambda >0\) is defined by Eq. (16).

Lemma 1

Assume that \(s(\eta )=\zeta (\eta )+iw(\eta )\) is the root of Eq. (5) near \(\eta =\eta _0\) satisfying \(\zeta (\eta _0)=0\), \(w(\eta _0)=w_0\), then the following transversality condition can be derived

$$\begin{aligned} \mathrm {Re}\Big [\frac{ds}{d\eta }\Big ] \Big |_{(w=w_0,\eta =\eta _0)}>0, \end{aligned}$$

where \(w_0\) and \(\eta _0\) denote the critical frequency and the bifurcation point of FONNs (1), respectively.

Proof

Using differential techniques for Eq. (5) with respect to \(\eta \), then one procures

$$\begin{aligned} \frac{d\eta }{ds}=\frac{qs^{q-1}+a\eta e^{-s\eta } +b\tau e^{-s\tau +\frac{2l\pi i}{n}}}{-ase^{-s\eta }}. \end{aligned}$$
(15)

In view of Eq. (15), it derives that

$$\begin{aligned} \mathrm {Re}\Big [\frac{d\eta }{ds}\Big ] \Big |_{(w=w_0,\eta =\eta _0)}=\frac{\varLambda }{a^2}, \end{aligned}$$
(16)

where \(\varLambda =qw_0^{q-2}\Big [w_0^q+k\cos \frac{q\pi }{2} -b\cos \Big (w_0\tau +\frac{(nq-4l)\pi }{2n}\Big )\Big ]+ab\tau \cos \frac{2l\pi }{n}\).

Taking advantage of \((\mathbf{H3} )\), it is evident that \(\mathrm {Re}\Big [\!\frac{ds}{d\eta }\!\Big ]\Big |_{(w=w_0,\eta =\eta _0)}\!>\!0\). It follows Lemma 1.

\(\square \)

Theorem 1

Under \((\mathbf{H1} )\)–\((\mathbf{H3} )\), the following results can be derived:

  1. (i)

    The origin of FONNs (1) is asymptotically stable for \(\eta \in [0,\eta _0)\) if \(\tau \in [0,\tau _0)\).

  2. (ii)

    FONNs (1) experiences a Hopf bifurcation at the origin if \(\tau \in [0,\tau _0)\) when \(\eta =\eta _0\), i.e., it has a branch of periodic solutions bifurcating from the origin near \(\eta =\eta _0\).

Remark 1

In this paper, self-connection delay \(\eta \) is viewed as a bifurcation parameter to discuss the bifurcations of high-order fractional NNs. The stability domains and self-connection delay \(\eta \) induced bifurcation results are completely established. As a matter of fact, \(\tau _i(i=1,2,\ldots ,n)\) in FONNs (1) can be taken as bifurcation parameter to explore the problem of bifurcation of FONNs (1) by fixing the parameter \(\eta \).

5 Numerical Tests

To authenticate the efficiency of the developed theory, two numerical examples are provided in this section.

5.1 Example 1

Consider the following FONN with three neurons

$$\begin{aligned} \left\{ \begin{aligned}&D^{q}x_{1}(t)=-\,kx_1(t)+p\tanh (x_1(t-\eta ))+c_1\tanh (x_3(t-\tau _1)),\\&D^{q}x_{2}(t)=-\,kx_2(t)+p\tanh (x_2(t-\eta ))+c_2\tanh (x_1(t-\tau _2)),\\&D^{q}x_{3}(t)=-\,kx_3(t)+p\tanh (x_3(t-\eta ))+c_3\tanh (x_2(t-\tau _3)),\\ \end{aligned} \right. \end{aligned}$$
(17)

where \(k=1\), \(p=-\,2\), \(c_1=1\), \(c_2=2\), \(c_3=4\), \(\tau _1=0.3\), \(\tau _2=0.4\), \(\tau _3=0.5\).

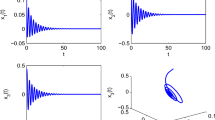
Choosing \(q=0.92\), it obtains as \(w_0=1.636\), then \(\eta _0=0.3897\). To confirm the derived bifurcation results, the initial values are taken as \(x_1(0),x_2(0),x_3(0)=(0.02,0.02,0.02)\). It is simple to verify that \((\mathbf{H1} )\)–\((\mathbf{H3} )\) hold. According to Theorem 1, the origin of FONN (17) is asymptotically stable when \(\eta =0.35<\eta _{0}\), which is depicted in Fig. 1. It can be observed that the origin of FONN (17) is unstable, Hopf bifurcation occurs from the origin when \(\eta =0.45>\eta _{0}\), as revealed in Fig. 2. Figure 3 reveals the influence of fractional order q on the bifurcation point \(\eta _0\) of FONN (17). This implies that the onset of bifurcation for FONN (17) can be postponed with the increment of fractional order q, which are diagrammatically confirmed in Figs. 4, 5 and 6 by choosing \(q=0.63, 0.65, 0.98\).

Fig. 1
figure 1

Waveform plots and portrait diagram of FONN (17) with \(q=0.92\), \(\eta =0.35<\eta _{0}=0.3897\)

Full size image
Fig. 2
figure 2

Waveform plots and portrait diagram of FONN (17) with \(q=0.92\), \(\eta =0.45>\eta _{0}=0.3897\)

Full size image
Fig. 3
figure 3

Impact of q on \(\eta _0\) of FONN (17)

Full size image
Fig. 4
figure 4

Waveform plots of FONN (17) with \(\eta =0.35\), \(q=0.63, 0.65, 0.98\)

Full size image
Fig. 5
figure 5

Waveform plots of FONN (17) with \(\eta =0.35\), \(q=0.63, 0.65, 0.98\)

Full size image
Fig. 6
figure 6

Waveform plots of FONN (17) with \(\eta =0.35\), \(q=0.63, 0.65, 0.98\)

Full size image

5.2 Example 2

Consider the following FONN with four neurons

$$\begin{aligned} \left\{ \begin{aligned}&D^{q}x_{1}(t)=-\,kx_1(t)+p\tanh (x_1(t-\eta ))+c_1\tanh (x_4(t-\tau _1)),\\&D^{q}x_{2}(t)=-\,kx_2(t)+p\tanh (x_2(t-\eta ))+c_2\tanh (x_1(t-\tau _2)),\\&D^{q}x_{3}(t)=-\,kx_3(t)+p\tanh (x_3(t-\eta ))+c_3\tanh (x_2(t-\tau _3)),\\&D^{q}x_{4}(t)=-\,kx_4(t)+p\tanh (x_4(t-\eta ))+c_4\tanh (x_3(t-\tau _4)),\\ \end{aligned} \right. \end{aligned}$$
(18)

where \(k=0.5\), \(p=-\,2.5\), \(c_1=1\), \(c_2=2\), \(c_3=3\), \(c_4=4\), \(\tau _1=0.2\), \(\tau _2=0.3\), \(\tau _3=0.4\), \(\tau _4=0.5\).

Selecting \(q=0.95\), it derives as \(w_0=6.6365\), then \(\eta _0=0.3798\). To demonstrate the bifurcation results, the initial values are selected as \(x_1(0),x_2(0),x_3(0),x_4(0)=(0.02,0.02,0.02,0.02)\). It is simple to confirm that \((\mathbf{H1} )\)–\((\mathbf{H3} )\) meet. In terms of Theorem 1, the origin of FONN (18) is asymptotically stable when \(\eta =0.3<\eta _{0}\), which is simulated in Figs. 7 and 8. It can be observed that the origin of FONN (18) is unstable, Hopf bifurcation occurs from the origin when \(\eta =0.4>\eta _{0}\), which is reflected in Figs. 9 and 10. Clearly, Fig.11 reflects the relation of fractional order q on the bifurcation point \(\eta _0\) of FONN (18). Fig.11 clearly displays that the onset of bifurcation for FONN (17) can be lagged as fractional order q increases. The observed results are nicely verified in Figs. 12, 13, 14 and 15 by selecting \(q=0.71, 0.72, 0.96\).

Fig. 7
figure 7

Waveform plots of FONN (18) with \(q=0.95\), \(\eta =0.3<\eta _{0}=0.3798\)

Full size image
Fig. 8
figure 8

Portrait diagrams of FONN (18) with \(q=0.95\), \(\eta =0.3<\eta _{0}=0.3798\)

Full size image
Fig. 9
figure 9

Waveform plots of FONN (18) with \(q=0.95\), \(\eta =0.4>\eta _{0}=0.3798\)

Full size image
Fig. 10
figure 10

Portrait diagrams of FONN (18) with \(q=0.95\), \(\eta =0.4>\eta _{0}=0.3798\)

Full size image
Fig. 11
figure 11

Impact of q on \(\eta _0\) of FONN (18)

Full size image
Fig. 12
figure 12

Waveform plots of FONN (18) with \(\eta =0.2\), \(q=0.71, 0.72, 0.96\)

Full size image
Fig. 13
figure 13

Waveform plots of FONN (18) with \(\eta =0.2\), \(q=0.71, 0.72, 0.96\)

Full size image
Fig. 14
figure 14

Waveform plots of FONN (18) with \(\eta =0.2\), \(q=0.71, 0.72, 0.96\)

Full size image
Fig. 15
figure 15

Waveform plots of FONN (18) with \(\eta =0.2\), \(q=0.71, 0.72, 0.96\)

Full size image

6 Conclusion

The issue of bifurcation for FONNs with n neurons and self-connection delay has been explored in this paper. Stability domain has been established, and self-connection delay induced bifurcation results have been determined in terms of self-connection delay as a bifurcation parameter. It has reflected that the stability performance of developed FONNs can be nicely maintained if taking a smaller connection delay, and Hopf bifurcation emerges upon self-connection delay negotiates the critical value. On the basis of theoretical calculations, the relation between the bifurcation points and fractional order has been revealed. It has manifested that fractional order plays an essential role in stabilizing the stability performance of the developed FONNs. Namely, the onset of bifurcation can be postponed with the enlargement of fractional order. Numerical simulations are performed to check the availability of obtained results.