Abstract
The theme of bifurcation for a class of fractional-order neural networks (FONNs) with unique delay has been incalculably elucidated. It exhibits that multiple delays are capable of increasing the complicacy of realistic FONNs, but this has been insufficiently probed into. This paper attempts to conduct a research on the stability and bifurcation for a FONN with two unequal delays. By intercalating one delay and taking remnant delay as a bifurcation parameter, the incongruent critical values of diverse delays-induced bifurcations are exactly gained. Eventually, confirmation experiments are offered to endorse the procured theory.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The explorations on the theory and applications of neural networks (NNs) have been garnered intense concerns thanks to their generally authentic applications [1,2,3,4,5,6,7]. Currently, fractional calculus has been favorably drawn into NNs in virtue of the pinpoint characterization for the dynamic response of the actual systems. It is exposed that fractional differentiation is emerged into NNs which can efficiently handle formation [8]. Some delightful results and applications have been founded for FONNs, such as image encryption [9], network approximation [10]. Therefore, it is requisite to explore the dynamics of FONNs. There has been an immensely ever-increasing attention in the explorations of FONNs, and some important and meritorious results were obtained [11,12,13,14,15]. In [11], the lag synchronization for delayed fractional-order memristive NNs was reached by the aid of switching jumps mismatch, and the lag quasi-synchronization conditions were further derived.
Researchers have the ability to develop prospective dynamical properties of nonlinear systems via impelling Hopf bifurcation methodology [16,17,18,19,20]. It is generally known that the bifurcations of integer-order systems have been excessively discussed. On account of high accurateness of describing NNs with the help of fractional calculus in comparison with accustomed ones, numerous scholars have been overwhelmingly enchanted by the bifurcations of fractional-order systems, and numerous valuable results have been reported [21,22,23,24,25,26,27,28]. In [21], the authors investigated a fractional delayed predator–prey model with Holling type II functional response including prey refuge and diffusion, and it indicated that the stability domain can be extended under the fractional order compared with integer-order one. In [24], the bifurcation control of a delayed fractional eco-epidemiological model with incommensurate orders was examined in terms of linear feedback strategy. It proclaimed that stability performance of the system can be varied by amplifying the control delay. In [25], the issue of bifurcation control for a delayed fractional-order predator–prey system was studied by using enhancing feedback method, and it divulged that the enhancing feedback can greatly diminish the control cost by comparison with dislocated feedback. In [26], the stability and bifurcation of a delayed fractional-order quaternion-valued neural network were considered. It manifested that the bifurcation phenomena transpire earlier as fractional order incrementally magnifies. Noticeably, the bulk of existing bifurcations results are focused on fractional-order systems including a single delay. Accordingly, it is reasonable and imperative to integrate multiple time delays into the fractional-order systems for accurately describing dynamical properties. Moreover, past findings has evidenced that the continuous state variables depending on different history, it is extremely essential to pierce the functions of diversified delays for NNs for well-implementing networks with electronic devices and enhancing the performance of optimizing networks in [29].
It is to be observed that some results available on bifurcations have been focused on investigating FONNs with a sole delay as a result of the more complicacy and difficulty for the academic inquiries involving multiple delays [30]. It is evident that systems with single delay can not well reflect the realistic dynamics of dynamical systems. Most currently, some scholars have tried to go a bit deeper and look at the effects of different delays with regard to the bifurcations for delayed FONNs [31, 32]. In [31], the authors considered the issue of bifurcation for a fractional-order predator–prey model comprising two discrepant delays, and the bifurcation points were deduced. The stability and bifurcation of a FONN with double delays, and the conditions of diverse delays-induced bifurcations were exactly derived in [32]. However, it should be pointed out that the investigations for the bifurcation of FONNs with multiple delays is insufficient with a vengeance.
Prompted by aforementioned discussions, we are dedicated to addressing a theoretical investigation of bifurcation for a FONN with two nonidentical delays in this paper. The essential benefits of this paper can be epitomized as follows: (1) It is a super-stretch challenging subject to identify the conditions of bifurcations for fractional order systems with multiple delays. This paper theoretically derives the exact bifurcation points based on disparate delays as the bifurcation parameters on account of the high complexity of stability analysis for dynamical systems with different delays. (2) Discriminating from [31, 32], this paper solves the bifurcation problems for a class of four-dimensional fractional-order system with two unequal delays. (3) This paper addresses an effectual scheme to theoretically investigate the bifurcation of higher dimensional FONNs with two different delays. It further provides an idea and framework to explore the issue of bifurcation for fractional-order systems with three or more delays.
The framework of the paper is portrayed in the following: In Sect. 2 addresses the fractional Caputo definition and basic stability results of fractional linear systems. In Sect. 3 formulates the mathematical model. Section 4 derives the outcomes of Hopf bifurcation by utilising different delays as bifurcation parameters. Section 5 gauges the efficiency of the proposed theory by exploiting simulation cases. Section 6 summaries the essential upshot.
2 Rudimentary Theoretical Tools
This section addresses the Caputo definition and lemma with respect to fractional calculus for the next theoretical analysis and simulations.
Definition 1
[33] The Caputo fractional-order derivative is defined by
where \(\iota -1<q\le \iota \in Z^+\), \(\varGamma (\cdot )\) is the Gamma function, \(\varGamma (s)=\int _0^\infty t^{s-1}e^{-t}dt\).
Based on the Laplace transform, we can express as
If \(f^k(0)=0\), \(k=1,2,\ldots ,n\), then \(L\{D^{q}f(t);s\}=s^q F(s).\)
Lemma 1
[34] Explore linear fractional-order systems with multiple variables
where \(q_i\in (0,1](i=1,2,\ldots ,n)\). Suppose that q is the lowest common multiple of the denominators \(\zeta _i\) of \(q_i\), where \(q_i=\frac{\sigma _i}{\zeta _i}\), \((\sigma _i,\zeta _i)=1\), \(\sigma _i,\zeta _i\in Z^+\), for \(i=1,2,\ldots ,n\). It is labeled as
Then the zero solution of system (1) is globally asymptotically stable in the Lyapunov sense if all roots s of the equation \(\det (\triangle (s))=0\) satisfy \(|\arg (s)|>q_i\pi /2\).
3 Mathematical Modeling
Due to the high-precision description of fractional calculus for NNs. In this paper, we hence incorporate fractional calculus into the dynamical model [35]. The developed model can be addressed as
where \(q_i\in (0,1](i=1,2,3,4)\), \(z_i(t)\) denote state variables, \(\nu _i>0\) represent real values, \(a_i\), \(b_i\) and \(c_i\) are connection weights, \(\varphi _i(\cdot )\), \(\psi _i(\cdot )\) denote activation functions, \(\tau _1\) and \(\tau _2\) are communication delays.
If setting up \(q_i=1\), then FONN (2) can be clearly inverted into the classical model in [35].
The following assumptions are addressed for catching the main results:
\((\mathbf{H1} )\)\(\varphi _i, \psi _i\in C(R,R)\), \(\varphi _i(0)=\psi _i(0)=0\), \(z\varphi _i(z)>0\), \(z\psi _i(z)>0\)\((i=1,2,3,4)\) for \(z\ne 0\).
4 Main Results
In this section, disparate delays are selected as a bifurcation parameter to study the stability and bifurcation for FONN (2), and the bifurcation points are exactly established.
4.1 The Existence of Bifurcation via \(\tau _1\) of FONN (2)
In this subsection, we select \(\tau _1\) as a bifurcation parameter to study the bifurcation of FONN (2). It is obvious that the origin is an equilibrium point of FONN (2) based on \((\mathbf{H1} )\). The linear equation of FONN (2) around the origin can be presented as
where \(k_i=\nu _i-a_i\varphi '_i(0)\), \(m_i=b_i\psi '_i(0)\), \(n_i=c_i\psi '_i(0)\)\((i=1,2,3,4)\).
In view of FONN (3), the following form characteristic equation can be gained
Multiplying \(e^{s\tau _1}\) on both sides of Eq. (4), it obtains as
The real and imaginary parts of \(U_l(s)(l=1,2,3)\) can be labeled by \(U_l^r\), \(U_l^i\), respectively. Assume that \(s=w(\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})\) is a purely imaginary root of Eq. (5), \(w>0\). Substituting s into Eq. (5) and separating the real and imaginary parts of it, it results in
Labeling
As far as Eq. (6), it concludes that
By means of Eq. (7), it procures that
It defines from Eq. (8) that
To establish the main results of this section, the following assumptions are useful and needed.
\((\mathbf{H2} )\) There exist positive real roots for Eq. (9).
Based on Eq. (7), it clearly derive as
Label the bifurcation point of FONN (2) as
where \(\tau _{10}^{(k)}\) is defined by Eq. (10).
Equation (4) can be transformed into the following form when renouncing \(\tau _1\)
where
If \(\tau _2=0\), it follows from Eq. (11) that
where
Assume that all roots s of the Eq. (12) obey Lemma 1, then we obtain that all the roots of Eq. (12) has negative real parts.
The real and imaginary parts of \(\ell _i(s)(i=1,2,3)\) can be designated by \(\ell _i^r\), \(\ell _i^i\), respectively. Multiplying \(e^{s\tau _2}\) on both sides of Eq. (11), it can be obtained as
Presume that \(s=\bar{w}(\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})(\bar{w}>0)\) is a purely imaginary root of Eq. (13), then we can reason out
It labels as
It concludes from Eq. (14) that
By means of Eq. (15), it procures that
It can be defined from Eq. (16) that
The following assumption is addressed.
\((\mathbf{H3} )\) There exists positive roots for Eq. (17).
By means of Eq. (17), the values of w can be obtained according to numerical software Maple 13, then the bifurcation point \(\tau _{20}^*\) of FONN (2) with \(\tau _1=0\) can be derived.
To throw out the bifurcation conditions, the following assumption is addressed
\((\mathbf{H4} )\)\(\frac{\varDelta _1\varLambda _1+\varDelta _2\varLambda _2}{\varLambda _1^2+\varLambda _2^2}\ne 0\), where \(\varDelta _1\), \(\varDelta _2\), \(\varLambda _1\), \(\varLambda _2\) are described by Eq. (20).
Lemma 2
Let \(s(\tau _1)=\xi (\tau _1)+i\rho (\tau _1)\) be the root of Eq. (4) near \(\tau _1=(\tau _1)_j\) complying with \(\xi ((\tau _1)_j)=0\), \(w((\tau _1)_j)=w_0\), then the following transversality condition holds
Proof
The real and imaginary parts of \(U'_p(s)p=1,2,3\) can be labeled by \(U_p^{'r}\), \(U_p^{'i}\). Using implicit function theorem to differentiate (4) with regard to \(\tau _1\), then
By mathematical operations from Eq. (18), we elicit
where
It educes from Eq. (19) that
where
\((\mathbf{H4} )\) indicates that transversality condition hold. It follows Lemma 2. \(\square \)
Based on the previous investigations, we can establish the following theorem.
Theorem 1
Under \((\mathbf{H1} )\)–\((\mathbf{H4} )\), the following results are procurable.
-
(1)
If \(\tau _2\in [0,\tau _{20}^*)\), then the origin of FONN (2) is asymptotically stable when \(\tau _1=\tau _{10}\).
-
(2)
If \(\tau _2\in [0,\tau _{20}^*)\), then FONN (2) undergoes a Hopf bifurcation at the origin when \(\tau _1=\tau _{10}\).
4.2 Impact of \(\tau _2\) on Bifurcation of FONN (2)
In this subsection, we turn our attention to choose \(\tau _2\) as a bifurcation parameter, the bifurcation point is further acquired.
Equation (4) can be rewritten equally as
Multiplying \(e^{s\tau _2}\) on both sides of Eq. (21), it obtains that
Marking the real and imaginary parts of \(J_l(s)(l=1,2,3)\) as \(J_l^r\), \(J_l^i\), respectively. Assume that \(s=\varpi (\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})\) is a purely imaginary root of Eq. (22), \(\varpi >0\). Then it results in
Labeling as
As far as Eq. (23), it concludes that
By means of Eq. (24), one reads
It labels from Eq. (25) that
To establish the main results of this section, the following assumptions is useful and needed.
\((\mathbf{H5} )\) Eq. (26) has one positive real roots.
Based on Eq. (24), it actualizes that
Define the bifurcation point of system (5) as follows:
where \(\tau _{20}^{(k)}\) is defined by Eq. (27).
If \(\tau _2=0\), then Eq. (21) can be inverted into
where
The real and imaginary parts of \(\hbar _i(s)(i=1,2,3)\) can be denoted by \(\hbar _i^r\), \(\hbar _i^i\), respectively. Multiplying \(e^{s\tau _1}\) on both sides of Eq. (28), it can be obtained as
Suppose that \(s=\bar{\varpi }(\cos \frac{\pi }{2}+i\sin \frac{\pi }{2})(\bar{\varpi }>0)\) is a purely imaginary root of Eq. (29), then we arrive at
It is further labeled as
As far as Eq. (30), it concludes that
It procures from Eq. (31) that
In terms of Eq. (32), it is clear that
The following assumption is addressed.
\((\mathbf{H6} )\) Eq. (33) has at least positive roots.
Based on Eq. (33), the values of \(\bar{\varpi }\) can be obtained using numerical software Maple 13, then the bifurcation point \(\tau _{10}^*\) of FONN (2) with \(\tau _2=0\) can be derived.
To throw out the bifurcation conditions, the following assumption is addressed
\((\mathbf{H7} )\)\(\frac{\varPi _1\varTheta _1+\varPi _2\varTheta _2}{\varTheta _1^2+\varTheta _2^2}\ne 0\),
where \(\varPi _1\), \(\varPi _2\), \(\varTheta _1\), \(\varTheta _2\) are described by Eq. (36).
Lemma 3
Let \(s(\tau _2)=\eta (\tau _2)+i\varpi (\tau _2)\) be the root of Eq. (21) near \(\tau _2=(\tau _2)_j\) complying with \(\eta ((\tau _2)_j)=0\), \(\varpi ((\tau _2)_j)=\varpi _0\), then the following transversality condition holds
Proof
The real and imaginary parts of \(J'_p(s)(p=1,2,3)\) can be labeled by \(J_p^{'r}\), \(J_p^{'i}\). Employing implicit function theorem to differentiate Eq. (21) concerning \(\tau _2\), then
Direct deduction from Eq. (34) yields
where
It educes from Eq. (35) that
where
\((\mathbf{H7} )\) indicates that transversality condition hold. We accomplish the proof of Lemma 3.
It follows from the prevenient analysis that the next theorem is obtainable. \(\square \)
Theorem 2
Under \((\mathbf{H1} )\), \((\mathbf{H5} )\)–\((\mathbf{H7} )\), the following results are available.
-
(1)
If \(\tau _1\in [0,\tau _{10}^*)\), then the origin of FONN (2) is asymptotically stable when \(\tau _2\in [0,\tau _{20})\).
-
(2)
If \(\tau _1\in [0,\tau _{10}^*)\), then FONN (2) undergoes a Hopf bifurcation at the origin when \(\tau _2\in [\tau _{20},+\infty )\).
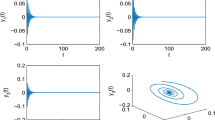
Time responses of FONN (37) with \(\tau _2=0.18\), \(\tau _1=1.2<\tau _{10}=1.4537\)
Phase diagrams of FONN (37) with \(\tau _2=0.18\), \(\tau _1=1.2<\tau _{10}=1.4537\)
Time responses of FONN (37) with \(\tau _2=0.18\), \(\tau _1=1.6>\tau _{10}=1.4537\)
Phase diagrams of FONN (37) with \(\tau _2=0.18\), \(\tau _1=1.6>\tau _{10}=1.4537\)
5 Simulation Examples
In this section, numerical results exemplify the effectiveness and practicability of our theoretical achievements.
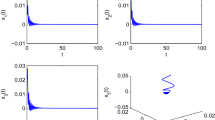
Time responses of FONN (38) with \(\tau _1=0.24\), \(\tau _2=0.6<\tau _{20}=0.8459\)
Phase portraits of FONN (38) with \(\tau _1=0.24\), \(\tau _2=0.6<\tau _{20}=0.8459\)
5.1 Example 1
Consider the following FONN model
Based on computation, we can first determine that \(\tau _{20}^*=1.6337\) in Theorem 1. Then the initial values are selected as \((z_1(0),z_2(0),z_3(0),z_4(0))=(0.02,0.03,0.05,0.04)\). If choosing \(\tau _2=0.18\in (0,\tau _{20}^*)\), we further procure \(w_0=0.9549\), \(\tau _{10}=1.4537\). It simply authenticates that the conditions in Theorem 1 are met. Figures 1 and 2 simulate that locally asymptotical steadiness of the zero equilibrium point of FONN (37) when \(\tau _1=1.2<\tau _{10}\), while Figs. 3 and 4 reflect that the instability of the zero equilibrium point FONN (37), Hopf bifurcation takes place when \(\tau _1=1.6>\tau _{10}\).
5.2 Example 2
Investigate the following FONN model
By calculation, it first derives that \(\tau _{10}^*=1.0859\) in Theorem 2. Next the initial values are taken as \((z_1(0),z_2(0),z_3(0),z_4(0))=(0.02,0.03,0.02,0.03)\). If setting up \(\tau _1=0.24\in (0,\tau _{10}^*)\), then we further procure that \(\varpi _0=1.1798\), \(\tau _{20}=0.8459\). It easily justifies that the conditions of in Theorem 2 hold. Figures 5 and 6 depict that the zero equilibrium point of FONN (38) is locally asymptotically steady when \(\tau _2=0.6<\tau _{20}\), while Figs. 7 and 8 describe that the zero equilibrium point of FONN (38) is precarious, Hopf bifurcation occurs when \(\tau _2=1>\tau _{20}\).
Time responses of FONN (38) with \(\tau _1=0.24\), \(\tau _2=1>\tau _{20}=0.8459\)
Phase portraits of FONN (38) with \(\tau _1=0.24\), \(\tau _2=1>\tau _{20}=0.8459\)
6 Conclusion
In this paper, one delay has been established and another has been delay selected as a bifurcation parameter, the critical values of bifurcation for a FONN with two different delays have been derived. It has been discovered that the bifurcation occurs when the selected delay passes through the critical value, and FONN turns unstable. To certificate the effectiveness of our analytic results, two simulation examples have been ultimately underpinned. There are some enchanting and essential issues that deserve further investigation in the future work, such as (i) how to analyze the problem of bifurcation of the NNs with different delays by using system parameter or fraction order as a bifurcation parameter. (ii) how to generalize the derived bifurcation results to more high-order FONNs with numerous delays.
References
Kim J, Kim H, Huh S, Lee J, Choi KY (2018) Deep neural networks with weighted spikes. Neurocomputing 311:373–386
Akter T, Desai S (2018) Developing a predictive model for nanoimprint lithography using artificial neural networks. Mater Des 160:836–848
Kobayashi M (2018) Twin-multistate commutative quaternion Hopfield neural networks. Neurocomputing 320:150–156
Lauriola I, Gallicchio C, Aiolli F (2020) Enhancing deep neural networks via multiple kernel learning. Pattern Recognit 101:107194
Castro FZ, Valle ME (2020) A broad class of discrete-time hypercomplex-valued Hopfield neural networks. Neural Netw 122:54–67
Wang XH, Wang Z, Song QK, Shen H, Huang X (2020) A waiting-time-based event-triggered scheme for stabilization of complex-valued neural networks. Neural Netw 121:329–338
Yao L, Wang Z, Huang X, Li YX, Shen H, Chen GR (2020) Aperiodic sampled-data control for exponential stabilization of delayed neural networks: a refined two-sided looped-functional approach. IEEE Trans Circuits Syst II Express Briefs. https://doi.org/10.1109/TCSII.2020.2983803
Lundstrom BN, Higgs MH, Spain WJ, Fairhall AL (2008) Fractional differentiation by neocortical pyramidal neurons. Nat Neurosci 11:1335–1342
Wu XJ, Li Y, Kurths J (2015) A new color image encryption scheme using CML and a fractional-order chaotic system. PLoS ONE 10:e0119660
Anastassiou GA (2012) Fractional neural network approximation. Comput Math Appl 64:1655–1676
Zhang LZ, Yang YQ, Wang F, Sui X (2018) Lag synchronization for fractional-order memristive neural networks with time delay via switching jumps mismatch. J Frankl Inst 355:1217–1240
Huang X, Fan YJ, Jia J, Wang Z, Li YX (2017) Quasi-synchronization of fractional-order memristor-based neural networks with parameter mismatches. IET Control Theory Appl 11:2317–2327
Fan YJ, Huang X, Wang Z, Li YX (2018) Improved quasi-synchronization criteria for delayed fractional-order memristor-based neural networks via linear feedback control. Neurocomputing 306:68–79
Fan YJ, Huang X, Wang Z, Li YX (2018) Global dissipativity and quasi-synchronization of asynchronous updating fractional-order memristor-based neural networks via interval matrix method. J Frankl Inst 355:5998–6025
Fan YJ, Huang X, Wang Z, Li YX (2018) Nonlinear dynamics and chaos in a simplified memristor-based fractional-order neural network with discontinuous memductance function. Nonlinear Dyn 93:611–627
Cao JD, Guerrini L, Cheng ZS (2019) Stability and Hopf bifurcation of controlled complex networks model with two delays. Appl Math Comput 343:21–29
Cao Y (2019) Bifurcations in an Internet congestion control system with distributed delay. Appl Math Comput 347:54–63
Li L, Wang Z, Li YX, Shen H, Lu JW (2018) Hopf bifurcation analysis of a complex-valued neural network model with discrete and distributed delays. Appl Math Comput 330:152–169
Wang Z, Li L, Li YX, Cheng ZS (2018) Stability and Hopf bifurcation of a three-neuron network with multiple discrete and distributed delays. Neural Process Lett 48:1481–1502
Wang XH, Wang Z, Shen H (2019) Dynamical analysis of a discrete-time SIS epidemic model on complex networks. Appl Math Lett 94:292–299
Alidousti J, Ghahfarokhi MM (2019) Stability and bifurcation for time delay fractional predator prey system by incorporating the dispersal of prey. Appl Math Model 72:385–402
Wang Z, Wang XH, Li YX, Huang X (2017) Stability and Hopf bifurcation of fractional-order complex-valued single neuron model with time delay. Int J Bifurc Chaos 27:1750209
Wang Z, Xie YK, Lu JW, Li YX (2019) Stability and bifurcation of a delayed generalized fractional-order prey–predator model with interspecific competition. Appl Math Comput 347:360–369
Wang XH, Wang Z, Xia JW (2019) Stability and bifurcation control of a delayed fractional-order eco-epidemiological model with incommensurate orders. J Frankl Inst 356:8278–8295
Huang CD, Liu H, Chen XP, Zhang MS, Ding L, Cao JD, Alsaedi A (2020) Dynamic optimal control of enhancing feedback treatment for a delayed fractional order predator-prey model. Physica 554:124136
Huang CD, Cao JD (2018) Impact of leakage delay on bifurcation in high-order fractional BAM neural networks. Neural Netw 98:223–235
Huang CD, Nie XB, Zhao X, Song QK, Tu ZW, Xiao M, Cao JD (2019) Novel bifurcation results for a delayed fractional-order quaternion-valued neural network. Neural Netw 117:67–93
Huang CD, Li H, Cao JD (2019) A novel strategy of bifurcation control for a delayed fractional predator–prey model. Appl Math Comput 347:808–838
Xu CJ, Shao YF, Li PL (2015) Bifurcation behavior for an electronic neural network model with two different delays. Neural Process Lett 42:541–561
Jia J, Huang X, Li YX, Cao JD, Ahmed A (2020) Global stabilization of fractional-order memristor-based neural networks with time delay. IEEE Trans Neural Netw Learn Syst 31(3):997–1009
Li H, Huang CD, Li TX (2019) Dynamic complexity of a fractional-order predator–prey system with double delays. Physica A 526:120852
Huang CD, Zhao X, Wang XH, Wang ZX, Xiao M, Cao JD (2019) Disparate delays-induced bifurcations in a fractional-order neural network. J Frankl Inst 356:2825–2846
Podlubny I (1999) Fractional differential equations. Academic Press, New York
Deng WH, Li CP, Lü JH (2007) Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn 48:409–416
Hu HJ, Huang LH (2009) Stability and Hopf bifurcation analysis on a ring of four neurons with delays. Appl Math Comput 213:587–599
Acknowledgements
The work was jointly supported by the Key Scientific Research Project for Colleges and Universities of Henan Province under Grant No. 20A110004 and the Nanhu Scholars Program for Young Scholars of Xinyang Normal University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Huang, C., Cao, J. Bifurcation Mechanisation of a Fractional-Order Neural Network with Unequal Delays. Neural Process Lett 52, 1171–1187 (2020). https://doi.org/10.1007/s11063-020-10293-w
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11063-020-10293-w