1 Introduction

In the past few decades, neural networks as an emerging field have been drawing attention from researchers due to their wide application in signal processing, pattern recognition, dynamic optimization, deep learning and so on [1,2,3,4,5,6]. As an important collective behavior, the synchronization of neural networks is an important topic because of its practical applications in biological systems [7,8,9,10,11,12,13].

As is well known, random noises widely exist in the signal transmission of neural networks due to environmental uncertainties, which usually lead to stochastic perturbation and uncertainties of the process for dynamic evolution. Based on the theory of stochastic system [14], a lot of stability and synchronization for neural networks with stochastic perturbations have been obtained [15,16,17]. In the hardware implementation of neural networks, it is impossible for neurons to respond and communicate simultaneously owing to time-delays. To reduce the negative influence of time-delays, delay-independent method is a powerful tool to check the stability and synchronization of neural networks by constructing Lyapunov–Krasovkii functional, see [18,19,20]. On the other hand, in the implementations of neural networks systems, parameter mismatches and stochastic perturbation mismatch are unavoidable. If parameter mismatch and stochastic perturbation mismatch are small, although the stochastic synchronization error can not converge to zero in the mean square with time increasing, but we may show that the error of system is small fluctuations about zero or even a nonzero mean value in the mean square. For background material on parameter mismatch of system, we can find in [21,22,23].

Pinning control, which is an effectively external control approach, has been widely used for a variety of purposes due to low cost. It is characterized that the controllers are added on only a small fraction of network nodes [24,25,26,27]. For example, in [26], the authors proposed a variety of pinning control methods of cluster synchronization in an array of coupled neural networks and proposed a new event-triggered sampled-data transmission strategy. Impulsive control is an energy-saving control due to the instantaneous perturbations input at certain moment, which has been applied efficiently in the fields of engineering, physics, and science as well [28, 29]. With the help of the impulsive system theory, a lot of synchronization results of dynamical networks with impulsive input have been obtained [30,31,32,33]. It is worth noting that the cost of control can be further reduce by adding the impulsive controllers to a small fraction of networks nodes, which can combine the advantage of pinning control and impulsive control. Recently, some research have been devoted to the synchronization of delayed neural networks with pinning and impulsive controls [34, 35]. For instance, in [34], the authors proposed a new pinning impulsive control scheme to investigate the synchronization problem for a class complex networks with time-varying delay.

Motivated by the above discussion, this paper focuses on stochastic quasi-synchronization of delayed neural networks under parameter mismatch and stochastic perturbation mismatch. Although the error of systems will not converge exponentially to zero in the mean square, some effectively sufficient condition are obtained to synchronize the error of systems up to a relatively small bound in the mean square via pinning impulsive control. The contributions in this paper are concluded as follows:

  1. (i)

    By pinning certain selected nodes of stochastic neural networks at each impulsive time, impulsive control strategy is proposed to achieve stochastic-synchronization.

  2. (ii)

    By establishing a new lemma of stochastic impulsive system, stochastic-synchronization criteria are derived to guarantee that the nodes of stochastic neural networks can synchronizes desired trajectory to small region in the mean square.

  3. (iii)

    If the bound of time delay does not exceed the length of impulsive interval, delay-independent method is used to overcome the effects of time delay and impulses by constructing Lyapunov–Krasovkii functional.

The rest of this paper is organized as follows. In Sect. 2, the stochastic neural network is presented and some definitions and lemmas are provided. In addition, a new lemma is established, which plays an important role in the proof of obtained theorems. In Sect. 3, some stochastic quasi-synchronization criteria are obtained via impulsive control technique. In Sect. 4, numerical example is presented to illustrate our results. Finally, some conclusions are given in Sect. 5.

Notations\(R^{n}\) and \(R^{n\times m}\) denote n dimensional Euclidean space and the set of \(n\times m\) real matrices. The superscript T denotes the transpose. \(I_{n}\) represents the identity matrix with n dimension. \(\Vert \cdot \Vert \) denotes the Euclidean norm for a vector and a matrix. \(\lambda _{\max }(A)\) and \(\lambda _{\min }(A)\) represent the maximum and minimum eigenvalues of matrix A. \(diag\{\cdots \}\) stands for a diagonal matrix. For real symmetric matrices X, the notation \(X>0(X<0)\) implies that the matrix X is positive (negative) definite. \(\otimes \) represents Kronecker product. Let \(\omega (t)=(\omega _{1}(t),\omega _{2}(t),\cdots ,\omega _{n}(t))^{T}\) be an n-dimensional Brownian motion on a complete probability space \((\Omega ,\mathcal {F}, P)\) with a natural filtration \(\{\mathcal {F}_{t}\}_{t\ge 0}\) satisfying the usual conditions.

2 Model Description and Preliminaries

Consider stochastic neural network with delay and N coupled nodes. The dynamics of ith neuron is described by the following form

$$\begin{aligned} dx_{i}(t)= & {} [C_{1}x_{i}(t)+B_{1}f(x_{i}(t))+D_{1}f(x_{i}(t-\tau (t)))+\sum \limits ^{N}_{j=1}a_{ij}\Gamma x_{j}(t)+u_{i}(t)]dt\nonumber \\&+h_{1}(t,x_{i}(t),x_{i}(t-\tau (t)))d\omega (t),i=1,2,\cdots ,N, \end{aligned}$$
(1)

where \(x_{i}(t)=(x_{i1}(t),x_{i2}(t),\cdots ,x_{in}(t))^{T}\) is the state vector of the i-th neural networks at time t; \(C_{1}=diag\{c_{11},c_{12},\cdots ,c_{1n}\}\) denotes the rate with which ith cell resets its potential to the resting state when being isolated from other cells and inputs, \(B_{1}=(b^{(1)}_{ij})_{n\times n},D_{1}=(d^{(1)}_{ij})_{n\times n}\in R^{n\times n}\) are the connection weight matrices; f(x) is the activation function at time t satisfying \(f(x_{i}(t))=(f_{1}(x_{i1}(t)),f_{2}(x_{i2}(t)),\ldots ,f_{n}(x_{in}(t)))^{T}\); \(h_{1}(t,x_{i}(t),x_{i}(t-\tau (t)))=(h_{11}(x_{i1}(t),x_{i1}(t-\tau (t))),h_{12}(x_{i2}(t),x_{i2}(t-\tau (t))),\cdots ,h_{1n}(x_{in}(t),x_{in}(t-\tau (t))))^{T}\); \(\tau (t)\) is transmittal delay, and there exist constant \(\tau \) and \(\sigma \) such that \(0<\tau (t)\le \tau \), \(\tau ^{'}(t)\le \sigma <1\); \(\Gamma =diag\{\gamma _{1},\gamma _{2},\cdots ,\gamma _{n}\}\) is the inner coupling positive definite matrix between two connected nodes i and j; and \(a_{ij}\) is defined as follows: if there is a connection from node j to node \(i(j\ne i)\), then \(a_{ij}\ne 0\); otherwise, \(a_{ij}>0\).

Let s(t) be the desired trajectory described by the following form:

$$\begin{aligned} \begin{array}{ll} ds(t)=[C_{2}s(t)+B_{2}f(s(t))+D_{2}f(s(t-\tau (t)))]dt +h_{2}(t,s(t),s(t-\tau (t)))d\omega (t), \end{array}\nonumber \\ \end{aligned}$$
(2)

where \(C_{2}=diag\{c_{21},c_{22},\cdots ,c_{2n}\}\), \(B_{2}=(b^{(2)}_{ij})_{n\times n}\), \(D_{2}=(d^{(2)}_{ij})_{n\times n}\in R^{n\times n}\); \(h_{2}(t,x_{i}(t),x_{i}(t-\tau (t)))=(h_{21}(x_{i1}(t),x_{i1}(t-\tau (t))),h_{22}(x_{i2}(t),x_{i2}(t-\tau (t))),\cdots ,h_{2n}(x_{in}(t),x_{in}(t-\tau (t))))^{T}\).

Define the error signal as \(e_{i}(t)=x_{i}(t)-s(t)\), \(i=1,2,\cdots ,N\), then we have the following error dynamical system

$$\begin{aligned} de_{i}(t)= & {} [C_{1}e_{i}(t)+\triangle Cs(t)+B_{1}(f(x_{i}(t))-f(s(t)))+\triangle Bf(s(t))\nonumber \\&+D_{1}(f(x_{i}(t-\tau (t)))-f(s(t-\tau (t))))+\triangle Df(s(t-\tau (t)))\nonumber \\&+\sum \limits ^{N}_{j=1}a_{ij}\Gamma e_{j}(t) +u_{i}(t)]dt\nonumber \\&+[h_{1}(t,x_{i}(t),x_{i}(t-\tau (t)))-h_{1}(t,s(t),s(t-\tau (t)))\nonumber \\&+\triangle h(t,s(t),s(t-\tau (t)))]d\omega (t), \end{aligned}$$
(3)

where \(\triangle C=C_{1}-C_{2}\), \(\triangle B=B_{1}-B_{2}\), \(\triangle D=D_{1}-D_{2}\) are parameter mismatch errors and \(\triangle h=h_{1}-h_{2}\) is stochastic perturbation mismatch error.

Due to the parameter mismatch and the stochastic perturbation mismatches, the origin \(e_{i}=0\) is not an equilibrium point of the error system (3), which means that it is impossible to be complete synchronization. However, by pinning impulsive control, stochastic quasi-synchronization with a relatively small error bound can considered.

Let \(t_{k}\ge 0\) be impulsive moments satisfying \(0=t_{0}<t_{1}<\cdots<t_{k}<t_{k+1}<\cdots \), \(\lim \limits _{k\rightarrow +\infty }t_{k}=+\infty \) and \(\sup \limits _{k\ge 0}\{\triangle _{k}\}<+\infty \), where \(\triangle _{k}=t_{k+1}-t_{k}\). For \(t=t_{k}\), the node errors are arranged in the following two forms

$$\begin{aligned} \begin{array}{ll} (i)\ \ \ \ E\Vert e_{i_{1}}(t_{k})\Vert \ge E\Vert e_{i_{2}}(t_{k})\Vert \ge \cdots \ge E\Vert e_{i_{s}}(t_{k})\Vert \ge E\Vert e_{i_{s+1}}(t_{k})\Vert \ge \cdots \ge E\Vert e_{i_{N}}(t_{k})\Vert , \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{ll} (ii)\ \ \ \ E\Vert e_{i_{1}}(t_{k})\Vert \le E\Vert e_{i_{2}}(t_{k})\Vert \le \cdots \le E\Vert e_{i_{s}}(t_{k})\Vert \le E\Vert e_{i_{s+1}}(t_{k})\Vert \le \cdots \le E\Vert e_{i_{N}}(t_{k})\Vert , \end{array} \end{aligned}$$

where \(i_{s}\in \{1,2,\cdots ,N\}\), \(s=1,2,\cdots ,N\), and \(i_{u}\ne i_{v}\) for \(u\ne v\). Furthermore, if \(E\Vert e_{i_{s}}(t_{k})\Vert =E\Vert e_{i_{s+1}}(t_{k})\Vert \), then \(i_{s}<i_{s+1}\). To reach stochastic quasi-synchronization of networks, the pinning impulsive control scheme is used on the nodes. Let \(\delta (\cdot )\) be a Dirac function. \(d_{k}\) denotes the impulsive gain. If \(-1<u_{k}<1\), the first q nodes are chosen as pinned nodes according to the arrangement (i). If \(u_{k}\ge 1\) or \(u_{k}\le -1\), then the first q nodes are chosen as the pinning nodes according to the arrangement (ii). The set of pinned nodes can be defined by \(\chi (t_{k})=\{i_{1},i_{2},\cdots ,i_{q}\}\subset \{1,2,\cdots ,N\}\) and \(\sharp \chi (t_{k})=q\). We design the pinning impulsive controller as follows:

$$\begin{aligned} u_{i}(t)=\left\{ \begin{array}{rl} &{}\sum \limits ^{+\infty }_{k=1}(v_{k}-1)e_{i}(t)\delta (t-t_{k}),i\in \chi (t_{k}),\\ &{}0,i\in \{1,2,\cdots ,N\}\backslash \chi (t_{k}). \end{array} \right. \end{aligned}$$
(4)

With the help of impulsive control, the error dynamical system can be obtained in the following form:

$$\begin{aligned} \left\{ \begin{array}{rl} de_{i}(t)&{}=[C_{1}e_{i}(t)+\triangle Cs(t)+B_{1}(f(x_{i}(t))-f(s(t)))+\triangle Bf(s(t))\\ &{}\quad +D_{1}(f(x_{i}(t-\tau (t)))-f(s(t-\tau (t))))+\triangle Df(s(t-\tau (t)))\\ &{}\quad +\sum \limits ^{N}_{j=1}a_{ij}\Gamma e_{j}(t)]dt +[h_{1}(t,x_{i}(t),x_{i}(t-\tau (t)))-h_{1}(t,s(t),s(t-\tau (t)))\\ &{}\quad +\triangle h(t,s(t),s(t-\tau (t)))]d\omega (t),\\ &{}\qquad i=1,2,\cdots ,N,t\ne t_{k},\\ e_{i}(t^{+}_{k})&{}=v_{k}e_{i}(t_{k}),i\in \chi (t_{k}),\\ e_{i}(t^{+}_{k})&{}=e_{i}(t_{k}),i\in \{1,2,\cdots ,N\}\backslash \chi (t_{k}), \end{array} \right. \end{aligned}$$
(5)

where \(e_{i}(t^{+}_{k})=\lim \limits _{h\rightarrow 0+}e_{i}(t_{k}+h),e_{i}(t_{k})=\lim \limits _{h\rightarrow 0-}e_{i}(t_{k}+h)\) is left-hand continuous at \(t=t_{k}\). The initial condition of \(e_{i}(t)\) is denoted as \(e_{i}(t)=\phi (t)\in PC_{\mathcal {F}_{t}}([-\tau ,0],R^{n})\), where \(PC_{\mathcal {F}_{t}}([-\tau ,0],R^{n})\) is the family of all \(\mathcal {F}_{t}\)-measurable, \(PC([-\tau ,0],R^{n})\)-value random variable \(\phi \) satisfied \(\int ^{0}_{-\tau }E[|\phi (\theta )|^{2}]d\theta <\infty \), \(PC([-\tau ,0],R^{n})\) is the family of piecewise continuous functions \(\phi \) with the norm \(\Vert \phi \Vert =\sup \limits _{-\tau \le \theta \le 0}\Vert \phi (\theta )\Vert \).

Remark 1

Based on the proposed scheme, the norm of synchronization error may vary with impulse time \(t_{k}\), which implies that the pinned nodes may be different at different \(t_{k}\). In view of control cost, if \(-1<v_{k}<1\), some nodes with large norm value are chosen to be pinned nodes. If \(v_{k}\le 1\) or \(v_{k}\ge 1\), some nodes with small norm value are considered to be pinned nodes.

Definition 1

Let \(\Phi \) be a region in the phase space of system (2). The neural networks (1) and (2) are said to be uniformly stochastic quasi-synchronized with error bound \(\overline{\theta }>0\) if there theists a \(\tilde{t}\ge 0\) such that for \(t\ge \tilde{t}\), \(E[\Vert x_{i}(0)\Vert ^{2}],E[\Vert s(0)\Vert ^{2}]\in \Phi \), \(i=1,2,\cdots ,N\)

$$\begin{aligned} \begin{array}{ll} E[\sum \limits ^{N}_{i=1}\Vert e_{i}(t)\Vert ^{2}] =E[\sum \limits ^{N}_{i=1}\Vert x_{i}(t)-s(t)\Vert ^{2}]\le \overline{\theta }. \end{array} \end{aligned}$$

Assumption 1

There exists constant \(l>0\) such that for \(\forall x,y\in R^{n}\)

$$\begin{aligned} \begin{array}{ll} \Vert f(x)-f(y)\Vert \le l\Vert x-y\Vert . \end{array} \end{aligned}$$

Assumption 2

There exist matrices \(M_{1}\in R^{n\times n}>0,M_{2}\in R^{n\times n}>0\) such that for \(x,y,u,v\in R^{n}\)

$$\begin{aligned}&trace[(h_{1}(t,x,y)-h_{1}(t,u,v))^{T}h_{1}(t,x,y)-h_{1}(t,u,v))]\\&\quad \le (x-u)^{T}M_{1}(x-u)+(y-v)^{T}M_{2}(y-v). \end{aligned}$$

Assumption 3

There exists constant \(\rho _{1}>0\) such that

$$\begin{aligned} \begin{array}{ll} \Vert \triangle C\Vert +l\Vert \triangle B\Vert +l\Vert \triangle D\Vert \le \rho _{1}. \end{array} \end{aligned}$$

Assumption 4

There exists constants \(\rho _{2}>0\), \(\rho _{3}>0\) such that

$$\begin{aligned} \begin{array}{ll} trace[\Delta h^{T}(t,x(t),x(t-\tau (t)))\Delta h(t,x(t),x(t-\tau (t)))]\le \rho ^{2}_{2}\Vert x(t)\Vert ^{2}+\rho ^{2}_{3}\Vert x(t-\tau (t))\Vert ^{2}. \end{array} \end{aligned}$$

For the following impulsive stochastic equation with delay:

$$\begin{aligned} \left\{ \begin{array}{rl} &{}dx(t)=F(t,x(t),x(t-\tau (t))dt +G(t,x(t),x(t-\tau (t))d\omega (t),t\ge 0,t\ne t_{k},\\ &{} \triangle x(t_{k})=I_{k}(t,x(t_{k})),\quad k=1,2,\cdots , \end{array} \right. \end{aligned}$$
(6)

where \(x(t)=(x_{1}(t),x_{2}(t),\cdots ,x_{n}(t))^{T}\), \(F:[0,+\infty )\times R^{n}\times PC([-\tau ,0];R^{n})\rightarrow R^{n}\), \(G:[0,+\infty )\times R^{n}\times PC([-\tau ,0];R^{n})\rightarrow R^{n\times n}\), \(\triangle x(t_{k})=x(t^{+}_{k})-x(t_{k})\), \(I:[0,+\infty )\times R^{n}\rightarrow R^{n}\).

Let \(\mathcal {C}^{2}_{1}([-\tau ,\infty )\times R^{n};[0,+\infty ))\) be the family of all nonnegative functions \(V(t,\phi )\) on \([-\tau ,\infty )\times R^{n}\), V, \(V_{t}\), \(V_{x}\), \(V_{xx}\) are continuous on \((t_{k-1},t_{k}]\times R^{n}\). For each \(V\in \mathcal {C}^{2}_{1}([-\tau ,\infty )\times R^{n};[0,+\infty ))\), \(\phi =\{\phi (\theta ):-\tau \le \theta \le 0\}\in PC_{\mathcal {F}_{t}}([-\tau ,0];R^{n})\), an operator \(\mathcal {L}V:(t_{k-1},t_{k}]\times PC_{\mathcal {F}_{t}}([-\tau ,0];R^{n})\rightarrow [0,+\infty )\) associated with Eq. (6) is defined as the following form:

$$\begin{aligned} \mathcal {L}V(t,\phi )= & {} V_{t}(t,\phi (0))+V_{x}(t,\phi (0))F(t,\phi (0),\phi (-\tau (t))\nonumber \\&+\frac{1}{2}trace[G_{1}^{T}(t,\phi (0),\phi )V_{xx}G(t,\phi (0),\phi (-\tau (t)). \end{aligned}$$
(7)

Lemma 1

Assume that \(V\in \mathcal {C}^{2}_{1}([-\tau ,\infty )\times R^{n};R^{+})\) and there exist constants \(d_{1}>0\), \(d_{2}>0\), \(\eta _{k}>0,k=1,2,\cdots \), \(\overline{\mu }\ge 0\), \(\hat{\mu }\ge 0\), \(\mu ,\delta \) such that

  1. (i)

    \(d_{1}\Vert x\Vert ^{2}\le V(t,x)\le d_{2}\Vert x\Vert ^{2}\);

  2. (ii)

    \(E[\mathcal {L}V(t,x(t))]\le \mu E[V(t,x(t))]+\overline{\mu }E[V(t,x(t-\tau (t)))]+\hat{\mu }\) for all \(t\in (t_{k-1},t_{k}]\);

  3. (iii)

    \(E[V(t^{+}_{k},x(t_{k})+I_{k}(t_{k},x(t_{k})))]\le \eta _{k}E[V(t_{k},x(t_{k}))]\);

  4. (iv)

    \(\ln \eta _{k}\le \delta \triangle _{k-1}\), \(k=1,2,\cdots \);

  5. (v)

    \(\mu +\beta \overline{\mu }+\delta <0\),

then the zero solution of Eq. (6) converges exponentially to small region \(\mathcal {K}=\{x(t)\in R^{n}|E[\Vert x(t)\Vert ^{2}]\le d\}\) in the mean square with exponent \(\lambda \), where \(\beta =\sup \limits _{1\le k<+\infty }\{\beta _{k}\}\), \(\beta _{k}=\max \{e^{\delta \triangle _{k-1}},e^{-\delta \triangle _{k-1}}\}\), \(\lambda \) is the unique solution of \(\lambda +\mu +\beta e^{\lambda \tau }\overline{\mu }+\delta =0\), \(d=\frac{-\beta \hat{\mu }}{\mu +\delta +\beta \overline{\mu }}\).

Proof

By It\(\hat{o}\) formula, we can obtain

$$\begin{aligned} \begin{array}{ll} dV(t,x)=\mathcal {L}V(t,x(t))+V_{x}(t,x(t))G(t,x(t),x(t-\tau (t)))d\omega (t). \end{array} \end{aligned}$$
(8)

For \(t\in (t_{k-1},t_{k}]\), we chose \(\varepsilon >0\) such that \(t+\varepsilon \in (t_{k-1},t_{k}]\). It follows from integrating the above inequality from t to \(t+\varepsilon \) and taking the expectations on both sides of (8) that

$$\begin{aligned}&E[V(t+\epsilon ,x(t+\epsilon ))]-E[V(t,x(t))])\nonumber \\&\quad =\int ^{t+\epsilon }_{t}E[\mathcal {L}V(s,x(s))]ds+E\int ^{t+\epsilon }_{t}V_{x}(s,x(s))G(s,x(s),x(s-\tau (s))d\omega (s).\nonumber \\ \end{aligned}$$
(9)

Let \(\varepsilon \rightarrow 0\), by (ii), it yields that for \(t\in (t_{k-1},t_{k}]\)

$$\begin{aligned} \begin{array}{ll} D^{+}V(t,x(t)) =E[\mathcal {L}V(t,x(t))]=\mu E[V(t,x(t))]+\overline{\mu }E[V(t,x(t-\tau (t)))]+\hat{\mu }. \end{array}\nonumber \\ \end{aligned}$$
(10)

Let \(V(t)=V(t,x(t))\) and \(z(t)=e^{-\mu t}E[V(t)]\). For \(t\in (t_{k-1},t_{k}]\), we have

$$\begin{aligned} \begin{array}{ll} D^{+}z(t)&{}=e^{-\mu t}D^{+}E[V(t)]-\mu e^{-\mu t}E[V(t)]\\ &{}=\overline{\mu }e^{-\mu t}E[V(t-\tau (t))]+\hat{\mu }e^{-\mu t}. \end{array} \end{aligned}$$
(11)

By (iii), we have

$$\begin{aligned} \begin{array}{ll} z(t^{+}_{k})=e^{-\mu t_{k}}E[V(t^{+}_{k})] \le \eta _{k}z(t_{k}). \end{array} \end{aligned}$$
(12)

For \(t\in [0,t_{1}]\), integrating the inequality (11) from 0 to t, we obtain

$$\begin{aligned} \begin{array}{ll} z(t)=z(0)+\int ^{t}_{0}\overline{\mu }e^{-\mu s}E[V(s-\tau (s))]ds+\int ^{t}_{0}\hat{\mu }e^{-\mu s}ds, \end{array} \end{aligned}$$
(13)

and

$$\begin{aligned} \begin{array}{ll} z(t_{1})=z(0)+\int ^{t_{1}}_{0}\overline{\mu }e^{-\mu s}E[V(s-\tau (s))]ds+\int ^{t_{1}}_{0}\hat{\mu }e^{-\mu s}ds. \end{array} \end{aligned}$$
(14)

For \(t\in (t_{1},t_{2}]\), by using the same method, we obtain

$$\begin{aligned} \begin{array}{ll} z(t)&{}=z(t^{+}_{1})+\int ^{t}_{t_{1}}\overline{\mu }e^{-\mu s}E[V(s-\tau (s))]ds+\int ^{t}_{t_{1}}\hat{\mu }e^{-\mu s}ds\\ &{}\le \eta _{1}\{z(0)+\int ^{t_{1}}_{0}\overline{\mu }e^{-\mu s}E[V(s-\tau (s))]ds+\int ^{t_{1}}_{0}\hat{\mu }e^{-\mu s}ds\}\\ &{}\quad +\int ^{t}_{t_{1}}\overline{\mu }e^{-\mu s}E[V(s-\tau (s))]ds+\int ^{t}_{t_{1}}\hat{\mu }e^{-\mu s}ds\\ &{}=\eta _{1}z(0)+\eta _{1}\int ^{t_{1}}_{0}\overline{\mu }e^{-\mu s}E[V(s-\tau (s))]ds+\int ^{t}_{t_{1}}\overline{\mu }e^{-\mu s}E[V(s-\tau (s))]ds\\ &{}\quad +\eta _{1}\int ^{t_{1}}_{0}\hat{\mu }e^{-\mu s}ds+\int ^{t}_{t_{1}}\hat{\mu }e^{-\mu s}ds. \end{array} \end{aligned}$$
(15)

By induction, it yields that for \(t\in (t_{k-1},t_{k}]\)

$$\begin{aligned} \begin{array}{ll} z(t)\le z(0)\prod \limits _{0\le t_{i}<t}\eta _{i}+\overline{\mu }\int ^{t}_{0}\prod \limits _{s\le t_{i}<t}\eta _{i}e^{-\mu s}E[V(s-\tau (s))]ds+\hat{\mu }\int ^{t}_{0}\prod \limits _{s\le t_{i}<t}\eta _{i}e^{-\mu s}ds, \end{array}\nonumber \\ \end{aligned}$$
(16)

which implies that for \(t>0\)

$$\begin{aligned} E[V(t)]\le & {} E[V(0)]e^{\mu t}\prod \limits _{0\le t_{i}<t}\eta _{i}+\overline{\mu }\int ^{t}_{0}e^{\mu (t-s)}\prod \limits _{s\le t_{i}<t}\eta _{i}E[V(s-\tau (s))]ds\nonumber \\&+\hat{\mu }\int ^{t}_{0}e^{\mu (t-s)}\prod \limits _{s\le t_{i}<t}\eta _{i}ds. \end{aligned}$$
(17)

For \(t>s\), the impulsive points in [s, t) can be denoted by \(t_{i1},_{i2},\cdots ,t_{ip}\) and \(t_{i1-1}\) is the first impulsive point before \(t_{i1}\). If \(\delta \ge 0\), by (iv), we have

$$\begin{aligned} \begin{array}{ll} \prod \limits _{s\le t_{i}<t}\eta _{i}&{}=\eta _{i1}\eta _{i2}\cdots \eta _{ip}\le e^{\delta (t_{i1}-t_{i1-1})}e^{\delta (t_{i2}-t_{i1})}\cdots e^{\delta (t_{ip}-t_{ip-1})}\\ &{}=e^{\delta (t_{ip}-t_{i1-1})}=e^{\delta (t-s)}e^{\delta (t_{ip}-t)}e^{\delta (s-t_{i1-1})}\\ &{}\le e^{\delta (t-s)}e^{\delta (s-t_{i1-1})}\le \beta e^{\delta (t-s)}. \end{array} \end{aligned}$$
(18)

If \(\delta <0\), by the similar methods, we can conclude that the above inequality holds. It follows that

$$\begin{aligned} E[V(t)]\le & {} \beta E[V(0)]e^{(\mu +\delta )t}+\beta \overline{\mu }\int ^{t}_{0}e^{(\mu +\delta )(t-s)}E[V(s-\tau (s))]ds\nonumber \\&+\beta \hat{\mu }\int ^{t}_{0}e^{(\mu +\delta )(t-s)}ds. \end{aligned}$$
(19)

Let \(\varphi (\lambda )=\lambda +\mu +\beta \overline{\mu }e^{\lambda \tau }+\delta \). By (v), we see that \(\varphi (0)<0,\varphi (+\infty )=+\infty \) and \(\varphi ^{'}(\lambda )=1+\beta \overline{\mu }\tau e^{\lambda \tau }>0\), which means that \(\varphi (\lambda )=0\) has a unique positive solution \(\lambda \). Next, we can claim that for \(t\ge -\tau \)

$$\begin{aligned} \begin{array}{ll} E[V(t)]\le \beta e^{-\lambda t}\sup \limits _{-\tau \le \varsigma \le 0}E[V(\varsigma )]+d. \end{array} \end{aligned}$$
(20)

Indeed, for \(t\in [-\tau ,0]\)

$$\begin{aligned} \begin{array}{ll} E[V(t)]\le \beta \sup \limits _{-\tau \le \varsigma \le 0}E[V(\varsigma )]\le \beta e^{-\lambda t}\sup \limits _{-\tau \le \varsigma \le 0}E[V(\varsigma )]+d. \end{array} \end{aligned}$$
(21)

Thus we only need to prove that (20) holds for \(t>0\). Otherwise, there exists a \(\tilde{t}>0\) such that

$$\begin{aligned} E[V(\tilde{t})]> & {} \beta e^{-\lambda \tilde{t}}\sup \limits _{-\tau \le \varsigma \le 0}E[V(\varsigma )]+d,\nonumber \\ E[V(t)]\le & {} \beta e^{-\lambda t}\sup \limits _{-\tau \le \varsigma \le 0}E[V(\varsigma )]+d,-\tau \le t<\tilde{t}. \end{aligned}$$
(22)

Noting \(\varphi (\lambda )=0\) and (20) (21) yields

$$\begin{aligned} E[V(\tilde{t})]&\le \beta E[V(0)]e^{(\mu +\delta )\tilde{t}}+\beta \overline{\mu }\int ^{\tilde{t}}_{0}e^{(\mu +\delta )(\tilde{t}-s)}E[V(s-\tau (s))]ds\nonumber \\&\quad + \beta \hat{\mu }\int ^{\tilde{t}}_{0}e^{(\mu +\delta )(\tilde{t}-s)}ds\nonumber \\&\le \beta \sup \limits _{-\tau \le \varsigma \le 0}E[V(\varsigma )]e^{(\mu +\delta )\tilde{t}}+\beta ^{2}\overline{\mu }e^{\lambda \tau }\sup \limits _{-\tau \le \varsigma \le 0}E[V(\varsigma )] \int ^{\tilde{t}}_{0}e^{(\mu +\delta )(\tilde{t}-s)}e^{-\lambda s}ds\nonumber \\&\quad +\beta \overline{\mu }d \int ^{\tilde{t}}_{0}e^{(\mu +\delta )(\tilde{t}-s)}ds+ \beta \hat{\mu }\int ^{\tilde{t}}_{0}e^{(\mu +\delta )(\tilde{t}-s)}ds\nonumber \\&=\beta e^{-\lambda \tilde{t}}\sup \limits _{-\tau \le \varsigma \le 0}E[V(\varsigma )]+d. \end{aligned}$$
(22)

\(\square \)

Lemma 2

[36]. For any vectors \(x,y\in R^{n}\), there exist constant \(\vartheta > 0\), and \(\Xi \in R^{n\times n}>0\) such that

$$\begin{aligned} \begin{array}{ll} 2x^{T}y\le \vartheta x^{T}\Xi x+\vartheta ^{-1}y^{T}\Xi ^{-1}y \end{array} \end{aligned}$$

Lemma 3

([36] Schur complement). The linear matrix inequality

$$\begin{aligned} \begin{array}{ll} U=\left( \begin{array}{cc} U_{11} &{} U_{12} \\ U^{T}_{12} &{} U_{22} \\ \end{array} \right) <0 \end{array} \end{aligned}$$

is equivalent to

$$\begin{aligned} \begin{array}{ll} U_{22}<0,\ \ \ \ \ \ U_{11}-U_{12}U^{-1}_{22}U^{T}_{12}<0, \end{array} \end{aligned}$$

where \(U_{11}=U^{T}_{11}\), and \(U_{22}=U^{T}_{22}\).

3 Stochastic Quasi-Synchronization in Mean Square

This section devotes to stochastic quasi-synchronization for stochastic neural networks by adding pinning impulsive control.

Theorem 1

Under Assumption 1–4. Let \(\Theta =\{y\in R^{n}|E(\Vert y\Vert ^{2})\le \theta \}\) is the range of system (2). If there exist matrices \(P\in R^{n\times n}>0\), \(L_{i}\in R^{n\times n}>0\), \(i=1,2,3\) and constants \(\alpha _{1}>0\), \(\alpha _{2}>0\), \(\alpha _{3}>0\), \(\mu _{1}\), \(\mu _{2}\), \(\nu \) such that

$$\begin{aligned}&\begin{array}{ll} \left( \begin{array}{cccc} \Xi &{} \sqrt{\alpha _{1}}I_{N}\otimes PB_{1} &{} \sqrt{\alpha _{2}}I_{N}\otimes PD_{1} &{} \sqrt{\alpha _{3}}I_{N}\otimes P \\ *&{} -I_{N}\otimes L_{1} &{} 0 &{} 0 \\ *&{} *&{} -I_{N}\otimes L_{2} &{} 0 \\ *&{} *&{} *&{} -I_{N}\otimes L_{3} \\ \end{array} \right) <0, \end{array} \end{aligned}$$
(23)
$$\begin{aligned}&\begin{array}{ll} \alpha ^{-1}_{2}l^{2}L_{2}+\lambda _{\max }(P)M_{2}<\mu _{2}P, \end{array} \end{aligned}$$
(24)
$$\begin{aligned}&\begin{array}{ll} \ln \xi _{k}\le \nu \triangle _{k-1}, \end{array} \end{aligned}$$
(25)

and

$$\begin{aligned} \begin{array}{ll} \mu _{1}+\overline{\nu }\mu _{2}+\nu <0, \end{array} \end{aligned}$$
(26)

then the error of system (3) can converge to small region \(\mathcal {D}=\{(e_{1}(t),e_{2}(t),\cdots ,e_{N}(t))^{T}|E[\sum \limits ^{N}_{i=1}\Vert e_{i}(t)\Vert ^{2})]\le \frac{\overline{d}}{\lambda _{\min }(P)},e_{i}(t)\in R^{n},i=1,2,\cdots ,N\}\) in the mean square with exponent \(\lambda \), where \(\Xi =I_{N}\otimes (PC+C^{T}P+\alpha ^{-1}_{1}l^{2}L_{1}+\lambda _{\max }(P)M_{1})+A\otimes P\Gamma +(A\otimes P\Gamma )^{T}-\mu _{1}I_{N}\otimes P\), \(\xi _{k}=v^{2}_{k}-(v_{k}-1)(v_{k}+1)\frac{\lambda _{\max }(P)(N-q)}{\lambda _{\min }(P)N}\), \(\overline{\nu }=\sup \limits _{1\le k<\infty }\{\nu _{k}\}\), \(\nu _{k}=\max \{e^{\nu \triangle _{k-1}},e^{-\nu \triangle _{k-1}}\}\), \(\overline{d}=\frac{-\overline{\nu }\theta [\alpha ^{-1}_{3}\lambda _{\max }(L_{3})\rho ^{2}_{1}+ \lambda _{\max }(P)(\rho ^{2}_{2}+\rho ^{2}_{3})]}{\mu _{1}+\overline{\nu }\mu _{2}+\nu }\), \(\lambda >0\) is the unique solution of \(\lambda +\mu _{1}+\overline{\nu }e^{\lambda \tau }\mu _{2}+\nu =0\).

Proof

Construct a Lyapunov function

$$\begin{aligned} \begin{array}{ll} V(t)=\sum \limits ^{N}_{i=1}e^{T}_{i}(t)Pe_{i}(t). \end{array} \end{aligned}$$
(27)

For \(t\in (t_{k-1},t_{k}]\), by (7), we have

$$\begin{aligned} \mathcal {L}V(t)= & {} 2\sum \limits ^{N}_{i=1}e^{T}_{i}(t)P[C_{i}e_{i}(t)+\triangle Cs(t)+B_{1}F(e_{i}(t))+\triangle Bf(s(t))\nonumber \\&+D_{1}F(e_{i}(t-\tau (t))) +\triangle Df(s-\tau (t))+\sum \limits ^{N}_{j=1}a_{ij}\Gamma e_{j}(t)]\nonumber \\&+\sum \limits ^{N}_{i=1}trace[H^{T}(t,e_{i}(t),e_{i}(t-\tau (t)))PH(t,e_{i}(t),e_{i}(t-\tau (t)))]\nonumber \\&+\sum \limits ^{N}_{i=1}trace[\triangle h^{T}(t,s(t),s(t-\tau (t)))Ph(t,s(t),s(t-\tau (t)))]. \end{aligned}$$
(28)

From Assumption 1 and Lemma 2, there exist \(\alpha _{1}>0\), \(\alpha _{2}>0\) and \(L_{1}\in R^{n\times n}>0\), \(L_{2}\in R^{n\times n}>0\) such that

$$\begin{aligned} 2e^{T}_{i}(t)PB_{1}F(e_{i}(t))\le & {} \alpha _{1} e^{T}_{i}(t)PB_{1}L^{-1}_{1}B^{T}_{1}Pe_{i}(t) +\alpha ^{-1}_{1}F^{T}(e_{i}(t))L_{1}F(e_{i}(t))\nonumber \\\le & {} \alpha _{1}e^{T}_{i}(t)PB_{1}L^{-1}_{1}B^{T}_{1}Pe_{i}(t) +\alpha ^{-1}_{1}l^{2}e^{T}_{i}(t)L_{1}e_{i}(t), \end{aligned}$$
(29)

and

$$\begin{aligned} 2e^{T}_{i}(t)PD_{1}F(e_{i}(t-\tau (t)))\le & {} \alpha _{2} e^{T}_{i}(t)PD_{1}L^{-1}_{2}D^{T}_{1}Pe_{i}(t)\nonumber \\&+\alpha ^{-1}_{2}F^{T}(e_{i}(t-\tau (t)))L_{2}F(e_{i}(t-\tau (t)))\nonumber \\\le & {} \alpha _{2} e^{T}_{i}(t)PD_{1}L^{-1}_{2}D^{T}_{1}Pe_{i}(t)\nonumber \\&+\alpha ^{-1}_{2}l^{2}e^{T}_{i}(t-\tau (t))L_{2}e_{i}(t-\tau (t)). \end{aligned}$$
(30)

In view of Assumption 2, we can obtain

$$\begin{aligned}&trace[H^{T}(t,e_{i}(t),e_{i}(t-\tau (t)))PH(t,e_{i}(t),e_{i}(t-\tau (t)))]\nonumber \\&\quad \le \lambda _{\max }(P)[e^{T}_{i}(t)M_{1}e_{i}(t)+e^{T}_{i}(t-\tau (t))M_{2}e_{i}(t-\tau (t))]. \end{aligned}$$
(31)

Let \(e(t)=(e^{T}_{1}(t),e^{T}_{2}(t),\cdots ,e^{T}_{N}(t))^{T}\), then

$$\begin{aligned} \begin{array}{ll} \ \ \ 2\sum \limits ^{N}_{i=1}e^{T}_{i}(t)P\sum \limits ^{N}_{j=1}a_{ij}\Gamma e_{j}(t)=2e^{T}(t)(A\bigotimes P\Gamma )e(t). \end{array} \end{aligned}$$
(32)

Noting that the parameter mismatches and stochastic perturbation mismatches satisfy Assumption 3 and Assumption 4, it follows from Lemma 2 that there exist \(\alpha _{3}>0\) and \(L_{3}\in R^{n\times n}>0\) such that

$$\begin{aligned}&2e^{T}_{i}(t)P[\triangle Cs(t)+\triangle Bf(s(t))+\triangle Df(s-\tau (t))]\nonumber \\&\quad \le \alpha _{3} e^{T}_{i}(t)PL^{-1}_{3}Pe_{i}(t)+\alpha ^{-1}_{3}[\triangle Cs(t)+\triangle Bf(s(t)) +\triangle Df(s-\tau (t))]^{T}\nonumber \\&\qquad L_{3}[\triangle Cs(t)+\triangle Bf(s(t))+\triangle Df(s-\tau (t))]. \end{aligned}$$
(33)

and

$$\begin{aligned}&trace[\triangle h^{T}(t,s(t),s(t-\tau (t)))P\triangle h(t,s(t),s(t-\tau (t)))]\nonumber \\&\quad \le \lambda _{\max }(P)(\rho ^{2}_{2}\Vert s(t)\Vert ^{2}+\rho ^{2}_{3}\Vert s(t-\tau (t))\Vert ^{2}). \end{aligned}$$
(34)

Substituting (29)–(34) into (28) yields

$$\begin{aligned} \mathcal {L}V(t)\le & {} \sum \limits ^{N}_{i=1}e^{T}_{i}(t)\Psi _{1}e_{i}(t) +2e^{T}(t)(A\bigotimes P\Gamma )e(t)+\sum \limits ^{N}_{i=1}e^{T}_{i}(t-\tau (t))\Psi _{2}e_{i}(t-\tau (t))\nonumber \\&+\alpha ^{-1}_{3}[\triangle Cs(t)+\triangle Bf(s(t)) +\triangle Df(s-\tau (t))]^{T}L_{3}[\triangle Cs(t)+\triangle Bf(s(t))\nonumber \\&+\triangle Df(s-\tau (t))]+\lambda _{\max }(P)(\rho ^{2}_{2}\Vert s(t)\Vert ^{2}+\rho ^{2}_{3}\Vert s(t-\tau (t))\Vert ^{2}), \end{aligned}$$
(35)

where \(\Psi _{1}=PC+C^{T}P+\alpha _{1} PB_{1}L^{-1}_{1}B^{T}_{1}P+\alpha ^{-1}_{1}l^{2}L_{1}+\alpha _{2}PD_{1}L^{-1}_{2}D^{T}_{1}P+\lambda _{\max }(P)M_{1}+\alpha _{3}PL^{-1}_{3}P\). \(\Psi _{2}=\alpha ^{-1}_{2}l^{2}L_{2}+\lambda _{\max }(P)M_{2}\). By (23) (24) and Lemma 3, we have

$$\begin{aligned} E[\mathcal {L}V(t)]\le & {} \mu _{1}E[V(t)]+\mu _{2} E[V(t-\tau (t))]+[\alpha ^{-1}_{3}\lambda _{\max }(L_{3})\rho ^{2}_{1}\nonumber \\&+\lambda _{\max }(P)(\rho ^{2}_{2}+\rho ^{2}_{3})]\theta . \end{aligned}$$
(36)

On the other hand, when \(t=t_{k}\), we have

$$\begin{aligned} \begin{array}{ll} V(t^{+}_{k})&{}=\sum \limits ^{N}_{i=1}e^{T}_{i}(t^{+}_{k})Pe_{i}(t^{+}_{k})\\ &{}=\sum \limits _{i\in \chi _{p}(t_{k})}e^{T}_{i}(t^{+}_{k})Pe_{i}(t^{+}_{k})+\sum \limits _{i\overline{\in } \chi _{p}(t_{k})}e^{T}_{i}(t^{+}_{k})Pe_{i}(t^{+}_{k})\\ &{}=u^{2}_{k}\sum \limits _{i\in \chi (t_{k})}e^{T}_{i}(t_{k})Pe_{i}(t_{k})+\sum \limits _{i\overline{\in } \chi (t_{k})}e^{T}_{i}(t_{k})Pe_{i}(t_{k})\\ &{}=u^{2}_{k}\sum \limits ^{N}_{i=1}e^{T}_{i}(t_{k})Pe_{i}(t_{k})-(u_{k}-1)(u_{k}+1)\sum \limits _{i\overline{\in } \chi (t_{k})}e^{T}_{i}(t_{k})Pe_{i}(t_{k}). \end{array} \end{aligned}$$
(37)

If \(-1<u_{k}<1\), in view of the selection of pinning nodes in set \(\chi _{p}(t_{k})\), we get

$$\begin{aligned}&\frac{1}{N-q}\sum \limits _{i\overline{\in } \chi (t_{k})}E[e^{T}_{i}(t_{k})Pe_{i}(t_{k})] \le \frac{\lambda _{\max }(P)}{N-q}\sum \limits _{i\overline{\in } \chi (t_{k})}E[e^{T}_{i}(t_{k})e_{i}(t_{k})]\nonumber \\&\quad \le \frac{\lambda _{\max }(P)}{N}\sum \limits ^{N}_{i=1}E[e^{T}_{i}(t_{k})e_{i}(t_{k})] \le \frac{\lambda _{\max }(P)}{\lambda _{\min }(P)N}\sum \limits ^{N}_{i=1}E[e^{T}_{i}(t_{k})Pe_{i}(t_{k})] \end{aligned}$$
(38)

Then we have

$$\begin{aligned} E[V(t^{+}_{k})]\le & {} v_{k}^{2}\sum \limits ^{N}_{i=1}E[e^{T}_{i}(t_{k})Pe_{i}(t_{k})]\nonumber \\&-(v_{k}-1)(v_{k}+1)\sum \limits ^{N}_{i=1}\frac{\lambda _{\max }(P)(N-q)}{\lambda _{\min }(P)N} E[e^{T}_{i}(t_{k})Pe_{i}(t_{k})]\nonumber \\= & {} \xi _{k}E[V(t_{k})], \end{aligned}$$
(39)

where \(\xi _{k}=v^{2}_{k}-(v_{k}-1)(v_{k}+1)\frac{\lambda _{\max }(P)(N-q)}{\lambda _{\min }(P)N}\). For \(v_{k}\le -1\) or \(v_{k}\ge 1\), we can conclude that (39) holds by the same method. It follows from (23)–(26) and Lemma 1 that there exists \(\overline{l}>0\) such that

$$\begin{aligned} \begin{array}{ll} E[V(t)]\le \overline{l}e^{-\lambda t}E\left[ \sup \limits _{-\tau \le \varsigma \le 0}V(\varsigma )\right] +\overline{d},t\ge 0 \end{array} \end{aligned}$$
(40)

which implies that

$$\begin{aligned} \begin{array}{ll} E\left[ \sum \limits ^{N}_{i=1}\Vert e_{i}(t)\Vert ^{2}\le \frac{\lambda _{\max }(P)\overline{l}}{\lambda _{\min }(P)}e^{-\lambda t}E\left[ \sup \limits _{-\tau \le \varsigma \le 0}\Vert e_{i}(\varsigma )\Vert ^{2}\right] +\frac{\overline{d}}{\lambda _{\min }(P)},t\ge 0.\right. \end{array} \end{aligned}$$
(41)

Therefore, the error system (3) can converges to small region in the mean square with exponent \(\lambda \). \(\square \)

Remark 2

From the proof of Theorem 1, the cluster synchronization criterion is related to \(\rho _{p}\), \(\eta _{k}\) and the impulsive interval \(t_{k+1}-t_{k}\). \(\eta _{k}\) depends on the impulsive gain \(d_{k}\) and the pinned number \(\rho _{p}\) at impulsive time \(t_{k}\). on the other hand, inequality (10) characterize the relation between \(\eta _{k}\) and \(t_{k+1}-t_{k}\). Therefore, a suitable pinning impulsive controller can be determined by selecting the value \(d_{k}\), \(\rho _{p}\) and \(t_{k+1}-t_{k}\).

Remark 3

According to Theorem 1, if \(-1<v_{k}<1\), we can conclude that the number of the pinned nodes is estimated as

$$\begin{aligned} \begin{array}{ll} q>[1+\frac{(e^{\nu \triangle _{k-1}}-v^{2}_{k})\lambda _{\min }(P)}{(v_{k}-1)(v_{k}+1)\lambda _{\max }(P)}]N. \end{array} \end{aligned}$$

Correspondingly, if \(v_{k}\le -1\) or \(v_{k}\ge 1\), we see that

$$\begin{aligned} \begin{array}{ll} q<[1+\frac{(e^{\nu \triangle _{k-1}}-v^{2}_{k})\lambda _{\min }(P)}{(v_{k}-1)(v_{k}+1)\lambda _{\max }(P)}]N. \end{array} \end{aligned}$$

Remark 4

The obtained conditions for stochastic quasi-synchronization are condition (23) (24) (25) and (26) in Theorem 1. To reduce the calculation burden, MATLAB LMI toolbox is used to determine \(\mu _{1}\) and \(\mu _{2}\) by fixing the values of \(\alpha _{i},i=1,2,3\). If taking \(P=L_{1}=L_{2}=L_{3}=I_{n},\alpha _{1}=\frac{l}{\sqrt{\lambda _{\max }(B_{1}B^{T}_{1})}},\alpha _{2}=\frac{l}{\sqrt{\lambda _{\max }(D_{1}D^{T}_{1})}},\alpha _{3}=1\), \(\mu _{1}=\lambda _{\max }(C_{1}+C^{T}_{1})+2l\sqrt{\lambda _{\max }(B_{1}B^{T}_{1})}+l\sqrt{\lambda _{\max }(D_{1}D^{T}_{1})} +\lambda _{\max }[(A\otimes \Gamma )+(A\otimes \Gamma )^{T}]+\lambda _{\max }(M_{1})+1\), \(\mu _{2}=l\sqrt{\lambda _{\max }(D_{1}D^{T}_{1})}+\lambda _{\max }(M_{2})\), \(\nu =\sup \limits _{1\le k<+\infty }\{\frac{\ln [v^{2}_{k}-(v_{k}-1)(v_{k}+1)\frac{\lambda _{\max }(P)(N-q)}{\lambda _{\min }(P)N}]}{\triangle _{k-1}}\}\), \(\overline{d}=\frac{-\overline{\nu }\theta (\rho ^{2}_{1}+ \rho ^{2}_{2}+\rho ^{2}_{3})}{\mu _{1}+\overline{\nu }\mu _{2}+\nu }\), we can derive the following practical corollary.

Corollary 1

Under Assumption 1–4. Let \(\Theta =\{y\in R^{n}|E(\Vert y\Vert ^{2})\le \theta \}\) is the range of system (2). If

$$\begin{aligned} \begin{array}{ll} \mu _{1}+\overline{\nu }\mu _{2}+\nu <0, \end{array} \end{aligned}$$

then the error of system (3) can converge to small region \(\mathcal {D}=\{(e_{1}(t),e_{2}(t),\cdots ,e_{N}(t))^{T}|E[\sum \limits ^{N}_{i=1}\Vert e_{i}(t)\Vert ^{2})]\le \overline{d},e_{i}(t)\in R^{n},i=1,2,\cdots ,N\}\) in the mean square.

Theorem 2

Under Assumption 1–4 and \(t_{k}-t_{k-1}\ge \tau \). Let \(\Theta =\{y\in R^{n}|E(\Vert y\Vert ^{2})\le \theta \}\) is the range of system (2). If there exist matrices \(P\in R^{n\times n}>0\), \(L_{i}\in R^{n\times n}>0\), \(i=1,2,3\) and constants \(\alpha _{1}>0\), \(\alpha _{2}>0\), \(\alpha _{3}>0\), \(\mu _{1}\), \(\mu _{2}\) satisfying (23), (24). Also if there exists a constant \(\lambda >0\) such that for \(k=1,2\cdots \)

$$\begin{aligned} \begin{array}{ll} \ln (\xi _{k}+\frac{\mu _{2}}{1-\sigma }\triangle _{k-1})+\rho \triangle _{k-1}\le -\,\lambda , \end{array} \end{aligned}$$
(42)

then the error of system (3) can converge to small region \(\mathcal {D}=\{(e_{1}(t),e_{2}(t),\cdots ,e_{N}(t))^{T}|E[\sum \limits ^{N}_{i=1}\Vert e_{i}(t)\Vert ^{2})]\le \frac{\widetilde{b}}{\lambda _{\min }(P)},e_{i}(t)\in R^{n},i=1,2,\cdots ,N\}\) in the mean square with exponent \(\frac{\lambda }{\overline{\triangle }}\), where \(\rho =\mu _{1}+\frac{\mu _{2}}{1-\sigma }\), \(\widetilde{b}=\frac{\varepsilon (e^{-\lambda }-\hat{d})e^{\rho \overline{\triangle }}}{\rho (1-e^{-\lambda })}+\frac{\varepsilon }{\rho }(e^{\rho \overline{\triangle }}-1)\), \(\varepsilon =[\alpha ^{-1}_{3}\lambda _{\max }(L_{3})\rho ^{2}_{1}+\lambda _{\max }(P)(\rho ^{2}_{2}+\rho ^{2}_{3})]\theta \), \(\overline{\triangle }=\sup \limits _{k\ge 1}\{\triangle _{k-1}\}\).

Proof

Consider a Lyapunov–Krasovskii functional

$$\begin{aligned} \begin{array}{ll} V(t)=V_{1}(t)+V_{2}(t), \end{array} \end{aligned}$$
(43)

where

$$\begin{aligned} \begin{array}{ll} V_{1}(t)=\sum \limits ^{N}_{i=1}e^{T}_{i}(t)Pe_{i}(t), \ \ \ \ \ \ \ V_{2}(t)=\frac{\mu _{2}}{1-\sigma }\int ^{t}_{t-\tau (t)}\sum \limits ^{N}_{i=1}e^{T}_{i}(s)Pe_{i}(s)ds. \end{array} \end{aligned}$$
(44)

Similar to the proof of Theorem 3.1, for \(t\in (t_{k},t_{k+1}]\), we see that

$$\begin{aligned} \begin{array}{ll} \mathcal {L}V_{1}(t)\le \mu _{1} V_{1}(t)+\mu _{2} V(t-\tau (t))+[\alpha ^{-1}_{3}\lambda _{\max }(L_{3})\rho ^{2}_{1}+\lambda _{\max }(P)(\rho ^{2}_{2}+\rho ^{2}_{3})]\theta . \end{array} \end{aligned}$$
(45)

For \(t\in (t_{k},t_{k+1}]\), it yields

$$\begin{aligned} \begin{array}{ll} \mathcal {L}V_{2}(t)\le \frac{\mu _{2}}{1-\sigma } V_{1}(t)-\mu _{2} V_{1}(t-\tau (t)). \end{array} \end{aligned}$$
(46)

Thus

$$\begin{aligned} \begin{array}{ll} E[\mathcal {L}V(t)]\le (\mu _{1}+\frac{\mu _{2}}{1-\sigma }) E[V_{1}(t)]+\varepsilon \le \rho E[V(t)]+\varepsilon , \end{array} \end{aligned}$$
(47)

where \(\rho =\mu _{1}+\frac{\mu _{2}}{1-\sigma }\), \(\varepsilon =[\alpha ^{-1}_{3}\lambda _{\max }(L_{3})\rho ^{2}_{1}+\lambda _{\max }(P)(\rho ^{2}_{2}+\rho ^{2}_{3})]\theta \). It follows that for \(t\in (t_{k},t_{k+1}]\)

$$\begin{aligned} \begin{array}{ll} E[V(t)]\le E[V(t^{+}_{k})]e^{\rho (t-t_{k})}+\frac{\varepsilon }{\rho }[e^{\rho (t-t_{k})}-1]. \end{array} \end{aligned}$$
(48)

When \(t=t_{k}\), according to the proof of Theorem 3.1 and by (48), we can obtain

$$\begin{aligned} \begin{array}{ll} E[V_{1}(t^{+}_{k})]\le \xi _{k}E[V_{1}(t_{k})]\le \xi _{k}E[V(t_{k})]\le \xi _{k}e^{\rho \triangle _{k-1}}E[V(t^{+}_{k-1})]+\frac{\varepsilon \xi _{k}}{\rho }[e^{\rho \triangle _{k-1}}-1]. \end{array} \end{aligned}$$
(49)

By (44), there exists a \(\bar{t}_{k}\in (t_{k-1},t_{k}]\) such that

$$\begin{aligned} \begin{array}{ll} V_{2}(t^{+}_{k})&{}=\frac{\mu _{2}}{1-\sigma }\int ^{t_{k}}_{t_{k}-\tau (t_{k})}V_{1}(s)ds\le \frac{\mu _{2}}{1-\sigma }\int ^{t_{k}}_{t_{k-1}}V_{1}(s)ds =\frac{\mu _{2}}{1-\sigma }\triangle _{k-1} V_{1}(\overline{t}_{k})\\ &{}\le \frac{\mu _{2}}{1-\sigma }\triangle _{k-1} V(\overline{t}_{k}). \end{array} \end{aligned}$$
(50)

It follows from (33) and the above inequality that

$$\begin{aligned} \begin{array}{ll} E[V_{2}(t^{+}_{k})] \le \frac{\mu _{2}}{1-\sigma }\triangle _{k-1}e^{\rho \triangle _{k-1}} E[V(t^{+}_{k-1})]+\frac{\mu _{2}\varepsilon }{(1-\sigma )\rho }\triangle _{k-1}(e^{\rho \triangle _{k-1}}-1). \end{array} \end{aligned}$$
(51)

Submitting (34) and (36) into (28), we have

$$\begin{aligned} \begin{array}{ll} E[V(t^{+}_{k})]&{}\le \left( \xi _{k}+\frac{\mu _{2}}{1-\sigma }\triangle _{k-1}\right) e^{\rho \triangle _{k-1}}E[V(t^{+}_{k-1})] +\frac{\varepsilon }{\rho }\left( \xi _{k}+\frac{\mu _{2}}{1-\sigma }\triangle _{k-1}\right) (e^{\rho \triangle _{k-1}}-1)\\ &{}\le e^{-\lambda }E[V(t^{+}_{k-1})]+\frac{\varepsilon }{\rho }(e^{-\lambda }-\overline{b}), \end{array} \end{aligned}$$
(52)

where \(\overline{b}=\inf \limits _{k\ge 1}\{\xi _{k}+\frac{\mu _{2}}{1-\sigma }\triangle _{k-1}\}\), which yields that

$$\begin{aligned} \begin{array}{ll} E[V(t^{+}_{k})]\le e^{-\lambda k} E[\sup \limits _{-\tau \le \varsigma \le 0}V(\varsigma )]+\frac{\varepsilon (e^{-\lambda }-\overline{b})}{\rho (1-e^{-\lambda })}. \end{array} \end{aligned}$$
(53)

For \(t\in (t_{k},t_{k+1}]\), by (26) (33), we see that

$$\begin{aligned} \begin{array}{ll} E[V(t)]&{}\le e^{\rho (t-t_{k})}E[V(t^{+}_{k})]+\frac{\varepsilon }{\rho }[e^{\rho (t-t_{k})}-1]\le e^{\rho \triangle _{k}}e^{-\lambda k} E[\sup \limits _{-\tau \le \varsigma \le 0}V(\varsigma )]+\widetilde{b}\\ &{}\le e^{\rho \triangle _{k}}e^{\frac{-\lambda t_{k}}{\overline{\triangle }}} E[\sup \limits _{-\tau \le \varsigma \le 0}V(\varsigma )]\\ &{}\quad +\widetilde{b}\le e^{\rho \triangle _{k}}e^{\frac{-\lambda (t_{k}-t_{k+1})}{\overline{\triangle }}}e^{\frac{-\lambda t_{k+1}}{\overline{\triangle }}} E[\sup \limits _{-\tau \le \varsigma \le 0}V(\varsigma )]+\widetilde{b}\\ &{}\le e^{\rho \overline{\triangle }+\lambda }e^{\frac{-\lambda t_{k+1}}{\overline{\triangle }}} E[\sup \limits _{-\tau \le \varsigma \le 0}V(\varsigma )]+\widetilde{b}\le e^{\rho \overline{\triangle }+\lambda }e^{\frac{-\lambda t}{\overline{\triangle }}} E[\sup \limits _{-\tau \le \varsigma \le 0}V(\varsigma )]+\widetilde{b}. \end{array} \end{aligned}$$
(54)

where \(\widetilde{b}=\frac{\varepsilon (e^{-\lambda }-\overline{b})e^{\rho \triangle _{k}}}{\rho (1-e^{-\lambda })}+\frac{\varepsilon }{\rho }(e^{\rho \triangle _{k}}-1)\). This completes the proof. \(\square \)

4 Numerical Simulations

In this section, a numerical example is given to demonstrate our results. Consider the following neural networks with stochastic perturbation as the leader:

$$\begin{aligned} \begin{array}{ll} ds(t)=[C_{2}s(t)+B_{2}f(s(t)) +D_{2}f(s(t-1))]dt+[h_{2}(t,s(t),s(t-1))]d\omega (t), \end{array} \end{aligned}$$
(55)

where \(s(t)=(s_{1}(t),s_{2}(t))^{T}\), \(f(s(t))=(f_{1}(s_{1}(t)),f_{2}(s_{2}(t)))^{T}\), \(f_{1}(s_{1}(t))=\arctan s_{1}(t)\), \(f_{2}(s_{2}(t))=\arctan s_{2}(t)\),

$$\begin{aligned} C_{2}= & {} \left( \begin{array}{cc} -1 &{} 0 \\ 0 &{} -1 \\ \end{array} \right) ,B_{2}=\left( \begin{array}{cc} 2 &{} -0.1 \\ -5 &{} 1.5 \\ \end{array} \right) ,D_{2}=\left( \begin{array}{cc} -1.5 &{} -0.1 \\ -0.2 &{} -1 \\ \end{array} \right) , \\ h_{2}(t,s(t),s(t-1))= & {} \left( \begin{array}{cc} 0.1s_{1}(t) &{} 0 \\ 0 &{} 0.03s_{2}(t) \\ \end{array} \right) +\left( \begin{array}{cc} -0.1s_{1}(t) &{} 0 \\ 0 &{} -0.05s_{2}(t) \\ \end{array} \right) \end{aligned}$$

Figure 1 depicts the trajectory of \((s_{1}(t),s_{2}(t))\) with value (0.2, 0.5). This is a chaotic attractor with stochastic perturbation and the range \(\Theta =\{s\in R^{2}|E[\Vert s\Vert ]\le 16\}\).

Fig. 1
figure 1

The state variables s(t) with initial value (0.2, 0.5)

Full size image

We assume the response neural networks is the following form:

$$\begin{aligned} \begin{array}{ll} dx_{i}(t)&{}=[C_{1}x_{i}(t)+B_{1}f(x_{i}(t)) +D_{1}f(x_{i}(t-1))+\sum \limits ^{4}_{j=1}a_{ij}\Gamma x_{i}(t)+u_{i}(t)]dt\\ &{}\quad +[h_{1}(t,x_{i}(t),x_{i}(t-1))]d\omega (t),\quad i=1,2,3,4, \end{array} \end{aligned}$$
(55)

where \(\Gamma =diag\{1.2,1.5\}\)

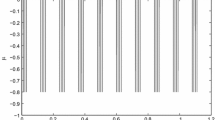
$$\begin{aligned} C_{1}= & {} \left( \begin{array}{cc} -1.002 &{} 0 \\ 0 &{} -1.003 \\ \end{array} \right) ,B_{1}=\left( \begin{array}{cc} 2.001 &{} -0.102 \\ -4.99 &{} 1.502 \\ \end{array} \right) ,\\ D_{1}= & {} \left( \begin{array}{cc} -1.502 &{} -0.09 \\ -0.203 &{} -1.002 \\ \end{array} \right) \\ A= & {} \left( \begin{array}{cccc} -2 &{} 0.6 &{} 0.8 &{} 0.6 \\ 0.5 &{} -3 &{} 0.5 &{} 2 \\ 1 &{} 0.2 &{} -2.5 &{} 1.3 \\ 0.8 &{} 0 &{} 1.2 &{} -2 \\ \end{array} \right) , \\ h_{1}(t,x_{i}(t),x_{i}(t-1))= & {} \left( \begin{array}{cc} -0.15x_{i1}(t) &{} 0 \\ 0 &{} 0.04x_{i2}(t) \\ \end{array} \right) +\left( \begin{array}{cc} -0.12x_{i1}(t) &{} 0 \\ 0 &{} -0.04x_{i2}(t) \\ \end{array} \right) . \end{aligned}$$

We design the pinning impulsive input with pinned nodes \(q=2\), \(t_{k}=0.02k\), \(v_{k}=0.25\). By simple calculation, we conclude that \(\mu _{1}+\overline{\nu }\mu _{2}+\nu \approx -13.8816<0\). By Corollary 1, we can estimate the convergence region \(\mathcal {D}=\{(e_{1},e_{2},e_{3},e_{4})|E[\sum \limits ^{4}_{i=1}\Vert e_{i}\Vert ^{2}]\le 0.098\}\). Figure 2 depicts the errors \(\Vert e_{1}\Vert \) and \(\Vert e_{2}\Vert \) of synchronization with initial value \((10,-5)\). Figure 2 depicts the errors \(\Vert e_{i}\Vert ,(i=1,2,3,4)\) of synchronization with initial value (0.2, 0.5). Figure 3 depicts the errors \(\Vert e_{i}\Vert ,(i=1,2,3,4)\) of synchronization without pinning impulsive input.

Fig. 2
figure 2

The errors \(\Vert e_{i}\Vert ,i=1,2,3,4\) of synchronization with initial value (0.2, 0.5)

Full size image
Fig. 3
figure 3

The errors \(\Vert e_{i}\Vert ,i=1,2,3,4\) of synchronization without pinning impulsive input

Full size image

Remark 5

It is necessary to select suitable nodes when applying pinning impulsive control scheme. In [24, 25], random nodes can be selected to control. However, since the expectation of synchronization error \(e_{i}(t)\) may be different at impulsive times \(t=t_{k}\), so the pinned nodes are not invariant. Figure 2 implies that our pinning algorithm is more general than ones in [24, 25, 35]. Figure 3 shows that pinning impulsive input plays an important role in stochastic quasi-synchronization of delayed networks.

5 Conclusions

In this paper, stochastic quasi-synchronization is studied in a leader-follower delayed neural networks by using pinning impulsive control scheme. First, by pinning selected nodes of stochastic neural networks and establishing a new lemma of stochastic impulsive system, a general criterion is obtained to ensure stochastic quasi-synchronization between the leader and the followers with two different topologies. Finally, an example is provided to illustrate the effectiveness of the obtained results.