Structural Reweight Sparse Subspace Clustering

Abstract

Subspace clustering aims to segment a group of data points into a union of subspaces. Reweight sparse subspace clustering is one of the state-of-the-art algorithms which proposed an iterative weighted subspace clustering. The reweight matrix helps to improve the performance of the affinity matrix construction process but it easily falls into a local minimization. In this paper, we propose a structural reweight sparse subspace clustering algorithm which introduces the structural information into reweight subspace clustering. The structural information achieved in spectral clustering process is useful for the subsequent iterative optimization process which helps to obtain a better local minimization. The experimental results on the Extended Yale B, Hopkins 155, and COIL 20 datasets demonstrate that our algorithm achieves a better performance on subspace clustering problem.

1 Introduction

In many real-world applications, plenty of high-dimensional datasets need to be segmented into low-dimensional subspaces, e.g., computer vision, machine learning and image processing. Because the high-dimensional data processing always require higher computational capability and larger memory spaces. It has been observed that these high-dimensional datasets usually are distributed in intrinsic low-dimensional subspaces. For instance, face images taken under different illuminations lie in respective subspaces of multiple subjects. To solve the high-dimensional face recognition problem, Wan et.al. proposed the local graph embedding dimensional reduction method based on maximum margin criterion via Fuzzy Set, which was helpful to extract the representative features [1]. The motion trajectories of multiple moving objects could be approximated by several low-dimensional subspaces. The images of one object which is rotated several degrees lie in one subspace. Subspace clustering methods have been proposed to segment a collection of data points into a union of subspaces [2].

Subspace clustering methods is traditionally divided into four main categories: algebraic, iterative, statistical, and spectral clustering-based methods. Algebraic algorithms include matrix factorization-based approaches and algebraic-geometric approaches. Matrix factorization-based methods first obtain a rank-r that r is the rank of input data matrix factorization of the data matrix, and then segment data points by the similarity matrix. So these approaches need to know the rank r and the subspaces should be independent. Generalized Principal Component Analysis (GPCA) is the typical algebraic-geometric method [3]. GPCA fits the high-dimensional data with a set of polynomials whose gradient at a data point gives the normal vector to the subspace including the point. So GPCA is sensitive to the outliers and its computation complexity grows exponential in terms of the dimensions of subspaces. Iterative methods first initialize the segmentation randomly, and fit a subspace using PCA. Then data points are assigned to its closest subspace. The iterative algorithms are sensitive to the initialization which will lead to a bad result. Statistical methods define proper generative models for subspaces. Mixtures of Probabilistic PCA (MPPCA) is based on Probabilistic PCA model and optimized by using Expectation Maximization (EM) algorithm [4]. MPPCA needs to known the number and dimensions of subspaces in advance. Agglomerative Lossy Compression (ALC) seeks for the minimization of the overall coding length of the segmented data [5]. The agglomerative procedure in ALC still need to be proved theoretically. Random Sample Consensus (RANSAC) is another statistical method [6], which randomly chooses d data points and computes a model for these points, then fit all data points to the model. RANSAC also needs to know the dimensions of subspaces. Spectral clustering-based methods are popular algorithms for subspace clustering. These methods divide subspace clustering into two steps: affinity matrix construction and spectral clustering. Spectral Local Best-fit Flats (SLBF) [7], Local Subspace Affinity (LSA) [8] and Locally Linear Manifold Clustering (LLMC) [9] cluster the data points based on the observation that a point and its neighbors always belong to the same subspace. SLBF and LSA can not handle the outliers near the subspace. When subspaces are independent, LLMC is hardly to select the number of nearest neighbors properly. SCC is based on the concept of polar curvature which is zero for data points in same subspace [10]. But its computation complexity grows fast. SSC (Sparse Subspace Clustering) introduces sparsity into the affinity matrix construction process [11]. Based on the hypothesis of data redundancy, the sparse constraint is used to separate data points of different subspaces. Because the data point could be represented by other data points of same subspace. In SSC, the ${l_1}$-norm as the convex relaxation of the ${l_0}$-norm is applied to achieve the sparsest self-expressive coefficient matrix. Then the affinity matrix could be obtained with the sparse coefficient matrix. Similar to SSC, Low Rank Representation (LRR) aims at finding the lowest-rank representation matrix [12]. Dong et al. proposed the method roboust low rank subspace segmentation via joint ${\ell _{21}}$-norm minimization (LR-L21) to learn low rank representation by jointing the nuclear norm and ${\ell _{21}}$-norm minimization [13].

SSC only need the number of subspaces as a priori knowledge. Consequently, many researches have carried out a great deal of improved algorithms based on SSC. For instances, Lin et al. proposed BD-SSC and BD-LRR that pursue the block-diagonal structure by graph Laplacian constraint [14]. Inspired by enhanced ${l_1}$ minimization [15], Reweighted Sparse Subspace Clustering (RSSC) was proposed for using iterative weighted ${l_1}$ minimization as an alternative to the ${l_1}$ minimization [16]. In order to do subspace clustering at a unified framwork, Structured Sparse Subspace Clustering (SSSC) was proposed in [17]. Similarly, Wu et al. proposed a novel robust spectral subspace clustering based on least square regression (${\text {R}}{{\text {S}}^2}{\text {CLSR}}$) to learn representation matrix through least square regression and the soft label was utilized to enhance the process [18].

Contributions RSSC proposes the iterative weighted ${l_1}$ minimization to be the alternative to the ${l_1}$ minimization. The main disadvantage of the method is that the optimization easily falls into a local minimization. It is observed that the structural information of the data helps to find a better local minimization. So our contributions can be summarized as follows.

1. We propose a structural reweight sparse subspace clustering model (SRSSC) by combining the structural sparse norm and weighted sparse norm into the cost function. 2. We prove that the structural information is used to help reweight subspace clustering find a better local minimum that more closely resembles the global minimum.

2 Related Works

Self-expressive model Let $\mathbf{X } \in {R^{D \times N}}$ be the input data whose columns stand for the data points. Suppose that all data points are distributed in a union of subspaces $S = \cup _{i = 1}^n\{ {S_i}\}$ whose dimension is ${d_i}$. n is the number of subspaces. The self-expressive model is proposed by SSC [11]. First, we need to assume that each data point ${{x}_j} \in \mathbf{X } = \{ {{x}_1},{{x}_2},\ldots ,{{x}_{ N}}\}$ can be efficiently reconstructed by a combination of other data points. So ${\mathbf{x }_\textit{j}}$ can be written as

$$\begin{aligned} {{x}_\textit{j}} = \mathbf X \mathbf{z _\textit{j}},\quad \mathbf{z _{\textit{jj}}} = 0, \end{aligned}$$

(1)

where ${\mathbf{z }_\textit{j}}$ is the j-th column of the representation coefficients matrix ${\mathbf{Z }} \in {R^{N \times N}}$. The function could also be written in matrix form as

$$\begin{aligned} \mathbf X = \mathbf X \mathbf{Z },\quad diag(\mathbf{Z }) = 0. \end{aligned}$$

(2)

The constrain $diag(\mathbf{Z }) = 0$ aims to eliminate the trivial solution that one data point is represented by itself. In order to obtain a sparse representation coefficient matrix ${\mathbf{Z }}$, the sparse norm is introduced into the cost function

$$\begin{aligned} \min {\left\| \mathbf{Z } \right\| _0}\quad s.t.\quad \mathbf X = \mathbf XZ , diag(\mathbf{Z }) = 0, \end{aligned}$$

(3)

where ${l_0}$-norm counts the number of nonzero elements in a matrix. Through minimize the ${l_0}$-norm of one matrix, we could achieve the sparsest representation matrix. But the ${l_0}$ minimization is the NP-hard problem. So the function should be relaxed as

$$\begin{aligned} \min {\left\| \mathbf{Z } \right\| _1}\quad s.t.\quad \mathbf X = \mathbf XZ , \quad diag(\mathbf{Z }) = 0. \end{aligned}$$

(4)

Reweight sparse subspace clustering As discussed in [15], the ${l_1}$ minimization penalizes larger elements more heavily than smaller elements while the ${l_0}$ minimization penalizes elements equally. An iterative weighted formulation of ${l_1}$ minimization is designed to more democratically penalize nonzero elements. In [15], the log-sum surrogate function $f(x) = \sum \nolimits _{i = 1}^n {\log (\left| {{x_i}} \right| + \varepsilon )}$ could closely resemble the ${l_0}$ minimization. So in RSSC [16], the penalty term is added into the cost function of the sparse subspace clustering,

$$\begin{aligned} \min {\left\| \mathbf{W \odot \mathbf{Z }} \right\| _1}\quad s.t.\quad \mathbf X = \mathbf XZ ,\quad diag(\mathbf{Z }) = 0, \end{aligned}$$

(5)

where $\mathbf{W }$ is the weight matrix related to the representation coefficient matrix ${\mathbf{Z }}$ and is updated by $\mathbf W = \frac{{{\varepsilon _2}}}{{\left| \mathbf{Z } \right| + {\varepsilon _1}}}$, ${{\varepsilon _1}}$ is used for numerical stability and to ensure that a zero-valued element will not lead to a nonzero estimate at the next iteration.

For the reason of the log-sum surrogate function is concave, RSSC easily falls into a local minimization.

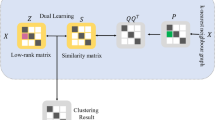
3 Structural Reweight Sparse Subspace Clustering

Inspired by the RSSC algorithm, we propose the Sparse Reweight Sparse Subspace Clustering (SRSSC) which introduces the structural information into the objective function.

$$\begin{aligned} \begin{aligned}&\mathop {\min }\limits _{{\mathbf{Z }},{\mathbf{E }}} {\left\| {\mathbf{W } \odot {\mathbf{Z }}} \right\| _1} + {\lambda _q}{\left\| \mathbf{Q \odot \mathbf{Z }} \right\| _1} + {\lambda _e}{\left\| {\mathbf{E }} \right\| _1}\\&\qquad s.t.\quad \mathbf X = \mathbf XZ + \mathbf{E }, {\mathbf{Z }^\textit{T}}{} \mathbf 1 = \mathbf 1 , \quad diag(\mathbf{Z }) = 0, \end{aligned} \end{aligned}$$

(6)

where ${\mathbf{E }}$ is the outliers, $\mathbf{Q }$ is the structural matrix. The parameters ${\lambda _q}$ and ${\lambda _e}$ balance the three terms in the objective function. As parameter ${\lambda _q}$ is equal to 0, the optimization of function (6) is equivalent to standard RSSC. $\odot$ denotes the element-wise product between two matrices. ${{\mathbf{Z }}^\textit{T}}{} \mathbf 1 = \mathbf 1$ is the constraint of affine subspaces.

The update on weight matrix $\mathbf{W }$ and structural matrix $\mathbf{Q }$ could be written as

$$\begin{aligned} {\mathbf{W }^{(k + 1)}}= & {} \frac{{{\varepsilon _2}}}{{\left| {{{\mathbf{Z }}^{(k + 1)}}} \right| + {\varepsilon _1}}}\end{aligned}$$

(7)

$$\begin{aligned} {\mathbf{Q }_{(t + 1)}}(i,j)= & {} \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1&{}{}&{}{{l_{(t + 1)}}(i) = {l_{(t + 1)}}(j)} \end{array}}\\ {\begin{array}{*{20}{c}} {}&{}{}&{}{} \end{array}}\\ {\begin{array}{*{20}{c}} 0&{}{}&{}{{l_{(t + 1)}}(i) \ne {l_{(t + 1)}}(j)} \end{array}} \end{array}} \right. , \end{aligned}$$

(8)

where ${{l_{(t + 1)}}(i)}$ and ${{l_{(t + 1)}}(j)}$ stand for the clustering labels of data point i and j after the t-th iteration. As shown in [16, 17], the updating of $\mathbf{W }$ and $\mathbf{Q }$ are not synchronous. Suppose we initialize the $\mathbf{W }$ as all the elements to be one, and the $\mathbf{Q }$ as zeros, the optimization is equivalent to a standard SSC.

The structural information is achieved after each iteration of weighted Z minimization. In detail, SRSSC could be divided into two steps: weighted Z minimization with fixed structural matrix $\mathbf{Q }$ and structural matrix $\mathbf{Q }$ updating with the result of spectral clustering. The two steps alternate until the formulation converged.

3.1 The Weighted Z Minimization

We fix the structural matrix $\mathbf{Q }$ as ${\mathbf{Q }_{(t)}}$ at the t-th iteration. The function (6) is changed into

$$\begin{aligned}&\mathop {\min }\limits _{{\mathbf{Z }},{\mathbf{E }}} {\left\| {\mathbf{W } \odot {\mathbf{Z }}} \right\| _1} + {\lambda _q}{\left\| {{\mathbf{Q }_{(t)}} \odot {\mathbf{Z }}} \right\| _1} + {\lambda _e}{\left\| {\mathbf{E }} \right\| _1}\nonumber \\&\qquad s.t. \quad \mathbf X = \mathbf XZ + \mathbf{E }, {{\mathbf{Z }}^\textit{T}}{} \mathbf 1 = \mathbf 1 , \quad diag(\mathbf{Z }) = 0. \end{aligned}$$

(9)

The function (9) could be solved by Alternating Direction Method of Multipliers (ADMM) [19].

First, we introduce an auxiliary matrix ${\mathbf{A }}$ into the function (9)

$$\begin{aligned}&\mathop {\min }\limits _{\mathbf{Z },\mathbf{E },\mathbf{A }} {\left\| \mathbf{W \odot \mathbf{Z }} \right\| _1} + {\lambda _q}{\left\| {{\mathbf{Q }_{(t)}} \odot {\mathbf{Z }}} \right\| _1} + {\lambda _e}{\left\| {\mathbf{E }} \right\| _1} + \frac{{{\lambda _n}}}{2}\left\| {\mathbf{X } - \mathbf{XA } - \mathbf{E }} \right\| _F^2\nonumber \\&\qquad s.t.\quad {{\mathbf{A }}^\textit{T}}{} \mathbf 1 = \mathbf 1 , \mathbf{A } = \mathbf{Z } - \quad diag(\mathbf{Z }). \end{aligned}$$

(10)

It’s clearly that the solution of function (9) is consistent with function (10). Then two penalty terms should be added into the function

$$\begin{aligned}&\mathop {\min }\limits _{{\mathbf{Z }},\mathbf{E },\mathbf{A }} {\left\| \mathbf{W \odot \mathbf{Z }} \right\| _1} + {\lambda _q}{\left\| {{\mathbf{Q }_{(t)}} \odot \mathbf{Z }} \right\| _1} + {\lambda _e}{\left\| \mathbf{E } \right\| _1} + \frac{{\lambda _n}}{2}\left\| \mathbf{X - \mathbf XA - \mathbf{E }} \right\| _F^2\nonumber \\&\qquad +\, \frac{\mu }{2}\left( {\left\| {{{\mathbf{Z }}^\textit{T}}{} \mathbf 1 - \mathbf 1 } \right\| _2^2 + \left\| {\mathbf{A } - (\mathbf{Z } - diag(\mathbf{Z }))} \right\| _F^2} \right) \nonumber \\&\qquad \quad s.t.\quad {\mathbf{A }^\textit{T}}{} \mathbf 1 = \mathbf 1 , \mathbf{A } = \mathbf{Z } - \quad diag(\mathbf{Z }). \end{aligned}$$

(11)

Note that adding the penalty terms does not change the optimal solution and makes the objective function to be strictly convex. Two Lagrangian multipliers $\delta \in {R^N}$ and $\varDelta \in {R^N}$ are augmented for two constraints. The Lagrangian function of (11) could be written as

$$\begin{aligned} L(\mathbf{A },\mathbf{Z },\mathbf W ,\mathbf Q ,\mathbf{E },\delta ,\varDelta )= & {} {\left\| \mathbf{W \odot \mathbf{Z }} \right\| _1} + {\lambda _q}{\left\| {{\mathbf{Q }_{(t)}} \odot {\mathbf{Z }}} \right\| _1}\nonumber \\&+\, {\lambda _e}{\left\| \mathbf{E } \right\| _1} + \frac{{{\lambda _n}}}{2}\left\| \mathbf{X - \mathbf XA - \mathbf{E }} \right\| _F^2\nonumber \\&+ \,\frac{\mu }{2}\left( {\left\| {{\mathbf{Z }^\textit{T}}{} \mathbf 1 - \mathbf 1 } \right\| _2^2 + \left\| {\mathbf{A } - (\mathbf{Z } - diag(\mathbf{Z }))} \right\| _F^2} \right) \nonumber \\&+\, {\delta ^T}\left( {{{\mathbf{A }}^\textit{T}}{} \mathbf 1 - \mathbf 1 } \right) + tr\left( {{\varDelta ^T}\left( {\mathbf{A } - \left( {\mathbf{Z } - diag\left( \mathbf{Z } \right) } \right) } \right) } \right) {,} \end{aligned}$$

(12)

where $tr( \cdot )$ is the trace operator.

Note that $\left( {{{\mathbf{Z }}^{(k)}},{{\mathbf{E }}^{(k)}},{{\mathbf{A }}^{(k)}}} \right)$ are the optimization variables at k-th iteration. $\left( {{\delta ^{(k)}},{\varDelta ^{(k)}}} \right)$ are the Lagrange multipliers at k-th iteration.

Update for${\mathbf{A }}$ Obtain ${{\mathbf{A }}^{(k + 1)}}$ by minimizing function (12) with respect to ${\mathbf{A }}$ while $\left( {{{\mathbf{Z }}^{(k)}},{{\mathbf{E }}^{(k)}},{\delta ^{(k)}},{\varDelta ^{(k)}}} \right)$ are fixed. Setting the derivative of function (12) to be zero, we can obtain

$$\begin{aligned} \left( {{\lambda _z}{\mathbf{X }^T}{} \mathbf X + \mu \mathbf I + \mu {\mathbf{11 }^T}} \right) {{\mathbf{A }}^{(k + 1)}} = {\lambda _z}{X^T}\left( {\mathbf{X } - {{\mathbf{E }}^{(k)}}} \right) + \mu \left( {{{\mathbf{11 }}^T} + {{\mathbf{Z }}^{(k)}}} \right) - 1{\delta ^{(k)T}} - {\varDelta ^{(k)}}. \end{aligned}$$

(13)

Update for${\mathbf{Z }}$ Obtain ${{\mathbf{Z }}^{(k + 1)}}$ by minimizing function (12) with respect to ${{\mathbf{Z }}}$ while $\left( {{{\mathbf{A }}^{(k+1)}},{{\mathbf{E }}^{(k)}},{\delta ^{(k)}},{\varDelta ^{(k)}}} \right)$ are fixed. The update on ${{\mathbf{Z }}^{(k + 1)}}$ has a closed-form solution

$$\begin{aligned} \begin{array}{l} {{\mathbf{Z }}^{(k + 1)}} = {{\tilde{Z}}^{(k + 1)}} - diag\left( {{{\tilde{Z}}^{(k + 1)}}} \right) \\ {{\tilde{Z}}^{(k + 1)}} \buildrel \varDelta \over = \varGamma _{(1 + {\lambda _q})/\mu }^{{\mathbf{Q }_{(t)}}}\left( {{{\mathbf{A }}^{(k + 1)}} + {{{\varDelta ^{(k)}}}\Bigg / \mu }}\right) , \end{array} \end{aligned}$$

(14)

where $\varGamma _\eta ^\mathbf W \left( \cdot \right)$ is the shrinkage-thresholding operator which is defined as

$$\begin{aligned} {\varGamma _{\eta }}^\mathbf{W }\left( \mathbf X \right) = \max \left( {\left| \mathbf X \right| - \eta \mathbf W ,0} \right) \odot {\mathrm {sgn}} (\mathbf X ). \end{aligned}$$

(15)

Update for${\mathbf{E }}$ Obtain ${{\mathbf{E }}^{(k + 1)}}$ by minimizing function (12) with respect to ${{\mathbf{E }}}$ while $\left( {{{\mathbf{A }}^{(k+1)}},{{\mathbf{Z }}^{(k+1)}},{\delta ^{(k)}},{\varDelta ^{(k)}}} \right)$ are fixed.

$$\begin{aligned} {{\mathbf{E }}^{(k + 1)}} = {\varGamma _{{{{\lambda _e}} / {{\lambda _n}}}}}\left( {\mathbf{X }{{\mathbf{A }}^{(k + 1)}} - \mathbf X } \right) . \end{aligned}$$

(16)

Update for$\delta$ and $\varDelta$ Obtain ${\delta ^{(k + 1)}}$ and ${\varDelta ^{(k + 1)}}$ with step size $\mu$ while $\left( {{{\mathbf{Z }}^{(k + 1)}},{{\mathbf{E }}^{(k + 1)}},{{\mathbf{A }}^{(k + 1)}}} \right)$ are fixed.

$$\begin{aligned} {\delta ^{(k + 1)}}= & {} {\delta ^{(k)}} + \mu \left( {{\mathbf{A }^{(k + 1)}}^T\mathbf 1 - \mathbf 1 } \right) \nonumber \\ {\varDelta ^{(k + 1)}}= & {} {\varDelta ^{(k)}} + \mu \left( {{{\mathbf{A }}^{(k + 1)}} - {{\mathbf{Z }}^{(k + 1)}}} \right) . \end{aligned}$$

(17)

Update for$\mathbf{W }$ Obtain ${\mathbf{W }^{(k + 1)}}$ while $\left( {{{\mathbf{Z }}^{(k + 1)}},{\mathbf{E }^{(k + 1)}},{\mathbf{A }^{(k + 1)}}} \right)$ are fixed.

$$\begin{aligned} {\mathbf{W }^{(k + 1)}} = \frac{{{\varepsilon _2}}}{{\left| {{\mathbf{Z }^{(k + 1)}}} \right| + {\varepsilon _1}}}. \end{aligned}$$

(18)

In summary, the optimization of function (9) with ADMM is summarized as Algorithm 1.

3.2 Spectral Clustering

After solving the weighted sparse optimization program in (9), we obtain the sparse representation matrix ${\mathbf{Z }_{(t + 1)}}$. Next, we build a symmetric non-negative similarity matrix $\mathbf G = \frac{1}{2}\left( {\left| {{\mathbf{Z }_{(t + 1)}}} \right| + \left| {{\mathbf{Z }_{(t + 1)}}^T} \right| } \right)$. Then we apply spectral clustering to find cluster label ${\mathbf{L }_{(t+1)}}$ which is essential to update $\mathbf{Q }$.

$$\begin{aligned} {\mathbf{Q }_{(t + 1)}}(i,j) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1&{}{}&{}{{l_{(t + 1)}}(i) = {l_{(t + 1)}}(j)} \end{array}}\\ {\begin{array}{*{20}{c}} {}&{}{}&{}{} \end{array}}\\ {\begin{array}{*{20}{c}} 0&{}{}&{}{{l_{(t + 1)}}(i) \ne {l_{(t + 1)}}(j)} \end{array}} \end{array}} \right. . \end{aligned}$$

(19)

In summary, the SRSSC program could be summarized as Algorithm 2.

3.3 Convergence Analysis

As shown in [16], the update on weight matrix $\mathbf W$ stems from the log-sum surrogate function. The log-sum heuristic function is concave and its minimization problem could be solved by an iterative linearization method [20]. In [15, 21, 22], the convergence of the reweight ${\ell _1}$ minimization with log-sum surrogate function has been proved that the minimization could converge to a local minimum. While the Algorithm 1 converges to a local minimum, the proposed method may not converge. The experimental results show that our proposed method converges in practice under optimal parameters.

4 Experiments and Analysis

In this section, we evaluate the clustering performance of the proposed method in dealing with images clustering, and motion segmentation problems. The datasets include the Extended Yale Database B, COIL 20 and Hopkins 155.

Experimental setup In this paper, we compare with some state-of-the-art subspace clustering algorithms, i.e., SSC [11], LRR [12], SCC [10], LSA [8], BD-SSC [14], BD-LRR [14], LR-L21 [13], RSSC [16], SSSC [17], S-SSSC [23], and SSC-OMP [24]. S-SSSC based on SSSC defines an alternative real-valued structural matrix to binary structural matrix. SSC-OMP changes the optimization method into OMP (Orthogonal Matching Pursuit). For most of the algorithms mentioned above, the code is released by the authors based on Matlab platform. All the parameters keep the same as mentioned in their paper. And for BD-SSC, BD-LRR and LR-L21, we directly cite the results shown in their papers.

We use the clustering error to measure the performance of algorithms

$$\begin{aligned} error = \frac{1}{N}\sum \limits _{i = 1}^N {\max \left( {\left| {{p_i} - g({q_i})} \right| ,0} \right) } , \end{aligned}$$

(20)

where ${{p_i}}$ is the ground truth label of point i, and ${{q_i}}$ is the clustering label. The function $g\left( \cdot \right)$ permutes clustering labels for matching the ground truth which could be Kuhn-Munkres method.

All the experiments are implemented in Matlab 2010b on a PC with Intel Core i3-3320 CPU at 3.30 GHz and 8.00 GB RAM.

Experimental results on Hopkins 155 dataset In this section, we evaluate the performance of our algorithm and other state-of-the-art algorithms on the Hopkins 155 dataset. Motion segmentation refers to the problem of motion trajectories segmentation according to their moving objects respectively. The Hopkins 155 dataset contains 155 video sequences where 120 of all videos contain two moving objects and 35 of all videos contain three moving objects, which means that the data lies in a union of 2 or 3 low-dimensional subspaces. In each video sequence, a set of N feature trajectories has been extracted and tracked by tracking algorithms. All trajectories data comprises a matrix $\mathbf X = [{{x}_1},{{x}_2},\ldots ,{{x}_\textit{N}}]$ and each column of $\mathbf X$ is a 2F-dimensional vector where F is the frame number.

For the motion segmentation experiments, we use the noisy variation, without the outlier term $\mathbf{E }$ and with the affine constraint in the optimization process. As shown in [11] , it gives the setting ${\lambda _Z} = {\alpha }/{\mu _Z}$ where ${\mu _Z} \buildrel \varDelta \over = \mathop {\min }\nolimits _i \mathop {\max }\nolimits _{j \ne i} \left| \mathbf{x _i^\textit{T}\mathbf{x _j}} \right|$. In SSC, we use $\alpha = 800$ as shown in [11]. In LRR, we use $\lambda = 4$ to achieve the best results without the post processing [12]. In SCC, the dimension $d = 3$ [10]. In LSA, the nearest neighbors number $kNeight = 6$ and dimension $d = 4$ [8]. In RSSC, the numerical stability parameters ${\varepsilon _1} = 0.001$ and ${\varepsilon _2} = 0.015$ [16]. In SSSC, we use $\alpha = 0.1$ [17]. In S-SSSC, we set $\alpha = 0.2$ [23]. In BD-SSC, BD-LRR and LR-L21, we directly cite the best results in their papers [13, 14]. In SSC-OMP, we use $K=50$ [24]. In our algorithm, we set the parameters value as ${\varepsilon _1} = 0.001 , {\varepsilon _2} = 0.015$ and ${\lambda _q} = 0.1$.

The final experimental results are represented in Table 1 where the average and median errors of subspace clustering are given.

Table 1 Clustering errors on the Hopkins 155 dataset with 2F-dimensional data points

First of all, our algorithm achieves the lowest clustering error in the Hopkins 155 dataset. The algorithms based on SSC have better performance than other algorithms which is a verification of SSC superiority over other subspace clustering algorithms based on spectral clustering. The clustering error of SSC-OMP is far worse than others. We consider the reason maybe that SSC-OMP could not deal with big data under the affine projection model successfully. Secondly, the clustering average error of our algorithm is reduced from 0.75 and 1.52 to 0.66% for the 2-motions case and from 1.68 and 4.41 to 1.34% for the 3-motion case respectively. Compared with RSSC and SSSC, we can find that the reweight sparse norm improves the performance of subspace clustering greatly. Compared with RSSC and ours, we can also find that ours reduces the cluster error greatly. So we can reach the conclusion that the reweight process is essential for the subspace clustering problem, and the structure information is also useful in achieving a better local minimization.

Fig. 1

The histogram of numbers of iterations to convergence

From the Fig. 1, we can find that our proposed algorithm mostly converges in 1 $\sim$ 3 iterations for all 155 video sequences. It proves that our algorithm could converge to a local minimum in a few iterations.

Experiments on Extended Yale B dataset In this section, we evaluate the performance of our algorithm and others on the Extended Yale B dataset. The dataset contains the frontal face images of 38 subjects. Every subject is required to take 64 frontal face images under different illumination conditions. The size of each image is $192 \times 168$. To reduce the computational complexity, each face image is down-sampled to $48 \times 42$ and represented as a 2016-dimensional vector. Following the protocol proposed in [11], we divide 38 subjects into 4 groups: 1–10, 11–20, 21–30, 31–38. We perform the combination of $n \in \left\{ {2,3,5,8,10} \right\}$ subjects for the first three groups and consider the all choices of $n \in \left\{ {2,3,5,8} \right\}$ subjects for the final groups.

For the face clustering experiments, we consider the condition of noisy variation, with outlier $\mathbf{E }$ and without the affine constrain. As shown in [11], outlier $\mathbf{E }$ could deal with small errors due to noise in practice. And the parameter is setting ${\lambda _e} = \alpha /{\mu _e}$ where ${\mu _e} \buildrel \varDelta \over = {\mathop {\min }\nolimits _i} {\mathop {\max }\nolimits _{j \ne i}} {\left\| {\mathbf{x _j}} \right\| _1}$. In SSC, we use $\alpha = 20$ as shown in [11]. In LRR, we use $\lambda = 0.18$ to achieve the same results in [12]. In SCC, the dimension $d = 9$ [10]. In LSA, the nearest neighbors number $kNeight = 8$ and dimension $d = 4$ [8]. In RSSC, the numerical stability parameters ${\varepsilon _1} = 0.0002$ and ${\varepsilon _2} = 0.0014$ [16]. In SSSC [17], we use $\alpha = 0.1$. In S-SSSC [23], we use $\alpha = 0.1$. In BD-SSC, BD-LRR and LR-L21, we directly cite the best results in their papers [13, 14]. In SSC-OMP , we use $K=5$ [24].

In our algorithm, we use ${\lambda _q} = 0.1$ and ${\varepsilon _1} = 0.006 , {\varepsilon _2} = 0.0001$. The experimental results are presented in Table 2.

Table 2 Clustering errors on the Extended Yale B dataset.

From Table 2, we can find that our algorithm achieves the best performance for most conditions on the Extended Yale B dataset. Compared with RSSC and SSC, we can find that the reweight sparse norm improves the performance of subspace clustering remarkebly. Compared with RSSC and our algorithm, the clustering errors are reduced from 0.49 to 0.41% for 2 objects case and from 5.73 to 4.43% for 10 objects case. When the object number increases, the numbers of outliers between clusters will increase synchronously.

Experiments on COIL 20 dataset In this section, we evaluate the performance of our algorithm and other state-of-the-art algorithms on COIL 20 dataset. COIL 20 contains 1440 images of 20 objects in which the background has been discard. Every object has been taken 72 images with a fixed camera while object is rotated through 360 degrees horizontally. The size of each image is $32 \times 32$, so the dimension of input data matrix $\mathbf X$ is 1024. Some examples are shown in Fig. 2.

Fig. 2

Examples from COIL 20 dataset

Following the protocol proposed in [10], we first divide the 20 objects into two groups: 1–10, 11–20, and consider all the choices of $n \in \left\{ {2,3,5,8} \right\}$ subjects in this experiment. An we consider the situation of noisy variation, with outlier $\mathbf{E }$ and without the affine constrain. For all methods, we adjust the parameters refer to experimental parameters on the Extend Yale Dataset B dataset to achieve the best result. In SSC [11], we set $\alpha = 10$. In LRR [12], we set $\lambda = 0.01$. In SCC [10], we set the dimension $d = 7$. In LSA [8], the nearest neighbors number is set $kNeight = 8$ and dimension $d = 7$. In RSSC [16], we set ${\varepsilon _1} = 0.1,{\varepsilon _2} = 0.005$. In SSSC [17], we use $\alpha = 0.1$.

In our algorithm, we use ${\lambda _q} = 0.1$ and ${\varepsilon _1} = 0.2,{\varepsilon _2} = 0.005$. The experimental results are shown in Table 3.

Table 3 Clustering errors on COIL 20 dataset

In Table 3, we can find that all the state-of-the-art algorithms achieve competitive performance on COIL20 datast, because the discarded images improve the dissimilarity. As we can seen in Table 3, SRSSC obtains the best performance for the all cases except for 8 objects case. At the same time, we find that the clustering error increases sharply when object number is 8. This phenomenon is due to the fast growing number of outliers. Structural information will disturb the optimization process in this situation. The clustering error increases from 7.53 to 9.82% for 8 objects cases. So our algorithm still need to be improved in the future.

Then, we calculate the percentage of clustering samples whose clustering accuracy is less than or equal to a certain value, which ranges in $\left\{ {0,0.1,\ldots ,0.9,1} \right\}$. The result are shown in Fig. 3.

Fig. 3

Percentage of clustering example whose clustering accuracy less than or equal to a given value

From Fig. 3, we can discovery that most of clustering samples achieve accuracy higher than 0.6 for SSC, RSSC, SSSC and our algorithm. And the accuracy of more than 90% clustering samples is higher than 0.9. Generally speaking, our algorithm improve the entire accuracy on COIL20 dataset.

From the above three experiments as a whole, the clustering errors demonstrate the effectiveness of the proposed SRSSC method.

5 Complexity Comparisions

In this section, we compare the computational and memory complexity of our algorithm with four related algorithms. The results are shown in Table 4. For the proposed method, there are standard matrix operations in the weighted Z minimization process such as matrix multiplication and matrix inversion. Assuming that the size of input data matrix is $m \times n$ and the maximal iteration numbers of ADMM is K, the computation complexity of the weighted Z optimization is $O\left( {K{n^3} + Km{n^2}} \right)$. It takes time $O\left( {{n^3}} \right)$ time to compute spectral clustering with Z. Then the total computational time of our proposed algorithm is $O\left( {K{n^3} + Km{n^2} + T{n^3}} \right)$ where T is the maximal iteration number of spectral clustering. The cost of memory is determined by the biggest matrices X and Z whose size are $m \times n$ and $n \times n$ respectively. The memory complexity of our algorithm is $O\left( {{n^2} + mn} \right)$.

Table 4 Computation and memory complexity comparison

where ${{n_s}}$ is the number of sampling iterations, d is the intrinsic dimension of input data, and c is the size of random sampling subsets of input data. The number of sampling iterations ${{n_s}}$ will grow fast as the data points grows.

6 Conclusions

In this paper, we propose a structural reweight subspace clustering (SRSSC) algorithm. The reweight sparse norm is used to make a greater approximation to the ${\ell _0}$-norm, and the structural information is added to find a better local minimum. From the results on the Hopkins 155 dataset, the Extended Yale B dataset, and the COIL 20 dataset, our algorithm has much better performance than other subspace clustering algorithms. It can illustrate that our method is reliable. But the SRSSC still has some drawbacks. SRSSC is sensitive to the three parameters which bring about the problem of parameters selection. Because SRSSC has two iterative procedures, it is time consuming. In the future work, we will improve the robustness and speed up our algorithm.