Optimal structure of particles-based superparamagnetic microrobots: application to MRI guided targeted drug therapy

Abstract

This paper presents an optimal design strategy for therapeutic magnetic micro carriers (TMMC) guided in real time by a magnetic resonance imaging (MRI) system. As aggregates of TMMCs must be formed to carry the most amount of drug and magnetic actuation capability, different clustering agglomerations could be arranged. Nevertheless, its difficult to predict the hydrodynamic behavior of any arbitrary-shaped object due to the nonlinear hydrodynamic effects. Indeed, the drag effect is related not only to the properties of the bolus but also to its interaction with the fluid viscosity, the free-stream velocity and the container geometry. In this work, we propose a mathematical framework to optimize the TMMC aggregates to improve the steering efficiency in experimental endovascular conditions. The proposed analysis is carried out on various sizes and geometries of microcarrier: spherical, ellipsoid-like, and chain-like of microsphere structures. We analyze the magnetophoretic behavior of such designs to exhibit the optimal configuration. Based on the optimal design of the boluses, experimental investigations were carried out in mm-sized fluidic artery phantoms to demonstrate the steerability of the magnetic bolus using a proof-of-concept setup. The experiments demonstrate the steerability of the magnetic bolus under different velocity, shear-stress, and trajectory constraints with a laminar viscous fluidic environment. Preliminary experiments with a MRI system confirm the feasibility of the steering of these TMMCs in hepatic artery microchannel phantom.

Introduction

Microrobots for targeted therapy by navigating in the cardiovascular system are a prolific research area for novel minimally invasive surgery procedures (Nelson et al. 2010). Among proposed approaches, magnetic targeting is one of the most advanced methods that attempts to concentrate navigable micro (Fusco et al. 2014) to nano-entities, such as therapeutic magnetic microcarriers (TMMC) in a targeted site by applying external magnetic fields (Pouponneau et al. 2011, 2014). The magnetic targeting of deep tissues is highly challenging and is not used in clinical practice (Alexiou et al. 2011). A new approach based on upgrading a typical clinical magnetic resonant imaging (MRI) scanner with adequate steering coils, referred as magnetic resonance navigation (MRN), has been proposed to guide TMMCs in deep tissues and keep the systemic carrier distribution under control (Pouponneau et al. 2014). In order to benefit both from a large motive force in the macrovasculature and from a possible break-up in the microvasculature (to avoid undesired thrombosis and to improve the targeting), a promising approach is to consider aggregates. Such aggregates of TMMC are binded either by a biodegradable ligand (Morgan et al. 2011; Korin et al. 2012) or by self-assembly properties (Vartholomeos and Mavroidis 2012). Already, polymer particles embedding doxorubicin as a therapeutic agent were successfully synthesized and steered in a rabbit liver using a 400 m/Tm unidirectional gradient coil (Pouponneau et al. 2011). However, usually several milliliters of TMMCs need to be injected in order to reach the required therapeutic drug dose. Therefore, navigation of such agents requires the injection of consecutive boluses (also referred as magnetic microrobot throughout the text) that will be serially steered from the injection site to the target location before to break-up into nanometer constituents, as shown in Fig. 1. Reliable navigation of such agents leads to know precisely the number, size, shape, and steering properties of the boluses to be injected with respect to the release location, the targeted site, and accessibility.

Fig. 1

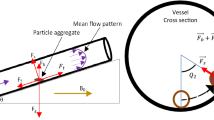
Schematic representation of the magnetic resonance navigation of boluses in the cardiovascular networks. The magnetic microrobots are released from a catheter in the arterial networks. By correctly applying magnetic gradients ${\nabla }{\mathbf {b}}$, the injected boluses follow a pre-planned path and navigate only toward the disease site (tumor, stenosis, etc.) preserving healthy tissues. The image zoom illustrates a cross section of the self-assembled magnetic bolus loaded with drug and SPIO particles

For this purpose, different designs of magnetic microrobots have been proposed in the literature (Nelson et al. 2010). First, biologically inspired magnetic microswimmers using helical propulsion (Zhang et al. 2010) or beating flagella (Dreyfus et al. 2005; Evans and Lauga 2010) have been designed. However, it has been shown that such propulsion schemes are mainly efficient in arterioles or capillaries where the Reynolds number (${{R_{\!e}}}$) remains small (Arcese et al. 2012). Another magnetic actuation, referred as bead pulling, has demonstrated its efficiency experimentally in the carotid artery of a living pig (Martel et al. 2007) and rabbit liver (Pouponneau et al. 2011).

Especially, this study aims to investigate the design of magnetic microrobots that are intended to be released from a catheter in the arterial system. The bolus is formed by aggregation of TMMCs that comprise superparamagnetic iron oxide (SPIO) particles and drug, as illustrated in Fig. 1. The MRI uniform magnetic field (e.g. $\mathbf {b}_0\ge 1.5 \hbox {T}$) ensures the saturation magnetization ($m_\mathrm {sat}$) of SPIO materials (Pouponneau et al. 2011). A relatively large aggregation could form clots in the small arteries or conversely, a very small one would be dragged away by the systemic circulation. Thus, the aggregation size and shape of the bolus is the main key factor for successful and efficient propulsion within the arteries. In the literature, spherical geometries have been mainly considered as magnetic microcarriers. As aggregates of TMMCs must be formed to carry the most amount of drug and magnetic actuation capability, different clustering agglomerations could be arranged. Nevertheless, its difficult to predict the hydrodynamic behavior of any arbitrary-shaped object. Indeed, the drag effect is related not only to the properties of the bolus but also to its interaction with the fluid viscosity, the free-stream velocity, and the container geometry. Therefore, in this work, spherical, ellipsoid-like, and chain-like of microsphere structures are mainly considered. We analyze the magnetophoretic behavior of such designs to exhibit the optimal configuration. Based on the optimal design of the bolus, experimental investigations are carried out in $mm$-sized fluidic artery phantoms to demonstrate the steerability of the magnetic bolus using a proof-of-concept setup. Secondly, preliminary MRN experiments using a clinical MRI scanner validate the feasibility of the proposed approach. The experimental results show the possibility to perform magnetic aggregation and mechanical break-up of boluses constituted of hundreds of SPIO particles of radius $r_p= 4.5\, \upmu{\hbox{m}}$.

Backgrounds

The use of therapeutic magnetic microrobots for targeted drug delivery aims to release high, localized concentrations of drug to specific sites through the selective application of a magnetic field. In particular, MRN-based microrobotic systems are considered here, since they require mainly a software upgrade of common MRI scanners. Moreover, to achieve efficient magnetic targeting, the microrobot has to navigate through the vascular network facing different values of vessel diameters, blood flow velocities, Reynolds numbers, among others. Classically, the dynamic model of a magnetic microrobot within the vasculature could be expresses as:

$$m\dot{\mathbf {v}}= \mathbf {f}_{\mathrm {m}} +\mathbf {f}_{\mathrm {Vasc}}$$

(1)

$$J \dot{\omega }= \mathbf {t}_{\mathrm {m}} + \mathbf {t}_\mathrm {Vasc}$$

(2)

where $\mathbf {v}$ and $\omega$ are the linear and angular velocities of the microrobot; $m$ its mass ; $J$ is the momentum of inertia; $\mathbf {f}_{\mathrm {m}}$ and $\mathbf {t}_{\mathrm {m}}$ are the controlled magnetic force and torque; $\mathbf {f}_{\mathrm {Vasc}}$ and $\mathbf {t}_\mathrm {Vasc}$ denote the external vascular forces and torques interactions, and take into account the dominant particle forces and particle-fluid coupling. Different cardiovascular dynamic behaviors could be considered in the above model, such as the hydrodynamic viscous drag, inertia, electrostatic, van der Waals, or contact forces (expressions of these forces are described in (Arcese et al. 2012). Especially, when the microrobot navigates close to the vessel centerline, it has been shown that the most dominant cardiovascular force is the hydrodynamic drag force $\mathbf {f}_{\mathrm {d}}$ induced by the blood flow (Arcese et al. 2012; Belharet et al. 2013).

Magnetic actuation

The basic principle of magnetic actuation is to manipulate a magnetic field $\mathbf {b}$ to induce a magnetic force ($\mathbf {f}_{\mathrm {m}}$) and torque ($\mathbf {t}_{\mathrm {m}}$) on the magnetized material:

$$\begin{aligned} \mathbf {f}_{\mathrm {m}}&= V_{\mathrm {m}}\ (\mathbf {m}\cdot \nabla ){\mathbf {b}}\end{aligned}$$

(3)

$$\begin{aligned} \mathbf {t}_{\mathrm {m}}&= V_{\mathrm {m}}\ (\mathbf {m}\times {\mathbf {b}}) \end{aligned}$$

(4)

with $V_{\mathrm {m}}$ the volume of the magnetic material; $\mathbf {m}=\left( m_x, m_y,m_z\right) ^{\!T}$ the microrobot’s magnetization; ${\mathbf {b}}=\left( b_x, b_y,b_z \right) ^T$ the magnetic field and $\nabla$ the gradient operator.

When using ferromagnetic or superparamagnetic material, the magnetic moment $\mathbf {m}$ tends to be aligned along the external applied magnetic field $\mathbf {b}_0$. Therefore, to actuate a magnetic microrobot, the magnetic field has to change spatially (e.g. thanks to a gradient field) or temporally, such as using rotating or oscillating field. Based on this consideration, different magnetic actuation schemes could be considered to manipulate the microrobot such as helical propulsion (Zhang et al. 2010), beating flagella (Dreyfus et al. 2005; Evans and Lauga 2010), or bead pulling (Floyd et al. 2009). Usually, the magnetic microrobot has to be released from the catheter within the arteries (e.g., about $10$ to $0.5\,\hbox {mm}$ of radii). From such vessel size, (Arcese et al. 2012) have demonstrated that bead pulling is the optimal actuation scheme. Actually, the other propulsion schemes, especially helical swimmers, provide sufficient actuation capabilities only from the arterioles size (i.e., below ${\sim }50$ μm). Considering bead pulling within an MRI device, the strong uniform magnetic field ($\mathbf {b}_0= 3\hbox {T}$) tends to align the magnetization moment $\mathbf {m}$ with $\mathbf {b}_0$. Thus, the orientation of the microrobot is maintained due to the magnetic torque $\mathbf {t}_{\mathrm {m}}$.

Hydrodynamic drag force

Classically, the hydrodynamic behavior of a magnetic microrobot is modeled using the Navier–Stokes equation. Assuming that the blood flow is incompressible, the drag force ($\mathbf {f}_{\mathrm {d}}$) and torque ($\mathbf {t}_{\mathrm {d}}$) on an arbitrary particle is expressed in the general case as follows (Happel and Brenner 1983):

$$\begin{aligned} \left( \begin{array}{c} \mathbf {f}_{\mathrm {d}} \\ \mathbf {t}_{\mathrm {d}} \end{array}\right) =-\left( \begin{array}{cc} \mathbf {A} &{} \mathbf {B}\\ \mathbf {B}^T &{} \mathbf {C} \end{array}\right) \left( \begin{array}{c} \mathbf {v}\\ \omega \end{array}\right) , \end{aligned}$$

(5)

with $\mathbf {v}$ the linear velocity, and $\omega$ the angular velocity of the microrobot with respect to the fluid flow. The resistance matrix defined by $\mathbf {A}$, $\mathbf {B}$ and $\mathbf {C}$, is a symmetric matrix function of the properties of the flow and of the microrobot. In particular, these parameters have some symmetric properties related to the microrobot geometry. For instance, if the body shape has three orthogonal symmetric planes (such as spheroid, cuboid, or chain-like structures), we get $\mathbf {B}={0}$. In addition, as the orientation of the microrobot within a MRI scanner is fixed due to the uniform field $\mathbf {b}_0$, there are no rotational motion and $\omega =0$. Thus the hydrodynamic behavior induces mainly a drag force that could be approximated by:

$$\mathbf {f}_{\mathrm {d}} =-\frac{1}{2}\rho _{f}A\ {C_\mathrm {d}}\cdot \Vert \mathbf {v}\Vert \mathbf {v},$$

(6)

where $\rho _{f}$ is the fluid density; $A$ is the microrobot hydrodynamic reference area; $\mathbf {v}$ is the motion of the microrobot relative to the fluid flow; and ${C_\mathrm {d}}$ is the dimensionless drag coefficient which is classically related to the Reynolds number ${{R_{\!e}}}$ (White and Corfield 1991), which is defined by:

$$\begin{aligned} {{R_{\!e}}}=\frac{a\rho _{f}\Vert \mathbf {v}\Vert }{\eta _f} \end{aligned}$$

(7)

with $\eta _f$ the fluid viscosity, and $a$ the characteristic length of the microrobot.

Hydrodynamic behavior of spherical microrobot

First, the hydrodynamic behavior of spherical particles has been deeply validated by many numerical and experimental studies on the drag force (Maccoll 1928; Davies 1949). For instance, for low Reynolds number (that is ${{R_{\!e}}}\ll 1$), we get:

$$C_{{\rm d}} {,\mathrm {Stoke}}=\frac{24}{{{R_{\!e}}}}$$

(8)

which leads to the well-known Stokes’ drag force in a creeping flow. Thus, for a spherical microrobot with a radius $r$, the Eq. (6) becomes:

$$\begin{aligned} {\mathbf {f}_{\mathrm {d}}}_{, \mathrm {Stoke}}=-6\pi \eta _f\ r^2\ \mathbf {v}\end{aligned}$$

(9)

This approximation is usually adequate in arterioles or capillaries, but remains inaccurate in arteries where the Reynolds number is in the range of ${{R_{\!e}}}{\sim }0.5$–$500$. A more accurate expression of the drag coefficient for a spherical body with a Reynolds number lower than ${{R_{\!e}}}< 2.5\times {10}^5$ has been proposed by White and Corfield (1991):

$$ C_{{\rm d}\infty} =\frac{24}{{{R_{\!e}}}}+\frac{6}{1+\sqrt{{{R_{e}}}}}+0.4 $$

(10)

Furthermore, the above Stoke’s approximation (9) also neglects the wall effect $\beta$. In endovascular applications the effect of the blood vessel walls on the drag force has to be accounted. The effect of the bounding walls is defined in terms of a wall correction factor which measures the relative change in the drag force $\mathbf {f}_{\mathrm {d}}$ with respect to the equivalent drag force ${{\mathbf{f}}_{{\rm d}\infty}}$ in unbounded environment. Therefore, this wall effect correction is usually defined as the ratio between the velocity $\mathbf {v}$ in a bounded medium and the velocity ${{\mathbf {v}}_\infty }$ in an infinite fluid, $\beta \equiv {\mathbf {v}}/{{\mathbf {v}}_\infty }$. Numerous studies have shown that this wall factor is mainly a function of the sphere-to-tube radius ratio, $\lambda ={r}/{R_v}$, assuming that the cylindrical vessel is sufficiently long to neglect the end effects. Especially, it is admitted that the wall correction depends only on $\lambda$ at both very low and high Reynolds number, whereas at the intermediate transition regime, the factor $\beta$ is a function of both $\lambda$ and ${{R_{\!e}}}$ parameters (Chhabra et al. 2003). For a spherical device in Stoke’s flow the Haberman and Sayre (1958) expression is the most reliable for $\lambda \le 0.9$:

$$\begin{aligned} \beta (\lambda )=\frac{1-2.1050\lambda +2.0865\lambda ^3-1.7068 \lambda ^5+0.72603\lambda ^6}{1-0.75857\lambda ^5} \end{aligned}$$

(11)

with $\lambda ={r}/{R_v}$, where $r$ and $R$ define the spherical microrobot and vessel radius, respectively. For intermediate Reynold number in the range $0.01<{{R_{\!e}}}<10,000$, the Kehlenbeck and Felice (1999) correlation could be recommended up to $\lambda =0.85$:

$$\begin{aligned} \beta (\lambda , {{R_{\!e}}})= \frac{1-\lambda ^{p}}{1+\left( \frac{\lambda }{\lambda _0}\right) ^{p}} \end{aligned},$$

(12)

where both $p$ and $\lambda _0$ are function of ${{R_{\!e}}}$ as follows:

$$\begin{aligned} \lambda _0&= \frac{0.283+0.0492 {{R_{\!e}}}^{0.524}}{1+0.041 {{R_{\!e}}}^{0.524}} \end{aligned}$$

(13)

$$ p= 1.44+0.5466\ {{R_{\!e}}}^{0.524} \text\quad {\rm if } \,{{\it R_{\!e}}}\le 35 $$

(14)

$$ p= 2.33+37.3\ {{R_{\!e}}}^{0.434} \text \quad{ \rm if }\, {{\it R_{\!e}}}>35$$

(15)

Hydrodynamic behavior of non-spherical microrobot

Secondly, the drag force experienced by a non-spherical object has been also considered for spheroids, cylinders, chain-like of spheres, or cuboids (Kasper et al. 1985; Madhav and Chhabra 1995; Filippov 2000). The main idea is to consider that the drag force experienced by a non-spherical microrobot acts in the direction of the velocity $\mathbf {v}$, and could be related to the equivalent spherical drag force, that is:

$${\mathbf {f}_{\mathrm {d}}}_\infty =\kappa _{f}\cdot {\mathbf {f}_{\mathrm {d}s}}_\infty (r_{e}), $$

(16)

where $\kappa _{f}$ is the dimensionless dynamic shape factor which is related to the microrobot geometry; and ${\mathbf {f}_{\mathrm {d}s}}_\infty (r_{e})$ is the equivalent drag force computed for a spherical device with the equivalent volume sphere radius $r_{e}$ in unbounded environment. This radius $r_{e}$ is defined as the radius of a sphere equal in volume to the non-spherical microrobot.

Furthermore, the wall effect plays a crucial role in the drag phenomena acting on non-spherical object. Efforts have been made to experimentally and numerically determine this drag correction factor for different object and channel shapes (Happel and Brenner 1983; Kasper et al. 1985; Unnikrishnan and Chhabra 1991; Kishore and Gu 2010). By analogy with spherical device, the wall correction is related to the object size-to-tube radius ratio ($\lambda$), the Reynolds number (${{R_{\!e}}}$), and the microrobot aspect ration ($\sigma$). Commonly, the wall factor $\beta$ is related to the Faxén’s correction (Happel and Brenner 1983), and could be expressed in the general form as:

$$\beta (\lambda ,{{R_{\!e}}},\sigma )={1-f(\lambda ,{{R_{\!e}}},\sigma )}, $$

(17)

where $f$ is a function of the ratio $\lambda =a/R_v$, with $a$ a characteristic length of the object and $R_v$ the radius of the channel.

Materials and methods

Microrobot design

To cope with the external vascular forces $\mathbf {f}_{\mathrm {Vasc}} =\mathbf {f}_{\mathrm {d}}$, we consider in this study a microrobot that is based either on a spherical or an aggregate of TMMC. Each TMMC comprises superparamagnetic iron oxide (SPIO) particles and a drug load, as illustrated in Fig. 2. The magnetic volume of a TMMC is then a fraction of the total volume, that is $V_{\mathrm {m}}=\tau _mV$. Although the saturation magnetization of SPIO particles is not optimal (e.g., $\mathbf {m}_\mathrm {sat}{\sim }30$–$60\,\hbox {emu}/\hbox {g}$), it is still acceptable with the advantage to being widely used clinically (Laurent et al. 2008). However, to be used as therapeutic agents, their very low value of magnetic material results in very high gradient fields that limit their application with MRI-guided delivery. To increase the effective volume $V_{\mathrm {m}}$ of magnetic material, novel approaches use self-assembled aggregates (dipole–dipole interactions) of magnetic nanoparticles (MNPs) (Vartholomeos and Mavroidis 2012) or biodegradable polymer (Pouponneau et al. 2011) to form large bolus of aggregates. We consider here three different structures: (i) a single spherical TMMC (Fig. 2a); (ii) an ellipsoid-like agglomerate of TMMCs (Fig. 2b); (iii) and a chain-like aggregation of TMMCs (Fig. 2c).

Fig. 2

Magnetic microrobot a single spherical TMMC, b ellipsoid-like aggregation, and c chain-like agglomerate of TMMC

Magnetic microrobot in viscous flow

The flow and drag phenomena spherical microrobot in viscous flow has been well investigated (Maccoll 1928; Davies 1949; Haberman and Sayre 1958; Kehlenbeck and Felice 1999), and could be directly obtained using Eqs. (6), (10) and (11), or (12). Usually, the hydrodynamic behavior of a non-spherical microrobot is related to its equivalent spherical drag force (16) through the dynamic shape factor $\kappa _{f}$. As experiments cannot be conducted on objects with a wide range of shapes in different orientations, a predictable model of the dynamic shape factor is required.

In the case of a longitudinally elliptic body of circular cross section (named prolate spheroid hereafter), the dimensionless shape correction depends on the direction of the movement. If the motion of a prolate ellipsoid is transverse to its major axis (i.e., direction $v_{\bot }$ in Fig. 2), the following approximation is proposed (Kasper et al. 1985):

$$\begin{aligned} {}^\mathrm {e}\kappa _{{\bot }} =\frac{8}{3}\frac{(\sigma ^{2}-1)}{\left( \frac{(2\sigma ^{2}-3)}{\sqrt{\sigma ^{2}-1}}\ln \left( \sigma +\sqrt{\sigma ^{2}-1}\right) +\sigma \right) } \end{aligned}$$

(18)

with $\sigma =\frac{a}{b}$ the aspect ratio of the prolate spheroid, where $a$ is the major axis and $b$ is the minor axis of the ellipsoid (cf. Fig. 2b). For a motion along the direction of the major axis (i.e., direction $v_{{/\!/}}$ in Fig. 2), the dynamic shape factor is given by (Kasper et al. 1985):

$$\begin{aligned} {}^\mathrm {e}\kappa _{{/\!/}} =\frac{4}{3}\frac{(\sigma ^{2}-1)}{\left( \frac{(2\sigma ^{2}-1)}{\sqrt{\sigma ^{2}-1}} \ln \left( \sigma +\sqrt{\sigma ^{2}-1}\right) -\sigma \right) } \end{aligned}$$

(19)

For chains of $N$-spheres, (Geller et al. 1993) have experimentally investigated the dynamic shape factor, and have proposed the following formula:

$${}^\mathrm {c}\kappa _{{\bot }}= \frac{4}{3}\frac{N^{2/3}}{\left( \log (2N)+0.26269+ \frac{0.38185}{\log ^{2}(2N)}\right) },$$

(20)

$${}^\mathrm {c}\kappa _{{/\!/}}= \frac{2}{3}\frac{N^{2/3}}{\left( \log (2N)-1.00401 +\frac{0.906526}{\log ^{2}(2N)}\right) },$$

(21)

where the subscript ${\bot }$ and ${/\!/}$ denote a motion perpendicular, and parallel, respectively, to the major axis of a straight chain of $N$-spheres (see Fig. 2c).

Remark 1

Let us notice that the above dynamic shape factors are defined for all aspect ratio $\sigma >1$ for ellipsoidal design, or $N>1$ for chain-like structure. If $\sigma =1$ or $N=1$, in both cases we get a spherical object leading to $\kappa _{f}=1$.

Furthermore, when exposed to an external magnetic field $\mathbf {b}_0$, the magnetic microrobot acquires a magnetic dipole moment. Therefore, a non-spherical microrobot get its major axis aligned along the field $\mathbf {b}_0$ direction, as illustrated in Fig. 3. As the controlled magnetic gradient ${\nabla }{\mathbf {b}}$ defines the motion direction $\mathbf {v}$, an angular deviation $\theta$ could occur. Thus, it influences the dynamic shape factor, and the above perpendicular and parallel factors could be seen as extrema values. The computation of the dynamic shape factor $\kappa _\theta$ for an angular deviation $\theta$ between the minor axis and the moving direction (see Fig. 3) is then given by (Kasper et al. 1985):

$$\begin{aligned} \frac{1}{\kappa _\theta }=\frac{1}{\kappa _{\bot }}+\left( \frac{1}{\kappa _{/\!/}}-\frac{1}{\kappa _{\bot }}\right) \sin ^2\theta \end{aligned}$$

(22)

Fig. 3

Magnetic microrobot in vessel-like environment

Fig. 4

Hydrodynamic drag forces $\mathbf {f}_{\mathrm {d}}$ for spherical, spheroid-like and chain-like superparamagnetic microrobots composed of TMMC aggregates as function of the bolus volume. The second abscissa shows the shape ratio $\sigma =b/a=1/N$ (left) and $\sigma =a/b=N$ (right). Dimensions: TMMC radius $r_0= 100$ μm, vessel radius $R_v= 750$ μm

As mentioned earlier, the wall effects have to be taken into account. The wall correction factor for prolate spheroids falling in the $v_{/\!/}$ direction has been first investigated at very low Reynolds number by Happel and Brenner (1983):

$$\begin{aligned} {}^e\beta _{/\!/}(\lambda ,\sigma )&=1-{}^\mathrm {e}\kappa _{{/\!/}} \lambda \sigma ^{1/3}\times\\ &\quad \times \left( 2.105+ 0.758\lambda ^2\sigma ^2 +1.329\lambda ^2\right) \end{aligned}$$

(23)

with the aspect ration $\sigma =a/b,$ where $a$ and $b$ denote the major and minor axes of the ellipsoid. However, no wall correction for orthogonal motion $v_{\bot }$ are proposed. For prolate spheroids falling in intermediate Reynolds number in the range $1\le {{R_{\!e}}}\le 200$ Kishore and Gu (2010) have proposed the following drag coefficient that embed the dynamic shape factor and the wall effect:

$$ {C_{\rm d}}=\frac{12}{{{R_{\!e}}}}\times \left( \frac{1.81+\lambda }{0.79+\lambda }\right) ^{4.16}\left( 1+0.304{{R_{\!e}}}^{0.685} \sigma ^{1.1}+ 0.15{{R_{\!e}}}^{-0.5}\sigma ^{3.3}+2.1\sigma ^{0.4}\right)$$

(24)

The above drag coefficient is defined for parallel motion with $\sigma =b/a$, and orthogonal motion with $\sigma =a/b$.

In contrast, few works have addressed the wall effect for chain-like structures. Commonly, researchers use the spheroid approximation. Particularly, in parallel orientation, spheroidal model appears adequate to approximate a straight chain structure, when $\lambda \ll 1$. Based on (Happel and Brenner 1983) studies, (Kasper et al. 1985) have proposed from their experimental results dedicated to chain-like structures of $N$-spheres in Stoke’s flow the following first-order approximations:

$$\begin{aligned} {}^c\beta _{/\!/}(\lambda ,\sigma =N)&= 1-2.105\ {}^\mathrm {e}\kappa _{{/\!/}} \lambda \sigma ^{1/3} \end{aligned}$$

(25)

$$\begin{aligned} {}^c\beta _{\bot }(\lambda ,\sigma =N)&= 1-0.76\ \lambda \sigma ^{0.7} \end{aligned}$$

(26)

with $\sigma =N$ the number of spheres. Tabulated values from series of experiments of the dynamic shape factor and wall effect of chain-like structure up to $N=30$ are also proposed in (Kasper et al. 1985).

Figure 4 shows the evolution of the drag forces $\mathbf {f}_{\mathrm {d}}$ for spherical, spheroid-like and chain-like superparamagnetic microrobots. The structures are composed by TMMC aggregates (radius $r_0= 100$ μm) navigating in a vessel of radius $R_v= 750$ μm. The left curves illustrate the drag behavior for a parallel motion along the vessel axis, while the right curves present the results for an orthogonal motion. As expected, the microrobotic shape plays a great role on its hydrodynamic behavior supporting the fact that the choice of the appropriated model is important for design optimization. When navigating in parallel, the ellipsoid-like, and chain-like designs clearly provide less drag force than the equivalent sphere. Especially, the ellipsoidal profile is the most efficient in such case. It should be noticed that for non-spherical microrobots, the hydrodynamic force is preponderant in an orthogonal motion rather than in a parallel motion due to the fact that the non-spherical shape presents a higher resistance to the flow. However, the chain-like microrobot seems to provide less drag in perpendicular direction than a spheroid design. It can be explained by that assumption that the flow can pass at intersections between the spheres reducing significantly the drag resistance. Finally, let us recall that only limited data is available for $\lambda >0.9$ and aspect ratio in the range of $0.25<\sigma <30$. Thus extreme caution must be exercised in using any of the available correlation under these conditions. In particular, the model of (Kasper et al. 1985) for chains of $N$-spheres structure provides significant correlation only up to $\lambda = 0.5$ in creeping flow.

MRI actuation

A clinical MRI is used to achieve the propulsion of the magnetic microrobot using the existing gradient coils of the scanner. These coils system is a set of electromagnetic coils, which allows the generation of magnetic gradients in the three-dimensional (3D) space within the MRI bore. We assume that the strong uniform magnetic field $\mathbf {b}_0= 3\hbox {T}$ of the MRI is sufficient to ensure the magnetization saturation $\mathbf {m}_{\mathrm {sat}}=(0,0,m_\mathrm {sat})^T$ of the embedded magnetic material. Furthermore, the uniform magnetic field $\mathbf {b}_0$ tends to align the magnetization moment $\mathbf {m}$ with $\mathbf {b}_0$. Thus, the orientation of the microrobot is maintained thanks to the magnetic torque $\mathbf {t}_{\mathrm {m}}$. The Eq. (3) can be then simplified as:

$$\begin{aligned} \left( \begin{array}{l} f_{m_x} \\ f_{m_y} \\ f_{m_z} \end{array}\right) = V_{\mathrm {m}}\cdot m_{\mathrm {sat}} \left( \begin{array}{l} \frac{\partial B_x}{\partial z} \\ \frac{\partial B_y}{\partial z} \\ \frac{\partial B_z}{\partial z} \end{array}\right) \end{aligned}$$

(27)

Obviously, the optimization of the magnetic propulsion capability is then related to the available magnetic volume ($V_{\mathrm {m}}$) and magnetization saturation ($\mathbf {m}_\mathrm {sat}$), together with the magnetic gradient strength (${\nabla }{\mathbf {b}}$). However, there are different technological constraints that actually limit the magnetic actuation. First, the limitations of the actuators are set here to $\Vert {\nabla }{\mathbf {b}}_{\mathrm{sat}}\Vert = 45\, {\rm m/Tm}$, which is consistent with the maximum magnetic gradients that are available in clinical MRI scanners. Furthermore, SPIO particles are currently extensively investigated as magnetic material for biomedical applications due to their excellent biocompatibility and reactive surface that can be readily modified with therapeutic molecules (Laurent et al. 2008; Pouponneau et al. 2011). Hence, after the break-up of the bolus and the drug release, the SPIO particles would be safely spread through the systemic circulation, and naturally removed by the body. Moreover, SPIO particles magnetization saturation $m_{\rm sat}$ commonly span the 30–60 emu/g range, lower than the bulk iron-oxide value (~100 emu/g). To improve the magnetic propulsion, one solution is then to increase the effective magnetic volume $V_{\mathrm {m}}$. Therefore, aggregates of TMMCs must be considered to maximize the magnetic force.

Magnetic microrobot for MRI-aided optimal drug delivery

This work aims to optimize the design of a magnetic microrobot that has to be released from the (small) arteries for targeted drug delivery using an MRI scanner. To transport the therapeutic agent, the microrobot comprises an agglomerate of TMMCs. In particular, to be consistent with the experiments, we consider hereafter that the magnetic parts of the TMMC are SPIO particles (BioMag BM547, Bang Laboratories, Inc.) with a saturation magnetization of $m_{\mathrm {sat},3T}= 58\,\hbox {emu}/\hbox {g}$ under a magnetic field $\mathbf {b}_0= 3\hbox {T}$ (Mathieu and Martel 2009). To optimize the drug delivery, the total volume $V$ of the microrobot should be maximized to provide a sufficient magnetic force $\mathbf {f}_{\mathrm {m}}$, and drug load to the targeted area. Nevertheless, this objective leads to increase the drag force $\mathbf {f}_{\mathrm {d}}$, and the risk of unwanted embolization. Especially, to control efficiently the microrobot, the driving force $\mathbf {f}_{\mathrm {m}}$ have to overcome the external drag force $\mathbf {f}_{\mathrm {d}}$. This design optimization is then related to the dimensionless magnetophoretic number $C_{\rm mt} =\frac{\mathbf {f}_{\mathrm {m}}}{\mathbf {f}_{\mathrm {d}}}$ ratio introduced by Mathieu et al. (2006).

Spherical magnetic microrobot

Fig. 5

Magnetophoretic number $C_{\rm mt} =\tfrac{\mathbf {f}_{\mathrm {m}}}{\mathbf {f}_{\mathrm {d}}}$ ratio as function of equivalent spherical radius $r_e$ and magnetization rate $\tau _m$ for spherical magnetic microrobots

The design optimization of spherical magnetic microrobots have been investigated from arteries to capillaries previously in (Arcese et al. 2012). In their studies the authors have considered the optimization of the design together with the trajectory, and thus fixed the magnetization rate to $\tau _m=45\,\%$. Here, we aim to consider the optimal structure that allows carrying the maximum drug load to the targeted area. Figure 5 shows the evolution of the magnetophoretic number $C_{\rm mt}$ for different spherical magnetic microrobot sizes that navigate in a small artery of $1.5\,\hbox {mm}$ size (cf. Table 1). The best ratio is given for a $C_{\rm mt} =1.96$ with a radius of $r_e= 285.5$ μm with a full magnetization rate of $\tau _m=100\,\%$. Moreover, this result exhibits that to control efficiently such spherical design, the equivalent radius $r_e$ must be within $127.8$ and $481.9$ μm range. For a spherical microcarrier in this range ($C_{\rm mt} =1$) the minimal magnetization rate $\tau _m=51.06\,\%$ is provided for a radius $r_e=269.3$ μm leading to a drug load of $V_d= 0.04\,{\hbox {mm}}^3$. As shown in Fig. 6, the optimum drug load of $0.098\,{\hbox {mm}}^3$ is obtained for a radius of $r_e= 415.8$ μm and $\tau _m=67.3\,\%$. However, for optimal delivery the size of the microrobot must be between $30$ and $60\,\%$ of the vessel size in small arteries (Arcese et al. 2012). Therefore, to ensure efficient magnetic controllability and drug load to deep location in the human body, the spherical microrobot is usable mainly in small arteries (about $R_v\gtrsim 175$ μm vessel size).

Table 1 Simulations parameters

Fig. 6

Evaluation of magnetization rate $\tau _m$   (a) and drug load  (b) as function of the radius for a magnetophoretic number $C_{\rm mt} =1$ for spherical magnetic microrobots

Fig. 7

Comparison of magnetophoretic number $C_{\rm mt} =\mathbf {f}_{\mathrm {m}}/\mathbf {f}_{\mathrm {d}}$ for an ellipsoidal (a)–(c) and a chain-like (b)–(d) microrobots in parallel (a)–(b) and perpendicular (c)–(d) motions

Non-spherical magnetic microrobot

To the authors’ knowledge, no studies have been investigated concerning the optimization of non-spherical bead pulling design for targeted drug delivery. Figure 7 presents the evolution of the $C_{\rm mt}$ ratio as a function of the equivalent radius $r_e$ and the magnetization rate $\tau _m$ for different microrobot structures. Specifically, these results consider ellipsoid (Fig. 7a, c) and chain-like (Fig. 7b, d) microrobots composed of TMMC aggregates. In the following, we consider TMMCs of radius $r_0=100$ μm. The considered ellipsoid design has a fixed minor radius $b=r_0$ while its major axis $a$ is increased with the equivalent volume sphere radius $r_e$. Therefore, for a given equivalent radius $r_e$ each magnetic microrobot has the same magnetic volume, and thus is propelled with the same magnetic force $\mathbf {f}_{\mathrm {m}}$ (27). As expected, non-spherical microrobots are more efficient in parallel direction rather than following a perpendicular motion. In terms of steering performances, the simulation results demonstrate better performance for chain-like structures compared to prolate-like structures. Obviously spheroids are not able to provide steering capability ($C_{\rm mt} <1$) in orthogonal motion. For the same equivalent volume, the reference surface of chain-like structures are greater than those of spheroids, but the former offers less drag resistance to the flow due to stream leakage at sphere contact.

Fig. 8

Drug volume as function of the equivalent radius $r_e$ when $C_{\rm mt} =1$ with TMMC of radius $r_0= 100$ μm

Fig. 9

Evaluation of the optimum a number of microspheres for chain-like structures, and b the drug load capability as function of the TMMCs radius $r_0$

Figure 8 compares the corresponding amount of drug volume carried by different microrobot structure when the ratio is settled to $C_{\rm mt} =1$. Once again, the chain-like geometry provides the optimal drug load as spheroid cannot be controlled properly in orthogonal motion. In small artery (radius $R_v= 750$ μm), only chain of up to $7$-TMMCs of radius $r_0= 100$ μm could be used in direction perpendicular to the vessel axis. Therefore, a maximal drug volume of $0.0107\,{\hbox {mm}}^{3}$ could be transported. In practice, such structures appear to be difficult to control properly without creating unwanted embolies at vessel bifurcations. Obviously, the best choice would be to navigate in vessels with a diameter close to the TMMC size. However, it would increase drastically wall effects and surface interactions (e.g., electrostatic, van der Waals, or contact microforces) which have been not addressed here. To overcome this limitation, a solution is to reduce the size of the TMMC radius $r_0$. Figure 9a illustrates the variation of the number of TMMCs in a chain-like agglomeration in orthogonal direction for maximum drug load. A minimum radius of $r_0= 60$ μm with at least $12$-microspheres could be magnetically steered in small artery of radius $R_v= 750$ μm. Below $r_0< 60$ μm there are not enough magnetic material to propel efficiently the microrobot in perpendicular direction. At the other end, for maximal values $r_0> 140$ μm, the drug load reaches a saturation level rapidly with only two TMMCs (Fig. 9b). The optimal number of TMMCs, and then the drug load capability, can be freely chosen wrt. the minimal vessel size of the targeted area.

Discussions

Actually, drug treatments utilize a manually operated syringe and single-lumen microcatheter to release the TMMC aggregates into the hepatic arterial supply with the intent of targeting downstream tumor sites. From the design point of view, the TMMCs has first to overcome the hepatic artery blood flow ($37\,{\text{mL}}/{\text{min}}$) with a minimum transient time. The simulation results show that in such a case the chains of microspheres aggregation provides the most efficient magnetophoretic ratio $C_{\rm mt} =\frac{\mathbf {f}_{\rm{m}}}{\mathbf {f}_{\rm{d}}}$ and drug load capability, particularly when its major axis is aligned along the vessel axis. Due to the magnetic chain-like aggregation of TMMCs, the magnetic volume to steer is drastically increased thereby reducing the transit time. These results are in full agreement with those experienced by (Pouponneau et al. 2009) with a MRI scanner. We found also that when navigating perpendicular to the vessel axis, such aggregates could have lengths exceeding the radius $R_v$ in smaller vessel (e.g., in arterioles or capillaries). The main problem foreseen is unwanted embolies. However, the simulations demonstrate that the conjunction of the endovascular shear-stress with the wall contact effects could induce a sufficient force to break-up the dipole–dipole interaction forces between the TMMCs allowing releasing the drug into arterioles and capillaries. As the small vessels are feeding the tumor, the drug delivery close to the targeted site seems feasible. Furthermore, the conducted optimal design analysis has mainly focused on the $C_{\rm mt} =1$ case. Indeed, this magnetophoretic ratio leads to provide the maximum amount of drug while offering sufficient magnetic volume to counteract the arterial blood flow. On the other hand, the optimal value $C_{\rm mt} \ge 1$ is only required to navigate against the hepatic blood flow. Such situations usually occur mainly in the vicinity of the first hepatic arterial bifurcation, and become less mandatory as the microrobot navigates in deeper locations. Therefore, one can slightly under evaluate the magnetic microrobot size.

Results and discussion

In this section, we demonstrate experimentally the steerability of TMMC aggregates composed of SPIO particles in different operating conditions. First, a steering Maxwell–Helmholtz coil system is developed as a proof-of-concept before to be used with a clinical MRI scanner.

Proof of concept validation

Experimental setup description

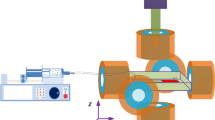
To validate experimentally the findings of model simulations, an experimental setup has been specifically developed by Aeon Scientific™ and is depicted in Fig. 10a. The system consists of three nested sets of Maxwell coils and one nested set of Helmholtz coils presented in Table 2. Such arrangement helps to generate magnetic gradient field in $x$-, $y$-, and $z$-axis direction in the workspace. Magnetic gradient forces will thus be exerted on the magnetic microrobot that is placed inside a Y-channel of the microfluidic chip (cf. Fig. 10b). This microchannel chip imitates a hepatic artery bifurcation, i.e., mother branch $R_{v1}= 2.5\,\hbox {mm}$ and daughter branch $R_{v2}= 750$ μm. To imitates the blood flow, this vascular phantom is filled with a viscous fluid that is made of $50\,\%\,$ glycerol–water mixture providing a viscosity of $\eta _f= 6\,\hbox {m}\hbox {Pa}\cdot \hbox {s}$ and density of $\rho _{f}= 1,130\,\hbox {k}\hbox {g}/{\hbox {m}}^3$.

Fig. 10

Experimental proof of concept setup a 3D Maxwell–Helmholtz coils setup; and b Y-shaped microfluidic arterial bifurcation chip

Table 2 Platform coils

The navigable bolus was synthesized with gel and SPIO particles (BioMag BM547, Bang Laboratories, Inc.) in a mixer before to be injected. By controlling the concentration of SPIO particles, we can design boluses with different magnetic rate $\tau _m$. Then, droplets containing SPIO particles are injected through a controlled syringe pump in the injection input via a flexible microcatheter. Figure 11 depicts an example of obtained ellipsoidal-like aggregates of TMMC (Fig. 11a) and a chain-like aggregation (Fig. 11b). TMMC depicted here has the following characteristics: an average radius of about $250$ μm; gel profile replacing the sustained release of drug; and an aspect ratio greater than $0.9$. Such value of aspect ratio leads to a dynamic shape factor that remains close to 1. Homogeneous magnetic flux densities and gradients of up to $300\,\hbox {mT}$ and 350 mT/m, respectively, can be generated in the workspace of $20 \hbox {mm}\times 20\hbox {mm}$. The Helmholtz coils corresponds to the $x$-axis to magnetize the SPIO microparticles with low remnant magnetization values. The system is set up on an CCD high-resolution miniature microscope camera (TIMM 400, Nanosensor) providing up to $26\,\hbox {mm}\times 20\,\hbox {mm}$ field of view. The motion of magnetic microcarrier is measured by real-time processing of the video images acquired by the microscope camera using Labview computer program.

Fig. 11

Navigable bolus being made of hundreds SPIO microparticles being embedded with the therapeutic load. The optimized structure is 75 % of magnetic material and 25 % of drug

Experimental validation

Successful targeting of magnetic microrobot at deep-seated lesions can be accomplished by steering the optimized boluses of SPIO particles through successive blood-vessel branches toward the lesion. The experimental platform can be used to determine the magnetic gradients that maximize the steering efficiency with a minimum of SPIO particles dispersion. This section describes the results of the proof of concept experiments that were conducted for validation purposes of the navigability of magnetic microrobot in a Y-channel microfluidic chip mimicking the hepatic arterial system. Figure 12 shows the CFD simulation (ANSYS©Fluent software) of the Y-shaped microfluidic device. This result helps to verify the laminar flow conditions when the microcatheter tip is inserted in the main vessel channel.

Fig. 12

Computational fluid dynamics simulation of a microcatheter delivering bolus of aggregates of magnetic microparticles in a Y-shaped microfluidic channel. As shown, the parabolic profile of laminar flow prevails in the mother and daughter vessels

Fig. 13

Magnetic bolus navigation experiments in microfluidic Y-shaped channels a the mother channel of radius $R_v= 2.5\,\hbox {mm}$; b the daughter channel of radius $R_v= 750$ μm

Microaggregates of SPIO particles with polymeric solutions demonstrate stability in aqueous liquid due to their hydrophobicity. As shown in Fig. 13a, the bolus of aggregates of particles keeps its shape when navigating far from the vessel’s walls. To measure the amount of particles lost during navigation, we analyzed the volume of the bolus through image processing techniques for different velocity values. Figure 14 shows clearly the linear dependence of the microrobot velocity on the volume of agglomerated particles. At relatively high motion conditions ($v= 6\,\hbox {mm}/\hbox {s}$) the microcarrier release less than $7\,\%$ of its volume of particles. It can be seen in Fig. 13 that for relatively large vessels (small artery of $R= 2.5\,\hbox {mm}$ of radius), the influence of the near-field surface forces such as the shear-stress ($\tau$) and the electrostatic forces does not play a great role in the break-up of the aggregate. The ratio $\lambda =r/R_{v1}$ between the bolus radii and the vessel radii is very small ($\lambda = 0.1$). The condition is verified when the distance between the microcarrier and the vessel’s wall ($\delta _{1}$) is superior to the bolus diameter. As shown in Fig. 13b, when the microcarrier enters in one daughter branch, the ratio $\lambda$ is close to $0.33$ that increases greatly the influence of shear-stress forces close to the wall’s vessel. Moreover, when the microrobot enters in the daughter branch, it has a spherical shape. While the shear-stress is increasing, the shape became more ellipsoidal-like. Hence, the form of the magnetic microrobot evolves during the navigation in smaller vessel.

Fig. 14

Evolution of particle losses wrt. navigation speed

Figure 15 illustrates the influence of the vessel’s wall on the bolus volume. We defined the non-dimensional value ($S/S_{0}$) as the ratio between the magnetic microrobot volume and the SPIO particle volume. The standard ratio is settled at $S/S_{0}=57$. One can see that for values less than $\delta = 350$ μm, the near-field surface forces dominates until to break-up the aggregate totally. The value highlighted in red corresponds to the specific case of the snapshots of Fig. 13b.

Fig. 15

Evolution of the aggregate volume wrt. to the distance at the vessel’s wall

Fig. 16

Evolution of the aggregate volume wrt. the shear-stress

Fig. 17

Navigation of a bolus of aggregates in a daughter channel of radius $750$ μm toward a microfluidic vascular stenosis model of radius $250$ μm. a navigation of a magnetic bolus of radius $r_0= 250$ μm in a stenosis vascular phantom and breaking in multiple clots due to shear-stresses; and b computational simulations using discrete particle modeling software

We see clearly that when the bolus is exposed to mechanical forces that overcome the attractive forces holding the microparticles together, such as hemodynamic shear-stresses, the aggregate break apart. To determine the shear-sensitivity of the microparticle deployment mechanism, we estimated from calculation the shear-stress for a cylindrical vessel as:

$$\begin{aligned} \tau _w=-\eta _f{Q}\frac{\left( R_v-\delta \right) }{R_v^3} \end{aligned}$$

(28)

with $Q$ the volumetric flow rate and $\delta$ the distance to the wall. The experimental results given in Fig. 16 demonstrates the great influence of the shear-stress mechanism on the break-up of the aggregate that produce repulsive forces and counteract the small magnetic dipole–dipole forces.

Finally, Fig. 17a shows a microfluidic vascular stenosis model demonstrating how large bolus of aggregates should remain intact in pre-stenotic region (daughter vessel), but then break-up into microparticles when they flow through a constriction (60 % lumen occlusion) and can accumulate in endothelial cells lining the bottom of the channel. As shown in experiments (Fig. 17a) and in simulation using discrete particle modeling software (Fig. 17b), shear-induced release of drug-coated microparticles could break-up back into its micrometer constituents, which are then driven by the blood flow into the thinner blood vessel toward the stenosis.

Preliminary MRI-aided experiments

A clinical MRI scanner has been used to evaluate the relevance of the model simulation. The MRI system used here is a standard Magnetom Verio $3$T (Siemens, Germany) scanner (see Fig. 18). As the MRI platform is still in used for clinical consultations, the system hardware has not been modified. However, the Siemens software environment has been upgraded. Specifically, a dedicated MRN architecture has been developed and embedded in the Siemens Integrated Development Environment for MR Applications (IDEA). The MRN architecture comprises novel MR-Imaging sequences, MR-Tracking algorithms, navigation planning, and magnetic control strategies (Folio et al. 2011). An external vision system is added to observe the evolution of the bolus.

Fig. 18

The clinical Siemens Mangetom Verio 3T MRI scanner with the square acrylic box filled with water that contains bolus of aggregates

To evaluate the capability to use magnetic bolus within a clinical MRI scanner, preliminary experiments have been conducted. To this aim, a magnetic microrobot was placed in an acrylic box filled with water inside the MRI bore, as shown in Fig. 18. The acrylic box allows ensuring that no magnetic material escapes into the system. Hence, the microrobot has to follow a simple planned path, as shown in Fig. 19. The motion of magnetic microrobot is measured by real-time processing of the MRI data using a dedicated MR-tracking algorithm from a fast low single shot (FLASH) sequences. Especially, the insertion of magnetic material into the MRI field of view implies some distortion in the MR-data, and leads to magnetic susceptibility artifact formation, as illustrated in Fig. 19a. The choice of FLASH sequences allows offering a MR-tracking providing a standard deviation of $0.1$ mm at $0.053$ mm in the x and y direction, respectively (Folio et al. 2011). In clinical practice the focus is usually on avoiding such artifacts to produce correct representation of anatomical structures. In contrast, in this study, susceptibility artifacts induced bythe particles-based superparamagnetic aggregates are exploited to localize the microrobot. Therefore, despite the strong artifact formation, the MRN architecture is able to drive the magnetic microrobot along the planned path (see Fig. 19). The results illustrate that an MRI device is able to control efficiently a bolus of aggregates.

Fig. 19

Navigation of a bolus of aggregates with a clinical MRI scanner a artifact imaging from MRI data; b observed path with external digital microscope

To assess the microrobot navigation capabilities in hepatic artery bifurcation phantom, a spherical aggregate of TMMCs with a radius of $r_0 = 250$ μm is injected into the mother channel. An average flow rate of $Q= 12\,{\text{mL}}/{\text{s}}$ has been generated using a pulsatile pump, and a gradient perpendicular to the flow switched to assist choosing a branch. For the sake of simplicity, a pre-planned isotropic navigation path is decomposed into two waypoints: one located at the bifurcation neighborhood, and the second at the end of the lower branch. Figure 20 illustrates the obtained results. These results show that despite the size of the spherical aggregate our MRN framework allows tracking in real time its position thanks to its significant magnetic susceptibility artifacts. Similar results have been obtained for chain-like and ellipsoid-like TMMC aggregates illustrated in Fig. 11. The experiments demonstrate that the use of magnetic gradient values limited to mT/m20 were sufficient to control the TMMC aggregates within a pulsatile flow of $12\,\hbox {mL}/\hbox {s}$.

Fig. 20

Magnetic resonant navigation in a hepatic artery bifurcation microchannel

Conclusion

The paper described an optimal design strategy for magnetic targeting of therapeutic drugs using magnetic SPIO particles aggregates. To propel these aggregations through the arteries (~5 mm) and small arteries (~500 μm) down to the thinner blood vessels to reach deep location in the human body requires important magnetic gradients leading to large boluses of agglomerates. To maximize the effect of the treatment and minimize adverse effects on the patient, different structures of magnetic microrobot have been addressed. As magnetic bead pulling actuation is the most efficient propulsion scheme in arteries, spherical, ellipsoidal-like, and chain-like agglomerations of TMMC are investigated and compared. It appears that chain-like structures provide the most efficient agglomerations to carry the most amount of drug. The preliminary experimental results demonstrate the relevance to use SPIO particles for targeted therapy. The experiments show that the bolus shape evolves during the navigation from spherical to ellipsoidal-like to chain-like structures, before to be break-up close to the targeted site.