Abstract
This article starts off with the observation that in certain cases, presuppositions triggered by an element inside a question nucleus may fail to project. In fact, in what looks like coordinated structures involving polar questions, presupposition projection patterns are exactly parallel to what is observed when the corresponding assertions are coordinated. The article further shows that these facts do not fall out straightforwardly from existing theories of polar questions, (apparent) coordinations of questions, and presupposition projection. It then proposes a trivalent extension of inquisitive semantics such that the observed pattern can be understood in terms of existing theories of presupposition projection. The proposal has the following properties: (a) apparent coordinations of questions are indeed coordinations of questions, and (b) the semantic denotation of polar questions is asymmetric with respect to the “yes” and “no” answers.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 How presuppositions project from polar questions
1.1 Introduction: presupposition projection and coordination
The issue of presupposition projection in coordinated structures has been the subject of a significant amount of attention within the formal semantics and pragmatics literature. The basic pattern to be explained is known at least since Karttunen (1973) and goes as follows: utterance (1) below presupposes that Syldavia is a monarchy, which means among other things that (1) can be judged to be of degraded felicity in a context where the nature of the Syldavian political system is in doubt. The presupposition is due to the presence of a trigger, here the definite DP the Syldavian monarch. When the clause in (1) occurs in an embedded context, the presupposition may or may not “project”, depending on certain factors. Of interest to us is the fact that the coordinated structures in (2) lack the presupposition that Syldavia is a monarchy.
-
(1)
The Syldavian monarch is a progressive.
-
(2)
-
a.
Syldavia is a monarchy, and the Syldavian monarch is a progressive.
-
b.
Syldavia is a republic, or the Syldavian monarch is a progressive.Footnote 1
-
a.
The lack of this presupposition for the examples in (2) is described and explained in various ways in the literature, going back in particular to the influential work of Karttunen (1973, 1974) and Heim (1983). At a minimum, an analysis of this data should derive the felicity conditions of (1) and (2) from more general assumptions about the semantics of declarative sentences, the semantics of the connectives and and or, and the semantics/pragmatics interface. For instance, Karttunen (1974) makes the following assumption about the semantics/pragmatics interface: a clause containing a trigger can be uttered felicitously if and only if its local context supports the trigger’s presupposition. He further gives rules to determine the local context of conjuncts and disjuncts, allowing us to derive that the local context of the second conjunct in (2a) will support that Syldavia is a monarchy even when the global context does not, which in turn explains why the presupposition trigger the Syldavian monarch can be used felicitously in such a global context. Heim (1983) recasts Karttunen’s (1974) analysis in a more general framework: she assumes that sentences denote Context Change Potentials (CCPs). In her model, one only has to specify how and and or string CCPs together to be able to derive the local context of every constituent clause.Footnote 2
1.2 The core data
What I am interested in here is a very similar pattern of presupposition projection that can be observed in what looks like coordinations of polar questions, rather than coordinations of declarative clauses. Consider, to begin with, the simple polar question in (3a). As is well known, (3a) presupposes that Syldavia is a monarchy, in the sense that it can be infelicitous in a context where that fact is under doubt. A similar presupposition is observed when an embedded polar question occurs in a declarative sentence, as in (3b).Footnote 3
-
(3)
-
a.
Is the Syldavian monarch a progressive?
-
b.
Mary wonders whether the Syldavian monarch is a progressive.
-
a.
The more general pattern is that a polar question, matrix or embedded, presupposes all that the corresponding declarative does — indeed, this fact is often used as a test to establish what declaratives presuppose.
English allows for what at least looks like conjunctions and disjunctions of polar questions.Footnote 4 We can investigate presupposition projection in such structures in much the same way as we do for declaratives. The result of this investigation is that presuppositions project from the second member in a coordination of questions following non-trivial patterns, and that the patterns in question are strikingly similar to what is observed for declaratives.
An example of what we will call a conjunctive question is given in (4). The apparent structure of (4) is ?p∧?q, where ? is a question-forming operator responsible for the auxiliary-fronting, p is Syldavia is a monarchy, and q is the Syldavian monarch is a progressive.Footnote 5 In spite of the fact that ?q, the second conjunct of (4), appears to be the question in (3a), the speaker who asks (4) is not understood to be presupposing that Syldavia is a monarchy. In fact, in a context where it is established that Syldavia is a monarchy, it is infelicitous to ask (4), because (4) presupposes that whether Syldavia is a monarchy is still not known.Footnote 6
-
(4)
Is Syldavia a monarchy, and is the Syldavian monarch a progressive?
Thus, in (4), the presupposition triggered by the definite DP fails to project. In this respect, (4) is just like the conjunction of assertions (2a). As in (2a), the failure to project is due in some way or other to the presence of the first conjunct; if we replace it with something unrelated, as in (5), the presupposition does project. Again as for assertions, the utterance becomes infelicitous if the order is reversed to yield ?q∧?p, as in (6).That (6) is infelicitous in any context can be explained as follows: the presupposition projects, but the second conjunct somehow triggers an ignorance inference about p, and the two inferences are incompatible. This explanation is very similar to how one can explain why (7), q∧p, is odd: the presupposition projects, but then the second conjunct is necessarily trivial.
-
(5)
Is Syldavia rich in mineral resources, and is the Syldavian monarch a progressive?
-
(6)
# Is the Syldavian monarch a progressive, and is Syldavia a monarchy?
-
(7)
# The Syldavian monarch is a progressive, and Syldavia is a monarchy.
More interestingly, we can try to replace the nucleus p of the first conjunct by a proposition \(p'\) that is (at least contextually) equivalent to ¬p, or to replace the first conjunct by an or not alternative question bearing upon the same proposition p. The reason these replacements are natural variants to test is that (8b) and (8c) intuitively raise the same issue as (8a), in the sense that the knowledge one needs in order to answer any of these three questions is the same. However, they turn out not to be interchangeable when it comes to presupposition projection: both replacement attempts, (9a) and (9b), yield sentences that are just infelicitous.
-
(8)
-
a.
Is Syldavia a monarchy?
-
b.
Is Syldavia a republic?
-
c.
Is Syldavia a monarchy or not?
-
a.
-
(9)
-
a.
# Is Syldavia a republic, and is the Syldavian monarch a progressive?
-
b.
# Is Syldavia a monarchy or not, and is the Syldavian monarch a progressive?
-
a.
The generalization that emerges is most easily phrased in terms of local contexts:
-
(10)
Generalization about conjunctive questions: In a conjunction of polar questions ?p∧?q (but not when or not questions are involved), while the local context of p is the global context, in at least some cases the local context of q is the global context enriched with p.
This generalization is entirely parallel to what Karttunen (1974) and Heim (1983) offer for the case of p∧q. It explains the felicity of (4), the infelicity of (6), the fact that the presupposition projects in (5),Footnote 7 and the infelicity of (9a) (the second conjunct’s presupposition is necessarily not met).
Let us now turn to the case of disjunctive questions. An example of what looks like a disjunction of polar questions is given in (11); we can schematize it as ?p∨?q, without committing to the idea it should be analysed that way. An immediate complication is that disjunctive questions of this sort are known to be systematically ambiguous between at least two readings. Using the terminology of Roelofsen and Farkas (2015), (11) has a closed reading where it presupposes (a) that one of John or Mary is here (exhaustiveness) and (b) that John and Mary are not both here (exclusivity). This reading is also known as the alternative question reading. The most natural way of bringing it out is to pronounce (11) with a falling intonation on the second disjunct. There is also an open reading, which is most easily made salient by having a rising intonation on the second disjunct. The open reading of (11) does not presuppose either (a) or (b), and is amenable to a negative answer (“Neither of them is here”).
-
(11)
Is John here or is Mary here?
With this distinction in mind, consider the crucial presuppositional example (12). The question in (12) can be uttered felicitously in a context where the political system of Syldavia is in doubt; in fact, as in the conjunctive case, (12) would be infelicitous otherwise.
-
(12)
Is Syldavia a republic, or is the Syldavian monarch a progressive?
These facts obtain both with the “open” and “closed” intonation, and both under the open and closed reading. Note that we do not have to rely on the intonation to disambiguate readings: specifying a richer context lets us select one or the other reading and establish the presuppositional facts as well; e.g. the discourse in (13) brings about the closed reading while the discourse in (14) brings about the open reading. In what follows, it will be helpful for the reader to keep these two discourses in mind to verify that all examples are compatible with both.
-
(13)
My conviction is that you never see a conservative monarch enacting progressive policies. With what you told me about Syldavia’s progressive laws, tell me, is Syldavia a republic, or is the Syldavian monarch a progressive? (closed reading)
-
(14)
I always thought Syldavia was a very conservative monarchy, but what I learned about their policies made me less certain about it. Tell me, is Syldavia a republic, or is the Syldavian monarch a progressive? (open reading)
Thus, in (12), as in the disjunction of assertions (2b), the presupposition triggered by the definite DP fails to project. We can in fact replicate all of the tests we applied to the conjunctive case to see how the failure to project depends on the first disjunct. An unrelated first disjunct, as in (15), fails to block projection. Reversing the order as in (16) leads to degraded felicity (the judgment is less sharp than for the conjunctive case, and in this respect questions do not differ from assertions; cf. (17)). Replacing the first disjunct by its “opposite” or adding or not, as in (18a) and (18b) respectively, leads to infelicity.
-
(15)
Is Syldavia rich in mineral resources, or is the Syldavian monarch a progressive?
-
(16)
?? Is the Syldavian monarch a progressive, or is Syldavia a republic?
-
(17)
?? The Syldavian monarch is a progressive or Syldavia is a republic.
-
(18)
-
a.
# Is Syldavia a monarchy, or is the Syldavian monarch a progressive?
-
b.
# Is Syldavia a republic or not, or is the Syldavian monarch a progressive?
-
a.
All of these observations lead us to the following generalization, which is strikingly similar to Karttunen’s (1974) generalization about disjunction in declaratives:
-
(19)
Generalization about disjunctive questions: In a disjunction of polar questions ?p∨?q (but not when or not questions are involved), under either an open or a closed reading, while the local context of p is the global context, in at least some cases the local context of q is the global context enriched with ¬p.
Thus, to conclude, presupposition projection in both (apparent) conjunctions and (apparent) disjunctions of polar questions obeys laws that are strikingly similar to those observed in conjunctions and disjunctions of declarative clauses. Yet as we are going to see, this pattern is puzzling from a theoretical point of view.Footnote 8
1.3 Some additional empirical points
A few other remarks can be made before we move on to the theoretical part of the paper. First, while we have been using matrix questions as examples, everything works exactly the same when looking at embedded questions; this is demonstrated below. In the disjunctive cases, the same ambiguity between open and closed reading is found in embedded examples, and as before it does not affect the projection facts we are interested in. In the rest of this article, we will switch between matrix and embedded examples depending on what makes a given point clearer, but as far as I can ascertain there is nothing in the discussion that does not apply equally to both.
-
(20)
Mary wonders whether Syldavia is a monarchy, and whether the Syldavian monarch is a progressive.
\(\not \leadsto \) (Mary believes that) Syldavia is a monarchy.
-
(21)
Mary wonders whether Syldavia is rich in mineral resources, and whether the Syldavian monarch is a progressive.
⇝ (Mary believes that) Syldavia is a monarchy.
-
(22)
-
a.
# Mary wonders whether the Syldavian monarch is a progressive, and whether Syldavia is a monarchy.
-
b.
# Mary wonders whether Syldavia is a republic, and whether the Syldavian monarch is a progressive.
-
c.
# Mary wonders whether Syldavia is a monarchy or not, and whether the Syldavian monarch is a progressive.
-
a.
-
(23)
Mary wonders whether Syldavia is a republic, or whether the Syldavian monarch is a progressive.
\(\not \leadsto \) (Mary believes that) Syldavia is a monarchy.
-
(24)
Mary wonders whether Syldavia is rich in mineral resources, or whether the Syldavian monarch is a progressive.
⇝ (Mary believes that) Syldavia is a monarchy.
-
(25)
-
a.
?? Mary wonders whether the Syldavian monarch is a progressive, or whether Syldavia is a republic.
-
b.
# Mary wonders whether Syldavia is a monarchy, or whether the Syldavian monarch is a progressive.
-
c.
# Mary wonders whether Syldavia is a republic or not, or whether the Syldavian monarch is a progressive.
-
a.
Second, alternative descriptions of the phenomenon that do not refer to local contexts would be possible. However, as pointed out by Schlenker (2009) (cf. also Singh 2007), when it comes to assertions, the generalization in terms of local contexts lets us predict certain cases of infelicity due to triviality effects, even in the absence of presuppositions. Such effects are also observed in polar questions. For instance, in (26a), the clause “Ann is in France” should always be in a local context where Ann is known to be in Paris, and therefore locally trivially true. Similarly in (26b), the clause “Ann is in London” should always be locally trivially false. We can therefore understand the infelicity of (26a) and (26b) in terms of our generalization.Footnote 9
Similar data can be observed in the case of disjunction, as seen in (27a) and (27b). For now, we are going to focus on the presupposition projection data; we will return to examples like (26a) and (26b) in Sect. 4.2.Footnote 10
-
(26)
-
a.
# Is Ann in Paris, and is she in France?
-
b.
# Is Ann in Paris, and is she in London?
-
a.
-
(27)
-
a.
# Is Ann away from Paris, or is she in France?
-
b.
# Is Ann away from Paris, or is she in London?
-
a.
2 Theoretical consequences and challenges
The fact that presupposition projection in coordinations of polar questions is very reminiscent of presupposition projection in coordinations of declarative clauses might seem expected. In this section, I am going to argue that it is actually puzzling, given established theories on polar questions, coordination of questions, and presupposition projection.
2.1 The need for a yes/no-asymmetry in polar questions
Some remarks can be made before we even attempt a formal analysis. To begin with, say we pursue an analysis where the following two properties hold:
-
(i)
in a conjunctive question like (4) (?p∧?q), there is actually a constituent identical or equivalent to the simple polar question (8a) (?p), as the syntax suggests;
-
(ii)
whether a presupposition triggered in a certain context projects or not is a function of the semantics of the sentence and of its subconstituents (a property true of all analyses of presupposition projection we will discuss).
If so, then we absolutely need our analysis of the simple polar question ?p to be asymmetric. What I mean by “asymmetric” here is that the semantic denotation of a polar question ?p should be such that the “yes” answer (p) and the “no” answer (¬p) do not play interchangeable roles in it. In particular, ?p and ?(¬p) should be different objects, and all three questions in (28)should be semantically distinct. The reason this is a necessity is that without a difference between these questions, there is no hope to account for the contrast between (4), on the one hand, and (9a) and (9b), on the other hand (a similar point can be made with the disjunctive examples).
-
(28)
-
a.
Is Syldavia a monarchy?
-
b.
Is Syldavia a republic?
-
c.
Is Syldavia a monarchy or not?
-
a.
The significance of this point comes from the fact that polar questions are frequently assigned denotations that are “yes/no-symmetric”, e.g.:
-
(29)
-
a.
in Hamblin semantics: {p,¬p};
-
b.
in partition semantics: \(\lambda w.\, \lambda w'.\, p(w) = p(w')\);
-
c.
in inquisitive semantics: {s | s⊢p∨s⊢¬p}.
-
a.
Such theories make (28c) indistinguishable from (28a), and make (28b) contextually equivalent to the other two, which is problematic given that these are not interchangeable as far as the phenomenon we are looking at is concerned. We therefore need a more fine-grained view of polar questions.
It is important to mention that the fact that there exist yes/no-asymmetries around polar questions is well known, at least since Bolinger (1978). Some specific asymmetric phenomena that have been studied include discourse patterns, both in terms of felicity conditions (e.g. Biezma and Rawlins 2012) and future discourse potential (e.g. Roelofsen and Farkas 2015), as well as epistemic and evidential biases (e.g. Büring and Gunlogson 2000; Sudo 2013). These authors acknowledge the need for asymmetric representations of questions in order to account for the phenomena at hand. What is generally assumed, however, is that symmetric denotations of the kind shown above are adequate to account for the resolution conditions of polar questions, even if they might not be an adequate representation of question meaning in general. Under this view, what our data tells us is that presupposition projection in questions and/or the mechanisms of question coordination cannot be derived purely from resolution conditions.Footnote 11
2.2 The failure of a direct reduction to the declarative case
A second remark has to do with the way we have to analyse the connectives. As already noted, the presupposition projection patterns we observe are very similar to those observed in the declarative case. Additionally, the basic facts we started from about how presuppositions project from declarative conjuncts and disjuncts are widely agreed-upon, and a large and diverse array of theories have been devised to derive them. If we can reduce our cases of “conjunctive questions” and “disjunctive questions” to conjunctions or disjunctions of declaratives, then said theories are going to make predictions about presupposition projection, which we might hope will match the observed pattern.
There is in fact an independent reason why we might want to reduce our examples to coordinations of assertions. The point would be to avoid committing to the fact that questions can be conjoined or disjoined at all. While the basic truth-conditional effect of and and or when acting upon declaratives is relatively well understood, there is much less of a consensus on what they do to questions. In various existing theories of questions, the meaning that should be assigned to and, to or, or to both to get non-degenerate results is unclear, or does not clearly relate to the declarative meaning, or there is a lack of uniformity between what has to be assumed for and and for or. Because of these pervasive issues, it has been proposed that questions can be conjoined but not disjoined, or at least not directly (e.g. Szabolcsi 1997; though see Szabolcsi 2016 and Ciardelli et al. 2018, Sect. 9.2.2 for counterpoints), or that they can be disjoined but not directly conjoined (e.g. Hirsch 2017), or that they can be neither directly conjoined nor directly disjoined (e.g. Krifka 2001).
In these accounts of question coordination, which I am going to refer to collectively as the reductionist view, an apparent coordination of questions can always be paraphrased as a coordination of declaratives. For instance, one would analyse (30a) in such a way that it is equivalent to either (30b) or (30c), and (31a) in such a way that it is equivalent to (31b) or (31c).Footnote 12
-
(30)
-
a.
Mary wonders whether John is here and whether it’s raining.
-
b.
Mary wonders whether John is here, and she wonders whether it’s raining.
-
c.
Mary wonders whether it is the case that John is here and it’s raining.
-
a.
-
(31)
-
a.
Mary wonders whether John is here or whether it’s raining.
-
b.
Mary wonders whether John is here, or she wonders whether it’s raining.
-
c.
Mary wonders whether it is the case that John is here or it’s raining.
-
a.
Unfortunately, such approaches do not lead to a satisfactory account. The low-scope strategy spelt out by (30c) and (31c) would make the presupposition projection facts unremarkable: the question nucleus would be a conjunctive or disjunctive proposition that is well known to lack a presupposition, and making a question out of this proposition should not change this. However, the problem is that our examples are not actually polar questions, or at the very least, some of the readings they allow for are not polar, and yet the presuppositions still fail to project. If (4) were a polar question, then the asker should be satisfied upon being told by a fully knowledgeable answerer that Syldavia’s leader is a conservative, without being told whether we are talking about a monarch or a president. This is wrong: someone who asks (4) wants to actually know whether Syldavia is a monarchy or a republic. Similarly for the disjunctive case (12): we expect the asker to be satisfied upon being told that Syldavia cannot possibly have a conservative monarch. Under the open reading, such an answer is actually judged to be incomplete, and only felicitous if it is all the answerer knows. Under the closed reading, the answer is completely infelicitous, which is fully expected given that the asker is already presupposing the fact in question. Thus, if either of our examples has a polar reading at all, it is not very salient, and the lack of presupposition projection that we observe is not dependent on it.Footnote 13
The high-scope strategy for conjunctive questions, as spelt out by (30b), has been argued to predict adequate truth conditions in general (Krifka 2001; Hirsch 2017). For disjunctive questions, it has been proposed as an analysis of certain cases of disjunctive constituent questions (e.g. Xiang 2021). However, as already pointed out by Hoeks and Roelofsen (2019), the resulting truth conditions are clearly wrong in the case of disjunctive polar questions: on its most natural reading, (31a) is not a wide-scope disjunction (it does not suggest speaker ignorance) and it does not indicate a disjunctive desire on Mary’s part.Footnote 14 Regardless of the truth conditions, in both the conjunctive and disjunctive cases, the high-scope strategy makes incorrect predictions about presupposition projection. Indeed, various theories of presupposition projection agree that “ϕ and ψ”, where ϕ and ψ are declarative sentences, is felicitous whenever the presuppositions of ϕ are satisfied, and it is sufficient to grant ϕ to satisfy the presuppositions of ψ (I am ignoring here any issues related to the so-called proviso problem, as they do not affect the discussion as far as I can tell). Applying this to our conjunctive example (20), we predict that it should be felicitous in a context where, if we come to know that Mary wonders whether Syldavia is a monarchy, then we can grant that Syldavia is a monarchy. Such a context is extremely odd, and we clearly do not need to accommodate it to accept (20). Similarly, in the disjunctive example, we predict the presupposition not to project as long as, if Mary does not wonder whether Syldavia is a republic, then she believes that Syldavia is a monarchy—which again is not a context that one needs to accommodate to accept (23).Footnote 15
To conclude, the low-scope reductionist view delivers inadequate polar interpretations for the questions we are looking at. The high-scope reductionist view makes specific predictions about presupposition projection, as long as we accept well-established facts about presupposition projection in declaratives, but these predictions do not bring us any closer to an explanation of what we observe. All this suggests that our data is problematic for reductionist accounts of question coordination, and that explaining this data will require that we actually engage with question semantics and with the thorny issue of question coordination.Footnote 16
2.3 Taking a broader look: our desiderata
In the previous two sections, I developed an argument that an analysis of our data should have the following two properties: it should feature a yes/no-asymmetric representation to polar questions, and it should not adopt a reductionist view of question coordination.
Some other properties are arguably desired in any account of question coordination. The effect of and and or when acting upon questions should relate in a natural way to their effect when acting upon propositions. Ideally, said relation should be the same for conjunction and for disjunction. The syntax we assume should be what we observe: two polar questions, each with auxiliary inversion or in embedded cases with whether, connected by and or or; in other words, ?p∧?q and ?p∨?q. Deviating from these requirements means that we need to assume a more complicated syntax/semantics interface. It might of course turn out that we need to violate some of them, but such a move requires good motivation.
Additionally, we want to account for the actual meaning of conjunctive and disjunctive questions (both open and closed), in terms of answerhood conditions, behaviour under embedding, and so on. This goes both as far as our specific examples are concerned and in the general case. The effect of or not should be explained as well.
The desiderata we listed so far bear entirely on the analysis of questions and of the question connectives that we adopt, and do not relate to the matter of presupposition projection directly. As I already mentioned, presupposition projection in declaratives is the subject of a large number of theories in the literature. These accounts have the following structure: they provide a system where the presuppositions of a complex declarative sentence can be derived from those of simpler sentences based on a few (ideally motivated) assumptions about the semantics/pragmatics interface and the denotation of sentences. Our goal here is to apply this methodology to questions. As we have seen above, we cannot get away with a reduction of our data to the sort of data that these theories have been designed to explain. However, we can still attempt to extend them in the most natural way. Concretely, what we want is to adopt the assumptions of an established theory of presupposition projection, apply them to an account of polar questions and coordinated questions, and derive the observed projection patterns.
How to do this, for a particular theory of presupposition projection and a particular theory of question semantics, is not necessarily obvious. In particular, it is difficult to extend a dynamic theory of presupposition projection, such as that of Heim (1983), to a static account of questions. In what follows, I am instead going to focus on theories of presupposition projection that are based on a static system, such as Schlenker’s (2008) Transparency Theory (and the related derivation of local contexts he offers in Schlenker (2009)), and what I am going to refer to as the trivalent theory (Beaver and Krahmer 2001; George 2014). The fact that these theories are based on a static and truth-conditional view of propositions will make it easier to extend them to various theories of questions.
My purpose in the rest of this section is to highlight the pervasive issues that one encounters when applying the methodology I described to various established accounts of questions. The end goal is to motivate a new approach to question semantics, which will be detailed in the next section. We will proceed in the following way: first, in Sect. 2.4, we will review in detail how one could try to understand the phenomenon at hand within the framework of Hamblin/Karttunen (H/K) semantics. Then, in Sect. 2.5, I will briefly show how parallel issues to those that arise for H/K semantics arise in other major theories as well. This will motivate the presentation of a new theory of questions in Sect. 3.
2.4 Case study: an analytical attempt based on answer set semantics and the Transparency Theory
Probably the most common approach in question semantics is to analyse questions as denoting a set of answers. This approach is known as the answer set theory or as Hamblin-Karttunen semantics, after Hamblin (1976) and Karttunen (1977). I will now attempt an analysis of our data within H/K semantics, in order to show the many issues that arise.
The basic idea of H/K semantics is that a question is at some level a set of propositions, and these propositions are construed as the possible answers to the question. Asking a question means prompting the participants in the conversation to identify one of the propositions as true. There are various implementations of the idea. In a thread of work based on Hamblin’s (1976) system, a question’s denotation is simply the set of all its possible answers, regardless of the present situation. In contrast, under the approach of Karttunen (1977), questions have an intension and an extension, and the extension is the set of true answers at the current world. We are going to adopt Hamblin’s view here for the sake of concreteness, but the choice does not really matter: the two systems map onto each other in a way that preserves the properties of interest to us (a formalization of this is offered in the Appendix, where both Hamblin’s and Karttunen’s systems are considered).
Presupposition projection
In what follows, I will assume that presupposition projection is governed by the Transparency Theory, for the sake of concreteness. My claim is that this choice is not crucial. The discussion can easily be recast in terms of local contexts or in trivalent terms, and in the Appendix I derive several formal results that illustrate the points made in the discussion in both the Transparency Theory and George’s (2014) trivalent theory. Moreover, at least certain dynamic accounts of presupposition projection would face very similar issues when being extended to questions.Footnote 17
I will not describe the Transparency Theory in full detail here, and only say how it applies to the examples: the Appendix contains proofs of some of the relevant formal results, as well as parallel results for trivalent theories of presupposition projection. The Transparency Theory’s predictions derive from a notion of contextual equivalence over sentence denotations. Thus, to apply this theory to questions, we need a notion of contextual equivalence over the domain of questions. The simplest possible one goes like this: two questions are equivalent if the sets that they denote are equal after each member proposition is contextually restricted. We can use this simple notion to derive the results discussed here; cf. the Appendix for a formal definition (under the name H-equivalence) as well as potential alternatives.
General considerations
In theories based on Hamblin (1976), a polar question like (32a) (repeated from (8a)) is traditionally analysed as denoting the two-element set in (32b). This analysis is based on the fact that the two propositions in (32b) are intuitively perceived to be the two ways one may felicitously answer (32a). More generally, one will analyse the polar question we schematize as ?p as denoting {p,¬p}.
-
(32)
-
a.
Is Syldavia a monarchy?
-
b.
{That Syldavia is a monarchy,That Syldavia is not a monarchy}
-
a.
Sets being unordered objects, ?p = {p,¬p} is indistinguishable from ?(¬p) (at least under a classical view of negation where it is involutive). Thus at first look, the traditional view in H/K semantics fails to meet one of our desiderata: it does not analyse polar questions in a yes/no-asymmetric way. However, in some accounts of the internal syntax of disjunctive and polar questions, there is a yes/no-asymmetric intermediate constituent with the type of a question, which is the entity that is assumed to be engaging in disjunction. In particular, Biezma and Rawlins (2012) propose that a polar question ?p really denotes the singleton set {p} rather than a two-element set, and that an additional “coercion operation” is responsible for adding ¬p to the set. In a very similar way, Karttunen (1977) offers a syntax involving a “proto-question” constituent whose denotation is the equivalent of {p} (translating from his system to Hamblin’s). The negative proposition is added by a special semantic rule. In both theories, while the denotation of a plain polar question is yes/no-symmetric, question coordination can involve yes/no-asymmetric (proto-)questions, and thus our desideratum is met.
For purposes of illustration I am going to give the sketch of an analysis in this vein. Proto-questions are formed by a question operator ? such that ?p = {p}. Then, a closure operator  , defined in (33), can apply. This operator generalizes the coercion operation of Biezma and Rawlins (2012) and the semantic rule of Karttunen (1977). What it does is add a “catch-all” answer to a question denotation — an answer that is true when all pre-existing answers are false. In particular, applied to {p}, it will give {p,¬p}. The definition given here is sufficiently general that the operator
, defined in (33), can apply. This operator generalizes the coercion operation of Biezma and Rawlins (2012) and the semantic rule of Karttunen (1977). What it does is add a “catch-all” answer to a question denotation — an answer that is true when all pre-existing answers are false. In particular, applied to {p}, it will give {p,¬p}. The definition given here is sufficiently general that the operator  could in principle apply to non-singleton sets as well. Neither Karttunen (1977) nor Biezma and Rawlins (2012) allow for this possibility, but it will prove worth considering for our purposes.
could in principle apply to non-singleton sets as well. Neither Karttunen (1977) nor Biezma and Rawlins (2012) allow for this possibility, but it will prove worth considering for our purposes.
-
(33)
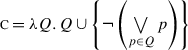
Following Karttunen (1977) as well as Biezma and Rawlins (2012), we assume that  is optional in at least some cases; in particular, we assume that while a plain polar question is essentially
is optional in at least some cases; in particular, we assume that while a plain polar question is essentially  , a disjunctive question might be just ?p∨?q.Footnote 18
, a disjunctive question might be just ?p∨?q.Footnote 18
It would be most natural to assume that and and or denote set intersection and set union respectively when applied to questions. For disjunction, this is indeed the assumption that is generally made in H/K semantics. However, for conjunction, such an assumption leads to degenerate results. In most cases, the two questions being conjoined are disjoint sets; there is no proposition that is an answer to both, and therefore their intersection is an empty set. We cannot hope to derive the felicity and answerhood conditions of conjunctive questions from the empty set. Because of that, one either needs to adopt a reductionist view of conjunction, or to assume that conjunction of questions applies pointwise inside the set. All this leaves us with the following definitions of question conjunction and disjunction:
-
(34)
-
a.
\(Q \land Q' = \{p \land p' \,|\, p \in Q, p' \in Q'\}\)
-
b.
\(Q \lor Q' = Q \cup Q'\)
-
a.
H/K semantics thus fails to fulfil another of our desiderata: the treatment of question conjunction and question disjunction is not uniform. This is disappointing in itself, inasmuch as it makes the syntax-semantics interface less transparent.Footnote 19 Additionally, it entails that we cannot hope to derive the presupposition projection patterns similarly for conjunction and disjunction, and therefore that the similarity between what is observed in questions and in declaratives will turn out to be a coincidence. This is an instance of a more general problem with H/K semantics, where the lack of parallelism makes the system not well-behaved from a formal perspective, leading to the impossibility of deriving formal properties and to strange predictions in edge cases (see Ciardelli et al. 2017 for a discussion of this point).
Conjunctive questions
These concerns aside, let us move to an account of presupposition projection in coordinated questions. We have the following building blocks: polar questions denoting singleton sets, conjunction and disjunction as defined above, and the closure operator  .
.
The most common analysis of a conjunctive question with the apparent structure of ?p∧?q in H/K semantics is that it should denote a 4-element set: {p∧q,p∧¬q,¬p∧q,¬p∧¬q}. I will call this set the quadripartition. The quadripartition leads to the prediction that the answerer to a conjunctive question has to specify the truth values of both propositions, resulting in four mutually exclusive answers. The received view is that this is indeed what conjunctive questions generally mean.
Recall that in the theory sketched above, ?p = {p}, ?q = {q}, and ∧ applies pointwise. Additionally,  may apply on top of question-type constituents. We can therefore generate the quadripartition if we assume that
may apply on top of question-type constituents. We can therefore generate the quadripartition if we assume that  applies to both conjuncts separately, resulting in a structure like
applies to both conjuncts separately, resulting in a structure like  .
.
Yet, the quadripartition is problematic for us. To predict the filtering observed in (35) (repeated from (4)), we would want the proposition expressed by p (that Syldavia is a monarchy) to be transparent in the position of q (the second conjunct’s nucleus). However, it is easy to verify that it is not; in fact, nothing non-trivial is transparent in the position of q in  in any context (cf. the Appendix for a proof). Regardless of the presupposition projection theory we adopt, we know at any rate that the quadripartition will not let us derive the observed pattern, because it is not yes/no-asymmetric: substituting ¬p for p in the quadripartition does not change the set.
in any context (cf. the Appendix for a proof). Regardless of the presupposition projection theory we adopt, we know at any rate that the quadripartition will not let us derive the observed pattern, because it is not yes/no-asymmetric: substituting ¬p for p in the quadripartition does not change the set.
-
(35)
Is Syldavia a monarchy, and is the Syldavian monarch a progressive?
Consequently, our data is problematic for the view that conjunctive questions always denote the quadripartition. It is also problematic for answer set theories not based on proto-questions, and where polar questions always denote {p,¬p}, as in these theories the quadripartition is the only thing that a conjunctive question could denote. In our system, however, it is possible to generate other denotations, as long as we give ourselves as much freedom as we want and allow for  to apply to any question-type constituent. This allows us to generate six alternative denotations for (35), which are listed in (36).Footnote 20 This wide use of
to apply to any question-type constituent. This allows us to generate six alternative denotations for (35), which are listed in (36).Footnote 20 This wide use of  is of course not at all in the spirit of Karttunen (1977) and Biezma and Rawlins (2012), for whom
is of course not at all in the spirit of Karttunen (1977) and Biezma and Rawlins (2012), for whom  is a last-resort coercion rule.
is a last-resort coercion rule.
-
(36)
-
a.
?p∧?q = {p∧q}
-
b.

-
c.

-
d.
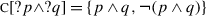
-
e.
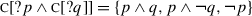
-
f.
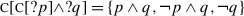
-
a.
Options (a), (b), and (c) are uninteresting. (a) leads to a question with only one possible answer; such a question is presumably not well-formed. (b) and (c) should correspond to readings where the answer to one of the conjuncts is presupposed, which is presumably banned on pragmatic grounds.
Option (d) leads to a yes/no question. We have already seen when discussing the reductionist view that (35) is not, or at least does not have to be, a yes/no question.
Option (f) is yes/no-symmetric as well (with respect to the first conjunct), leaving us with option (e). Option (e) is in fact what we want. First, p is transparent in the position of q. Intuitively, this is because in the denotation, “q” always appears somewhere after “p∧”.Footnote 21 We therefore correctly predict (4) to lack a presupposition that Syldavia is a monarchy.Footnote 22 Furthermore, the three mutually exclusive propositions in the set, which I will refer to as the tripartition, correspond exactly to the possible answers to (35):
-
(37)
-
a.
Syldavia is not a monarchy. (¬p)
-
b.
Syldavia is a monarchy and/but the Syldavian monarch is not a progressive. (p∧¬q)
-
c.
Syldavia is a monarchy and the Syldavian monarch is a progressive. (p∧q)
-
a.
Thus, what we now have is a new analysis for conjunctive questions within H/K semantics, schematized by (e), such that both the presupposition projection facts and the answerhood conditions of (35) are easily understood.Footnote 23
In my view, the analysis in question is not entirely satisfactory. Other than the general problems with H/K semantics and pointwise conjunction I mentioned above, the main issue is with the asymmetric structure of (e). This asymmetry raises a number of challenges if we make the natural assumption that  is in the syntax and that it is some sort of complementizer. First, assuming that coordination can only occur between constituents of the same category, we need to explain why a constituent like
is in the syntax and that it is some sort of complementizer. First, assuming that coordination can only occur between constituents of the same category, we need to explain why a constituent like  is at all possible. Second, we need to explain why (e) is allowed, whereas the alternative tripartition in (f), which is not attested, is not. Even the polar reading predicted by (d) might have to be ruled out, as the evidence for such a reading is scarce.Footnote 24 Finally, it is puzzling that nothing in the surface syntax of (35) suggests there is left/right asymmetry in the structure. This is probably why, to my knowledge, the possibility of something like (e) (or (f)) has in fact never been considered worth discussing before.Footnote 25 None of these problems is insurmontable, but they will require us to complicate the syntax, or else to find another analysis of the mechanism responsible for the operation performed by
is at all possible. Second, we need to explain why (e) is allowed, whereas the alternative tripartition in (f), which is not attested, is not. Even the polar reading predicted by (d) might have to be ruled out, as the evidence for such a reading is scarce.Footnote 24 Finally, it is puzzling that nothing in the surface syntax of (35) suggests there is left/right asymmetry in the structure. This is probably why, to my knowledge, the possibility of something like (e) (or (f)) has in fact never been considered worth discussing before.Footnote 25 None of these problems is insurmontable, but they will require us to complicate the syntax, or else to find another analysis of the mechanism responsible for the operation performed by  where they become easier to deal with.
where they become easier to deal with.
To conclude, while H/K semantics provides the necessary ingredients to understand our cases of conjunctive questions, doing so requires non-standard assumptions about conjunctive questions’ internal composition (with unconstrained, asymmetric application of a closure operation), so as to allow them to be interpreted as a tripartition, and possibly suffers from an overgeneration of readings.
Disjunctive questions
We can apply the same methodology to our disjunctive example (38) (repeated from (12)). The most common analysis of closed disjunctive questions (alternative questions) within H/K semantics is that a question with the apparent structure ?p∨?q denotes {p,q}, based on the intuition that the two potential answers to the question are the two disjuncts (cf. discussion by Roelofsen and Farkas 2015). Both Karttunen (1977) and Biezma and Rawlins (2012) essentially adopt this view.
-
(38)
Is Syldavia a republic, or is the Syldavian monarch a progressive?
Assuming that disjunction is set union, {p,q} can easily be derived as the direct disjunction of the proto-questions {p} and {q}, i.e. ?p∨?q. This is in fact part of the motivation for proto-questions: if a polar question denoted {p,¬p} from the get-go, a disjunction of two such questions would be {p,¬p,q,¬q}. Yet there is no reading of disjunctive questions such that the set of felicitous answers is this 4-element set. For instance, a fully knowledgeable speaker cannot cooperatively answer “John is not here” (¬p) to (39), whatever the intonation.
-
(39)
Is John here, or is Mary here?
The version of H/K semantics we are working with here partially solves the problem by allowing for ?p∨?q = {p,q}. We do generate  , but we can rule it out by assuming a unique-answer constraint: at every contextually permissible world, there should be exactly one answer that is true. It can be verified that there is no context where {p,¬p,q,¬q} satisfies this constraint without making some of the answers trivially false in the context (see Hoeks and Roelofsen (2019) for extensive discussion of the interaction between disjunctive questions and various refinements of the unique-answer constraint).
, but we can rule it out by assuming a unique-answer constraint: at every contextually permissible world, there should be exactly one answer that is true. It can be verified that there is no context where {p,¬p,q,¬q} satisfies this constraint without making some of the answers trivially false in the context (see Hoeks and Roelofsen (2019) for extensive discussion of the interaction between disjunctive questions and various refinements of the unique-answer constraint).
The open reading of disjunctive questions has been the subject of less theorizing, as it is often mischaracterized as a polar reading. As Roelofsen and Farkas (2015) argue, the open reading is not polar and in fact allows for three possible answers corresponding to the disjuncts (p, q) and to their joint negation (¬p∧¬q). The natural analysis, therefore, is {p,q,¬p∧¬q}. We can generate it as  , as Roelofsen and Farkas (2015) propose (they work within the framework of inquisitive semantics, but the variant of H/K semantics that we are using here is close enough that the analysis carries over).Footnote 26
, as Roelofsen and Farkas (2015) propose (they work within the framework of inquisitive semantics, but the variant of H/K semantics that we are using here is close enough that the analysis carries over).Footnote 26
We therefore have two potential denotations, {p,q} and {p,q,¬p∧¬q}. Unfortunately for us, neither of them leads to an immediate explanation of the projection facts. Recall that in the conjunctive case, the key property that we could capitalize on, under the Transparency Theory but also under other theories of presupposition projection, is that q always appeared after “p∧” in the denotation. There is no similar property in either of our proposed denotations: q appears on its own.Footnote 27 This translates into a failure of transparency: for ¬p to be transparent in the position of q in either case, a necessary condition is that {p,q} = {p,¬p∧q} for any arbitrary proposition q (cf. also the Appendix). There is no reason for this to be the case in any realistic example.
At this point, one might remark that the notion of question equivalence that we have been using so far is naïve and excessively fine-grained. To fix this, first, we would have to define equivalence relative to a context, as Schlenker (2008) in fact does. Additionally, we might want to take the unique-answer presupposition into account. There are many natural approaches that one could think of to that effect — Schlenker’s theory as laid out in Schlenker 2008 does not cover the case of multiple sources of presupposition in the same sentence — and in the Appendix I prove for a number of them that they do not let us derive the desired result. Thus (12)/(38) remain entirely mysterious from the perspective of H/K semantics and the Transparency Theory.
In the end, H/K semantics lets us explain presupposition projection in conjunctive questions under the Transparency Theory (among others), if we are ready to make certain ad hoc assumptions on question composition. More problematically, while there is a natural analysis for open and closed disjunctive questions within H/K semantics, the observed presupposition filtering does not follow in a similar, mostly theory-neutral way, and neither does engaging in detail with the Transparency Theory (as is done in the Appendix) let us derive it. At any rate, the fact that conjunctive and disjunctive questions receive a very different treatment and that considerations from one case do not extend straightforwardly to the other is unsatisfactory, given that we hope to explain the parallelism between questions and assertions. Thus, given the desiderata exposed above, our data is problematic for the H/K analysis of polar questions, even in its proto-question-based yes/no-asymmetric form.
2.5 Other theories in question semantics
We have seen that our data is puzzling from the perspective of the answer set theory of questions. We are naturally prompted to look for alternative views on question semantics that do not suffer from the same problems as H/K semantics. While I lack the space to review these views at the same level of detail, I will discuss the most common approaches here and show that largely the same issues arise.Footnote 28
Questions as partitions
Groenendijk and Stokhof (1984) propose (as a component of a more complex theory) an analysis of questions based on the following intuition: what questions contribute to the conversation is that they raise an issue, and the issue is a partition of the logical space. Thus, the denotation of a question will be a partition, represented in the form of an equivalence relation over possible worlds (type s→s→t). Two worlds are related if and only if they resolve the issue in the same way. Concretely, this will be the denotation of a polar question ?p:
-
(40)
λu. λv. p(u)=p(v)
The partition theory fails to meet our desiderata in a more fundamental way than H/K semantics. First, the denotation of a polar question is yes/no-symmetric: substituting ¬p for p in (40)would keep the object unchanged. Unlike in the answer set theory, there is no obvious fix without deeply changing the account. A related fact is that a conjunction of two questions will denote what I have called earlier the quadripartition, where the desired transparency property does not obtain, and there is no obvious way to derive the tripartition that we want. Finally, since a disjunction of equivalence relations is not in general an equivalence relation, the partition theory predicts that disjunctions of questions will be ill-formed. It therefore needs to resort to reductionist techniques to analyse question disjunction; we have seen why this is problematic for our purposes.
Inquisitive semantics
Inquisitive semantics (Ciardelli et al. 2013) is a framework in which questions and assertions are analysed as having the same type. Both are sets of sets of worlds, construed as the epistemic states that resolve the question or make the assertion true. Concretely, a proposition p is the set of sets of worlds such that p is uniformly true in the classical sense, as in (41a). Here “s⊢p” is to be read as “s supports p” and means that all worlds in s are p-worlds. I will write P for the inquisitive denotation to distinguish it from the classical one, and I will use Q, \(Q'\), etc. for abstract variables denoting inquisitive propositions, even though that is not standard practice. A polar question over proposition P is assumed to have the structure ?P, where ? is an operator defined in (41b), which adds to its argument all the sets that have no intersection with anything in it. The result is given in (41c). Notice that P is yes/no-asymmetric, but ?P is not.
-
(41)
-
a.
P = {s | s⊢p}
-
b.
\(? = \lambda Q.\, Q \cup \{s \,|\, \forall s'\in Q.\, s \cap s' = \varnothing \}\)
-
c.
?P = {s | s⊢p}∪{s | s⊢¬p}
-
a.
The structure of the analysis is actually extremely similar to our version of H/K semantics. The basic denotation of a question/assertion is yes/no-asymmetric and derives directly from the corresponding proposition. Then, an additional operator adds the negative case. (42)gives an helpful translation table from H/K semantics to inquisitive semantics; notice that the main innovation at this point is the loss of the distinction between propositions and proto-questions.
-
(42)
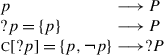
Taking the maximal elements (under set inclusion) in an inquisitive proposition, called the alternatives, in fact lets us perform the opposite translation to H/K denotations. The operator  defined in (43)does just that.
defined in (43)does just that.
-
(43)
-
a.
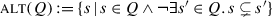
-
b.
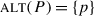
-
c.
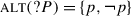
-
a.
Unlike H/K semantics, inquisitive semantics allows for parallel definitions of conjunction and disjunction as set intersection and set union respectively, which, as we already discussed, is desirable from a theoretical perspective. Relative to the H/K definitions, the inquisitive connectives do the same thing to alternatives in simple cases, and where they differ, the inquisitive behaviour has been argued to be preferable (Ciardelli et al. 2017). The definitions are given in (44).
-
(44)
-
a.
\(Q \land Q' = Q \cap Q'\)
-
b.
\(Q \lor Q' = Q \cup Q'\)
-
a.
Unfortunately, even though I made such uniform definitions part of our desidarata, in this case the uniformity does not bring us any closer to understanding presupposition projection. In fact, the discussion of H/K semantics above carries over almost entirely to inquisitive semantics, translating the structures as per (42) and using  to recover the predicted answers. For conjunctive questions, ?P∧?Q is the quadripartition, and we need ?(P∧?Q) to get the desired tripartition and transparency to obtain. The treatment of disjunctive questions is again not uniform with that of conjunctive questions: ?P∨?Q has to be ruled out on semantic or pragmatic grounds (Hoeks and Roelofsen 2019) and we most naturally analyse alternative questions as P∨Q and open disjunctive questions as ?(P∨Q) (Roelofsen and Farkas 2015). Either way, we do not straightforwardly get transparency.
to recover the predicted answers. For conjunctive questions, ?P∧?Q is the quadripartition, and we need ?(P∧?Q) to get the desired tripartition and transparency to obtain. The treatment of disjunctive questions is again not uniform with that of conjunctive questions: ?P∨?Q has to be ruled out on semantic or pragmatic grounds (Hoeks and Roelofsen 2019) and we most naturally analyse alternative questions as P∨Q and open disjunctive questions as ?(P∨Q) (Roelofsen and Farkas 2015). Either way, we do not straightforwardly get transparency.
In fact, by switching to inquisitive semantics we might even have lost our explanation of presupposition projection in assertions, at least within the theories of presupposition projection that we focus on here. When we derive why the Transparency Theory predicts a presupposition to the effect that ¬p is true to be satisfied in the second disjunct of p∨q, the following property is crucial: p∨⊤ = p∨¬p, where ⊤ is a tautology (cf. Schlenker 2008). This property does not hold in inquisitive semantics (here Ω is the set of all worlds and \(\mathcal{P}\) maps sets to their powerset).
-
(45)
-
a.
\(P \lor \top = \{s \,|\, s \vdash p\} \cup \mathcal{P}(\Omega ) = \mathcal{P}(\Omega )\)
-
b.
\(P \lor \neg P = \{s \,|\, s \vdash p\} \cup \{s \,|\, s \vdash \neg p\} = ?P \neq \mathcal{P}(\Omega )\)
-
a.
A similar problem will arise when we derive local contexts in the manner of Schlenker (2009) or when we derive trivalent connectives in the manner of George (2014). The natural way around this issue is to look at the logical properties of !(P∨Q) rather than P∨Q; in inquisitive semantics, !(P∨Q) is essentially a classical disjunction. However, since the presence of the operator ! is assumed to be specific to assertions, predicating our derivation of projection facts upon it makes it so that our analysis does not extend to questions. Equivalently, we could say that what matters to presupposition projection is not full equivalence between propositions, but rather informational equivalence (the notion obtained by ignoring inquisitiveness); however, this would lead to undesirable predictions and require further amendments to the system (e.g., all polar questions would become equivalent, so that we might end up predicting an absence of projection from polar nuclei).
Categorial theories
The final approach to question semantics that I will mention is the categorial approach. In categorial theories, questions are assigned a complex functional type that depends on the kind of question we are looking at. Thus a polar question might have a type isomorphic to a proposition, or a more complex type (e.g. ((st)st)st for Krifka (2001)), while a who question would be a one-place property of individuals (type e→s→t or s→e→t). The appeal is, among other things, that this allows for finer-grained distinctions than other theories. In particular, categorial theories always avoid yes/no-symmetry.
The main challenge for categorial theories is that questions behave in a way that suggests they all have the same type: they can be relatively freely coordinated, and a number of attitude verbs can embed any kind of question. In order to solve the former problem, proponents of categorial approaches usually resort to the reductionist view in its higher-order type variant (see in particular Krifka (2001) and Xiang (2021)), with the problems that we have seen. Alternatively, they fall back to one of the above theories to account for coordination and embedding. Categorial theories thus do not help us towards understanding our phenomenon.
3 A proposal: questions as trivalent inquisitive predicates
3.1 Introduction and background
In this section, I propose a novel view of what kind of object questions denote, which is rich enough to let us derive presupposition projection patterns while avoiding the issues we have encountered in our earlier attempts.
While this choice is not a necessity, it will make the motivation for the proposal and the exposition clearer if we adopt a trivalent view of propositions and presuppositions; in Sect. 4.2 we will see how the system can function with bivalent propositions as well. The trivalent approach consists in reifying presuppositions by assuming that there are three truth values: 0, to which propositions map worlds where they are false; 1, to which propositions map worlds where they are true; and #, to which propositions map worlds where their presuppositions are not satisfied. Presupposition projection can then be derived from a trivalent semantics for logical operators (Peters 1979; Beaver and Krahmer 2001; George 2014).
It is customary in the formal semantics literature to entertain two perspectives on propositions at the same time: propositions are functions from worlds to truth values but they are also sets of worlds. In a bivalent setting, these two domains are isomorphic and the mapping between them is trivial. In a trivalent setting, the domain of functions from worlds to (trivalent) truth values is richer than the domain of sets of worlds, so in what follows I will distinguish between the functional type s→t of trivalent propositions and the set type {s} of sets of worlds, as that will make certain things clearer. The operator  maps a trivalent proposition to its truth set:
maps a trivalent proposition to its truth set:
-
(46)
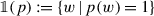
Finally, the trivalent perspective lets us define an operator that maps a trivalent proposition to “its” presupposition. This operator will be denoted as π; it is defined in (47a). Note that what π returns is a set of worlds (there is no sense in which the presupposition of a proposition could itself have a presupposition). The identity in (47b) will be useful to have in mind.Footnote 29
-
(47)
-
a.
π(p): = {w | p(w)∈{0,1}}
-
b.
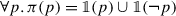
-
a.
3.2 Trivalent homogeneous polar questions
The system I present here is a trivalent theory of polar questions. We consider a polar question ?p to be a predicate over sets of worlds (construed as epistemic states). This predicate is potentially undefined: we take ?p to be defined at a state s if and only if s settles p, i.e. s supports p or ¬p. Thus:
-
(48)
\(?p = \lambda s.\, \begin{cases} 1 & \text{if $s \vdash p$,} \\ 0 & \text{if $s \vdash \neg p$,} \\ \# & \text{in all other cases.} \end{cases}\)
Here p is a trivalent proposition. As before, s⊢p is read as “s supports p” and means that p maps all worlds in s to 1. Thus s⊢¬p will hold when s maps all worlds in s to 0. If s does not support the presuppositions of p — that is, if there are #-worlds in s — neither s⊢p nor s⊢¬p can hold. There are therefore two reasons why we can have ?p(s)=#: (i) if s includes both 1-worlds and 0-worlds, i.e. s does not settle p; (ii) if s includes #-worlds, i.e. s does not satisfy the presuppositions of p. These two reasons are of course compatible with each other.
It is helpful to compare our denotation to what is assumed in inquisitive semantics. Inquisitive semantics also assumes that questions are predicates over sets of worlds, but it does not distinguish positive and negative answers. Thus, the standard inquisitive treatment of polar questions, when converted from set notation to functional notation, is essentially what is given in (49):
-
(49)
\(?_{\text{inq}}p = \lambda s.\, \begin{cases} 1 & \text{if $s \vdash p$ or $s \vdash \neg p$,} \\ 0 & \text{otherwise.} \end{cases}\)
The system I propose here can therefore be seen as an extension of the inquisitive account of polar questions. Unlike the basic inquisitive account, it assigns to them a yes/no-asymmetric denotation: ?p and ?(¬p) are different objects.Footnote 30 Also unlike the basic inquisitive account, it is integrated within a trivalent logic, making it easy to develop a theory of presupposition projection based on it, as we will see. One may wonder how the usage of the third value (#) in question denotations relates to its usual usage: is the system based on the idea that questions presuppose something? Tentatively, I submit that the fact that undecided states are mapped to # can be related to the pragmatic effect of questions, which require the addressees to address them before the conversation can move on. Thus questions arguably do presuppose that certain states will not be undecided: specifically, they presuppose that future Common Grounds will have addressed them (see also footnote 38). At this point, however, I do not have a definitive answer as to how to interpret the distinction between positive answers; I certainly do not intend here to develop a system where questions can be “true” or “false”. While I believe that this distinction could be linked to certain pragmatic phenomena, this will not be discussed here. Instead, we can presume for now that the distinction is relevant to nothing other than question coordination. The most conservative interpretation would be that it is merely a formal device.Footnote 31
The inquisitive denotation can be defined in terms of the denotation under our proposal; we call it the “domain” of a question. Intuitively, as in inquisitive semantics, the domain is the set of states where the question is resolved. Also as in inquisitive semantics (cf. (43)), we can define the “alternatives” of a question, the least specific states where the question is resolved, which correspond intuitively to the possible answers. For a polar question ?p,  will be
will be  , i.e. the denotation that is generally assumed in Hamblin-Karttunen semantics.Footnote 32
, i.e. the denotation that is generally assumed in Hamblin-Karttunen semantics.Footnote 32
-
(50)
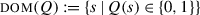
-
(51)
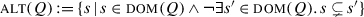
-
(52)
-
a.
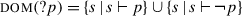
-
b.
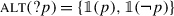
-
a.
Finally, we define an operator that maps a question to its informational commitment, the union of all states where the question is defined. Intuitively, this is (a superset of) what the questioner takes for granted (the intuition is that the questioner is assuming that the question can be resolved; we will formalize it in Sect. 3.4).
-
(53)
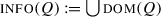
In the case of a polar question ?p,  will return the union of p’s truth worlds and p’s falsity worlds, leaving out the #-worlds. This is essentially the presupposition of p:
will return the union of p’s truth worlds and p’s falsity worlds, leaving out the #-worlds. This is essentially the presupposition of p:
-
(54)

This identity will let us derive the fact that a polar question has the same presuppositions as the corresponding assertion.
To give a concrete illustration of how all the definitions I just introduced work, consider (55a). This sentence presupposes that John once smoked. We therefore assign to it, under a trivalent view of presuppositions, the denotation in (55b). The corresponding polar question in (56a) is assigned the denotation in (56b). In (57) we see that the domain of the question is the union of the set of 1-states and the set of 0-states; these are all the subsets of the set of 1-worlds ( ) and the set of 0-worlds (
) and the set of 0-worlds ( ) respectively. The domain therefore has two maximal elements, the set of 1-worlds and the set of 0-worlds, and these constitute the alternatives as seen in (58). Finally, the informational commitment, seen in (59), is the union of the domain, which is equivalent in our case to the union of the alternatives: the set of worlds where John used to smoke and either stopped or still does, i.e. the set of all the worlds where John used to smoke.
) respectively. The domain therefore has two maximal elements, the set of 1-worlds and the set of 0-worlds, and these constitute the alternatives as seen in (58). Finally, the informational commitment, seen in (59), is the union of the domain, which is equivalent in our case to the union of the alternatives: the set of worlds where John used to smoke and either stopped or still does, i.e. the set of all the worlds where John used to smoke.
-
(55)

-
(56)

-
(57)
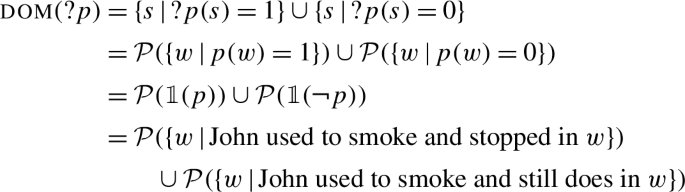
-
(58)

-
(59)

3.3 Defining the connectives
The extension of the system to conjunctions and disjunctions of polar questions is straightforward. The type we assign to questions is conjoinable, and we are going to assume that and and or apply to it directly. In a trivalent theory, there are several sensible candidates for conjunction and disjunction. Peters (1979) argues that presupposition projection patterns suggest we should adopt left/right-asymmetric connectives. These connectives are known as Peters connectives or Middle Kleene connectives (in contrast to Strong and Weak Kleene; cf. Beaver and Krahmer 2001); their definitions are given in the tables below (rows represent the left-hand argument).Footnote 33
-
(60)
\(\begin{array}{r@{\quad }|@{\quad }r@{\quad }r@{\quad }r} \land & 0 & 1 & \# \\ \hline 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \# \\ \# & \# & \# & \# \end{array} \qquad \begin{array}{r@{\quad }|@{\quad }r@{\quad }r@{\quad }r} \lor & 0 & 1 & \# \\ \hline 0 & 0 & 1 & \# \\ 1 & 1 & 1 & 1 \\ \# & \# & \# & \# \end{array}\)
Our assumption will be that question coordination obeys Middle Kleene rules. From this we immediately get a denotation for conjunctive and disjunctive questions, and we can compute their domain and therefore their resolution conditions (under the assumption that a question is resolved when a proposition in its domain is known to be true).
Here we see that the distinction between positive and negative answers, which has played no role so far, will crucially affect the denotation of coordinated questions.
3.4 Deriving presupposition projection
To give an account of presupposition projection in our system, we need a version of Stalnaker’s bridge for questions, or in other words, we need to specify what in a question’s denotation makes it felicitous to ask or not in a given context.
As mentioned above, we are going to identify the presuppositions of a question with the output of  . The motivation for this view goes as follows: in general, questions do not modify the set of worlds in the context set, but they restrict what continuations are allowed, in the sense that unless the participants contribute an assertion that addresses the question, the conversation will be at an impasse.Footnote 34 It seems natural then to consider that a speaker should not ask a question if it is not established (in the Common Ground) that the participants are capable in principle of contributing such an assertion. It should be necessary, then, that when a question is asked, the Common Ground entail that there exists a proposition that is true at the actual world and addresses the question. Going back to our system, the speaker should only utter Q if it is established that there exist states in
. The motivation for this view goes as follows: in general, questions do not modify the set of worlds in the context set, but they restrict what continuations are allowed, in the sense that unless the participants contribute an assertion that addresses the question, the conversation will be at an impasse.Footnote 34 It seems natural then to consider that a speaker should not ask a question if it is not established (in the Common Ground) that the participants are capable in principle of contributing such an assertion. It should be necessary, then, that when a question is asked, the Common Ground entail that there exists a proposition that is true at the actual world and addresses the question. Going back to our system, the speaker should only utter Q if it is established that there exist states in  that contain the actual world, or equivalently that the Common Ground supports
that contain the actual world, or equivalently that the Common Ground supports  .
.
We have already seen that  . Thus, we predict a polar question to presuppose the same thing as the corresponding assertion. This is a well-known fact, and is sometimes used as a test or even a definition for presuppositions.Footnote 35
. Thus, we predict a polar question to presuppose the same thing as the corresponding assertion. This is a well-known fact, and is sometimes used as a test or even a definition for presuppositions.Footnote 35
3.5 Conjunctive questions
We can now see what our system predicts conjunctive questions to mean.
Denotation and presuppositions
The denotation of a conjunction of questions ?p∧?q is as follows:
-
(61)
\(?p \land ?q = \lambda s.\, \begin{cases} 1 & \text{if $s \vdash p$ and $s \vdash q$,} \\ 0 & \text{if $s \vdash \neg p$ or if $s \vdash p$ and $s \vdash \neg q$,} \\ \# & \text{in all other cases.} \end{cases}\)
From this we can compute the domain and the alternatives. The domain being the downwards closure of the alternatives, it is sufficient to give the alternatives:
-
(62)
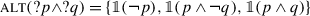
The alternatives are mutually exclusive. If p has no presupposition, they form a three-cell partition of the logical space. The three cells are essentially those I called the tripartition when discussing H/K semantics, and we have seen that they correspond intuitively to the possible answers to our presuppositional conjunctive question (4).
We can compute the predicted presupposition of a conjunctive question, as follows:
-
(63)
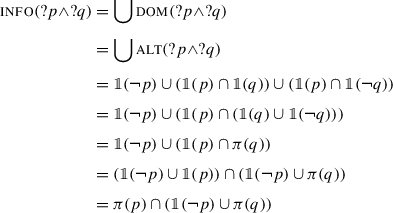
The end result is an intersection of two terms. The first term is π(p), the presupposition of p: for ?p∧?q to be felicitous, all worlds in the context therefore have to satisfy the presuppositions of p. The second term means that worlds in the context set should either make p false or satisfy the presuppositions of q. Essentially, this is equivalent to saying that they should satisfy the material conditional p→π(q). These two conditions on the context are exactly the ones that have been argued since Karttunen (1973, 1974) to describe presupposition projection in conjunctive assertions, and that I have argued in Sect. 1 to also describe presupposition projection in conjunctive questions. This is not surprising, because once we have derived the tripartition, this projection pattern follows in a fairly theory-agnostic way.
The main difference with H/K semantics and inquisitive semantics here is that the way we derive the tripartition is significantly different. In these other theories, a conjunction of polar questions ?p∧?q most naturally corresponds to what I called the quadripartition, and the tripartition can only be derived by assuming a left/right-asymmetric structure (?(p∧?q) in inquisitive semantics), if it can be derived at all. Within the present proposal, we get the tripartition from a left/right-symmetric structure because our conjunction is left/right-asymmetric in its semantics.
Contrast with earlier accounts
The reason that earlier accounts derive the quadripartition is of course not just that it naturally falls out from the formalism, but also that it is thought to be an empirically adequate characterisation of what conjunctive questions mean in general, absent presuppositional effects. It is of course desirable that we maintain this empirical coverage.Footnote 36
There are several ways in which we can derive the quadripartition in our system. First, we can assume that and may also denote a Weak Kleene trivalent conjunction. Second, we can assume there is an operator  , defined as in (64), that makes all the answers positive. If so, then
, defined as in (64), that makes all the answers positive. If so, then  (or
(or  ) would have the alternatives of the quadripartition. Finally, we can assume that whenever we think we observe the quadripartition, what we are actually seeing is two separate questions, the coordination of which takes place at the level of attitude or speech acts. The result of high-level coordination is indeed virtually indistinguishable in most cases from the quadripartition: if I know the answer to both conjuncts, I know the answer to the quadripartition. This is the basis of what we have called reductionist theories (e.g. Hirsch 2017; Xiang 2021).
) would have the alternatives of the quadripartition. Finally, we can assume that whenever we think we observe the quadripartition, what we are actually seeing is two separate questions, the coordination of which takes place at the level of attitude or speech acts. The result of high-level coordination is indeed virtually indistinguishable in most cases from the quadripartition: if I know the answer to both conjuncts, I know the answer to the quadripartition. This is the basis of what we have called reductionist theories (e.g. Hirsch 2017; Xiang 2021).
-
(64)
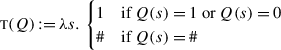
Whatever solution we adopt, we end up with a system where conjunctive questions can have the resolution conditions of either the tripartition or the quadripartition. We assume that examples of presuppositional filtering involve the tripartition; recall that because it is yes/no-symmetric, the quadripartition cannot be the basis of an analysis of this phenomenon. When there is no presuppositional trigger that forces the tripartition, conjunctive questions should in principle be ambiguous. This raises the following question: why do we generally observe quadripartitive readings, and are there counterexamples?
I would like to claim that, in an appropriate context, conjunctive questions can have the answerhood conditions of the tripartition even when no presupposition is present to force such a reading. An example is given in (65). (65a) has the form ?p∧?q, and a fully knowledgeable speaker may answer it felicitously with ¬p, even though that should be under-informative relative to the quadripartition. This tends to show that the tripartition does exist. The tripartition also predicts that ¬q as an answer should be judged uncooperative. What might in fact be the case, even though the judgment is not clear, is that ¬q as an answer implicates p. While the present account does not offer an immediate explanation for this fact, it would be impossible to derive it from the quadripartition due to its yes/no-symmetry; the tripartition does not have this problem.Footnote 37 Additionally, the quadripartition would predict that if p is replaced by \(p'\), which is equivalent to ¬p, as in (65b), then we should see no difference. What we observe is that \(p'\) becomes an uncooperative answer.
-
(65)

A related example is given in (66a). Here the context guarantees that the quadripartition cannot possibly be addressed by the participants in the conversation, while the tripartition can. A conjunctive question is perfectly felicitous, suggesting that the issue it raises is the tripartition. An advocate of the quadripartition will of course argue that we have not independently established that it is infelicitous to ask a conjunctive question that cannot be fully addressed, but if conjunctive questions always denote the quadripartition and not being able to tell between some of the cells is fine, there is no reason why reversing the order of the conjuncts as in (66b), or replacing the left-hand nucleus with its negation as in (66c), leads to infelicity.
-
(66)

Thus, the tripartition can be observed in non-presuppositional cases. What both our examples have in common is that the reason the speaker is not interested in the quadripartitive issue is clear from the context: in (65), it is more information than they need to establish whether they can carry out their plan or not, and in (66a), it is more information than the listener can possibly be knowledgeable about.Footnote 38 This suggests that the reason that most examples found in the literature lend themselves to quadripartitive readings is purely pragmatic: in the absence of an explicit context, the quadripartitive reading is more natural because it requires less specific assumptions on the speaker’s motivations. Indeed, if p and q are arbitrary, unrelated propositions, it is hard to see why a speaker would be interested in the tripartition formed from ?p∧?q, while being interested in the quadripartition is just being interested in both ?p, and ?q, possibly for different reasons.
It should be noted as a counterpoint that most speakers seem to judge matrix conjunctive questions somewhat degraded out-of-the-blue. This is puzzling if conjunctive questions can easily denote the quadripartition, which I have just argued should be easy to accept without context. It would be consistent, however, with the view that conjunctive questions always denote the tripartition, and that the quadripartition is an artefact of high-scope coordination, which might be unavailable or marked in matrix questions.
Another counterpoint is that apparent quadripartitive readings of conjunctive questions do not necessarily constitute strong evidence that these questions denote the quadripartition. First, it is in general felicitous for answerers to provide more information than the questioner was explicitly asking for. (67)is a felicitous dialogue and is not taken to provide evidence that B’s utterance is a semantic answer to A’s question. Thus the fact that a conjunctive question ?p∧?q can generally be answered with ¬p∧¬q is not necessarily incompatible with a tripartitive analysis. In contrast, being less precise than was asked is not felicitous in general, which is why (65) is puzzling from a quadripartitive perspective.
-
(67)
A: Is the weather nice outside?
B: Yes, but there is no charcoal left.
3.6 Disjunctive questions
Disjunctive questions work very similarly.
Denotation and presuppositions
We derive for them the following denotation and alternatives:
-
(68)
\(?p \lor ?q = \lambda s.\, \begin{cases} 1 & \text{if $s \vdash p$ or if $s \vdash \neg p$ and $s \vdash q$,} \\ 0 & \text{if $s \vdash \neg p$ and $s \vdash \neg q$,} \\ \# & \text{in all other cases.} \end{cases}\)
-
(69)
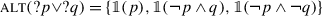
The predicted presupposition is derived as follows:
-
(70)
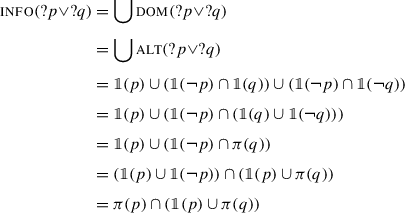
The only difference with conjunction is that we have p instead of ¬p in the second term. Thus, we again predict the presuppositions of p to project, but the material conditional that should hold throughout the context set is now ¬p→π(q) rather than p→π(q). Once again, these contextual requirements are exactly what Karttunen (1973, 1974) argues should be derived for disjunctive assertions, and what I argued in Sect. 1 to be the observed pattern in disjunctive questions.
Contrast with earlier accounts: the open reading
Per (69), we predict that the issue raised by a disjunctive question involves three mutually incompatible possibilities, corresponding essentially to the answer set {p,¬p∧q,¬p∧¬q}. This is intuitively a good match for the open reading of disjunctive questions, which also has three good answers. However, our partition cells do not exactly align with what Roelofsen and Farkas (2015) derive in their inquisitive account (and what we derived earlier in our H/K reconstruction of it). Roelofsen and Farkas (2015) assume the structure ?(p∨q) for open disjunctive questions, from which we get the equivalent of {p,q,¬p∧¬q}. Thus our alternatives exhibit a left/right asymmetry that is not found in their account. Concretely, they predict that the question is resolved when the participants know the positive answer to either disjunct, even though they might be ignorant about the other one, while in our system the participants need to know for sure what the truth value of p is.
It is not clear which prediction is more correct: an example like (71)shows some left/right asymmetry in the resolution conditions, as we predict: if the answerer says q, we draw the inference that ¬p, which would be consistent with the idea that the partition cell being identified here really is ¬p∧q. With a symmetric approach, it is formally impossible to account for the contrast. The characterization that the question has not been resolved if one is ignorant about John might nevertheless be too strict.
-
(71)
A: Did John↗ arrive or did Mary?↗
-
a.
B: John arrived. ⇝ Mary might or might not have arrived.
-
b.
B: Mary arrived. \(\overset{?}{\leadsto}\) (B thinks) John didn’t arrive.
-
a.
We can add that, in some other cases, no asymmetry can clearly be detected:Footnote 39
-
(72)
A: Can I call you tomorrow at 3pm↗ or on Friday at 1pm?↗
-
a.
B: You can call me tomorrow. ⇝ B does not want A to call them on Friday.
-
b.
B: You can call me on Friday. ⇝ B does not want A to call them tomorrow.
-
a.
This could suggest that, in at least some cases, {p,q,¬p∧¬q} really is the answer set that we want. We can generate it within our system by assuming that disjunction can denote a Strong Kleene rather than Middle Kleene connective, or that it always does. If that is the case, we expect to observe presupposition filtering not just from the right-hand disjunct through the left-hand one, but also the other way round. Recall that the data is unclear on this point: we do observe a left-right contrast, but it is much less clear than for conjunction, and in the case of assertions, Rothschild (2011) among others has argued that the data does not support an asymmetric view of filtering. In a way, our discussion whether the resolution conditions of open disjunctive questions are left/right-asymmetric or not reflects the earlier debate whether presupposition filtering in disjunctive assertions is left/right-asymmetric or not. We will leave both questions open, but venture that they should receive a common answer.
Contrast with earlier accounts: the closed reading
Disjunctive questions also have a closed reading (or alternative question reading). In an alternative question like (73), the two propositions p and q inside each disjunct are presupposed to be exhaustive (p∨q holds) and exclusive (p∧q does not hold). In H/K semantics, alternative questions are generally assigned the denotation {p,q}; the equivalent move in inquisitive semantics is to assign to them the structure p∨q. Alternative questions can be resolved by asserting either of the two disjuncts, p or q.
-
(73)
Did John↗ arrive or did Mary?↘
To derive a two-element answer set from the denotation of ?p∨?q, it seems natural to assume a mechanism through which a presupposition that a question can be answered positively can be generated, for instance an operator  :
:
-
(74)
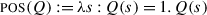
-
(75)
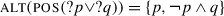 .
.
If that is our account of alternative questions, we correctly predict that they have two possible answers, and that p and q are good answers in a context where exhaustiveness (p∨q) and exclusivity (¬(p∧q)) hold (since in such a context, q and ¬p∧q are equivalent). We also derive the exhaustiveness presupposition. We do not derive the exclusivity presupposition in any way, however, so we have to assume that it arises from a separate mechanism, perhaps as an effect of focus structure in the question nucleus: cf. Sect. 4.5 for discussion. Under the Strong Kleene variant of the theory, the alternatives are {p,q}, as in the traditional account, but again the exclusivity presupposition is not derived.
Finally, recall that in inquisitive semantics and H/K semantics, a structure like ?p∨?q will result in the answer set {p,¬p,q,¬q}, which has to be ruled out one way or another, as there is no reading of disjunctive questions that looks like it. The system here does not generate this problematic answer set.
3.7 Interim conclusion
At this point, I have given an account of conjunctive questions and disjunctive questions such that the presupposition projection patterns that we observed in Sect. 1 can be easily derived. I have argued that the predicted resolution conditions for conjunctive and disjunctive questions are attested, and that those predicted by earlier accounts can also be generated, with only a few, simple extra assumptions.
The analysis offers a fully parallel account of conjunctions and disjunctions of polar questions. They are both assumed to have the structure that the surface syntax suggests, that is to say, ?p□?q, where □ is the (generalized) truth-conditional binary connective that you would expect, in its Middle Kleene variant.
Furthermore, assuming that propositions receive a classical trivalent denotation (type s→t, where t is the type of trivalent truth values), we can give a single entry for “and” and for “or” that applies to both questions and propositions. We just have to make them polymorphic truth-conditional connectives, in a way similar to what Partee and Rooth (1983) propose (with the added twist that we understand truth values to be trivalent):
-
(76)
-
a.
\(\left [\!\![\text{and} \right ]\!\!]= \lambda Q_{\alpha \rightarrow t}.\, \lambda P_{\alpha \rightarrow t}.\, \lambda x_{\alpha}.\, P(x) \land Q(x)\)
-
b.
\(\left [\!\![\text{or} \right ]\!\!]= \lambda Q_{\alpha \rightarrow t}.\, \lambda P_{\alpha \rightarrow t}.\, \lambda x_{\alpha}.\, P(x) \lor Q(x)\) (type ∀α. (α→t)→(α→t)→α→t in both cases)
-
a.
Thus all our desiderata as listed in Sect. 2.3 are met.
Of course, the theory presented here is probably not the only way to achieve these desiderata, and slight reformulations as well as radically different (possibly dynamic) theories could probably be offered. I do believe that they would involve some form of the following idea: there is some notion of a positive and a negative answer to a question, even beyond polar questions (cf. footnote 31), and the connectives should interact with this distinction in a similar manner to the way they interact with propositions. At an even more abstract level, the way we analyse a question should be more parallel to the way we analyse related propositions than it currently is. As I discussed in Sect. 2 and demonstrated for the case of answer set semantics, the lack of such properties in earlier accounts makes it very difficult to deal with the data presented here.
4 Further predictions and challenges for the trivalent inquisitive theory of questions
This final section explores in more detail the theory we have just developed: we first revisit some data points that we have set aside so far, and show how we are able to deal with them, and then briefly show we could develop the theory into a general theory of questions.
4.1 The effect of or not
Recall that, even though an alternative question using or not such as (77) has the same resolution conditions as the corresponding polar question, when such questions occur in a coordinated structure, they do not license presupposition filtering (cf. (9b)/(18b)).
-
(77)
Did John come or not?
Within our framework, or not questions are naturally analysed as instantiating the structure ?p∨?(¬p), which we will abbreviate as \(\tilde{?}p\). Thus, they receive the denotation in (78). This makes or not questions completely similar to polar questions in terms of their domain, their alternatives, and their informational commitment, as seen in (79).
-
(78)
\(\tilde{?}p = \lambda s.\, \begin{cases} 1 & \text{if $s \vdash p$ or $s \vdash \neg p$,} \\ \# & \text{otherwise.} \end{cases}\)
-
(79)
-
a.
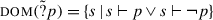
-
b.
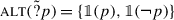
-
c.
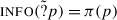
-
a.
The main way in which or not questions are predicted to differ from polar questions is that they behave differently with respect to coordination. Consider for instance \(\tilde{?}p \land ?q\):
-
(80)
\(\tilde{?}p \land ?q = \lambda s.\, \begin{cases} 1 & \text{if $s \vdash p \land q$ or $s \vdash \neg p \land q$,} \\ 0 & \text{if $s \vdash p \land \neg q$ or $s \vdash \neg p \land \neg q$,} \\ \# & \text{in all other cases.} \end{cases}\)
-
(81)
-
a.
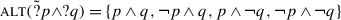
-
b.
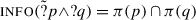
-
a.
Unlike ?p∧?q, \(\tilde{?}p \land ?q\) evokes a four-cell partition. Furthermore, the presuppositions of the second conjunct are predicted to project no matter what. Thus, we predict (82) (repeated from (9b)) to be infelicitous.
-
(82)
# Is Syldavia a monarchy or not, and is the Syldavian monarch a progressive?
4.2 Local contexts, triviality, and bivalent propositions
In Sect. 1, we stated a generalization about the observed data in terms of local contexts. The point was to also capture certain redundancy effects, seen in (83a) and (83b) (repeated from (26a) and (26b)), and in (84a) and in (84b) (repeated from (27a) and (27b)).
-
(83)
-
a.
# Is Ann in Paris and is she in France?
-
b.
# Is Ann in Paris and is she in London?
-
a.
-
(84)
-
a.
# Is Ann away from Paris or is she in France?
-
b.
# Is Ann away from Paris or is she in London?
-
a.
The infelicity of all these examples is predicted by a generalization in terms of local contexts (the local context of q in ?p∧?q entails p, the local context of q in ?p∨?q entails ¬p), together with a triviality constraint: no constituent should be trivially true or false in its local context.
Here, we have been adopting a trivalent theory of presuppositions, and we have not mentioned local contexts so far. It is nevertheless straightforward to derive local contexts that are exactly the ones we need, by applying Schlenker’s (2009) procedure to our question denotations.Footnote 40 The facts above will then be correctly predicted.
If we derive local contexts in this way, since they can also be used to predict presupposition projection, as shown by Schlenker (2009), we no longer need trivalent connectives at the propositional level. Thus the Middle Kleene connectives would exclusively serve for questions, and the present proposal would come down to the fact that question coordination obeys some form of Middle Kleene logic, without tying it as closely to presupposition projection. Since the empirical predictions are the same in the cases that we have been looking at so far, the choice between these two approaches has to be made on other grounds.
It should be noted that at least as far as these particular facts are concerned, we do not absolutely need a theory of local contexts. The various infelicitous examples listed above run afoul of plausible pragmatic constraints on question denotation:
-
(83a) would be banned by a global redundancy constraint: we predict it to be equivalent to its first conjunct on its own.
-
(83b) is predicted to only have 0-alternatives, as its 1-alternative is a contradiction. It is plausible that this is pragmatically deviant: the yes/no-asymmetries in polar questions identified in the literature (Büring and Gunlogson 2000; Roelofsen and Farkas 2015, a.o.) suggest that the positive answer has to have some special significance in the discourse context.Footnote 41
-
Within existing H/K approaches, (84a) would be banned by a unique-answer constraint: the two disjuncts overlap in natural contexts. In our system, the disjunction is equivalent to “Is Ann away from Paris or not?”, and could be banned by a global redundancy constraint similarly to (83a).
-
A unique-answer constraint would also ban (84b) in H/K theory. In our system, the disjunction is in fact equivalent to its first disjunct, “Is Ann away from Paris?”, so a global redundancy constraint would ban it.
4.3 Embedding and the relation between questions and propositions
Predicates like know can embed both questions, as in (85a), and propositions, as in (85b). It is of course desirable to analyse these two examples with a single entry for know, while accounting for the major difference in meaning between them.
-
(85)
-
a.
John knows whether Mary came.
-
b.
John knows that Mary came.
-
a.
Uegaki (2019) compares several approaches, including:
-
the Q-to-P approach: assuming that know embeds propositions, and that there is an operator that converts questions into propositions;
-
the P-to-Q approach: assuming that know embeds questions, and that there is an operator that converts propositions into questions;
-
the uniformitarian approach: giving the same kind of denotation to propositions and questions.
He argues that the Q-to-P approach cannot account for certain phenomena that are easy to analyze under the P-to-Q and uniformitarian approaches.Footnote 42
At any rate, our theory can in principle be made compatible with all three strategies. Here I will briefly describe an implementation of P-to-Q.Footnote 43 The P-to-Q approach can be implemented in our system in a fairly conservative way, mostly following the same lines as what would be done in answer set semantics. We can assume, as we have been doing so far, that propositions have type s→t, where t is the type of trivalent truth values. The following conversion operator converts a proposition to a question (type {s}→t, where {s} is the type of (non-trivalent) sets of worlds):
-
(86)
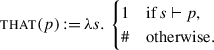
Note that  . Then, the following entry for know will deliver the appropriate truth conditions and presuppositions for (85a) and (85b).
. Then, the following entry for know will deliver the appropriate truth conditions and presuppositions for (85a) and (85b).
-
(87)
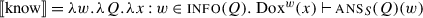
where  is an answerhood operator that computes the answer to a question:
is an answerhood operator that computes the answer to a question:
-
(88)
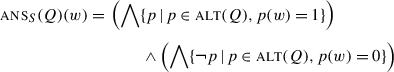
Applied to a polar question ?p,  returns p if p is true and ¬p if p is false. The definition does not have to be as complicated as it is to get this result, but it will also extend to constituent questions, as we will see below. In the propositional case, we correctly capture that “know that p” presupposes that p is true, as
returns p if p is true and ¬p if p is false. The definition does not have to be as complicated as it is to get this result, but it will also extend to constituent questions, as we will see below. In the propositional case, we correctly capture that “know that p” presupposes that p is true, as  .
.
4.4 Extending the proposal to constituent questions
I will only sketch an extension of the system to constituent questions here, in order to show what it might look like. I will be making a specific assumption on how constituent questions should be formalized, though alternative approaches can certainly be pursued. There are of course a number of issues that might prove challenging to tackle, and I will mention a few.
Trivalent existential quantification
To extend our system to constituent questions like (89), we need to give them a denotation that is a trivalent predicate upon sets of worlds, as for polar questions.
-
(89)
Who came?
The assumption that we make here, then, is that constituent questions are existentially quantified-into polar questions. This is consistent with the fact that wh-words are crosslinguistically similar to indefinites, and it is going to deliver the alternatives that we want. We can implement the idea as follows:
-
(90)
\(\left [\!\![\text{who} \right ]\!\!]= \lambda P.\, \lambda s.\, \exists x \in \text{\textbf {human}}.\, ?(P(x))(s)\)
-
(91)
\(\left [\!\![\text{(89)} \right ]\!\!]= \lambda s.\, \exists x \in \text{\textbf {human}}.\, ?(\text{\textbf {came}}(x))(s)\)
For the sake of perspicuity, we will ignore the restriction to humans and adopt the following notation:
-
(92)
?x. P(x)≡λs. ∃x. ?P(x)(s)
What the denotation we derive actually comes down to depends on what kind of trivalent existential quantifier we adopt. I propose to adopt the lazy trivalent existential quantifier defined by Beaver and Krahmer (2001) and George (2014), which is described in (93).Footnote 44
-
(93)
\(\exists x \in D.\, P(x) = \begin{cases} 0 & \text{if for all $y \in D$, $P(y) = 0$,} \\ 1 & \text{if there is $y \in D$ such that $P(y) = 1$,} \\ \# & \text{in all other cases.} \end{cases}\)
We then derive the following domain, alternatives, and informational commitment:
-
(94)
-
(95)

-
(96)
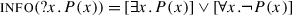
The alternatives are the mention-some answers to (89), plus the negative answer. The presupposition we predict for a constituent question involving a presuppositional predicate, such as (97), is a roughly existential presupposition similar to what George (2014) predicts for existential quantification: at least one person has a dog and is walking it, or everyone has a dog and nobody is walking their dog.Footnote 45
-
(97)
Who’s walking their dog?
Answerhood operators for constituent questions
Much of the discussion in the literature about the semantics of constituent questions is applicable to our system as long as we are able to redefine the various notions of answers that have been established in the literature. Since the alternatives that we derive are very similar to what is commonly assumed in Hamblin-Karttunen semantics, this is relatively straightforward to accomplish.
As we have seen, our alternatives already correspond to the mention-some answers to the question. A second kind of answer is found in the strongly exhaustive answers, which provide full information about the truth of the alternatives. The strongly exhaustive answer to “Who came?”, for instance, is the proposition asserting that the people who came came, and that the people who did not come did not come. We have already seen above, in (88), the definition of an operator computing the strongly exhaustive answer, and an entry for know based on it. Finally, some question-embedding predicates like surprise are thought to be sensitive to weakly exhaustive answers. The weakly exhaustive answer to “Who came?” is the proposition that the people who came came, with no information about the fact that nobody else did. Thus, (98) means that John was surprised that the people who came came, as opposed to being surprised that the people who did not come did not come.
-
(98)
It surprised John who came.
It is also straightforward to define an operator that computes the weakly exhaustive answer through a conjunction, as seen in (99). Here we are exploiting the difference between alternatives that are mapped to 0 and to 1; this enables us to go around the fact that our alternatives include an extra element (“nobody came”) relative to what is generally assumed in H/K semantics, where it is often assumed that the negative answer is not a semantic answer (e.g. Dayal 1996).
-
(99)
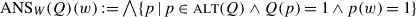
To conclude, the system proposed here can be extended to constituent questions in a way that is fairly close to H/K semantics and lets us replicate its basic ingredients, with the main difference (which we can get around if we wish) lying in our assumption that the negative answer to a constituent question is an actual semantic alternative. The parallelism with H/K semantics makes it so that much of the discussion found in the literature is applicable to the trivalent system.
4.5 Some potential challenges
A problem with plurals and Dayal’s presupposition
A common alternative to the definition of weakly exhaustive answers found above involves maximization rather than conjunction, following Dayal (1996). If the domain includes Ann and Bill, and who is taken to also range over plural individuals, under standard assumptions a constituent question like (89) should denote the set in (100)in H/K semantics.
-
(100)
{Ann came,Bill came,Ann and Bill came}
Because the set is closed under conjunction, the weakly exhaustive answer is always in the set, and it can be recovered without a conjunction operation. Instead, it can be defined as the maximal element (under entailment) within the true answers:
-
(101)
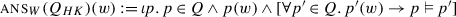
The expression above is only defined if there is a single p verifying the scope of ιp. It is frequently assumed that questions in fact presuppose that the actual world makes the expression above defined: this is Dayal’s presupposition, also known as the strongest-answer presupposition. Under this assumption, among other niceties, the difference in presuppositions between “Which student came?” (assumed to be as in (102)) and “Which students came?” (assumed to be as in (100)) follows naturally.
-
(102)
{Ann came,Bill came}
Unfortunately, this line of thought is not directly transferable to our system. Indeed, because we define alternatives as maximal elements under set inclusion, we are committed to the fact that alternatives are logically independent. Thus, we cannot have an alternative set that looks like (100). The set of positive alternatives for (89) can only look like (102), whether the wh-word ranges over singular individuals only or over both singular and plural individuals.
This has at least two consequences. First, we need to define weakly exhaustive answers in the conjunctive manner above. Second, the uniqueness presupposition of “Which student came?” cannot be derived from a more general presupposition of questions. Instead, it has to be analyzed as a presupposition specific to which questions.Footnote 46
Deriving the exclusivity inference in alternative questions
A related issue is that, as we have seen above, we do not derive the exclusivity presupposition of alternative questions. Recall that an alternative question or closed disjunctive question carries the presupposition that exactly one of the disjuncts is true. The presupposition can be further decomposed into exhaustiveness (at least one disjunct is true: p∨q) and exclusivity (the two disjuncts are not both true: ¬(p∧q)). With the denotation that is traditionally assumed in H/K semantics, {p,q}, both exhaustiveness and exclusivity can be derived from a strongest-answer constraint in the spirit of Dayal (1996). In our system, assuming that a closed disjunctive question denotes  (as predicted by a Middle Kleene view of disjunction), the alternatives are {p,¬p∧q}. A strongest- or unique-answer constraint, applied to our alternatives, derives exhaustiveness but not exclusivity. Worse than that, it is in fact impossible to construct a constraint that derives exclusivity from {p,¬p∧q}, because the desired presupposition (¬(p∧q)) is not expressible as a function of p and ¬p∧q. The Strong Kleene view of disjunction is more promising: the alternatives for
(as predicted by a Middle Kleene view of disjunction), the alternatives are {p,¬p∧q}. A strongest- or unique-answer constraint, applied to our alternatives, derives exhaustiveness but not exclusivity. Worse than that, it is in fact impossible to construct a constraint that derives exclusivity from {p,¬p∧q}, because the desired presupposition (¬(p∧q)) is not expressible as a function of p and ¬p∧q. The Strong Kleene view of disjunction is more promising: the alternatives for  are {p,q}, and a unique-answer constraint will derive the exclusivity presupposition. Adding a unique-answer presupposition will not affect our analysis of conjunctive cases (where the alternatives form a partition anyway). We will need to assume that it is not operative in open disjunctive questions, which do not seem to presuppose anything, but this problem is already present in earlier accounts. If we want instead to maintain the Middle Kleene view, which, as we have seen, helps explain certain left/right asymmetries, one solution might be to adopt a similar approach as in the case of which questions, consisting in the proposal that the individual alternatives entail the exclusivity inference. However, unlike in the case of which, there is no independent motivation for the move.
are {p,q}, and a unique-answer constraint will derive the exclusivity presupposition. Adding a unique-answer presupposition will not affect our analysis of conjunctive cases (where the alternatives form a partition anyway). We will need to assume that it is not operative in open disjunctive questions, which do not seem to presuppose anything, but this problem is already present in earlier accounts. If we want instead to maintain the Middle Kleene view, which, as we have seen, helps explain certain left/right asymmetries, one solution might be to adopt a similar approach as in the case of which questions, consisting in the proposal that the individual alternatives entail the exclusivity inference. However, unlike in the case of which, there is no independent motivation for the move.
5 Conclusion
In this long paper, we have identified a striking parallelism between the presupposition projection patterns observed when a trigger is in the second of two coordinated polar questions, and when a trigger is in the second of two coordinated assertions. We have seen that existing views on the semantics of coordinated questions struggle to explain the projection pattern in itself, and that they would have an even harder time explaining the parallelism, because they do not analyse coordinated questions in a way that adequately relates them to coordinated assertions. The system proposed here, a trivalent extension of inquisitive semantics, solves the initial problem of deriving the projection facts by making polar questions more closely related to assertions. Through this proposal, we also make polar questions yes/no-asymmetric, and we give a uniform account of question conjunction and question disjunction — two issues that have proven problematic for some theories of questions. While we do not have the space to explore further implications here, a natural next step will be to identify which other phenomena the resulting system might help us with, such as, possibly, question bias. Additionally, while I think I have shown here a defect in existing theories of questions taken as-is, there certainly exist other ways of extending extant theories, following the same basic conceptions that I followed when extending inquisitive semantics, which would deliver the same welcome results; we will have to see whether some of them might not improve on the present system in some respects.
Notes
(2b) does presuppose that Syldavia is either a republic or a monarchy. I ask the reader to assume that this is a well-known fact about countries in the part of the world where Syldavia is located. The issue will not substantially affect the discussion.
What (3b) presupposes is arguably “Mary believes that Syldavia is a monarchy” rather than “Syldavia is a monarchy”, or possibly both readings are possible. Whether the inferences I describe are attributed to the speaker or the attitude holder when they differ does not affect my discussion of them.
Most connectives other than and and or, such as for instance but, do not seem to ever occur between two questions. Complex disjunctions such as either... or... cannot embed matrix questions either.
We are going to discuss in time whether (4) should indeed be analysed as ?p∧?q.
In general, matrix questions pragmatically presuppose that their answer has not yet been established in the discourse. Thus, the first conjunct in (4), uttered on its own, presupposes that Syldavia might or might not be a monarchy as far as the Common Ground allows. How this presupposition arises exactly in the case of (4) is an interesting question, but I will not attempt to address it here.
To be precise, the fact that we infer from (5) that Syldavia is a monarchy, and not that if Syldavia is rich in mineral resources it is a monarchy, is an instance of the proviso problem. The proviso problem occurs in exactly the same cases for questions as for assertions, as far as I can tell.
The availability of filtering in conjunctive questions has not been noted before to my knowledge, but Groenendijk (1998) (cited by Dotlačil and Roelofsen 2019) mentions the example in (20), which demonstrates a parallel pattern when it comes to anaphoric dependencies. Both Groenendijk (1998) and Dotlačil and Roelofsen (2019) propose dynamic theories under which this example cannot be accounted for.
-
(i)
Did you see a man? and was he angry?
Meanwhile, in a recent article, Abenina-Adar and Sharvit (2021) observe that filtering is available in disjunctive questions in certain cases similar to those we discuss here. They propose an account of disjunction based on alternative semantics where the observed projection pattern is specified by the semantics of the connective. We are going to adopt a very different approach here, among other things because we seek to understand conjunctive and disjunctive questions in parallel.
-
(i)
An anonymous reviewer points out that under certain intonations, these two examples can be felicitous. Discourse markers like actually, in fact etc. can help bring out such readings.
-
(i)
Is Ann in Paris? And (actually) is she (even) in France?
Intuitively, in these cases, the speaker changes discourse strategy between the two conjuncts, and they would have asked the second question first, had they thought it through. The fact that the second conjunct is a correction is signalled through discourse markers and emphatic intonation. There is also a clear sentence break between the conjuncts.
The judgments reported here are based on a different intonation pattern, where there is no full sentence break between the clauses (which I have tried to indicate through punctuation) and the second conjunct does not bear any emphasis, and where there is no perception that the speaker changed their mind. Attempting an analysis of discourse-level uses of question coordination is beyond the scope of this paper.
-
(i)
In particular, we will see that under the theory we are going to propose, it will be possible to explain the infelicity of (26a) and (26b) in terms of global redundancy or similar pragmatic constraints, without necessarily referring to local contexts.
I thank a reviewer for stressing the importance of this distinction.
Two strategies are possible. One option consists in assuming that the connective takes higher or lower scope than the surface syntax would suggest, with ellipsis or semantically inert elements potentially involved. For instance, Hirsch (2017) proposes that apparent conjunctive questions actually involve “and” taking high scope. The second option, proposed among others by Krifka (2001), consists in lifting the question from whatever type α our theory of simple questions would assign to it to the higher-order type (α→t)→t, as shown in (i), and then assuming that conjunction and disjunction apply (classically) to this higher-order denotation. The second strategy only delivers “high” readings, as in (30b) and (31b).
-
(i)
 (type (α→t)→t)
(type (α→t)→t)
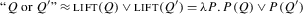
To apply either strategy to the case of matrix questions, we need to assume that there are silent truth-conditional speech act operators above them, such as a silent I wonder or a silent you should tell me. Alternatively, along with the second strategy, we might assume that the higher-order type is the “normal” type of questions, and that there are no linguistic constituents with semantic type α. I use embedded examples in this section to avoid dealing with the issue.
-
(i)
Another reason to think that our questions are not polar questions is that “yes” and “no” are not good answers to them. My impression from an informal survey is that in the conjunctive case (4), speakers’ initial intuition is to accept “yes” and “no” as answers, but they are not sure as to how to interpret either. In the disjunctive case (12), with the “open” intonation, “no” is a felicitous answer, meaning that both disjuncts are false, but “yes” is of unclear interpretation. With the alternative question intonation, both “yes” and “no” are unacceptable. More generally, “yes” and “no” as answers to an alternative question can sometimes be interpreted as “both are true” and “neither is true”, respectively, but they tend to come across as joke answers.
An analysis following Xiang (2021), where wonder is decomposed into want and know, and disjunction takes scope in between the two, would predict such a disjunctive desire: Mary wants it to be the case that either she knows whether John is here or she knows whether it is raining.
Under the ‘want’>‘or’>‘know’ scope analysis, the condition for filtering would instead be something like: “According to Mary’s beliefs, if she does not know whether Syldavia is a republic, then Syldavia is a monarchy”, which is nonsensical.
A potential reductionist counter-argument worth commenting upon is that if we attempt to explicitly spell out the semantics that a reductionist account would give to our examples, it is not entirely clear whether the presupposition projects in the resulting sentence. This is especially true in the conjunctive case, (i), which is only somewhat degraded in my judgment. In the disjunctive case, the sentence we obtain, (ii), is somewhat involved and hard to interpret.
-
(i)
? Mary wonders / wants to know whether Syldavia is a monarchy and she wonders / wants to know whether the Syldavian monarch is a progressive.
-
(ii)
?? Mary wants to know whether Syldavia is a republic or to know whether the Syldavian monarch is a progressive.
A counter-counter-argument is that using complex conjunctions and disjunctions to make the scope explicit, even though it does not affect presupposition projection in the general case, makes both our attempts more clearly contradictory:
-
(iii)
-
a.
Not only is Syldavia a monarchy, but the Syldavian monarch is a progressive.
-
b.
# Not only does Mary wonder whether Syldavia is a monarchy, but she wonders whether the Syldavian monarch is a progressive.
-
a.
-
(iv)
-
a.
Either Syldavia is a republic or the Syldavian monarch is a progressive.
-
b.
# Mary wants either to know whether Syldavia is a republic or to know whether the Syldavian monarch is a progressive.
-
a.
-
(i)
The presentation here is not true to Karttunen (1977) and Biezma and Rawlins (2012) in the sense that neither theory actually features such an operator, and the corresponding device is more like an interpretation rule.
Additionally, Biezma and Rawlins (2012) assume that the corresponding coercion operation only occurs in embedded questions. Since the phenomenon we are interested in is not affected by the distinction between matrix and embedded questions, it will be easier to follow Karttunen (1977) and assume that both kinds are composed uniformly.
Here there are several things to say to defend H/K semantics. First, pointwise composition is independently motivated, not only to analyse the internal composition of questions (Hamblin 1976) but also for other phenomena, such as focus (Rooth 1992). Second, given that non-pointwise conjunction leads to degenerate results, it seems unproblematic to assume that the syntax allows for it just as it allows for non-pointwise disjunction, but that it is banned on semantic grounds.
Adding extra
 ’s would only add logical contradictions to the sets, as the reader can verify. We are going to assume that it would make the questions unacceptable.
’s would only add logical contradictions to the sets, as the reader can verify. We are going to assume that it would make the questions unacceptable.Since all theories of presupposition projection are designed so that a presupposition that p is true does not project after “p∧”, here we can see that the choice of the Transparency Theory was not crucial. See also the derivations in the Appendix.
Our generalization in terms of local contexts given in (10) also follows if we derive local contexts in the spirit of the Transparency Theory, along the lines of Schlenker (2009).
We will discuss in Sect. 3.5 the implications of the resolution conditions predicted by (e) in non-presuppositional examples.
Hoeks and Roelofsen (2019) note that, like the theory we are sketching here, inquisitive semantics predicts conjunctive questions to have polar readings, and they claim that this prediction is correct. My own judgment is that the reading they characterize as polar is the one corresponding to the tripartition, that is, option (e). In my view, the issue remains to be investigated more thoroughly.
In particular, the extensive discussion of potential structures for conjunctive questions offered by Hoeks and Roelofsen (2019) does not mention the possibility of (e) or (f).
In contrast, Biezma and Rawlins (2012) analyse both open and closed questions as {p,q}, but with different presuppositions.
As in the conjunctive case, there are in principle other possibilities, such as
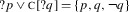 and
and 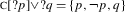 . These options do not have the required property either; I will ignore them here to keep the discussion contained.
. These options do not have the required property either; I will ignore them here to keep the discussion contained.All the theories discussed in what follows are static; while there exist also dynamic accounts of questions, I will set them aside for lack of space. In general, these accounts’ handling of the connectives is derivative of a static theory, and the issues that we are going to discuss carry over. This applies for instance to Dotlačil and Roelofsen 2019 (based on inquisitive semantics) and to Li 2019 (based on answer set theory).
Here ¬ denotes trivalent negation: it maps 0 to 1, 1 to 0, and # to #.
The basic idea of adding yes/no-asymmetry to inquisitive semantics has already been explored by Roelofsen and Farkas (2015), but their system is conceptually quite different. Roelofsen and Farkas (2015) propose a two-dimensional theory where ?p has its usual inquisitive denotation on the ordinary dimension (essentially {p,¬p}). On the second dimension, called the “highlighting” dimension, ?p essentially denotes p.
Under the proposal presented here, answers to a complex question will all be assigned a certain category (positive or negative). For instance, p∧q will be a positive answer to ?p∧?q, while p∧¬q will be a negative one. As an anonymous reviewer points out, there is no clear intuition on how to make this distinction beyond simple polar questions that we could evaluate the proposal against. My claim is that this particular way of dividing up “positive” and “negative” answers will lead to an adequate account of question coordination and presupposition projection, which is enough to justify it. Unless we ascertain that another phenomenon involves a more fine-grained distinction or a different one, there is no reason to be concerned about the premise of categorizing answers beyond what is intuitively obvious.
In the possible extension to constituent questions based on \(\exists _{G}\) that we are going to discuss in Sect. 4.4,
 will specifically return (roughly) the Hamblin-Karttunen answers to the question, as opposed to propositions corresponding to the partition cells in the sense of Groenendijk and Stokhof (1984). For polar questions, there is no difference between Hamblin answers and partition cells.
will specifically return (roughly) the Hamblin-Karttunen answers to the question, as opposed to propositions corresponding to the partition cells in the sense of Groenendijk and Stokhof (1984). For polar questions, there is no difference between Hamblin answers and partition cells.George (2014) motivates the MK connectives by showing how they can be derived from classical bivalent logic together with some general assumptions about definedness conditions.
This is of course an idealization where we ignore, among other things, the possibility of avowing complete or partial ignorance (“I don’t know”, “Probably”, etc.), the possibility of rejecting the question (“Who cares?”), the possibility of providing an implicit answer (“A: Did John come? B: He was sick.”), the existence of rhetorical questions, and so on.
I am ignoring here the various pragmatic presuppositions that are associated to asking a question: that the facts have not been established before in the discourse, that the answer is accessible, etc.
H/K semantics and inquisitive semantics generate a variety of other readings, as we have seen. In particular, there is a polar reading ({p∧q,¬(p∧q)}) and a reverse tripartition ({¬q,p∧q,¬p∧q}). Without further assumptions, our system generates none of these either. In principle, the polar reading can be generated if we assume that and can take scope below ?, or if we have an operation that collapses the 0-alternatives into one. The reverse tripartition can be generated if we assume that and can also denote a right-to-left rather than left-to-right Middle Kleene connective, or equivalently that it can combine either with the first or the second conjunct first. The reverse tripartition is unattested and, pending further investigation, my judgment is that the polar reading is not available either (cf. footnote 24), so these extra assumptions are not necessary.
One could in particular use the fact that p∧¬q is a good answer and entails ¬q. Asserting ¬q always raises the contextual probability of p∧¬q relative to the other two cells, from which an inference that p∧¬q holds might follow as a relevance implicature.
One might in fact argue that both (65) and (66a) do involve presupposition filtering, but with pragmatic presuppositions. In (65), the presupposition that the second question is relevant to some greater issue is not satisfied in the context: it only matters whether there is charcoal if the weather is nice, as the goal is to take out the grill. In (66a), similarly, the presupposition that knowledge of the answer to the second question is accessible to the participants is not satisified, but what is true is that if the mail has arrived, participants have a chance knowing whether Mary got her grant. This is consistent with the interpretation of the trivalent system offered in Sect. 3.2: a polar question ?q on its own presupposes that future Common Grounds will entail q or ¬q, but when it is in the second conjunct of ?p∧?q, this presupposition can be filtered, and it is fine if the question is uninteresting or unknowable when p is false.
I thank an anonymous reviewer for this example.
Schlenker (2009) applies his procedure to bivalent propositions, but the procedure is mostly agnostic with respect to the type of what it is looking at, and it is straightforward to adapt it to functions from states to trivalent values. The one thing we need to specify is how contextual restriction works with states: we take it that if the context set is C, the set of contextually permissible states is the set of subsets of C.
I think the distinction between 1-alternatives and 0-alternatives would be helpful in a theory of question bias, but this is not the place to develop this idea.
For discussion of the differences between P-to-Q and uniformitarian approaches, see Roelofsen (2019) and references therein.
Q-to-P can be implemented through answerhood operators; cf. Section (97). The uniformitarian approach can be implemented by assigning to propositions the same type as questions. The simplest approach consists in assigning to propositions the same denotation as to the corresponding polar question, and distinguishing them only at the highest level (above any connective), by assuming either that polar questions are embedded under
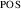 (then the entry for know would presuppose that we are in a 1-state), or that assertions are embedded under something similar to
(then the entry for know would presuppose that we are in a 1-state), or that assertions are embedded under something similar to  (then the entry for know needs not be changed).
(then the entry for know needs not be changed).A natural alternative would be a universally-projecting existential quantifier, such that \(\exists x.\, \phi _{x}\) is defined only if \(\phi _{x}\) is defined for all x. This would make the alternatives to the question congruent with its strongly exhaustive answers, which is unwelcome because there is no obvious way to derive weakly exhaustive and mention-some answers from strongly exhaustive answers.
The matter of how presuppositions project from questions beyond simple polar cases has received relatively little attention in the literature and is subject to debate. Schwarz and Simonenko (2018) argue that while universal projection is generally observed in constituent questions (as noted in earlier work, e.g., Abruśan 2011), it can be obviated in certain contexts. In a paper published after the present one was written, Theiler (2021) proposes a generalization whereby what we observe is universal projection over an answer set that can be smaller than the H/K question denotation under certain conditions. Integrating Theiler’s observations and proposal with the present framework is left to future work.
Champollion et al. (2017) defend a localist account of which’s presupposition within the framework of inquisitive semantics, where the same problem occurs. Decoupling the presuppositions of which questions from answerhood operators is also argued for by Uegaki (2020) and Hirsch and Schwarz (2019) within H/K semantics. An alternative solution to the issue consists in making singular and plural which questions different again through extensions of the inquisitive system; see for instance the dynamic inquisitive proposal of Dotlačil and Roelofsen (2020).
Both the second and third approach are reminiscent of the definition of Strawson entailment proposed by von Fintel (1999).
This condition should clearly be met in any realistic example. Possibly a weaker condition would suffice to validate the result.
We would need to define an explicit fragment to properly prove this fact, but I think it is reasonable to take it for granted.
If d contextually entails p, then the unique-answer presupposition of {p,d∧q} will be contradictory, whatever q is. d is actually W-transparent in this case, but not in an interesting way.
The fact that we look at equivalence in \(C'\) rather than in C here constitutes the crucial difference between C-equivalence and W-equivalence.
An entirely parallel result obtains in the case of the Simple Dynamic Answer set Theory (SDAT):

Li (2019) proposes a system of this kind.
Note that we could relativize everything to a context set, as is done in the definition of K-equivalence, while preserving all the results.
As before, this condition should be met in any realistic example.
This can also be stated as “p entails π(q)”, where π is defined as in (47).
References
Abenina-Adar, Maayan, and Yael Sharvit. 2021. On the presuppositional strength of interrogative clauses. Natural Language Semantics 29(1): 47–90. https://doi.org/10.1007/s11050-020-09169-5.
Abruśan, Marta. 2011. Presuppositional and negative islands. A semantic account. Natural Language Semantics 19(3): 257–321. https://doi.org/10.1007/s11050-010-9064-4.
Beaver, David, and Emiel Krahmer. 2001. A partial account of presupposition projection. Journal of Logic, Language and Information 10(2): 147. https://doi.org/10.1023/A:1008371413822.
Biezma, Maria, and Kyle Rawlins. 2012. Responding to alternative and polar questions. Linguistics and Philosophy 35(5): 361–406. https://doi.org/10.1007/s10988-012-9123-z.
Bolinger, Dwight. 1978. Yes-no questions are not alternative questions. In Questions, ed. Henry Hiż, 87–105. Dordrecht: Reidel. https://doi.org/10.1007/978-94-009-9509-3_3.
Büring, Daniel, and Christine Gunlogson. 2000. Aren’t positive and negative polar questions the same? Ms., UCSC/UCLA. https://semanticsarchive.net/Archive/mYwOGNhO/polar_questions.pdf.
Champollion, Lucas, Ivano Ciardelli, and Floris Roelofsen. 2017. On questions and presuppositions in typed inquisitive semantics. Handout, NYU.
Ciardelli, Ivano, Jeroen Groenendijk, and Floris Roelofsen. 2013. Inquisitive semantics. A new notion of meaning. Language and Linguistics Compass 7(9): 459–476. https://doi.org/10.1111/lnc3.12037.
Ciardelli, Ivano, Jeroen Groenendijk, and Floris Roelofsen. 2018. Inquisitive semantics. London: Oxford University Press.
Ciardelli, Ivano, Floris Roelofsen, and Nadine Theiler. 2017. Composing alternatives. Linguistics and Philosophy 40(1): 1–36. https://doi.org/10.1007/s10988-016-9195-2.
Dayal, Veneeta. 1996. Locality in WH-quantification. Questions and relative clauses in Hindi. Dordrecht: Kluwer.
Dotlačil, Jakub, and Floris Roelofsen. 2019. Dynamic inquisitive semantics: Anaphora and questions. In Proceedings of Sinn und Bedeutung 23, eds. M. Teresa Espinal et al., 365–382. Konstanz: University of Konstanz. https://doi.org/10.18148/sub/2019.v23i1.538.
Dotlačil, Jakub, and Floris Roelofsen. 2020. A dynamic semantics of single-wh and multiple-wh questions. In Proceedings of SALT 30, eds. Joseph Rhyne et al., 376–395. Washington: Linguistic Society of America. https://doi.org/10.3765/salt.v30i0.4839.
von Fintel, Kai. 1999. NPI licensing, Strawson entailment, and context dependency. Journal of Semantics 16(2): 97–148. https://doi.org/10.1093/jos/16.2.97.
George, Benjamin R. 2014. Some remarks on certain trivalent accounts of presupposition projection. Journal of Applied Non-Classical Logics 24(1–2): 86–117. https://doi.org/10.1080/11663081.2014.911521.
Groenendijk, Jeroen. 1998. Questions in update semantics. In Formal semantics and pragmatics of dialogue: Proceedings of the 13th Twente Workshop on language technology (Twendial ’98), eds. Joris Hulstijn and Anton Nijholt, 125–137. Enschede: University of Twente.
Groenendijk, Jeroen, and Martin Stokhof. 1984. Studies on the semantics of questions and the pragmatics of answers, PhD thesis, University of Amsterdam.
Hamblin, Charles L. 1976. Questions in Montague English. In Montague grammar, ed. Barbara H. Partee, 247–259. San Diego: Academic Press. https://doi.org/10.1016/B978-0-12-545850-4.50014-5.
Heim, Irene. 1983. On the projection problem for presuppositions. In Proceedings of WCCFL 2, eds. Daniel P. Flickinger, Michael Barlow, and Michael T. Wescoat, 114–126. Stanford: Stanford University.
Hirsch, Aron. 2017. An inflexible semantics for cross-categorial operators, PhD thesis, MIT.
Hirsch, Aron, and Bernhard Schwarz. 2019. Singular which, mention-some, and variable scope uniqueness. In Proceedings of SALT 29, eds. Katherine Blake et al., 748–767. Washington: Linguistic Society of America. https://doi.org/10.3765/salt.v29i0.4637.
Hoeks, Morwenna, and Floris Roelofsen. 2019. Coordinating questions: The scope puzzle. In Proceedings of SALT 29, eds. Katherine Blake et al., 562–581. Washington: Linguistic Society of America. https://doi.org/10.3765/salt.v29i0.4632.
Karttunen, Lauri. 1973. Presuppositions of compound sentences. Linguistic Inquiry 4(2): 169–193.
Karttunen, Lauri. 1974. Presupposition and linguistic context. Theoretical Linguistics 1(1–3): 181–194.
Karttunen, Lauri. 1977. Syntax and semantics of questions. Linguistics and Philosophy 1: 1–44.
Krifka, Manfred. 2001. For a structured meaning account of questions and answers. In Audiatur vox sapientia. A festschrift for Arnim von Stechow, eds. Caroline Féry and Wolfgang Sternefeld, 287–319. Berlin: Akademie Verlag. https://doi.org/10.1515/9783050080116.287.
Li, Haoze. 2019. Deriving short answers from Hamblin sets: A case study of Mandarin wh-conditionals. In Proceedings of SALT 29, eds. Katherine Blake et al., 138–159. Washington: Linguistic Society of America. https://doi.org/10.3765/salt.v29i0.4604.
Partee, Barbara, and Mats Rooth. 1983. Generalized conjunction and type ambiguity. In Meaning, use, and interpretation of language, eds. Rainer Bäuerle, Christoph Schwarze, and Arnim von Stechow, 361–384. Berlin: de Gruyter. https://doi.org/10.1515/9783110852820.361.
Peters, Stanley. 1979. A truth-conditional formulation of Karttunen’s account of presupposition. Synthese 40(2): 301–316. https://doi.org/10.1007/BF00485682.
Roelofsen, Floris. 2019. Semantic theories of questions. In Oxford Research Encyclopedia of Linguistics. Oxford: Oxford University Press. https://doi.org/10.1093/acrefore/9780199384655.013.504.
Roelofsen, Floris, and Donka F. Farkas. 2015. Polarity particle responses as a window onto the interpretation of questions and assertions. Language 91(2): 359–414. https://doi.org/10.1353/lan.2015.0017.
Rooth, Mats. 1992. A theory of focus interpretation. Natural Language Semantics 1(1): 75–116. https://doi.org/10.1007/BF02342617.
Rothschild, Daniel. 2011. Explaining presupposition projection with dynamic semantics. Semantics and Pragmatics 4(3): 1–43. https://doi.org/10.3765/sp.4.3.
Schlenker, Philippe. 2008. Be articulate. A pragmatic theory of presupposition projection. Theoretical Linguistics 34(3): 157–212. https://doi.org/10.1515/THLI.2008.013.
Schlenker, Philippe. 2009. Local contexts. Semantics and Pragmatics 2(3): 1–78. https://doi.org/10.3765/sp.2.3.
Schwarz, Bernhard, and Alexandra Simonenko. 2018. Decomposing universal projection in questions. In Proceedings of Sinn und Bedeutung 22, eds. Uli Sauerland and Stephanie Solt, 361–374. Konstanz: University of Konstanz.
Singh, Raj. 2007. Assertability constraints and absurd assertions. Ms., MIT.
Sudo, Yasutada. 2013. Biased polar questions in English and Japanese. In Beyond expressives: Explorations in use-conditional meaning, eds. Daniel Gutzmann and Hans-Martin Gärtner, 275–295. Leiden: Brill. https://doi.org/10.1163/9789004183988_009.
Szabolcsi, Anna. 1997. Quantifiers in pair-list readings. In Ways of scope taking, ed. Anna Szabolcsi, 311–347. Dordrecht: Kluwer. https://doi.org/10.1007/978-94-011-5814-5_9.
Szabolcsi, Anna. 2016. Direct vs. indirect disjunction of wh-complements, as diagnosed by subordinating complementizers. Ms., New York University. https://ling.auf.net/lingbuzz/003090.
Theiler, Nadine. 2021. An epistemic bridge for presupposition projection in questions. In Proceedings of SALT 30, eds. Joseph Rhyne et al., 252–272. Washington: Linguistic Society of America. https://doi.org/10.3765/salt.v30i0.4817.
Uegaki, Wataru. 2019. The semantics of question-embedding predicates. Language and Linguistics Compass 13(1). https://doi.org/10.1111/lnc3.12308.
Uegaki, Wataru. 2020. The existential/uniqueness presupposition of wh-complements projects from the answers. Linguistics and Philosophy. https://doi.org/10.1007/s10988-020-09309-4.
Xiang, Yimei. 2021. A hybrid categorial approach to question composition. Linguistics and Philosophy 44: 587–647. https://doi.org/10.1007/s10988-020-09294-8.
Acknowledgements
My thanks go to the great number of people with whom I discussed part or all of this work and who provided me with helpful remarks, including in particular Benjamin Spector and two anonymous reviewers for Natural Language Semantics.
This work has benefitted from funding from the Agence Nationale de la Recherche (ANR-17-EURE-0017 FrontCog, ANR-10-IDEX-0001-02 PSL).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Formal companion to Sect. 2.4
Appendix: Formal companion to Sect. 2.4
This appendix contains a formal development that demonstrates the problems encountered when one combines answer set semantics with either the Transparency Theory or trivalent theories, as cursorily explained in Sect. 2.4. We will derive the fact that the observed presupposition filtering pattern is expected in conjunctive questions if they are analysed as the tripartition, but not if they are analysed as the quadripartition. Meanwhile, the observed pattern in disjunctive questions is not derived in any natural way.
Note that throughout the Appendix we work with question denotations, rather than with declarative sentences containing embedded questions, and therefore the results might only directly apply to matrix questions. In principle, at least under the Transparency Theory, we could predict different filtering patterns under certain embeddings (in particular, we might expect more filtering predictions). While I do not think this would lead to different results in practice, no attempt is made to prove it here.
When the proof of a result is omitted, it is because it is immediate.
1.1 1 Equivalence relations on questions
The Transparency Theory requires a notion of equivalence; we define several natural ones below. As in the main text, we identify questions with Hamblin denotations (sets of propositions). We will use Q, \(Q'\), etc. to name our abstract variables representing questions. In order to show that the results extend to Karttunen’s approach, we will also deal with Karttunen denotations (functions from worlds to sets of propositions), which we will refer to as Q̂, \(\hat{Q}'\), etc. The following relations let us map each kind of denotation into the other:
Definition 1
Relation between Hamblin and Karttunen denotations
For a question Q, we define:
As long as Q does not contain a logical contradiction, the following relation lets us reverse the mapping:
Note that it is not true in general that all Karttunen questions can be derived from a Hamblin question (i.e., that they can be written as Q̂ for some Q). However, all the questions that we consider here are representable as Hamblin questions.
In the main text, we left the notion of equivalence we were using somewhat implicit. Here we define several reasonable notions of equivalence. These notions are all relativised to a context set C (they are notions of contextual equivalence). The purpose of this wealth of definitions is to show that the issues outlined in the main text do not depend on specific implementational choices within the general framework of H/K semantics. In particular, whether we adopt H-equivalence, which is the most natural approach from the perspective of a Hamblin-style theory, or K-equivalence, which is the most natural approach from the perspective of a Karttunen-style theory, does not matter, showing that our discussion applies to Hamblin- and Karttunen-style accounts equally.
For the notions based on a presuppositional answerhood operator, I implement a variety of ways of dealing with the unique-answer presupposition. The first approach treats it essentially as an entailment, a second one only considers worlds where it is true, and a third one only considers contexts where it is true.Footnote 47
Non-contextual versions of the non-presuppositional notions can be obtained by taking C to be the set of all possible worlds.
Definition 2
Pointwise contextual restriction
-
(i)
For a proposition p and a context set C, \(p_{|C}\) is the function from C to truth values that is identical to p at all points (the contextual restriction of p to C).
-
(ii)
For a question Q and a context set C, the contextual restriction of Q to C is \(Q_{|C}\), where:
$$ Q_{|C} := \{p_{|C} \,|\, p \in Q\} $$
Definition 3
Hamblin equivalence
Q and \(Q'\) are H-equivalent relative to context set C iff \(Q_{|C} = Q_{|C}'\).
Definition 4
Karttunen equivalence
Q and \(Q'\) are K-equivalent relative to context set C iff:
Definition 5
Unique-answer answerhood operator
We define:

Definition 6
Unique-answer equivalence: entailed presupposition
Q and \(Q'\) are U-equivalent relative to a context set C iff:
-
(i)
the unique-answer presuppositions of Q and \(Q'\) are equivalent in C,
-
(ii)
calling \(C'\) the subset of C where the presuppositions are met, we have:
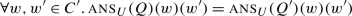
Definition 7
Unique-answer Strawson equivalence — world-level version
Q and \(Q'\) are W-equivalent relative to a context set C iff for any world w in C such that the unique-answer presuppositions of both Q and \(Q'\) are true at w, we have:

Definition 8
Unique-answer Strawson equivalence — context-level version
Q and \(Q'\) are C-equivalent relative to a context set C iff for any subset \(C'\) of C where the unique-answer presuppositions of both Q and \(Q'\) are true, we have

Result 1
H-equivalence and K-equivalence are almost the same thing
-
(i)
If C is a context set and Q and \(Q'\) are two questions, then if Q and \(Q'\) are H-equivalent in C, they are K-equivalent in C.
-
(ii)
If C is a context set and Q and \(Q'\) are two questions that do not contain any proposition that is false throughout C, then if Q and \(Q'\) are K-equivalent in C, they are H-equivalent in C.
Result 2
Order of the answer-based equivalences by strength
If C is a context set and Q and \(Q'\) are two questions, then if Q and \(Q'\) are U-equivalent in C, they are W-equivalent in C, and if they are W-equivalent in C, they are C-equivalent in C.
Result 3
K-equivalence is stronger than unique-answer equivalences
If C is a context set and Q and \(Q'\) are two questions, then if Q and \(Q'\) are K-equivalent in C, they are U-equivalent and therefore also W-equivalent and C-equivalent in C.
Result 4
Collapse of the equivalences
If C is a context set and Q and \(Q'\) are two questions whose unique-answer presuppositions are satisfied in C, then for any pair of letters α, β within H, K, U, W, and C, Q and \(Q'\) are α-equivalent in C iff they are β-equivalent in C.
1.2 2 The Transparency Theory
Here we derive the announced results under Schlenker’s (2008) Transparency Theory. Schlenker (2008) proposes that in a context C, a presuppositional clause is acceptable if and only if the proposition being presupposed is transparent in the clause’s position. Transparency is defined as follows (some details are simplified or left implicit; the reader is referred to Schlenker 2008):
Definition 9
Transparency; Schlenker 2008
Let αβγ be a sentence where β is an embedded clause, and δ be another clause denoting a proposition d. d is transparent in the position of β if and only if for any completion \(\gamma '\) that makes \(\alpha \beta \gamma '\) well-formed, and for any clause \(\beta '\), the two sentences \(\alpha \beta ' \gamma '\) and \(\alpha (\text{$\delta $ and $\beta '$}) \gamma \) are contextually equivalent in C.
The definition of Transparency depends on a notion of contextual equivalence; it is straightforward to apply it to questions as long as we have defined equivalence over them. Thus we can in principle define H-transparency, K-transparency, and so on in terms of the definitions above.
The relations between our notions of equivalence immediately translate into relations between our notions of transparency:
Result 5
Relations between the transparencies
-
(i)
H-transparency implies K-transparency.
-
(ii)
K-transparency implies U-transparency.
-
(iii)
U-transparency implies W-transparency.
-
(iv)
W-transparency implies C-transparency.
We can now derive the results that we are interested in. The first one below establishes that under the quadripartitive account, no presupposition filtering should ever be observed when the trigger is in the second conjunct of a conjunctive question.
Result 6
The quadripartition
Let C be a context set, and p a proposition such that there exists a proposition \(q_{0}\) that is not related by contextual entailment to p or ¬p.Footnote 48 A proposition d is H-transparent (as well as K/U/W/C-transparent) in the position of q in  if and only if C supports d.
if and only if C supports d.
Proof
The direction “If C supports d, then d is transparent” is immediate.
For the other direction, it suffices to show that if d is C-transparent, then C supports d, as C-transparency is the weakest form of transparency. Note that the definedness condition of  is always met if the answers form a logical partition as they do here, and therefore we do not need to consider subcontexts at all.
is always met if the answers form a logical partition as they do here, and therefore we do not need to consider subcontexts at all.
Assume then that d is C-transparent. We will write  ; the fact that d is C-transparent means that
; the fact that d is C-transparent means that  is equivalent in C to
is equivalent in C to  for any q and any w∈C (taking \(\beta '\) to be q, and \(\gamma '\) to be the empty string).
for any q and any w∈C (taking \(\beta '\) to be q, and \(\gamma '\) to be the empty string).
It follows from the existence of \(q_{0}\) that p is not trivially true or false in C. Let then w, \(w'\) be two worlds such that p(w)=1 and \(p(w') = 0\). We have  and
and  .
.
-
If \(d(w) = d(w') = 0\), then
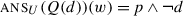 , from which it follows that p∧¬d is equivalent to p, i.e. that p entails ¬d. We also have
, from which it follows that p∧¬d is equivalent to p, i.e. that p entails ¬d. We also have 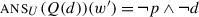 , from which it follows similarly that ¬p entails ¬d. The only way these two entailments can hold is if d is a trivial falsehood. But then, we have
, from which it follows similarly that ¬p entails ¬d. The only way these two entailments can hold is if d is a trivial falsehood. But then, we have  , which is equivalent to p, so p is equivalent to
, which is equivalent to p, so p is equivalent to 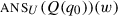 , which is either \(p \land q_{0}\) or \(p \land \neg q_{0}\). This contradicts the assumption that p and \(q_{0}\)/\(\neg q_{0}\) are not related by entailment.
, which is either \(p \land q_{0}\) or \(p \land \neg q_{0}\). This contradicts the assumption that p and \(q_{0}\)/\(\neg q_{0}\) are not related by entailment. -
If d(w)=1 and \(d(w') = 0\), then
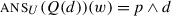 and
and 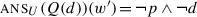 . It follows that p entails d and that ¬p entails ¬d. Hence p is equivalent to d. Then, we have
. It follows that p entails d and that ¬p entails ¬d. Hence p is equivalent to d. Then, we have 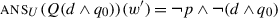 , which is equivalent to ¬p, so ¬p is equivalent to
, which is equivalent to ¬p, so ¬p is equivalent to 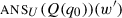 , which is either \(\neg p \land q_{0}\) or \(\neg p \land \neg q_{0}\). It follows that \(\neg q_{0}\) or \(q_{0}\) entails ¬p, against assumption.
, which is either \(\neg p \land q_{0}\) or \(\neg p \land \neg q_{0}\). It follows that \(\neg q_{0}\) or \(q_{0}\) entails ¬p, against assumption. -
If d(w)=0 and \(d(w') = 1\), the same reasoning as in the previous case applies, replacing any occurrence of p with ¬p and vice versa, and replacing \(w'\) with w.
The only remaining possibility is that \(d(w) = d(w') = 1\). Since w can be any p-world and \(w'\) can be any ¬p-world, d has to be a trivial truth in C. □
The next result shows that if conjunctive questions denote the tripartition, then we predict the observed pattern of presupposition filtering in the second conjunct.
Result 7
The tripartition
Let C be a context set, and p a proposition such that there exists a proposition \(q_{0}\) that is not related by contextual entailment to p or ¬p. A proposition d is H-transparent (as well as K/U/W/C-transparent) in the position of q in  if and only if C supports the material conditional p→d.
if and only if C supports the material conditional p→d.
Proof
We define:  .
.
Assume that C supports p→d, and let q be an arbitrary proposition. p∧d∧q is equivalent in C to p∧q, and this relation can equivalently be written as \([p \land d \land q]_{|C} = [p \land q]_{|C}\). Moreover, we have p∧¬(d∧q)=(p∧¬d)∨(p∧¬q), which is equivalent to p∧¬q (as p∧¬d is a contextual contradiction). It follows that Q(q) and Q(d∧q) are H-equivalent in C. Then, for any completion γ, Q(q)γ and Q(d∧q)γ are also H-equivalent in C.Footnote 49 Therefore, d is H-transparent in the position of q in Q(q), and it is also K/U/W/C-transparent.
As for the other direction, assume that d is C-transparent in the position of q in Q(q) in C. As before, it follows from the existence of \(q_{0}\) that p is not trivially true or false in C. Let us then take w∈C such that p(w)=1. If d(w)=0, since  and
and  , p and p∧¬d are contextually equivalent, which is equivalent to saying that C supports p→¬d. Assume without loss of generality (as we could replace \(q_{0}\) by \(\neg q_{0}\)) that \(q_{0}(w) = 1\). Then, we have
, p and p∧¬d are contextually equivalent, which is equivalent to saying that C supports p→¬d. Assume without loss of generality (as we could replace \(q_{0}\) by \(\neg q_{0}\)) that \(q_{0}(w) = 1\). Then, we have  . Since p entails ¬d, it also entails \(\neg d \lor q_{0}\), and therefore
. Since p entails ¬d, it also entails \(\neg d \lor q_{0}\), and therefore  is equivalent to p. By C-transparency, p is thus equivalent to
is equivalent to p. By C-transparency, p is thus equivalent to  , i.e. p is equivalent to \(p \land q_{0}\), or equivalently, p contextually entails \(q_{0}\), against assumptions. Therefore this case is impossible, and d(w)=1. Since this holds for any w such that p(w)=1, C supports p→d. □
, i.e. p is equivalent to \(p \land q_{0}\), or equivalently, p contextually entails \(q_{0}\), against assumptions. Therefore this case is impossible, and d(w)=1. Since this holds for any w such that p(w)=1, C supports p→d. □
Moving on to disjunction, the next result shows that no filtering is predicted to be possible with H/K/U-transparency. The subsequent result is an extension to W-transparency (that an additional condition is needed is essentially a bug in the definition). A final result shows that C-transparency derives a degenerate pattern where everything is transparent.
Result 8
No filtering in alternative questions (H/K/U)
Let C be a context set. A proposition d is H/K/U-transparent in the position of q in ?p∨?q in C if and only if C supports d.
Proof
The direction “If C supports d, then d is transparent” is immediate.
We define Q(q): = ?p∨?q = {p,q}. Assume that d is U-transparent in C. The unique-answer presupposition of Q(⊤) is equivalent to ¬p, from which it follows that the unique-answer presupposition of Q(d) is equivalent to ¬p, i.e. that p⊻d is equivalent to ¬p (⊻ represents an exclusive disjunction). This can be verified to be equivalent to the fact that d is trivially true in C. □
Result 9
No filtering in alternative questions (W)
Let C be a context set, and let d be a proposition that does not contextually entail p.Footnote 50d is W-transparent in the position of q in ?p∨?q if and only if C supports d.
Proof
Once again, define Q(q): = ?p∨?q = {p,q}.
The direction “If C supports d, then d is transparent” is immediate.
Assume that d is W-transparent. Let w be a world such that p(w)=0 and d(w)=1 (such a world exists by assumption).  and
and  , so d is contextually equivalent to ⊤. □
, so d is contextually equivalent to ⊤. □
Result 10
C-equivalence derives a degenerate pattern in alternative questions
Let C be a context set, and let d be a proposition. d is C-transparent in the position of q in ?p∨?q .
Proof
Once again, define Q(q): = ?p∨?q = {p,q}.
Take q to be an arbitrary proposition, and call \(C'\) the set of worlds in C such that p∨(d∧q) and ¬(p∧q) are true. \(C'\) is the biggest subset of C such that the unique-answer presupposition of both Q(q) and Q(d∧q) is met. What we need to prove is that  and
and  define the same two-place predicate over \(C'\), or equivalently that for any \(w \in C'\), both operators return equivalent propositions when applied to w, with equivalence being taken in \(C'\).Footnote 51 Take then w in \(C'\).
define the same two-place predicate over \(C'\), or equivalently that for any \(w \in C'\), both operators return equivalent propositions when applied to w, with equivalence being taken in \(C'\).Footnote 51 Take then w in \(C'\).
-
If p(w)=1, then
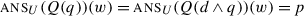 .
. -
If p(w)=0, from the definition of \(C'\) we have d(w)=q(w)=1. It follows that
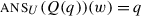 and
and 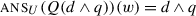 . Due to the way \(C'\) is defined, both q and d∧q are equivalent to ¬p in \(C'\) and therefore to one another, as desired.
. Due to the way \(C'\) is defined, both q and d∧q are equivalent to ¬p in \(C'\) and therefore to one another, as desired.
Thus, d is C-transparent. □
These results are essentially preserved if we look at {p,q,¬(p∨q)} rather than {p,q}; the proofs are omitted to save space.
1.3 3 Trivalent theories: a compositional approach
We now turn to trivalent theories. The simplest way of adapting trivalent theories to our problem is to consider that conjunction and disjunction of propositions are trivalent, and that question conjunction and disjunction just do what they usually do in H/K semantics, except that questions are sets of trivalent propositions. Below we define such a system, called the Simple Trivalent Answer set Theory (STAT). It is straightforward to verify that under STAT, essentially the same results as with the Transparency Theory obtain: the conjunctive case can be dealt with through the tripartition, while the disjunctive case remains puzzling.Footnote 52
Concretely, assume the following:
Definition 11
STAT
-
(i)
Questions are sets of trivalent propositions.
-
(ii)
Question conjunction is pointwise Middle Kleene conjunction.
-
(iii)
Question disjunction is set union.
-
(iv)
Questions are felicitous only if all their answers return 0 or 1 at all worlds in the context.
Result 11
Predictions of STAT
Under the assumptions given in Definition 11:
-
(i)
If a conjunctive question (schema: ?p∧?q) denotes the quadripartition {p∧q,p∧¬q,¬p∧q,¬p∧¬q}, it should presuppose π(p) and π(q).
-
(ii)
If a conjunctive question (schema: ?p∧?q) denotes the tripartition {p∧q,p∧¬q,¬p}, it should presuppose π(p) and p→π(q).
-
(iii)
Whether a disjunctive question (schema: ?p∨?q) denotes {p,q} or {p,q,¬p∧¬q}, it should presuppose π(p) and π(q).
In order to deal with disjunction, one might think that case (iv) in Definition 11 should be relaxed to an existential presupposition: at least one answer should be defined at a given world in the context. We can in fact unify the constraint with the independent assumption, generally made in H/K theories, that questions presuppose that one of their answers is true:
Definition 12
Existential variant of STAT
-
(iv’)
Questions presuppose that at least one answer is defined and true at each world in the context.
The observed case of filtering is immediately predicted, but we derive no order effects.
1.4 4 Trivalent deployment of the connectives
Another way of extending trivalent theories to questions is to apply the methodology of “Peters-Kleene deployment”, as described by George (2014), to derive trivalent meanings for the question connectives from their bivalent meanings. Below we provide an implementation of George’s idea, and derive the same results as with the Transparency Theory: presupposition filtering is predicted for the tripartition but not for the quadripartition as far as conjunction is concerned, and not at all as far as disjunction is concerned (only the case of {p,q} is discussed, as using {p,q,¬p∧¬q} instead does not make a difference).
The idea behind Peters-Kleene deployment is as follows: assume that you want to derive how potential undefinedness in p will project in the environment F(p). What you know is the specification of F in the bivalent world (i.e., you know what F(p) is for a total proposition p). Now define the repair set of a trivalent proposition p: it is the set of all propositions that agree with p wherever p is defined.
Definition 13
Repair set of a trivalent proposition
If p is a trivalent proposition, the repair set of p is written as \(p^{R}\) and given by:
(Here Ω is the set of possible worlds, and therefore \(\{0,1\}^{\Omega}\) is the set of total/bivalent propositions.)
From the repair set of p, we derive the deployment of F, \(F^{D}\). Unlike F(p), \(F^{D}(p)\) is potentially defined for some trivalent inputs p. Those inputs are those where, no matter how p is repaired to form a bivalent proposition \(p'\), \(F(p')\) is the same.
Definition 14
Deployment of a functor
If F is a function whose input is a bivalent proposition, the deployment of F is written as \(F^{D}\) and given by:
-
(i)
If there is an output X such that for all \(p' \in p^{R}\), \(F(p') = X\), then \(F^{D}(p) = X\).
-
(ii)
Otherwise, \(F^{D}(p) = \#\).
In our case, F will be the function from q to the denotation of the question schematized as ?p∧?q or ?p∨?q. The desired result is that even if q is potentially undefined, F(q) might be defined in some cases.
Applying this methodology is most naturally done within a Karttunen-style account. Thus, the output of K will be a Karttunen question (type s(st)t). The definition of deployment above presupposes a notion of equality on the outputs of F; the natural choice in our case is the usual definition of set equality.Footnote 53
We can now prove the results promised above:
Result 12
Deployment of conjunction (quadripartition)
For total propositions p and q, define \(F_{p}(q)\) to represent the Karttunen denotation of a quadripartitive conjunctive question:
Let p be a total proposition that is true in at least two worlds and false in at least two worlds.Footnote 54\(F^{D}_{p}(q)\) is defined if and only if q is total.
Proof
It is clear that if q is total, \(F^{D}_{p}(q)\) is defined (it is just \(F_{p}(q)\)).
Assume that q is not total, i.e. that there is w such that q(w)=#. Take \(q' \in q^{R}\) such that \(q'(w) = 1\), and \(q'' \in q^{R}\) that is exactly the same as \(q'\), except that \(q''(w) = 0\).
-
If p(w)=1, then \(F_{p}(q')(w) = \{p \land q'\}\) and \(F_{p}(g'')(w) = \{p \land \neg q''\}\). Let \(w'\) be another world where p is true: we have \([p \land q'](w') = q'(w')\) and \([p \land q''](w') = q''(w')\). By construction, \(q'(w') \neq q''(w')\), so \(F_{p}(q')(w) \neq F_{p}(g'')(w)\).
-
If p(w)=0, then \(F_{p}(q')(w) = \{\neg p \land q'\}\) and \(F_{p}(q'')(w) =\{\neg p \land \neg q''\}\). Let \(w'\) be another world where p is false: we have \([\neg p \land q'](w') = q'(w')\) and \([\neg p \land q''](w') = q''(w')\). By construction, \(q'(w') \neq q''(w')\), so \(F_{p}(q')(w) \neq F_{p}(g'')(w)\).
Either way, \(F_{p}^{D}(q)\) is not defined. By contraposition, if \(F_{p}^{D}(q)\) is defined, q is total. □
Result 13
Deployment of conjunction (tripartition)
For total propositions p and q, define \(F_{p}(q)\) to represent the Karttunen denotation of a tripartitive conjunctive question:
Let p be a total proposition that is true in at least two worlds. \(F^{D}_{p}(q)\) is defined if and only if all #-worlds for q are 0-worlds for p.Footnote 55
Proof
Assume that q is only undefined at worlds where p is false. Take \(q', q''\) in \(q^{R}\), and let w be a world.
-
If p(w)=0, then \([p \land q'](w) = [p \land q''](w) = 0\), and \([p \land \neg q'](w) = [p \land \neg q''](w) = 0\)
-
If p(w)=1, then q is defined at w and \(q'(w) = q''(w) = q(w)\). If q(w)=1, we have \([p \land q'](w) = [p \land q''](w) = 1\) and \([p \land \neg q'](w) = [p \land \neg q''](w) = 0\). If q(w)=0, we have \([p \land q'](w) = [p \land q''](w) = 0\) and \([p \land \neg q'](w) = [p \land \neg q''](w) = 1\).
Then, \(p \land q' = p \land q''\) and \(p \land \neg q' = p \land \neg q''\), from which the fact that \(F_{p}(q') = F_{p}(q'')\) immediately follows. Therefore \(F_{p}^{D}(q)\) is defined.
As for the other direction, the same reasoning as in the previous result shows that if there is w such that q(w)=# and p(w)=1, then \(F_{p}^{D}(q)\) is not defined. By contraposition, if \(F_{p}^{D}(q)\) is defined, there is no such w. □
Result 14
Deployment of disjunction
For total propositions p and q, define \(F_{p}(q)\) to represent the Karttunen denotation of a disjunctive question:
Let p be a total proposition that is true in at least two worlds. \(F^{D}_{p}(q)\) is defined if and only if q is total.
Proof
It is clear that if q is total, \(F^{D}_{p}(q)\) is defined.
Assume that there is w such that q(w)=#. Take \(q' \in q^{R}\) such that q(w)=1, and \(q'' \in q^{R}\) that is the same as \(q'\), except that \(q''(w) = 0\).
-
If p(w)=0, we have \(F_{p}(q')(w) = \{q'\}\) and \(F_{p}(q'')(w) = \varnothing \).
-
If p(w)=1, we have \(F_{p}(q')(w) = \{p, q'\}\) and \(F_{p}(q'')(w) = \{p\}\). If \(q' \neq p\), \(F_{p}(q')(w) \neq F_{p}(q')(w)\). If \(q' = p\), take \(w'\) such that \(p(w') = 1\). We have \(F_{p}^{D}(q')(w') = \{p, q'\} = \{p\}\) and \(F_{p}(q'')(w') = \{p, q''\}\) (recall that \(q''\) agrees with \(q'\), and therefore with p, at \(w'\)). Since \(q'' \neq q'\) by construction, \(F_{p}(q')(w') \neq F_{p}(q'')(w')\).
Either way, \(F_{p}^{D}(q)\) is not defined. By contraposition, if \(F_{p}^{D}(q)\) is defined, q is total. □
Rights and permissions
About this article
Cite this article
Enguehard, É. Explaining presupposition projection in (coordinations of) polar questions. Nat Lang Semantics 29, 527–578 (2021). https://doi.org/10.1007/s11050-021-09182-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11050-021-09182-2




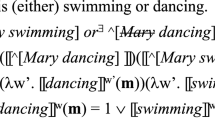
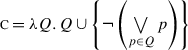


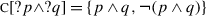
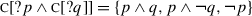
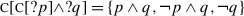
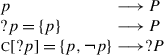
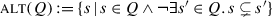
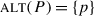
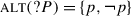
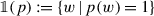
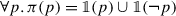
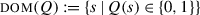
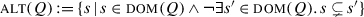
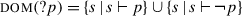
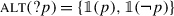
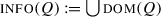



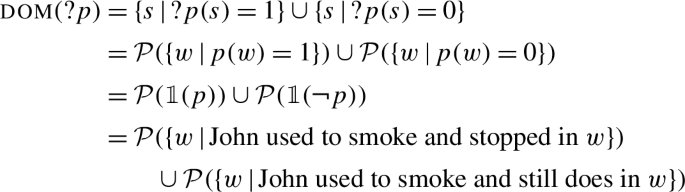


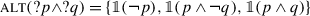
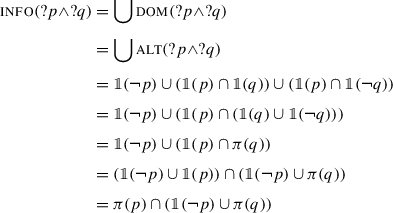
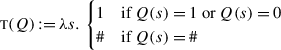


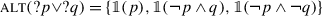
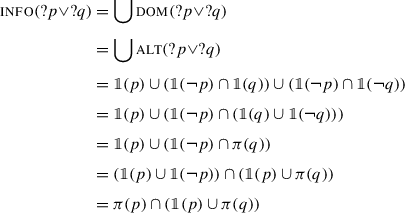
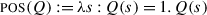
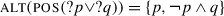 .
.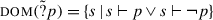
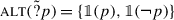
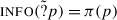
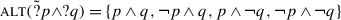
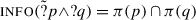
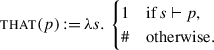
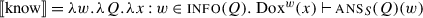
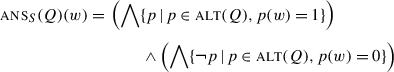

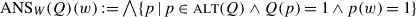
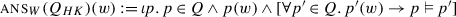
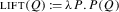 (type (α→t)→t)
(type (α→t)→t)
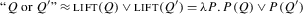
 ’s would only add logical contradictions to the sets, as the reader can verify. We are going to assume that it would make the questions unacceptable.
’s would only add logical contradictions to the sets, as the reader can verify. We are going to assume that it would make the questions unacceptable. and
and 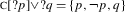 . These options do not have the required property either; I will ignore them here to keep the discussion contained.
. These options do not have the required property either; I will ignore them here to keep the discussion contained. will specifically return (roughly) the Hamblin-Karttunen answers to the question, as opposed to propositions corresponding to the partition cells in the sense of Groenendijk and Stokhof (
will specifically return (roughly) the Hamblin-Karttunen answers to the question, as opposed to propositions corresponding to the partition cells in the sense of Groenendijk and Stokhof ( (then the entry for know would presuppose that we are in a 1-state), or that assertions are embedded under something similar to
(then the entry for know would presuppose that we are in a 1-state), or that assertions are embedded under something similar to  (then the entry for know needs not be changed).
(then the entry for know needs not be changed).
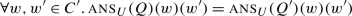
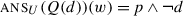 , from which it follows that p∧¬d is equivalent to p, i.e. that p entails ¬d. We also have
, from which it follows that p∧¬d is equivalent to p, i.e. that p entails ¬d. We also have 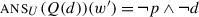 , from which it follows similarly that ¬p entails ¬d. The only way these two entailments can hold is if d is a trivial falsehood. But then, we have
, from which it follows similarly that ¬p entails ¬d. The only way these two entailments can hold is if d is a trivial falsehood. But then, we have  , which is equivalent to p, so p is equivalent to
, which is equivalent to p, so p is equivalent to 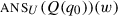 , which is either
, which is either 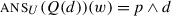 and
and 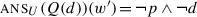 . It follows that p entails d and that ¬p entails ¬d. Hence p is equivalent to d. Then, we have
. It follows that p entails d and that ¬p entails ¬d. Hence p is equivalent to d. Then, we have 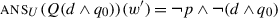 , which is equivalent to ¬p, so ¬p is equivalent to
, which is equivalent to ¬p, so ¬p is equivalent to 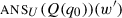 , which is either
, which is either 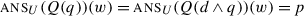 .
.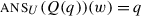 and
and 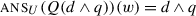 . Due to the way
. Due to the way