1 Introduction

Radar system encounters a great challenge in detecting maneuvering targets with high order motion parameters, e.g. acceleration and jerk (Liu et al. 2016; Xu et al. 2015; Wang et al. 2016). Usually, the target echo is hidden in the noise, prolonging the coherent integration time is an effective approach to increase the signal-to-noise ratio (SNR). However, the complex motions will lead to range migration (RM) and Doppler frequency migration (DFM), which deteriorate the focusing performance.

To correct FRM induced by velocity, the keystone transform (KT) (Perry et al. 1999; Shun-Sheng et al. 2005; Dai et al. 2016) is proposed to rescale the slow time axis and it has an excellent detection performance of multi-targets even in the low SNR environment. However, in order to detect high speed targets, there is a need for the search of Doppler ambiguous integers through high-complexity KT operators. To reduce the computational complexity, Xu et al. (2011) presented the Radon-Fourier transform (RFT) to realize the long time coherent integration. However, RFT still needs to perform a jointly searching along range and velocity directions.

To correct SRM induced by acceleration, the Radon-fractional Fourier transform (RFRFT) (Chen et al. 2013, 2014) is proposed to search the target trajectory and remove DFM by FRFT. In addition, Sun et al. (2011) proposed the SOKT-MFrRT method combing the second-order KT and modified fractional Radon transform. Besides the traditional dechirp (Liu et al. 2003) and FRFT (Qi et al. 2004; Guan et al. 2012) methods, a novel linear frequency-modulated (LFM) signal time-frequency distribution called Lv’s distribution (LVD) (Lv et al. 2011; Luo et al. 2013) is proposed and it has an excellent estimation performance without a heavy searching process. Based on LVD, a method combing KT and LVD (Li et al. 2016) is introduced to estimate the velocity and acceleration of the maneuvering target with a low computational load.

To remove TRM induced by Jerk, Xu et al. (2012) presented the generalized Radon Fourier transform (GRFT). It realizes the coherent integration by a jointly searching process along four parameter directions. Besides a huge amount of computation, GRFT suffers a loss of integration performance with the blind speed sidelobe (BSSL) appearing in the output result. In order to reduce the computational cost, Wang et al. (2015) proposed the modified discrete polynomial-phase transform (MDPT). Utilizing the symmetrical characteristic of discrete slow time, Huang et al. (2015) proposed an acceleration separation method which includes TOKT and Hough transform (HT) Ballard 1987.

Motivated by the previous works, we propose a novel method to correct RM and estimate motion parameters of the maneuvering target. Firstly, TOKT is applied to the range compressed signal to remove TRM. Then, a pair of frequency shifting operations is conducted and the residual RM is removed by cross correlation. After extracting the self term, the velocity and acceleration of the target can be estimated by LVD and compensated. Finally, the jerk can be estimated through the searching process. The main contributions of this paper lie in the following.

  • Proposing a novel algorithm to remove high order RM and estimate motion parameters by LVD, which eliminates the brute-force searching procedure and is effective for the detection of both mono and multiple targets.

  • The proposed method achieves a higher computational efficiency than GRFT.

The rest of this paper is organized as follows. Section 2 presents the signal model and the effect on target detection brought by the motion parameters. Section 3 introduces the proposed method with mono and multiple targets. Section 4 gives the computational complexity analysis of the proposed method. Section 5 provides several simulation results and the anti-noise performance analysis. Finally, the conclusions are given in Sect. 6.

2 Signal model

Suppose that the radar transmits a LFM signal as follows

$$\begin{aligned} s\left( {t_m ,\tau } \right) =\hbox {rect}\left( {\frac{\tau }{T_p }} \right) \exp \left( {j\pi K\tau ^{2}} \right) \hbox {exp}\left( {j2\pi f_c t_m } \right) \end{aligned}$$
(1)

where \(\hbox {rect}\left( x \right) =\left\{ {{\begin{array}{l} {1,\quad \left| x \right| \le 1/2} \\ {0,\quad \left| x \right| > 1/2} \\ \end{array} }} \right. \), \(T_p \) is the pulse duration, K is the frequency modulated rate and \(f_c \) is the carrier frequency.

Assume that the radar emits N pulses during the integration time,\(T_r \) is the pulse repetition interval, \(t_m =mT_r \) is the slow time and \(\tau \) is the fast time. The received baseband signal of a moving target can be stated as

$$\begin{aligned} s_r \left( {t_m ,\tau } \right) =A_1 \hbox {rect}\left[ {\frac{\tau -2R\left( {t_m } \right) /c}{T_p }} \right] \exp \left[ {j\pi K\left( {\tau -\frac{2R\left( {t_m } \right) }{c}} \right) ^{2}} \right] \hbox {exp}\left[ {-j\frac{4\pi }{\lambda }R\left( {t_m } \right) } \right] \nonumber \\ \end{aligned}$$
(2)

where \(A_1 \) is the received signal’s amplitude, \(R\left( {t_m } \right) \) is the instantaneous range between radar and target at the slow time \(t_m \),\(\tau _m (\tau _m =2R\left( {t_m } \right) /c)\) denotes the delay time of the mth received pulse and \(\lambda (\lambda =c/f_c )\) denotes the wavelength of the transmitted signal.

After pulse compression, the compressed signal in the range time domain can be stated as (Huang et al. 2015b)

$$\begin{aligned} s_c \left( {t_m ,\tau } \right) =A_2 \hbox {sinc}\left[ {B\left( {\tau -\frac{2R\left( {t_m } \right) }{c}} \right) } \right] \hbox {exp}\left[ {-j\frac{4\pi }{\lambda }R\left( {t_m } \right) } \right] \end{aligned}$$
(3)

where \(A_2 \) denotes the signal amplitude and B denotes the bandwidth of the transmitted signal.

Considering a maneuvering target with jerk motion, the instantaneous range can be expressed as \(R\left( {t_m } \right) =R_0 +c_1 t_m +c_2 t_m^2 +c_3 t_m^3 \), where \(R_0 \) is the initial range from radar to the target, and \(c_1 ,c_2 ,c_3 \) denote the target’s radial velocity, acceleration and jerk respectively.

From (3), it can be seen that FRM, SRM and TRM are respectively caused by \(c_1 \), \(c_2 \) and \(c_3 \). During the short integration time, SRM and TRM are not obvious and can be neglected. However, with the increasing coherent integration time, the high order RM will deteriorate the detection result. Meanwhile, the quadratic and cubic phases will induce DFM, which makes signal energy defocused.

After performing FT to the variable \(\tau \) in (3), the compressed signal in the range frequency domain can be expressed as

$$\begin{aligned} S_c \left( {t_m ,f} \right) =A_3 \hbox {rect}\left( {\frac{f}{B}} \right) \exp \left[ {-j\frac{4\pi }{c}\left( {f+f_c } \right) R\left( {t_m } \right) } \right] \end{aligned}$$
(4)

where \(A_3 \) denotes the amplitude of the compressed signal after FT.

In the scenario of Doppler ambiguity, the radial velocity can be expressed as \(c_1 =N_a v_a +c_0 \), where \(v_a =\lambda /2T_r\) is the blind velocity, \(N_a \) is the Doppler ambiguity number and \(c_0 =\hbox {mod}\left( {c_1 ,v_a } \right) \) is the unambiguous velocity which satisfies \(\left| {c_0 } \right| <v_a /2\). In this situation, \(S_C \left( {t_m ,f} \right) \) can be expressed as

$$\begin{aligned} S_c \left( {t_m ,f} \right)= & {} A_3 \hbox {rect}\left( {\frac{f}{B}} \right) \exp \left[ {-j\frac{4\pi }{c}\left( {f+f_c } \right) \left( {R_0 +c_0 t_m +c_2 t_m^2 +c_3 t_m^3 } \right) } \right] \nonumber \\&\times \exp \left( {-j\frac{4\pi }{c}fN_a v_a t_m } \right) \end{aligned}$$
(5)

3 Proposed method

3.1 Proposed method with mono-target

3.1.1 Correction of TRM through TOKT

To correct TRM caused by the target’s jerk motion, TOKT is performed in (5) to decouple the range frequency f from \(t_m^3 \), we define the scaled slow time \(t_n \) and perform the scale transform as follows

$$\begin{aligned} t_m =\left( {\frac{f_c }{f_c +f}} \right) ^{1/3}t_n \end{aligned}$$
(6)

After performing TOKT, we can obtain

$$\begin{aligned} S_c \left( {t_n ,f} \right)= & {} A_3 \hbox {rect}\left( {\frac{f}{B}} \right) \exp \left[ {-j\frac{4\pi }{c}\left( {f+f_c } \right) R_0 } \right] \nonumber \\&\times \, \hbox {exp}\left\{ {-j\frac{4\pi }{c}\left[ {c_0 f_c^{1/3} \left( {f+f_c } \right) ^{2/3}t_n +c_2 f_c^{2/3} \left( {f+f_c } \right) ^{1/3}t_n^2 +c_3 f_c t_n^3 } \right] } \right\} \nonumber \\&\times \, \hbox {exp}\left[ {-j\frac{4\pi }{c}f\left( {\frac{f_c }{f_c +f}} \right) ^{1/3}N_a v_a t_n } \right] \end{aligned}$$
(7)

Considering the narrowband environment (\(f\ll f_c )\) and taking Taylor series expansion around range frequency f, we have

$$\begin{aligned} S_c \left( {t_n ,f} \right)= & {} A_3 \hbox {rect}\left( {\frac{f}{B}} \right) \exp \left[ {-j\frac{4\pi }{c}\left( {f+f_c } \right) R_0 } \right] \nonumber \\&\times \, \hbox {exp}\left[ {-j\frac{4\pi f}{c}\left( {\frac{2}{3}c_0 t_n +N_a v_a t_n +\frac{1}{3}c_2 t_n^2 } \right) } \right] \nonumber \\&\times \, \hbox {exp}\left[ {-j\frac{4\pi f_c }{c}\left( {c_0 t_n +c_2 t_n^2 +c_3 t_n^3 } \right) } \right] \end{aligned}$$
(8)

Performing IFT to the variable f in (8), we can obtain the signal in the range time domain as follows

$$\begin{aligned} s_c \left( {t_n ,\tau } \right)= & {} A_4 \hbox {sinc}\left[ {B\left( {\tau -R_T \left( {t_n } \right) } \right) } \right] \hbox {exp}\left( {-j\frac{4\pi f_c }{c}R_0 } \right) \nonumber \\&\times \, \hbox {exp}\left[ {-j\frac{4\pi f_c }{c}\left( {c_0 t_n +c_2 t_n^2 +c_3 t_n^3 } \right) } \right] \end{aligned}$$
(9)

where \(A_4 \) denotes the amplitude after IFT, \(R_T \left( {t_n } \right) =R_0 +\frac{2}{3}c_0 t_n +N_a v_a t_n +\frac{1}{3}c_2 t_n^2\), which represents the residual RM change with the variety of \(t_n\) after TOKT.

It is obvious that TRM has been corrected after TOKT. However, residual RM exists and the coupling effect is still remaining in the linear and quadratic exponential terms, thus it is necessary to perform the decoupling operation.

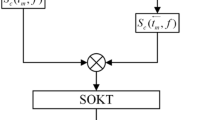
Normally, the Doppler spectrum of a maneuvering target is located in one pulse repetition frequency (PRF) band which satisfies \(f_m \in N_a PRF+\left[ {-PRF/2,PRF/2} \right] \), as it is shown in Fig. 1a. In this situation, TOKT result will be a curve containing the residual RM as the aforementioned analysis. However, the Doppler spectrum may span over two neighboring PRF bands during a long integration time as shown in Fig. 1b, and the trajectory after TOKT will be split into two parts with different slopes. Here it is necessary to perform a direct PRF/2 spectrum shifting before TOKT by multiplying the compensation function in (10) with (5) yields (Zhu et al. 2011).

$$\begin{aligned} H_{shift} \left( {t_m ,f} \right) =\hbox {exp}\left[ {-j\frac{4\pi }{c}\left( {f+f_c } \right) \frac{\lambda }{4T_r }t_m } \right] \end{aligned}$$
(10)

After shifting, the Doppler spectrum can be located in one PRF band and the resultant trajectory will become continuous. The above two cases are based on the condition that the bandwidth of Doppler spectrum is narrower than PRF / 2. However, if the bandwidth is wider than PRF / 2 as shown in Fig. 1c, direct shifting by PRF / 2 will become invalid and we need to employ the azimuth deramp method presented by Sun et al. (2013).

Fig. 1
figure 1

Doppler spectrum in the azimuth dimension. a Case 1: Spectrum entirely in one PRF band (\(B_m <PRF/2)\), b Case 2: Spectrum spanning over two neighboring PRF bands (\(B_m <PRF/2)\), c Case 3: Spectrum spanning over two neighboring PRF bands (\(B_m >PRF/2)\)

Full size image

3.1.2 Correction of FRM and SRM

In what follows, we propose a novel method to remove FRM and SRM simultaneously. A cross correlation function implemented in the range frequency domain is constructed as

$$\begin{aligned} s_{c2} \left( {t_n ,\tau } \right)= & {} \mathop {\hbox {IFT}}\limits _f \left[ {\hbox {S}_c^*\left( {t_n ,f-\frac{B}{4}} \right) S_c \left( {t_n ,f+\frac{B}{4}} \right) }\right] \nonumber \\= & {} A_5 \hbox {sinc}\left( {\frac{B}{2}\tau } \right) \hbox {exp}\left[ {-j\frac{2\pi B}{c}R_T \left( {t_n } \right) } \right] \end{aligned}$$
(11)

where \(A_5 \) is the amplitude after cross correlation.

In (11), \(S_c \left( {t_n ,f} \right) \) is separately shifted by \(-B/4\) and B / 4 on the variable f, and then the conjugate multiplication of the two frequency shifted signals and IFT are conducted. It can be seen that FRM and SRM are simultaneously corrected, and the target’s energy is located in the same range cell which corresponds the zero time delay (\(\tau =0)\).

After extracting the signal from \(s_{c2} \left( {t_n ,\tau }\right) \) at zero delay cell, we can obtain a LFM signal with the centroid frequency \(f_0 \) and chirp rate \(K_{0} \) as follows

$$\begin{aligned} s_0 \left( {t_n } \right) =A_5 \hbox {exp}\left( {-j\frac{2\pi B}{c}R_0 } \right) \hbox {exp}\left( {j2\pi f_0 t_n +j\pi K_0 t_n^2 } \right) \end{aligned}$$
(12)

where

$$\begin{aligned} f_0= & {} -\frac{B}{c}\left( {\frac{2}{3}c_0 +N_a v_a } \right) \end{aligned}$$
(13)
$$\begin{aligned} K_0= & {} -\frac{2B}{3c}c_2 \end{aligned}$$
(14)

3.1.3 Estimating radial velocity and acceleration through LVD

The LVD method can estimate the centroid frequency and chirp rate of a certain LFM signal by obtaining an impulse in the centroid frequency and chirp rate (CFCR) domain. Here, we employ LVD to estimate \(f_0 \) and \(K_0 \) of \(s_0 \left( {t_n } \right) \), detailed implementation process of LVD are discussed in the follows.

The parametric symmetric instantaneous autocorrelation function (PSIAF) of (12) is defined by

$$\begin{aligned} R_0^C \left( {t_n ,\tau _k } \right)= & {} s_0 \left( {t_n +\frac{\tau _k +a}{2}} \right) s_0^*\left( {t_n -\frac{\tau _k +a}{2}} \right) \nonumber \\= & {} A_5^2 \hbox {exp}\left[ {j2\pi f_0 \left( {\tau _k +a} \right) +j2\pi K_0 \left( {\tau _k +a} \right) t_n } \right] \end{aligned}$$
(15)

where \(\tau _k \) denotes a lag variable and a denotes a constant time delay related to a scaling operator.

From (15), it is easily seen that the time variable \(t_n \) and lag variable \(\tau _k \) couple with each other in the exponential terms. Such a coupling between \(t_n \) and \(\tau _k \) in the 2-D linear phase component is the underlying mechanism for the blurred representation of the LFM signals on the 2-D parameter plane due to the linear frequency migration. In order to remove the coupling, we do the scale transform as follows

$$\begin{aligned} t_n =\frac{t_k }{h\left( {\tau _k +a} \right) } \end{aligned}$$
(16)

where \(t_k \) is called the scaled time and h is a scaling factor.

Applying the scale transform (16) to (15), we have

$$\begin{aligned} R_0^C \left( {t_k ,\tau _k } \right) =A_5^2 \hbox {exp}\left[ {j2\pi f_0 \left( {\tau _k +a} \right) +j2\pi \frac{K_0 }{h}t_k } \right] \end{aligned}$$
(17)

Generally a = 1 and h = 1, after performing 2-D FT on (17) with respect to \(\tau _k \) and \(t_k \), we can obtain

$$\begin{aligned} L_0 \left( {f,\gamma } \right) =A_6 \hbox {exp}\left( {j2\pi f} \right) \hbox {sinc}\left( {f-f_0 } \right) \hbox {sinc}\left( {\gamma -K_0 } \right) \end{aligned}$$
(18)

where \(A_6 \) denotes the amplitude after 2-D FT.

It can be seen clearly that after decoupling procedure and 2-D FT, the LFM signal is accumulated as a peak in the CFCR domain, then \(f_{0} \) and \(K_0 \) can be estimated from the peak position.

According to (13) and (14), the estimated value of \(c_1 \) and \(c_2 \) can be expressed as

$$\begin{aligned} \hat{c}_1= & {} \frac{1}{2}\hbox {mod}\left( {-\frac{c}{B}f_0 ,v_a } \right) -\frac{c}{B}f_0 \end{aligned}$$
(19)
$$\begin{aligned} \hat{c}_2= & {} -\frac{3c}{2B}K_0 \end{aligned}$$
(20)

3.1.4 Estimation of jerk

After compensating \(c_1 \) and \(c_2 \) of the compressed signal \(S_c \left( {t_m ,f} \right) \) in (4), we can obtain

$$\begin{aligned} S_c^{\prime } \left( {t_m ,f} \right) =A_3 \hbox {rect}\left( {\frac{f}{B}} \right) \exp \left[ {-j\frac{4\pi }{c}\left( {f+f_c } \right) \left( {R_0 +c_3 t_m^3 } \right) } \right] \end{aligned}$$
(21)

Utilizing the searching jerk \(c_{3,search} \) to construct the corresponding matched function as follows

$$\begin{aligned} H_m \left( {t_m ,f} \right) =\exp \left[ {j\frac{4\pi }{c}\left( {f+f_c } \right) c_{3,search} t_m^3 } \right] \end{aligned}$$
(22)

Then, the estimated value of \(c_3 \) can be expressed as

$$\begin{aligned} \hat{c}_{3} =\mathop {\hbox {argmax}}\limits _{c_{3,search} } \left| {\mathop {\hbox {FT}}\limits _{t_m } \left\{ {\mathop {\hbox {IFT}}\limits _f \left[ {S_c^{\prime } \left( {t_m ,f} \right) H_m \left( {t_m ,f} \right) } \right] } \right\} } \right| \end{aligned}$$
(23)

3.2 Proposed method with multi-targets

From the aforementioned analysis, it is demonstrated that the motion parameters of a single target can be effectively estimated by the proposed method. However, it should be noted that in the scenario of multiple targets, the cross terms exist and it is necessary to consider their effect on the performance of parameter estimation. In this circumstance, the pulse compressed signal in the range frequency domain can be expressed as

$$\begin{aligned} S_c \left( {t_m ,f} \right)= & {} \mathop \sum \limits _{i=1}^N A_{3,i} \hbox {rect}\left( {\frac{f}{B}} \right) \exp \left[ {-j\frac{4\pi }{c}\left( {f+f_c } \right) R_{0,i} } \right] \nonumber \\&\times \exp \left[ {-j\frac{4\pi }{c}\left( {f+f_c } \right) \left( {c_{1,i} t_m +c_{2,i} t_m^2 +c_{3,i} t_m^3 } \right) } \right] \end{aligned}$$
(24)

where N denotes the number of targets,\(A_{3,i} \) denotes the signal amplitude of the ith target, and \(R_i \left( {t_m } \right) =R_{0,i} +c_{1,i} t_m +c_{2,i} t_m^2 +c_{3,i} t_m^3\) denotes the instantaneous range of the ith target.

After performing TOKT and cross correlation, we have

$$\begin{aligned} s_{c2} \left( {t_n ,\tau } \right) =s_{c2,\hbox {self}} \left( {t_n ,\tau } \right) +s_{c2,\hbox {cross}} \left( {t_n ,\tau } \right) \end{aligned}$$
(25)

where

$$\begin{aligned} s_{c2,\hbox {self}} \left( {t_n ,\tau } \right)= & {} \mathop \sum \limits _{i=1}^N A_{5,i} \hbox {sinc}\left( {\frac{B}{2}\tau } \right) \hbox {exp}\left( {-j\frac{2\pi B}{c}R_{0,i} } \right) \nonumber \\&\times \,\hbox {exp}\left[ {-j\frac{2\pi B}{c}\left( {\frac{2}{3}c_{0,i} t_n +N_{a,i} v_a t_n +\frac{1}{3}c_{2,i} t_n^2 } \right) } \right] \end{aligned}$$
(26)
$$\begin{aligned} s_{c2,\hbox {cross}} \left( {t_n ,\tau } \right)= & {} \mathop \sum \limits _{i=1}^N \mathop \sum \limits _{j=1,j\ne i}^N A_{5,ij} \hbox {sinc}\left\{ {\frac{B}{2}\left[ \tau +\frac{2\left( {R_{T,i} \left( {t_n } \right) -R_{T,j} \left( {t_n } \right) } \right) }{c} \right] } \right\} \nonumber \\&\times \, \hbox {exp}\left[ {j\frac{4\pi f_c }{c}R_\Delta \left( {t_n } \right) } \right] \hbox {exp}\left\{ {-j\frac{\pi B}{c}\left[ {R_{T,i} \left( {t_n } \right) +R_{T,j} \left( {t_n } \right) } \right] } \right\} \end{aligned}$$
(27)
$$\begin{aligned} R_{T,i} \left( {t_n } \right)= & {} R_{0,i} +\frac{2}{3}c_{0,i} t_n +N_{a,i} v_a t_n +\frac{1}{3}c_{2,i} t_n^2 \end{aligned}$$
(28)
$$\begin{aligned} R_\Delta \left( {t_n } \right)= & {} R_{0,i} -R_{0,j} +\left( {c_{0,i} -c_{0,j} } \right) t_n +\left( {c_{2,i} -c_{2,j} } \right) t_n^2 +\left( {c_{3,i} -c_{3,j} } \right) t_n^3\nonumber \\ \end{aligned}$$
(29)

\(s_{c2,\hbox {self}} \left( {t_n ,\tau } \right) \) denotes the self terms, \(s_{c2,\hbox {cross}} \left( {t_n ,\tau } \right) \) denotes the cross terms and \(R_{T,i} \left( {t_n } \right) \) represents the residual RM of the ith target after TOKT.

From (25) to (29), it can be seen that the self terms’ energy are located in the same range cell which corresponds the zero time delay. As for the cross terms, their energy spread over a number of cells and can be removed. The extracted self terms are multicomponent LFM signals as follows

$$\begin{aligned} s_0 \left( {t_n } \right) =\sum _{i=1}^N {A_{5,i} \exp \left( {-j\frac{2\pi B}{c}R_{0,i} } \right) \exp \left( {j2\pi f_{0,i} t_n +j\pi K_{0,i} t_n^2 } \right) } \end{aligned}$$
(30)

where

$$\begin{aligned} f_{0,i}= & {} -\frac{B}{c}\left( {\frac{2}{3}c_{0,i} +N_{a,i} v_a } \right) \end{aligned}$$
(31)
$$\begin{aligned} K_{0,i}= & {} -\frac{2B}{3c}c_{2,i} \end{aligned}$$
(32)

It is demonstrated that LVD has an excellent performance on the estimation of multicomponent LFM signals (Lv et al. 2011), thus the velocity and acceleration of each target can be estimated respectively. After compensating the velocity and acceleration of each target, the jerk searching method can be performed to estimate the jerk of each target. The flowchart of the proposed method is shown in Fig. 2.

Fig. 2
figure 2

Flowchart of the proposed method

Full size image
Table 1 Parameters of radar
Full size table

4 Computational complexity analysis

The computational complexity of the proposed method is analyzed in the follows in terms of the number of complex multiplications. It is noted that LVD is implemented by the scaled FT and IFFT (SFT-IFFT) which has a lower computational cost than utilizing discrete FT and inverse fast FT (DFT-IFFT) (Lv et al. 2010).

Fig. 3
figure 3

Simulation results of a single maneuvering target. a Result after range compression. b Result after performing TOKT. c LVD result after without Doppler shifting. d Chirp rate section of LVD result (dB form). e Frequency section of LVD result (dB form). f TOKT result after Doppler shifting. g LVD result after Doppler shifting. h Chirp rate section of LVD result (dB form). i Frequency section of LVD result (dB form). j Search result of jerk

Full size image

Denote that \(N_r \), \(N_p \), M, \(N_{c_3 } \) respectively represent the number of range cells, echo pulses, lag samples and searching jerk. For TOKT, the computational complexity is \(\mathrm{O}\left( {N_p^2 N_r } \right) \). For the cross correlation to remove FRM and SRM, the computational complexity is \(\mathrm{O}\left( {N_p N_r log_2 N_r } \right) \). For LVD and the compensation of radial velocity and acceleration, the computational complexity is \(\mathrm{O}\left( {5MN_p log_2 N_p +MN_p log_2 M+N_p N_r } \right) \). The radial jerk estimation process includes two 1-D FFT operations, and the computational complexity is \(\mathrm{O}\left( {N_{c_3 } N_p N_r log_2 N_r +N_{c_3 } N_p N_r log_2 N_p } \right) \). Suppose that \(N_r =N_p =M=N_{c_3 } =N\), then the computational complexity of the proposed method is \(\mathrm{O}\left( {N^{3}log_2 N} \right) \), whereas the computational complexity of GRFT is \(\mathrm{O}\left( {N^{5}} \right) \). It can be seen that GRFT has a heavier computational burden than the proposed method due to the 4-D searching process. However, the proposed method can remove FRM and SRM simultaneously and then estimate the velocity and acceleration through LVD, the only searching process is applied to the estimation of the jerk.

5 Numerical experiments and performance analysis

In this section, several simulation experiments are provided to demonstrate the performance of the proposed method.

5.1 Proposed method with a Doppler compensation process

From the aforementioned analysis, it is discussed that when the Doppler spectrum of a maneuvering target spans over two neighboring PRF bands, a direct PRF/2 shifting can be utilized to obtain a continuous trajectory after TOKT. In what follows, we consider a single maneuvering target in this situation. The parameters of radar are listed in Table 1.

Assume that the radial velocity, acceleration and jerk of the target are 50 m/s, 6 m/s\(^{2}\) and 2 m/s\(^{3}\) respectively. SNR after range compression is 6 dB.

Fig. 4
figure 4

Simulation results of two maneuvering targets. a Result after range compression. b Result after performing TOKT. c Result after performing frequency shift and cross correlation process. d LVD result. e Jerk searching result of target A. f Jerk searching result of target B

Full size image

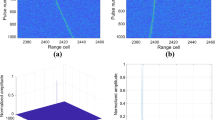
Figure 3 shows the simulation results of the maneuvering target by the proposed method. Figure 3a shows the range compression result. It can be seen that the target trajectory spans over 43 range cells, which includes FRM, SRM and TRM. After performing TOKT, the trajectory is split into two parts as shown in Fig. 3b. This phenomenon occurs for the reason that the Doppler spectrum spans from the first to the second PRF band during the integration time. Figure 3c–e show the LVD result without Doppler shifting process. Figure 3f shows the result after performing the Doppler shifting and TOKT, it can be seen that the trajectory turns into a continuous curve. The LVD result with Doppler shifting process is shown in Fig. 3g–i, compared with the focusing results in Fig. 3c–e, it is observed that the output SNR is effectively improved. Figure 3j shows the searching result of jerk.

5.2 Proposed method with two maneuvering targets

In what follows, we consider two maneuvering targets. The radar system parameters are the same as those listed in Table 1. For target A, \(c_{1,1} \)= 80 m/s, \(c_{2,1} \)= 12 m/s\(^{2}\), \(c_{3,1} \)= 3 m/s\(^{3}\); for target B, \(c_{1,2} \)= 160 m/s, \(c_{2,2} \)= 6 m/s\(^{2}\), \(c_{3,2} = 5\) m/s\(^{3}\). SNR after range compression is 6 dB.

Figure 4 shows the simulation results of the proposed method. Figure 4a shows the range compression result in the range time domain. It can be seen that the RM number of the two targets are respectively 71 and 120. Figure 4b shows the simulation result after performing TOKT, it can be seen that after the correction of TRM, the RM numbers of the two targets are respectively 55 and 105, which involve the residual FRM and SRM.

Figure 4c shows the result after performing frequency shift and cross correlation process. To show the trajectories clearly, the noise is removed from the processing result. It can be seen that there is a straight line in the zero delay cell and it involves two LFM signals, which separately correspond to the two self terms. Meanwhile, there are two cross terms correspond to the two curves which distribute on both sides of the zero delay range cell. Extracting the signal from the zero delay cell is the approach to obtain the self terms and remove the cross terms simultaneously.

After performing LVD, two peaks can be obtained in the CFCR domain. As shown in Fig. 4d, the energy of each target can be integrated respectively, thus the velocity and acceleration of each target can be estimated according to the peak position. Figure 4e, f respectively show the jerk searching result of target A and target B.

5.3 Detection performance analysis

Figure 5 compares the detection performances among the proposed method, the acceleration separation method, RFT, GRFT and MTD. 1000 times of Monte Carlo simulations are done under the Gaussian noises environment, and the probability of false alarm is set to be 10\(^{-6}\). It can be seen that although the acceleration separation method can estimate all the motion parameters, it suffers a serious SNR loss due to the non-linear operations while isolating the acceleration and HT procedure. GRFT has a better detection performance than the proposed method with a much heavier computational burden. The proposed method can obtain a balance between the imaging quality and computational cost, and is effective for multi-targets detection due to the ability to remove the cross terms.

Fig. 5
figure 5

Detection probability of the five methods

Full size image

6 Conclusions

The RM and DFM caused by the velocity, acceleration and jerk of the maneuvering target degrade the performance of correlation integration. In this paper, a novel method is proposed to correct TRM via TOKT, then remove FRM and SRM simultaneously by constructing the cross correlation function of two frequency shifted signals. Thereafter, LVD is applied to estimate the velocity and acceleration by obtaining a peak in the CFCR domain. Finally, the corresponding matched function is constructed to estimate the jerk of the target. Compared with some existing methods, the proposed method has a lower computational cost without a heavy searching procedure. The simulation result of detection probabilities shows that the proposed method has a better detection performance than some other existing methods. In addition, it is validated that the proposed method can be utilized to multi-targets detection.