1 Introduction

With the development of aerospace technology, high-speed maneuvering targets bring challenges to detection ability of radar. High-speed maneuvering targets detection has attracted much more attention for modern radar due to the increasing demands in practical applications, such as motion parameters estimation, target tracking and identification and high-resolution imaging (Xing et al. 2011; Tian et al. 2014; Bar-Shalom et al. 2001; Zhang et al. 2015; Sun et al. 2013; Chen and 2010). Li and Jilkov (2002), gave a comprehensive introduction of techniques for tracking maneuvering targets containing the maneuvering decision methods, which has a high reference value. Nevertheless, as for high-speed weak maneuvering target detection before tracking, tradition accumulation methods may have poor performance. Long-time coherent integration is an effective method to improve the signal-to-noise ratio (SNR) of target. Unfortunately, the long observation time and maneuvering target’s complex motions, e.g., high velocity, acceleration and jerk, will result in range migration (RM) and Doppler frequency migration (DFM) during a coherent integration time, which may seriously deteriorate integration performance.

As for first-order range migration (FRM) caused by target’s radial velocity, several methods have been proposed. The keystone transform (KT) (Perry et al. 1999; Zhu et al. 2007; Li et al. 2008) can correct the FRM without any prior knowledge. The Radon Fourier transform (RFT) (Xu et al. 2011a, b; Yu et al. 2012) eliminates FRM and achieves target detection by jointly searching range and velocity. The axis rotation moving target detection (AR-MTD) (Rao et al. 2014) and the improved axis rotation moving target detection (IAR-MTD) (Xuan et al. 2019) remove FRM by axis rotation. The modified location rotation transform (MLRT) (Sun et al. 2018) can rotate the locations of data coordinates to eliminate FRM. Besides, the scaled inverse Fourier transform (SCIFT) (Zheng et al. 2015) can eliminate FRM and realize coherent integration in low SNR environment.

However, when target maneuvers with a relatively large acceleration, the above-mentioned methods may suffer significant performance loss because they may not efficiently compensate the second-order range migration (SRM) and linear DFM caused by target’s radial acceleration. As for these problems, some effective methods have been proposed recently. The second-order keystone transform (SOKT) (Zhou et al. 2007) can be applied to eliminate the SRM without any searching procedures. The Radon-based methods (Chen et al. 2014; Li et al. 2015) including the Radon-fractional Fourier transform (RFRFT) (Chen et al. 2014) and Radon Lv’s distribution (RLVD) (Li et al. 2015) eliminate FRM and SRM by jointly searching velocity and acceleration, then realize coherent integration by FRFT and LVD. The KT with matched filtering process (KTMFP) (Sun et al. 2017) corrects the LRM caused by unambiguous velocity and then target’s Doppler ambiguity number and acceleration are jointly searched to remove the residual RM and DFM. The SOWVD-based method is proposed in Huang et al. (2016b). This method uses KT and matched filtering process to remove FRM and SRM respectively, and then SOWVD method is applied to realize the target refocusing. Besides, the KT with discrete polynomial-phase transform (KTDPT) (Xin et al. 2017) and a method based on deramp-SOKT-phase difference (deramp-SOKT-PD) (He et al. 2018) have been proposed to achieve target coherent integration without any prior knowledge.

However, for maneuvering target with jerk motion, the third-order range migration (TRM) and quadratic DFM will occur in the long integration time. Unfortunately, the above-mentioned methods don’t take into account the effects of target’s radial jerk, and thus they may not be appropriate.

In order to address these problems, the generalized Radon Fourier transform (GRFT) (Xu et al. 2012), which can remove the RM and DFM via jointly searching target’s range, radial velocity, acceleration and jerk, is proposed to achieve coherent integration for maneuvering targets with jerk motion. Unfortunately, it has high computational complexity because of the 4-D searching of motion parameters. Besides, the GRFT method may result in blind speed side-lobe (BSSL), which brings about serious false alarm. Kong et al. (2015) proposed the generalized KT and generalized dechirp process (GKTGDP). This method corrects TRM, SRM and FRM by third-order KT (TOKT), six-order KT and SOKT, respectively, and removes DFM by searching target’s acceleration and jerk. Although GKTGDP algorithm can achieve a good integration performance, it is still computationally complex because the 3-D searching is performed in the motion parameters space. The KT-based method, which employs the KT and 3-D searching of Doppler ambiguity number, acceleration and jerk to remove the RM and DFM, is recently proposed in Huang et al. (2015). The detection ability and parameters estimation capability of this method are close to GRFT method, but its computational effort is still heavy. Next, several methods (Huang et al. 2016a, 2017, 2018) based on time–frequency analysis are introduced. Huang et al. (2016a), the Radon high-order time chirp rate transform (RHTRT) is proposed, which employs Radon transform (RT) to correct RM and achieves coherent integration as well as jerk estimation by HTRT. However, this method may occur the significant performance loss, because TRM is ignored and high-order nonlinear transforms will lead to cross-terms suppression performance degradation. The method based on generalized Hough-high-order ambiguity function (GHHAF) transform (Huang et al. 2017) removes SRM and FRM by employing SOKT and Hough transform (HT), respectively, and then realizes coherent integration in time–frequency domain by generalized high-order ambiguity function (GHAF) with HT. Although the computational cost of this method is low, the integration performance may severely deteriorate because the cross-terms rejection performance is limited and FRM may not be absolutely correct by incoherent HT. Besides, the TRM caused by target’s radial jerk is also ignored. To address the above problems, Huang et al. (2018) proposed the scaled GHAF (SGHAF), SGHAF can achieve better cross-terms rejection performance than GHHAF method by employing generalized KT instead of incoherent HT. Nevertheless, this method still only employs SOKT and HT to correct RM, which may not correct the RM absolutely. Li et al. (2016) developed the adjacent cross-correlation function iteratively (IACCF) method. This method applies ACCF twice to eliminate RM and DFM. Though the computational cost of IACCF method is very low, this method will result in the coherent integration performance degradation on account of the application of two nonlinear transforms and error propagation effect.

In this paper, we develop a novel method for high-speed maneuvering target detection and motion parameters estimation. The TOKT is carried out to correct the TRM related to radial jerk at first. Then, the matched filtering function, via searching in jerk domain, is conducted to remove quadratic DFM related to radial jerk. If the searching jerk is equal to target’s radial jerk, the third-order phase will be transformed into second-order phase. After that, the second-order phase is reduced to first-order phase by performing the FDPT (Xin et al. 2017) in range-frequency and slow-time domain. Though the SRM and linear DFM caused by acceleration have been removed, the FRM related to radial acceleration still exists. Hence, the TOKT is again carried out to correct the FRM, and then target’s coherent integration is achieved after range IFFT and azimuth FFT. According to the position of peak, the Doppler ambiguity number, acceleration and jerk can be estimated accurately. Finally, we construct a compensation function related to estimated motion parameters in order to eliminate the RM and DFM resulted from blind velocity, acceleration and jerk, and then unambiguous velocity will be effectively estimated after KT. Simulation results testify the effectiveness of the proposed algorithm.

Compared with the methods in Zhou et al. (2007), Chen et al. (2014), Li et al. (2015), Sun et al. (2017), Huang et al. (2016a, b, 2017, 2018), Xin et al. (2017) and He et al. (2018), the proposed method takes into consideration the effects of TRM and quadratic DFM induced by radial jerk, and can remove the TRM and quadratic DFM effectively. In addition, the proposed method has a better anti-noise and cross-terms suppression performance due to only employing once nonlinear transform in comparison with the method in Li et al. (2016). Besides, the computational complexity of the proposed method is lower in comparison with the methods in Xu et al. (2012), Kong et al. (2015) and (Huang et al. 2015), because only target’s jerk whose value is usually small needs to be searched in the proposed method and the TOKT can be quickly implemented by scaling principle (Zhu et al. 2007; He et al. 2018). Therefore, the proposed method can balance the computational complexity and detection ability very well.

The remainder of this paper is organized as follows. In Sect. 2, the mathematical model of received signal for high-speed maneuvering target is established. In Sect. 3, we introduce the proposed method in detail and give the computational complexity analysis. Section 4 gives several simulation experiments to evaluate the coherent integration performance, detection ability and motion parameters estimation capability. In the end, conclusions are drawn in Sect. 5.

2 Signal model

Suppose that the radar transmits a linear frequency modulated (LFM) signal, which can be stated as follows:

$$ s_{t} (t,t_{m} ) = {\text{rect}}\left( {t/T_{p} } \right)\exp \left( {{\text{j}}\uppi\mu t^{2} } \right)\exp \left( {{\text{j2 }\uppi}f_{c} \left( {t_{m} + t} \right)} \right) $$
(1)

where \( {\text{rect}}\left( {\frac{t}{{T_{p} }}} \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {1,} & {\left| t \right| \le T_{p} /2} \\ \end{array} } \\ {\begin{array}{*{20}c} {0,} & {\left| t \right| \ge T_{p} /2} \\ \end{array} } \\ \end{array} } \right. \), t denotes the fast time, \( T_{p} \) denotes the pulse duration, \( \mu \) denotes the frequency modulated rate, \( f_{c} \) denotes the carrier frequency, \( t_{m} = mT_{r} \left( {m = - M/2, \ldots ,M/2 - 1} \right) \) denotes the slow time, \( T_{r} \) is the pulse repetition time, M denotes integrated pulses number.

Supposed that there are K maneuvering targets with complex motions. The instantaneous slant range between the radar and ith target is expressed as

$$ R_{i} \left( {t_{m} } \right) = R_{0,i} + c_{1,i} t_{m} + c_{2,i} t_{m}^{2} + c_{3,i} t_{m}^{3} $$
(2)

where \( R_{0,i} \) represents the initial slant range between the radar and ith target, \( c_{1,i} \), \( c_{2,i} \) and \( c_{3,i} \) are ith target’s radial velocity, acceleration, and jerk, respectively.

After demodulation, the received baseband signal of targets is expressed as

$$ s_{r} \left( {t,t_{m} } \right) = \sum\limits_{i = 1}^{K} {A_{0,i} {\text{rect}}\left( {\frac{{t - 2R_{i} \left( {t_{m} } \right)/c}}{{T_{p} }}} \right)\exp \left( { - j\frac{{4{{\uppi }}f_{c} R_{i} \left( {t_{m} } \right)}}{c}} \right)\exp \left( {j{{\uppi }}\mu \left( {t - \frac{{2R_{i} \left( {t_{m} } \right)}}{c}} \right)^{2} } \right)} $$
(3)

where c indicates the speed of light, and \( A_{0,i} \) is the ith target’s reflectivity.

After pulse compression, the compressed signal can be expressed as

$$ s_{r} \left( {t,t_{m} } \right) = \sum\limits_{i = 1}^{K} {A_{1,i} {\text{sinc}}\left( {B\left( {t - \frac{{2R_{i} \left( {t_{m} } \right)}}{c}} \right)} \right)\exp \left( { - j\frac{{4{{\uppi }}f_{c} R_{i} \left( {t_{m} } \right)}}{c}} \right)} $$
(4)

where A1,i is the amplitude after pulse compression, B denotes the signal bandwidth.

The first term of Eq. (4) represents the envelope of echo signal. It is observed that the peak position of sinc() changes with the slow time duo to the time delay varying with tm, which indicates that the envelope of echo signal changes with the slow time. If the offset exceeds the range resolution, the RM effect will occur. To be more specific, the target’s radial velocity, acceleration, and jerk will result in FRM, SRM and TRM during the coherent integration time, respectively, which may cause the target energy to spread to different range units. Furthermore, the quadratic and cubic terms of tm in the exponential term of Eq. (4) will bring about Doppler frequency migration, which may cause the target energy to spread to different Doppler units.

3 Algorithm description

After performing the FFT on (4) corresponding to the fast time, the compressed signal is stated as

$$ s_{r} \left( {f,t_{m} } \right) = \sum\limits_{i = 1}^{K} {A_{2,i} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left( { - j\frac{{4{{\uppi }}\left( {f + f_{c} } \right)R_{i} \left( {t_{m} } \right)}}{c}} \right)} $$
(5)

where A2,i is the amplitude after performing FFT in fast time domain, f is the range frequency corresponding to the fast time.

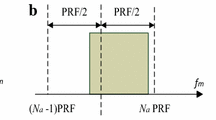
Generally, there is the problem of Doppler ambiguity on account of the low pulse repetition frequency and high speed of targets. As a result, the radial velocity of ith target can be expressed as

$$ c_{1,i} = n_{am,i} v_{a} + v_{0,i} $$
(6)

where \( v_{a} = \lambda PRF/2 \) is the blind velocity, \( \lambda = c/f_{c} \) is the wavelength, \( n_{am,i} \) denotes the Doppler ambiguity number of ith target, \( v_{0,i} \) represents the unambiguous velocity of ith target which meets \( \left| {v_{0,i} } \right| < v_{a} /2 \).

Substituting (6) into (5), it yields

$$ \begin{aligned} s_{r} \left( {f,t_{m} } \right) & = \sum\limits_{i = 1}^{K} {A_{2,i} {\text{rect}}\left( {\frac{f}{B}} \right)} \exp \left[ { - j\frac{4\pi }{c}\left( {f + f_{c} } \right)n_{am,i} v_{a} t_{m} } \right] \\ & \quad \times \exp \left[ { - j\frac{4\pi }{c}\left( {f + f_{c} } \right)\left( {R_{0,i} + v_{0,i} t_{m} + c_{2,i} t_{m}^{2} + c_{3,i} t_{m}^{3} } \right)} \right] \\ \end{aligned} $$
(7)

with \( \exp \left[ { - j4\pi f_{c} n_{am,i} v_{a} t_{m} /c} \right] = 1 \), (7) can be rewritten as

$$ \begin{aligned} s_{r} \left( {f,t_{m} } \right) & = \sum\limits_{i = 1}^{K} {A_{2,i} {\text{rect}}\left( {\frac{f}{B}} \right)} \exp \left[ { - j\frac{4\pi f}{c}n_{am,i} v_{a} t_{m} } \right] \\ & \quad \times \exp \left[ { - j\frac{4\pi }{c}\left( {f + f_{c} } \right)\left( {R_{0,i} + v_{0,i} t_{m} + c_{2,i} t_{m}^{2} + c_{3,i} t_{m}^{3} } \right)} \right] \\ \end{aligned} $$
(8)

3.1 Proposed algorithm for single target

The echo for single target in range frequency and slow time domain is expressed as

$$ \begin{aligned} s_{1} \left( {f,t_{m} } \right) & = A_{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left( { - j\frac{{4\pi R_{0} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)} \right)\exp \left( { - j\frac{{4\pi v_{0} t_{m} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)} \right) \\ & \quad \times \exp \left( { - j\frac{{4\pi c_{2} t_{m}^{2} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)} \right)\exp \left( { - j\frac{{4\pi c_{3} t_{m}^{3} }}{\lambda }\left( {1 + \frac{f}{{f_{c} }}} \right)} \right) \\ & \quad \times \exp \left( { - j\frac{{4\pi n_{am} v_{a} t_{m} }}{\lambda }\frac{f}{{f_{c} }}} \right) \\ \end{aligned} $$
(9)

in order to eliminate the TRM resulted from radial jerk of moving target, the TOKT is applied, which performs scaling transform in the range frequency and slow time domain. The TOKT (Kong et al. 2015) is represented as follows

$$ t_{m} = \left( {f_{c} /\left( {f + f_{c} } \right)} \right)^{1/3} t_{n} $$
(10)

where tn is the new slow time variable.

Substituting the scaling formula into (9), it yields

$$ \begin{aligned} s_{1} \left( {f,t_{n} } \right) & = A_{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left( { - j\frac{{4\pi R_{0} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)} \right)\exp \left( { - j\frac{{4\pi v_{0} t_{n} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{2/3} } \right) \\ & \quad \times \exp \left( { - j\frac{{4\pi c_{2} t_{n}^{2} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{1/3} } \right)\exp \left( { - j\frac{{4\pi c_{3} t_{n}^{3} }}{\lambda }} \right) \\ & \quad \times \exp \left( { - j\frac{{4\pi n_{am} v_{a} t_{n} }}{\lambda }\frac{f}{{f_{c} }}\left( {\frac{{f_{c} }}{{f + f_{c} }}} \right)^{1/3} } \right) \\ \end{aligned} $$
(11)

From Eqs. (9)–(11), it is observed that the \( \exp \left( { - j\frac{{4\pi c_{3} t_{m}^{3} }}{\lambda }\frac{f}{{f_{c} }}} \right) \) has been eliminated after the TOKT operation. In other words, the cubic coupling between tm and f has been eliminated and the TRM has been corrected. However, the quadratic DFM caused by radial jerk still exists. Therefore, a matched filtering function is constructed to eliminate the cubic phase term. The expression of the matched filtering function can be stated as

$$ H_{m} \left( {t_{n} } \right) = \exp \left( {j\frac{{4\pi a_{3} t_{n}^{3} }}{\lambda }} \right) $$
(12)

where a3 denotes the searching jerk. When a3 is equal to c3, multiplying (12) to (11) is represented as

$$ \begin{aligned} s_{1} \left( {f,t_{n} } \right) & = A_{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left( { - j\frac{{4\pi R_{0} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)} \right)\exp \left( { - j\frac{{4\pi v_{0} t_{n} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{2/3} } \right) \\ & \quad \times \exp \left( { - j\frac{{4\pi c_{2} t_{n}^{2} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{1/3} } \right)\exp \left( { - j\frac{{4\pi n_{am} v_{a} t_{n} }}{\lambda }\frac{f}{{f_{c} }}\left( {\frac{{f_{c} }}{{f + f_{c} }}} \right)^{1/3} } \right) \\ \end{aligned} $$
(13)

From (13), it is observed that the quadratic DFM caused by radial jerk has been eliminated. Nevertheless, the FRM caused by target’s unambiguous velocity \( v_{0} \) as well as blind velocity \( v_{a} \) still exists. Besides, the linear DFM and SRM caused by radial acceleration c2 are also present.

To solve the issues above, we utilize FDPT, which can be used to reduce the target phase order, to eliminate the SRM and linear DFM simultaneously. The FDPT (Xin et al. 2017) is represented as

$$ s_{2} \left( {f,t_{n} } \right) = s_{1} \left( {f,t_{n} + \frac{{\tau_{0} }}{2}} \right) \cdot \left[ {s_{1} \left( {f,t_{n} - \frac{{\tau_{0} }}{2}} \right)} \right]^{ * } $$
(14)

where \( \tau_{0} \) represents the fixed lay time and * denotes the conjugate operation. Substituting (13) into (14) yields

$$ \begin{aligned} s_{2} \left( {f,t_{n} } \right) & = A_{2}^{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left( { - j\frac{{4\pi v_{0} \tau_{0} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{2/3} } \right) \\ & \quad \times \exp \left( { - j\frac{{8\pi c_{2} t_{n} \tau_{0} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{1/3} } \right)\exp \left( { - j\frac{{4\pi n_{am} v_{a} \tau_{0} }}{\lambda }\frac{f}{{f_{c} }}\left( {\frac{{f_{c} }}{{f + f_{c} }}} \right)^{1/3} } \right) \\ \end{aligned} $$
(15)

From (15), it is observed that the order of slow time tn has been reduced from second-order to first-order. Meanwhile, the SRM and linear DFM have been eliminated. Also, the FRM caused by blind speed is corrected. However, the FRM related to radial acceleration c2 is still present, which would also result in the dispersion of target energy in different range units and a serious integration performance loss. Therefore, we utilize TOKT to remove the coupling between range frequency f and slow time tn once again. The expression of TOKT (Kong et al. 2015) is as shown in (10).

Substituting (10) into (15), it yields

$$ \begin{aligned} s_{2} \left( {f,t_{n} } \right) & = A_{2}^{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left( { - j\frac{{4\pi v_{0} \tau_{0} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{2/3} } \right) \\ & \quad \times \exp \left( { - j\frac{{8\pi c_{2} t_{a} \tau_{0} }}{\lambda }} \right)\exp \left( { - j\frac{{4\pi n_{am} v_{a} \tau_{0} }}{\lambda }\frac{f}{{f_{c} }}\left( {\frac{{f_{c} }}{{f + f_{c} }}} \right)^{1/3} } \right) \\ \end{aligned} $$
(16)

where ta is the new slow time variable. We have \( f \ll f_{c} \) under narrowband condition. Thus, on the basis of first-order Tylor series expansion, we have

$$ \left( {\frac{{f_{c} }}{{f + f_{c} }}} \right)^{1/3} = 1 - \frac{f}{{3f_{c} }},\quad \left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{2/3} = 1 + \frac{2f}{{3f_{c} }} $$
(17)

Substituting (17) into (16), we have

$$ \begin{aligned} s_{2} \left( {f,t_{a} } \right) & = A_{2}^{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left( { - j\frac{{8\pi v_{0} \tau_{0} f}}{3c}} \right)\exp \left( { - j\frac{{4\pi n_{am} v_{a} \tau_{0} f}}{c}} \right) \\ & \quad \times \exp \left( { - j\frac{{4\pi v_{0} \tau_{0} }}{\lambda }} \right)\exp \left( { - j\frac{{8\pi c_{2} t_{a} \tau_{0} }}{\lambda }} \right) \\ \end{aligned} $$
(18)

known from He et al. (2018), \( \exp \left( {j\frac{{4\pi n_{am} v_{a} \tau_{0} }}{c}\frac{{f^{2} }}{{3f_{c} }}} \right) \) can be ignored because it is much smaller than \( \pi /4 \). In addition, it is observed that the residual FRM related to radial acceleration c2 has been removed from (18). Therefore, after performing IFFT along range frequency and FFT along slow time, the coherent integration of high speed maneuvering target can be achieved, i.e.,

$$ \begin{aligned} s_{3} \left( {t,f_{m} } \right) & = {\text{FFT}}_{{t_{a} }} \left\{ {{\text{IFFT}}_{f} \left[ {s_{2} \left( {f,t_{a} } \right)} \right]} \right\} \\ & \quad = A_{3} {\text{sinc}}\left[ {B\left( {t - \left( {\frac{{4v_{0} }}{3} + 2n_{am} v_{a} } \right)\frac{{\tau_{0} }}{c}} \right)} \right] \\ & \quad \times \sin c\left[ {T_{a} \left( {f_{m} + \frac{{4c_{2} \tau_{0} }}{\lambda }} \right)} \right]\exp \left( { - j\frac{{4\pi v_{0} \tau_{0} }}{\lambda }} \right) \\ \end{aligned} $$
(19)

where A3 denotes the target’s amplitude after coherent integration, fm is the Doppler frequency corresponding to slow time, and Ta is the integration time. Furthermore, \( {\text{FFT}}_{{t_{a} }} \left[ {} \right] \) and \( {\text{IFFT}}_{f} \left[ {} \right] \) represent the FFT operation along slow time variable ta and IFFT operation along range frequency variable f, respectively.

From (12)–(19), we can find that the target will be well focused at \( t = \left( {4v_{0} /3 + 2n_{am} v_{a} } \right)\tau_{0} /c \) and \( f_{m} = - 4c_{2} \tau_{0} /\lambda \) as long as the target’s jerk c3 is matched exactly. Using the peak detection technique (Su et al. 2010), the estimations of target’s acceleration c2, Doppler ambiguity number nam and jerk c3 are as follows:

$$ \hat{c}_{2} = {{ - \frac{{\hat{f}_{m} \lambda }}{{4\tau_{0} }}\quad \hat{n}_{am} = \left\lfloor {\frac{{c\hat{t}}}{{\tau_{0} v_{a} }}} \right\rfloor } \mathord{\left/ {\vphantom {{ - \frac{{\hat{f}_{m} \lambda }}{{4\tau_{0} }}\quad \hat{n}_{am} = \left\lfloor {\frac{{c\hat{t}}}{{\tau_{0} v_{a} }}} \right\rfloor } 2}} \right. \kern-0pt} 2} $$
(20)
$$ \hat{c}_{3} = \mathop {\arg \hbox{max} }\limits_{{a_{3} }} \left| {{\text{FFT}}_{{t_{a} }} \left\{ {{\text{IFFT}}_{f} \left\{ {{\text{TOKT}}\left[ {{\text{DPT}}\left[ {{\text{TOKT}}\left[ {s_{1} \left( {f,t_{m} } \right)} \right]H_{m} \left( {t_{n} } \right)} \right]} \right]} \right\}} \right\}} \right| $$
(21)

where ⌊⌋ denotes round down operation. Besides, \( {\text{TOKT}}\left[ {} \right] \) and \( {\text{DPT}}\left[ {} \right] \) represent the third-order KT operation and first-order DPT operation, respectively. According to Eq. (21), we have

$$ \begin{aligned} s_{3} \left( {t,t_{a} ,f_{m} } \right) & = A_{3} {\text{sinc}}\left[ {B\left( {t - \left( {\frac{{4v_{0} }}{3} + 2n_{am} v_{a} - 4\left( {c_{3} - a_{3} } \right)t_{a}^{2} } \right)\frac{{\tau_{0} }}{c}} \right)} \right] \\ & \quad \times {\text{FFT}}_{{t_{a} }} \left[ {\exp \left( { - j\frac{{8\pi c_{2} t_{a} \tau_{0} }}{\lambda }} \right)\exp \left( { - j\frac{{12\pi t_{a}^{2} \tau_{0} }}{\lambda }\left( {c_{3} - a_{3} } \right)} \right)} \right] \\ & \quad \times \exp \left( { - j\frac{{\pi \tau_{0}^{3} }}{\lambda }\left( {c_{3} - a_{3} } \right)} \right)\exp \left( { - j\frac{{4\pi v_{0} \tau_{0} }}{\lambda }} \right) \\ \end{aligned} $$
(22)

From (22), we can find that only when the radial jerk c3 is exactly matched by searching jerk a3 can the RM and DFM be eliminated absolutely, and the target energy can be well accumulated as a peak in fast time-Doppler frequency domain as shown in (19). Nevertheless, if the above condition is not satisfied, the target energy will still be spread to different range bins and Doppler frequency bins, which may result in the deterioration of accumulation performance. Therefore, while we apply Eq. (21) to estimate the radial jerk c3, the searching jerk which maximizes the target energy after coherent integration is what we want.

Then, based on the estimated parameters, a compensation function \( H_{match} \left( {f,t_{m} ,\hat{c}_{2} ,\hat{c}_{3} ,\hat{n}_{am} } \right) \) will be constructed to eliminate RM and DFM resulted from \( v_{a} \), c2, c3. The compensation function can be expressed as

$$ \begin{aligned} H_{match} \left( {f,t_{m} ,\hat{c}_{2} ,\hat{c}_{3} ,\hat{n}_{am} } \right) & = \exp \left( {j\frac{4\pi }{\lambda }\frac{{\left( {f + f_{c} } \right)}}{{f_{c} }}\left( {\hat{c}_{2} t_{m}^{2} + \hat{c}_{3} t_{m}^{3} } \right)} \right) \\ & \quad \times \exp \left( {j\frac{{4\pi \hat{n}_{am} v_{a} t_{m} }}{\lambda }\frac{f}{{f_{c} }}} \right) \\ \end{aligned} $$
(23)

Substituting (23) into (9), it yields

$$ s_{4} \left( {f,t_{m} } \right) = A_{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left[ { - j\frac{4\pi }{\lambda }\frac{{\left( {f + f_{c} } \right)}}{{f_{c} }}\left( {R_{0} + v_{0} t_{m} } \right)} \right] $$
(24)

From (24), it is seen that the RM and DFM induced by \( v_{a} \), c2, and c3 have been eliminated. Nevertheless, the FRM related to target’s unambiguous velocity \( v_{0} \) is still present, which may cause defocusing of maneuvering target. Then, the KT is applied to correct the FRM. The KT (Perry et al. 1999; Zhu et al. 2007; Li et al. 2008) can be stated as follows:

$$ t_{m} = \frac{{f_{c} }}{{f + f_{c} }}\eta_{m} $$
(25)

where \( \eta_{m} \) represents the new slow time variable.

Substituting (25) into (24) and performing range IFFT and azimuth FFT, it yields

$$ s_{5} \left( {t,f_{m} } \right) = A_{4} {\text{sinc}}\left( {B\left( {t - \frac{{2R_{0} }}{c}} \right)} \right){\text{sinc}}\left( {T_{a} \left( {f_{m} + \frac{{2v_{0} }}{\lambda }} \right)} \right) $$
(26)

where A4 denotes the integrated amplitude. We can find that a peak will occur at \( t = 2R_{0} /c \) and \( f_{m} = - 2v_{0} /\lambda \) from (26), and then the unambiguous velocity \( v_{0} \) can be estimated as \( \hat{v}_{0} = - \hat{f}_{m} \lambda /2 \). Therefore, the target’s radial velocity c1 is calculated as

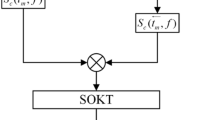
$$ \hat{c}_{1} = \frac{{ - \hat{f}_{m} \lambda }}{2} + \hat{n}_{am} \frac{\lambda PRF}{2} $$
(27)

From the above procedures, we come to the conclusions that the proposed algorithm has the ability to achieve refocusing of high-speed maneuvering target only with 1-D motion parameter searching procedure. In addition, the proposed method can reduce radar system complexity obviously by reducing the parameters searching dimension in comparison with methods in (Xu et al. 2012; Kong et al. 2015; Huang et al. 2015). Besides, the proposed method can get better parameters estimation performance in comparison with the parameters estimation methods in Huang et al. (2016a, 2017, 2018), because the RM and FRM are compensated completely. The flowchart of proposed algorithm is shown in Fig. 1.

Fig. 1
figure 1

Flowchart of the proposed algorithm

Full size image

According to the analysis above, an example is given to prove how the proposed method eliminates target’s RM and DFM and achieves target refocusing.

Example 1

Assume there is a maneuvering target with jerk motion in the scene. Radar parameters are: the pulse repetition frequency PRF is 1000 Hz, the number of integration pulse is 1000, the carrier frequency fc is 1 GHz, the signal bandwidth B is 15 MHz, the sample frequency fs is 60 MHz. The parameters of this maneuvering target are set as: initial slant range R0 = 100.9 km, velocity c1 = 1500 m/s, acceleration c2 = 40 m/s2 and jerk c3 = 30 m/s3. Simulation results are given in Fig. 2.

Fig. 2
figure 2

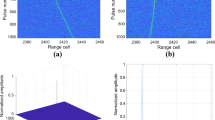
Accumulation results for signal target. a Maneuvering target trajectory after range compression. b Echoes of 1th and 1000th pulses after range compressed. c Third-order KT result. d Echoes of 1th and 1000th pulses after third-order KT. e RM correction result. f Accumulation result of the proposed method. g Searching result of jerk

Full size image

The target echo in range frequency and slow time domain is given in Fig. 2a, and the results of 1th and 1000th pulses after range compressed are given in Fig. 2b. Obviously, it is observed that the serious RM (FRM, SRM and TRM) occurs in the scene and the number of RM is 603. The results after performing TOKT are shown in Fig. 2c, d. It is observed that the number of RM is reduced to 599, which is 4 range cells less than Fig. 2b. The result after performing first-order DPT and TOKT is given in Fig. 2e. We can find that the target motion trajectory is a straight line parallel to the slow time axis and target’s RM has been corrected. Then, a well-focused peak occurs in Fig. 2f after the range IFFT and azimuth FFT, which demonstrates that the proposed method can eliminate the effect of high-order RM and DFM. Meanwhile, according to the peak position, the Doppler ambiguity number and acceleration can be respectively estimated as 10 and 39.92 m/s2. Figure 2g shows the searching result of jerk. Obviously, we can easily find that jerk can be estimated as 30 m/s3 according to peak position. Then, after compensation and KT procedure, the unambiguous velocity can be estimated as − 0.02 m/s, so we can estimate target’s velocity as 1499.98 m/s.

3.2 Proposed algorithm for multiple targets

As for multiple targets detection, the proposed method will introduce cross-terms interference inevitably because FDPT is the nonlinear transform. Next, the effects of cross-terms on coherent integration for multiple targets will be analyzed. After carrying out TOKT on multiple targets motion model as shown in (8), it yields

$$ \begin{aligned} s_{mul,1} \left( {f,t_{n} } \right) & = \sum\limits_{i = 1}^{K} {A_{2,i} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left( { - j\frac{{4\pi R_{0,i} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)} \right)} \\ & \quad \times \exp \left( { - j\frac{{4\pi v_{0,i} t_{n} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{2/3} } \right)\exp \left( { - j\frac{{4\pi c_{2,i} t_{n}^{2} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{1/3} } \right) \\ & \quad \times \exp \left( { - j\frac{{4\pi c_{3,i} t_{n}^{3} }}{\lambda }} \right)\exp \left( { - j\frac{{4\pi n_{am,i} v_{a} t_{n} }}{\lambda }\frac{f}{{f_{c} }}\left( {\frac{{f_{c} }}{{f + f_{c} }}} \right)^{1/3} } \right) \\ \end{aligned} $$
(28)

From (28), it is observed that the TRM has been corrected after TOKT. Multiplying the matched filtering function as shown in (12)–(28), it yields

$$ \begin{aligned} s_{mul,1} \left( {f,t_{n} } \right) & = \sum\limits_{i = 1}^{K} {A_{2,i} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left( { - j\frac{{4\pi R_{0,i} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)} \right)} \\ & \quad \times \exp \left( { - j\frac{{4\pi v_{0,i} t_{n} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{2/3} } \right)\exp \left( { - j\frac{{4\pi c_{2,i} t_{n}^{2} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{1/3} } \right) \\ & \quad \times \exp \left( { - j\frac{{4\pi \left( {c_{3,i} - a_{3} } \right)t_{n}^{3} }}{\lambda }} \right)\exp \left( { - j\frac{{4\pi n_{am,i} v_{a} t_{n} }}{\lambda }\frac{f}{{f_{c} }}\left( {\frac{{f_{c} }}{{f + f_{c} }}} \right)^{1/3} } \right) \\ \end{aligned} $$
(29)

After performing FDPT on (29), we have

$$ \begin{aligned} s_{mul,2} \left( {f,t_{n} } \right) & = \sum\limits_{i = 1}^{K} {A_{2,i}^{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left( { - j\frac{{4\pi v_{0,i} \tau_{0} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{2/3} } \right)} \\ & \quad \times \exp \left( { - j\frac{{8\pi c_{2,i} t_{n} \tau_{0} }}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{1/3} } \right) \\ & \quad \times \exp \left( { - j\frac{{4\pi \left( {c_{3,i} - a_{3} } \right)\left( {3t_{n}^{2} \tau_{0} + \tau_{0}^{3} /4} \right)}}{\lambda }} \right) \\ & \quad \times \exp \left( { - j\frac{{4\pi n_{am,i} v_{a} \tau_{0} }}{\lambda }\frac{f}{{f_{c} }}\left( {\frac{{f_{c} }}{{f + f_{c} }}} \right)^{1/3} } \right) + s_{cross} \left( {f,t_{n} } \right) \\ \end{aligned} $$
(30)

where

$$ \begin{aligned} s_{cross} \left( {f,t_{n} } \right) & = \sum\limits_{l = 1}^{K} {\sum\limits_{j = 1,j \ne l}^{K} {A_{2,l} A_{2,j} {\text{rect}}\left( {\frac{f}{B}} \right)} } \exp \left[ { - j\frac{{4\pi \left( {R_{0,l} - R_{0,j} } \right)}}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)} \right] \\ & \quad \times \exp \left[ { - j\frac{{4\pi \left( {\left( {v_{0,l} - v_{0,j} } \right)t_{n} + \left( {v_{0,l} + v_{0,j} } \right)\tau_{0} /2} \right)}}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{2/3} } \right] \\ & \quad \times \exp \left[ { - j\frac{{4\pi \left( {\left( {c_{2,l} - c_{2,j} } \right)\left( {t_{n}^{2} + \tau_{0}^{2} /4} \right) + \left( {c_{2,l} + c_{2,j} } \right)t_{n} \tau_{0} } \right)}}{\lambda }\left( {\frac{{f + f_{c} }}{{f_{c} }}} \right)^{1/3} } \right] \\ & \quad \times \exp \left[ { - j\frac{{4\pi \left( {\left( {c_{3,l} - c_{3,j} } \right)\left( {t_{n}^{3} + 3t_{n} \tau_{0}^{2} /4} \right) + \left( {c_{3,l} + c_{3,j} - 2a_{3} } \right)\left( {\tau_{0}^{3} /8 + 3t_{n}^{2} \tau_{0} /2} \right)} \right)}}{\lambda }} \right] \\ & \quad \times \exp \left[ { - j\frac{{4\pi v_{a} \left( {\left( {n_{am,l} - n_{am,j} } \right)t_{n} + \left( {n_{am,l} + n_{am,j} } \right)\tau_{0} /2} \right)}}{\lambda }\frac{f}{{f_{c} }}\left( {\frac{{f_{c} }}{{f + f_{c} }}} \right)^{1/3} } \right] \\ \end{aligned} $$
(31)

From (30) and (31), we can find that the cross-terms are generated after FDPT. After performing the TOKT on (31) and simplifying by first-order Tylor series expansion, we have

$$ \begin{aligned} s_{mul,3} \left( {f,t_{a} } \right) & = \sum\limits_{i = 1}^{K} {A_{2,i}^{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left( { - j\frac{{8\pi v_{0,i} \tau_{0} f}}{3c}} \right)} \exp \left( { - j\frac{{4\pi n_{am,i} v_{a} \tau_{0} f}}{c}} \right) \\ & \quad \times \exp \left( { - j\frac{{4\pi v_{0,i} \tau_{0} }}{\lambda }} \right)\exp \left( { - j\frac{{8\pi c_{2,i} t_{a} \tau_{0} }}{\lambda }} \right)\exp \left( { - j\frac{{\pi \left( {c_{3,i} - a_{3} } \right)\tau_{0}^{3} }}{\lambda }} \right) \\ & \quad \times \exp \left( { - j\frac{{12\pi \left( {c_{3,i} - a_{3} } \right)t_{a}^{2} \tau_{0} }}{\lambda }\left( {1 - \frac{2f}{{3f_{c} }}} \right)} \right) + s_{cross} \left( {f,t_{a} } \right) \\ \end{aligned} $$
(32)

where

$$ \begin{aligned} s_{cross} \left( {f,t_{a} } \right) & = \sum\limits_{l = 1}^{K} {\sum\limits_{j = 1,j \ne l}^{K} {A_{2,l} A_{2,j} {\text{rect}}\left( {\frac{f}{B}} \right)} } \exp \left[ { - j\frac{{4\pi \left( {R_{0,l} - R_{0,j} } \right)}}{\lambda }\left( {1 + \frac{f}{{f_{c} }}} \right)} \right] \\ & \quad \times \exp \left[ { - j\frac{4\pi }{\lambda }\left[ {\left( {v_{0,l} - v_{0,j} } \right)\left( {1 - \frac{f}{{3f_{c} }}} \right)t_{a} + \frac{{\left( {v_{0,l} + v_{0,j} } \right)\tau_{0} }}{2}} \right]\left( {1 + \frac{2f}{{3f_{c} }}} \right)} \right] \\ & \quad \times \exp \left[ - j\frac{4\pi }{\lambda }\left[ \left( {c_{2,l} - c_{2,j} } \right)\left( {\left( {1 - \frac{2f}{{3f_{c} }}} \right)t_{a}^{2} + \frac{{\tau_{0}^{2} }}{4}} \right)\right.\right.\\ &\quad\left. \left.+ \left( {c_{2,l} + c_{2,j} } \right)\left( {1 - \frac{f}{{3f_{c} }}} \right)t_{a} \tau_{0} \right]\left( {1 + \frac{f}{{3f_{c} }}} \right) \right] \\ & \quad \times \exp \left[ { - j\frac{{4\pi \left( {c_{3,l} - c_{3,j} } \right)}}{\lambda }\left( {\left( {1 - \frac{f}{{f_{c} }}} \right)t_{a}^{3} + \left( {1 - \frac{f}{{3f_{c} }}} \right)\frac{{3t_{a} \tau_{0}^{2} }}{4}} \right)} \right] \\ & \quad \times \exp \left[ { - j\frac{{4\pi \left( {c_{3,l} + c_{3,j} - 2a_{3} } \right)}}{\lambda }\left( {\frac{{\tau_{0}^{3} }}{8} + \frac{{3t_{a} \tau_{0} }}{2}\left( {1 - \frac{2f}{{3f_{c} }}} \right)} \right)} \right] \\ & \quad \times \exp \left[ - j\frac{{4\pi v_{a} }}{\lambda }\left( {\left( {n_{am,l} - n_{am,j} } \right)\left( {1 - \frac{f}{{3f_{c} }}} \right)t_{a} + \frac{{\left( {n_{am,l} + n_{am,j} } \right)\tau_{0} }}{2}} \right)\right.\\ &\quad\left. \frac{f}{{f_{c} }}\left( {1 - \frac{f}{{3f_{c} }}} \right) \right] \\ \end{aligned}$$
(33)

Similarly, we can ignore the \( \exp \left( {j\frac{{4\pi n_{am,i} v_{a} \tau_{0} }}{c}\frac{{f^{2} }}{{3f_{c} }}} \right) \) on (32), because it is much smaller than \( \pi /4 \) (He et al. 2018). From (32) and (33), we can find that, in auto-terms, when searching jerk \( a_{3} \) is equal to ith target’s radial jerk \( c_{3,i} \), the RM and quadratic DFM caused by radial jerk of ith target are removed. However, for other targets, the TRM and quadratic DFM still exist since the radial jerk is not compensated completely. Besides, it is also observed that, in the cross-terms, the linear, quadratic, and cubic couplings between slow time and range frequency still exist simultaneously. In addition, the cross-terms are the cubic phase functions of slow time, which indicate the presence of DFM.

Assuming \( a_{3} = c_{3,i} \) and carrying out IFFT along range frequency domain and FFT along slow time domain respectively, it yields

$$ \begin{aligned} s_{mul,4} \left( {t,f_{m} } \right) & = A_{3,i} {\text{sinc}}\left[ {B\left( {t - \left( {\frac{{4v_{0,i} }}{3} + 2n_{am,i} v_{a} } \right)\frac{{\tau_{0} }}{c}} \right)} \right] \\ & \quad \times \sin c\left[ {T_{a} \left( {f_{m} + \frac{{4c_{2,i} \tau_{0} }}{\lambda }} \right)} \right]\exp \left( { - j\frac{{4\pi v_{0,i} \tau_{0} }}{\lambda }} \right) \\ & \quad + {\text{FFT}}_{{t_{a} }} \left[ {{\text{IFFT}}_{f} \left[ {s_{other,3} \left( {t,f_{m} } \right)} \right]} \right] \\ & \quad + {\text{FFT}}_{{t_{a} }} \left[ {{\text{IFFT}}_{f} \left[ {s_{cross,3} \left( {t,f_{m} } \right)} \right]} \right] \\ \end{aligned} $$
(34)

where \( A_{3,i} \) denotes ith target’s amplitude after coherent integration. Form (34), one can see that ith target’s energy is well refocused. However, the other targets and cross-terms can’t be well integrated because of RM and DFM.

According to analysis above, we can find, though the proposed algorithm introduces cross-terms interference, the cross-terms interference can be ignored because it can’t be well focused. Therefore, the proposed method can realize target coherent integration effectively under multi-targets environment.

Nevertheless, when amplitudes of multi-targets differ greatly, the weak targets will be drowned in cross-terms which are related to strong targets. For addressing the problem mentioned above, the CLEAN technique proposed in (Misiurewicz et al. 2012) will be applied to remove the effects of strong targets. Next, we will give some simulation experiments to prove that the proposed method can effectively suppress the cross-terms and accumulate the auto-terms.

Example 2

Three maneuvering targets exist in the scene. The motion parameters of target A: initial slant range \( R_{0,1} = 100.9\;{\text{km}} \), velocity \( c_{1,1} = 1500\;{\text{m/s}} \), acceleration \( c_{2,1} = 40\;{\text{m/s}}^{2} \) and jerk \( c_{3,1} = 30\;{\text{m/s}}^{3} \). The motion parameters of target B: initial slant range \( R_{0,2} = 100.9\;{\text{km}} \), velocity \( c_{1,2} = 1200\;{\text{m/s}} \), acceleration \( c_{2,2} = - 40\;{\text{m/s}}^{2} \) and jerk \( c_{3,2} = 30\;{\text{m/s}}^{3} \). The motion parameters of target C: initial slant range \( R_{0,3} = 100.8\;{\text{km}} \), velocity \( c_{1,3} = 1200\;{\text{m/s}} \), acceleration \( c_{2,3} = 40\;{\text{m/s}}^{2} \) and jerk \( c_{3,3} = - 30\;{\text{m/s}}^{3} \). Besides, the radar parameters in this simulation are same as example 1. Figure 3 shows the results of simulation experiments.

Fig. 3
figure 3

Accumulation results for multiple targets. a Maneuvering targets trajectory after range compression. b Searching result of jerk. c Accumulation results for target A and B. d Accumulation result for target C

Full size image

The maneuvering targets trajectory after range compression is shown in Fig. 3a. Obviously, it can be seen that serious RM occurs in the scene and target energy is spread across different range units. The jerk searching result is given in Fig. 3b, from which it is observed that two peaks corresponding to searching jerk \( - \,30\;{\text{m/s}}^{3} \) and \( 30\;{\text{m/s}}^{3} \) respectively are present. Figure 3c shows the focused result corresponding to searching jerk \( - \,30\;{\text{m/s}}^{3} \). Obviously, we can see that target A and target B are well refocused, while cross-terms and target C are still severely defocused because of RM and DFM even though \( R_{0,1} = R_{0,2} \) and \( c_{3,1} = c_{3,2} \). Figure 3d shows the focused result corresponding to searching jerk \( 30\;{\text{m/s}}^{3} \). It is observed that the target C is well integrated as a peak from Fig. 3d, while the energy of other targets and cross-terms are spread in the different range and Doppler frequency units because RM and DFM still exist even though \( c_{1,2} = c_{1,3} \) and \( c_{2,1} = c_{2,3} \). Hence, the proposed method can remove the cross-terms interference and realize the coherent integration of maneuvering targets effectively under multi-targets environment. According to the positions of target peaks, the motion parameters of three targets can be respectively estimated as follows: \( \hat{n}_{am,1} = 10 \), \( \hat{c}_{2,1} = 40.01\;{\text{m/s}}^{2} \) and \( \hat{c}_{3,1} = 30\;{\text{m/s}}^{3} \) for target A;\( \hat{n}_{am,2} = 8 \), \( \hat{c}_{2,2} = - 39.99\;{\text{m/s}}^{2} \) and \( \hat{c}_{3,2} = 30\;{\text{m/s}}^{3} \) for target B;\( \hat{n}_{am,3} = 8 \), \( \hat{c}_{2,3} = 39.98m/s^{2} \) and \( \hat{c}_{3,3} = - 30\;{\text{m/s}}^{3} \) for target C. Then, after compensation and first-order KT procedure, the velocity of three targets are respectively estimated as \( \hat{c}_{1,1} = 1499.99\;{\text{m/s}} \), \( \hat{c}_{1,2} = 1200.02\;{\text{m/s}} \) and \( \hat{c}_{1,3} = 1200\;{\text{m/s}} \). Therefore, the results of parameters estimation prove the proposed algorithm can realize target parameters estimation effectively under multi-targets environment.

3.3 Computational complexity analysis

In the following, the computational complexity of GKTGDP (Kong et al. 2015), IACCF (Li et al. 2016) and the proposed method will be analyzed. Assume that the number of range cells, echo pulses, searching velocity, searching acceleration, searching jerk and searching Doppler ambiguity number are denoted as N, M, N1, N2, N3, Na. The proposed algorithm mainly includes two TOKT operations, a FDPT operation and a 1-D searching operation. In addition, the computational cost of a TOKT operation based on the scaling principle (Zhu et al. 2007; He et al. 2018) is about \( {\text{O}}\left( {NM\log_{2} M} \right) \) and the computational complexity of a FDPT operation is about \( {\text{O}}\left( {NM} \right) \). So the total computational cost of the proposed algorithm is about \( {\text{O}}\left( {NM\log_{2} M} \right) + N_{3} {\text{O}}\left( {NM{ + }3NM\log_{2} M} \right) \). The procedures of IACCF mainly include FFT operations and IFFT operations. The computational complexity of FFT operation or IFFT operation is about \( {\text{O}}\left( {M\log_{2} M} \right) \), so the total computational cost of IACCF is about \( {\text{O}}\left( {3NM\log_{2} N + 3NM\log_{2} M} \right) \). Moreover, the computational cost of GKTGDP based on 3-D searching operation is about \( {\text{O}}\left( {N_{a} N_{2} N_{3} NM\log_{2} M} \right) \).

Supposed that \( N = M = N_{1} = N_{2} = N_{3} = N_{a} \), then the computational complexity of the proposed algorithm, IACCF and GKTGDP is about \( {\text{O}}\left( {N^{3} \log_{2} N} \right) \), \( {\text{O}}\left( {N^{2} \log_{2} N} \right) \) and \( {\text{O}}\left( {N^{5} \log_{2} N} \right) \), respectively. In order to better show the computational complexity of these methods, we give the computational time in Table 1. In this simulation, the radar parameters and motion parameters are same as those in example 1. Besides, the main configurations of computer are: Intel (R) Core (TM) i7-4790 CPU @3.60 GHz, RAM (8 GB), and Matlab 2014a. From Table 1, we can find that the proposed method is computationally efficient compared with GKTGDP method since the 3-D searching problem has been reduced to 1-D searching problem. Though the IACCF algorithm has the lowest computational effort among those methods, its accumulation performance is poor duo to the application of two nonlinear transforms. As a result, the proposed algorithm achieves a balance between the computational effort and the accumulation capability.

Table 1 Computational time comparison
Full size table

4 Simulation results analysis

In what follows, several simulation experiments are performed to analyze the integration ability, detection probability and parameters estimation performance of the proposed method for a maneuvering target with jerk motion under Gaussian noise environment, where the parameters of radar and maneuvering target are same as those in example 1. As a contrast, we will carry out MTD, RFT (Xu et al. 2011a, b; Yu et al. 2012), RLVD (Li et al. 2015), IACCF (Li et al. 2016) and GKTGDP (Kong et al. 2015) to better demonstrate the superior performance of the proposed algorithm.

4.1 Integration ability

The coherent integration results obtain by different methods for a maneuvering target is given in Fig. 4, where the SNR after range compressed is 4 dB. Figure 4a shows the maneuvering target trajectory after range compression. Obviously, the serious RM occurs. The integration result of the proposed method is given in Fig. 4b. It is observed the target energy is well refocused by the proposed algorithm, which contributes to target detection and parameters estimation in the next step. The integration result of MTD method is given in Fig. 4c. We can find that the target is still defocused for the reason that the DFM and RM related to target’s velocity, acceleration and jerk still exist after MTD method. The integration result of RFT algorithm is shown in Fig. 4d. It is observed that the target energy is still spread in different range and Doppler frequency units because the RM and DFM related to acceleration and jerk still exist after RFT algorithm. Figure 4e gives coherent integration result of RLVD method. We can find that the energy of maneuvering target can’t be effectively accumulated as one peak because the TRM and quadratic DFM caused by jerk still exist after RLVD method. Figure 4f gives the coherent accumulation result of IACCF algorithm. We can find the target energy is drowned in the noise for the reason that two nonlinear transforms, which may lead to a serious decline of accumulation performance in the low SNR environment, are used in IACCF algorithm. The coherent accumulation result of GKTGDP algorithm is given in Fig. 4g. Obviously, the coherent integration performance of GKTGDP algorithm is better than the proposed algorithm. Nevertheless, the computational cost of GKTGDP method is too high due to three dimension searching of Doppler ambiguity number, acceleration and jerk.

Fig. 4
figure 4

Integration results under the noise environment. a Maneuvering target trajectory after range compression. b Result after the proposed method. c Result after MTD method. d Result after RFT method. e Result after RLVD method. f Result after IACCF method. g Result after GKTGDP method

Full size image

According to the above analysis, we will get the conclusions that the proposed method can achieve better integration performance for the reason that it can completely eliminate the effects of RM and DFM related to target’s radial velocity, acceleration and jerk only by one nonlinear transform. Besides, though the integration performance of GKTGDP method is best in this simulation experiment, the computational cost of the proposed method is much lower than GKTGDP method for the reason that only the jerk need to be searched.

4.2 Maneuvering target detection ability

In what follows, the target detection ability of the proposed algorithm, MTD, RFT, RLVD, IACCF and GKTGDP will be analyzed via Monte Carlo experiments. In addition, the zero-mean white Gaussian noise is added to the target echoes and the range compressed SNRs vary from − 5 to 20 dB with the step of 1 dB. Besides, the constant false alarm probability Pfa= 10−4. After performing 200 times of Monte Carlo trials, Fig. 5 gives the curves of detection probability varying with range compressed SNRs. It is seen that target detection capability of the proposed method is better than MTD, RFT and RLVD for the reason that RM and DFM related to radial velocity, acceleration and jerk are absolutely removed. Furthermore, the target detection capability of the proposed method is also superior to IACCF method, because IACCF algorithm needs two nonlinear transforms, which causes significant detection performance loss. The GKTGDP algorithm has the optimal target detection capability in this simulation. Nevertheless, the optimal detection capability of GKTGDP method is at the expense of huge computational effort, which limits its practical application. Furthermore, when the input SNR is larger than 2 dB, the proposed algorithm has similar detection capability to GKTGDP method and much less computational complexity than GKTGDP method. Moreover, we can find that the proposed algorithm suffers from serious detection capability degradation under low SNR environment, which is the reason of application of nonlinear transform.

Fig. 5
figure 5

Curves of detection probability varying with range compressed SNRs

Full size image

4.3 Parameters estimation capability

In this subsection, the parameters estimation capability of the proposed algorithm, GKTGDP algorithm and IACCF algorithm will be analyzed via Monte Carlo experiments, where the input SNRs after range compressed vary from − 5 to 20 dB with the step of 1 dB. After performing 200 times of Monte Carlo trials, Fig. 6 gives the relationships between the root mean square errors (RMSEs) of motion parameters and input SNRs. In addition, Fig. 6a–c show the RMSEs of estimated speed, acceleration and jerk vary with different input SNRs, respectively. From the figures, it can be seen that the proposed method has the generally close parameters estimation capability with GKTGDP method when the input SNR is larger than 2 dB. Unfortunately, on account of the application of two nonlinear transforms, the motion parameters estimation performance of IACCF method is poor.

Fig. 6
figure 6

Relationships between RMSEs of motion parameters and input SNRs. a RMSE of estimated speed varying with input SNRs. b RMSE of estimated acceleration varying with input SNRs. c RMSE of estimated jerk varying with input SNRs

Full size image

According to the simulation results above (Figs. 4, 5, 6), we get the following conclusions: the proposed algorithm has better integration performance and target detection capability in comparison with IACCF, RLVD, RFT and MTD under the noise environment. In addition, compared with GKTGDP method, the proposed method makes 3-D searching problem become 1-D searching problem, which will significantly cut down the computational effort. Besides, in high SNR environment, the proposed algorithm has generally similar integration ability, detection probability and parameters estimation capability with GKTGDP algorithm. Therefore, as for long-time coherent integration, target detection and parameters estimation for high-speed maneuvering target with jerk motion, the proposed method is the best choice in comparison with the existing methods for the reason that it can achieve a balance between the computational complexity and the detection ability as well as motion parameters estimation capability.

5 Conclusions

This paper has put forward a new detection and motion parameters estimation method for high speed moving target with complex motions mainly based on TOKT and FDPT, referring to high-order RM, DFM and Doppler ambiguity during coherent processing time. For the reason that the effects of high order motion parameters have been taken into consideration, the proposed algorithm can eliminate RM and DFM completely and achieve coherent integration of maneuvering target in comparison with traditional methods, which is beneficial for target detection and motion parameters estimation in the next step. With respect to multi-targets refocusing, the proposed algorithm has the ability to eliminate cross-terms interference absolutely in which RM and DFM is still present. Besides, the proposed algorithm has lower computational effort since it mainly includes jerk searching whose value usually is small and two TOKT operations which can be quickly realized. In addition, compared with GKTGDP method, the proposed algorithm can not only obtain generally close target detection and motion parameters estimation performance but also need much lower computational effort under relatively high SNR environment. Numerical results have proved the effectiveness of the proposed algorithm.

Duo to the application of nonlinear transform, the proposed algorithm is more suitable for the coherent accumulation of maneuvering targets in relatively high SNR case. How to improve the integration performance of maneuvering targets in case of low SNR will be our future work. Besides, detection and parameters estimation of moving targets with higher-order motions will be also concerned in our future work.