1 Introduction

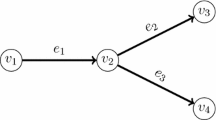
Aspects of temporal and spatial stability are investigated for infinite cascades of stable linear time-invariant (LTI) systems. Specifically, interconnections of the kind shown in Fig. 1 are studied. Such models arise in various application domains, such as vehicle platoons (Levine and Athans 1966; Chu 1974; Ioannou and Chien 1993; Darbha and Hedrick 1996; Eyre et al. 1998; Seiler et al. 2004; Klinge and Middleton 2009; Knorn 2013), air traffic control (Weitz 2011; Arneson and Langbort 2012), supply chains (Huang et al. 2007; Disney et al. 2004), and automated irrigation channels (Cantoni et al. 2007; Soltanian and Cantoni 2013), for example.

Fig. 1
figure 1

Cascade of heterogeneous dynamical systems

Full size image

In Fig. 1, the interconnection signal \(u_{i+1}\) at the output of subsystem \(i \ge 0\) is related to the interconnection signal \(u_i\) at the corresponding input, according to an LTI dynamic input–output relationship \(u_{i+1}=G_iu_{i}\). The corresponding spatial boundary condition is \(u_0=d(t)\), where d(t) is a time-dependent input signal. The constant value w(i) is an input associated with non-zero initialization of a state-space realization for \(G_i\). As such, the sequence \(\{w(0),w(1),\ldots \}\) constitutes a space-dependent temporal boundary condition for a state-space realization of the cascade. An important aspect of such system interconnections is the unidirectional propagation of information in both space, from right to left as shown in Fig. 1, and in time.

Many papers in the literature consider the propagation of boundary disturbances and/or initial conditions along a chain or string of dynamical subsystems. Early work in this direction was carried out within the context of optimal error control for a platoon of vehicles (Levine and Athans 1966). In Chu (1974), “stability of a string” is defined in terms of requiring bounded position error fluctuations that also tend to zero in steady state, in response to bounded initial conditions for all vehicles. See Knorn (2013) for a recent overview of various definitions of string-stability.

In this paper, cascades of the kind described above are studied from the perspective of \(L_2\)-to-\(L_\infty \) string-stability. That is, in terms of desiring uniformly bounded, across time and space, interconnection signals in response to bounded finite-energy spatial and temporal boundary conditions. Limiting attention to finite-energy boundary conditions is motivated by the finite duration of typical spatial boundary inputs and the finite extent of cascades in practice. The infinite cascade abstraction is nonetheless relevant, as uniformity requirements within such a context translate to time- and space-horizon independent bounds, which is important within the context of long chains.

The main result is a decentralized \(L_2\)-to-\(L_\infty \) string-stability certificate applicable to heterogeneous cascades, subject to the requirement that constant spatial boundary conditions are asymptotically matched by the interconnection signals along the chain of subsystems. This is motivated by the operation of automated irrigation channels, where a steady-state objective at each flow regulating structure is to match the downstream load, as may also arise in other application domains. The string-stability certificate involves verification of the location independent property that the \(H_\infty \) norm of the interconnection-signal transfer function of each subsystem is no greater than unity. This is more amenable to design and synthesis than impulse-response based certificates, which ensure a related but more stringent string-stability property (Soltanian and Cantoni 2013; Soltanian 2014). The main result extends earlier work reported in Knorn (2013), Knorn and Middleton (2013), where the stability of homogeneous platoons of vehicles are studied in a similar fashion, via Lyapunov-based stability analysis (see e.g. Du and Xie 2002) of a two-dimensional (2-D) Roesser model for the cascade, although an analog of the steady-state matching requirement is not considered explicitly therein.

The main result is also distinct from similar conditions in the literature in that the corresponding \(H_\infty \)-norm bound condition is non-strict, as required to accommodate the aforementioned steady-state matching requirement, unlike the strict norm-bound conditions presented in Shaw and Hedrick (2007), Darbha and Hedrick (1996), Dabkowski et al. (2012) for various notions of string stability. It is interesting to note that the non-strict certificate developed here is necessary for the different notion of string stability considered in Peppard (1974). Indeed, this observation is presented in Peppard (1974) as a motivation for using bi-directional information exchange in vehicle platoons, as it is not possible to achieve the necessary condition with uni-directional information flow. Bi-directional information exchange would be disadvantages within the context of irrigation channels, and other distribution networks, in view of the typically limited availability of downstream storage. It is also of note that results of the kind considered in Lestas and Vinnicombe (2006), which are also applicable to interconnections of heterogeneous subsystems, do not directly yield the uniform \(L_\infty \) bounds on the system response to boundary conditions, as required here.

The decentralized nature of the string-stability certificate developed in this paper can facilitate the design of cascades on a subsystem-by-subsystem basis. This scalability aspect of the result is explored within the context of so-called distributed distant-downstream control architectures for automated irrigation channels. Within this context, it is desirable from an engineering perspective for each distributed component of the controller to be designed using only the model of the corresponding section of the channel dynamics. This can be advantageous in terms of the tractability of systematic approaches to controller synthesis and system maintainability.

The paper is structured as follows. Section 2 sets some basic notation and preliminary technical results. A 2-D Roesser model is then developed for a heterogeneous cascade in Sect. 3. The main \(L_2\)-to-\(L_\infty \) string-stability analysis results, including the aforementioned decentralized certificate, are presented in Sect. 4. Section 5 contains an application of the analysis within the context of irrigation channel control-system design. Some final remarks are provided in a concluding section.

2 Notation and preliminaries

The symbol \(\mathbb {Z}_{+}\) denotes the subset \(\{i\in \mathbb {Z}\,:\,i\ge 0\}\) of the integers \(\mathbb {Z}\), \(\mathbb {R}_+\) denotes the subset \(\{t\in \mathbb {R}\,:\,t\ge 0\}\) of the real numbers \(\mathbb {R}\), and \(\mathbb {C}_{-}\) denotes the subset \(\{z\in \mathbb {C}\,:\, \mathfrak {R}(z) < 0\}\) of the complex numbers \(\mathbb {C}=\{\alpha +j\beta \,:\,\alpha ,\beta \in \mathbb {R}\}\), where \(\mathfrak {R}(z)\) denotes the real part \(\alpha \) of \(z=\alpha +j\beta \) and \(j{:=}\sqrt{-1}\). The symbol \(\mathbb {R}^n\) denotes the linear space of column vectors with n real-valued entries. \(\mathbb {F}^{p\times m}\) denotes the linear space p-row-by-m-column matrices with entries in \(\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}\). A superscript \(*\) denotes the (complex conjugate) transpose of a matrix or column vector considered as an \(n\times 1\) matrix.

Given a vector \(x=(x_1,\ldots ,x_n)^*\in \mathbb {R}^n\), \(|x|_2 {:=} (\sum _{i=1}^{n}x_i^2)^{\frac{1}{2}}\) and \(|x|_\infty {:=} \max \{|x_i|\,:\,i=1,2,\ldots ,n\}\). Note that \(|x|_\infty \le |x|_2=\sqrt{x^*x}\) for all \(x\in \mathbb {R}^n\). Given \(A\in \mathbb {R}^{p\times m}\) with elements \(a_{ij}\in \mathbb {R}\), \(\Vert A\Vert _{2\rightarrow 2}{:=}\sup _{x\ne 0}|Ax|_2/|x|_2\) and \(\Vert A\Vert _{\infty \rightarrow \infty }{:=} \sup _{x\ne 0}|Ax|_\infty /|x|_\infty =\max _{i}\sum _ja_{ij}\). The set of eigenvalues of A is denoted by \(\sigma (A)=\{{\lambda }\in \mathbb {C}~:~Ax={\lambda } x,~x\ne 0\}\). Clearly, \({\lambda }\in \sigma (A)\Leftrightarrow -{\lambda }\in \sigma (-A)\) and \({\lambda }\in \sigma (A) \Leftrightarrow (1+{\lambda }) \in \sigma (I+A)\), where I denotes the identity matrix.

A symmetric matrix \(P=P^*\in \mathbb {R}^{n\times n}\) has eigenvalues that are real and \({\lambda }_{\text {max}}(P)\) (resp. \({\lambda }_{\text {min}}(P)\)) denotes the maximum (resp. minimum) eigenvalue. It is said to be positive definite (resp. semi-definite) if \(x^*Px \ge c x^*x\) (resp. \(x^*Px \ge 0\)) for all \(x\in \mathbb {R}^n\) and some \(c>0\), which is denoted by \(P>0\) (resp. \(P\ge 0\)). Also, \(P<0\Leftrightarrow -P>0\) and \(P\le 0 \Leftrightarrow -P\ge 0\). Note that \(P>0 \Leftrightarrow {\lambda }_{\text {min}}(P)>0\) and \(P<0 \Leftrightarrow {\lambda }_{\text {max}}(P)<0\). Given \(P> 0\), there exists a unique matrix \(0 < P^{\frac{1}{2}}=(P^{\frac{1}{2}})^*\in \mathbb {R}^{n\times n}\) such that \(P=P^{\frac{1}{2}}P^{\frac{1}{2}}\).

\(L_2^n\) denotes the space of functions \(x:\mathbb {R}_+\rightarrow \mathbb {R}^n\) with \(\Vert x\Vert _2{:=}(\int _{0}^\infty |x(t)|_2^2 dt)^\frac{1}{2}<\infty \). The space of functions \(x:\mathbb {R}_+\rightarrow \mathbb {R}^n\) such that \(\Vert x\Vert _\infty {:=} \sup _{t}|x(t)|_\infty <\infty \) is denoted by \(L_\infty ^n\). Similarly, \(\ell _2^n\) and \(\ell _\infty ^n\) denote the subspaces of sequences \(x:\mathbb {Z}_+\rightarrow \mathbb {R}^n\) such that \(\Vert x\Vert _2{:=}(\sum _{i=0}^\infty |x(i)|_2^2)^\frac{1}{2}<\infty \) and \(\Vert x\Vert _\infty {:=}\sup _i |x(i)|_\infty <\infty \), respectively. The dimension n of the function value is often suppressed for convenience.

The following technical lemma, a version of which can be found in Knorn (2013) for example, is used subsequently in Lyapunov-type analysis of a 2-D Roesser model for heterogeneous cascades.

Lemma 1

Let \(V_t,V_s:\mathbb {R}_+\times \mathbb {Z}_+\rightarrow \mathbb {R}\). If \(V_t(t,i) \ge 0\), \(V_s(t,i) \ge 0\) and

$$\begin{aligned} \varDelta (t,i) {:=} \frac{\partial V_t}{\partial t}(t,i) + V_s(t,i+1) - V_s(t,i) \le 0 \end{aligned}$$

for all \((t,i)\in \mathbb {R}_+\times \mathbb {Z}_+\), then

$$\begin{aligned}&\sum _{k=0}^i V_t(t,k)\le \sum _{k=0} ^i V_t(0,k)+\int _0^tV_s(\tau ,0)d\tau \quad \text {and} \end{aligned}$$
(1)
$$\begin{aligned}&\int _0^tV_s(\tau ,i)d\tau \le \int _0^tV_s(\tau ,0)d\tau +\sum _{k=0}^iV_t(0,k), \end{aligned}$$
(2)

for all \((t,i)\in \mathbb {R}_+\times \mathbb {Z}_+\).

Proof

Since \(\varDelta (t,i) \le 0\) for all \((t,i)\in \mathbb {R}_+\),

$$\begin{aligned} 0\ge \sum _{k=0}^i \int _0^t \varDelta (\tau ,k) d\tau = \sum _{k=0}^i (V_t(t,k)- V_t(0,k))+\int _0^t(V_s(\tau ,i)-V_s(\tau ,0))d\tau , \end{aligned}$$

Therefore,

$$\begin{aligned} \sum _{k=0}^i V_t(t,k)+\int _0^tV_s(\tau ,i)d\tau \le \sum _{k=0}^i V_t(0,k)+\int _0^tV_s(\tau ,0)d\tau , \end{aligned}$$

whereby (1) and (2) hold because \(V_t(t,i)\ge 0\) and \(V_s(t,i)\ge 0\). \(\square \)

The following non-strict version of the so-called Bounded Real Lemma plays a role in subsequently establishing a decentralized string-stability certificate for heterogeneous cascades of stable LTI subsystems with rational transfer functions.

Lemma 2

Let \(G(s)=C(sI-A)^{-1}B\) be a state-space realization of a strictly-proper matrix transfer function, with \(A\in \mathbb {R}^{n\times n}\) Hurwitz (i.e. \(\sigma (A)\subset \mathbb {C}_{-}\)).The following are equivalent:

  1. (i)

    \(\Vert G\Vert _\infty {:=}\sup _{\mathfrak {R}(s)>0}\Vert G(s)\Vert _{2\rightarrow 2}=\sup _{\omega \in \mathbb {R}}\Vert G(j\omega )\Vert _{2\rightarrow 2} \le 1\);

  2. (ii)

    there exists a unique real matrix \(X=X^*\ge 0\) such that

    $$\begin{aligned} A^*X+XA+XBB^*X+C^*C=0 \end{aligned}$$
    (3)

    and \(\sigma (A+BB^*X)\subset \mathbb {C}_-\cup j\mathbb {R}\).

Proof

\(\Vert G\Vert _\infty \le 1\) is equivalent to

$$\begin{aligned} \phi (j\omega ){:=}\,&I-G^*(j\omega )G(j\omega )\nonumber \\ =&\begin{bmatrix}B^*(-j\omega I-A^*)^{-1}&\quad I\end{bmatrix}\begin{bmatrix} -C^*C&\quad 0\\ 0&\quad I\end{bmatrix}\begin{bmatrix} (j\omega I-A)^{-1}B\\ I \end{bmatrix}\ge 0. \end{aligned}$$
(4)

Applying Zhou et al. (1996, Lemma 13.17) \(\phi (j\omega )\ge 0 \text { for all } \omega \ge 0 \) is equivalent to the existence of a unique real \(Y=Y^*\le 0\) such that

$$\begin{aligned} A^*Y+YA-YBB^*Y-C^*C=0 \end{aligned}$$

and \(\sigma (A-BB^*Y)\in \mathbb {C}_{-}\cup j\mathbb {R}\). By taking \(X=-Y\), this is in turn equivalent to the existence of \(X\ge 0\) such that (3) holds with \(\sigma (A+BB^*X)\in \mathbb {C}_{-}\cup j\mathbb {R}\). \(\square \)

In the case that additional hypotheses on the state-space realization of G hold, an eigenvalue upper bound for the solution of (3) follows as summarised below. This bound also plays a role in subsequent analysis.

Lemma 3

Let \(G(s) = B(sI-A)^{-1}C\), with \(A\in \mathbb {R}^{n\times n}\) Hurwitz, (A, B) controllable and (C, A) observable; i.e. (A, B, C) is a minimal realization of \(G(\cdot )\). If \(\Vert G\Vert _\infty \le 1\), then the unique positive semi-definite solution of (3) such that \(\sigma (A+BB^*X)\in \mathbb {C}_{-}\cup j\mathbb {R}\), also satisfies \(X>0\). Moreover, \({\lambda }_{\text {max}}(X) \le 1/{\lambda }_{\text {min}}(P)\), where \(P=P^*\in \mathbb {R}^{n\times n}>0\) is the unique solution of

$$\begin{aligned} AP + PA^* + BB^* = 0. \end{aligned}$$
(5)

Proof

Since \(\Vert G\Vert _\infty \le 1\), there exists a unique \(X=X^*\ge 0\) such that (3) holds with \(\sigma (A+BB^*X)\in \mathbb {C}_{-}\cup j\mathbb {R}\) by Lemma 2. Note that (C, A) observable implies \(X>0\). To see this, suppose to the contrary that \(\ker (X)\ne \{0\}\) and observe the following: (a) \(\ker (X)\subset \ker (C)\), which can be seen by left and right multiplying (3) by \(x^*\) and x, to yield \(Cx=0\) whenever \(x\in \ker (X)\); and (b) \(A\ker (X)\subset \ker (X)\), which can be seen by right multiplying (3) by \(x\in \ker (X)\) so that using (a) it follows that \(XAx=0\) and thus, \(Ax\in \ker (X)\). In particular, (b) implies there exists \(0\ne x\in \ker (X)\) and \({\lambda }\in \sigma (A)\subset {\mathbb {C}_-}\) such that \(Ax={\lambda } x\). Moreover, \(Cx=0\) by (a), which contradicts the hypothesis that (C, A) is observable. As such, \(\ker (X)=\{0\}\), whereby \(X>0\) as claimed.

Now, let \(Z=X^{-1}>0\). Using (3) yields

$$\begin{aligned} AZ + ZA^* + BB^* + ZC^*CZ = 0 \end{aligned}$$
(6)

and

$$\begin{aligned} A(Z-P) + (Z-P)A^* + ZC^*CZ = 0, \end{aligned}$$
(7)

where \(P=P^*\) is the unique solution of (5), which satisfies \(P>0\) because A is Hurwitz and (A, B) is controllable; see Zhou et al. (1996, Lemma 3.18(iii)). Since \(C^*C\ge 0\), it follows from (7) that \(A(Z-P) + (Z-P)A^* \le 0\), whereby Zhou et al. (1996, Lemma 3.18(ii)) implies \(Z-P \ge 0\). As such, \(0\le X^{-1}-P = X^{-\frac{1}{2}}(I-X^{\frac{1}{2}}PX^{\frac{1}{2}})X^{-\frac{1}{2}}\), which is equivalent to \(0\le I - X^{\frac{1}{2}}P X^{\frac{1}{2}}\). In particular, \(0 \le {\lambda }_{\text {min}}(I- X^{\frac{1}{2}}P X^{\frac{1}{2}}) = 1 - {\lambda }_{\text {max}}(X^{\frac{1}{2}}P X^{\frac{1}{2}}) = 1 - {\lambda }_{\text {max}}(XP)\), where \({\lambda }_{\text {max}}(X)>0\) or \({\lambda }_{\text {max}}(P)>0\) can be used to establish the last equality. The inequality \({\lambda }_{\text {min}}(P) {\lambda }_{\text {max}}(X) \le {\lambda }_{\text {max}}(XP)\), which holds by Wang and Zhang (1992, Theorem 2) as \(X>0\) and \(P>0\), thus leads to the bound \({\lambda }_{\text {max}}(X) \le 1/{\lambda }_{\text {min}}(P)\). \(\square \)

Remark 1

In Lemma 3, if (A, B, C) is also a balanced realization of G, so that \(P=\mathrm {diag}(\sigma _1,\cdots ,\sigma _n)\) is a diagonal matrix of the Hankel singular values of G in descending order \(\sigma _1\ge \cdots \ge \sigma _n>0\) and \(PA+A^*P +CC^*=0\), then \({\lambda }_{\text {max}}(X) \le 1/ \sigma _n\).

3 A 2-D Roesser model for heterogeneous cascades

Recall the cascade of heterogeneous LTI systems shown in Fig. 1. Let

$$\begin{aligned}G_i(s)=C(i)(sI-A(i))^{-1}B(i)\end{aligned}$$

be a state-space realization for the transfer function of subsystem \(i\in \mathbb {Z}_+\). In the frequency domain,

$$\begin{aligned} U_{i+1}(s)=G_i(s)U_{i}(s)+H_i(s)w(i) \end{aligned}$$
(8)

for \(i\in \mathbb {Z}_+\), with \(U_0(s)=D(s)\) and \(H_i(s) {:=} C(i)(sI-A(i))^{-1}\), where \(U_{i}(s)\) and D(s) denote the Laplace transforms of \(u_i\) and d, respectively. In the time domain,

$$\begin{aligned} \dot{x}_i(t)&=A(i)x_i(t)+B(i)u_{i}(t),\nonumber \\ u_{i+1}(t)&= C(i)x_i(t), \end{aligned}$$
(9)

with initial state \(x_i(0)=w(i)\) and spatial boundary condition \(u_{0}(t)=d(t)\). Defining the semi-states \(x_t(t, i) {:=} x_i(t)\) and \(x_s(t,i){:=}u_{i}(t)\) yields the following mixed-continuous-discrete spatially-varying 2-D Roesser model (see Xiao 2001):

$$\begin{aligned} \begin{bmatrix} \dot{x}_t(t,i) \\ x_s(t,i+1) \end{bmatrix}=&\begin{bmatrix} A(i)&\quad B(i) \\ C(i)&\quad 0 \end{bmatrix} \begin{bmatrix} {x}_t(t,i) \\ x_s(t,i) \end{bmatrix}, \end{aligned}$$
(10)

with boundary conditions \(x_t(0,\cdot )=w(\cdot )\) and \(x_s(\cdot ,0)=d(\cdot )\). The evolution of the semi-states given boundary conditions \(x_t(0,.)\in \ell _2\) and \(x_s(., i)\in L_2\cap L_\infty \) is of particular interest in this paper.

Before proceeding, it is instructive to note that the aforementioned steady-state matching requirement considered in this paper simply translates to the requirement that \(\lim _{s\rightarrow 0}G_i(s)=1\) for all \(i\in \mathbb {Z}_+\). It is for this reason that sufficient conditions for string-stability which need the \(H_\infty \) norm of each \(G_i\) to be strictly less than unity (see e.g. Shaw and Hedrick 2007) do not apply directly. This is overcome via the analysis developed below.

4 String-stability analysis

Consider the cascade shown in Fig. 1. Let \(G_i\) denote the rational transfer function from the input signal \(u_i\) to the output signal \(u_{i+1}\), at the LTI subsystem labelled \(i\in \mathbb {Z}_+\), which has initial state w(i).

Definition 1

The cascade in Fig. 1 is called \(L_2\)-to-\(L_\infty \) string-stable if there exists finite constants \(M_1,M_2,M_3>0\) such that the bound

$$\begin{aligned}\Vert u_{i} \Vert _\infty \le M_1\Vert d\Vert _2 + M_2\Vert d\Vert _\infty + M_3 \Vert w\Vert _2\end{aligned}$$

holds for all \(i\in \mathbb {Z}_+\) and arbitrary boundary conditions \(u_0=d\in L_2\cap L_\infty \) and \(w=\{w(0),w(1),\ldots \}\in \ell _2\).

The following theorem provides a sufficient condition for \(L_2\)-to-\(L_\infty \) string-stability in terms of appropriate state-space realizations (A(i), B(i), C(i)) of the subsystem transfer functions \(G_i\) and the corresponding 2-D Roesser model (10). This is used subsequently to establish another sufficient, but importantly decentralized, string-stability certificate for the cascade.

Theorem 1

Given (A(i), B(i), C(i)) for \(i\in \mathbb {Z}_+\), consider the spatially-varying 2-D Roesser model (10). Suppose the following exist:

  1. 1.

    finite constants \(\beta , \gamma , {\lambda }, \kappa >0\) such that, for all \(i\in \mathbb {Z}_{+}\),

    $$\begin{aligned}\Vert B(i)\Vert _{\infty \rightarrow \infty } \le \beta ,~\Vert C(i)\Vert _{\infty \rightarrow \infty }\le \gamma ,\text { and } \Vert e^{A(i)t}\Vert _{\infty \rightarrow \infty } \le \kappa e^{-{\lambda } t}~\forall t\in \mathbb {R}_+;\end{aligned}$$
  2. 2.

    positive-semi-definite matrix sequences \(\{P_t(0)\!=\!P_t(0)^*,P_t(1)\!=\!P_t(1)^*,\ldots \}\) and \(\{P_s(0)\!=\!P_s(0)^*,P_s(1)\!=\!P_s(1)^*,\ldots \}\), and finite constants \({\lambda }_s, {\lambda }_t>0\) such that, for all \(i\in \mathbb {Z}_{+}\),

    1. (a)

      \({\lambda }_{\text {min}}(P_s(i)) \ge {\lambda }_s\), \({\lambda }_{\text {max}}(P_t(i)) \le {\lambda }_t\) and

    2. (b)

      \(Q(i) {:=} \tilde{A}(i)^*\tilde{P}_t(i)+\tilde{P}_t(i) \tilde{A}(i)+\tilde{A}(i)^*\tilde{P}_s(i+1)\tilde{A}(i)-\tilde{P}_s(i) \le 0 ,\)

    where

    $$\begin{aligned} \tilde{A}(i) {:=} \begin{bmatrix}A(i)&\quad B(i) \\ C(i)&\quad 0 \end{bmatrix},\quad \tilde{P}_t(i) {:=} \begin{bmatrix}P_t(i)&\quad 0 \\ 0&\quad 0 \end{bmatrix} \quad \text { and }\quad \tilde{P}_s(i) {:=} \begin{bmatrix}0&\quad 0 \\ 0&\quad P_s(i) \end{bmatrix}. \end{aligned}$$
    (11)

Then there exist finite constants \(M_1, M_2, M_3 > 0\) such that

$$\begin{aligned}|x(t,i)|_\infty \le M_1\Vert x_t(0,\cdot )\Vert _2 + M_2\Vert x_s(\cdot ,0)\Vert _2 + M_3\Vert x_s(\cdot ,0)\Vert _\infty \end{aligned}$$

for all \((t,i)\in \mathbb {R}_+\times \mathbb {Z}_{+}\) and arbitrary boundary conditions \(x_s(\cdot ,0)\in L_2\cap L_\infty \) and \(x_t(0,\cdot )\in \ell _2\).

Proof

Let \(V_t(t,i) {:=} x_t(t,i)^* P_t(i) x_t(t,i)\) and \(V_s(t,i) {:=} x_s(t,i)^* P_s(i) x_s(t,i)\) for \((t,i)\in \mathbb {R}_+\times \mathbb {Z}_+\). Using (10) and hypothesis 2(b), it follows that

$$\begin{aligned} \frac{\partial V_t}{\partial t}(t,i)&+ V_s(t,i+1) - V_s(t,i) \nonumber \\&=x(t,i)^*(\tilde{A}(i)^*\tilde{P}_t(i)+\tilde{P}_t(i) \tilde{A}(i)+\tilde{A}(i)^*\tilde{P}_s(i+1)\tilde{A}(i)-\tilde{P}_s(i)) x(t,i)\nonumber \\&=x(t,i)^*Q(i)x(t,i) \le 0 \quad \text { for all } (t,i)\in \mathbb {R}_+\times \mathbb {Z}_+. \end{aligned}$$
(12)

Since \(V_t(t,i)\ge 0\) and \(V_s(t,i)\ge 0\), the inequality (12) implies (2) holds by Lemma 1. Combining this with the properties of \(P_s(i)>0\) and \(P_t(i)\ge 0\) identified in hypothesis 2(a) yields

$$\begin{aligned} \int _0^t x_s(\tau ,i)^*x_s(\tau ,i)d\tau&\le \frac{1}{{\lambda }_s} \int _0^t V_s(\tau ,i) d\tau \nonumber \\&\le \frac{1}{{\lambda }_s} \int _0^t V_s(\tau ,0)d\tau + \frac{1}{{\lambda }_s}\sum _{k=0}^iV_t(0,k) \nonumber \\&= \frac{1}{{\lambda }_s} \int _0^t x_s(\tau ,0)^*P_s(0)x_s(\tau ,0) d\tau + \frac{1}{{\lambda }_s}\sum _{k=0}^{i} x_t(0,k)^*P_t(k)x_t(0,k) \nonumber \\&\le \frac{{\lambda }_{\text {max}}(P_s(0))}{{\lambda }_s}\Vert x_s(\cdot ,0)\Vert _2^2 + \frac{{\lambda }_t}{{\lambda }_s} \Vert x_t(0,\cdot )\Vert _2^2. \end{aligned}$$
(13)

Now bearing in mind hypothesis 1, and noting that \(x_t(0,\cdot )\in \ell _2\) implies \(|x_t(0,i)|_\infty \le |x_t(0,i)|_2 \le \Vert x_t(0,\cdot )\Vert _2\) for all \(i\in \mathbb {Z}_+\), it follows that

$$\begin{aligned} |x_t\left( t,i\right) |_\infty&=|x_t\left( 0,i\right) e^{A\left( i\right) t}+\int _0^te^{A\left( i\right) \left( t-\tau \right) }B\left( i\right) x_s\left( \tau ,i\right) d\tau |_\infty \nonumber \\&\le \kappa e^{-{{\lambda }}t}|x_t\left( 0,i\right) |_\infty + \kappa \sup _i\Vert B\left( i\right) \Vert _{\infty \rightarrow \infty }\int _0^t e^{-{{\lambda }}\left( t-\tau \right) }|x_s\left( \tau ,i\right) |_{\infty }d\tau \nonumber \\&\le \kappa \Vert x_t\left( 0,\cdot \right) \Vert _2 + \kappa \beta \left( \int _0^t\left( e^{-{{\lambda }}\left( t-\tau \right) }\right) ^2d\tau \right) ^\frac{1}{2} \left( \int _0^t|x_s\left( \tau ,i\right) |_\infty ^2d\tau \right) ^\frac{1}{2} \end{aligned}$$
(14)
$$\begin{aligned}&\le \kappa \Vert x_t\left( 0,\cdot \right) \Vert _2 + \kappa \beta \left( \frac{1-e^{-2{{\lambda }}t}}{2{{\lambda }}}\right) ^\frac{1}{2} \left( \int _0^t |x_s\left( \tau ,i\right) |_2^2d\tau \right) ^\frac{1}{2} \end{aligned}$$
(15)
$$\begin{aligned}&\le \kappa \Vert x_t\left( 0,\cdot \right) \Vert _2 + \frac{\kappa \beta }{\sqrt{2{{\lambda }}}}\sqrt{\int _0^t x_s^*\left( \tau ,i\right) x_s\left( \tau ,i\right) d\tau }\nonumber \\&\le \kappa \Vert x_t\left( 0,\cdot \right) \Vert _2 + \frac{\kappa \beta }{\sqrt{2{{\lambda }}}} \sqrt{\frac{{\lambda }_{\text {max}}\left( P_s\left( 0\right) \right) }{{\lambda }_s}\Vert x_s\left( \cdot ,0\right) \Vert _2^2 + \frac{{\lambda }_t}{{\lambda }_s} \Vert x_t\left( 0,\cdot \right) \Vert _2^2} \end{aligned}$$
(16)
$$\begin{aligned}&\le \kappa \left( 1+\frac{\beta \sqrt{{\lambda }_t}}{\sqrt{2{\lambda }{\lambda }_s}}\right) \Vert x_t\left( 0,\cdot \right) \Vert _2 + \frac{\kappa \beta \sqrt{{\lambda }_{\text {max}}\left( P_s\left( 0\right) \right) }}{\sqrt{2{\lambda }{\lambda }_s}}\Vert x_s\left( \cdot ,0\right) \Vert _2\nonumber \\&{:=}\, \mu _1\Vert x_t\left( 0,\cdot \right) \Vert _2 + \mu _2\Vert x_s\left( \cdot ,0\right) \Vert _2 \end{aligned}$$
(17)

for all \((t,i)\in \mathbb {R}_+\times \mathbb {Z}_+\). In particular, (14) holds by the Cauchy–Schwartz inequality, (15) holds because \(|x_s(\tau ,i)|_\infty \le |x_s(\tau ,i)|_2\) and (16) holds in view of (13).

Finally, note that \(x_s(t,i+1)= C(i)x_t(t,i)\) by (10). Hence,

$$\begin{aligned} |x_s(t,i+1)|_\infty \le \sup _i\Vert C(i)\Vert _{\infty \rightarrow \infty }|x_t(t,i)|_\infty \le \gamma (\mu _1\Vert x_t(0,\cdot )\Vert _2 + \mu _2\Vert x_s(\cdot ,0)\Vert _2)\end{aligned}$$

for all \((t,i)\in \mathbb {R}_+\times \mathbb {Z}_+\), where (17) and hypothesis 1 have been used. Moreover, \(x_s(\cdot ,0)\in L_2\cap L_\infty \) implies \(|x_s(t,0)|_\infty \le \Vert x_s(\cdot ,0)\Vert _\infty \). As such, it follows that

$$\begin{aligned} |x(t,i)|_\infty&= \max \{|x_t(t,i)|_\infty ,|x_s(t,i)|_\infty \} \\&\le \max \{\mu _1\Vert x_t(0,\cdot )\Vert _2 + \mu _2\Vert x_s(\cdot ,0)\Vert _2,\\&\quad \quad \quad \quad \max \{\gamma (\mu _1\Vert x_t(0,\cdot )\Vert _2 + \mu _2\Vert x_s(\cdot ,0)\Vert _2),\Vert x_s(\cdot ,0)\Vert _\infty \}\} \\&\le \max \{1,\gamma \}\mu _1\Vert x_t(0,\cdot )\Vert _2 + \max \{1,\gamma \}\mu _2\Vert x_s(\cdot ,0)\Vert _2 + \Vert x_s(\cdot ,0)\Vert _\infty \end{aligned}$$

for all \((t,i)\in \mathbb {R}_+\times \mathbb {Z}_+\), as claimed. \(\square \)

Theorem 1 and the following lemma lead to the main decentralized string-stability certificate summarised in Theorem 2 below.

Lemma 4

For all \(i\in \mathbb {Z}_+\), suppose that \(G_i(s){:=}C(i)(sI-A(i))^{-1}B(i)\) with \(A(i)\in \mathbb {R}^{n(i)\times n(i)}\) Hurwitz, and that \(\Vert G_i\Vert _\infty \le 1\). Then there exist positive-semi-definite matrix sequences \(\{P_t(0)\!=\!P_t(0)^*,P_t(1)\!=\!P_t(1)^*,\ldots \}\) and \(\{P_s(0)\!=\!P_s(0)^*,P_s(1)\!=\!P_s(1)^*,\ldots \}\) such that

$$\begin{aligned} Q(i){:=}\tilde{A}(i)^*\tilde{P}_t(i)+\tilde{P}_t(i) \tilde{A}(i)+\tilde{A}(i)^*\tilde{P}_s(i+1)\tilde{A}(i)-\tilde{P}_s(i) \le 0 \end{aligned}$$
(18)

for all \(i\in \mathbb {Z}_+\), where \(\tilde{A}(i)\), \(\tilde{P}_t(i)\) and \(\tilde{P}_s(i)\) are as defined in (11). Specifically, take \(P_s(i)=I\) and \(P_t(i)=P_t(i)^*\ge 0\) to be the unique solution of

$$\begin{aligned} A(i)^*P_t(i)+P_t(i)A(i)+P_t(i)B(i)B(i)^*P_t(i)+C(i)^*C(i)=0 \end{aligned}$$
(19)

that satisfies \(\sigma (A(i)+B(i)B(i)^*P_t(i))\in \mathbb {C}_-\cup j\mathbb {R}\).

Proof

In view of Lemma 2, there exists a real matrix \(X(i)=X^*(i)\ge 0\) such that

$$\begin{aligned}&X(i)A(i)+A(i)^*X(i)+X(i)B(i)B(i)^*X(i)+C(i)^*C(i)=0. \end{aligned}$$
(20)

Applying the Schur complement to (20) gives

$$\begin{aligned} \left[ \begin{array}{cc} X(i)A(i)+A(i)^*X(i)+C(i)^*C(i) &{}\quad X(i)B(i)\\ B(i)^*X(i) &{}\quad -I \end{array}\right]&\le 0. \end{aligned}$$
(21)

Note that with \(P_t(i)=X(i)\) and \(P_s(i)=I\),

$$\begin{aligned} Q(i) = \begin{bmatrix} X(i)A(i)+A(i)^*X(i)+C(i)^*C(i)&\quad X(i)B(i)\\ B(i)^*X(i)&\quad -I \end{bmatrix}, \end{aligned}$$

whereby (21) implies (18). \(\square \)

Theorem 2

Consider a cascade of stable LTI systems, as shown in Fig.  1. Let \(G_i(s)=C(i)(sI-A(i))^{-1}B(i)\), with \(A(i)\in \mathbb {R}^{n(i)\times n(i)}\) Hurwitz, be a minimal balanced realization for subsystem \(i\in \mathbb {Z}_+\) and suppose that the following hold:

  1. 1.

    there exists a constant \(\varsigma >0\) such that the minimum Hankel singular value of \(G_i\) satisfies \(\sigma _{n(i)} \ge \varsigma \) for all \(i\in \mathbb {Z}_+\).

  2. 2.

    there exist finite constants \(\beta , \gamma , {\lambda }, \kappa >0\) such that

    $$\begin{aligned} \Vert B(i)\Vert _{\infty \rightarrow \infty } \le \beta ,~\Vert C(i)\Vert _{\infty \rightarrow \infty }\le \gamma \text { and }\Vert e^{A(i)t}\Vert _{\infty \rightarrow \infty } \le \kappa e^{-{\lambda } t}\text {for all } (t,i)\in \mathbb {R}_+\times \mathbb {Z}_{+}. \end{aligned}$$

If \(\Vert G_i\Vert _\infty \le 1\) for all \(i\in \mathbb {Z}_+\), then the cascade is \(L_2\)-to-\(L_\infty \) string-stable in the sense of Definition 1.

Proof

Let \(\Vert G_i\Vert _\infty \le 1\) for all \(i\in \mathbb {Z}_+\), so that in view of Lemma 2, Lemma 3, Remark 1 and hypothesis 1 above, the unique solution of \(P_t(i)\ge 0\) of (19) such that \(\sigma (A(i)+B(i)B(i)^*P_t(i))\in \mathbb {C}_-\cup j\mathbb {R}\) also satisfies \(P_t(i)>0\) and \({\lambda }_{\text {max}}(P_t(i)) \le 1/\varsigma \) for all \(i\in \mathbb {Z}_+\). Using Lemma 4 and hypothesis 2, it follows that Theorem 1 applies to yield the required bound on the semi-state evolution of the corresponding 2-D Roesser model (10), given boundary conditions \(x_s(\cdot ,0)=d\in L_2\cap L_\infty \) and \(x_t(0,\cdot )=w\in \ell _2\). As such, the result holds since \(u_i(t)=x_s(t,i)\). \(\square \)

Fig. 2
figure 2

Section (pool) of an irrigation channel under decentralized distant-downstream control

Full size image

5 Distant-downstream control of irrigation channels

Irrigation channels are used around the world to distribute fresh water for agriculture. The channels are typically sectioned into pools that stretch between gates that can be adjusted to locally impose gravity-powered flow downstream and at supply points. Figure 2 shows the block diagram for a section of an automated irrigation channel that has a so-called distant-downstream control architecture (Clemmens and Replogle 1989; Schuurmans et al. 1999; Weyer 2002; Mareels et al. 2005; Li 2006; Litrico and Fromion 2009; Soltanian 2014). The local feedback controller \(C_i(s)\) is used to regulate the water-level \(y_i\) at the downstream gate, which reflects the capacity of the section to supply flow locally and downstream, under the power of gravity. This is achieved via adjustment of the inflow \(u_i\) at the upstream gate, in response to variation of the outflow load \(v_i\). The controlled inflow \(u_i\) is a load on the upstream section. A correspondingly automated irrigation channel is therefore a cascade of subsystems on the kind shown in Fig. 2. Importantly, the distant-downstream control architecture translates to demand-driven release of water from upstream storage, which has merit from an operations perspective in light of the limited availability of storage in the channels.

In this section, a heterogeneous channel of pools with specifications as in Table 1 is considered, where the pool delay and integrator constant are denoted by \(\tau _i\) and \(k_i\), respectively, and PI controller is represented by \(C_i(s)=K_i\frac{(s+z_i)}{s(s+p_i)}\) for each pool i.

Table 1 Pool model and controller parameters, \(n=0,1,2,\ldots \)
Full size table

The conventional decentralized distant-downstream control architecture corresponds to \(F_i(s)=0\) in Fig. 2. For a homogeneous channel and integral action in identical decentralized controllers C(s), transient flow peaks produced along the channel in response to a step increase in downstream flow, are amplified as these propagate upstream (Li et al. 2005; Cantoni et al. 2007). Indeed, it is not possible to achieve \(\Vert G\Vert _\infty \le 1\), where \(G=\frac{C(s)k/s}{1+C(s)ke^{-s\tau }/s}\) is the transfer function from outflow v to inflow u. Even in the case of heterogeneous channels, under a purely decentralized distant-downstream control architecture transient water flow peaks can be amplified, as shown in Fig. 3 for the channel and controller data summarised in Table 1. Note that in this case, \(\Vert G_1\Vert _\infty = 1.66\), \(\Vert G_2\Vert _\infty = 2.16\), \(\Vert G_3\Vert _\infty =\Vert G_4\Vert _\infty =\Vert G_5\Vert _\infty =1.836\), and so on.

Fig. 3
figure 3

Response of channel under decentralized distant-downstream control—i.e., \(F_i(s)=0\) and \(C_i(s)=K_i\frac{(s+z_i)}{s(s+p_i)}\)

Full size image

As first considered in Soltanian and Cantoni (2013), Soltanian (2014), the local feed-forward controller \(F_i(s)\) provides scope for shaping the transfer function \(G_i(s)\) from \(v_i\) to \(u_i\) for each section of the automated channel, as desired. Of course, there is a price to pay; the steady-state offset in water-level relative to a constant reference for a step increase in flow load becomes non-zero. For a given PI controller \(C_i(s)\) (i.e., given \(K_i,z_i,p_i>0\)), a desired stable strictly-proper transfer function \(G_i(s)\), which must satisfy \(G_i(0)=1\) to ensure steady-state matching of inflow to outflow, can be achieved by setting

$$\begin{aligned} F_i(s) = \frac{k_i}{s}(1-G_i(s)e^{-s\tau _i}) - \frac{G_i(s)}{C_i(s)}. \end{aligned}$$
(22)

Note that \(F_i(s)\) is stable, because \(G_i(s)\) is stable, \((1-G_i(s)e^{-s\tau _i})\) has at least one zero at \(s=0\) and the zero of \(C_i(s)\) has negative real part. Note that it is also reasonable to use a rational approximation of the delay transfer function \(e^{-s\tau _i}\), provided the error is sufficiently small up to the loop-gain crossover frequency, as the closed-loop behaviour is insensitive to such modeling uncertainty. For example, the Padé approximation \((1-s\tau _i/2)/(1+s\tau _i/2)\) is acceptable provided the controller gain \(K_i\) and corresponding loop-gain crossover frequency are sufficiently small, which is necessary to achieve reasonable control performance and robustness anyway (Li 2006).

Fig. 4
figure 4

Response of channel under decentralized distant-downstream control with \(F_i(s)\) set as in (22) so that \(G_1(s)=1/(20s+1),G_2(s)=1/(10s+1),G_3(s)=G_4(s)=G_5(s)=1/(40s+1),\ldots \)

Full size image

By Theorem 2, choosing \(F_i(s)\) to achieve \(\Vert G_i\Vert _\infty \le 1\) for each pool would imply \(L_2\)-to-\(L_\infty \) string-stability of the automated channel. That is, uniformly bounded flow peaks in response to finite-duration step-changes of flow load. One possible choice is \(G_i(s)=1/(T_is+1)\) for some time-constant \(T_i>0\); note \(G_i(0)=1\). In this case, \(\Vert g_i\Vert _1{:=}\int _{0}^\infty |g_i(t)|dt \le 1\), where \(g_i(\cdot )\) denotes the impulse response associated with the transfer function \(G_i\) (i.e. \(g_i(t)=e^{-t/T_i}\) here). In fact, \(\Vert g_i\Vert _1 \le 1\), which implies \(\Vert G_i\Vert _\infty \le 1\) (in general), is a condition that ensures non-amplification of peaks as these propagate; see Soltanian and Cantoni (2013). This is illustrated in Fig. 4, where again a \(17\text {m}^3/\text {min}\) step change in the outflow of the bottom pool is considered.

With \(F_i(s)\) selected to achieve \(G_1(s)=0.03/(s^2+0.28s+0.03)\), \(G_2(s)=0.06/(s^2+0.35s+0.06)\), and \(G_3(s)=G_4(s)=G_5(s)=0.01/(s^2+0.15s+0.01)\), one has \(G_i(0)=1\) and \(\Vert G_i\Vert _\infty =1\) for all i. Thus, \(L_2\)-to-\(L_\infty \) stability would be achieved by Theorem 2. The controlled flow responses to a \(17\text {m}^3/\text {min}\) step change in the outflow at the bottom pool are shown in Figs. 5 and 6. It can be seen that, while there is amplification of flow peaks as these propagate along the bottom pools, this does not persist and the peak flows remain uniformly bounded along the channel as expected.

Fig. 5
figure 5

Response of channel under decentralized distant-downstream control with \(F_i(s)\) set as in (22) so that \(\Vert G_i\Vert _\infty =1\)

Full size image
Fig. 6
figure 6

Response channel under decentralized distant-downstream control with \(F_i(s)\) set as in (22) so that \(\Vert G_i\Vert _\infty =1\)(zoomed in)

Full size image

6 Conclusion

An \(L_2\)-to-\(L_\infty \) string-stability property is defined and analyzed for a heterogeneous cascade of stable LTI subsystems, subject to the requirement that the interconnection signals match constant spatial boundary conditions in steady state. A sufficient condition is established in terms of state-space realizations for the subsystems. This is subsequently used to develop a decentralized string-stability certificate, which simply involves a location independent bound on the \(H_\infty \) norm of the transfer function relating the interconnection signals associated with each subsystem. An application of this is explored within the context of scalable distant-downstream controller design in irrigation channels. It would be of interest to understand if the \(H_\infty \) norm condition is necessary for \(L_2\)-to-\(L_\infty \) stability of homogeneous cascades. The robustness properties of the presented local feed-forward approach to satisfying the decentralized string-stability certificate within the context of irrigation channel control-system design also requires further investigation.