1 Introduction

VFD digital filters belong to the branch of variable digital filters which are applied to where frequency characteristics need to be adjusted online without redesigning the system. For the past decade, several works have been proposed for the design of variable digital filters (Shyu et al. 2009a, b; Shyu et al. 2010; Deng 1998a, b, 2001, 2003; Deng 2005, 2007a, b, 2010; Deng et al. 2003; Deng and Soma 1995a, b; Zarour and Fahmy 1989; Farrow 1998; Laakso et al. 1996; Lu and Deng 1999; Tseng 2002a; Tseng 2002b, 2003; Johansson and Löwenborg 2003; Deng and Lian 2006; Zhao and Yu 2006; Tsui et al. 2007; Kwan and Jiang 2009; Pei and Lin 2009; Tseng and Lee 2010; Deng and Lu 2000) due to their wide applications in signal processing and communication systems. By the function, they are generally classified into two main categories. One is the filters with variable magnitude characteristics such as cutoff frequencies or magnitude responses (Deng 1998a, b, 2001, 2003; Deng 2005; Deng and Soma 1995a, b; Zarour and Fahmy 1989; Deng et al. 2003; Shyu et al. 2009b), and the other is the filters with variable fractional delay (Shyu et al. 2009a, 2010; Farrow 1998; Laakso et al. 1996; Lu and Deng 1999; Tseng 2002a; Tseng 2002b, 2003; Johansson and Löwenborg 2003; Deng and Lian 2006; Zhao and Yu 2006; Deng 2007a; Deng 2007b, 2010; Tsui et al. 2007; Kwan and Jiang 2009; Pei and Lin 2009; Tseng and Lee 2010; Deng and Lu 2000).

In this paper, the design of VFD 2-D FIR digital filters will be investigated. Conventionally, the transfer function of a variable fractional-delay (VFD) 2-D FIR digital filter is given by

$$\begin{aligned} Hc\left( {z_1 ,z_2 ,p_1 ,p_2 } \right)=\sum _{n_1 =0}^{N_1 } {\sum _{n_2 =0}^{N_2 } {h_{n_1 n_2 } \left( {p_{1} ,p_2 } \right) } } z_1^{-n_1 } z_2^{-n_2 } \end{aligned}$$
(1)

where

$$\begin{aligned} h_{n_1 n_2 } \left( {p_1 ,p_2 } \right)=\sum _{m_1 =0}^M {\sum _{m_2 =0}^M {h\left( {n_1 ,n_2 ,m_1 ,m_2 } \right) } } p_1^{m_1 } p_2^{m_2 }. \end{aligned}$$
(2)

Hence, (1) can be represented by

$$\begin{aligned} Hc\left( {z_1 ,z_2 ,p_1 ,p_2 } \right)=\sum _{m_1 =0}^M {\sum _{m_2 =0}^M {\hat{{G}}_{m_1 m_2 } \left( {z_1 ,z_2 } \right)} } p_1^{m_1 } p_2^{m_2 } \end{aligned}$$
(3)

where the 2-D subfilters

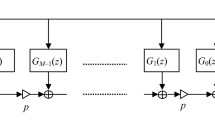
$$\begin{aligned} \hat{{G}}_{m_1 m_2 } \left( {z_1 ,z_2 } \right)=\sum _{n_1 =0}^{N_1 } {\sum _{n_2 =0}^{N_2 } {h\left( {n_1 ,n_2 ,m_1 ,m_2 } \right) } } z_1^{-n_1 } z_2^{-n_2 } , \end{aligned}$$
(4)

and the system can be implemented by a 2-D Farrow structure as in Fig. 1 (Shyu et al. 2009a).

Fig. 1
figure 1

The conventional structure for a VFD 2-D FIR digital filter. (\(M=5\))

Full size image

Comparing with the conventional 2-D Farrow structure presented recently in (Shyu et al. 2009a), a prefilter–subfilter cascaded structure is proposed in this paper. The structure is developed based on the Taylor series expansion of the desired frequency response. In (Shyu et al. 2009a), there are four types of 2-D quadrantally symmetric/antisymmetric filters (Pei and Shyu 1995; Zhao and Lai 2011) to be designed. But, only two 1-D differentiating prefilters and one type of 2-D quadrantally symmetric subfilters are needed to be designed in the proposed structure. By the proposed experiments in this paper, it will be shown that the required number of independent coefficients of the designed system is much less than that in (Shyu et al. 2009a) while the performance of the designed filters is still better than that in (Shyu et al. 2009a) under the cost of larger delays.

This paper is organized as follows. In Sect. 2, the proposed prefilter–subfilter cascaded structure is derived from the Taylor series expansion of the desired frequency response. And the design of the mentioned prefilters and subfilters for even \(M\) is presented in Sect. 3. For simplicity, the general least-squares method (Shyu et al. 2009a, 2010; Zhao and Lai 2011, 2012) is applied, and design examples will be presented to demonstrate the effectiveness of the presented method. As to the design of VFD 2-D FIR digital filters for odd \(M\), it is shown in Sect. 4 accompanying also a design example. Finally, the conclusions are given in Sect. 5.

2 The proposed structure

For designing a VFD 2-D FIR filter, the desired frequency response is given by

$$\begin{aligned} H_d \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)=M\left( {\omega _1 ,\omega _2 } \right)e^{-j\left[ {\omega _1 \left( {I_1 +p_1 } \right)+\omega _2 \left( {I_2 +p_2 } \right)} \right]} \end{aligned}$$
(5)

where \(M\left( {\omega _1 ,\omega _2 } \right)\) is the desired magnitude response, \(I_1 \) and \(I_2 \) are the prescribed group-delays with respect to \(\omega _1\) and \(\omega _2\)-axis, respectively, and \(p_1 ,p_2 \in \left[ {-0.5,0.5} \right].\)For simplicity, only quadrantally symmetric magnitude response \(M\left( {\omega _1 ,\omega _2 } \right)\) is considered in this paper. By Taylor series expansion,

$$\begin{aligned} e^{-j\left( {\omega _{1}p_{1} +\omega _{2} p_{2} } \right)}&= \sum _{m_{1}=0}^{\infty } {\frac{\left( {-j\omega _{1} p_{1}} \right)^{m_{1}}}{m_{1}!}}\cdot \sum _{m_{2}=0}^{\infty }{\frac{\left( {-j\omega _{2} p_{2}}\right)^{m_{2}}}{m_{2}!}} \nonumber \\&\approx \sum _{m_{1}=0}^{M} {\frac{\left({-j\omega _{1} p_{1}} \right)^{m_{1}}}{m_{1}!}}\cdot \sum _{m_{2}=0}^{M}{\frac{\left( {-j\omega _{2}p_{2}}\right)^{m_{2}}}{m_{2}!}} \end{aligned}$$
(6)

for sufficiently large \(M\). In this paper, the case for odd \(M\) is considered first, and the case for even \(M\) will be discussed in Sect. 4. Let \(M=2\hat{{M}}+1\), then (6) becomes

$$\begin{aligned} e^{-j\left({\omega _{1} p_{1}+\omega _{2} p_{2}}\right)}&\approx \left[{\sum _{m_{1}=0}^{\hat{{M}}}{\left({-1}\right)^{m_{1}}\frac{\left( {\omega _{1}p_{1}}\right)^{2m_{1}}}{\left({2m_{1}}\right)!}+} \left( {-j\omega _{1}} \right)p_{1}\sum _{m_{1}=0}^{\hat{{M}}} {\frac{\left( {-1} \right)^{m_{1}}}{2m_{1}+1}\frac{\left({\omega _{1}p_{1}} \right)^{2m_{1}}}{\left({2m_{1}}\right)!}}} \right] \nonumber \\&\quad \times \left[{\sum _{m_{2}=0}^{\hat{{M}}}{\left({-1} \right)^{m_{2}}\frac{\left({\omega _{2}p_{2}} \right)^{2m_{2}}}{\left( {2m_{2}}\right)!}+}\left({-j\omega _{2}}\right)p_{2}\sum _{m_{2} =0}^{\hat{{M}}}{\frac{\left({-1}\right)^{m_{2}}}{2m_{2} +1}\frac{\left({\omega _{2}p_{2}}\right)^{2m_{2}}}{\left({2m_{2}} \right)!}}} \right] \nonumber \\&= \sum _{m_{1}=0}^{\hat{{M}}}{\sum _{m_{2}=0}^{\hat{{M}}} {\left( {-1} \right)^{m_{1} +m_{2}}\frac{\left({\omega _{1} p_{1}}\right)^{2m_{1}}\left({\omega _{2}p_{2}}\right)^{2m_{2}}}{\left( {2m_{1}}\right)!\left({2m_{2}}\right)!}} } \nonumber \\&\quad +\left( {-j\omega _{1}} \right)p_{1}\sum _{m_{1}=0}^{\hat{{M}}} {\sum _{m_{2}=0}^{\hat{{M}}}{\frac{\left({-1}\right)^{m_{1}+m_{2} }}{2m_{1}+1}\frac{\left({\omega _{1} p_{1}} \right)^{2m_{1} }\left( {\omega _{2} p_2 } \right)^{2m_{2}}}{\left( {2m_1} \right)!\left( {2m_2} \right)!}} } \nonumber \\&\quad +\left( {-j\omega _2 } \right)p_2 \sum _{m_{1} =0}^{\hat{{M}}} {\sum _{m_{2}=0}^{\hat{{M}}} {\frac{\left( {-1} \right)^{m_{1} +m_{2} }}{2m_{2} +1}\frac{\left( {\omega _{1}p_{1}} \right)^{2m_{1}}\left( {\omega _{2}p_{2}}\right)^{2m_{2}}}{\left({2m_{1}}\right)!\left( {2m_2} \right)!}} } \nonumber \\&\quad +\left({-j\omega _1}\right)\left({-j\omega _2}\right)p_{1} p_{2} \sum _{m_{1}=0}^{\hat{{M}}} {\sum _{m_{2}=0}^{\hat{{M}}} {\frac{\left( {-1} \right)^{m_{1} +m_{2}}}{\left({2m_{1}+1} \right)\left( {2m_{2} +1} \right)}} } \frac{\left( {\omega _{1} p_{1}} \right)^{2m_1}\left( {\omega _{2}p_{2}}\right)^{2m_2}}{\left( {2m_1 } \right)!\left({2m_2 } \right)!}\nonumber \\ \end{aligned}$$
(7)

By (5) and (7), the applied transfer function of the VFD 2-D FIR filter in this section is represented by

$$\begin{aligned} H\left( {z_1 ,z_2 ,p_1 ,p_2} \right)&= z_{1}^{-\frac{N_{d1}}{2}} z_{2}^{-\frac{N_{d2}}{2}}\sum _{m_{1}=0}^{\hat{{M}}} {\sum _{m_{2} =0}^{\hat{{M}}} {G_{2m_{1} ,2m_{2}}\left({z_1 ,z_2 } \right)} } p_{1}^{2m_{1}} p_{2}^{2m_{2}} \nonumber \\&\quad + z_{2}^{-\frac{N_{d2} }{2}} D_{1} \left( {z_1} \right)\sum _{m_{1}=0}^{\hat{{M}}}{\sum _{m_{2}=0}^{\hat{{M}}} {\frac{1}{2m_{1}+1}G_{2m_{1} ,2m_{2}} \left( {z_1 ,z_2} \right)} } p_{1}^{2m_{1}+1} p_{2}^{2m_2}\nonumber \\&\quad + z_{1}^{-\frac{N_{d1} }{2}} D_{2}\left( {z_2 } \right)\sum _{m_{1}=0}^{\hat{{M}}}{\sum _{m_{2}=0}^{\hat{{M}}} {\frac{1}{2m_{2}+1}G_{2m_{1},2m_{2}}\left({z_1,z_2} \right)} } p_{1}^{2m_1 } p_{2}^{2m_2 +1} \nonumber \\&\quad +D_{1} \left( {z_1}\right)D_{2}\left({z_2}\right)\sum _{m_{1} =0}^{\hat{{M}}} \sum _{m_{2}=0}^{\hat{{M}}}\frac{1}{\left({2m_{1} +1} \right)\left({2m_{2}+1}\right)}G_{2m_{1},2m_{2}}\nonumber \\&\quad \times \left({z_1,z_2 } \right) p_{1}^{2m_{1} +1} p_2^{2m_2 +1} \end{aligned}$$
(8)

and the proposed structure is shown in Fig. 2. In (8), the quadrantally symmetric subfilters \(G_{2m_{1},2m_{2}}\left({z_1 ,z_2 }\right)\) are characterized by

$$\begin{aligned} G_{2m_{1},2m_{2}}\left({z_{1},z_{2}} \right)=\sum _{n_{1}=0}^{N_{g}} {\sum _{n_{2}=0}^{N_{g}} { g_{m_{1} m_{2}}\left({n_1 ,n_2 } \right)} z_1^{-n_1 } z_2^{-n_2 } } \end{aligned}$$
(9)

where \(N_g \) is assumed to be even while the Type III linear-phase prefilters \(D_i \left( {z_i } \right)\), \(i=1, 2,\) are characterized by

$$\begin{aligned} D_i \left( {z_i } \right)=\sum _{n=0}^{N_{di}} {d_i \left( n \right)z_i^{-n} } , N_{di}:\text{ even},\quad i=1, 2. \end{aligned}$$
(10)

After some algebraic operations, the frequency response of (8) can be represented by

$$\begin{aligned} H\left( {e^{j\omega _{1}},e^{j\omega _{2}},p_1 ,p_2 } \right)=e^{-j\left( {\frac{N_{d1}}{2}+\frac{N_g }{2}} \right)\omega _1 }e^{-j\left( {\frac{N_{d2} }{2}+\frac{N_g }{2}} \right)\omega _2 }\hat{{H}}\left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right) \end{aligned}$$
(11)

where

$$\begin{aligned} \hat{{H}}\left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)&= \sum _{m_1 =0}^{\hat{{M}}} {\sum _{m_2 =0}^{\hat{{M}}} {\hat{{G}}_{2m_1 ,2m_2 } \left( {\omega _1 ,\omega _2 } \right)} } p_1^{2m_1 } p_2^{2m_2 } \nonumber \\&\quad +\,j\hat{{D}}_1 \left( {\omega _1 } \right)\sum _{m_1 =0}^{\hat{{M}}} {\sum _{m_2 =0}^{\hat{{M}}} {\frac{1}{2m_1 +1}\hat{{G}}_{2m_1 ,2m_2 } \left( {\omega _1 ,\omega _2 } \right)} } p_1^{2m_1 +1} p_2^{2m_2 } \nonumber \\&\quad +\,j\hat{{D}}_2 \left( {\omega _2 } \right)\sum _{m_1 =0}^{\hat{{M}}} {\sum _{m_2 =0}^{\hat{{M}}} {\frac{1}{2m_2 +1}\hat{{G}}_{2m_1 ,2m_2 } \left( {\omega _1 ,\omega _2 } \right) } } p_1^{2m_1 } p_2^{2m_2 +1} \nonumber \\&\quad -\,\hat{{D}}_1 \left( {\omega _1 } \right)\hat{{D}}_2 \left( {\omega _2 } \right)\sum _{m_1 =0}^{\hat{{M}}} \sum _{m_2 =0}^{\hat{{M}}} \frac{1}{\left( {2m_1 +1} \right)\left( {2m_2 +1} \right)} \nonumber \\&\quad \times \hat{{G}}_{2m_1 ,2m_2 } \left( {\omega _1 ,\omega _2 } \right) p_1^{2m_1 +1} p_2^{2m_2 +1},\end{aligned}$$
(12a)
$$\begin{aligned} \hat{{G}}_{2m_1 ,2m_2 } \left( {\omega _1 ,\omega _2 } \right)&= \sum _{n_{1} =0}^{\frac{N_g}{2}}{\sum _{n_{2}=0}^{\frac{N_g }{2}} \hat{{g}}_{m_{1}m_2} \left( {n_1,n_2}\right)\cos \left( {n_{1}\omega _{1}}\right)}\cos \left({n_{2}\omega _{2}}\right),\end{aligned}$$
(12b)
$$\begin{aligned} \hat{{D}}_i \left( {\omega _i } \right)&= \sum _{n=1}^{\frac{N_{di} }{2}} {\hat{{d}}_i \left( n \right)\sin \left( {n\omega _i } \right)} , i=1, 2,\end{aligned}$$
(12c)
$$\begin{aligned} \hat{{g}}_{m_1 m_2 } \left( {n_1 ,n_2 } \right)&= \left\{ {{\begin{array}{ll} {g_{m_{1} m_2 } \left( {\frac{N_g }{2},\frac{N_g }{2}} \right),}&{n_1 =n_2 =0,} \\ {2g_{m_{1} m_2 } \left( {\frac{N_g }{2}-n_1 ,\frac{N_g }{2}} \right),}&{1\le n_1 \le \frac{N_g }{2}, \quad n_2 =0,} \\ {2g_{m_{1} m_2 } \left( {\frac{N_g }{2},\frac{N_g }{2}-n_2 } \right),}&{n_1 =0, \quad 1\le n_2 \le \frac{N_g }{2},} \\ {4g_{m_{1} m_2 } \left( {\frac{N_g }{2}-n_1 ,\frac{N_g }{2}-n_2 } \right),}&{1\le n_1, n_2 \le \frac{N_g }{2},} \\ \end{array} }} \right.\end{aligned}$$
(12d)
$$\begin{aligned} \hat{{d}}_i \left( n \right)&= 2d_i \left( {\frac{N_{di} }{2}-n} \right), \quad i=1, 2. \end{aligned}$$
(12e)

Obviously, the integers \(I_1 \) and \(I_2 \) in (5) can be set as \(I_i =\frac{N_{di} }{2}+\frac{N_g }{2}\),   \(i=1, 2.\)

Fig. 2
figure 2

The proposed structure of a VFD 2-D FIR digital filter. (\(M=5\))

Full size image

3 Design of 2-D VFD FIR digital filters with odd \(M\)

In this paper, we first deal with the design of the prefilters \(D_1 \left( {z_1 } \right)\) and \(D_2 \left( {z_2 } \right)\), and then these prefilters will be applied for the design of the subfilters \(G_{2m_{1} ,2m_2 } \left( {z_1 ,z_2 } \right)\). Design examples will be given to demonstrate the effectiveness of the presented method.

3.1 Design of the prefilters \(D_{1}\left({z_1}\right)\) and \(D_{2}\left({z_2}\right)\)

By (7) and (8), the prefilters \(D_1\left({z_1} \right)\) and \(D_2\left({z_2}\right)\) are used as differentiators with magnitudes \(-\omega _1\) and \(-\omega _2\), respectively, and their specifications depend on the magnitude response \(M\left({\omega _1 ,\omega _2}\right)\) in (5). For example, when the designed filter is an elliptically low-pass VFD filter with

$$\begin{aligned} M\left( {\omega _1 ,\omega _2 } \right)= \left\{ {{\begin{array}{ll} {1,}&{\frac{\omega _1^2 }{\omega _{p1}^2 }+\frac{\omega _2^2 }{\omega _{p2}^2 }\le 1,} \\ {0,}&{\frac{\omega _1^2 }{\omega _{s1}^2 }+\frac{\omega _2^2 }{\omega _{s2}^2 } \ge 1,} \\ \end{array} }} \right. \end{aligned}$$
(13)

the prefilters \(D_1 \left( {z_1 } \right)\) and \(D_2 \left( {z_2 } \right)\) are designed with passband edges \(\omega _{p1} \) and \(\omega _{p2} \), respectively, while their stopband edges are \(\omega _{s1} \) and \(\omega _{s2} \), respectively.

Defining

$$\begin{aligned}&\mathbf{d}_i =\left[ {\hat{{d}}_i \left( 1 \right),\;\hat{{d}}_i \left( 2 \right), \ldots , \hat{{d}}_i \left( {\frac{N_{di} }{2}} \right)} \right]^{T},\end{aligned}$$
(14a)
$$\begin{aligned}&\mathbf{s}_i \left( {\omega _i } \right)=\left[ {\sin \left( {\omega _i } \right),\;\sin \left( {2\omega _i } \right), \ldots , \sin \left( {\frac{N_{di} }{2}\omega _i } \right)} \right]^{T}, \end{aligned}$$
(14b)

the magnitude responses \(\hat{{D}}_i \left( {\omega _i } \right)\) of the prefilters can be represented by

$$\begin{aligned} \hat{{D}}_i \left( {\omega _i } \right)=\mathbf{d}_i^T \mathbf{s}_i \left( {\omega _i } \right),\quad i=1,2 \end{aligned}$$
(15)

where the superscript \(T\) denotes a transpose operator. Hence, the objective error functions for designing the prefilters in least-squares sense can be defined by

$$\begin{aligned} e\left( {\mathbf{d}_i } \right)&= \int \limits _0^{\omega _{pi} } {\left[ {-\omega _i -\hat{{D}}_i \left( {\omega _i } \right)} \right]^{2}} \;d\omega _i +\int \limits _{\omega _{si} }^{\pi } {\left[ {\hat{{D}}_i \left( {\omega _i } \right)} \right]^{2}} \;d\omega _i \nonumber \\&= u_i +\mathbf{r}_i^T \mathbf{d}_i +\mathbf{d}_i^T \mathbf{Q}_i \mathbf{d}_i \end{aligned}$$
(16)

where

$$\begin{aligned} u_i&= \int \limits _0^{\omega _{pi} } {\omega _i^2 } \;d\omega _i =\frac{\omega _{pi}^2 }{3},\end{aligned}$$
(17a)
$$\begin{aligned} \mathbf{r}_i&= 2\int \limits _0^{\omega _{pi} } {\omega _i \mathbf{s}_i \left( {\omega _i } \right)} \;d\omega _i ,\end{aligned}$$
(17b)
$$\begin{aligned} \mathbf{Q}_i&= \int \limits _0^{\omega _{pi} } {\mathbf{s}_i \left( {\omega _i } \right)\mathbf{s}_i^T \left( {\omega _i } \right)} \;d\omega _i +\int \limits _{\omega _{si} }^\pi {\mathbf{s}_i \left( {\omega _i } \right)\mathbf{s}_i^T \left( {\omega _i } \right)} \;d\omega _i , \end{aligned}$$
(17c)

and the solutions are

$$\begin{aligned} \mathbf{d}_i =-\frac{1}{2}\mathbf{Q}_i^{-1} \mathbf{r}_i,\quad i=1, 2. \end{aligned}$$
(18)

3.2 Design of the subfilters \(G_{2m_{1},2m_2}\left({z_{1},z_2 }\right)\)

Similarly, by defining

$$\begin{aligned} \mathbf{g}&= \left[ {\hat{{g}}_{00} \left( {0,0} \right),\;\ldots ,\;\hat{{g}}_{00} \left( {\frac{N_g }{2},\frac{N_g }{2}} \right),\;\ldots ,\;} \hat{{g}}_{\hat{{M}}\hat{{M}}} \left( {0,0} \right),\;\ldots ,\; \right.\nonumber \\&\left.\hat{{g}}_{\hat{{M}}\hat{{M}}} \left( {\frac{N_g }{2},\frac{N_g }{2}} \right) \right]^{T},\end{aligned}$$
(19a)
$$\begin{aligned} \mathbf{c}_{ee}&= \left[ {1,\;\ldots ,\;\cos \left( {\frac{N_g }{2}\omega _1 } \right)\cos \left( {\frac{N_g }{2}\omega _2 } \right),\;\ldots ,\;} p_1^{2\hat{{M}}} p_2^{2\hat{{M}}} ,\;\ldots ,\; \right.\nonumber \\&\left. p_1^{2\hat{{M}}} p_2^{2\hat{{M}}} \cos \left( {\frac{N_g }{2}\omega _1 } \right)\cos \left( {\frac{N_g }{2}\omega _2 } \right) \right]^{T},\end{aligned}$$
(19b)
$$\begin{aligned} \mathbf{c}_{oe}&= \left[ {p_1 ,\;\ldots ,\;p_1 \cos \left( {\frac{N_g }{2}\omega _1 } \right)\cos \left( {\frac{N_g }{2}\omega _2 } \right),\;\ldots ,\;} \frac{1}{M}p_1^M p_2^{2\hat{{M}}} ,\;\ldots ,\; \right.\nonumber \\&\left.\frac{1}{M}p_1^M p_2^{2\hat{{M}}} \cos \left( {\frac{N_g }{2}\omega _1 } \right)\cos \left( {\frac{N_g }{2}\omega _2 } \right) \right]^{T},\end{aligned}$$
(19c)
$$\begin{aligned} \mathbf{c}_{eo}&= \left[ {p_2 ,\;\ldots ,\;p_2 \cos \left( {\frac{N_g }{2}\omega _1 } \right)\cos \left( {\frac{N_g }{2}\omega _2 } \right),\;\ldots ,\;} \frac{1}{M}p_1^{2\hat{{M}}} p_2^M ,\;\ldots ,\; \right.\nonumber \\&\left.\frac{1}{M}p_1^{2\hat{{M}}} p_2^M \cos \left( {\frac{N_g }{2}\omega _1 } \right)\cos \left( {\frac{N_g }{2}\omega _2 } \right) \right]^{T},\end{aligned}$$
(19d)
$$\begin{aligned} \mathbf{c}_{oo}&= \left[ {p_1 p_2 ,\;\ldots ,\;p_1 p_2 \cos \left( {\frac{N_g }{2}\omega _1 } \right)\cos \left( {\frac{N_g }{2}\omega _2 } \right),\;\ldots ,\;} \frac{1}{M^{2}}p_1^M p_2^M ,\;\ldots ,\; \right. \nonumber \\&\left.\frac{1}{M^{2}}p_1^M p_2^M \cos \left( {\frac{N_g }{2}\omega _1 } \right)\cos \left( {\frac{N_g }{2}\omega _2 } \right) \right]^{T}, \end{aligned}$$
(19e)

(12a) can be represented by

$$\begin{aligned} \hat{{H}}\left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)&= \mathbf{g}^{T}\mathbf{c}_{ee} +j\hat{{D}}_1 \left( {\omega _1 } \right)\mathbf{g}^{T}\mathbf{c}_{oe} +j\hat{{D}}_2 \left( {\omega _2 } \right)\mathbf{g}^{T}\mathbf{c}_{eo} \nonumber \\&- \hat{{D}}_1 \left( {\omega _1 } \right)\hat{{D}}_2 \left( {\omega _2 } \right)\mathbf{g}^{T}\mathbf{c}_{oo}. \end{aligned}$$
(20)

Therefore, the objective error function for designing the subfilters \(G_{2m_1 ,2m_2 } \left( {z_1 ,z_2 } \right)\) can be defined by

$$\begin{aligned} e\left( \mathbf{g} \right)&= \int \limits _R {\left| {H_d \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)-H\left( {e^{j\omega _1 },e^{j\omega _2 },p_1 ,p_2 } \right)} \right|^{2}{\varvec{dv}}} \nonumber \\&= \int \limits _R {\left| {M\left( {\omega _1 ,\omega _2 } \right)e^{-j\left( {\omega _1 p_1 +\omega _2 p_2 } \right)}-\hat{{H}}\left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)} \right|^{2}{\varvec{dv}}} \nonumber \\&= \int \limits _R \left| {M\left( {\omega _1 ,\omega _2 } \right)\cos \left( {\omega _1 p_1 +\omega _2 p_2 } \right)} -\mathbf{g}^{T}\mathbf{c}_{ee} +\hat{{D}}_1 \left( {\omega _1 } \right)\hat{{D}}_2 \left( {\omega _2 } \right)\mathbf{g}^{T}\mathbf{c}_{oo} \right|^{2}{\varvec{dv}} \nonumber \\&\quad +\int \limits _R \left| {-M\left( {\omega _1 ,\omega _2 } \right)\sin \left( {\omega _1 p_1 +\omega _2 p_2 } \right)} -\hat{{D}}_1 \left( {\omega _1 } \right)\mathbf{g}^{T}\mathbf{c}_{oe} -\hat{{D}}_2 \left( {\omega _2 } \right)\mathbf{g}^{T}\mathbf{c}_{eo} \right|^{2}{\varvec{dv}} \nonumber \\&= u+\mathbf{r}^{T}\mathbf{g}+\mathbf{g}^{T}\mathbf{Qg} \end{aligned}$$
(21)

where

$$\begin{aligned}&\int \limits _{R}\stackrel{\Delta }{=} \int \int \limits _{R_p } \int \int \limits _{R_\omega },\end{aligned}$$
(22a)
$$\begin{aligned}&{\varvec{dv}}\stackrel{\Delta }{= }d\omega _1 d\omega _2 dp_1 dp_2 ,\end{aligned}$$
(22b)
$$\begin{aligned}&R=R_p \cup R_\omega = \left\{ {-0.5\le p_1 ,p_2 \le 0.5} \right\} \cup \left\{ \left( {\omega _1 ,\omega _2 } \right)\right. \nonumber \\&\qquad \quad \left.\in \text{ passbands} \text{ or} \left( {\omega _1 ,\omega _2 } \right) \in \text{ stopbands} \right\} \end{aligned}$$
(22c)

and

$$\begin{aligned} u&= \int \limits _R {\left| {M\left( {\omega _1 ,\omega _2 } \right)\cos \left( {\omega _1 p_1 +\omega _2 p_2 } \right)} \right|^{2}{\varvec{dv}}} +\int \limits _R {\left| {M\left( {\omega _1 ,\omega _2 } \right)\sin \left( {\omega _1 p_1 +\omega _2 p_2 } \right)} \right|^{2}{\varvec{dv}}} \nonumber \\&= \int \limits _R {\left| {M\left( {\omega _1 ,\omega _2 } \right)} \right|^{2}{\varvec{dv}}} \nonumber \\&= \int \int \limits _{R_\omega } {\left| {M\left( {\omega _1 ,\omega _2 } \right)} \right|^{2}d\omega _1 d\omega _2 } , \end{aligned}$$
(23a)
$$\begin{aligned} \mathbf{r}&= -2\int \limits _R {M\left( {\omega _1 ,\omega _2 } \right)\cos \left( {\omega _1 p_1 +\omega _2 p_2 } \right)} \left[ {\mathbf{c}_{ee} -\hat{{D}}_1 \left( {\omega _1 } \right)\hat{{D}}_2 \left( {\omega _2 } \right)\mathbf{c}_{oo} } \right]{\varvec{dv}} \nonumber \\&\quad +\,2\int \limits _R {M\left( {\omega _1 ,\omega _2 } \right)\sin \left( {\omega _1 p_1 +\omega _2 p_2 } \right)} \left[ {\hat{{D}}_1 \left( {\omega _1 } \right)\mathbf{c}_{oe} +\hat{{D}}_2 \left( {\omega _2 } \right)\mathbf{c}_{eo} } \right]{\varvec{dv}}, \end{aligned}$$
(23b)
$$\begin{aligned} \mathbf{Q}&= \int \limits _R {\left[ {\mathbf{c}_{ee} -\hat{{D}}_1 \left( {\omega _1 } \right)\hat{{D}}_2 \left( {\omega _2 } \right)\mathbf{c}_{oo} } \right]} \left[ {\mathbf{c}_{ee} -\hat{{D}}_1 \left( {\omega _1 } \right)\hat{{D}}_2 \left( {\omega _2 } \right)\mathbf{c}_{oo} } \right]^{T}{\varvec{dv}} \nonumber \\&\quad +\int \limits _R {\left[ {\hat{{D}}_1 \left( {\omega _1 } \right)\mathbf{c}_{oe} +\hat{{D}}_2 \left( {\omega _2 } \right)\mathbf{c}_{eo} } \right]} \left[ {\hat{{D}}_1 \left( {\omega _1 } \right)\mathbf{c}_{oe} +\hat{{D}}_2 \left( {\omega _2 } \right)\mathbf{c}_{eo} } \right]^{T}{\varvec{dv}}. \end{aligned}$$
(23c)

The least-squares solution can be obtained by differentiating (21) with respect to the coefficient vector g and setting the result to zero, which yields

$$\begin{aligned} \mathbf{g}=-\frac{1}{2}\mathbf{Q}^{-1}\mathbf{r}. \end{aligned}$$
(24)

3.3 Design examples

In this subsection, design example is presented and the results are compared with those of the conventional method (Shyu et al. 2009a). To evaluate the performance, several measured criterions are defined as below:

$$\begin{aligned} \varepsilon _{m,rms}&= \left[{\frac{\int _R {\left| {H_d \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)-H\left( {e^{j\omega _1 },e^{j\omega _2 },p_1 ,p_2 } \right)} \right|^{2}{\varvec{dv}}} }{\int _R {\left| {H_d \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)} \right|^{2}{\varvec{dv}}} }} \right]^{1/2}\times 100\,\% ,\qquad \end{aligned}$$
(25a)
$$\begin{aligned} \varepsilon _{mp}&= \max \left\{ {\left| {H_d \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)-H\left( {e^{j\omega _1 },e^{j\omega _2 },p_1 ,p_2 } \right)} \right|,} \right.\nonumber \\&\quad \left. {\left( {\omega _1 ,\omega _2 } \right)\in \text{ passbands},-0.5\le p_1 ,p_2 \le 0.5} {}\right\} \end{aligned}$$
(25b)
$$\begin{aligned} \varepsilon _{ms}&= \max \left\{ {\left| {H_d \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)-H\left( {e^{j\omega _1 },e^{j\omega _2 },p_1 ,p_2 } \right)} \right|,} \right.\nonumber \\&\quad \left. {\left( {\omega _1 ,\omega _2 } \right)\in \text{ stopbands}, -0.5\le p_1 ,p_2 \le 0.5} {} \right\} \end{aligned}$$
(25c)
$$\begin{aligned} \varepsilon _{\tau _1 ,rms}&= \left[ {\frac{\int _R {\left| {\tau _{d1} \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)-\tau _1 \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)} \right|^{2}{\varvec{dv}}} }{\int _R {p_1^2 {\varvec{dv}}} }} \right]^{1/2}\times 100\,\%, \end{aligned}$$
(25d)
$$\begin{aligned} \varepsilon _{\tau _2 ,rms}&= \left[ {\frac{\int _R {\left| {\tau _{d2} \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)-\tau _2 \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)} \right|^{2}{\varvec{dv}}} }{\int _R {p_2^2 {\varvec{dv}}} }} \right]^{1/2}\times 100\,\% ,\end{aligned}$$
(25e)
$$\begin{aligned} \varepsilon _{\tau _1 }&= \max \left\{ {\left| {\tau _{d1} \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)-\tau _1 \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)} \right|} \right.\left. \left( {\omega _1 ,\omega _2 } \right) \right.\nonumber \\&\quad \in \left.\text{ passbands}, -0.5\le p_1 ,p_2 \le 0.5 \right\} ,\end{aligned}$$
(25f)
$$\begin{aligned} \varepsilon _{\tau _2 }&= \max \left\{ {\left| {\tau _{d2} \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)-\tau _2 \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)} \right|} \left( {\omega _1 ,\omega _2 } \right) \right.\nonumber \\&\quad \in \left.\text{ passbands}, -0.5\le p_1 ,p_2 \le 0.5 \right\} \end{aligned}$$
(25g)

where \(\tau _{di} \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)\) and \(\tau _i \left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)\) denote the desired and actual group delays, respectively, with respect to \(\omega _i\)-direction, \(i=1, 2\). Meanwhile, the numbers of independent coefficients are also taken into account for comparison, which are computed as below:

$$\begin{aligned}&\text{ Proposed} \text{ method} \text{(including} \text{ scale} \text{ factors):}\nonumber \\&\quad N_d +\left( {\frac{N_g }{2}+1} \right)^{2}\left( {\hat{{M}}+1} \right)^{2}+4\hat{{M}}+3\hat{{M}}^{2}\end{aligned}$$
(26a)
$$\begin{aligned}&\text{ Conventional} \text{ method} \text{(Shyu} \text{ et} \text{ al.} 2009a) \nonumber \\&\quad \left( {\frac{N}{2}+1} \right)^{2}\left( {M_c +1} \right)^{2}+\left( {\frac{N}{2}} \right)^{2}M_s^2 +2\left( {\frac{N}{2}+1} \right)\frac{N}{2}\left( {M_c +1} \right)M_s \end{aligned}$$
(26b)

where

$$\begin{aligned} \left\{ {{\begin{array}{ll} {M_c =M_s =\frac{M}{2},}&{\;\;\text{ for} \text{ even}\;M,} \\ {M_c +1=M_s =\frac{M+1}{2},}&{\;\;\text{ for} \text{ odd}\;M.} \\ \end{array} }} \right. \end{aligned}$$
(27)

To compute the errors in (25), the frequencies \(\omega _1 \) and \(\omega _2 \) are uniformly sampled at step size \(\pi /{100}\), and the variable parameters \(p_1 \) and \(p_2 \) are uniformly sampled at step size 1/50.

Example 1

In this example, an elliptically symmetric low-pass VFD FIR filter is designed and the desired magnitude response has been given in (13). When \(\omega _{p1} =0.45\pi , \,\omega _{p2} =0.6\pi , \,\omega _{s1} =0.7\pi , \,\omega _{s2} =0.85\pi , \,N_{d1} =N_{d2} =30, \,N_g =20, \,M=5\), the obtained magnitude responses for \(( {p_1 ,p_2})=({0,0}), \,({0.25,0.25}), \,({0.5,0.5}), \,({0.5,-0.5})\) are shown in Fig. 3a, the group-delay responses at \(({p_1,p_2})=( {0.25,0.25})\) and \(({0.5,-0.5})\) are shown in Fig. 3b, c, while the variable group-delay responses and magnitude responses for both \(\omega _2 =0, \,p_2 =0\) and \(\omega _1 =0\), \(p_1 =0\) are shown in Fig. 3d, e, respectively. The errors defined in (25) are tabulated in Table 1, accompanying those of the conventional method with \(N=20\).

Fig. 3
figure 3figure 3

Design of an elliptically symmetric low-pass VFD FIR filter. a Magnitude responses at \(({p_1,p_2})=({0,0}), ({0.25,0.25}), ({0.5,0.5}), ({0.5,-0.5})\). b \(\omega _1\)-directional and \(\omega _2\)-directional group-delay responses in the passband at \(({p_1,p_2} )=({0.25,0.25})\). c \(\omega _1\)-directional and \(\omega _2\)-directional group-delay responses in the passband at \(({p_1,p_2})=({0.5,-0.5})\). d Variable group-delay response in the passband and magnitude response at \(\omega _2 =0\), \(p_2 =0\). e Variable group-delay response in the passband and magnitude response at \(\omega _1 =0\), \(p_1 =0\)

Full size image
Table 1 Comparisons for the proposed method and the conventional method (Shyu et al. 2009a)
Full size table

4 Design of 2-D VFD FIR digital filters with even \(M\)

For even \(M\) in (6), let \(M=2\hat{{M}}\) then

$$\begin{aligned}&e^{-j\left( {\omega _1 p_1 +\omega _2 p_2 } \right)} \approx \left[ {\sum _{m_1 =0}^{\hat{{M}}} {\left( {-1} \right)^{m_1 }\frac{\left( {\omega _1 p_1 } \right)^{2m_1 }}{\left( {2m_1 } \right)!}+} \left( {-j\omega _1 } \right)p_1 \sum _{m_1 =0}^{\hat{{M}}-1} {\frac{\left( {-1} \right)^{m_1 }}{2m_1 +1}\frac{\left( {\omega _1 p_1 } \right)^{2m_1 }}{\left( {2m_1 } \right)!}} } \right]\nonumber \\&\qquad \times \left[ {\sum _{m_2 =0}^{\hat{{M}}} {\left( {-1} \right)^{m_2}\frac{\left( {\omega _2 p_2 } \right)^{2m_2 }}{\left( {2m_2 } \right)!}+} \left( {-j\omega _2 } \right)p_2 \sum _{m_2 =0}^{\hat{{M}}-1} {\frac{\left( {-1} \right)^{m_2 }}{2m_2 +1}\frac{\left( {\omega _2 p_2 } \right)^{2m_2 }}{\left( {2m_2 } \right)!}} } \right] \nonumber \\&\quad = \sum _{m_1 =0}^{\hat{{M}}} {\sum _{m_2 =0}^{\hat{{M}}} {\left( {-1} \right)^{m_1 +m_2 }\frac{\left( {\omega _1 p_1 } \right)^{2m_1 }\left( {\omega _2 p_2 } \right)^{2m_2 }}{\left( {2m_1 } \right)!\left( {2m_2 } \right)!}} } \nonumber \\&\qquad +\left( {-j\omega _1 } \right)p_1 \sum _{m_1 =0}^{\hat{{M}}-1} {\sum _{m_2 =0}^{\hat{{M}}} {\frac{\left( {-1} \right)^{m_1 +m_2 }}{2m_1 +1}\frac{\left( {\omega _1 p_1 } \right)^{2m_1 }\left( {\omega _2 p_2 } \right)^{2m_2 }}{\left( {2m_1 } \right)!\left( {2m_2 } \right)!}} } \nonumber \\&\qquad +\left( {-j\omega _2 } \right)p_2 \sum _{m_1 =0}^{\hat{{M}}} {\sum _{m_2 =0}^{\hat{{M}}-1} {\frac{\left( {-1} \right)^{m_1 +m_2 }}{2m_2 +1}\frac{\left( {\omega _1 p_1 } \right)^{2m_1 }\left( {\omega _2 p_2 } \right)^{2m_2 }}{\left( {2m_1 } \right)!\left( {2m_2 } \right)!}} } \nonumber \\&\qquad +\left( {-j\omega _1 } \right)\left( {-j\omega _2 } \right)p_1 p_2 \sum _{m_1 =0}^{\hat{{M}}-1} {\sum _{m_2 =0}^{\hat{{M}}-1} {\frac{\left( {-1} \right)^{m_1 +m_2 }}{\left( {2m_1 +1} \right)\left( {2m_2 +1} \right)}} } \frac{\left( {\omega _1 p_1 } \right)^{2m_1 }\left( {\omega _2 p_2 } \right)^{2m_2 }}{\left( {2m_1 } \right)!\left( {2m_2 } \right)!} \nonumber \\ \end{aligned}$$
(28)

Hence, the applied transfer function in this section is represented by

$$\begin{aligned} H\left( {z_1 ,z_2 ,p_1 ,p_2 } \right)&= z_1^{-\;\frac{N_{d1} }{2}} z_2^{-\;\frac{N_{d2} }{2}} \sum _{m_1 =0}^{\hat{{M}}} {\sum _{m_2 =0}^{\hat{{M}}} {G_{2m_1 ,2m_2 } \left( {z_1 ,z_2 } \right)\; } } p_1^{2m_1 } p_2^{2m_2 } \nonumber \\&+\,z_2^{-\;\frac{N_{d2} }{2}} D_1 \left( {z_1 } \right)\sum _{m_1 =0}^{\hat{{M}}-1} {\sum _{m_2 =0}^{\hat{{M}}} {\frac{1}{2m_1 +1}G_{2m_1 ,2m_2 } \left( {z_1 ,z_2 } \right)\; } } p_1^{2m_1 +1} p_2^{2m_2 } \nonumber \\&+\,z_1^{-\;\frac{N_{d1} }{2}} D_2 \left( {z_2 } \right)\sum _{m_1 =0}^{\hat{{M}}} {\sum _{m_2 =0}^{\hat{{M}}-1} {\frac{1}{2m_2 +1}G_{2m_1 ,2m_2 } \left( {z_1 ,z_2 } \right)\; } } p_1^{2m_1 } p_2^{2m_1 +1} \nonumber \\&+\,D_1 \left( {z_1 } \right)D_2 \left( {z_2 } \right)\times \sum _{m_1 =0}^{\hat{{M}}-1} \sum _{m_2 =0}^{\hat{{M}}-1} \frac{1}{\left( {2m_1 +1} \right)\left( {2m_2 +1} \right)}\nonumber \\&\times G_{2m_1 ,2m_2 } \left( {z_1 ,z_2 } \right)\; p_1^{2m_1 +1} p_2^{2m_1 +1} \end{aligned}$$
(29)

where \(G_{2m_{1} ,2m_2}({z_1 ,z_2} )\) and \(D_i({z_{i}}), \,i=1, 2\) have been characterized in (9) and (10), respectively, and the frequency response of (29) is

$$\begin{aligned} H\left( {e^{j\omega _1 },e^{j\omega _2 },p_1 ,p_2 } \right)=e^{-j\left( {\frac{N_{d1} }{2}+\frac{N_g }{2}} \right)\omega _1 }e^{-j\left( {\frac{N_{d2} }{2}+\frac{N_g }{2}} \right)\omega _2 }\hat{{H}}\left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right) \end{aligned}$$
(30)

where

$$\begin{aligned} \hat{{H}}\left( {\omega _1 ,\omega _2 ,p_1 ,p_2 } \right)&= \sum _{m_1 =0}^{\hat{{M}}} {\sum _{m_2 =0}^{\hat{{M}}} {\hat{{G}}_{2m_1 ,2m_2 } \left( {\omega _1 ,\omega _2 } \right)\; } } p_1^{2m_1 } p_2^{2m_2 } \nonumber \\&\quad +\,j\hat{{D}}_1 \left( {\omega _1 } \right)\sum _{m_1 =0}^{\hat{{M}}-1} {\sum _{m_2 =0}^{\hat{{M}}} {\frac{1}{2m_1 +1}\hat{{G}}_{2m_1 ,2m_2 } \left( {\omega _1 ,\omega _2 } \right)\; } } p_1^{2m_1 +1} p_2^{2m_2 } \nonumber \\&\quad +\,j\hat{{D}}_2 \left( {\omega _2 } \right)\sum _{m_1 =0}^{\hat{{M}}} {\sum _{m_2 =0}^{\hat{{M}}-1} {\frac{1}{2m_2 +1}\hat{{G}}_{2m_1 ,2m_2 } \left( {\omega _1 ,\omega _2 } \right) } } p_1^{2m_1 } p_2^{2m_2 +1} \nonumber \\&\quad -\,\hat{{D}}_1 \left( {\omega _1 } \right)\hat{{D}}_2 \left( {\omega _2 } \right)\sum _{m_1 =0}^{\hat{{M}}-1} \sum _{m_2 =0}^{\hat{{M}}-1} \frac{1}{\left( {2m_1 +1} \right)\left( {2m_2 +1} \right)}\nonumber \\&\quad \times \hat{{G}}_{2m_1 ,2m_2 } \left( {\omega _1 ,\omega _2 } \right)\; p_1^{2m_1 +1} p_2^{2m_2 +1} \end{aligned}$$
(31)

in which \(\hat{{G}}_{2m_1 ,2m_2 } \left( {\omega _1 ,\omega _2 } \right)\) and \(\hat{{D}}_i \left( {\omega _i } \right)\), \(i=1, 2\) are the same as (12b) and (12c), respectively. So, the technique in Sect. 3 can also be applied to the design of 2-D VFD FIR filters with even \(M\).

Example 2

This example will deal with the design of a circularly symmetric low-pass VFD FIR filter whose magnitude response is shown in (13) with \(\omega _{p1} =\omega _{p2} =\omega _p \) and \(\omega _{s1} \!=\!\omega _{s2} \!=\!\omega _s \). Figure 4a presents the obtained magnitude responses for \(({p_1 ,p_2 })\!=\!({0,0}), ({0.25,0.25}), \,({0.5,0.5}), \,({0.5,-0.5})\) if \(N_{d1} =N_{d2} =30, \,N_g =16, \,M=4, \omega _p =0.5\pi , \omega _s =0.75\pi \) are used, Fig. 4b, c present the group-delay responses at \(({p_1 ,p_2})=({0.25,0.25})\) and \(({0.5,-0.5})\), and Fig. 4d, e present the variable group-delay responses and magnitude responses for \(\omega _2 =0\), \(p_2 =0\) and \(\omega _1 =0\), \(p_1 =0\), respectively. The error defined in (25) are also tabulated in Table 1, accompanying those of the conventional method with \(N=16\), \(M=4\).

Fig. 4
figure 4figure 4

Design of a circularly symmetric low-pass VFD FIR filter. a Magnitude responses at \(({p_1,p_2})=({0,0}), ({0.25,0.25}), ({0.5,0.5}), ({0.5,-0.5})\). b \(\omega _1\)-directional and \(\omega _2\)-directional group-delay responses in the passband at \(({p_1,p_2})=({0.25,0.25})\). c \(\omega _1\)-directional and \(\omega _2\)-directional group-delay responses in the passband at \(({p_1,p_2})=({0.5,-0.5})\). d Variable group-delay response in the passband and magnitude response at \(\omega _2 =0\), \(p_2 =0\). e Variable group-delay response in the passband and magnitude response at \(\omega _1 =0\), \(p_1 =0\)

Full size image

5 Conclusions

In this paper, a prefilter–subfilter cascaded structure for the design of VFD 2-D FIR digital filters has been proposed, which is derived basing on the Taylor series expansion of the desired frequency response. By the specified relationships among the presented structure, it has been shown that the required number of independent coefficients is much less than that of the existing structure, while the performance of the designed filters is still better. Design examples have been presented to demonstrate the effectiveness of the presented method.