1 Introduction

Nearest neighbor search is a fundamental problem in many computer science domains such as computer vision, massive data processing and information retrieval [9, 13, 21, 27, 29, 33, 34, 39,40,41]. For example, it is a key component of large-scale image search [34], and classification tasks with a large number of classes [18, 23]. In high-dimensional spaces, the exact nearest neighbor search performs even worse than a linear scan due to the curse of dimensionality, and thus approximate nearest neighbor search is often solicited by trading answer quality for efficiency [3, 22, 26, 42, 43].

In the last few years, two promising indexing paradigms for similarity search have drawn much attention in both academic and industry fields. The first one focuses on compact codes based on various quantization methods, by which image descriptors consisting of a few hundred or even thousand components are compressed employing only 8-32 bytes per descriptor. Typical methods include product quantization (PQ) [24], optimized PQ [20], additive quantization [4], and other PQ extensions [1, 5, 7, 28, 32, 37, 44]. Compact representation reduces memory footprint for indexing, and thus is capable of supporting billion-scale image sets.

In contrast, the graph-based similarity search paradigm offers high accuracy and efficiency, paying little attention to the memory constraint. For example, the successful approach hierarchical navigable small worlds (HNSW) by Malkov et al. [35] can easily achieve 95% recall with an order of magnitude speedup over other search methods [10]. Such outstanding performance, however, does not come for free – it needs both the original vectors and a full graph structure to be stored in the main memory, which severely limits the scalability. To the best of our knowledge, none of this class of approaches scaled up to a billion vectors on one commercial server [19].

Douze et al. take the first step to conciliate these two trends by proposing Link&Code (L&C) [17], which represents vectors in the compressed domain and builds a search graph using only the compact codes of vectors. In this way, L&C tries to strike a balance between the two extreme sides of the spectrum of operating points. By consuming around one hundred bytes per vectorFootnote 1, it scales to a billion vectors in one commercial server with better accuracy/speed trade-off.

Our preliminary experiments indicate that L&C still suffers the accuracy saturation problem. For instance, the performance saturates at around 65% and 51% recall (rank@1) for Deep1B and Sift1B respectively, i.e., the accuracy grows very slowly as the increase of search time. The in-depth analysis shows that the reasons are two folds: 1) the link number is too small with respect to the cardinality of billion-scale datasets, which is detrimental to the search accuracy of graph-based methods, and 2) the quantization error is over large even with the help of quantized regression from neighbors invented by L&C.

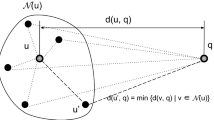
A naive way to tackle this problem is allocating more bytes per vector. This, however, contradicts with the original purpose of L&C and may jeopardize the scalability. To address this issue, we propose a simple yet effective solution that fulfills all design goals of L&C and offers much higher accuracy and efficiency. Specifically, we employ a two-layer graph structure, instead of a single giant one, to organize all vectors. The top-layer graph is composed of centroids obtained by partitioning the whole dataset into multiple clusters via the standard K-means algorithm. The bottom-layer consists of a set of subgraphs, each of which corresponds to a cluster as illustrated in Fig. 1. Such a hierarchical structure improves the graph search accuracy significantly using the same number of links as L&C. The other benefit of this design is that we only need 2 bytes to keep track of one link identifier if the sizes of all clusters are limited to 216, which is easy to enforce. Considering that L&C requires 4 bytes for one link, it saves us quite a few bytes for the compact representation of vectors.

Fig. 1
figure 1

Overview of the two-layer graph structure of HiL&C

Full size image

To minimize the reconstruction error, we introduce dual residual encoding to represent vectors in the compressed domain. Particularly, the compact codes of the first-level residuals are used to construct all subgraphs in the bottom-layer, and we employ those of the second-level residuals to re-rank the candidate list obtained through graph search. Preliminary study shows that dual residual quantization provides smaller reconstruction error than L&C even if using the same length of codes.

To sum up, the contributions of this paper are:

  • Through preliminary experiments we show that a hierarchical structure of small graphs provides better accuracy than a single giant one. Interestingly, it takes only 1/2 of the space cost required by L&C for storing link identifiers and saves quite a number of bytes for compression.

  • We demonstrate that the dual residual encoding scheme offers much less reconstruction error, suggesting better approximation of original vectors is attained than the regression-from-neighbors strategy adopted by L&C.

  • We introduce a hierarchical graph-based similarity search method with dual residual quantization (HiL&C), which takes full advantage of the precious memory budget. Extensive experiments show that our proposal achieves the state-of-the-art performance. To be specific, HiL&C attains 90%+ 1-recall@10 and 1-recall@100 on two billion-sized benchmarks at the cost of 10ms per query in the single thread setting.

The chapters are organized as follows. In Section 2 introduces the related work and preparatory knowledge, Section 3 compares the different design alternatives, Section 4 details our approach and Section 5 performs detailed comparative experiments and conclude.

2 Related work

Suppose \(\mathcal {X} = \{x_{1}, \cdots , x_{n}\} \subset \mathbb {R}^{d}\) is a dataset containing n vectors. The goal of approximate nearest neighbor search is to find the nearest neighbor \(\mathcal {N}_{\mathcal {X}}(y) \subset \mathcal {X}\) of the query vector \(y \in \mathbb {R}^{d}\) by minimizing d(y,x). For distance calculation \(d: \mathbb {R}^{d} \times \mathbb {R}^{d} \rightarrow \mathbb {R}\), We use the most commonly used distance calculation function in ANNS - d = ℓ2.

For high-dimensional Euclidian space, the majority of research effort turns to the approximate nearest neighbor search because of the difficulty in finding exact results [12, 14]. For instance, locality sensitive hashing (LSH) schemes exploit the hashing properties resulting from the Johnson-Lindenstrauss lemma to provide c-approximate nearest neighbors with constant probability by trading accuracy for efficiency [15]. Due to space limitation, we mainly present a brief review of the quantization-based and graph-based nearest neighbor search methods next.

Quantization-based methods

Product Quantization (PQ) [24] partitions the original high-dimensional vectors \(x\in \mathbb {R}^{d}\) into m \(\frac {d}{m}\)-dimensional subvectors \(x = \left [ x^{1},\ldots ,x^{m} \right ]\). Then PQ encodes these m \(\frac {d}{m}\)-dimensional subvectors using m different subquantizers qi(x), each of which is associated with a codebook ci. Therefore the final codebook C is the Cartesian product of the m sub-codebooks

$$ C=c_{1}\times ... \times c_{m} $$

Each codebook includes s codewords (centroids), where s is typically set to 256 in order to fit a codeword into 1 byte. Thus, a compressed vector occupies only \(m \log {(s)} \) bits. To process a query, all vectors are reproduced on-the-fly by consulting the codebooks and their distances to the query are evaluated to get the best answers.

The idea of re-rank with source coding is proposed in [25] to refine the hypotheses of a query with an imprecise post-verification scheme, i.e., After quantizing the vectors using the first-level quantizer, the residuals are quantized using the second-layer quantizer. In this way, we avoid the costly post-verification scheme adopted in most state-of-the-art approximate search techniques [15, 38].

The inverted-file indexing(IVF) method [5, 25] goes one step further to solve the problem that the PQ method requires a brute force search for all vectors. The IVF method also builds a two layers structure, and the first layer uses a clustering method to cluster and assign the dataset vectors to the nearest inverted list, thus avoiding sequential searching. Only a small number of inverted lists, of which the centroid are close enough to the query, are examined. Interested readers are referred to [36] for a comprehensive survey of quantization-based methods.

Graph-based methods

Graph-based methods are currently the most efficient similarity search method, not considering the main memory constraint. Malkov et al. [35] introduced an hierarchical navigable small world graphs (HNSW), one of the most accomplished graph-based search algorithms. The main idea of HNSW is distributing vectors into multiple layers and introducing the long-range links to speedup the search procedure. Empirical study shows that HNSW exhibits \(O(\log {n})\) search complexity, which is rather appealing in practice. A recent proposal named NSG outperforms HNSW by constructing the so-called monotonic relative neighbor graph [19]. Quite a number of graph-based algorithms are proposed in the last few years and we would like to refer readers to [2, 11, 22, 30, 31, 45] for more details.

Link&Code

HNSW requires to store both the original vectors and the graph index in main memory, which jeopardize the scalability. In contrast, PQ-based methods supports billion-scale datasets but suffer the accuracy saturation problem.

L&C encodes the vectors using PQ-based methods and organizes them with a single HNSW graph. It is demonstrated that L&C beats the state-of-the-art on operating points considering 64-128 bytes per vectors.

3 Motivations

This section describes our original idea and experimental arguments for Section 4. First, we focus on how the size of dataset affects the performance when the number of neighbors per vector on the base layer of HNSW are fixed and relatively small. Then we demonstrate the superiority of the hierarchical graph structure consisting of a number of small subgraphs over L&C. Finally, we present a detailed comparison with other methods to demonstrate the superiority of our approach. This leads us to favor dual residual quantization over quantized regression method adopted by L&C.

3.1 The impact of dataset size on accuracy

Due to the limited memory budget, L&C can only use a relatively small number of links pointing to the corresponding approximate neighbors for each point. We first examine the impact of dataset cardinality on the performance of L&C for a fixed number of links, which is set to 7 by default on the base layer of graph structure. All these evaluations are performed on Sift10K, Sift1M, Sift10M and Sift100M datasets, where Sift10K consists of the first 10K descriptors of Sift1B dataset, and so on and so forth.

We select standard parameter settings for vector quantization and regression coefficient encoding, where OPQ32 (32 bytes) is used for the first-level vector approximation and the regression coefficient takes 8 bytes per descriptor. Figure 2 reports the recall and search time for different datasets. The plot shows that 1) the accuracy increases as more search time is taken but tends to saturate because of the existence of reconstruction error; 2) smaller the dataset is, higher the accuracy will be. Since the memory footprint for quantization is identical for all evaluations, one can see that the accuracy is negatively correlated with the size of datasets for a fix number of links per vector. This motivates us to consider a set of small subgraphs rather than a big one.

Fig. 2
figure 2

Accuracy vs. search time. 10K means the first 10 kilo descriptors of SIFT1B dataset, and so on and so forth

Full size image

The other benefit of using small subgraphs is that we could reduce the memory cost for storing graph links. In the original implementation of L&C, each neighbor identifier occupies 4 bytes to support billion-sized address space. Suppose we somehow could partition the big dataset into a set of small ones, of which the cardinality is less than 216. Then, only 2 bytes are enough to store each neighbor identifier, reducing the space cost by half. This saves us quite a few bytes for longer compact representation of vectors given the limited memory budget.

3.2 A big graph or a set of small subgraphs?

The previous experiment shows that using a set of small graphs might be promising in improving the accuracy and reducing the memory occupation for graph links. Inspired by IVFPQ [25], we design a hierarchical structure as illustrated in Fig. 1. The top layer is a standard HNSW graph, of which vertices are the centroids obtained by employing the K-means algorithm over the whole dataset. Please note that these centroids are not quantized, i.e., the original centroid vectors are used to build the top layer graph.

Suppose we have \(\mathcal {K}\) clusters in hand, then we use L&C to index vectors in each cluster and all these \(\mathcal {K}\) L&C graphs constitute the bottom layer. A pointer is associated with each centroid in the top layer, following which one can visit its corresponding L&C graph. We call such an index structure the hierarchical link and code graph (HiL&C).

We use Sift100M to evaluate the performance of the standard L&C and HiL&C. Particularly, a single big graph is constructed following the L&C index building strategy. For HiL&C, we first use K-means to partition Sift100M into 5000 clusters, enforcing the size of each cluster is less than 216. A HNSW graph is built using these 5000 centroids, and then L&C is applied for each clusters to build 5000 L&C subgraphs. For both L&C and HiL&C the parameter settings are identical, where the numbers of links are set to 7 and OPQ32 (32 bytes) is used for vector approximation.

To answer a query, L&C traverses the graph, evaluates the distances between query y and reconstructed vectors in the candidate set, and outputs the best results after the refinement stage. Since HiL&C owns a two-layer index structure, it starts the search procedure by traversing the top-layer HNSW graph first, and identify k∗ centroids that are closest to y. Then, the corresponding k∗ L&C subgraphs are searched and the results from each subgraph are merged into a temporary candidate set, in which the closest vectors to y are chosen and output as the final answers.

We adjust the number of visited L&C subgraphs, i.e., k∗, to make the search times are identical for both L&C and HiL&C. Figure 3 reports the accuracy as a function of search time for both methods. As one can see, HiL&C provides much higher accuracy than L&C with the same time cost. The reasons are 1) the k∗ clusters already cover most nearest neighbors of y, and 2) recall increases as the dataset cardinality decreases for a fixed number of links as discussed in Section 3.1.

Fig. 3
figure 3

L&C vs. HiL&C on SIFT100M: accuracy as a function of the search time

Full size image

3.3 Regression from neighbors or dual residual encoding?

In this section, we evaluate two kind of candidate refinement strategies given a memory budget, i.e., the method of L&C and dual residual encoding in our proposal.

Regression from neighbors

L&C employs OPQ for the first approximation of vectors plus refinement stage using regression coefficients (also stored in the compact code form) learned during the index construction phase. L&C adopts a two-stage search strategy. During the first stage, the first approximation induced by the quantizer is used to select a short-list of potential neighbor candidates. The indexed vectors are reconstructed on-the-fly from their compact codes. The second stage solicits compressed regression coefficients and applied only them on this short-list to re-rank the candidates, which will be discussed briefly next.

Assuming that we have reconstructed the best regression coefficients \(\hat {\beta }\) from their compact representation, and k nearest neighbors of x stored in matrix form as \(\textbf {N}(x) = [\hat {n_{1}}, \hat {n_{2}}, ... , \hat {n_{k}}\)], L&C estimates x as the weighted average

$$ \hat{x}=\hat{\beta} \left( x \right)^{\top}\textbf{N}(x) $$
(1)

then computes the exact ℓ2 distance between \(\hat {x}\) and query y to re-rank the potential neighbor candidates.

Dual residual encoding

Recall that HiL&C adopts a hierarchical graph structure to organize vectors. At the top layer, the whole dataset is divided into \(\mathcal {K}\) clusters \(C_{c} = \{c_{1}, \cdots , c_{\mathcal {K}} \}\), which can be viewed as a coarse quantizer qc. Each vector x is mapped to its nearest cluster centroid by

$$ q_{c}\left( x \right) =\underset{c\in C_{c}}{arg\min}\ \lVert x - \ c \rVert^{2} $$
(2)

Quantization error occurs through the coarse quantization progress, between the original vector and its approximation. We can decompose x into the coarse quantization centroid and the first-level residual vector r1(x)

$$ r_{1}(x)= x - q_{c}(x) $$
(3)

The energy of r1(x) is reduced significantly compared with x itself, which limits the impact of residuals on distance estimation. Inspired by IVFPQ, we use PQ to quantize and encode r1(x)

$$ q_{r_{1}}\left( r_{1}\left( x \right) \right) =arg\ \underset{c\in C_{r_{1}}}{\min}\ \lVert r_{1}\left( x \right) -c \rVert^{2} $$
(4)

Similar to L&C, we also adopt a two-stage search strategy. In the first stage, we use the estimation of x, i.e., \(\hat {x}=q_{c}\left (x \right ) + q_{r_{1}}\left (r_{1}\left (x \right ) \right )\), to select a short-list of potential neighbor candidates. In order to obtain more precise results, we re-rank the candidates in the short-list using compact code of the second-level residual of each candidate. The second-level residual r2(x) is computed as

$$ r_{2}(x) = x - q_{c}(x) - q_{r_{1}}\left( r_{1}\left( x \right) \right) $$
(5)

In the similar vein, we use PQ to quantize and encode r2(x)

$$ q_{r_{2}}\left( r_{2}\left( x \right) \right) =arg\ \underset{c\in C_{r_{2}}}{\min}\ \lVert r_{2}\left( x \right) -c \rVert^{2} $$
(6)

Table 1 compares the quantization error, i.e., \({\sum }_{x \in \mathcal {X}}\lVert x - \hat {x} \rVert ^{2}\), for estimators obtained using regression-from-neighbors and dual residual encoding over Deep100M datasetFootnote 2. To identify unambiguously the parameter setting, we adopt a notation of the form L13&OPQ32 following [17]. L13 means that each vector stores only 13 neighbor IDs, and OPQ32 means that we use a 32 bytes OPQ method for PQ encoding. For L&C, M = 8 suggests that the regression-from-neighbors is enabled, allocating 8 bytes per vector. For our proposal, R2 = 8 means that 8 types is used to compress the second-level residuals.

Table 1 Quantization error comparison on Deep100M
Full size table

The immediate observation drawn from Table 1 is that the total square loss of dual residual encoding is smaller than that of regression from neighbors under the same length of codewords, i.e., OPQ32 M = 8 vs. OPQ32 R2 = 8. This suggests that dual residual encoding alone can beat the regression method in L&C, which is more complicated and time consuming.

Recall that each link occupies only two bytes in HiL&C, enabling us to allocate more bytes spared from links to codec and represent the vectors more accurately. As a quick example, the quantization error in the case of L13&OPQ48 R2 = 16 is an order of magnitude smaller than that of L&C, where the same amount of memory per vector (96 bytes) is used for both methods.

To sum up, dual residual encoding is far more effective, along with the hierarchical graph structure, than L&C in reducing the reconstruction loss. This translates to higher recall as will be discussed shortly.

4 Hierarchical link and code with dual residual encoding

In this section, we introduce our approach named hierarchical link and code with dual residual encoding (HiL&C). It uses a hierarchical graph structure and two-level residual quantization to build an index that scales to billion-sized datasets for efficient similarity search. We then describe the architecture of our indexing and searching method, we present the detailed indexing and search algorithms of HiL&C. Finally, we conclude by describing our tradeoffs in links and refinements structure in terms of bytes.

4.1 Overview of the index structure

Hierarchical graph-based structure

Motivated by the discussion in Section 3.2, we employ a two-layer HNSW index structure as illustrated in Fig. 1, and we adapt the HNSW index structure to fit our data partitioning and dual residual encoding strategies. To be specific, we use PQ encoding to save storage space so that ADC can be used on the HNSW structure. Since the construction complexity of HNSW scales as O(Log(N)), so the search complexity of HiL&C scales as O(log(N)).

Vector approximation

All vectors are first partitioned into \(\mathcal {K}\) clusters via the K-means algorithm, and the \(\mathcal {K}\) corresponding centroids are inserted into the top-layer graph and stored in the original vector format. Please note that the number of clusters is rather small compared with the dataset cardinality, and thus is not a dominating factor of the index size. After subtracting each vector from its corresponding centroid, all first-level residuals are compressed with a coding method independent of the structure. Formally, it is a quantizer, which maps any vector \(x \in \mathbb {R}^{d} \mapsto q(x) \in \mathcal {C}\), where \(\mathcal {C}\) is a finite set subset of \(\mathbb {R}^{d}\) meaning that q(x) is stored as a code. Although vector residuals are assigned to different bottom-layer subgraphs, they share the same first-level codebook for coding and decoding.

Candidate refinement

Recall that HiL&C adopts a two-stage search strategy similar to [17, 25]. To re-rank a short-list of potential neighbor candidates, we compute the second-level residual for each vector and compress them using the other quantizer. To answer a query more precisely, the short-list of candidates are re-ranked using the vector estimation reconstructed on-the-fly from their second-level compact code. This trades a little extra computation per vector for better accuracy.

It is worth noting that HiL&C is a more generalized indexing framework for similarity search than L&C. Actually, if we set \(\mathcal {K} = 1\) and replace the second-level residual encoding with the regression method for candidate refinement, HiL&C will reduce to L&C.

4.2 Algorithm description

This subsection presents the details of the indexing and query processing algorithms of HiL&C.

The algorithm for building a HiL&C index

  1. 1.

    Learning \(\mathcal {K}\) clusters on a training dataset using K-Means and insert all centroids into the top-layer HNSW graph. The value of \(\mathcal {K}\) is chosen judiciously to make the sizes of all clusters are smaller than 216. For example, \(\mathcal {K}\) is set to around 40000 for the billion-scale datasets in our experiment setup. Each \(x \in \mathcal {X} \) is assigned to its closest centroid qc(x).

  2. 2.

    For all vectors, the first-level residuals r1(x) are computed by (3). After learning the first-level PQ quantizer \(q_{r_{1}}(\cdot )\) with a sample set of r1(x), we insert r1(x) into its corresponding HNSW subgraph, where r1(x) is stored in the compact form of \(q_{r_{1}}(r_{1}(x))\). Please note that we uses the internal ID of x rather than the global one to store the neighbor identifier in the subgraph. This design saves two bytes per link. To map an internal ID to a global one during query processing, we maintain a lookup table for each subgraph, which occupies extra 4 bytes per vector.

  3. 3.

    To re-rank the short-list of potential candidates, we learn a second-level PQ quantizer \(q_{r_{2}}(\cdot )\) with a sample of second-level residuals r2, which is computed by (5). Similarly, the codebook is shared by all r2(x).

The algorithm for similarity search

  1. 1.

    To get the nearest neighbors of a query vector y, HiL&C starts the search by traversing the top-layer HNSW graph and return k∗ closest centroids to y. The residual r1(y) = q − qc(y) is computed for each of the k∗ subgraphs. k∗ is an important parameter by tuning which we can trade speed for accuracy.

  2. 2.

    For each of the k∗ subgraphs, we perform the graph-based similarity search using r1(y) and get t best answers. The first-level residuals r1(x) of the results are reconstructed on-the-fly by first consulting the lookup table to map the internal ID into the global one, and then approximated using the corresponding compact code.

  3. 3.

    The short-list of potential candidates consists of all k∗∗ t results obtained in Step 2. The second-level residual r2(x) are used to re-rank these candidates. Specifically, the distance between y and x in the short-list is computed as \({d\left (x,y \right )} = \lVert y-q_{c}\left (x \right ) -q_{r_{1}}\left (r_{1}\left (x \right ) \right ) -q_{r_{2}}\left (r_{2}\left (x \right ) \right ) \rVert \). We select the best results based on \(d\left (x,y \right )\) as the final answers.

4.3 Memory allocation trade-offs

In this subsection, we analyze HiL&C when imposing a fixed memory budget per vector. Four factors contributes to the marginal memory fingerprint: (a) the number of graph links per vector (2 bytes per link); (b) the code used for the first-level residual approximation, for instance OPQ32 (32 bytes); (c) the R2 bytes used by the refinement method to re-rank the short-list of candidates; (d) the lookup table mapping internal ID to the global ID (4 bytes per vector).

Since the memory occupation for the lookup table is fixed, we only focus on the compromise among the first three factors next.

Linking vs Coding

We first study the impact of the number of links on the performance of HiL&C. Note that increasing the number of links means one has to reduce the number of bytes allocated to the compression codec. Figure 4 illustrates the trade-off using a simple example on Deep1M with R2 = 0. t is set to 150 by default.

Fig. 4
figure 4

Performance on Deep1M by varying the number of links for a fixed memory budget of 64 bytes

Full size image

HNSW has an obvious drawback that when the number of links is low, HNSW cannot provide a high recall because the graph structure is too sparse.

Examining more subgraphs shifts the curves upwards, meaning improved accuracy at the cost of more time consumption.

First-level approximation vs refinement codec

We now fix the number of links to 6 and consider the compromise between the number of bytes allocated to the first-level and second-level residuals under fixed memory constraint. Recall that the first-level residual is used to generate a short-list of potential candidates and the second-level quantization is used for the re-rank procedure. We denote the number of bytes allocated for them by R1 and R2, respectively. The number of subgraphs examined are fixed to 5.

Table 2 shows that the effectiveness of refinement procedure depends heavily on the amount of memory budget. When the total number of bytes per vector is very small, say 16, allocating bytes to the second-level residual codec hurts recall at all ranks listed, i.e., recall@1, @10 and @100. We have investigated the reason for this observation, and discovered that 1) 16 bytes are essentially not enough to obtain precise approximation of the first-level residuals, considering the size of the dataset; 2) the reconstruction error of the first approximation increases dramatically when decreasing R1 from 16 to 8.

Table 2 Trade-offs for allocating bytes to quantizers for the first-level and second-level residuals on SIFT1M
Full size table

The picture is totally different if the memory budget is more sufficient, which is the operating point we are interested in. For example, in the case of 64 bytes per vector, allocating these bytes evenly to the two-level residual codecs improves recall@1 significantly but hardly affects recall@10 and @100, compared with R2 = 0.

5 Experiments and analysis

In this section we present the experimental comparison of HiL&C with several state-of-the-art algorithms. All experiments are carried out on a server with E5-2620 v4@2.10GHz CPU, 256GB memory and 2T mechanical hard drive. Following the methodology in [17], the search time is obtained with a single thread and given in milliseconds per query.

5.1 Baselines and algorithm implementation

We choose Inverted Multi-Index [5] (IMI) and L&C as two baseline methods because most recent works on large-scale indexing build upon IMI [6, 8, 16, 28], and L&C outperforms IMI for most operating points as reported in [17]. We use the implementation of FaissFootnote 3 (in CPU mode) as the IMI and L&C baselines. All results are obtained using the optimal parameters selected by automatic hyperparmeter tuning for them. HiL&C is implemented using the same code base of Faiss as L&C. OPQ is used to facilitate the encoding in both levels. By default, we set \(\mathcal {K}=40000\) and t = 150 for billion-sized datasets.

The indexing cost is an important factor for real applications. It takes much less time for HiL&C to build the index compared with L&C (20 vs. 28 hours on SIFT1B and 28 vs. 34 hours on DEEP1B). The main reason is that building multiple small graphs is cheaper than constructing a giant one.

5.2 Empirical evaluation on billion-sized image sets

We perform all the experiments on the two publicly available billion-scale datasets, which are widely adopted by the computer vision community:

  1. 1.

    SIFT1B [25] contains 1 billion 128-dimensional SIFT vectors, where each vector requires 512 bytes to store.

  2. 2.

    DEEP1B [8] consists of 1 billion 96-dimensional feature vectors extracted by a CNN, where each vector occupies 384 bytes.

For encoding, all three methods use 104 bytes per vector for Deep1B and 72 bytes per vector for SIFT1B. Please note HiL&C requires only two bytes for each link, and maintains an additional lookup table (4 bytes per vector) for ID mapping.

Figure 5 compares the performance in terms of search time vs accuracy for different algorithms. As depicted in Fig. 5(a), HiL&C is much faster than L&C and IMI for almost all operating points. For example, HiL&C achieves 6.1x and 3.1x speedup at 65% recall@1 compared with L&C and IMI, respectively. Moreover, HiL&C attains much higher accuracy, e.g., it provides around 85% recall@1 using 10ms per query whereas L&C has already saturated at 65%, indicating a 30%+ gain in accuracy.

Fig. 5
figure 5

Performance comparison of HiL&C, L&C and IMI on Deep1B

Full size image

Recall@10 is an important metric to evaluate if one would like to pay extra random access to the original data stored on the external memory. As shown Fig. 5(b), HiL&C is slightly worse than L&C at the low precision region while outperforms it after reaching the high precision region (above recall@10 of 80%), which is of great interest in real applications. IMI is inferior to the other two algorithms due to its low selectivity as discussed in [17]. Figure 5(c) shows that recall@100 exhibits the similar trends as recall@10.

Figure 6 compares three algorithms on Sift1B. For most operating points, HiL&C delivers much higher accuracy than L&C and IMI. To be specific, HiL&C is 7.7x and 1.12x faster than L&C and IMI to attain a recall@1 of 51% (the saturation point of L&C), respectively. Around 39% improvement in recall@1 is achieved by HiL&C compared with L&C at the operating point of 10ms per query. For recall@10 and recall@100, HiL&C also demonstrates the superiority over the others.

Fig. 6
figure 6

Performance comparison of HiL&C, L&C and IMI on Sift1B

Full size image

5.3 Comparison with other competing algorithms

Table 3 shows the comparison between HiL&C and other methods, although HiL&C uses more bytes, since the design goal of both methods is reducing space occupation and increasing recall. When one needs a higher recall@1, HiL&C is far more attractive than the other methods.

Table 3 Performance evaluation on two billion-sized datasets
Full size table

The design philosophy of PQ-like paradigm is to trade approximation accuracy for memory consumption. Thus, it is difficult for them to achieve high Recall@1 unless a large proportion of the dataset is examined. In contrast, HiL&C and L&C are aimed at obtaining high Recall@1 by only visiting a small number of points in the dataset. This is why Recall@10 and Recall@100 of HiL&C are inferior to other baselines. Please note that Recall@10 and Recall@100 are only meaningful unless we evaluate the exact distances between the original vectors and the query, which will incur more memory access and computation time. Considering the popularity of computers with large main memory, we believe that it is affordable to trade memory for more precise vector approximation and higher Recall@1.

Considering the increasing popularity of servers with 256G+ main memory, our approach offers an competitive effects for most real-life computer vision applications.

6 Conclusion

In this paper, we introduced a simple yet effective approach for efficient approximate nearest search on billion-scale datasets on one commercial server. The proposed method, HiL&C, adopts the hierarchical graph index structure and dual residual encoding to take full advantage of the limited memory budget. The search efficiency and quantization error are both improved thanks to the delicate design choices. Empirical study shows that HiL&C outperforms the state-of-the-arts significantly.