1 Introduction

With the rapid development of computer technology, computer vision has gradually refined and formed its scientific system, in which image segmentation, as an important branch of the field of image processing, plays an increasingly important role. Image segmentation refers to the division of images into disjoint, meaningful sub-regions, the pixels in the same area have a certain correlation, and the pixels in different areas have certain differences, that is, the process of assigning the same label to pixels with the same nature in the picture [18]. Threshold segmentation is one of the classical segmentation techniques, and it is also the simplest, most practical, and efficient method [42]. The target of threshold segmentation is to select one or more specific thresholds to divide the image into several different regions. The main purpose of the threshold segmentation method is to obtain the most appropriate and effective thresholds for image segmentation. Common segmentation methods are the maximum class method, minimum error method, maximum entropy method, and so on. Kapur’s entropy is also a popular segmentation method in recent years and has been applied to many fields by many researchers. This method is an image segmentation technique based on the entropy threshold transformation, which combines the probability distribution of image histogram in the process of use. When the threshold value is selected accurately, the entropy will get the maximum value. Therefore, how to find the best threshold quickly and accurately is the focus of threshold segmentation. When threshold segmentation is performed by a common exhaustive search, the computation time is long and the limitations are large.

With the rise and development of swarm intelligence optimization algorithms, it has been widely used in image segmentation because of its strong global optimization ability and fast convergence speed, which has played a role in reducing the segmentation time and improving the accuracy of the segmentation. Akay et al. [3] applied classical particle swarm algorithm and artificial bee swarm algorithm to multi-threshold image segmentation. Kapur’s entropy and Otsu were selected as fitness functions to search for thresholds to obtain the best segmentation results. Mohamed Abd El Aziz [1] uses WOA and Moth-Flame Optimization (MFO) to solve the multi-threshold image segmentation problem. The results show that the two algorithms have better segmentation quality than other algorithms. Fayad et al. [15] proposed an image segmentation algorithm based on ACO. Upadhyay [46] proposed the Crow search algorithm to handle the multi-threshold segmentation problem, which has a good segmentation effect. Xing [29] applies TLBO to image segmentation. Zhou Y et al. [58] proposed a moth swarm algorithm for image segmentation. At the same time, to further obtain the optimal segmentation effect, scholars improved some algorithms and better handle the threshold segmentation problem. For example, Wachs-Lopes G et al. [13] proposed an improved Firefly algorithm to deal with the threshold search problem. It uses Gaussian mutation and neighborhood strategy to improve search efficiency and global searchability. Wang [47] introduced Levy flight into the salp swarm algorithm, which showed better pioneering ability and searchability, and made the segmentation quality better. Yang Z et al. [54] proposed a non-revisiting quantum-behaved PSO (NRQPSO) algorithm for image segmentation. Xin Lv et al. [49] proposed a multi threshold segmentation method based on improved sparrow search algorithm (ISSA). ISSA adopts the idea of bird swarm algorithm to improve the search and development ability of the algorithm and can find the best threshold quickly and accurately. Bao x et al. [7] proposed a method to solve the multi-threshold segmentation problem based on differential Harris Hawks Optimization. The results show that HHO-DE is an effective color image segmentation tool. Jia et al. [28] proposed a mutation strategy, Harris Hawks Optimization, to handle the multi-threshold segmentation problem, and achieved good results in the quality of the segmentation. Zhao D et al. [56] proposed the horizontal and vertical search ACO, which effectively reduces the probability of the algorithm falling into the local optimal, has better searchability, and makes the segmentation result better. Ismail S G et al. [44] proposed a chaotic optimal foraging algorithm for leukocyte segmentation in microscopic images. Pare S et al. [36] proposed CS and egg-laying radius-cuckoo search optimizer to solve multilevel threshold problems for color images using different parametric analysis methods. However, the global optimization capabilities of the above algorithms are still inadequate and can fall into local states in complex datasets. Before optimization, a large number of experiments are needed to select appropriate algorithm parameters, which makes the workload and efficiency of these algorithms significantly unbalanced.

Manta ray foraging optimization (MRFO) is a new swarm intelligence optimization algorithm proposed in 2020. It is stronger than Particle Swarm Optimization (PSO) [31], Genetic Algorithm (GA) [48], Differential Evolution (DE) [9], Cuckoo Search (CS) [53], Gravitational Search Algorithm (GSA) [40], and Artificial Bee Colony (ABC) [30] in function optimization. It has the advantages of few parameters, easy to understand, and strong global optimization [57]. So far, it has been successfully applied to solar energy [14, 23], ECG [24], generator [6, 21], power system [20], cogeneration energy system [45], geophysical inversion problem [8], directional overcurrent relay [4], feature selection [17], hybrid energy system [5], and sewage treatment [12]. MRFO has flexible searchability and strong global searchability, but it lacks local development ability. For example, the ordered search between individuals will cause greater dependence and lack of initiative, resulting in a better overall search range, but poor local search performance.

Inspired by the above literature, this paper presents a multi-strategy learning manta ray foraging optimization (MSMRFO) algorithm. It introduces saltation learning, which enables individuals to communicate closely and obtain important information in different locations. Then, a behavior selection strategy is presented, which introduces Tent disturbance and Gauss mutation to prevent the convergence shortage and local optimum in the later stage. This strategy makes an important judgment on the current situation and effectively improves the global optimization ability of the algorithm. The specific workload and contributions of this article are as follows:

  1. (1)

    Firstly, Saltation learning is introduced to speed up the information exchange of the population and improve the search efficiency of the algorithm.

  2. (2)

    A behavioral selection strategy is designed, which uses Tent disturbance and Gauss mutation to improve Manta ray convergence and trap into local optimum.

  3. (3)

    In the CEC 2017 test set, MSMRFO is compared with 8 algorithms, among which the firefly algorithm with courtship learning (FA_CL) [37] and ASBSO [55] proposed in recent years are also compared. The results verify that the algorithm has good searching ability and universality.

  4. (4)

    MSMRFO is used to optimize the threshold segmentation. It is also the first time that MRFO performs threshold segmentation in the underwater image. Nine underwater image datasets are used to validate the optimal segmentation from different thresholds. The result shows that MSMRFO has better segmentation quality than other algorithms.

The main part of the paper is structured as follows: Section 2 mainly introduces the background knowledge, including Kapur’s entropy and basic MRFO. Section 3 introduces and analyses the content and process of MSMRFO. Section 4 is to test and analyze the algorithms in CEC 2017. Section 5 describes the process of Kapur’s entropy threshold segmentation based on MSMRFO. Section 6 introduces and analyses the threshold segmentation experiments of each algorithm. The seventh section summarizes the full text, and the last section discusses the future work.

2 Background

2.1 Multi-threshold segmentation based on Kapur entropy

Kapur’s entropy is one of the early methods applied to single-threshold image segmentation, and it has been applied to the field of multi-threshold segmentation by many scholars. This segmentation method is a more effective image segmentation technique based on the entropy threshold transformation method, which combines the probability distribution of the image histogram. When the optimal threshold value is correctly selected and allocated, the maximum entropy will go. The ultimate goal of this method is to search for the optimal threshold value, which is the maximum direct value.

Assume that K is the gray level of 0-K-1 for a given picture, N is the total number of pixels, and f(i) is the frequency of the i-th intensity level.

$$ N=f(0)+f(1)+\cdots +f\left(K-1\right) $$
(1)

The probability of the i-th strength level can be expressed as:

$$ {p}_i=f(i)/N $$
(2)

Assume there are G thresholds: {th1, th2, ⋯, thG}, where 1 ≤ G ≤ K − 1. Use these thresholds to divide a given picture into G + 1 classes, each represented by the following symbols:

$$ {\displaystyle \begin{array}{c} Class(0)=\left\{0,1,2,\cdots, {th}_1-1\right\}\\ {} Class(1)=\left\{{th}_1,{th}_1+1,\cdots, {th}_2-1\right\}\\ {}\vdots \\ {} Class\left(G+1\right)=\left\{{th}_{G-1},{th}_{G-1}+1,\cdots, {th}_G\right\}\end{array}} $$
(3)

The combination entropy is obtained by calculating the sum of each type of entropy. Entropy-based methods are calculated as follows:

$$ {\displaystyle \begin{array}{c}{E}_0=-\sum \limits_{i=0}^{i={th}_1-1}\frac{p_i}{w_0}\ln \frac{p_i}{w_0},{w}_0=\sum \limits_{i=0}^{i={th}_1-1}{p}_i\\ {}{E}_1=-{\sum}_{i={th}_1}^{i={th}_2-1}\frac{p_i}{w_1}\ln \frac{p_i}{w_1},{w}_1={\sum}_{i={th}_1}^{i={th}_2-1}{p}_i\\ {}\begin{array}{c}\vdots \\ {}{E}_G=-\sum \limits_{i={th}_G}^{i=K-1}\frac{p_i}{w_G}\ln \frac{p_i}{w_G},{w}_G=\sum \limits_{i={th}_G}^{i=K-1}{p}_{\mathrm{i}}\end{array}\end{array}} $$
(4)

Where Ei represents the entropy of class i. The final current function is as follows:

$$ F(th)={E}_0+{E}_1+\cdots +{E}_G $$
(5)

For the best threshold, the higher the F(th) value, the better.

2.2 Manta ray foraging optimization

Inspired by the foraging behavior of manta rays, the algorithm is divided into three stages: chain foraging, spiral foraging, and somersault foraging.

2.2.1 Chain foraging

When manta rays are foraging, the higher the food concentration at a certain location, the better the location. Although the specific location of the best food source is not known, assuming that the location with the highest known food concentration is the best food source, manta rays will observe and swim to the best food source first. During swimming, the first manta ray moves to the best food source, while other manta rays move to the best food source and the manta ray in front of it at the same time, forming a foraging chain from head to tail. That is, in each iteration, each manta ray updates its position according to the best food source position found so far and the manta ray in front of it. The mathematical model of the chain foraging process can be expressed as follows:

$$ {x}_i^d\left(t+1\right)=\left\{\begin{array}{c}{x}_i^d(t)+r\cdotp \left({x}_{best}^d(t)-{x}_i^d(t)\right)+\alpha \cdotp \left({x}_{best}^d(t)-{x}_i^d(t)\right)\kern3.5em i=1\\ {}{x}_i^d(t)+r\cdotp \left({x}_{i-1}^d(t)-{x}_i^d(t)\right)+\alpha \cdotp \left({x}_{best}^d(t)-{x}_i^d(t)\right)\kern0.75em i=2,3,\dots, N\end{array}\right. $$
(6)

In eq. (6), \( {x}_i^d(t) \) represents the d-dimensional information of the location of the i-th manta ray in the t-generation, and r is a random number subject to [0,1] uniform distribution. \( \alpha =2\cdot r\cdot \sqrt{\mid \log\ (r)\mid } \) is the weight coefficient, \( {x}_{best}^d(t) \) is the d-dimensional information of the best location found at present. The manta ray in position i depends on the manta ray in position i-1 and the best food location currently found. The update of the first manta ray depends on the optimal location.

2.2.2 Cyclone foraging

When a manta ray finds a high-quality food source in a certain space, each manta ray in the manta ray population will connect the head to the tail and spiral to the food source. During the aggregation process, the movement mode of the manta ray population changed from simple chain movement to spiral movement around the optimal food source. The cyclone foraging process can be represented by the following mathematical model:

$$ \left(t+1\right)=\left\{\begin{array}{c}{x}_{best}^d(t)+r\cdotp \left({x}_{best}^d(t)-{x}_i^d(t)\right)+\beta \cdotp \left({x}_{best}^d(t)-{x}_i^d(t)\right)\kern3.5em i=1\\ {}{x}_{best}^d(t)+r\cdotp \left({x}_{i-1}^d(t)-{x}_i^d(t)\right)+\beta \cdotp \left({x}_{best}^d(t)-{x}_i^d(t)\right)\kern0.75em i=2,3,\dots, N\end{array}\right. $$
(7)

Among them, \( \beta =2{e}^{\frac{r_1\left(T-t+1\right)}{T}}\cdotp \sin \left(2\pi {r}_1\right) \) represents the weight coefficient of helical motion, t is the maximum number of iterations, r1 is the rotation factor and obeys the uniform random number of [0,1]. In addition, to improve the efficiency of group foraging, MRFO randomly generates a new location in the optimization process and then performs a spiral search at that location. Its mathematical model is:

$$ {x}_i^d\left(t+1\right)=\left\{\begin{array}{c}{x}_{rand}^d(t)+r\cdotp \left({x}_{best}^d(t)-{x}_i^d(t)\right)+\beta \cdotp \left({x}_{best}^d(t)-{x}_i^d(t)\right)\kern3.5em i=1\\ {}{x}_{rand}^d(t)+r\cdotp \left({x}_{i-1}^d(t)-{x}_i^d(t)\right)+\beta \cdotp \left({x}_{best}^d(t)-{x}_i^d(t)\right)\kern0.75em i=2,3,\dots, N\end{array}\right. $$
(8)

\( {x}_{rand}^d(t) \) represents a new position in space.

2.2.3 Somersault foraging

When a manta ray finds a food source, it regards the food source as a fulcrum, rotates around the fulcrum, and somersaults to a new position to attract the attention of other manta rays. For the manta ray population, somersault foraging is a random, local and frequent action, which can improve the foraging efficiency of the manta ray population. The mathematical model is as follows:

$$ {x}_i^j\left(t+1\right)={x}_i^j(t)+S\left({r}_1{x}_{best}^j(t)-{r}_2{x}_i^j(t)\right)\kern0.5em i=1,\dots, N $$
(9)

S is the somersault factor, which determines the flip distance. r2 and r3 are two random numbers that are uniformly distributed [0,1]. As S values vary, individual bats somersault to locations in search space that are symmetrical to the optimal solution at their current location.

3 Manta ray foraging optimization based on fusion mutation and learning

3.1 Algorithm analysis

From these equations, it can be seen that more communication between individuals and orderly work can improve the searchability of the algorithm and perform a wide search. However, the lack of initiative among individuals in the population limits their ability to develop. On the other hand, updates within the population are related to the best location. When encountering high-bit complex problems, the change of the optimal position is similar, which results in less change in the two updates before and after the algorithm, and limits the algorithm’s optimization ability. Therefore, a flexible change strategy is needed to improve the development ability and local convergence effect of the algorithm.

3.2 Related work

At present, Scholars are also constantly exploring new technologies to make MRFO play a better optimization ability. For example, Mohamed Abd Elaziz [2] will combine fractional calculus with MRFO to provide the direction of manta ray movement. CEC 2017 has verified the feasibility of the algorithm and applied it to image segmentation with good results. Mohamed H. Hassan [19] combines a gradient optimizer with MRFO to reduce the probability that the algorithm will fall into a local optimum and has been successfully applied in single- and multi-objective economic emission scheduling. Haitao Xu [51] uses adaptive weighting and chaos to improve MRFO to efficiently handle thermodynamic problems. Essam H. Houssein [25] uses reverse learning to initialize the population, enhances the diversity of the population, and applies it to threshold image segmentation problems with good segmentation quality. Bibekananda Jena [27] adds an attack capability to MRFO, which allows it to jump out of local optimization and find a globally optimal solution. It is then applied to the image segmentation problem of 3D Tsallis. Mihailo Micev [33] fuses SA with MRFO and applies it to the PID controller, which is better than other algorithms. In addition, Serdar Ekinci [11] uses a reverse learning and fusion simulated annealing algorithm to improve the convergence speed of the algorithm. It has good control performance when applied to the FOPID controller.

Although the above work has achieved some results, there are still some problems: Firstly, simple fusion can not show good results in different optimization environments. Secondly, adaptive strategy and reverse learning still have drawbacks in the face of high-dimensional complex problems, and can not jump out of local optimum later.

3.3 Proposed algorithm

3.3.1 Saltation learning (SL)

In the process of searching for the MRFO, the individuals are connected and the location update is only related to the optimal location, which results in a lack of learning ability and monotonous searching methods. Therefore, an individual learning behavior needs to be enhanced to improve the searchability of the algorithm in different environments.

Saltation learning is a new learning strategy proposed by Penghu et al. [38]. It can learn in different dimensions. It calculates candidate solutions through the best location, the worst location, and the randomly selected location, which increases the population diversity and has good searchability. This reduces the chance of falling into a local optimum. SL is described as follows:

$$ {x}_{i,j}^{t+1}={x}_{best,k}^t+r\cdotp \left({x}_{a,l}^t-{x}_{worst,n}^t\right) $$
(10)

In eq. (10), \( {x}_{best}^t \) and \( {x}_{worst}^t \) represents the best and worst position of the t iterations, k, l, n are three different integers selected from [1, D]. D is the dimension, r is the random number of [−1,1], exploring positions in different directions by changing the sign. a is a random integer of [1,P], and P is the population number. As shown in Fig. 1, assuming a dimension of 3, individuals from three different dimensions guide the selection of the next location, which accelerates information exchange within the population and improves search efficiency.

Fig. 1
figure 1

SL Diagram

Full size image

3.3.2 Gaussian mutation (GM)

A search chain is formed between individuals of the algorithm, which can perform a good search, but it is small on local development problems. Individuals are lazy and cannot search freely. Gauss mutation can solve this problem well and perform a good local search.

The Gauss variance comes from the Gauss distribution. Specifically, in the process of performing the variance, the original parameter value is replaced by a random number that fits the normal distribution of the mean μ and variance σ2 [16, 22]. The variance equation is:

$$ mutaion(x)=x\left(1+N\left(0,1\right)\right) $$
(11)

In the eq. (11), x is the original parameter value, and N (0,1) indicates the expected value is 0. A random number with a standard deviation of 1; mutaion(x) represents the value after the Gaussian mutation.

From the characteristics of normal distribution, it can be seen that the Gaussian distribution focuses on the local scope of the individual, carries out an efficient search, and improves the local search ability of the algorithm. For function problems with many local extremum points, it helps the algorithm to find global minimum points efficiently and accurately. it also improves the robustness of the algorithm.

3.3.3 Tent disturbance (TD)

Later individual manta rays are prone to fall into the local optimum, so chaotic disturbance is needed to make the algorithm jump out of the local optimum and improve the global searchability and optimization accuracy of the algorithm.

Chaos represents a nonlinear phenomenon in nature, so chaotic variables have the characteristics of randomness, ergodicity, and regularity, which can effectively improve the search efficiency of the algorithm. At present, the sequence generated by Tent mapping is more uniform than that generated by Logistic mapping. Therefore, using Tent mapping can effectively enable individuals to find quality positions [50]. The mathematical expression of Tent mapping is as follows:

$$ {x}_{n+1}=\left\{\begin{array}{c}2{x}_n,0\le {x}_n\le \frac{1}{2}\\ {}2\left(1-{x}_n\right),\frac{1}{2}\le {x}_n\le 1\end{array}\right. $$
(12)

The Tent mapping is expressed as follows after Bernoulli shift transformation:

$$ {x}_{n+1}=\left(2{x}_n\right)\mathit{\operatorname{mod}}\ 1 $$
(13)

Therefore, the steps of introducing Tent disturbance are as follows:

  • Step 1, generate chaotic variable x according to xn + 1;

  • Step 2, apply chaotic variables to the solution of the problem to be solved:

$$ {X}_d={\mathit{\min}}_d+\left({\mathit{\max}}_d-{\mathit{\min}}_d\right)\cdotp {x}_{n+1} $$
(14)

mind and maxd are the minimum and maximum values of the d-th dimension x, respectively.

  • Step 3, make a chaotic disturbance to the individual according to the following equation:

$$ {newX}^{,}=\left({X}^{,}+ newX\right)/2 $$
(15)

In the equation, X, represents the individual requiring chaotic perturbation, newX is the chaotic variable generated, and newX, is the individual after chaotic perturbation.

3.3.4 Selection of mutation and disturbance

First, to minimize the objective function, assume that Fave is the average fitness value within the population. If the fitness value of an individual is less than Fave, then clustering occurs. Gauss mutation makes these individuals slightly dispersed and improves the local search ability of the algorithm. Conversely, this means that individuals diverge, their current position is unreliable and disturbances are needed to improve their quality. Individuals after mutation and disturbance will change their position if they are better than those before, otherwise, the position will not change. The specific behavior selection (BC) equation is as follows:

$$ {x}_i^d(t)=\left\{\begin{array}{c} GM, if\ {F}_i<{F}_{ave}\\ {} TD, if\ {F}_i\ge {F}_{ave}\end{array}\right. $$
(16)

\( {x}_i^d(t) \) represents the updated individual, Fi represents the fitness value of the i-th individual.

3.3.5 Fusion multi-strategy learning manta ray foraging optimization

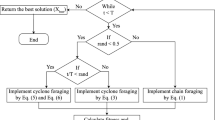
To improve the local development and learning ability of the manta ray foraging optimization, this paper proposes a multi-strategy learning manta ray foraging optimization algorithm. The algorithm uses saltation learning to speed up the internal communication of the population and improve the learning ability of the algorithm to adapt to different environments. Then a behavior selection strategy is presented, which uses Tent disturbance and Gauss mutation to balance the global search and local development capabilities of the algorithm by comparing the current and average fitness values, thus improving the quality of each optimal solution. The algorithm flow is as follows:

figure a

Algorithm: The framework of the MSMRFO.

3.3.6 Time complexity analysis

Time complexity is an important index to measure an algorithm, so it is necessary to balance the optimization ability and time complexity of the algorithm in order to improve it effectively. The basic MRFO consists of only three stages: chain foraging, spiral foraging, and somersault foraging, in which chain foraging and spiral foraging are in the same cycle. Set the population number to N, the maximum number of iterations to T, and the dimension to D, so the time complexity of MRFO can be summarized as follows:

$$ O(MRFO)=O\left(T\left(O\left( cyclone\ foraging+ chain\ foraging\right)+O\left( somersault\ foraging\right)\right)\right)=O\left(T\left( ND+ ND\right)\right)=O(TND) $$
(17)

MSMRFO can be summarized as:

$$ O(MSMRFO)=O\left(T\left(O\left( cyclone\ foraging+ chain\ foraging\right)+O(SL)+O\left( somersault\ foraging\right)+O(BC)+O\left( somersault\ foraging\right)\right)\right)=O(TND) $$
(18)

Therefore, it can be seen that the time complexity of MSMRFO has not changed radically.

3.3.7 Strategy effectiveness test

In order to test whether MSMRFO can really improve the optimization mechanism of the original algorithm, this paper takes sphere function as an example, and tests on MRFO and MSMRFO respectively. The population number is 50, the maximum number of iterations is 5, the theoretical optimal value of sphere function is 0, and the location is x∗ = (0, …, 0). The final individual distribution of the two algorithms is given as shown in Fig. 2.

Fig. 2
figure 2

Algorithmic Personal Distribution Map (a)MRFO (b)MSMRFO

Full size image

As shown in Fig. 2, it is clear that MRFO does not find an optimal value and is in a dispersed state, while MSMRFO has been clustered near the theoretical optimal value. Therefore, MSMRFO has a very fast convergence rate and a high accuracy. It can be seen that the introduction of multiple strategies significantly improves the optimization methods of the MRFO algorithm, speeds up the population exchange speed, and improves the quality of each solution obtained.

4 Performance testing

To verify the optimization capability of the MSMRFO algorithm, this paper tests each algorithm on the CEC 2017 test set, and compares eight algorithms with MSMRFO. The population number is 100, the number of assessments is 100 × D, and D is the dimension. To better reflect the effectiveness of the MSMRFO algorithm, this paper compares it with PSO, whale optimization algorithm (WOA) [34], sparrow search algorithm (SSA) [52], naked mole-rat algorithm (NMRA) [43], MRFO, Grey Wolf Optimizer (GWO) [35], and compares the two algorithms proposed in recent years, FACL and ASBSO, which have a good performance on the test set of CEC. PSO, GWO, and WOA are classical algorithms. SSA, MRFO, and NMRA are new swarm intelligence algorithms proposed in recent years. Because the parameters of some algorithms do not need special declaration and internal parameters do not need to be set, the parameters of some algorithms are shown in Table 1 In this paper, the Wilcoxon rank test is used to show whether there is a significant difference between each algorithm, which is tested at 5% significant level. “+” means that MSMRFO has more optimization capabilities than other algorithms, “-” conversely, “=“means that the optimization performance between the two algorithms is equal, and “N/A” means that the values of the two algorithms are the same and cannot be compared. Specific test results are shown in Tables 2 and 3 in the Appendix.

Table 1 Parameters of each algorithm
Full size table

The results of 30 operations of each algorithm are counted, and the five indexes of each algorithm, namely, optimal value, worst value, median, average value, and standard deviation, are calculated. In addition, the rank of each algorithm in each function is calculated, and the average rank is calculated to measure the universality of the algorithm. In order to clearly see the stability and optimization interval of each algorithm, a box diagram of 30 times the results of these functions in F3–6, F11–14, and F22–25 is given as shown in Fig. 3. These functions represent different types.

Fig. 3
figure 3figure 3

Statistical chart of algorithm operation results (a)F3 (b)F4 (c)F5 (d)F6 (e)F11 (f)F12 (g)F13 (h)F14 (i)F22 (j)F23 (k)F24 (l)F25

Full size image

From Tables 2 and 3 and Fig. 3, we can see that MSMRFO has a great advantage in searchability and stability, especially in functions that show better searchability. Although some functions do not show better performance indicators, most of them have shown better search performance. Based on the fact that there is no free lunch theorem in the world, it is impossible to find an algorithm that performs well on any optimization problem, so MSMRFO is generally applicable. From the test results and average ranking, the average ranking of MSMRFO in the two tables is 1.34 and 1.7241 respectively. NMRA, PSO, and MRFO are second only to MSMRFO. And are the lowest ranking. MSMRFO has better advantages and is more perfect than the algorithm proposed in recent years. From the box diagram, the optimization effect of MSMRFO in each function is relatively stable, and the accuracy of the solution is also high. Generally speaking, the saltation learning and behavior selection strategy introduced by MSMRFO effectively avoids the phenomenon that the algorithm falls into local optimum and greatly improves the searchability of the algorithm.

5 Threshold segmentation process based on MSMRFO

Assuming a k-dimensional threshold segmentation of the image, the solution vector is T = [t1, t2, ⋯, tk], which takes a positive integer and satisfies 0 < t1 < t2 < ⋯ < tn < L. Multi-threshold segmentation is the process of finding a set of thresholds [t1, t2, ⋯, tk] (K > 0) in the image f(x, y) to be segmented according to a certain criterion and dividing it into K + 1 parts. In this paper, Kapur’s entropy is used as the segmentation criterion, MSMRFO is used to optimize the selection among L gray levels in solution space, and the maximization of eq. (1) is used as the objective function to solve. The multi-threshold segmentation process based on MSMRFO is shown in Fig. 4, and the detailed process is as follows:

  • Step1, Read the image to be split (grayscale image);

  • Step2, Get gray histogram of read-in image;

  • Step3, Initialization of MSMRFO parameters and setting of segmentation threshold K;

  • Step4, Initialization of the manta ray population. The individual position of a manta ray represents a threshold vector for image segmentation, and the component value of each vector ranges from [0,255] to an integer;

  • Step5, Perform MSMRFO;

  • Step6, if the algorithm reaches the preset end condition, the algorithm finishes the optimization and returns the best fitness of the bat location information. That is, the optimal threshold segmentation, otherwise jump to step 5.

  • Step7, Segment gray-scale images by the optimal threshold vector obtained, and output it.

Fig. 4
figure 4

MSMRFO-based threshold segmentation flowchart

Full size image

6 Threshold segmentation experiment

6.1 Evaluating indicator

It is impossible to see the difference between each algorithm in image segmentation by human eyes. Therefore, three commonly used image segmentation indicators, PSNR, SSIM, and FSIM, are selected to measure the quality of each algorithm.

PSNR is mainly used to measure the difference between the segmented image and the original image. The equation is as follows:

$$ PSNR=20\cdotp {\mathit{\log}}_{10}\left(\frac{255}{RMSE}\right) $$
(19)
$$ RMSE=\sqrt{\frac{\sum_{i=1}^M{\sum}_{j=1}^Q{\left(I\left(i,j\right)- Seg\left(i,j\right)\right)}^2}{M\times Q}} $$
(20)

In the equation, RMSE represents the root mean square error of the pixel; M × Q represents the size of the image; I(i, j) represents the pixel gray value of the original image; Seg(i, j) represents the pixel gray value of the segmented image. The larger the PSNR value, the better the image segmentation quality.

SSIM is used to measure the similarity between the original image and the segmented image. The larger the SSIM, the better the segmentation results. SSIM is defined as:

$$ SSIM=\frac{\left(2{\mu}_I{\mu}_{seg}+{c}_1\right)\left(2{\sigma}_{I,\mathit{\operatorname{seg}}}+{c}_2\right)}{\left({\mu}_I^2+{\mu}_{seg}^2+{c}_1\right)\left({\sigma}_I^2+{\sigma}_{seg}^2+{c}_2\right)} $$
(21)

In the equation, μI and μseg represent the average value of the original image and the segmented image. σI and σseg represent the standard deviation between the original image and the segmented image; σI, seg represents the covariance between the original image and the segmented image; c1, c2 are constants used to ensure stability.

FSIM is a measure of feature similarity between the original image and the segmentation quality, used to evaluate local structure and provide contrast information. The value range of FSIM is [0,1], and the closer the value is to 1, the better the result is. FSIM is defined as follows:

$$ FSIM=\frac{\sum_{l\in \Omega}{S}_L(X)P{C}_m(X)}{\sum_{l\in \Omega}P{C}_m(X)} $$
(22)
$$ SL(X)={\mathrm{S}}_{PC}(X){S}_G(X) $$
(23)
$$ {S}_{PC}(X)=\frac{2P{C}_1(X)P{C}_2(X)+{T}_1}{PC_1^2(X)P{C}_2^2(X)+{T}_1} $$
(24)
$$ {S}_G(X)=\frac{2{G}_1(X){G}_2(X)+{T}_2}{G_1^2(X){G}_2^2(X)+{T}_2} $$
(25)
$$ G=\sqrt{G_x^2+{G}_y^2} $$
(26)
$$ PC(X)=\frac{E(X)}{\left(\varepsilon +{\sum}_m{A}_n(X)\right)} $$
(27)

In the above equation, Ω is all the pixel areas of the original image; SL(X) is the similarity score; PCm(X) is a measure of phase consistency; T1 and T2 are constant; G is a gradient descent; E(X) is the size of the response vector at position X and the scale is n; ε is a very small number; An(X) is the local size at scale n.

6.2 Experiment and analysis

To verify the effectiveness and feasibility of the MSMRFO algorithm, nine underwater image test sets [26] are selected in this paper. The underwater environment is complex and has a lot of debris, so the optimum performance of an algorithm can be tested most. At the same time, in order to prove that MSMRFO is competitive, it is compared with ten algorithms: MRFO, PSO, WOA, Teaching Learning Based Optimization (TLBO) [39], SSA, ISSA, GWO, BSA [32], CPSOGSA [41], HHO-DE. These ten algorithms have been applied to threshold image segmentation by researchers, so they are very persuasive. Each algorithm has experimented with 4 thresholds from 2 to 5. Each algorithm has a population of 30 and a maximum number of iterations of 100. A stop parameter of 10 is set in the experiment. If the solution found 10 times is the same in the optimization, it is assumed that the convergence has been completed. The significance of this is to reflect the value of the algorithm and find an algorithm with higher search efficiency. The experimental environment is Window10 64bit, the software is matlab2019b, the memory is 16GB, and the processor is Intel(R) Core(TM) i5-10200H CPU @ 2.40GHz. The MSMRFO algorithm segmentation image is shown in Fig. 5. The results of each algorithm are shown in Tables 4, 5, 6 and 7 in the Appendix. If MSMRFO has the best performance Indicators, the font will be bold. Among them, Table 4 shows the average fitness value (F(th)) of each algorithm to verify the optimization ability of the algorithm, and Tables 5, 6 and 7 show the PSNR, SSIM and FSIM performance indicators of each algorithm to verify the segmentation quality of the algorithm, respectively.

Fig. 5
figure 5

Threshold segmentation image based on MSMRFO

Full size image

From Table 4, it can be seen that the number of optimal indicators of MSMRFO is higher relative to other algorithms, which shows the stronger optimization ability of MSMRFO, on the other hand, the indicators are not optimal in the case that its values are close to other optimal indicators want. Taken together, MSMRFO is effective in optimizing Kapur’s Entropy and has sufficient generalizability.

It can see from Fig. 5, the image after MSMRFO segmentation becomes clearer with the increase of the threshold value, so MSMRFO has a good application value in threshold segmentation. From Table 5, 6 and 7, we can see that there are more optimal indicators for MSMRFO. In Test 05, the PSNR of each threshold segmentation is better than other algorithms. In Test 08, the SSIM indicators of each threshold segmentation is the best. In the individual images in Table 7, the FSIM indicators is optimal for MSMRFO with a threshold of 3 or more categories. Other algorithms have optimal criteria, but they are small in number and have better segmentation quality only at a certain threshold. Overall, MSMRFO has better segmentation quality at high thresholds and generally worse at low thresholds.

In order to better show the quality of MSMRFO segmentation under each threshold, the Friedman test [10] is applied to three performance indicators of each threshold, the ranking of each algorithm under different thresholds is calculated, and the final average rank is calculated to evaluate the segmentation effect of an algorithm. The test results are shown in Tables 8 and 9 in the Appendix. Table 8 shows the ranking results of MSMRFO and classical algorithms, and Table 9 shows the ranking of MSMRFO and the new algorithms and variant algorithms proposed in recent years. Similarly, if MSMRFO ranks best, its value will be bolded.

It can be seen from Tables 8 and 9 that MSMRFO has a large number of optimal values, indicating that MSMRFO has a better optimization effect than the classical algorithm or compared with the algorithm proposed in recent years. At the same time, it also shows that MSMRFO has good universality in threshold segmentation and can show good application value in underwater images.

7 Conclusion

To better determine the optimal threshold in threshold segmentation, a Kapur’s entropy image segmentation based on multi-strategy manta ray foraging optimization is presented. At the same time, a multi-strategy learning manta ray foraging optimization algorithm is proposed to improve the local development capability of the original algorithm and the probability of falling into the local optimum. The algorithm uses saltation learning to communicate among individuals, which accelerates the convergence speed of the algorithm. A new selection behavior strategy is proposed to make a better judgment on the current optimization stage, to prevent the algorithm from falling into local optimization and insufficient convergence, and to improve the global search ability of the algorithm. Tests on CEC 2017 show that the algorithm has good optimization ability and strong universality. Finally, nine underwater image data sets are segmented by MSMRFO. According to the segmented indicators, MSMRFO has better advantages and better quality in high threshold segmentation. From the Friedman test, MSMRFO ranked the highest, indicating that MSMRFO is generally good at segmentation in nine datasets.

8 Future work

Firstly, saltation learning has some randomness, so the final result is not maintained at a good level. Secondly, in some functions, no theoretical optimal value is found. At the same time, the fitness value does not yet achieve a certain advantage when optimizing the threshold. Thirdly, in many image data collections, it is not guaranteed that the three evaluation indicators in the same segmented image are optimal. For example, in Test 08, PSNR is not optimal with a threshold of 3, but the values of the other two indicators are the best. Finally, poor segmentation quality is common in low threshold processing. For example, in Test 02, none of the three MSMRFO indicators with a threshold of 3 was optimal. Therefore, The next step is to balance the optimization ability of the algorithm at high and low thresholds. In the aspect of image segmentation, we need to balance the quality of one image to ensure that the three indicators of image quality obtained at each time are excellent.