1 Introduction

Hyperspectral imagery is commonly acquired from hyperspectral sensors and typically denoted as a data cube, where each pixel consists of plentiful spectral information to reflect the specific land cover [20, 38]. In general, hyperspectral image (HSI) data are collected from various spectral channels and represented as high-dimensional features, which may contain noisy, irrelevant and redundant information [23, 25]. To tackle the remote sensing problems with such data, the Hughes phenemenon may happen and the performance may be degraded for the limited number of instances with plentiful redundant features.

To avoid the Hughes phenemenon induced by high-dimensional hyperspectral data, dimensionality reduction should be taken into consideration [8, 15, 24]. Being a dimensionality reduction technique, feature selection is conducted according to a specific criterion, which can locate the discriminative feature subset. In [29], the multiobjective feature selection method for hyperspectral data is developed on a novel discrete sine cosine algorithm, where the redundancy is minimized and the relevance is maximized for the selected hyperspectral features. In [28], the high dimensional model representation approach for hyperspectral imagery calculates the class labels of auxiliary training instances by a k-nearest neighbor (KNN), which are used for ranking the importance of features. In [26], the Gabor hyperspectral feature selection model is related to symmetrical uncertainty and Markov blanket, where the extracted Gabor features are firstly ranked by the classification information and then evaluated their redundancy. In [6], the fast forward feature selection method is based on a Gaussian mixture model, which improves the classification accuracy via k-fold cross validation to select discriminative spectral features. However, the above feature selection methods for hyperspectral imagery are linear models and required the explicit labels. In reality, it is difficult and expensive to acquire abundant label information for hyperspectral data. Besides, the nonlinear characteristic of hyperspectral data is hard to extract by a linear model.

To address the aforementioned problems, in this paper, we propose a latent representation learning based autoencoder feature selection (LRLAFS) model, which can nonlinearly select the informative hyperspectral features for classification. The autoencoder is an unsupervised neural network model for efficient data codings [13]. By imposing the ℓ2,1-norm regularization on the network parameters connecting the input and hidden layers, the autoencoder can be used to perform feature selection [11]. To steer the feature selection process, the adjacency matrix of hyperspectral data is decomposed to obtain the latent representation of original data, which is used for approximating a new feature representation learnt by the autoencoder. To solve the proposed model, a helpful alternative optimization algorithm is advanced. Experiments on three HSI datasets confirm the effectiveness of the proposed model.

The rest of this paper is structured as follows. Related work is briefly introduced in Section 2. Section 3 advances the proposed latent representation learning based autoencoder feature selection model, followed by the optimization algorithm in Section 4. Experiments and comparisons on HSI data are demonstrated in Section 5. We finally conclude the paper in Section 6.

2 Related work

2.1 Unsupervised feature selection

Being a data preprocessing technique, feature selection is used for dimensionality reduction, which requires less memory space and alleviates the computational cost [10, 37]. According to the availability of label information, feature selection methods are grouped into the supervised, semi-supervised and unsupervised methods. Unsupervised feature selection approaches are required to preserve the intrinsic geometric data structure and select a subset of informative features without using any label information [22, 30]. Recently, a large number of unsupervised feature selection approaches have been proposed, which are broadly split into the filter, wrapper and embedded approaches according to previous literatures [10, 19].

The filter approaches design an evaluation measure to independently score the importance of features. This is a simple kind of strategy for feature selection. The variance score is the simplest measure to select useful features with the assumption that better representation ability is along with larger variance. The laplacian score (LS) is a measure to select discriminative features for locality preservation of data with the assumption of manifold structure [12]. Filters usually require less computational complexity than wrappers, but are independent of predictive model. The wrapper approaches score the significance of each feature accompanied by a predictive model. Clustering and classification are commonly employed as predictive models in wrappers. The multi-cluster feature selection (MCFS) method utilizes a regression algorithm to promote unsupervised feature selection [4]. In addition, the embedded approaches are trained by all features and conduct feature selection during the model learning process, where the computational complexity is between filters and wrappers. Existing embedded approaches exploit the potential information and correlation to distinguish informative features by imposing different penalty terms for different purposes, such as sparsity restriction [39], nonnegative restriction [32] and redundancy control [17].

2.2 Autoencoder

The autoencoder [9, 14] is a special unsupervised neural network framework for learning auxiliary feature representations, where the same neurons are in the output layer as inputs to reconstruct the original input data instead of determining their predicted the target values. During the learning process, the autoencoder firstly converts the input data to an auxiliary encoded representation and then decodes it to reconstruct a representation that approximates to the original input data as possible [36]. The above descriptions are respectively the encoding and decoding procedures, which can be also regarded as a nonlinear self-representation model. With the special learning process, the autoencoder can extract the discriminative encoded representation via the hidden layer, which contains the underlying information inherent in the original data. In diverse applications, different kinds of autoencoders are utilized to extract informative feature representations for further learning [3, 34].

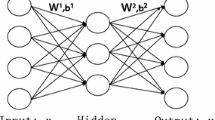
In addition to feature extraction, the autoencoder can be also used to perform feature selection [1, 5]. When integrating a feature selection regularized term into the autoencoder, the network weights will be sparse in row to fulfill feature selection, which is shown as in Fig. 1. Since the relationships of features may be linear or nonlinear, the conventional linear feature selection methods may ignore the nonlinear characteristic and can not correctly capture the real relationships among features. In contrast, autoencoder based models can select informative features by excavating both linear and nonlinear information among features. In [31], the feature selection guided autoencoder (FSAE) method is proposed, which integrates an autoencoder and a general feature selection regularizer to distinguish relevant and irrelevant features. In [11], the autoencoder feature selection (AEFS) approach is advanced by imposing the ℓ2,1-norm regularization on the connecting parameters between the input and hidden layers, which can retain the most discriminative information among features. Following the previous work [11], the graph regularized autoencoder feature selection (GAFS) model [7] is proposed by adding the local data geometric structure regularization, which achieves promising performance. The above autoencoder based methods are superior to some linear approaches on feature selection, which mainly attribute to the special encoding and decoding procedures.

Fig. 1
figure 1

Autoencoder network for feature selection. The blue dotted lines mean that the features are less important in the learning task, which can fulfill feature selection

Full size image

3 Proposed method

The autoencoder is an extraordinary unsupervised neural network learning model, where the output layer is to reconstruct the original inputs instead of predicting their target values [33]. Here, we employ a typical autoencoder network with only one hidden layer as an example. Given a hyperspectral data matrix \(\mathbf {X}\in \mathbb {R}^{N\times d}\), the learning process of autoencoder is separated into two components: an encoder to transform the original data into a different representation \(f(\mathbf {X})=\sigma _{1}(\mathbf {W}^{(1)}\mathbf {X}+\mathbf {B}^{(1)})\) and a decoder to convert the new representation into the reconstructed input data \(\hat {\mathbf {X}}=g(f(\mathbf {X}))= \sigma _{2}(\mathbf {W}^{(2)}f(\mathbf {X})+\mathbf {B}^{(2)})\). In the above learning process, σ1 and σ2 are respectively set to be nonlinear and linear activation functions for the hidden and output layers, \({\mathscr{H}}=\{\mathbf {W}^{\mathbf (1)},\mathbf {W}^{(2)},\mathbf {B}^{(1)},\mathbf {B}^{(2)}\}\) are the network weights to connect two adjacent layers of the autoencoder and the biases for the hidden and output layers.

During the learning process, the autoencoder aims at minimizing the difference between the original inputs and the reconstructed data, which is represented as the following equation:

$$ \min_{\mathcal{H}} || \mathbf{X} - g(f(\mathbf{X})) ||_{F}^{2} $$
(1)

where ||⋅||F is the Frobenius norm. From (1), we can learn that the autoencoder encodes the data matrix X to generate a representation matrix f(X) and then decodes it to get the reconstructed data matrix \(\hat {\mathbf {X}}=g(f(\mathbf {X}))\). According to nonlinear activation function used in the hidden layer, the autoencoder is normally treated as a nonlinear self-representation learning model.

When using the autoencoder model of (1), all features are adopted to solve hyperspectral image applications. However, the original hyperspectral data may contain noisy, irrelevant and redundant information. To eliminate the negative effect from these information, the associated network parameters (i.e., W(1)) of the autoencoder should be set as zeros or small values. This is typically regarded as feature selection [11]. To this end, the ℓ2,1-norm constraint imposed on W(1) is as follows:

$$ ||\mathbf{W}^{(1)}||_{2,1} = {\sum\limits_{i}^{d}} ||\boldsymbol{w}_{i}^{(1)}||_{2} = {\sum\limits_{i}^{d}}\sqrt{{\sum\limits_{j}^{l}}(w^{(1)}_{ij})^{2}}. $$
(2)

where \(\boldsymbol {w}_{i}^{(1)}\) is the i th row vector and \(w^{(1)}_{ij}\) is the i th row and j th column element in matrix W(1). Equation (2) can produce a row-sparse matrix W(1), where the i th row vector \(\boldsymbol {w}_{i}^{(1)}\) is to measure the importance of the i th feature. Therefore, the autoencoder based feature selection model is formulated as follows:

$$ \min_{\mathcal{H}} ||\mathbf{X} - g(f(\mathbf{X}))||_{F}^{2} + \alpha || \mathbf{W}^{(1)}|_{2, 1} $$
(3)

where α is a parameter to balance the reconstruction loss and the ℓ2,1-norm regularizer.

In general, the overfitting problem and the slow convergence issue commonly occur on neural network learning models. To avoid overfitting and promote convergence for an autoencoder, a weight decay regularization is imperative. By adding the weight decay regularization, the above learning model is denoted as follows:

$$ \min_{\mathcal{H}} || \mathbf{X} - g(f(\mathbf{X})) ||_{F}^{2} + \alpha ||\mathbf{W}^{(1)}||_{2, 1} + \beta\sum\limits_{i=1}^{2}{||\mathbf{W}^{(i)}||_{F}^{2}} $$
(4)

where β is a parameter for the weight decay regularization. Equation (4) describes a basic autoencoder feature selection model, which can effectively select discriminative features.

In an autoencoder, f(X) is the representation encoding from X, which denotes the latent compact or sparse information. In reality, the latent representations of X are various according to different learning scenarios. Uncovering latent representations from the original data benefits diverse learning tasks and has gained increasingly attention [27]. For networked data, the link information reflects that instances often connect to each other for their underlying relationships. Usually, latent representations can be learnt from the link information via a symmetric nonnegative matrix factorization model [18]. For hyperspectral image data, the similarity matrix A can be constructed by a KNN graph, which describes the correlation between instances. Motivated by this, we employ latent representation learning to steer autoencoder based feature selection. By decomposing A with symmetric matrix factorization, we can get the following equation:

$$ \min_{\mathbf{V}} ||\mathbf{A}-\mathbf{V}\mathbf{V}^{\mathrm{T}}||_{F}^{2}; $$
(5)

where V is the latent representation of X. Equation (5) captures the underlying data information and represents the original data in a different representation. For a same data matrix, different latent representations should consistently share the same information [27]. Therefore, the latent representations f(X) and V should be consistent. To minimize the difference between f(X) and V, we can obtain the following equation:

$$ \min_{\mathcal{H}, \mathbf{V}} ||f(\mathbf{X}) - \mathbf{V}||_{F}^{2}. $$
(6)

Equation (6) builds a connection between two different latent representations. Equations (4)–(6) represent the important components of the proposed model. It is clear that these separated equations cannot guarantee an optimal result. We integrate (5) and (6) into the basic model of (4). Therefore, the formulation of our proposed model is represented as the following equation:

$$ \mathcal{J}{\kern-.5pt}(\mathcal{H},{\kern-.1pt} \mathbf{V}) {}={} \min_{\mathcal{H}, \mathbf{V}} ||\mathbf{X}-\hat{\mathbf{X}}||_{F}^{2} + \alpha||\mathbf{W}^{(1)}||_{2, 1} + \beta{}\sum\limits_{i = 1}^{2}{{\kern-.1pt}||\mathbf{W}^{(i)}||_{F}^{2}}\\ +{\kern-.5pt} \gamma||f(\mathbf{X}) - \mathbf{V}||_{F}^{2} + \lambda||\mathbf{A} - \mathbf{V}\mathbf{V}^{\mathrm{T}}||_{F}^{2} \\ $$
(7)

During the learning process, we can select informative features from the advanced techniques of autoencoder and latent representation learning. Once W(1) is learned, we can sort all features to select the top ranked features by means of the descending order of \(||\boldsymbol {w}_{i}^{(1)}||_{2}~(i=1,...,d)\).

4 Optimization algorithm

Since the proposed model is based on an autoencoder network to perform feature selection, it is hard to solve (7) for the complex nonlinearity. Therefore, the gradient descent method [2] is employed as an alternating optimization algorithm to iteratively update the network parameters \({\mathscr{H}}=\{\mathbf {W}^{(1)},\mathbf {W}^{(2)},\mathbf {B}^{(1)},\mathbf {B}^{(2)}\}\) and the latent representation V. To calculate the derivatives of (7) w.r.t variables W(1), W(2), B(1), B(2) and V, the calculation of the error terms for the output and hidden layers is required for the chain rule. Specifically, the error terms of the output and hidden layers are determined as follows:

$$ \delta^{(o)} = 2(\mathbf{X}-g(f(\mathbf{X}))) \odot g^{\prime}(f(\mathbf{X})); $$
(8)
$$ \delta^{(h)} = (\delta^{(o)}{\mathbf{W}^{(2)}}^{\mathrm{T}})\odot f^{\prime}(\mathbf{X}); $$
(9)

where ⊙ denotes the element-wise product. Given the above error terms in (8) and (9), the derivatives of (7) w.r.t different variables can be consecutively determined.

  1. 1)

    Derivative w.r.t W(2): With a fixed W(1), B(1), B(2) and V, the optimization problem of (7) w.r.t W(2) can be rewritten as \(\mathcal {J}(\mathbf {W}^{(2)}) = ||\mathbf {X}-\hat {\mathbf {X}}||_{F}^{2} + \beta ||\mathbf {W}^{(2)}||_{F}^{2}\). The derivative w.r.t W(2) is given as:

    $$ \frac{\partial \mathcal{J}}{\partial \mathbf{W}^{(2)}} = {\mathbf{Z}^{(o)}}^{\mathrm{T}}\delta^{(o)} + \beta\mathbf{W}^{(2)}. $$
    (10)
  2. 2)

    Derivative w.r.t B(2): With a fixed W(1), W(2), B(1) and V, the optimization problem of (7) w.r.t B(2) can be rewritten as \(\mathcal {J}(\mathbf {B}^{(2)}) = ||\mathbf {X}-\hat {\mathbf {X}}||_{F}^{2}\). The derivative w.r.t B(2) is given as:

    $$ \frac{\partial \mathcal{J}}{\partial \mathbf{B}^{(2)}} =\delta^{(o)} $$
    (11)
  3. 3)

    Derivative w.r.t W(1): With a fixed W(2), B(1), W(2) and V, the optimization problem of (7) w.r.t W(1) can be rewritten as \(\mathcal {J}(\mathbf {W}^{(1)}) = ||\mathbf {X}-\hat {\mathbf {X}}||_{F}^{2} + \alpha ||\mathbf {W}^{(1)}||_{2, 1} + \beta ||\mathbf {W}^{(1)}||_{F}^{2} + \gamma ||f(\mathbf {X}) - \mathbf {V}||_{F}^{2}\). The derivative w.r.t W(1) is given as:

    $$ \frac{\partial \mathcal{J}}{\partial \mathbf{W}^{(1)}} = \mathbf{X}^{\mathrm{T}}\delta^{(h)} + \alpha\mathbf{D}\mathbf{W}^{(1)} + \beta\mathbf{W}^{(1)} + 2\gamma\mathbf{X}^{T}((f(\mathbf{X}) - \mathbf{V}) \odot f^{\prime}(\mathbf{X}). $$
    (12)

    In (12), D is a diagonal matrix updated in each iteration, where each diagonal element is calculated as \(d_{ii}=\frac {1}{2||\boldsymbol {w}_{i}^{(1)}||_{2}}\).

  4. 4)

    Derivative w.r.t B(1): With a fixed W(1), W(2), B(1) and V, the optimization problem of (7) w.r.t B(1) can be rewritten as \(\mathcal {J}(\mathbf {B}^{(1)}) = ||\mathbf {X}-\hat {\mathbf {X}}||_{F}^{2} + \gamma ||f(\mathbf {X}) - \mathbf {V}||_{F}^{2}\). The derivative w.r.t W(1) is given as:

    $$ \frac{\partial \mathcal{J}}{\partial \mathbf{B}^{(1)}} = \delta^{(h)} + 2\gamma(f(\mathbf{X})-\mathbf{V}) \odot f^{\prime}(\mathbf{X}). $$
    (13)
  5. 5)

    Derivative w.r.t V: With a fixed W(1), W(2), B(1) and B(2), the optimization problem of (7) w.r.t V can be rewritten as \(\mathcal {J}(\mathbf {V}) = \gamma ||f(\mathbf {X}) - \mathbf {V}||_{F}^{2} + \lambda ||\mathbf {A} - \mathbf {V}\mathbf {V}^{\mathrm {T}}||_{F}^{2}\). The derivative w.r.t W(1) is given as:

    $$ \frac{\partial \mathcal{J}}{\partial \mathbf{V}} = 2\gamma(f(\mathbf{X}) - \mathbf{V}) + 4\lambda(\mathbf{A} - \mathbf{V}\mathbf{V}^{\mathrm{T}})\mathbf{V}. $$
    (14)

Given the above derivatives, a novel alternative optimization algorithm is devised to alternatively update variables W(1), W(2), B(1), B(2) and V. The update rule of the alternating solution for the proposed model is provided as follows:

$$ \left\{ \begin{array}{ll} & \mathbf{W}^{(1)}:=\mathbf{W}^{(1)} - \eta \frac{\partial \mathcal{J}}{\partial \mathbf{W}^{(1)}}\\ & \mathbf{B}^{(1)}:=\mathbf{B}^{(1)} - \eta \frac{\partial \mathcal{J}}{\partial \mathbf{B}^{(1)}}\\ & \mathbf{W}^{(2)}:=\mathbf{W}^{(2)} - \eta \frac{\partial \mathcal{J}}{\partial \mathbf{W}^{(2)}}\\ & \mathbf{B}^{(2)}:=\mathbf{B}^{(2)} - \eta \frac{\partial \mathcal{J}}{\partial \mathbf{B}^{(2)}}\\ & \mathbf{V}:=\mathbf{V} - \eta \frac{\partial \mathcal{J}}{\partial \mathbf{V}} \end{array}{} \right. $$
(15)

where η is the learning rate for the update rule. The pseudocode of the proposed method is exhibited in Algorithm 1.

figure a

5 Experiments and results

5.1 Hyperspectral data

To validate the performance of different feature selection approaches, three public HSI datasetsFootnote 1 are utilized for experimental studies, including Indian Pine, University of Pavia and Salinas Scene.

The Indian Pine dataset was acquired by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor over Northwest Indiana. This scene consists of 145 × 145 pixels with 200 valid spectral bands and records 16 land covers of different plants. The false color composition and ground truth for the Indian Pines dataset are respectively shown in Figs. 2a and d.

Fig. 2
figure 2

The false color composition (in the upper row) and ground truth (in the bottom row) of three hyperspectral image datasets. a and d Indian Pines. b and e University of Pavia. c and f Salinas Scene

Full size image

The University of Pavia dataset was captured by the Reflective Optics System Imaging Spectrometer (ROSIS-3) sensor to record a scene from the University of Pavia, Italy. This scene contains 610×340 pixels with 103 informative spectral bands and includes 9 different land covers. The false color composition and ground truth for the University of Pavia dataset are respectively shown in Figs. 2b and e.

The Salinas Scene dataset was collected by the AVIRIS sensor to record a scene from Salinas Valley, California, USA. There are 512 × 217 pixels with 204 useful spectral bands in this scene, which is associated with 16 diverse land covers. The false color composition and ground truth for the Salinas Scene dataset are respectively shown in Figs. 2c and f.

5.2 Comparison method and experimental setting

In the experiments, the proposed LRLAFS method is compared with the following methods. SpaBS is based on sparse representation to perform feature selection, where the histogram of the coefficient matrix decomposed from hyperspectral image data is calculated to select the most discriminative features [16]. AEFS selects informative features by combining autoencoder regression and group lasso tasks, which can take full advantage of linear and nonlinear information among features [11]. GAFS integrates manifold learning into the basic autoencoder feature selection model, where spectral graph analysis is considered into the learning process for local data geometry preservation [7]. AllFeas is the baseline method with all original features for hyperspectral image classification.

For a fair comparison, k-nearest neighbors (KNN) [21] is employed as the classifier to validate all compared methods. The parameter k in KNN is empirically set to be 5. Overall accuracy (OA), average accuracy (AA) and Kappa coefficient are popularly used as evaluation measures in HSI classification. The experiments are conducted on a computer with Intel(R) Core(TM) 2.90 GHZ CPU and 8 GB RAM. In the proposed LRLAFS model, parameters α, β, γ and λ are tuned from {10− 3,10− 2,...,103} by means of a grid-search strategy. Besides, the numbers of hidden neurons are tuned from {5,15,25,...,95}, while the numbers of selected features are varying from {3%,6%,9%,...,66%} of the number of features. The best results presented in the following sections are achieved by setting the optimal parameters [35].

5.3 Experimental results

The experimental results of all competing feature selection approaches on the three HSI datasets are discussed in this section.

  1. (1)

    Comparison for the Indian Pines data: The experimental results on the Indian Pines data are summarized in Table 1. From Table 1, the proposed LRLAFS method is superior to AllFeas and other competing methods are inferior to AllFeas. It demonstrates that the proposed LRLAFS method can select informative features and remove uninformative features from the original Indian Pines data, which benefits the classification performance. While SpaBS, AEFS and GAFS may select uninformative features from the original feature space, which degrades the further classification performance. For autoencoder based models, AEFS, GAFS and LRLAFS show the increasing performance on feature selection, which mainly attributes to the manifold learning in GAFS and the latent representation learning in LRLAFS. Accordingly, the classification maps of all competing approaches are presented in Fig. 3, which are consistent with our previous observation.

    Fig. 3
    figure 3

    Classification maps of all competing approaches on the Indian Pines dataset. a AllFeas. b SpaBS. c AEFS. d GAFS. e LRLAFS

    Full size image
    Table 1 Experimental comparison of different feature selection approaches on the Indian Pines dataset
    Full size table
  2. (2)

    Comparison for the University of Pavia data: We report the experimental results on the University of Pavia data in Table 2. According to Table 2, AEFS and GAFS demonstrate the worst and the second worst performance compared to other feature selection methods, while LRLAFS shows the best performance. Compared to AEFS, the improvement of GAFS and LRLAFS is at 1.4% and 6.6% for overall accuracy, 1.2% and 7.8% for average accuracy, and 1.9% and 9.5% for Kappa coefficient. Compared to AllFeas, LRLAFS can choose discriminative features from the original University of Pavia features, which alleviates computational burden and improves the further classification performance. For SpaBS, the overall accuracy is 85.42%, the average accuracy is 83.28%, and the Kappa coefficient is 0.8051, which shows inferior performance compared to AllFeas and achieves superior performance compared to AEFS and GAFS. More detailed comparisons can be discovered in Table 2 and the classification maps for all compared methods are shown in Fig. 4.

    Table 2 Experimental comparison of different feature selection approaches on the University of Pavia dataset
    Full size table
    Fig. 4
    figure 4

    Classification maps of all competing approaches on the University of Pavia dataset. a AllFeas. b SpaBS. c AEFS. d GAFS. e LRLAFS

    Full size image
  3. (3)

    Comparison for the Salinas Scene data: Table 3 presents the experimental results on the Salinas Scene data. According to Table 3, LRLAFS exhibits superior performance (90.76% for overall accuracy, 95.47% for average accuracy, and 0.8972 for Kappa coefficient) than AllFeas and other feature selection methods, which mainly attributes to the latent representation learning embedding in the feature selection process. AllFeas and SpaBS present comparative performance and slightly outperform AEFS and GAFS, which means that SpaBS is good at choosing informative features on the Salinas Scene data. In details, the overall accuracy of SpaBS, AEFS and GAFS is 90.51%, 90.20% and 90.43%, respectively. From Table 3, more detailed comparisons can be observed. Besides, Fig. 5 shows the classification maps for all compared methods.

    Table 3 Experimental comparison of different feature selection approaches on the Salinas Scene dataset
    Full size table
    Fig. 5
    figure 5

    Classification maps of all competing approaches on the Salinas Scene dataset. a AllFeas. b SpaBS. c AEFS. d GAFS. e LRLAFS

    Full size image

5.4 Parameter sensitivity study

In LRLAFS, parameters α, β, γ and λ are utilized in the objective function, which are needed to be set in advance. Here, we study the sensitivity of these four parameters and observe how they influence the final results. These four parameters are tuned from {10− 3,10− 2,10− 1,1,101,102,103}. The experimental results of parameter sensitivity study on three HSI datasets are depicted in Fig. 6. For the Indian Pines data, the proposed LRLAFS shows superior performance with α = 10 (presented in Fig. 6a). For the University of Pavia data, the inferior result is achieved with ω = 1, which is shown in Fig. 6k. For the Salinas Scene data, the superior results is obtained with β = 0.001, which is displayed in Fig. 6f. Therefore, it is important to determine appropriate values for the four parameters to conduct feature selection.

Fig. 6
figure 6

Performance variation of LRLAFS for α (in the first column), β (in the second column), γ (in the third column) and λ (in the fourth column) on hyperspectral image datasets. a, b, c and d Indian Pines. e, f, g and h University of Pavia. i, j, k and l Salinas Scene

Full size image

6 Conclusions

In this paper, we propose a novel latent representation learning based autoencoder feature selection (LRLAFS) model for hyperspectral image (HSI) data. To select informative features from HSI data, we incorporate the latent representation learning into the basic autoencoder feature selection model, where the latent representations learnt by the hidden layer of the autoencoder and decomposed by matrix factorization from the adjacency matrix are used to steer the nonlinear feature selection. An alternative optimization algorithm is introduced to solve the optimization for LRLAFS. Experimental comparisons on three HSI datasets prove the potential of LRLAFS and LRLAFS consistently outperforms other compared methods.