1 Introduction

Hyperspectral imaging sensors provide the ability to sample a scene’s spectral properties more densely. Whereas a normal RGB imaging sensors roughly divides the observation into red, green, and blue, a hyperspectral imaging sensors can easily obtain thirty or more distinct bands across the visible spectrum. Having detailed spectral information can be very useful to remote sensing [44] and computer vision tasks ranging from object recognition and tracking [9], as RGB alone is often insufficient to identify the materials within a scene. However, due to the physical limitations of imaging sensors, the hyperspectral image (HSI) is often of low spatial resolution. This is due to the fact that hyperspectral imaging systems need a large number of exposures to simultaneously acquire many bands within a narrow spectral window. To ensure sufficient signal-to-noise ratio, long exposures are often necessary, resulting in the sacrifice of spatial resolution. Simply increasing the spatial resolution of image sensors would not be effective for hyperspectral imaging because the average amount of photons reaching the sensors would be further reduced leading to even lower signal-to-noise ratio. Consequently, the low spatial resolution hyperspectral images (LR-HSIs) are often fused with high spatial resolution multispectral images (HR-MSIs) to reconstruct high spatial resolution hyperspectral images (HR-HSIs). This procedure is referred to as HSI super-resolution or HSI-MSI fusion.

The goal of this paper is to recover a HR-HSI Z ∈ RL × N from a LR-HSI X ∈RL × n and a HR-MSI image Y ∈ Rl × N of the same scene, where L is the number of spectral bands of Z (L » l), N and n (N = W × H, n = w × h, w « W and h « H) denote pixel number in Z and X respectively. The reconstruction of Z from X and Y is an ill-posed inverse problem. For such ill-posed inverse problems, regularization is a popular tool for exploiting the prior knowledge about the unknown. Sparsity prior has been shown effective for solving hyperspectral image reconstruction [1, 2, 22, 24, 39], the target image Z can be written as [17, 23],

$$ \boldsymbol{Z}=\boldsymbol{DA}+\boldsymbol{E} $$
(1)

where D = [d1, · · ·, dK]∈\( {\mathrm{R}}_{+}^{L\times K} \) is the spectral dictionary, K(K ≥ L) is the number of atoms, A = [a1, · · ·, aN] ∈\( {\mathrm{R}}_{+}^{K\times N} \) is the sparse coefficient matrix, and E is the approximation error. Both X and Y result from linear degradations of Z,

$$ \boldsymbol{X}=\boldsymbol{ZH}+{\boldsymbol{E}}_1,\boldsymbol{Y}=\boldsymbol{PZ}+{\boldsymbol{E}}_2 $$
(2)

where H ∈ RN × n denotes the blurring and down-sampling degradation operator, P is a spectral transformation matrix, E1 and E2 denote the approximation error matrix. Many LR-HSI and HR-MSI fusion methods rely on a similar linear model of (2) [8, 24, 28, 29, 31, 35, 36, 38, 42, 46]. Combining (1) and (2) leads to

$$ \boldsymbol{X}=\boldsymbol{DAH}+{\boldsymbol{E}}_1=\boldsymbol{DB}+{\boldsymbol{E}}_1,\boldsymbol{Y}=\boldsymbol{PDA}+{\boldsymbol{E}}_2=\overline{\boldsymbol{D}}\boldsymbol{A}+{\boldsymbol{E}}_2 $$
(3)

where B = AH∈RK × n denotes the transformed sparse coefficient matrix, \( \overline{\boldsymbol{D}}=\boldsymbol{PD} \) denotes the transformed spectral dictionary. The spectral dictionary D and coefficient matrix A in (3) are unknown. For scenes satisfying the sparsity assumption, coefficient matrix A have to be sparse. It follows that D and A can be solved by sparse matrix decomposition.

Besides the spectral information, some methods [8, 30,31,32, 36] also used the spatial structure to regularize the fusion problem. Dong et al. [8] proposed a non-negative structured sparse representation (NSSR) method which exploited the clustering-based sparsity of hyperspectral images. The limitation of [8] is that the structured sparse representation is only used to estimate the coefficient matrix, not for the spectral dictionary learning.

In this paper, we present a novel hyperspectral image super-resolution method. The main contributions of our work are as follows.

(1) A non-negative clustering-based sparse representation (NNCSR) model is proposed. The reconstruction of HR hyperspectral image is formulated as a joint estima-tion of the hyperspectral dictionary and the sparse coefficients based on the spatial-spectral sparsity of the hyperspectral image. To improve the accuracy, both spectral dictionary and sparse coefficients exploit the clustering-based sparsity of hyperspectral images.

(2) We present an experimental valuation, where the proposed method is compared against several state-of-the-art approaches. Results of these experiments show our method outperforms these state-of-the-art approaches in objective quality metrics and visual performance.

2 Related work

Reconstructing a HR-HSI from a LR-HSI and HR-MSI, although challenging, is a crucial inverse problem that has been addressed in various scenarios [18,19,20,21]. As this inverse problem is generally ill-posed, introducing prior distributions to regularize the target image has been widely explored and some methods use Bayesian inference to regularize the problem [2, 12, 36, 37]. Based on prior knowledge and on the observation model, these Bayesian fusion methods build the posterior distribution, which is the Bayesian inference engine. The work [12, 36] computed the maximum a posteriori (MAP) estimator in an optimization framework to solve the fusion problem. The work [37] formed the likelihoods of the observations and developed a fast Sylvester based solver. Akhtar et al. [2] proposed a method using non-parametric Bayesian dictionary learning.

Many fusion methods are based on matrix factorization (MF) [1, 8, 22, 24, 26, 30,31,32, 36, 38, 39, 42] or nonnegative matrix under- approximation (NMU) [4]. Assuming that the HR-HSI only contains a small number of pure spectral signatures, these approaches first unfold the HR-HSI as a matrix and then factor it into a basis matrix and a coefficient matrix. The work [22] firstly introduced MF into fusion by factorizing the HSI into a dictionary of basis vectors and a set of sparse coefficients. The work [39] proposed a non-negative sparse framework to integrate LR-HSI and RGB data into a HR hyperspectral set of data. Akhtar et al. [1] exploited signal sparsity, non-negativity and the spatial structure in the scene. A coupled non-negative matrix factorization (CNMF) method [42] alternately applied NMF unmixing to LR hyperspectral and HR multispectral data. Since non-negative matrix factorization is not always unique [25, 26], the results of [42] are often not satisfactory. A similar fusion and unmixing framework was introduced in [24]. The common point of [24, 42] is to learn the spectral bases from the LR-HSI and sparse coefficients from the HR-MSI alternatively instead of using both LR-HSI and HR-MSI jointly. To fully exploit the data information, Wei et al. [38] used an optimization formulation similar to [24, 42], but both LR-HSI and HR-MSI images contributed to the estimation of spectral bases and sparse coefficients.

Recently, the work [6, 7, 27, 40] used tensor factorization. Different from MF based methods, the hyperspectral image was approximated by a core tensor multiplied by dictionaries of the width, height, and spectral modes. Dian et al. [7] first proposed a nonlocal sparse tensor factorization for HSI-MSI fusion, where they approximate the HR-HSI by dictionaries of three modes and a sparse core tensor. Li et al. [27] solved the fusion problem by simultaneously conducting sparse Tucker decomposition on the HR-MSI and LR-HSI, where the core tensor and three dictionaries are alternatively updated until convergence. Xu et al. [40] propose a non-local tensor sparse representation model, and the main difference between [7, 40] is that they use different tensor sparse representation model.

Besides the spectral information, some methods [6, 8, 30,31,32, 36] also used the spatial structure to regularize the fusion problem. Veganzones et al. [32] exploited the low rank of the hyperspectral images, while the work [30, 36] exploited the low intrinsic dimensionality of hyperspectral images. Dong et al. [8] proposed a non-negative structured sparse representation (NSSR) method. They exploited the clustering-based sparsity of hyperspectral images. A similar work was proposed in [31]. The limitation of [8, 31] is that the structured sparse representation is only used to estimate the coefficient matrix, not for the spectral dictionary learning. Dian et al. [6] proposed a subspace based low tensor multi-rank (LTMR) regularization method for HSI super-resolution. The LTMR mainly exploited two prior information of HR-HSI: high correlations among spectral bands and non-local self-similarities. Their work achieved state-of-art performance.

Recently, considerable improvements in performance have been achieved by exploiting learning methods [15, 16]. Spectral information and spatial structure can be learned from the images. To fully exploit the data information, our work exploits the clustering-based sparsity of the high spatial resolution hyperspectral images for both the coefficient matrix estimation and the spectral dictionary learning.

3 Hyperspectral image super-resolution

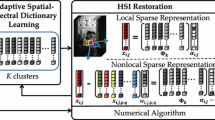
In this section, we explain the proposed hyperspectral image super-resolution method. The flowchart of the proposed method is illustrated in Fig. 1. The reconstruction of HR-HSI Z is formulated as a joint estimation of the hyperspectral dictionary D and the sparse coefficient matrix A based on the spatial-spectral sparsity of the hyperspectral image. First, we learn the hyperspectral dictionary D from the LR-HSI X. Once the spectral dictionary D is estimated, we estimate the sparse coefficient matrix A from LR-HSI X and the corresponding HR-MSI Y. To improve the accuracy, both spectral dictionary learning and sparse coefficients estimation are imposed a structural sparsity constraint, which exploits the clustering-based sparsity of hyperspectral images - namely reconstructed spectral pixels should be similar to those learned centroids. At last, we reconstruct the HR-HSI Z with the hyperspectral dictionary D and the sparse coefficient matrix A.

Fig. 1
figure 1

Flowchart of the proposed hyperspectral image super-resolution method

Full size image

3.1 NNCSR model

For spectral dictionary D, it is reasonable to assume that the LR-HSI X contains the same spectral dictionary as the HR-HSI Z, but due to the spectral degradation P, only l spectral channels cannot contain sufficient information to reconstruct L (L » l) spectral channels [24], thus spectral dictionary D is estimated by solving the following sparse nonnegative matrix decomposition problem

$$ \left(\boldsymbol{D},\boldsymbol{B}\right)=\underset{\boldsymbol{D},\boldsymbol{B}}{argmin}\frac{1}{2}{\left\Vert \boldsymbol{X}-\boldsymbol{DB}\right\Vert}_2^2+{\lambda}_1{\left\Vert \boldsymbol{B}\right\Vert}_1,s.t.{\mathbf{b}}_i\ge 0,{d}_k\ge 0 $$
(4)

where D = [d1, · · ·, dK]∈\( {\mathrm{R}}_{+}^{L\times K} \) is the spectral dictionary, K(K ≥ L) is the number of atoms, B = [b1, · · ·, bN] ∈\( {\mathrm{R}}_{+}^{K\times N} \) is the sparse coefficient matrix. In this formulation, \( \frac{1}{2}{\left\Vert \boldsymbol{X}-\boldsymbol{DB}\right\Vert}_2^2\kern0.5em \)is a term modeling data fidelity, ‖B‖1 is the regularization prior on the image to recover, and λ1 is a parameter controlling the trade-off between these two terms.

Once the spectral dictionary D is estimated, the coefficient matrix A can be estimated from both the HR-MSI image Y and the LR-HSI X by solving the following sparse nonnegative matrix decomposition problem

$$ \boldsymbol{A}=\underset{\boldsymbol{A}}{argmin}{\left\Vert \boldsymbol{Y}-\overline{\boldsymbol{D}}\boldsymbol{A}\right\Vert}_2^2+\tau {\left\Vert \boldsymbol{X}-\boldsymbol{DAH}\right\Vert}_2^2+{\eta}_2{\left\Vert \boldsymbol{A}\right\Vert}_1,\mathrm{s}.\mathrm{t}.{\boldsymbol{\alpha}}_i\ge 0 $$
(5)

where A = [a1, · · ·, aN] ∈\( {\mathrm{R}}_{+}^{K\times N} \) is the sparse coefficient matrix. In this formulation, \( {\left\Vert \boldsymbol{Y}-\overline{\boldsymbol{D}}\boldsymbol{A}\right\Vert}_2^2\kern0.5em \)and \( {\left\Vert \boldsymbol{X}-\boldsymbol{DAH}\right\Vert}_2^2 \) are two terms of modeling data fidelity, ‖A‖1 is the regularization prior on the image to recover, and τ, η2 are two parameters controlling the trade-off between these terms. A typical natural scene usually contains a collection of similar patches from all over the image. These non-local similar patches can be exploited to enhance the performance of image restoration tasks [10, 11]. But the l1-norm nonnegative sparse model of (4) and (5) cannot exploit the spatial correlations among local and nonlocal similar neighbors. To address this issue, we propose the following non-negative clustering-based sparse representation (NNCSR) model,

$$ \left(\boldsymbol{D},\boldsymbol{B},\boldsymbol{U}\right)=\underset{\boldsymbol{D},\boldsymbol{B},\boldsymbol{U}}{argmin}\frac{1}{2}{\left\Vert \boldsymbol{X}-\boldsymbol{DB}\right\Vert}_2^2+{\lambda}_1{\left\Vert \boldsymbol{B}\right\Vert}_1+{\lambda}_2{\sum}_{q=1}^Q\sum \limits_{i\in {S}_q}{\left\Vert {\boldsymbol{D}\boldsymbol{\alpha}}_i-{\boldsymbol{\mu}}_q\right\Vert}_2^2,s.t.{\mathbf{b}}_i\ge 0,{\mathbf{d}}_k\ge 0 $$
(6)
$$ \left(\boldsymbol{A},\boldsymbol{U}\right)=\underset{\boldsymbol{A},\boldsymbol{U}}{argmin}{\left\Vert \boldsymbol{Y}-\overline{\boldsymbol{D}}\boldsymbol{A}\right\Vert}_2^2+\tau {\left\Vert \boldsymbol{X}-\boldsymbol{DAH}\right\Vert}_2^2+{\eta}_1{\sum}_{q=1}^Q\sum \limits_{i\in {S}_q}{\left\Vert {\boldsymbol{D}\boldsymbol{\alpha}}_i-{\boldsymbol{\mu}}_q\right\Vert}_2^2+{\eta}_2{\left\Vert \boldsymbol{A}\right\Vert}_1,\mathrm{s}.\mathrm{t}.{\boldsymbol{\alpha}}_i\ge 0 $$
(7)

where μq denotes the centroid of the q-th cluster\( {\boldsymbol{S}}_q=\left\{i\left|{\left\Vert \overline{{\boldsymbol{y}}_i}-\overline{{\boldsymbol{y}}_q}\right\Vert}_2^2<t\right.\right\},\overline{{\boldsymbol{y}}_i} \)and \( \overline{{\boldsymbol{y}}_q} \)denote the image patches of Y centered at positions i and q respectively. Recently, clustering learning has been widely used [13, 14, 43]. The efficient k-Nearest Neighbour (k-NN) clustering method is used to group similar spectral pixels for each spectral pixel [18]. Due to the structural similarity between Z and Y, we perform the k-NN clustering on the HR-MSI image patches to search for similar neighbors of \( \overline{{\boldsymbol{y}}_q} \). The vector μq is computed as

$$ {\boldsymbol{\mu}}_q=\sum \limits_{i\in {\boldsymbol{S}}_q}{w}_i\left({\boldsymbol{Da}}_i\right) $$
(8)

where \( {w}_i=\frac{1}{c}\mathit{\exp}\left(-{\left\Vert \overline{{\boldsymbol{y}}_i}-\overline{{\boldsymbol{y}}_q}\right\Vert}_2^2/h\right) \) is the weighting coefficients. The proposed NNCSR model exploits the structural prior that the reconstructed spectral pixels should be similar to those learned centroids.

In practice, both D and ai for each pixel zi of Z are unknown, μq cannot be directly computed via (8). This difficulty can be overcome by estimating μq from the current estimates of D and ai. We estimate D and ai alternatively. For notation convenience, Eq. (6) and (7) can be rewritten as

$$ \left(\boldsymbol{D},\boldsymbol{B},\boldsymbol{U}\right)=\underset{\boldsymbol{D},\boldsymbol{B},\boldsymbol{U}}{argmin\frac{1}{2}}{\left\Vert \boldsymbol{X}-\boldsymbol{DB}\right\Vert}_2^2+{\lambda}_1{\left\Vert \boldsymbol{B}\right\Vert}_1+{\lambda}_2{\left\Vert \boldsymbol{DA}-\boldsymbol{U}\right\Vert}_2^2,s.t.{\mathbf{b}}_i\ge 0,{\mathbf{d}}_k\ge 0 $$
(9)
$$ \left(\boldsymbol{A},\boldsymbol{U}\right)=\underset{\boldsymbol{A},\boldsymbol{U}}{argmin}{\left\Vert \boldsymbol{Y}-\overline{\boldsymbol{D}}\boldsymbol{A}\right\Vert}_2^2+\tau {\left\Vert \boldsymbol{X}-\boldsymbol{DAH}\right\Vert}_2^2+{\eta}_1{\left\Vert \boldsymbol{DA}-\boldsymbol{U}\right\Vert}_2^2+{\eta}_2{\left\Vert \boldsymbol{A}\right\Vert}_1,\mathrm{s}.\mathrm{t}.{\boldsymbol{\alpha}}_i\ge 0 $$
(10)

where U = [μ1, …, μq, …, μQ].

3.2 Spectral dictionary learning

First, the spectral dictionary D can be learned from X by solving (4),i.e., the first two terms of (9). As both D and B are constrained to be nonnegative, existing dictionary learning algorithms and online dictionary learning cannot be used. In [39], the alternating direction method of multipliers (ADMM) is adopted to convert a constrained dictionary learning problem into an unconstrained version and solved the unconstrained dictionary learning problem via alternative optimization. For a fixed D, the subproblem with respect to B becomes

$$ \boldsymbol{B}=\underset{\boldsymbol{B}}{argmin}\frac{1}{2}{\left\Vert \boldsymbol{X}-\boldsymbol{DB}\right\Vert}_2^2+{\lambda}_1{\left\Vert \boldsymbol{B}\right\Vert}_1,s.t.{\mathbf{b}}_i\ge 0 $$
(11)

which is convex and can be efficiently solved by any convex optimization solver. For fast convergence rate, we use ADMM technique to solve (11). We reformulate (11) into

$$ \boldsymbol{B}=\underset{\boldsymbol{B}}{argmin}\frac{1}{2}{\left\Vert \boldsymbol{X}-\boldsymbol{DS}\right\Vert}_2^2+{\lambda}_1{\left\Vert \boldsymbol{B}\right\Vert}_1,s.t.\mathbf{B}=\mathbf{S},{\mathbf{b}}_i\ge 0 $$
(12)

Applying ADMM [3], there is the following augmented Lagrangian function.

Algorithm 1

Spectral dictionary learning

figure a
$$ {\boldsymbol{L}}_{\mu}\left(\boldsymbol{B},\boldsymbol{S},\boldsymbol{R}\right)=\frac{1}{2}{\left\Vert \boldsymbol{X}-\boldsymbol{DS}\right\Vert}_2^2+{\lambda}_1{\left\Vert \boldsymbol{B}\right\Vert}_1,+\mu {\left\Vert \boldsymbol{S}-\boldsymbol{B}+\frac{\boldsymbol{R}}{2\mu}\right\Vert}_2^2,s.t.\mathbf{B}=\mathbf{S},{\mathbf{b}}_i\ge 0 $$
(13)

where R is the Lagrangian multiplier (μ > 0). Then, solving (12) consists of the following alternative iterations,

$$ {\displaystyle \begin{array}{c}{\boldsymbol{S}}^{\left(t+1\right)}=\underset{\boldsymbol{S}}{argmin}{L}_{\mu}\left({\boldsymbol{B}}^{(t)},\boldsymbol{S},{\boldsymbol{R}}^{(t)}\right)\\ {}{\boldsymbol{B}}^{\left(t+1\right)}=\underset{\boldsymbol{B}}{argmin}{L}_{\mu}\left(\boldsymbol{B},{\boldsymbol{S}}^{\left(t+1\right)},{\boldsymbol{R}}^{(t)}\right),s.t.{\mathbf{b}}_i\ge 0\end{array}} $$
(14)

where t is the iteration number and Lagrangian multiplier R is updated by

$$ {\boldsymbol{R}}^{\left(t+1\right)}={\boldsymbol{R}}^{(t)}+\mu \left({\boldsymbol{S}}^{\left(t+1\right)}-{\boldsymbol{B}}^{\left(t+1\right)}\right) $$
(15)

The sub-problems in (14) have closed-form solutions,

$$ {\displaystyle \begin{array}{c}{\boldsymbol{S}}^{\left(t+1\right)}={\left({\boldsymbol{D}}^{\mathrm{T}}\boldsymbol{D}+\mathbf{2}\mu \boldsymbol{I}\right)}^{-1}\left({\boldsymbol{D}}^{\mathrm{T}}\boldsymbol{X}+\mathbf{2}\mu \left({\boldsymbol{B}}^{(t)}-\frac{{\boldsymbol{R}}^{(t)}}{2\mu}\right)\right)\\ {}{\boldsymbol{B}}^{\left(t+1\right)}={\left[\boldsymbol{Soft}\left({\boldsymbol{S}}^{\left(t+1\right)}+\frac{{\boldsymbol{R}}^{(t)}}{2\mu },\frac{\lambda_1}{2\mu}\right)\right]}_{+}\end{array}} $$
(16)

where Soft(.) denotes a soft-shrinkage operator and [x]+ = max{x, 0}.For a fixed B, spectral dictionary D can be updated by solving

$$ \boldsymbol{D}=\underset{\boldsymbol{D}}{argmin}{\left\Vert \boldsymbol{X}-\boldsymbol{DB}\right\Vert}_2^2,s.t.{\mathbf{d}}_k\ge 0 $$
(17)

Eq. (17) can be solved using block coordinate descent [8] or be solved analytically

$$ \boldsymbol{D}={\boldsymbol{XB}}^T{\left({\boldsymbol{BB}}^T\right)}^{-1} $$
(18)

The algorithm for the initial spectral dictionary learning is summarized in Algorithm 1. Once the initial spectral dictionary D is estimated, sparse coefficient matrix A can be estimated by solving (10). We will elaborate on the sparse coefficient estimation in the next section. When the sparse coefficient matrix A is estimated, the last term of (9) can be solved analytically,

$$ \boldsymbol{D}={\boldsymbol{UA}}^T{\left({\boldsymbol{AA}}^T\right)}^{-1} $$
(19)

3.3 Sparse coefficient estimation

With respect to the learned spectral dictionary D, we estimate the sparse coefficient matrix A by solving (10). Eq. (10) is convex and can be efficiently solved by any convex optimization solver. For fast convergence, we use ADMM technique to solve (10), and obtain the following Lagrangian function:

$$ {\boldsymbol{L}}_{\mu}\left(\boldsymbol{A},\boldsymbol{Z},\boldsymbol{S},{\boldsymbol{R}}_{\mathbf{1}},{\boldsymbol{R}}_2\right)={\left\Vert \left[\begin{array}{c}\boldsymbol{Y}\\ {}\tau \boldsymbol{X}\\ {}{\eta}_1\boldsymbol{DS}\end{array}\right]-\left[\begin{array}{c}\overline{\boldsymbol{D}}\boldsymbol{S}\\ {}\tau \boldsymbol{ZH}\\ {}{\eta}_1\boldsymbol{U}\end{array}\right]\right\Vert}_2^2+{\eta}_2{\left\Vert \boldsymbol{A}\right\Vert}_1+\mu {\left\Vert \boldsymbol{DS}-\boldsymbol{Z}+\frac{{\boldsymbol{R}}_1}{2\mu}\right\Vert}_2^2+\mu {\left\Vert \boldsymbol{S}-\boldsymbol{A}+\frac{{\boldsymbol{R}}_2}{2\mu}\right\Vert}_2^2,\mathrm{s}.\mathrm{t}.{\boldsymbol{a}}_i\ge 0 $$
(20)

where R1, R2 are Lagrangian multipliers (μ > 0). Minimizing the augmented Lagrangian function leads to the following iterations:

$$ {\displaystyle \begin{array}{c}{A}^{\left(t+1\right)}=\underset{A}{\mathrm{argmin}}{L}_{\mu}\left(A,{Z}^{(t)},{S}^{(t)},{R_1}^{(t)},{R_2}^{(t)}\right),\\ {}{Z}^{\left(t+1\right)}=\underset{Z}{\mathrm{argmin}}{L}_{\mu}\left({A}^{\left(t+1\right)},Z,{S}^{(t)},{R_1}^{(t)},{R_2}^{(t)}\right),\\ {}{S}^{\left(t+1\right)}=\underset{S}{\mathrm{argmin}}{L}_{\mu}\left({A}^{\left(t+1\right)},{Z}^{\left(t+1\right)},S,{R_1}^{(t)},{R_2}^{(t)}\right),\end{array}} $$
(21)

where the Lagrangian multipliers are updated by

$$ {{\boldsymbol{R}}_1}^{\left(t+1\right)}={{\boldsymbol{R}}_1}^{(t)}+\mu \left({\boldsymbol{DS}}^{\left(t+1\right)}-{\boldsymbol{Z}}^{\left(t+1\right)}\right),{{\boldsymbol{R}}_2}^{\left(t+1\right)}={{\boldsymbol{R}}_2}^{(t)}+\mu \left({\boldsymbol{S}}^{\left(t+1\right)}-{\boldsymbol{A}}^{\left(t+1\right)}\right) $$
(22)

All sub-problems in (20) can have closed-form solutions,

$$ {\displaystyle \begin{array}{c}S={\left[{\overline{D}}^T\overline{D}+\left({\eta}_1+\mu \right){D}^TD+\mu I\right]}^{-1}\left[{\overline{D}}^TY+{\eta}_1{D}^TU+{\mu D}^T\left({Z}^{(t)}-\frac{{R_1}^{(t)}}{2\mu}\right)+\mu \left({A}^{(t)}-\frac{{R_1}^{(t)}}{2\mu}\right)\right],\\ {}Z=\left[\tau X{H}^T+\mu \left(D{S}^{(t)}+\frac{R_1}{2\mu}\right)\right]{\left(\tau H{H}^T+\mu I\right)}^{-1},\kern0.5em A={\left[ Soft\left({S}^{(t)}-\frac{{R_2}^{(t)}}{2\mu },\frac{\eta_2}{2\mu}\right)\right]}_{+}\end{array}} $$
(23)

As the matrix to be inverted in the equation of updating Z is large, we use conjugate gradient algorithm to compute the matrix inverse. The overall algorithm for reconstruction Z is summarized in Algorithm 2.

4 Experiments and discussion

4.1 Experimental datasets

To verify the performance of our proposed method, we have test the algorithm on two different public datasets of hyperspectral images. The first dataset is Columbia computer vision laboratory (CAVE) [41]. The CAVE dataset consists of 32 indoor HSIs. The images have 31 spectral bands, and each band has a size of 512 × 512. We take the hyperspectral images from the dataset as ground-truth images and use these images to simulate LR-HSIs and HR-MSI images. As in [8, 22], the original HR-HSIs Z are downsampled by averaging over disjoint 32 × 32 blocks to simulate the LR-HSIs X. Similar to [8, 42], HR RGB images Y are generated by downsampling the hyperspectral images Z along the spectral dimension using the spectral transform matrix derived from the response of a Nikon D700 camera.

Algorithm 2

Hyperspectral image super-resolution with NNCSR model.

figure b

The second dataset is Pavia University [5], acquired by the reflective optics system imaging spectrometer optical sensor over the area of Pavia University. The Pavia University have the 115 spectral bands and 610 × 340 spectral pixels. As in [6, 7], by removing the bands of low SNR, we reduce the HSI as 93 bands and select the up-left 256 × 256 × 93-pixel-size image as the ground truth. To simulate the LR-HSI, we firstly filter each band of HR-HSI by a 7 × 7 Gaussian blur (standard deviation 2) and then downsample every four pixels in two spatial modes. The HR-MSI of four bands is simulated by using IKONOS-like reflectance spectral response filter [36].

4.2 Compared approaches

We compare the proposed NNCSR method with Bayesian sparse representation (BSR) [36], MF [22], CNMF [42], NSSR [8], CSTF [27] and low tensor multi-rank (LTMR) [6], which represent the state-of-the-arts of modern hyperspectral image super-resolution method. Among the compared approaches, BSR is based on Bayesian inference, CSTF and LTMR are based on tensor factorization, MF, CNMF and NSSR are based on matrix factorization.

4.3 Quantitative metrics

Five indexes are utilized to measure the quality of the fusion results.

The first index is the peak signal-to-noise ratio (PSNR) for HSI defined as,

$$ \kern0.5em PSNR\left(\boldsymbol{Z},\overset{\sim }{\boldsymbol{Z}}\right)=\frac{1}{L}{\sum}_{i=1}^L PSNR\left(\ {\boldsymbol{Z}}_{\boldsymbol{i}},{\overset{\sim }{\boldsymbol{Z}}}_i\ \right) $$
(24)

where Z ∈ RL × N and \( \overset{\sim }{\boldsymbol{Z}}\in {R}^{L\times N} \) are ground-truth and reconstructed HSIs respectively, \( {\boldsymbol{Z}}_{\boldsymbol{i}}\ \mathrm{and}\ {\overset{\sim }{\boldsymbol{Z}}}_i \) represent i-th band of Z ∈ RL × N and \( \overset{\sim }{\boldsymbol{Z}}\in {R}^{L\times N} \) . The higher the PSNR, the better the quality of the reconstructed image.

The second index is the root mean square error (RMSE) defined as

$$ \mathrm{RMSE}\left(\boldsymbol{Z},\overset{\sim }{\boldsymbol{Z}}\right)=\sqrt{\frac{{\left\Vert \boldsymbol{Z}-\overset{\sim }{\boldsymbol{Z}}\right\Vert}_F^2}{LN}} $$
(25)

where Z ∈ RL × N and \( \overset{\sim }{\boldsymbol{Z}}\in {R}^{L\times N} \) are scaled to the range [0, 255]. RMSE is a measure of the estimation error. The smaller the RMSE, the better the quality of the reconstructed image.

The third index is the spectral angle mapper (SAM) [36, 45], which is defined as the averaged angle between the estimated pixel \( {\overset{\sim }{\boldsymbol{z}}}_j \) and the ground truth pixel zj, i.e.

$$ \mathrm{SAM}\left(\boldsymbol{Z},\overset{\sim }{\boldsymbol{Z}}\right)=\frac{1}{LN}{\sum}_{j=1}^{LN} arcos\frac{{\overset{\sim }{\boldsymbol{z}}}_j^T{\boldsymbol{z}}_j\ }{{\left\Vert {\overset{\sim }{\boldsymbol{z}}}_j\right\Vert}_2{\left\Vert {\boldsymbol{z}}_j\ \right\Vert}_2} $$
(26)

SAM is given in degrees. The smaller SAM, the less spectral distortions.

The fourth index is the relative dimensionless global error in synthesis (ERGAS) [33] defined as

$$ \mathrm{ERGAS}\left(\boldsymbol{Z},\overset{\sim }{\boldsymbol{Z}}\right)=\frac{100}{d}\sqrt{\ \frac{1}{L}{\sum}_{i=1}^L\frac{MSE\left(\ {\boldsymbol{Z}}_{\boldsymbol{i}},{\overset{\sim }{\boldsymbol{Z}}}_i\ \right)}{\mu_{{\overset{\sim }{\boldsymbol{Z}}}_i}^2}} $$
(27)

where d is the spatial downsampling factor, and \( {\mu}_{{\overset{\sim }{\boldsymbol{Z}}}_i} \) is the mean value of\( \kern0.5em {\overset{\sim }{\boldsymbol{Z}}}_i \). ERGAS reflects the overall quality of the reconstruction image. The smaller ERGAS, the better quality of the reconstructed results.

The fifth index is the universal image quality index (UIQI) [34], which is calculated on a sliding window of size 32 × 32 and averaged on all windows. The UIQI for two windows a and b is given by

$$ \mathrm{UIQI}\left(\mathbf{a},\mathbf{b}\right)=\frac{4{\sigma}_{\mathbf{a}\mathbf{b}}^2}{\sigma_{\mathbf{a}}^2+{\sigma}_{\mathbf{b}}^2}\frac{\mu_{\mathbf{a}}{\mu}_{\mathbf{b}}}{\mu_{\mathbf{a}}^2+{\mu}_{\mathbf{b}}^2} $$
(28)

where σab is the sample covariance between a and b, and σa and μa denote the standard deviation and mean value of a, respectively.

4.4 Parameters discussion

In our method, four key parameters: the number of atoms K, the parameter k of k-NN, the regularization parameters η1 and η2 need to be discussed.

To discuss the effects of these parameters, we plot the PSNR curves of the fused results of Balloons (an HSI in the CAVE dataset) varying from these parameters in Fig. 2. As we can see from Fig. 2 (a), the proposed method performs best when the number of atoms is in the range of 75 ∼ 125 and is insensitive to the variation in the values of K in this range. Therefore, 75 atoms are enough to preserve the spectral information. In our implementation, we set K = 75. From Fig. 2 (b), we can see the PSNR rises as k changed from 1 to 60, and then it keeps relatively stable as k increases further. Therefore we can select k = 60. From Fig. 2(c), we can see that the performance of the proposed method rises as η1 varies from 0.01 to 0.025, and then it declines as η1 grows further. The PSNR for Balloons rises as η2 varies from 3*10−5 to 8*10−5, and then it declines as η2 is greater than 8*10−5. So we set η1 = 0.025 and η2 = 8*10−5. Similar observations can be obtained for other test images.

Fig. 2
figure 2

The PSNR as functions of parameters K, k, η1 and η2, respectively. (a) The atoms K, (b) The parameter k of k-NN, (c) The parameter η1, (d) The parameter η2

Full size image

4.5 Experimental results

Table 1 reports the average quality metrics of competing methods on the CAVE dataset. We highlight the best results in bold. For fair comparison, the results of BSR [36], MF [22], CNMF [42] and NSSR [8] are directly obtained from [8]. From Table 1, we can see that our NNCSR method performs consistently better than other testing methods according to these quality metrics, which indicates that HR-HSIs recovered by our method have better spatial and spectral qualities in CAVE dataset. For example, the PSNR of our method is greater than that of the state-of-the-art CSTF method by 1.12 dB, and the SAM is reduced by 0.22 degrees compared with NSSR. The improvement mainly comes from one aspect. Both NNCSR and NSSR exploit the clustering-based sparsity of hyperspectral images. The main difference is that NNCSR exploits the clustering-based sparsity for both sparse coefficient estimation and dictionary learning, while the NSSR only for sparse coefficient estimation, not for dictionary learning. The CSTF does not exploit the clustering-based sparsity. For visual comparison, the recovered HR-HSIs, corresponding error images of the competing approaches at band 16 and 26 for Oil_Painting (an HSI in CAVE dataset) are shown in Fig. 3. A representative region of each reconstructed image is magnified. As can be seen from the magnified images and error images, the HR-HSI reconstructed by NNCSR has fewer artifacts than that produced by NSSR and CSTF.

Table 1 The average results of the competing methods on the CAVE dataset
Full size table
Fig. 3
figure 3

Reconstructed images and corresponding error images of Oil-Painting from CAVE dataset [41] at band 16 and 26. The first two rows show the reconstructed images. The next two rows show the error images. (a) Ground truth, (b) NNCSR, (c) NSSR [8], (d) CSTF [27]

Full size image

The quality metrics of the competing approaches on the Pavia University are shown in Table 2. For fair comparison, the results of LTMR [6] are directly obtained from its original paper. Our NNCSR method has obvious advantages over CSTF in terms of all quality indexes. Meanwhile, the LTMR and NSSR delivers comparable performance to the NNCSR. Figure 4 shows the reconstructed images and error images at band 30 of the competing approaches for the Pavia University. We can see that all testing approaches can reconstruct the spatial structures of the HR-HSIs. As we can see from the error images, the HR-HSIs produced by NNCSR and NSSR have fewer errors than that produced by CSTF.

Table 2 The results of the competing methods on the Pavia University dataset
Full size table
Fig. 4
figure 4

Reconstructed images and corresponding error images of the competing approaches for the Pavia University at 30-th band. The first row shows the reconstructed images. The second row shows the error images. (a) Ground truth; (b) NNCSR; (c)NSSR [8]; (d)CSTF [27]

Full size image

4.6 Computation efficiency

In algorithm 2, the computational complexity mainly consists of three parts: 1) the initial spectral dictionary learning, 2) k-NN nearest neighbor searching each patch within a window of size h × h, 3) the sparse coding. The complexity of solving the initial dictionary is O(num1T1(K2n + K3 + KLn)) in algorithm 1. The complexity of computing the k-NN per patch isO(Nk1h2). The complexity of updating S is the same as that of D, i.e. O(K2L + KN2 + K3 + KLN). The complexity of updating Z and A is\( O\left( LN\sqrt{N} logN\right) \)and O(N) respectively. The propose algorithm is implemented with Matlab R2016a on an Intel(R) Core(TM) i7-6700T CPU @2.80GHz 2.81GHz. A running time comparison between the proposed method and other competing methods on a 512 × 512 × 31 test image is shown in Table 3. From Table 3, it can be seen that the proposed NNCSR method is quicker than CSTF [27]. And it is slightly slower than NSSR [8], this is because NNCSR exploits the clustering-based sparsity prior for both dictionary learning and sparse codes estimation, while NSSR [8] exploits the clustering-based sparsity prior only for sparse codes estimation.

Table 3 Average run time (seconds) of different methods on a test image of size 512 × 512 × 31
Full size table

5 Conclusions

A non-negative sparse representation model for hyperspectral image super-resolution is proposed. The hyperspectral dictionary is learned from the LR hyperspectral image. The sparse codes with respect to the learned dictionary are estimated from LR hyperspectral image and the corresponding HR multispectral image. To improve the accuracy, both spectral dictionary learning and sparse coefficients estimation exploit the clustering-based sparsity of the hyperspectral image. Experiments show that the proposed method outperforms several state-of-the-art methods in objective quality metrics and visual performance.