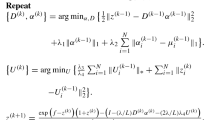A mixed model with multi-fidelity terms and nonlocal low rank regularization for natural image noise removal

Abstract

Reconstructing an original image from its corrupted observation is an important and fundamental problem in many image processing applications. Generally, the L₁-norm or L₂-norm combined with a regularization term (the total variation (TV), total generalized variation (TGV) or nuclear norm) is used to fit the impulse noise and Gaussian noise, respectively. However, these methods can only be used to remove a single type of noise from images, and traditional regularization terms often have difficulties in capturing some important prior knowledge of images, such as nonlocal self-similarity, low rank and sparsity. To overcome the above issues, we propose a mixed noise removal model with L₁-L₂ fidelity terms and a popular nonlocal low-rank regularization term, which has been shown to have more effective image denoising performance than traditional regularization methods. To solve this model, the split Bregman iteration method (SBIM) is adopted to decompose the difficult minimization optimization problem into four simple subproblems. Extensive experiments on natural images demonstrate that the effectiveness of the proposed method is better than that of other state-of-the-art methods.

1 Introduction

Reconstructing a true image from its poor-quality observation is one of the most important issues in image processing applications [5, 37, 38, 41]. Generally, we encounter two types of noise during the image acquisition process: impulse noise (IN) and additive white Gaussian noise (AWGN). IN is generally produced due to transmission errors and damaged pixels in camera sensors, and AWGN is generally produced during the image acquisition itself [4]. Many methods have been developed for removing either AWGN or IN. However, a mixture of IN and AWGN is normally encountered in real-life applications, which makes image denoising a challenging problem.

Formally, the aim of the denoising problem is to solve the inverse problem

$$ Au = f $$

(1)

Here, A is an identity operator or blurring operator, and f is the known data (observed image) from the sensors, which may be of poor quality. u : Ω ⊂ R^d → R denotes the unknown object (uncorrupted image).

Assume that u is an instance of a random variable U itself, and the corrupted image follows the conditional probability density p(f;u) = p(f|U = u) = p(f|u). Given f, we can obtain the posteriori probability density for u based on the Bayesian formula $p(u|f) = \frac {{p(f|u)p(u)}}{{p(f)}}$.

To resolve u when it is polluted by Gaussian noise only, we can rewrite (1) as follows: $Au + \varepsilon = f,\begin {array}{*{20}{c}} \end {array}where\begin {array}{*{20}{c}} \end {array}\varepsilon \sim N(0,{\sigma ^{2}})$. Therefore, we can effectively remove the Gaussian noise by solving the optimization problem in (2), where we dropped every term that is independent of u.

$$ \hat u = \mathop {\arg \min }\limits_{u \in {L^{1}}\left( {\varOmega} \right)} \left\{ {\frac{1}{{2{\sigma^{2}}}}\left\| {Au - f} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2} - \log \left( {p\left( u \right)} \right)} \right\} $$

(2)

Because Ω in (2) is bounded with a finite measure and ${L^{\infty } }\left ({\varOmega } \right ) \subset {L^{2}}\left ({\varOmega } \right ) \subset {L^{1}}\left ({\varOmega } \right )$, the L₂-norm can fit the Gaussian noise [55]. In the last term $- \log \left ({p\left (u \right )} \right )$, we can add some prior information about images u (e.g., piecewise smoothness [46] and the sparsity prior [14, 15, 35, 40, 41, 62, 64, 65]). We often choose the Gibbs function [25] as the prior, i.e., $p\left (u \right ) \sim {e^{- \lambda R\left (u \right )}}$. Here, $R:{L^{1}}\left ({\varOmega } \right ) \to [0,\infty ]$ is a convex energy function. Therefore, we can rewrite (2) as follows:

$$ \hat u = \mathop {\arg \min }\limits_{u \in {L^{1}}\left( {\varOmega} \right)} \left\{ {\left\| {Au - f} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2} + \lambda R\left( u \right)} \right\} $$

(3)

Here, $R\left (u \right )$ is a regularization term.

For images polluted by IN only, which may be random-valued IN and salt-and pepper noise in real-life applications, we can replace the L₂ fidelity term $\left \| {Au - f} \right \|_{{L^{2}}\left ({\varOmega } \right )}^{2}$ with L₁ fidelity, which performs well in removing outliers and IN. Then, we can obtain the following optimization problem for IN removal:

$$ \hat u = \mathop {\arg \min }\limits_{u \in {L^{1}}\left( {\varOmega} \right)} \left\{ {{{\left\| {Au - f} \right\|}_{{L^{1}}\left( {\varOmega} \right)}} + \lambda R\left( u \right)} \right\} $$

(4)

The aforementioned approaches mainly concentrate on AWGN or IN denoising. However, a mixture of AWGN and IN is frequently encountered in practice, which makes the problem of image noise reduction considerably more challenging due to the very different distributions of the two types of noises. Based on the above derivations for the image affected by either Gaussian noise or IN, we can define a flexible mixed noise removal framework as follows, and many previous mixed AWGN and IN noise removal methods [8, 26, 29, 52, 55] can be expressed under this framework:

$$ \underset{{u \in {L^{1}}\left( {\varOmega} \right)}}{\arg\min} \left\{ \begin{array}{l} \begin{array}{*{20}{c}} \end{array}{\mu_{1}}{\left\| {Au - f} \right\|_{{L^{1}}\left( {\varOmega} \right)}}\begin{array}{*{20}{c}} \end{array}\\ \begin{array}{*{20}{c}} \end{array} + {\mu_{2}}\left\| {Au - f} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}\begin{array}{*{20}{c}} \end{array}\\ \begin{array}{*{20}{c}} \end{array} + \lambda R\left( u \right)\begin{array}{*{20}{c}} \end{array} \end{array} \right\} $$

(5)

Here, μ₁, μ₂ and λ are weight parameters which balance the mixed noise and regularization term. The noise parameters are unknown and need to be estimated in real-world denoising applications. The L₁ and L₂ data fidelity terms in (5) restrain the solution of minimization problem (5) to preserve the origianl image information as much as possible by fitting the noise distribution. The L₁ data fidelity has been proved to be more appropriate for fitting the impulse noise, while L₂ data fidelity is offten used to modeling the Gaussian noise distribution. The regularization term R(u) places limits on u and forces the solution of (5) to show the supposed properties of our prior knowledge.

Inspired by the different prior knowledge studied over the past decades, we proposed a variational model that combines various popular image denoising techniques. Specifically, L1 [57] and L2 [25] norms are used to capture the IN and the GN noise, respectively. The TV norm [46] is employed to preserve the edge information of the image with sharp discontinuity. In addition, to maintain the nonlocal similarity and sparsity of natural images, a nonlocal low-rank regularization (NLR) [17] term is introduced.

In the experiments, we compare our method with other state-of-the-art methods on natural images. The extensive experimental results have verified that the proposed method performs better than all compared methods.

The main contributions of this work are as follows: (1) A mixed noise removal model is proposed, which combines multifidelity terms, TV norm and NLR. (2) SBIM is used to solve the proposed model by decomposing the minimization problem of the model into multiple simple subproblems and obtains a solution to a large global optimization problem by coordinating the solutions of the subproblems. (3) The performance of visual quantitative indicators is improved compared with other state-of-the-art mixed noise removal methods.

The remainder of this paper is organized as follows. Section 2 describes some related works. The details of the proposed method are given in Section 3. Section 4 presents the convergence analysis of the proposed model. In Section 5, we present the experimental results that demonstrate our model’s performance using a variety of real-world images. Finally, the conclusions are drawn in Section 6.

2 Related work

Numerous previous methods have been developed for image denoising over the past decades, and they can be roughly divided into three categories: filtering methods, variational optimization methods and machine learning methods.

(1). Filtering methods modify the noisy image such that the denoised image can maintain several characteristics in the spatial domain or dictionary domain. In the spatial domain, clean images normally maintain local similarity, nonlocal self-similarity (NSS) and low-rank properties. Local similarity refers to the fact that the pixel value is closely related to its surrounding neighbors, and the local filters estimate the original pixel of the noisy image by averaging the values of neighbors, such as a linear filter (Gaussian filter, mean filter) and a nonlinear filter (bilateral filter, median filter) [43]. NSS refers to the fact that for a given local patch in a natural image, one can find many patches that are similar to it across the image. To capture the NSS of images, nonlocal filters must first collect similar patches into groups and then remove noise according to the features of similar patches. For example, the nonlocal means filter (NLM) [5] takes the mean of all pixels in the image, weighted by how similar these pixels are to the target pixel. To remove AWGN and IN simultaneously, [54] introduced the robust outlyingness ratio (ROR) to NLM as an IN detection mechanism. [39] proposed a fast nonlocal means filter (FNLM), which accelerates the NLM algorithm by eliminating pixels that have small weights. [18] proposed an adaptive NLM that tunes the parameters of the NLM-based patch regularity. [21] proposed a parameter-free NLM that precomputes the optimal parameters of NLM in an image database.

Low rank assumes that the clean image matrix or patch matrices often have a low-rank property, and we can recover a low-rank matrix approximation (LRMA) as the denoising result from the noise observation. Low-rank matrix factorization (LRMF) and nuclear norm minimization (NNM) are two popular classes of methods for solving the LRMA problem. LRMF factorizes the noise image matrix into the product of two low-rank matrices while simultaneously constraining certain fidelity on the noisy image. For example, according to the Eckart–Young–Mirsky theorem [19], the basic LRMF problem under the Frobenius norm can be solved by truncating the rank of the singular value matrix to k. [47] proposed a weighted Frobenius norm to measure the deviation between the reconstructed image and noisy image and solved the new LRMA problem by an EM algorithm. Instead, the noisy image is decomposed into different parts, and NNM recovers the underlying low-rank matrix u from the corrupted image f by minimizing the nuclear norm of u. For example, [9] proved that many NNM problems can easily be solved in closed form by imposing a soft-thresholding operation on the singular values of the observation matrix. [30] proposed a weighted low-rank model (WLRM) for mixed noise removal, which assigned the residuals in the objective function different weights. [59] propose a truncated nuclear norm (TNNR) to approximate the rank function, which minimizes the k smallest singular values of the low-rank image matrix. [53] proposed a weighted Schatten p-norm minimization (WSNM) method that generalizes the NNM to the Schatten p-norm minimization with weights assigned to different singular values.

In the dictionary domain, noisy images or patches are projected into the dictionary domain, and the coding of clean images shows a sparse property. The methods mainly differ in how to choose the dictionary and how to sparsify the encoding. One approach to choose the dictionary is from a fixed set of transforms (steerable wavelet, curvelet, contourlets, bandlets). When the noisy image is transformed, the denoising method shrinks the coefficients of coding and reconstructs images through an inverse transform [3]. Another approach is learning the dictionary from an image database or patches. For example, K-SVD [41] learns the optimal dictionary by performing a k-means algorithm on the singular value decomposition of clean images, and once the dictionary is constructed, we can denoise the image by orthogonal matching pursuit (OMP). PCA filters construct orthogonal dictionaries by performing principal component analysis on image patches and then shrinks the coefficients of the principal components by different functions, such as PB-PCA, PGPCA, PLPCA and PHPCA [3]. [13] proposed a clustering-based method (K-LLD) that bridged dictionary-based approaches with regression-based frameworks.

The above methods mainly exploit single image characteristics to remove noise; however, some works are combine NSS, low rank and sparse coding. For example, BM3D [35] exploits NSS by grouping similar patches into a 3D block and collaborative filtering of the block in the transform domain. [40] proposed a method that extends and combines nonlocal means and sparse coding by learned simultaneous sparse coding (LSSC) such that similar patches share the same dictionary elements in their sparse decomposition. [51] proposed a powerful image model for mixed noise removal that connects low-rank methods with simultaneous sparse coding by spatially adaptive iterative singular-value thresholding (SAIST). The weighted encoding and sparse nonlocal regularization are unified in the weighted encoding model for mixed noise removal (WESNR) [29] by weighting the encoding residual to follow a Gaussian distribution. [27] grouped similar patches in the spatiotemporal domain and formulated the video restoration problem as a joint sparse and low-rank matrix approximation problem. [16] proposed nonlocally centralized sparse representation (NCSR), which exploits NSS to estimate the sparse coding coefficients of the original image.

(2) Variational optimization-based image denoising methods have been studied for several decades. Most of these works use different regularization terms to add prior knowledge on u. Traditional regularizers mainly include Tikhonov regularization [48], total variation (TV) regularization [11, 42, 46], total generalized variation (TGV) regularization [6, 34] and sparsity-based regularization [62, 64, 65]. For example, if we choose the regularization term in (3) as $R\left (u \right ) = {\left \| {\nabla u} \right \|_{{L^{1}}\left ({\varOmega } \right )}}$, then the resulting model will become the famous ROF model [46].

The TV-L1 model [57] improved ROF by replacing the squared L₂-norm in the data fidelity term with the robust L₁-norm. Although there is only a slight difference between the ROF and TV-L1, the TV-L1 model has the following advantages: 1) It is shown to be contrast invariant. 2) The TV-L1 model is considerably more effective at removing noise containing strong IN (e.g., salt-and-pepper noise). Because of the efficient performance of the TV-L1 model in removing strong IN, the L1-data fidelity term ${\left \| {f - Au} \right \|_{1}}$ has been widely used in related studies [31, 33, 45]. In addition, some scholars have improved the TV-L1 model by introducing a second regularization term, as in the following equation:

$$ \hat u = \underset{u}{\arg\min} \left\{ {\frac{{{\gamma_{1}}}}{2}{{\left\| {f - Au} \right\|}_{1}} + \frac{\alpha }{2}\left\| {\nabla u\left( x \right)} \right\|_{2}^{2} + {{\left\| {\nabla u\left( x \right)} \right\|}_{1}}} \right\} $$

(6)

Since (6) is nonconvex, it is difficult to directly solve the minimization problem. Cai et al. [10] proposed the following two-stage segmentation method based on the Mumford–Shah model which replaced the L1 norm with L2 norm.

$$ \hat u = \underset{u}{\arg\min} \left\{ {\frac{{{\gamma_{1}}}}{2}\left\| {f - Au} \right\|_{2}^{2} + \frac{\alpha }{2}\left\| {\nabla u\left( x \right)} \right\|_{2}^{2} + {{\left\| {\nabla u\left( x \right)} \right\|}_{1}}} \right\} $$

(7)

Here, γ₁ and α are positive weight parameters. To remove the mixed Gaussian noise and IN, a combined L₁ − L₂ data fidelity term was suggested, and Shi et al. [28] proposed the following model by combining (6) with (7):

$$ \hat u = \underset{u}{\arg\min} \left\{ \begin{array}{l} \frac{{{\gamma_{1}}}}{2}{\left\| {f - Au} \right\|_{1}} + \frac{{{\gamma_{2}}}}{2}\left\| {f - Au} \right\|_{2}^{2}\\ \begin{array}{*{20}{c}} {} \end{array} + \frac{\alpha }{2}\left\| {\nabla u\left( x \right)} \right\|_{2}^{2} + {\left\| {\nabla u\left( x \right)} \right\|_{1}} \end{array} \right\} $$

(8)

Here, α > 0, γ₁ ≥ 0, and γ₂ ≥ 0 are parameters for balancing the data fidelity terms and the regularization terms.

The sparse-based regularization models can be expressed as the following problem [26], where the regularization term enforces the code of result to be sparse in the dictionary domain. As described in the filtering method, the dictionary can be precomputed in an image database or built on corrupted patches.

$$ \hat u = \underset{u \in {L^{1}}\left( {\varOmega} \right)}{\arg\min} \left\{ {\begin{array}{*{20}{c}} {\left\| {Au - f} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}}\\ { + \eta \sum\limits_{i = 1}^{M} {\left\| {{R_{i}}u - D{\alpha_{i}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}} }\\ { + \lambda \sum\limits_{i = 1}^{M} {\varphi \left( {{\alpha_{i}}} \right)} } \end{array}} \right\} $$

(9)

Here, R_i ∈ R^n×N is the matrix that is extracted from an image patch with size $\sqrt n \times \sqrt n$ centered at the pixel position i, D ∈ R^n×k denotes the dictionary, and $\varphi \left ({{\alpha _{i}}} \right )$ denotes the sparsity penalty on the sparse codes α_i ∈ R^K.

Since the sparse coding can be connected with a low-rank approximation [51], Dong et al. [17] proposed an NLR to maintain the low rank and sparsity of the image. Huang et al. [26] developed an efficient mixed noise removal model that exploits a Laplacian scale mixture (LSM) to model mixed noise and NLR to model prior knowledge. In the nonlocal rank regularization methods, the key is to solve the rank minimization subproblem, and it can be approximately solved by minimizing the following optimization problem [17]:

$$ E\left( {u,\varepsilon } \right) = \log \det \left( {u + \varepsilon I} \right) $$

(10)

Here, u ∈ R^n×n is a symmetric positive semidefinite matrix, and ε denotes a small constant value.

(3) Machine learning methods have been applied to many domains over the past decade, and such methods can be exploited for image denoising in two different ways. The first approach employs the learned model to solve a subproblem of other image denoising methods more quickly and efficiently. For example, Zhang et al. [61] decomposed the AWGN denoising model into a fidelity-term-related subproblem and a denoising subproblem by half quadratic splitting (HQS) and then trained a set of CNN denoisers to solve the denoising subproblem. Wang et al. [50] decomposed the mixed denoising model into four subproblems by the alternating direction method of multipliers (ADMM), and then they used a CNN as a Gaussian denoiser for the u subproblem.

Another approach removes the noise directly based on the learned model. Such methods are typical supervised learning methods that train models in a clean-noise paired dataset, such as the traditional machine learning methods Markov random fields (MRFs) [36], linear regression [63] and multilayer perceptrons [7]. Recently, many deep learning methods have been proven to be powerful tools for image denoising. [60] proposed a blind Gaussian denoising convolutional neural network (DnCNN) that predicts the residual image between the noisy observation and the latent clean image. [2] proposed a block-matching convolutional neural network (BMCNN) method that contains the denoising and averaging operations on the image patches. [2] proposed a blind denoising method GAN-CNN that employs a generative adversarial network (GAN) to build paired training datasets for CNN [2]

3 Proposed mixed noise removal method

Based on (5), we can reformulate our proposed mixed noise removal model as follows:

$$ \hat u = \underset{u \in {L^{1}}\left( {\varOmega} \right)}{\arg \min} \left\{ \begin{array}{l} {\mu_{1}}{\left\| {Au - f} \right\|_{{L^{1}}\left( {\varOmega} \right)}} + {\mu_{2}}\left\| {Au - f} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}\\ + {\lambda_{1}}{\left\| {\nabla u} \right\|_{{L^{1}}\left( {\varOmega} \right)}} + {\lambda_{2}}\sum\limits_{i} {rank\left( {{{\tilde R}_{j}}u} \right)} \end{array} \right\} $$

(11)

Here, the regularization term ${R(u)=(\left \| {\nabla u} \right \|_{{L^{1}}\left ({\varOmega } \right )}},\sum \limits _{i} {rank\left ({{{\tilde R}_{j}}u} \right ))}$ combines the TV with NLR [17] and λ = (λ₁, λ₂) denotes the weight parameter of TV and NLR regularization terms. ${\tilde R_{j}}u = \left [ {{R_{{j_{0}}}}u,{R_{{j_{1}}}}u,{R_{{j_{2}}}}u,...,{R_{{j_{m - 1}}}}u} \right ] \in {R^{n \times m}}$ denotes the matrix formed by the similar patch set of the exemplar image patch u_j ∈ Rⁿ that is $\sqrt n \times \sqrt n$ in size and centered at position j, and ${\tilde R_{j}}$ is an operator to extract the similar patches.

The rank minimization problem can be approximated using the surrogate function $E\left ({u,\varepsilon } \right )$, which has been proven to be better than the nuclear norm [17]. For a general matrix X_i ∈ C^m×n, n ≤ m, which is neither square nor positive semidefinite, Dong et al. [17] slightly modified (10) into the following:

$$ \begin{array}{l} L\left( {X,\varepsilon } \right) = \log \det \left( {{{\left( {{X}{X}^{T}} \right)}^{\frac{1}{2}}} + \varepsilon I} \right)\\ \begin{array}{*{20}{c}} \end{array} = \log \det \left( {{{\left( {\varSigma} \right)}^{\frac{1}{2}}} + \varepsilon I} \right)\\ \begin{array}{*{20}{c}} \end{array} = \sum\limits_{r = 1}^{{r_{0}}} {\log \left( {{\sigma_{r}}\left( X \right) + \varepsilon } \right)} \end{array} $$

(12)

Here, Σ is a diagonal matrix whose diagonal elements are eigenvalues of the matrix XX^T, i.e., XX^T = UΣU^− 1, Σ^1/2 is the diagonal matrix whose diagonal elements are the singular values of the matrix, and ${\sigma _{r}}\left (X \right )$ denotes the r^th singular value of X, ${r_{0}} = {\min \limits } \left ({n,m} \right )$. By combining the above energies, we formulate the nonlocal low-rank-based mixed noise removal model as follows:

$$ \hat u = \underset{u \in {L^{1}}\left( {\varOmega} \right)}{\arg\min} \left\{ \begin{array}{l} {\mu_{1}}{\left\| {Au - f} \right\|_{{L^{1}}\left( {\varOmega} \right)}} + {\mu_{2}}\left\| {Au - f} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}\\ \begin{array}{*{20}{c}} {} \end{array} + {\lambda_{1}}{\left\| {\nabla u} \right\|_{{L^{1}}\left( {\varOmega} \right)}} + {\lambda_{2}}\sum\limits_{i} {L\left( {{{\tilde R}_{j}}u}, \varepsilon \right)} \end{array} \right\} $$

(13)

Here, $L\left ({{{\tilde R}_{j}}u,\varepsilon } \right )$ refers to

$$ \begin{array}{l} L\left( {{{\tilde R}_{j}}u,\varepsilon } \right) = \log \det \left( {{{\left( {{{\tilde R}_{j}}u{{\left( {{{\tilde R}_{j}}u} \right)}^{T}}} \right)}^{\frac{1}{2}}} + \varepsilon I} \right)\\ \begin{array}{*{20}{c}} {}&{}&{}& = \end{array}\log \det \left( {{{\left( {\varSigma} \right)}^{\frac{1}{2}}} + \varepsilon I} \right)\\ \begin{array}{*{20}{c}} {}&{}&{}& = \end{array}\sum\limits_{r = 1}^{{r_{0}}} {\log \left( {{\sigma_{r}}\left( {{{\tilde R}_{j}}u} \right) + \varepsilon } \right)} \end{array} $$

(14)

Numerous methods can be used to solve model (13), such as the split Bregman iteration method (SBIM) [22], the primal-dual approach [12, 20], ADMM [23, 24] and the augmented Lagrange multipliers (ALM) method [32].

ALM transforms constrained optimization problems into unconstrained optimization problems by combining the Lagrange multiplier term with a quadratic penalty function. ADMM extends ALM by breaking the ALM optimization problem into several subproblems and obtaining the corresponding solutions alternately. However, in image processing, because the objective function generally contains L1 and L2 norms, the subproblems must optimize the L1 and L2 norms simultaneously, which is not an easy task. SBIM introduces several auxiliary variables and decouples the L1 and L2 norms into different subproblems. Therefore, the algorithm could solve the L1 subproblem with Bergen iteration and the L2 subproblem with other efficient convex optimization methods separately. In addition, SBIM uses less memory and is easy to code. Therefore, in this paper, we choose SBIM to solve (13).

We separate the optimization problem (13) into multiple simple subproblems. Specifically, we first introduce auxiliary variables h = f − Au, d = ∇u and ${L_{j}} = {\tilde R_{j}}u$, and then we turn (13) into the optimization problem (15).

$$ \left\{ {\begin{array}{*{20}{c}} {\arg \min \limits_{u \in {L^{1}}\left( {\varOmega} \right)} \left\{ {\begin{array}{*{20}{l}} {{\mu_{1}}{{\left\| {Au - f} \right\|}_{{L^{1}}\left( {\varOmega} \right)}} + {\mu_{2}}\left\| {Au - f} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}}\\ { + {\lambda_{1}}{{\left\| {\nabla u} \right\|}_{{L^{1}}\left( {\varOmega} \right)}} + {\lambda_{2}}\sum\limits_{i} {L\left( {{{\tilde R}_{j}}u}, \varepsilon \right)} } \end{array}} \right\}}\\ {s.t.\begin{array}{*{20}{c}} {}&{}&{} \end{array}h = f - Au,d = \nabla u,{L_{j}} = {{\tilde R}_{j}}u} \end{array}} \right. $$

(15)

The augmented Lagrangian equation for (15) is as shown in (16):

$$ \begin{array}{@{}rcl@{}} &&L\left( {{u^{k + 1}},{h^{k + 1}},{d^{k + 1}},L_{j}^{k + 1}} \right)\\ &&= {\mu_{1}}{\left\| h \right\|_{{L^{1}}\left( {\varOmega} \right)}} + {\mu_{2}}\left\| {Au - f} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2} + {\lambda_{1}}{\left\| d \right\|_{{L^{1}}\left( {\varOmega} \right)}}\\ &&\quad+ {\lambda_{2}}\sum\limits_{j} {L\left( {{L_{j}}} \right)} + {\gamma_{1}}\left\| {h - \left( {f - Au} \right) - {b_{1}^{k}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}\\ &&\quad+ {\gamma_{2}}\left\| {d - \nabla u - {b_{2}^{k}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2} + {\gamma_{3}}\sum\limits_{j} {\left\| {{L_{j}} - {{\tilde R}_{j}}u - {U_{j}^{k}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}} \end{array} $$

(16)

Therefore, we solve the u, h, d, and L_j-subproblems as follows.

3.1 u-subproblem

By applying the variable splitting method to (16), u has the minimization problem (17).

$$ {u^{k + 1}} = \underset{u \in {L^{1}}\left( {\varOmega} \right)}{\arg\min} \left( \begin{array}{l} \begin{array}{*{20}{c}} \end{array}{\mu_{2}}\left\| {Au - f} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}\\ \begin{array}{*{20}{c}} \end{array} + {\gamma_{1}}\left\| {h - \left( {f - Au} \right) - {b_{1}^{k}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}\\ \begin{array}{*{20}{c}} \end{array} + {\gamma_{2}}\left\| {d - \nabla u - {b_{2}^{k}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}\\ \begin{array}{*{20}{c}} \end{array} + {\gamma_{3}}\sum\limits_{j} {\left\| {{L_{j}} - {{\tilde R}_{j}}u - {U_{j}^{k}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}} \end{array} \right) $$

(17)

The optimal value of u^k+ 1 must satisfy the following Euler-Lagrange equation:

$$ \begin{array}{l} \left( {{\mu_{2}} - {\gamma_{1}}} \right){A^{T}}Au - {\gamma_{2}}{\varDelta} u + {\gamma_{3}}\sum\limits_{j} {\tilde {R_{j}^{T}}{{\tilde R}_{j}}} u\\ \begin{array}{*{20}{c}} \end{array} = {\mu_{2}}{A^{T}}f + {\gamma_{1}}{A^{T}}\left( {f - h + {b_{1}^{k}}} \right)\\ \begin{array}{*{20}{c}} \end{array} \quad- {\gamma_{2}}div\left( {{d^{k}} - {b_{2}^{k}}} \right) + {\gamma_{3}}\sum\limits_{j} {\tilde {R_{j}^{T}}\left( {{L_{j}} - {U_{j}^{k}}} \right)} \end{array} $$

(18)

Here, $\tilde {R_{j}^{T}}{L_{j}} = \sum \limits _{r = 0}^{m - 1} {R_{{j_{r}}}^{T}{u_{{j_{r}}}}}$, $\tilde {R_{j}^{T}}{\tilde R_{j}} = \sum \limits _{r = 0}^{m - 1} {R_{{j_{r}}}^{T}{R_{{j_{r}}}}}$, and ${R_{{j_{r}}}}$ is a matrix, which is the image patch in the j_r position. We can use the FFT technique or the Gauss-Seidel method to solve this equation. Therefore, (18) can be efficiently solved in the discrete Fourier domain by assuming a periodic boundary condition by denoting ${\mathcal F}\left (u \right )$ as the Fourier transform of u.

3.2 h-subproblem

Similar to the u-subproblem, h has the following minimization problem:

$$ {h^{k + 1}} = \underset{h \in {L^{1}}\left( {\varOmega} \right)}{\arg\min} \left\{ {{\mu_{1}}{{\left\| h \right\|}_{{L^{1}}\left( {\varOmega} \right)}} + {\gamma_{1}}\left\| {h - \left( {f - Au} \right) - {b_{1}^{k}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}} \right\} $$

(19)

This convex L₁-problem is quite easy to solve, and it has an approximate solution through the shrinkage operator [49]:

$$ {h^{k + 1}} = Shrink\left( {f + {b_{1}^{k}} - A{u^{k}},\frac{{{\mu_{1}}}}{{{\gamma_{1}}}}} \right) $$

(20)

Here, $shrink\left ({s,t} \right )$ is the shrinkage operator, and it is defined at each point $\alpha \in {\left [ {0,1} \right ]^{2}}$:

$$ shrink\left( {{s_{\alpha} },{t_{\alpha} }} \right) = \frac{{{s_{\alpha} }}}{{\left| {{s_{\alpha} }} \right|}}\max \left( {\left| {{s_{\alpha} }} \right| - {t_{\alpha} },0} \right) $$

(21)

3.3 d-subproblem

Because d is also a convex L₁-problem, the same procedure may easily be adapted to obtain

$$ {d^{k + 1}} = \arg \min \limits_{d \in {L^{1}}\left( {\varOmega} \right)} \left\{ {{\lambda_{1}}{{\left\| d \right\|}_{{L^{1}}\left( {\varOmega} \right)}} + {\gamma_{2}}\left\| {d - \nabla {u^{k + 1}} - {b_{2}^{k}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}} \right\} $$

(22)

As in (20), we can apply the shrinkage operator again and obtain the following closed-form solution:

$$ {d^{k + 1}} = Shrink\left( {\nabla {u^{k}} + {b_{2}^{k}},\frac{{{\lambda_{1}}}}{{{\gamma_{2}}}}} \right) $$

(23)

3.4 L_j-subproblem

As a consequence of the variable splitting technique, L_j has the following minimization problem:

$$ L_{j}^{k + 1} = \arg \min \limits_{{L_{j}} \in {L^{1}}\left( {\varOmega} \right)} \left\{ \begin{array}{l} {\lambda_{2}}\sum\limits_{j} {L\left( {{{\tilde R}_{j}}u,\varepsilon } \right)} \\ + {\gamma_{3}}\sum\limits_{j} {\left\| {{L_{j}} - {{\tilde R}_{j}}u - {U_{j}^{k}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}} \end{array} \right\} $$

(24)

In summary, the optimization problem (24) is equivalent to the following minimization problem (25):

$$ L_{j}^{k + 1} = \underset{{{L_{j}} \in {L^{1}}\left( {\varOmega} \right)}}{\arg\min} \left\{ \begin{array}{l} {\lambda_{2}}\sum\limits_{r = 1}^{{r_{0}}} {\log \left( {{\sigma_{r}}\left( {{L_{j}}} \right) + \varepsilon } \right)} \\ \begin{array}{*{20}{c}} {}&{} \end{array} + {\gamma_{3}}\left\| {{L_{j}} - {Y_{j}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2} \end{array} \right\} $$

(25)

Here, ${Y_{j}} = {\tilde R_{j}}u$, ${r_{0}} = {\min \limits } \left ({n,m} \right )$, and ${\sigma _{r}}\left ({{L_{j}}} \right )$ denotes the r^th singular value of L_j. Let $g(\sigma ) = \sum \limits _{j = 1}^{n} {\log \left ({{\sigma _{j}} + \varepsilon } \right )}$. Then, g(σ) can be formulated as follows:

$$ g(\sigma ) = g({\sigma^{\left( k \right)}}) + \left\langle {\nabla g({\sigma^{\left( {\text{k}} \right)}}),\sigma - {\sigma^{\left( k \right)}}} \right\rangle $$

(26)

Here, ${\sigma ^{\left (k \right )}}$ is the solution in the k^th iteration. Therefore, we can rewrite (25) as follows:

$$ L_{j}^{k + 1} = \mathop {\arg \min }\limits_{{L_{j}} \in {L^{1}}\left( {\varOmega} \right)} \left\{ {{\lambda_{2}}\sum\limits_{r = 1}^{{r_{0}}} {\frac{{{\sigma_{j}}}}{{\sigma_{j}^{\left( k \right)} + \varepsilon }}} + {\gamma_{3}}\left\| {{L_{j}} - {Y_{j}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}} \right\} $$

(27)

For simplicity, we set up $\theta = \frac {{{\lambda _{2}}}}{{{\gamma _{3}}}}$, $\omega _{j}^{\left (k \right )} = \frac {1}{{\left ({\sigma _{j}^{\left (k \right )} + \varepsilon } \right )}}$, and $\phi \left ({{L_{j}},\omega } \right ) = \sum \limits _{j = 1}^{{r_{0}}} {\omega _{j}^{\left (k \right )}} {\sigma _{j}}$. Consequently, we obtain the following formula:

$$ L_{j}^{k + 1} = \underset{{L_{j}} \in {L^{1}}\left( {\varOmega} \right)}{\arg\min} \left\{ {\left\| {{L_{j}} - {Y_{j}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2} + \theta \phi \left( {{L_{j}},\omega } \right)} \right\} $$

(28)

Theorem 1 (Proximal Operator of the Weighted Nuclear Norm)

For each Y ∈ C^m×n, $0 \le {\omega _{1}} \le {\omega _{2}} \le ... \le {\omega _{{r_{0}}}}$ and ${r_{0}} = {\min \limits } \left ({m,n} \right )$, the minimization optimization problem is as follows:

$$ \min\limits_{L \in {L^{1}}\left( {\varOmega} \right)} \frac{1}{2}\left\| {Y - L} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2} + \theta \phi \left( {L,\omega } \right) $$

(29)

It can be changed to the following closed-form solution using the weighted singular value thresholding method:

$$ {S_{\omega ,\theta }}\left( Y \right)\mathop = \limits^{{\varDelta}} U{\left( {{\varSigma} - \theta diag\left( \omega \right)} \right)_ + }{V^{T}} $$

(30)

Here, UΣV^T is the SVD of Y, and ${\left (w \right )_ + }\mathop = \limits ^{{\varDelta }} {\max \limits } \left ({w,0} \right )$. To obtain more details about the proof of Theorem 1, please reference the Appendixof [17].

Based on Theorem 1, the optimization problem (25) has a closed-form solution:

$$ L_{j}^{k + 1}{\text{ = U}}{\left( {\tilde {\varSigma} {\text{ - }}\frac{{{\lambda_{2}}}}{{{\gamma_{3}}}}{\text{diag}}\left( {{{\text{w}}^{\left( k \right)}}} \right)} \right)_ + }{V^{T}} $$

(31)

Here, $U\tilde {\varSigma } {V^{T}}$ is the SVD of ${\tilde R_{j}}u$, $\omega _{j}^{\left (k \right )} = \frac {1}{{\left ({\sigma _{j}^{\left (k \right )} + \varepsilon } \right )}}$, and ${\sigma _{r}}\left ({{L_{j}}} \right )$ denotes the r^th singular value of L_j.

3.5 Update multipliers

After resolving all subproblems, we also need to update the Lagrangian multipliers b₁, b₂, and U on the ${\left ({k + 1}\right )^{th}}$ iteration using the following update equations:

$$ \begin{array}{l} b_{1}^{k + 1} = {b_{1}^{k}} + \left( {f - A{u^{k + 1}}} \right) - {h^{k + 1}}\\ b_{2}^{k + 1} = {b_{2}^{k}} + \nabla {u^{k + 1}} - {d^{k + 1}}\\ U_{j}^{k + 1} = {U_{j}^{k}} + \rho \left( {L_{j}^{k + 1} - {{\tilde R}_{j}}{u^{k + 1}}} \right) \end{array} $$

(32)

In this paper, we decompose the difficult optimization problem (15) into four subproblems (the u, h, d and L_j-subproblems) based on SBIM. All the subproblems have fast and accurate techniques for obtaining solutions. For example, the u-subproblem can be efficiently solved using the FFT technique or the Gauss-Seidel iteration method. The h-subproblem and d-subproblem can be successfully resolved by applying the shrinkage operator. Furthermore, the L_j-subproblem keeps the closed-form solution by using the weighted SVD. The optimization procedure is summarized in Algorithm 1.

4 Convergence analysis

In this section, we provide the convergence analysis of the proposed algorithm (Algorithm 1). The following convergence analysis is motivated by the theorem in [58]. We can view the unconstrained minimization problem (11) as the constrained problem (15).

Based on the operator splitting algorithm, the augmented Lagrangian function of the problem (15) is as shown in (33):

$$ \begin{array}{l} L\left( {{u^{k + 1}},{h^{k + 1}},{d^{k + 1}},L_{j}^{k + 1},\eta ,{\eta_{1}},{\eta_{2}}} \right)\\ \begin{array}{*{20}{c}} \end{array} = {\mu_{1}}{\left\| h \right\|_{{L^{1}}\left( {\varOmega} \right)}} + {\mu_{2}}\left\| {Au - f} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}\\ \begin{array}{*{20}{c}} \end{array} \quad+ {\lambda_{1}}{\left\| d \right\|_{{L^{1}}\left( {\varOmega} \right)}} + {\lambda_{2}}\sum\limits_{j} {L\left( {{L_{j}}} \right)} - \left\langle {\eta ,d - \nabla u} \right\rangle \\ \begin{array}{*{20}{c}} \end{array} \quad- \left\langle {{\eta_{1}},h - f + Au} \right\rangle - \left\langle {{\eta_{2}},{L_{j}} - {{\tilde R}_{j}}u} \right\rangle \\ \begin{array}{*{20}{c}} \end{array} + {\gamma_{1}}\left\| {h - \left( {f - Au} \right) - {b_{1}^{k}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}\\ \begin{array}{*{20}{c}} \end{array} + {\gamma_{2}}\left\| {d - \nabla u - {b_{2}^{k}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}\\ \begin{array}{*{20}{c}} \end{array} + {\gamma_{3}}\sum\limits_{j} {\left\| {{L_{j}} - {{\tilde R}_{j}}u - {U_{j}^{k}}} \right\|_{{L^{2}}\left( {\varOmega} \right)}^{2}} \end{array} $$

(33)

Here, η, η₁, and η₂ are dual variables. Set ${x^{*}} = \left ({{u^{*}},{h^{*}},{d^{*}},L_{j}^{*},{\eta ^{*}},\eta _{1}^{*},\eta _{2}^{*}} \right )$ to be Karush-Kuhn-Tucker (KKT) conditions as follows:

$$ \left\{ {\begin{array}{*{20}{c}} {0 \in {\mu_{1}}\partial {{\left\| {{h^{*}}} \right\|}_{1}} + \eta_{1}^{*}}\\ {0 = {\mu_{2}}{A^{T}}\left( {A{u^{*}} - f} \right) - div\eta_{1}^{*}}\\ {0 \in {\lambda_{1}}\partial {{\left\| {{d^{*}}} \right\|}_{1}} + {\eta^{*}}}\\ {0 \in {\lambda_{1}}\partial \left( {\sum\limits_{j} {L\left( {{L_{j}}} \right)} } \right) + \eta_{2}^{*}}\\ {\int {\eta_{1}^{*}dx = 0} }\\ {\int {\eta_{2}^{*}dx = 0} }\\ {f - A{u^{*}} = {h^{*}}}\\ {\nabla {u^{*}} = {d^{*}}}\\ {L_{j}^{*} = {{\tilde R}_{j}}{u^{*}}} \end{array}} \right. $$

(34)

Theorem 2

Set ${x^{k}} = \left ({{u^{k}},{h^{k}},{d^{k}},{L_{j}^{k}},{b_{1}^{k}},{b_{2}^{k}},{U_{j}^{k}}} \right )$ to be the iterates in Algorithm 1 and ${\tilde x^{k}} = \left ({{u^{k}},{h^{k}},{d^{k}},{L_{j}^{k}},{\gamma _{1}}{b_{1}^{k}},{\gamma _{2}}{b_{2}^{k}},{\gamma _{3}}{U_{j}^{k}}} \right )$. Suppose that

$$\mathop {\lim }\limits_{k \to \infty } \left( {{x^{k}} - {x^{k - 1}}} \right) = 0.$$

Then, any accumulation point of ${\tilde x^{k}}$ is a KKT point of (34).

Proof. First, the SBIM subproblem (16) of u is equivalent to (17), which leads to the optimality condition (18). From the optimality conditions for all variables, we can obtain equalities

$$ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \left( {{\mu_{2}} - {\gamma_{1}}} \right){A^{T}}A\left( {{u^{k + 1}} - {u^{k}}} \right)\\ - {\gamma_{2}}{\varDelta} \left( {{u^{k + 1}} - {u^{k}}} \right) + {\gamma_{3}}\sum\limits_{j} {\tilde {R_{j}^{T}}{{\tilde R}_{j}}} \left( {{u^{k + 1}} - {u^{k}}} \right)\\ \begin{array}{*{20}{c}} \end{array} = {\mu_{2}}{A^{T}}f + {\gamma_{1}}{A^{T}}\left( {f - {h^{k}} + {b_{1}^{k}}} \right)\\ \begin{array}{*{20}{c}} \end{array} - {\gamma_{2}}div\left( {{d^{k}} - {b_{2}^{k}}} \right) + {\gamma_{3}}\sum\limits_{j} {\tilde {R_{j}^{T}}\left( {{L_{j}^{k}} - {U_{j}^{k}}} \right)} \\ \begin{array}{*{20}{c}} \end{array} - \left( {{\mu_{2}} - {\gamma_{1}}} \right){A^{T}}A{u^{k}} + {\gamma_{2}}{\varDelta} {u^{k}} - {\gamma_{3}}\sum\limits_{j} {\tilde {R_{j}^{T}}{{\tilde R}_{j}}} {u^{k}} \end{array}\\ {{h^{k + 1}} - {h^{k}} = Shrink\left( {f + {b_{1}^{k}} - A{u^{k}},\frac{{{\mu_{1}}}}{{{\gamma_{1}}}}} \right) - {h^{k}}}\\ {{d^{k + 1}} - {d^{k}} = Shrink\left( {\nabla {u^{k}} + {b_{2}^{k}},\frac{{{\mu_{1}}}}{{{\gamma_{1}}}}} \right) - {d^{k}}}\\ {L_{j}^{k + 1}{\text{ - }}{L_{j}^{k}}{\text{ = U}}{{\left( {\tilde {\varSigma} {\text{ - }}\frac{{{\lambda_{2}}}}{{{\gamma_{3}}}}{\text{diag}}\left( {{{\text{w}}^{\left( k \right)}}} \right)} \right)}_ + }{V^{T}}{\text{ - }}{L_{j}^{k}}}\\ {b_{1}^{k + 1} - {b_{1}^{k}} = \left( {f - A{u^{k + 1}}} \right) - {h^{k + 1}}}\\ {b_{2}^{k + 1} - {b_{2}^{k}} = \nabla {u^{k + 1}} - {d^{k + 1}}}\\ {U_{j}^{k + 1} - {U_{j}^{k}} = \rho \left( {L_{j}^{k + 1} - {{\tilde R}_{j}}{u^{k + 1}}} \right)} \end{array}} \right. $$

(35)

Because of $\mathop {\lim }\limits _{k \to \infty } \left ({{x^{k}} - {x^{k - 1}}} \right ) = 0$, the right-hand side of each equality in (35) goes to zero as $k \to \infty$. Therefore, all the terms go to zero as $\to \infty$

$$ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \left( {{\mu_{2}} - {\gamma_{1}}} \right){A^{T}}A{u^{k}} - {\gamma_{2}}{\varDelta} u + {\gamma_{3}}\sum\limits_{j} {\tilde {R_{j}^{T}}{{\tilde R}_{j}}} {u^{k}} - \\ \begin{array}{*{20}{c}} \end{array}\left( \begin{array}{l} {\mu_{2}}{A^{T}}f + {\gamma_{1}}{A^{T}}\left( {f - h + {b_{1}^{k}}} \right)\\ - {\gamma_{2}}div\left( {{d^{k}} - {b_{2}^{k}}} \right) + {\gamma_{3}}\sum\limits_{j} {\tilde {R_{j}^{T}}\left( {{L_{j}^{k}} - {U_{j}^{k}}} \right)} \end{array} \right) \to 0 \end{array}\\ {Shrink\left( {f + {b_{1}^{k}} - A{u^{k}},\frac{{{\mu_{1}}}}{{{\gamma_{1}}}}} \right) - {h^{k}} \to 0}\\ {Shrink\left( {\nabla {u^{k}} + {b_{2}^{k}},\frac{{{\mu_{1}}}}{{{\gamma_{1}}}}} \right) - {d^{k}} \to 0}\\ {{\text{U}}{{\left( {\tilde {\varSigma} {\text{ - }}\frac{{{\lambda_{2}}}}{{{\gamma_{3}}}}{\text{diag}}\left( {{{\text{w}}^{\left( k \right)}}} \right)} \right)}_ + }{V^{T}}{\text{ - }}{L_{j}^{k}} \to 0}\\ {\left( {f - A{u^{k + 1}}} \right) - {h^{k + 1}} \to 0}\\ {\nabla {u^{k + 1}} - {d^{k + 1}} \to 0}\\ {\left( {L_{j}^{k + 1} - {{\tilde R}_{j}}{u^{k + 1}}} \right) \to 0} \end{array}} \right. $$

(36)

From (35), we can easily obtain the following equation:

$$ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \left( {{\mu_{2}} - {\gamma_{1}}} \right){A^{T}}A{u^{*}} - {\gamma_{2}}{\varDelta} {u^{*}} + {\gamma_{3}}\sum\limits_{j} {\tilde {R_{j}^{T}}{{\tilde R}_{j}}} {u^{*}}\\ \begin{array}{*{20}{c}} \end{array} = {\mu_{2}}{A^{T}}f + {\gamma_{1}}{A^{T}}\left( {f - {h^{*}} + b_{1}^{*}} \right)\\ \begin{array}{*{20}{c}} \end{array} - {\gamma_{2}}div\left( {{d^{*}} - b_{2}^{*}} \right) + {\gamma_{3}}\sum\limits_{j} {\tilde {R_{j}^{T}}\left( {L_{j}^{*} - U_{j}^{*}} \right)} \end{array}\\ {{h^{*}} = Shrink\left( {f + b_{1}^{*} - A{u^{*}},\frac{{{\mu_{1}}}}{{{\gamma_{1}}}}} \right)}\\ {{d^{*}} = Shrink\left( {\nabla {u^{*}} + b_{2}^{*},\frac{{{\mu_{1}}}}{{{\gamma_{1}}}}} \right)}\\ {L_{j}^{*}{\text{ = U}}{{\left( {\tilde {\varSigma} {\text{ - }}\frac{{{\lambda_{2}}}}{{{\gamma_{3}}}}{\text{diag}}\left( {{{\text{w}}^{\left( * \right)}}} \right)} \right)}_ + }{V^{T}}} \end{array}} \right. $$

(37)

Therefore, any accumulation of ${\tilde x^{k}}$ satisfies the KKT conditions (34) due to (35). However, since the minimization problem (15) is nonconvex, the KKT conditions are the only necessary optimal conditions for (15). Therefore, we cannot ensure that an accumulation point of x^k is an optimal point of (33).

5 Experimental results

In this section, we evaluate the validity of the proposed model. We first introduce the process for selecting the model parameters, and then we compare the denoising effects with other models using different noise levels. We choose four image denoising methods as the baseline in our experiment: nonlocal filter method NLM [5], sparse coding method WESNR [29], nonlocal low regularization method LSM_NLR [26] and the recently proposed deep learning method BdCNN [1] for blind noise whose learned network model is open sourced on GitHub. Because NLM was originally proposed for AWGN, we only show the result of NLM in the AWGN noise removal experiment. We choose the following classic images in the experiments: parrot, monarch, boat, cameraman, house and Lena (Fig. 1).

Fig. 1

The six classic ground truths (a-f): a is the parrot, b is the monarch, c is the boat, d is the cameraman, e is the house, f is Lena

We utilize the improvement in the signal-to-noise ratio (ISNR), the peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) to evaluate the effectiveness of all methods for removing the noise, and the three metrics can be defined as follows:

$$ISNR\left( {{u_{*}},\hat u,\tilde u} \right) = 10{\log_{10}}\left( {\frac{{\sum {{{\left( {{u_{*}} - \tilde u} \right)}^{2}}} }}{{{{\sum {\left( {{u_{*}} - \hat u} \right)} }^{2}}}}} \right)$$

$$PSNR\left( {{u_{*}},\hat u} \right) = 10{\log_{10}}\left( {\frac{{{{255}^{2}}mn}}{{\left\| {{u_{*}} - \hat u} \right\|_{2}^{2}}}} \right)$$

$$SSIM\left( {{u_{*}},\hat u} \right) =\frac{2\mu_{u_{*}}\mu_{u}+C_{1}}{\mu^{2}_{u_{*}}{\mu^{2}_{u}}+C_{1}} * \frac{2\sigma_{u_{*}}\sigma_{u}+C_{2}}{\sigma^{2}_{u_{*}}{\sigma^{2}_{u}}+C_{2}} *\frac{2\sigma_{u_{*}}\sigma_{u}+C_{3}}{\sigma^{2}_{u_{*}}{\sigma^{2}_{u}}+C_{3}}$$

where u_∗ ∈ R^m×n is the clean image, $\hat u \in {R^{m \times n}}$ is the restored image, $\tilde u \in {R^{m \times n}}$ is the contaminated image, $\mu _{u_{*}},\mu _{u}$ is the mean of u_∗, u, $\sigma _{u_{*}},\sigma _{u}$ is the covariance and C₁, C₂, C₃ are constants. Note that a high value (ISNR, PSNR and SSIM) indicates a better restoration result.

5.1 Parameter selection

The proposed algorithm needs to choose seven parameters: μ₁, μ₂, λ₁, λ₂, γ₁, γ₂ and γ₃. Generally, there are two methods for parameter selection: 1) the first is that parameters are chosen based on the experience of the experimenters, and 2) the second method is to fix the values of some parameters and adjust other parameter values to obtain the optimal parameters [20, 22]. In this paper, we choose the second method to select our parameters. The appendix section shows a demo parameter selection process for GN0.01 noise removal, and in our real parameter selection process, we tried more values to select the optimal parameters. It can be found from the appendix that the parameter value of λ₂ affects the denoising result most, and therefore the parameter selection for other noise level can firstly fixed the value of λ₂ and then adjust the value of μ₁, μ₂, λ₁, γ₁, γ₂ respectively.

Because the proposed algorithm is not guaranteed to converge to the optimal value as the update operation continues to run, the loop iteration can be determined by the researcher’s experience. For example, as other algorithms implement [26, 29], we can divide the parameter value into several regions and set different loop iteration times for each region. In addition, we can also collect experimental results on some image databases to determine the loop iteration. For example, we can first fix the inner loop iteration, record the PSNR value of every outer iteration step on 100 images and select the iteration times that make most images finally achieve the optimal performance. As shown in Fig. 2, the best loop iteration is 3 for the image database. Note that for other image databases, the best loop iteration may be different.

Fig. 2

a PSNRs of 10 iteration steps for 100 images b Frequencies of outer loop number which has best performace on given images

Both the proposed algorithm and the LSM_NLR algorithm have an NLR term and two layers of a loop structure in their algorithms. For fairness, we set the outer loop and inner loop iteration times of the two methods to be 3 and 4, respectively, in the successive experiments, and the main parameter of the nonlocal regularization term in the LSM_NLR model and the proposed model are the same at different noise levels. We also set the same patch size and number of patches as the LSM_NLR in [17]. We first select the optimal λ₂ value of the LSM_NLR and then iteratively determine the other parameters of the proposed model.

For NLM [5] and WESNR [29], the parameters are setted as in the published papers, which may lead to a diffrent result when the images in our experiments are not the same as in the original papers. The parameters of BdCNN [1] are trained on images database and we employed the network published by [1] in the successive experiments, which may slightly affects the denoising result due to the training image database. Table 1 shows the parameter values that are selected in this paper for different types and levels of noise.

Table 1 The parameter selection

5.2 Experimental comparison of single noise

In this section, we compared the denoising effects of different models on images with a single type of noise. The types of noise are impulse noise(IN) and Gaussian noise(GN), which are added to the image using the MATLAB function imnoise, and the noise levels are (0.01, 0.04 and 0.1) and (0.01, 0.1 and 0.4), respectively.

The quantitative indicator (ISNR, PSNR and SSIM) results of the four models are shown in Tables 2 and 3. The GN0.04 denoising visualization effect of parrots, monarch, boats, cameraman, house and Lena is shown in Fig. 3. The IN0.4 denoising visualization effect of parrots, monarch, boats, cameraman, house and Lena is shown in Fig. 4.

Fig. 3

Denoising effect of noisy images (GN0.1): The first column is the NLM, the second column is the WESNR, the third column is the LSM_NLR, the fourth column is BdCNN, and the fifth column is Oursx

Fig. 4

Denoising effect of noisy images (IN0.4): The first column is the WESNR, the second column is the LSM_NLR, the third column is the BdCNN, and the fourth column is Ours

Table 2 The quantitative indicators for the AWGN

Table 3 The quantitative indicators for the in

As shown in Tables 2 and 3, for Gaussian noise, only the three GN0.01 polluted images’ (parrots, cameraman, Lena) ISNR and PSNR values are lower than that of LSM_NLR, and the other 15 noise-added images are better than all the other models in the three indicators. For the IN noise, the denoising effect of the proposed model is significantly better than the other three models on all images, and the restored local visual quality is also better than the other models. Especially when IN noise level is low, the proposed method can not only preserve the nonlocal self-similarity (NSS) and nonlocal low-rank properties, but also distinguish and remove IN noises better than other methods. The BdCNN and WESNR methods remove all types of noise as same way by averaging the noise patches or restraining the low-rank property of denoising image, therefore the denoising result of these two methods are lower than that of LSM_NLR and the proposed method.

To investigate the algorithm, we count each step’s PSNR value of the images in which our model’s denoising effect is lower than the LSM_NLR (GN0.01 parrot), and we find that during the processing of these images, the PSNR value will first increase to the peak value in the first round of the inner loop and then follow an overall downward trend (see Fig. 5b). We plotted the PSNR values for each step of the two models for the parrot image with the GN0.01 noise level, and it can be observed that the PSNR values of both the LSM_NLR and our model (not just the proposed model) follow an overall downward trend during the iterative processing. However, for the situation in which the PSNR value of the proposed model is better than that of the LSM_NLR (e.g., boat image with GN0.01 noise), both models present an upward trend (see Fig. 5a). Therefore, we attempted several methods and finally found that adjusting the number of iterations can improve this situation. We set the number of inner loop iterations to 2, and the iterative PSNR values of the parrot with GN0.01 are shown in Fig. 5c. The PSNR values of both models show an overall upward trend, and the final PSNR value of our model is better than the LSM_NLR results.

Fig. 5

PSNRs for different noisy images and iteration steps: a Boat with GN0.01 noise, b parrot with GN0.01 noise and c parrot with GN0.01 noise after adjusting the iteration step

In real applications, the real image and the PSNR value are unknown. The inner loop iteration number can be statistically determined by the best number in an image database, as shown in Fig. 3. Through this approach, although the selected loop iteration is not the best for every image, it can obtain the best performance for most noisy images in the same situation.

5.3 Experimental comparison of mixed noise

In this subsection, we evaluate the effectiveness of the proposed model to remove the mixed noises. The mixed noises are IN and AWGN, and the noise levels are GN0.01+IN0.01, GN0.01+IN0.1 and GN0.1+IN0.01. The results for the denoising quantitative indicators (ISNR, PRSR and SSIM) of the four models are shown in Table 4, and the denoising visual effects of the four models with GN0.1+IN0.01 noise are shown for parrots, monarch, boats, cameraman, house and Lena in Fig. 6.

Table 4 The quantitative indicators for mixed noise

Fig. 6

Denoising effect of noisy images (GN0.1+IN0.01): The first column is the WESNR, the second column is the LSM_NLR, the third column is the BdCNN, and the fourth column is Ours

Similar to the denoising results of the Gaussian noise, it can be observed from Table 4 that all quantitative indicators of the proposed model algorithm in this paper is better than the other three models for the 16 images with mixed noise. In addition, the quality of the local visualization after recovery is better than that of other models. However, the ISNR and PSNR values of the GN0.01+IN0.01 and GN0.01+IN0.1 picture parrots are lower than that of the LSM_NLR model.

This situation mainly happens when Gaussian noise is low, and in such situation, the Laplacian scale mixture (LSM) part in LSM_NLR model is more suitable for modeling Gaussian noise than the proposed model in some particular cases. We can validate that the denoising effect of GN0.01+IN0.01 and GN0.01+IN0.1 parrots can be improved by adjusting the number of iterations. Since WENSNR and BdCNN don’t distinguish different types of noise in their noise removal process, the quantitative indicators of WENSNR and BdCNN are relatively lower for mixed noise image removal.

Although the denoising result of the proposed method is better than other models in most polluted images, the time efficiency of our model has no advantages. For example, the time consumed for GN0.01+IN0.01 parrots noise removal in our experimental computer is (OURS:54.6s,LSM_NLR:55.2s,WESNR:31.2s,BdCNN:15.7s). The running time of our algorithm is mainly consumed to solve the approximation low-rank optimization problem iterately, which has no advantage of time efficiency than other methods escpically for pretrained method BdCNN. This shortcoming is also a limitation of the proposed method in real applications, which could be improved by combining the proposed method with other pretrained methods or more efficient optimization methods.

6 Conclusion

In this paper, we proposed a mixed noise removal model that combines multifidelity terms with the nonlocal low-rank and TV regularization terms. In the proposed model, the L1 and L2 fidelity terms are employed to fit the IN and Gaussian noise, respectively. TV and NLR regularization impose edge, NSS, low-rank and sparsity prior knowledge on the natural images. We also use the nonconvex function logdet(X) as a smooth surrogate function for the rank approximation rather than the convex nuclear norm. To solve this model, we use SBIM to decompose the difficult minimization problem of (15) into four simple subproblems. Through many experiments on many images and different noise levels, it is shown that the ISNR, PSNR and SSIM values on almost noisy images of the proposed model are better than the values of four state-of-the-art models. In addition, the proposed model can retain the local information of the images and provide a better visualization effect.

Howerver, there are still several limitations to our current study. Firstly, in some cases, the PSNR indicator follows an overall downward trend as the iterations increase. This problem can be solved to some extent by adjusting the number of iterations. However, determining this situation during the runtime processing of the algorithm and automatically adjusting the number of iterations is an important issue to be solved in our future work. Secondly, the time efficiency need to be further improved for real application, and we can utilize Laplacian smoothing-gradient descent [44] or other methods to speed up the objective function optimization process. Thirdly, since this study follows a traditional image processing approach, the parameters can not be setted automatically to adapt to various noise level. Therefore, in the future, we could exploit the deep split Bregman algorithm such as ADMM-Nets [56] to solve this problem, which combines the deep learning methods with traditional variational optimization model.

Appendix: Demo parameters selection process for GN0.01 noise removal

Table 5