1 Introduction

Chaos is a kind of nonlinear phenomenon in the physical world. The first chaotic system was proposed by Lorenz in [11]. After then, many different kinds of chaotic systems have been provided and constructed, eg, Logistic map [13], Tent map [6], Henon Map [7], Chen system [12], coupled map lattices [9], and very recently, Bulban map [1], Lorenz-like system [2], spatiotemporal chaotic system [19], et al.

In these studies, the high-dimensional chaotic system and hyper-chaotic systems have received much more attentions than one-dimension map. One of the main reasons is that the control parameter of the one-dimensional chaotic map is rather limited, which makes the chaotic map easier to be attacked. As we know, one-dimensional chaotic map is easy to implement and can also provide good chaotic characteristics, which is also important for practical use. Therefore, in this paper, we propose a new simple one-dimensional chaotic map with two control parameters, where one of the parameter can be infinite, which greatly increase the parameter space. We theoretically analyze the linear stability of the fixed points of this new map, and use numerical simulations to reveal the bifurcation and Lyapunov exponent, the results show that the chaotic performance is only related to one of the system parameter, and has no correlation to the other.

With the rapid development in internet technology and multimedia technology, communications with images have become more and more popular. In order to ensure communication security, image encryption has become an increasingly serious issue and urgently needed [18]. However, traditional encryption algorithms, such as RSA, DES and IDEA, are not suitable for image encryption due to image’s intrinsic properties such as bulky data capacity, strong redundancy and strong correlations among adjacent pixels [4, 5, 10].

Recently, chaotic systems have been widely used in image encryption for their significance nonlinear performance, such as sensitivity to both initial value and parameter, unpredictability, and pseudorandomness, et al. [8, 15,16,17, 20]. Wang and Guo [17] proposes an image alternate encryption algorithm based on Logistic map. In this algorithm, the shuffling and diffusion stages are combined in encryption process. However, Logistic map is proved to be not secure enough for its small key space and some other weaknesses [10]. Zhou and Liao [20] presents a digital image encryption algorithm with different precisions by three collision-based dynamical systems. This algorithm induces three chaotic systems, which increases its implementation cost. Sun et al. [15] proposes a new image encryption algorithm based on a new spatial chaos system. Tong et al. [16] proposes a new high-dimensional chaotic system, and presents a novel image encryption based on this map and Cat map. In order to enhance the security, a new separated Cat map with variable parameters is designed for the permutation process. These two algorithms are based on high-dimensional chaotic systems. Although the security performances are quite good, the encryption speed is not satisfactory. Hua et al. [8] proposes an image encryption algorithm based on new two-dimensional Sine Logistic modulation map. This map is derived from Logistic map and Sine map, while the use of original Logistic map makes this algorithm not that convincing.

In this paper, we propose a new image encryption algorithm based on our new one-dimensional chaotic map. Both shuffling and substitution algorithms are related to this new map. Many statistical tests and security analysis are carried out to evaluate the performances of our algorithm, including histogram analysis, information entropy analysis, key space analysis, key sensitivity analysis, correlation analysis, resistance to differential attack analysis, and randomness analysis. The results prove that our algorithm has a high security level, and can be competitive with other recently proposed image encryption algorithms.

The rest of this paper is organized as follows. The mathematically model of this new chaotic map is introduced in Section 2, and its dynamical performances are revealed in Section 3. In Section 4, we propose a new image encryption algorithm based on the new chaotic map. Statistical tests and security analysis of our algorithm are presented in Section 5. Finally, Section 6 concludes the whole paper.

2 A new one-dimensional chaotic map

The mathematical model of our new one-dimensional chaotic map is described as follow

$$ {x}_{n+1}=f\left({x}_n\right)=\sqrt{-{ax}_n^2+{bx}_n} $$
(1)

here, n is the iteration number, a, b > 0 are the two control parameters of this equation, f: I → I is the nonlinear iterative function, xn = f(n)(x0) is the one-dimensional state variable after n times iteration by initial condition x0.

A chaotic map must be bounded. By Eq. (1), obviously, we have 0 < xn < b/a, for every n. Thus, I = [0, b/a]. The nonlinear function f can be estimated as

$$ f(x)=\sqrt{-a{\left(x-\frac{b}{2a}\right)}^2+\frac{b^2}{4a}}\le \frac{b}{2\sqrt{a}} $$
(2)

the “=” holds if and only if x = b/2a. In order to make the state variable x bounded in the interval I, it should have

$$ \frac{b}{2\sqrt{a}}\le \frac{b}{a} $$
(3)

Eq. (3) indicates that a ≤ 4. Set a = 4, b = 3, the trajectory diagram is shown in Fig. 1.

Fig. 1
figure 1

(a) The trajectory diagram of Eq. (1); (b) Enlargement of (a)

Full size image

3 Dynamical performances

In this section, we will analyze the dynamical characteristics of our new chaotic map, including fix point, linear stability and bifurcation analysis.

3.1 Fixed points, linear stability and bifurcation analysis

We consider the fixed points and also the equilibrum points of our map, which can be calculated as x* = f(x*). After calculation, there exist two fixed points, which are found as

$$ {x}^{\ast }=0\kern0.5em \mathrm{and}\kern0.75em {x}^{\ast }=\frac{b}{1+a}, $$
(4)

respectively. In order to get bifurcation, the fixed points should be unstable. We consider a point xn close to the fixed point x* with a small difference Δx, we get

$$ \Delta {x}_n={x}_n-{x}^{\ast } $$
(5)

Afterward, we do the Taylor expansion of function f, and get

$$ {x}^{\ast }+\Delta {x}_{n+1}={x}_{n+1}=f\left({x}_n\right)=f\left(x\ast \right)+{f}^{\hbox{'}}\left({x}^{\ast}\right)\Delta {x}_n+\cdots $$
(6)

Here f'(x) is the derivation of function f at point x, which can be calculated as

$$ {f}^{\hbox{'}}(x)=\frac{-2 ax+b}{2\sqrt{-{ax}^2+ bx}} $$
(7)

Put x* = f(x*) into Eq. (6), Eq. (6) can be simplified as

$$ \Delta {x}_{n+1}={f}^{\hbox{'}}\left({x}^{\ast}\right)\Delta {x}_n+\cdots $$
(8)

Therefore, if |f'(x*)| is larger than 1, we have that the difference |Δxn + 1| is larger than |Δxn|, which means that the fixed point is unstable.

Next, we consider the value of |f'(x*)|. Substituting x* = 0 into Eq. (7), we have |f'(x*)| approach to infinity. Thus, the fixed point 0 becoming unstable. When substituting x* = b/(1 + a) into Eq. (7), we get

$$ {f}^{\hbox{'}}\left({x}^{\ast}\right)=\frac{-2a\cdot \frac{b}{1+a}+b}{2\sqrt{-a\cdot \frac{b^2}{{\left(1+a\right)}^2}+b\cdot \frac{b}{1+a}}}=\frac{1-a}{2} $$
(9)

In order to make the fixed point x* unstable, it should have

$$ {f}^{\hbox{'}}\left({x}^{\ast}\right)=\frac{1-a}{2}>1 $$
(10)

or

$$ {f}^{\hbox{'}}\left({x}^{\ast}\right)=\frac{1-a}{2}<-1 $$
(11)

From Eq. (10), we can get a < −1. This contradicts the requirement that a > 0, and thus, be neglected. From Eq. (11) we have that a > 3. This solution gives the first bifurcation point on a > 3, and the fixed point becoming unstable, which means the chaotic behavior of Eq. (1). Furthermore, the second bifurcation point can be calculated using the period 2 points of f(2)(xn).

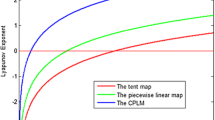
$$ {f}^{(2)}\left({x}_n\right)=f\left(f\left({x}_n\right)\right)=\sqrt{-a{\left(-{ax}_n^2+{bx}_n\right)}^2+b\left(-{ax}_n^2+{bx}_n\right)} $$
(12)

By using the similar method of fixed points, the second bifurcation point can be approximately calculated as a > 3.6451. Moreover, by using simulations on Matlab, the bifurcation diagram of parameter a is shown in Fig. 2. From Fig. 2 we have that this map will be chaotic when 3.7835 < a ≤ 4. Another interesting result is that the bifurcation point has no relevance to the parameter b, the similar result can also be achieved in the Lyapunov exponent analysis. Parameter b only affects the interval I.

Fig. 2
figure 2

Bifurcation diagram of parameter a (a) b = 4; (b) b = 6; (c) b = 8; (d) b = 10

Full size image

3.2 Lyapunov exponent

The one-dimensional chaotic map has only one largest Lyapunov exponent. The largest Lyapunov exponent is used to measure whether the map is chaotic or not. For an exponent larger than zero, the map is chaotic, and vice versa. The larger the Lyapunov exponent is, the more complex (less predictable) the map is. The largest Lyapunov exponent can be calculated as [14]:

$$ LE=\underset{n\to \infty }{\lim}\frac{1}{n}\sum \limits_{i=1}^n{\lambda}_i $$
(13)

where

$$ {\lambda}_n=\ln \mid {f}^{\hbox{'}}\left({x}_n\right)\mid $$
(14)

f'(xn) is given by Eq. (7). For different parameter b, Fig. 3 show the Lyapunov exponents with the variation of parameter a. From Fig. 3 we have that the Lyapunov exponent diagram is the same with different parameter b, which means that the chaotic characteristics has no relevance to parameter b. This gets the same conclusion as bifurcation analysis. The Lyapunov exponent of Eq. (1) reaches its maximum value when a = 4, which is about LE = 0.5547. The convergence process is shown in Fig. 4.

Fig. 3
figure 3

Lyapunov exponent with the variation of parameter a (a) b = 10; (b) b = 8; (c) b = 6; (d) b = 4

Full size image
Fig. 4
figure 4

Convergence of the Lyapunov exponent for a = 4

Full size image

Based on the above analysis, the significant advantages of this map can be described as

  1. 1)

    This map is one-dimensional, which is much easier to implement than high dimensional maps. For most of 1D chaotic maps, such as Logistic map, Chebyshev map, Tent map, et al., they have only one control parameter, which leads to a relatively small key space. While in our map, there are two control parameters, and the key space is larger, which is more suitable for image encryption.

  2. 2)

    Generally, the dynamics of chaotic map will be influenced by its control parameters. All the parameters will affect the dynamics of chaotic map, such as [1], which makes the dynamical behavior of map hard to control. For our map, the chaotic performance is only related to one of the system parameter, and has no correlation to the other, which indicates that our map is easier to control in this sense.

4 A new image encryption algorithm

In this section, we propose a new image encryption algorithm based on this new one-dimensional chaotic map. Our new algorithm is combined with two steps, shuffling algorithm and substitution algorithm.

4.1 Shuffling algorithm

The shuffling algorithm is used to disturb the positions of each pixel of a plain image A, which can reduce the correlationship between adjacent pixels. In our algorithm, we use the proposed chaotic map Eq. (1) to shuffle the pixels.

Assume {Aij} be the pixel matrix of M × N plain image A, and a real-valued sequence {xk} is generated by the Eq. (1) with a given initial value with length MN. Rearrange the sequence {xk} according to the ascending order, and get the rearranged sequence

$$ {x}_{k_1},{x}_{k_2},\dots, {x}_{k_{MN}} $$
(15)

where

$$ {x}_{k_1}<{x}_{k_2}<\cdots <{x}_{k_{MN}} $$
(16)

and kl∈{1, 2, ...,MN}, 1 < l < MN, is different from each other. Now, the integer sequence {kl} is used as the shuffling sequence. Scanning the matrix A into a sequence {bs} as

$$ {b}_{\left(i-1\right)N+j}={A}_{ij},\kern0.5em 1\le i\le M,1\le j\le N $$
(17)

Then, the shuffled sequence {ct} can be calculated as

$$ {c}_{k_i}={b}_i,\kern0.5em 1\le i\le MN $$
(18)

Finally, reconstruct the sequence {ct} to a matrix as

$$ {C}_{ij}={c}_t $$
(19)

where

$$ i= floor\left\lfloor \left(t-1\right)/N\right\rfloor +1 $$
(20)

and

$$ j=t-\left(i-1\right)N $$
(21)

Thus, the matrix C is the shuffled matrix of plain A by using our shuffling algorithm. This shuffled matrix is based on the chaotic sequence {xk}, which can be regarded as unpredictable and randomness.

4.2 Substitution algorithm

The Substitution algorithm is used to change the pixel value of plain image A. Based on the chaotic characteristics of our proposed map, here, we also use this map in our substitution algorithm.

Also, assume a real-valued sequence {xk} is generated by the Eq. (1) with a given initial value with length MN. In order to get good statistical properties, we first change the sequence {xk} into a uniformly distributed integer sequence {dk}. In this paper, we propose the following coding algorithm to generate uniformly distributed integer sequence

$$ {d}_k=600000\left({x}_k+2350\right)\kern0.5em \operatorname{mod}256\kern0.5em $$
(22)

The distribution of sequence {xk} and {dk} are shown in Fig. 5, which indicate that our uniformly distributed algorithm is quite effective.

Fig. 5
figure 5

Distribution of (a) chaotic sequence {xk}; (b) coding sequence {dk}

Full size image

Change the sequence {dk} into a substitution matrix D by using the same method as Eq. (19), (20) and (21). The substituted image matrix E can be written as

$$ {\displaystyle \begin{array}{cc}{E}_{ij}={D}_{ij}+{C}_{ij}& \operatorname{mod}256\end{array}}\kern0.5em $$
(23)

Remark 1

In our algorithm, the newly proposed chaotic map is the key factor to ensure the security of encrypted images. Eq. (22) is used to improve the statistical characteristics of chaotic sequences. The randomness tests are provided in Section 5.8. Certainly, we can replace this generator by another one. If other generators can make the sequence {dk} with good randomness, there will have no much differences in the security of encrypted images.

4.3 The new image encryption algorithm

In order to have a high chaotic characteristics of Eq. (1), we always set a = 4 in our algorithm. The detailed steps of our algorithm are described as follows.

  1. Step 1:

    Read the plain image A. Assume the size of plain image A be M × N, and set R = 1.

  2. Step 2:

    Set secret values x0,1, x0,2, ..., x0,T, y0,1, y0,2, ..., y0,T and b1, b2, ..., bT for T round encryption. Secret values x0,1, x0,2, ..., x0,T are used in the shuffling phase, and y0,1, y0,2, ..., y0,T are used in the substitution phase. b1, b2, ..., bT are the parameters of our chaotic map which are used in both shuffling and substitution phases.

  3. Step 3:

    Generate the real-valued chaotic sequences {xk} and {yk} with length MN based on Eq. (1) by the initial values x*i = x0,i + mean{A}/256 mod (bi/4), and y*i = y0,i + mean{A}/256 mod (bi/4), i = 1, 2, ..., T, and denote as {X1}, {X2}, …, {XT} and {Y1}, {Y2}, …, {YT} respectively. Here, x0,i and y0,i can be selected arbitrarily in the interval I. In generating the chaotic sequences, the average pixel value of plain image A is used, which makes our algorithm to resist the chosen-plaintext attack. The item mod (bi/4) is used to ensure the initial values locates in the interval I.

  4. Step 4:

    Change the real-valued sequences {XR} into shuffling matrix according to Eq. (15), (16) and (17), and then generate the shuffled matrix {CR} by Eq. (18), (19), (20) and (21).

  5. Step 5:

    Change the sequence {YR} into uniformly distributed sequence by Eq. (22), and construct this sequence into matrix according to Eq. (19), (20) and (21).

  6. Step 6:

    Encrypt the shuffled matrix {CR} by Eq. (23).

  7. Step 7:

    Set R = R + 1.

  8. Step 8:

    If R ≤ T, go to step 4. Else, break out.

  9. Step 9:

    Save as encrypted image A*.

The flowchart of our algorithm is shown in Fig. 6. The values x0,1, x0,2, ..., x0,T, y0,1, y0,2, ..., y0,T and b1, b2, ..., bT can be used as the security keys. The decryption algorithm is the inverse process of our encrypt algorithm which is neglected here.

Fig. 6
figure 6

The flowchart of our image encryption algorithm

Full size image

Our encryption algorithm is based on our newly proposed 1D chaotic map. In order to enhance the security, we use Eq. (22) to generate a uniformly distributed sequence. Our encryption scheme is quite different from other chaotic image encryption algorithms since the chaotic source used here is completely different from others.

As we know, the security of the encrypted image is mainly depended on the chaotic sequences generated by chaotic sources. In our algorithm, the parameter is selected in the chaotic region, and Eq. (22) is used to improve its statistical characteristics. Therefore, the output chaotic sequence is with good randomness (We use NIST test suite to confirm the randomness of the output chaotic sequence in Section 5.8), and thus the encrypted images have relatively high security (uniformly distribution, weak correlation between pixels, large entropy, et al.). Furthermore, the average pixel value of plain image A is used in generating the chaotic sequences to resist the chosen-plaintext attack.

5 Statistical tests and security analysis

In this section, we make some experiments to evaluate the security and statistical properties of our image encryption algorithm, and compare the results with some other algorithms in [8, 15,16,17, 20]. The experiment image is 256 × 256 plain image, and the encryption round is one. All the tests are processed by Matlab 7.0 on computer with 1.99 GHz CPU and 1.92 GB memory. The security keys are selected as x0,1 = 0.1236, y0,1 = 0.3278 and b1 = 4.

5.1 Encryption and decryption experiment tests

The encryption and decryption results are shown in Fig. 7. Four plain images are used in the encryption phase, including “Lena”, “Horse”, “Cameraman” and “Cameo”, where “Cameo” is a computer generated image. From Fig. 7 we know that all the encrypted images are completely unrecognized. In the decryption phase, as the results are quite similar, so we only present the decryption results of Lena image here. By using the correct keys, the decrypted image is the same as the plain image, while with a wrong key, the decrypted image is also unrecognized.

Fig. 7
figure 7

Encryption and decryption results (a) Lena plain image; (b) Lena encrypted image; (c) Horse plain image; (d) Horse encrypted image; (e) Cameo plain image; (f) Cameo encrypted image; (g) Cameraman plain image; (h) Cameraman encrypted image; (i) Decryption of Lena image with correct key; (j) Decryption of Lena image with wrong key

Full size image

5.2 Histogram analysis

The histogram is use to evaluate the distribution of ciphered image. In order to withstand the statistical attack and cipher-only attack, the histogram should be uniform. The histogram of plain Lena image and the encrypted Lena image are shown in Fig. 8, which indicates that the distribution of our encrypted image is rather uniform comparing to the plain image.

Fig. 8
figure 8

Statistical histogram of (a) Lena plain image; (b) Lena encrypted image

Full size image

5.3 Information entropy analysis

Information entropy, proposed by Shannon, is widely used to evaluate the uncertainty or unpredictability, and can be calculated as

$$ H(m)=-\sum \limits_{i=1}^Mp\left({m}_i\right){\log}_2p\left({m}_i\right) $$
(24)

here, M is the total number if symbols, and p(mi) is the probability of symbol mi. For a random image with 256 Gy levels, the entropy should ideally be 8. In this test, the entropies of plain image and encrypted image are calculated in Table 1, which indicates that the entropies of the encrypted images by our encryption algorithm are all close to 8, and is better than the results in [15, 17, 20], but a little less than the entropy in [16].

Table 1 Information entropy analysis of plain image and encrypted image
Full size table

5.4 Key space analysis

The key space should be large enough to resist brute-force attacks. In our proposed encryption algorithm, values x0,1, x0,2, ..., x0,T, y0,1, y0,2, ..., y0,T and b1, b2, ..., bT are always be selected as security keys. If the precision of a real number is 10−14, the key space of our algorithm can be approximately written as.

$$ {\left(\frac{1}{4}\cdot {10}^{14}\cdot {10}^{14}\cdot {10}^{14}\right)}^T $$
(25)

Set the round T = 2. the key space is about 0.25 × 1084 ≈ 2277, which is large enough to resist all kinds of brute-force attacks and is much larger than some recently proposed algorithms, such as 2160 in [17], 2140 in [16], and 2256 in [8], under the same precision.

5.5 Key sensitivity analysis

A good encryption scheme should be extremely sensitive to its security key. Key sensitivity means that for the same plain image, if there is a small change (only 1 bit) of the secret keys, the encrypted image should be totally different. In this test, we test the key sensitivity of x0,1 and b1, the sensitivity of y0,1 is similar which we omitted here. Change each secret key by only 10−14, the test results are shown in Fig. 9.

Fig. 9
figure 9

Key sensitivity analysis in the encryption process

Full size image

Figure 9a is the encrypted image by changing the key x0,1 to 0.1236 + 10−14. Figure 9b shows the difference between Fig. 9a and Fig. 7b, which is vastly different from each other. Figure 9c is the encrypted image by changing the key b1 to 4 + 10−14. Figure 9d shows the difference between Fig. 9c and Fig. 7b, which is totally different from each other as well. These results show that the security keys have good sensitivity.

5.6 Correlation analysis

The pixels of a plain image always have a high correlation with their neighboring pixels, either in horizontal, vertical or diagonal directions. Therefore, a good image encryption algorithm should remove this strong correlation between adjacent pixels.

In this test, we first randomly select 2040 pairs of adjacent pixels along with the horizontal, vertical and diagonal directions. The distributions of these pixel sequence pairs are plot in Fig. 10. From Fig. 10, we have that the points of plain Lena image are located nearby the diagonal line, while the points of encrypted Lena image are uniformly located in the whole space. These results show that we can remove the correlation between adjacent pixels.

Fig. 10
figure 10

Distributions of adjacent pixel sequence pairs of Lena image (a) horizontal of plain image; (b) vertical of plain image; (c) diagonal of plain image; (d) horizontal of encrypted image; (e) vertical of encrypted image; (f) diagonal of encrypted image

Full size image

Furthermore, we test the correlation coefficient of pixel sequence pairs by using the following equation

$$ Corr=\frac{N{\sum}_{i=1}^N\left({x}_i\times {y}_i\right)-{\sum}_{i=1}^N{x}_i\times {\sum}_{i=1}^N{y}_i}{\sqrt{\left(N{\sum}_{i=1}^N{x}_i^2-{\left({\sum}_{i=1}^N{x}_i\right)}^2\right)\times \left(N{\sum}_{i=1}^N{y}_i^2-{\left({\sum}_{i=1}^N{y}_i\right)}^2\right)}} $$
(26)

where xi and yi be the two pixel sequences, N is the length. If the correlation value is close to 1, then these two sequences have a high correlation. If the correlation value is close to 0, then these two sequences have little correlation with each other. The value of Corr for each pair is shown in Table 2. From Table 2 we have that the correlation coefficients of our encrypted images are all close to 0, which also means that our algorithm has successfully disrupted the correlation between adjacent pixels. Some comparisons to other proposed methods show that our algorithm is quite competitive.

Table 2 Correlation analysis
Full size table

5.7 Resistance to differential attack analysis

The differential attack, also called the chosen-plaintext attack, is a well-known and effective image analysis method. To resist the differential attack, the algorithm should have good sensitivity to plaintext. Two measures are often used to evaluate this property, which are the number of pixels change rate (NPCR) and unified average changing intensity (UACI), and can be calculated as Eq. (27) and (29), respectively [3].

$$ \mathrm{NPCR}=\frac{\sum \limits_{i,j}D\left(i,j\right)}{L}\times 100\% $$
(27)
$$ D\left(i,j\right)=\left\{\begin{array}{l}0,\kern0.75em {C}_1\left(i,j\right)={C}_2\left(i,j\right)\\ {}1,\kern0.75em {C}_1\left(i,j\right)\ne {C}_2\left(i,j\right)\end{array}\right. $$
(28)
$$ \mathrm{UACI}=\frac{1}{L}\left[\sum \limits_{i,j}\frac{\mid {C}_1\left(i,j\right)-{C}_2\left(i,j\right)\mid }{H}\right]\times 100\% $$
(29)

Where C1 and C2 are two images with the same size, L is the number of pixels and H is the largest allowed pixel value in the images. In our test, L = 65,536, H = 255. For the random gray image, the ideal value of NPCR and UACI are 0.9961 and 0.3346, respectively.

We randomly change 1 bit of the plain image. The values of NPCR and UACI of two encrypted images with the same keys are shown in Table 3. Table 3 indicates that both NPCR and UACI values of all images are close to the ideal value, which means that our encryption algorithm has good performance to resist the differential attack.

Table 3 Sensitivity to plaintext test
Full size table

5.8 Randomness analysis

In our substitution algorithm, we use Eq. (22) to generate the sequence {dk} with uniformly distributed. Here, we further evaluate the randomness of these sequences by using NIST sp-800-22 test suites.

The significance level of each test in NIST is set to 0.01, which means that 99% of test samples pass the tests if the random numbers are truly random. The P-value ≥ 0.01 would mean that the sequence would be considered to be random with a confidence of 0.99. In this test, we have generated 500 different sequences randomly by using different initial values and parameter, each sequence having a length of 125,000. Use Eq. (22) to change these sequences into integer sequences. By coding dk into binary sequence with 8 b, (as: 0 is encoded into “00000000” and 255 is encoded into “11,111,111”), we can totally get 500 pseudorandom binary sequences with length 1,000,000. We test the passing ratio of each test from the NIST test suite and the uniformity of the p-values of each test. The results are shown in Table 4. From Table 4 we know that the sequences have passed all tests suite, which can be regarded as random.

Table 4 The passing ratio and the uniformity of the p-values of each test from the NIST suite
Full size table

6 Conclusions

In this paper, we propose a new simple one-dimensional chaotic map. The bifurcation of this system is analyzed by both theoretical and experimental methods. The Lyapunov exponent is also calculated by numerical simulation. The results show that the chaotic characteristics of this new map have no correlation to the parameter b. Furthermore, we propose a new image encryption algorithm based on this new chaotic map. Many statistical tests and security analysis are carried out to evaluate our algorithm, including histogram analysis, information entropy analysis, key space analysis, key sensitivity analysis, correlation analysis, resistance to differential attack analysis, and randomness analysis. The results show that our algorithm has an excellent security performance, and can be competitive with some other recently proposed image encryption algorithms. Four different plain images are test here, including natural image and computer generated image. The results also show that our algorithm is effective to different images, and has no content dependency.