Semi-supervised minimum redundancy maximum relevance feature selection for audio classification

Abstract

It is still a changing problem of choosing the most relevant ones from multiple features for their specific machine learning tasks. However, feature selection provides an effective solution to it, which aims to choose the most relevant and least redundant features for data analysis. In this paper, we present a feature selection algorithm termed as semi-supervised minimum redundancy maximum relevance. The relevance is measured by a semi-supervised filter score named constraint compensated Laplacian score, which takes advantage of the local geometrical structures of unlabeled data and constraint information from labeled data. The redundancy is measured by a semi-supervised Gaussian mixture model-based Bhattacharyya distance. The optimal feature subset is selected by maximizing feature relevance and minimizing feature redundancy simultaneously. We apply our algorithm in audio classification task and compare it with other known feature selection methods. Experimental results further prove that our algorithm can lead to promising improvements.

1 Introduction

In the field of machine learning, especially in audio related fields, there are numerous features for choices in model construction for each specific application. However, it is still a challenging problem that how we can choose the most relevant features to construct a more effective model. It may need very professional background knowledge, yet it can be solved by automatic feature selection [39]. Feature selection produces features which are more discriminative or easier for statistical modeling and hence promises higher accuracy by removing the irrelevant and redundant features [17].

From class information utilizations, feature selection can be divided into three categories: supervised [30], unsupervised [9, 10], or semi-supervised [33]. Supervised approaches need lots of labeled data, and they are apt to ignore the internal structures of data whereas focus too much on label information. Due to the absence of class labels, unsupervised feature selection fails to extract more discriminative features which may yield worse performance. Semi-supervised feature selection focuses on solving the small-labeled-sample problem [37], where the amount of unlabeled data is much larger than that of labeled data. This type of algorithm has attracted more attentions for its comprehensive considerations of label information and data intrinsic structure characteristics.

From the perspective of selection strategy, feature selection are categorized as filter, wrapper and embedded. The filter methods use scores or confidences to evaluate the relevance of features to the learning tasks. There are various kind of filter based algorithms, for example, Laplacian score (LS) [18], constraint score (CS) [36] and constraint compensated Laplacian score (CCLS) [34]. The wrapper approaches evaluate the different subsets of features by some specific learning algorithms and select the one with the best performance. The embedded model techniques search the most relevant and effective features for models while their constructions. The most common embedded methods are regularization-based [11], e.g., C4.5 [24] and LARS [12].

Since the filter methods are irrelevant to any specific classification or learning methods, they have been widely used for their better generalization properties. However, it may be very simple to select the top-ranked features only based on the feature relevance, because these features could be correlated among themselves. In other words, the set of selected features contains a certain redundancy, and this redundancy will degrade the learning performances and complicate the models. Several studies have addressed influences of such redundancy [2, 8, 35]. Among them, the most famous one is minimum redundancy maximum relevancy (mRMR) algorithm [23] in which the features are selected by simultaneously optimizing the minimum redundancy and the maximum relevance conditions. For mRMR algorithm, either redundancy between features or relevance between the features and the corresponding classes is measured by mutual information (MI). However, when the values of feature vectors are continuous, both types of MI are difficult to compute because it needs to calculate integral which limits the application ranges of mRMR algorithm most in discrete data like genes.

In this paper, we propose a new feature selection algorithm which selects the optimal feature set similar to mRMR. Rather than using MI to measure relevance and redundancy, a novel semi-supervised relevance measurement named constraint compensated Laplacian score (CCLS) is proposed and a semi-supervised Gaussian mixture model (GMM)-based Bhattacharyya distance [5] is used as the score of minimum redundancy. In traditional Laplacian score, the features are evaluated according to their locality preserving abilities. Compared to unsupervised constructions of local and global structures in Laplacian score, CCLS uses constraint information generated from a small amount of labeled data to compensate these constructions. The GMM-based Bhattacharyya distance first classifies the unlabeled data in training dataset according to the labeled data, and then a GMM is used to model the data of each class. Finally, the redundancy is measured by the Bhattacharyya distance calculated from these GMMs. Because the relevance and redundancy measurements in our algorithm are both semi-supervised, our algorithm is termed as semi-Supervised minimum redundancy maximum relevance (SSMRMR).

We use SSMRMR in audio classification. In this application, there are dozens of features to be utilized and we have to pick up effective ones or their combinations. The experimental results proved that CCLS outperformed classical LS and CS and the GMM-based Bhattacharyya distance was superior to the correlation-based or mutual information-based redundancy measurements. Moreover, the SSMRMR could remove irrelevant features and improve classification accuracy significantly.

The outline of this paper is as follows: definitions and notations are given in Section 2. Section 3 enumerates several main methods used in feature selections. Then we present our SSMRMR algorithm in Section 4. Section 5 depicts the backgrounds of audio classifications, experimental setup and analysis results. Finally, the conclusion is given in Section 6.

2 Definitions and notations

In this section, we will provide basic terminologies and notations which are necessary for the understanding of subsequent algorithms.

In this work, let the training dataset with N instances be X = {x _i  ∈ ℝ ^M| i = 1, 2,  ⋯ , N}. LetF ₁ , F ₂ ,  ⋯  , F _M denote the M features of X and f ₁ , f ₂ ,  ⋯  , f _M denote the corresponding feature vectors. Let f _ri denote the r-th feature of the i-th instance x _i , i = 1 , 2 ,  ⋯  , N, r = 1 , 2 ,  ⋯  , M. More specifically,

$$ \mathrm{X}=\left[{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots, {\mathbf{x}}_N\right]=\left[\begin{array}{cccc}\hfill {f}_{11}\hfill & \hfill {f}_{12}\hfill & \hfill \cdots \hfill & \hfill {f}_{1N}\hfill \\ {}\hfill {f}_{21}\hfill & \hfill {f}_{22}\hfill & \hfill \cdots \hfill & \hfill {f}_{2N}\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill \\ {}\hfill {f}_{M1}\hfill & \hfill {f}_{M2}\hfill & \hfill \cdots \hfill & \hfill {f}_{MN}\hfill \end{array}\right]={\left[{\mathbf{f}}_1^{\mathrm{T}},{\mathbf{f}}_2^{\mathrm{T}},\cdots, {\mathbf{f}}_M^{\mathrm{T}}\right]}^{\mathrm{T}} $$

(1)

which means f _r  = [f _r1, f _r2,  ⋯ , f _rN ]^T and x _i  = [f _1i , f _2i ,  ⋯ , f _Mi ]^T.

In semi-supervised learning, the training dataset X can be divided into two subsets. The first contains data X^l = {x ₁, x ₂,  ⋯ , x _L } with labels Y^l = {y ₁, y ₂,  ⋯ , y _L | y _i  = 1, 2,  ⋯ , C}, where C is the number of classes and L is the number of labeled data. And the second one only has the unlabeled data X^u = {x _L + 1, x _L + 2,  ⋯ , x _N }.

Define ${\mu}_r^l={\sum}_{i\Big|{\mathbf{x}}_i\in {\mathrm{X}}^l}{f}_{ri}/L$ is the mean of the r-th feature of the labeled data. Define μ _r and ${\mu}_r^{(c)}$ be the r-th feature means of the whole dataset and the c-th class respectively, ${\sigma}_r^2$ and ${\left({\sigma}_r^{(c)}\right)}^2$ denote its corresponding variances. n _c is the number of instances corresponding to the class c.

For any pair of instances (x _i , x _j ) in X^l, there are two types of constraints: must-link (ML) and cannot-link (CL). The ML constraint is constructed if x _i and x _j have the same class label, and the CL constraint is formed when x _i and x _j belong to different classes. Then, according to ML and CL constraints, the data are grouped into two sets Ω _ML and Ω _CL , respectively.

From the consideration of data geometric structure, there are a set of pairwise instances similarity measures which can be used to represent the relationships between two instances. In this paper, we choose the RBF kernel function to be the similarity measure for its unsupervised property. The similarity w _ij between x _i and x _j is defined by:

$$ {w}_{ij}={e}^{-\frac{{\left\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\right\Vert}^2}{2{\sigma}^2}} $$

(2)

where, σ is a constant and ${\left\Vert \cdotp \right\Vert}^2$ is the square of Euclidian norm.

3 Related work

In this section, we shall list a collection of scores which are bases for the score functions of our framework. We illustrate both advantages and disadvantages of Laplacian score and constraint score. Moreover, the framework of mRMR is presented.

3.1 Laplacian score

Laplacian Score is a recently proposed unsupervised feature selection method [18]. The basic idea is to evaluate the features according to their locality preserving ability. If two data points are close to each other, they belong to the same class with high probability. So the local structure is more important than global structure in many machine learning problems, especially for classification tasks. The Laplacian score of the r-th feature is computed as follows:

$$ {L}_r=\frac{\sum_{i,j}{\left({f}_{ri}-{f}_{rj}\right)}^2{S}_{ij}}{\sum_i{\left({f}_{ri}-{u}_r\right)}^2{D}_{ii}} $$

(3)

where, ${u}_r={\sum}_{i=1}^N{f}_{ri}/N$ denotes the mean of the r-th feature of the whole data set, D is a diagonal matrix with D _ii  = ∑ _j S _ij , and S denotes the similarity matrix whose nonzero element is the RBF kernel function defined in Eq. (2):

$$ {S}_{ij}=\left\{\begin{array}{l}{w}_{ij}\kern2.5em \mathrm{if}\kern0.5em {\mathbf{x}}_i\kern0.5em \mathrm{and}\kern0.5em {\mathbf{x}}_j\kern0.5em \mathrm{are}\kern0.5em \mathrm{neighbors}\\ {}0\kern3.4em \mathrm{otherwise}\end{array}\right. $$

(4)

where, x _i and x _j are neighbors which means that x _i is among k nearest neighbors of x _j or x _j is among the k nearest neighbors of x _i .

In the score function in Eq. (3), the numerator indicates the locality preserving power of the r-th feature, the smaller the better. The denominator is the estimated variance of the r-th feature, the bigger the better. Thus, the criterion of LS for choosing a good feature is to minimize the object function in Eq. (3).

Compared to other unsupervised feature selection algorithms [9, 10], the main advantage of LS is its powerful locality preserving ability which can be thought of as the degree a feature respects the nearest neighbor graph structure. However, there is some blindness when LS constructs the local structure of data space without supervised information.

3.2 Constraint score

Constraint Score is a supervised feature selection algorithm which need small amount of labeled data [36]. Firstly, the pairwise instances level constraints between any two data points, ML and CL constraints, are generated using the data labels, and the score function C _r is computed as follows using these pairwise constraints:

$$ {C}_r=\frac{\sum_{\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)\in {\Omega}_{ML}}{\left({f}_{ri}-{f}_{rj}\right)}^2}{\sum_{\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)\in {\Omega}_{CL}}{\left({f}_{ri}-{f}_{rj}\right)}^2} $$

(5)

In this score function, a good feature means that two ML-constraint point pair should be close to each other, CL-constraint point pair should be far away from each other. So the constraint score of the r-th feature should be minimized. CS feature selection algorithm is particularly applied to the cases where very few labeled training data are available. In these cases, CS can select a reliable feature subset only based on the limited training data. However, when there are large amount of unlabeled data in the training set, how to use these unlabeled samples to improve performance is still a challenge problem.

3.3 Minimum redundancy maximum relevancy

The mRMR algorithm focuses on MI-based feature selection. Given two random variables z ₁ and z ₂, suppose that p(z ₁), p(z ₂), and p(z ₁, z ₂) are their marginal and joint probabilistic density functions. Their mutual information is defined as follows:

$$ I\left({z}_1,{z}_2\right)=\int \int p\left({z}_1,{z}_2\right) \log \frac{p\left({z}_1,{z}_2\right)}{p\left({z}_1\right)p\left({z}_2\right)}{dz}_1{dz}_2 $$

(6)

The mRMR feature set is obtained by minimum redundancy condition and maximum relevance condition simultaneously, either in quotient form:

$$ \underset{\Lambda \subset \Omega}{ \max}\left\{{\sum}_{{\mathbf{f}}_i\in \Lambda}I\left(\mathrm{Y},{\mathbf{f}}_i\right)/\left[\frac{1}{\left|\Lambda \right|}{\sum}_{{\mathbf{f}}_i,{\mathbf{f}}_j\in \Lambda}I\left({\mathbf{f}}_{i,}{\mathbf{f}}_j\right)\right]\right\} $$

(7)

or in difference form:

$$ \underset{\Lambda \subset \Omega}{ \max}\left\{{\sum}_{{\mathbf{f}}_i\in \Lambda}I\left(\mathrm{Y},{\mathbf{f}}_i\right)-\left[\frac{1}{\left|\Lambda \right|}{\sum}_{{\mathbf{f}}_i,{\mathbf{f}}_j\in \Lambda}I\left({\mathbf{f}}_{i,}{\mathbf{f}}_j\right)\right]\right\} $$

(8)

where, Λ is the features subset under seeking and Ω is the set of entire candidate features. |Λ| is the number of features in Λ. I(Y, f _i ) is the MI between the feature f _i and its corresponding classes Y. I(f _i , f _j ) is MI between feature f _i and f _j .

For discrete (categorical) feature variables, the MI is easy and straightforward to be calculated, because the integral operation is reduces to summation, and moreover the probability can be approximated by counting the instances of discrete variables in the data based on ML criterion.

However, it is hard to compute the MI when the feature variables are continuous. Because only based on a limited number of instances, it is difficult to compute the integral in the continuous space. To solve this problem, one can either discretize the continuous data before computing MI [28], or use density estimation method to estimate MI approximately [19].

4 Semi-supervised minimum redundancy maximum relevance feature selection

In the following sections, we present the score of maximum relevance (constraint compensated Laplacian score) and the score of minimum redundancy (GMM-based Bhattacharyya distance) in our framework for feature selection. We also present the objective function of our algorithm and its approximate solution.

4.1 Feature relevance

4.1.1 Score function

In order to take advantages of both LS and CS as well as to overcome their shortcomings, we propose the constraint compensated Laplacian score algorithm [34]. The score function, which should be minimized, is defined as follows:

$$ {\eta}_r=\frac{\sum_{i,j}{\left({f}_{ri}-{f}_{rj}\right)}^2\left({S}_{ij}+{\overline{\mathcal{N}}}_{ij}\right)}{\Sigma_r+{\Sigma}_r^b-{\Sigma}_r^w} $$

(9)

where,

$$ {\overline{\mathcal{N}}}_{ij}=\left\{\begin{array}{l}1-{w}_{ij}\kern1em {\mathbf{x}}_i\kern0.5em \mathrm{and}\kern0.5em {\mathbf{x}}_j\kern0.5em \mathrm{are}\kern0.5em \mathrm{neighbors}\kern0.5em \\ {}\kern4.6em \mathrm{and}\kern0.5em \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)\in {\Omega}_{ML}.\\ {}-\gamma {w}_{ij}\kern0.9em {\mathbf{x}}_i\kern0.5em \mathrm{and}\kern0.5em {\mathbf{x}}_j\kern0.5em \mathrm{are}\kern0.5em \mathrm{neighbors}\\ {}\kern4.6em \mathrm{and}\kern0.5em \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)\in {\Omega}_{CL}.\\ {}\lambda \kern3.6em {\mathbf{x}}_i\kern0.5em \mathrm{and}\kern0.5em {\mathbf{x}}_j\kern0.5em \mathrm{are}\kern0.5em \mathrm{not}\kern0.5em \mathrm{neighbors}\\ {}\kern4.3em \mathrm{and}\kern0.5em \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)\in {\Omega}_{ML}.\\ {}0\kern3.7em \mathrm{otherwise}\kern0.5em \end{array}\right. $$

(10)

where, x _i and x _j are neighbors which means that x _i is among k nearest neighbors of x _j or x _j is among the k nearest neighbors of x _i . γ and λ are the parameters set using the empirical values of 0.9 and 0.5 respectively [34], S _ij is the same as Eq. (4) and is computed using both labeled and unlabeled data. Σ _r is the variance of the whole dataset X, ${\Sigma}_r^w$ and ${\Sigma}_r^b$ are inner-class variance and inter-class variance of the labeled dataset X^l, respectively.

$$ {\Sigma}_r={\sum}_i{\left({f}_{ri}-{\mu}_r\right)}^2{D}_{ii} $$

(11)

$$ {\Sigma}_r^b={\sum}_c{n}_c{\left({\mu}_r^{(c)}-{\mu}_r^l\right)}^2 $$

(12)

$$ {\Sigma}_r^w={\sum}_c{n}_c{\left({\sigma}_r^{(c)}\right)}^2 $$

(13)

And let Ψ = [η _r |r = 1, 2,  ⋯ , M] be the relevancy vector which represent the interior relevance of feature series in each dimension.

4.1.2 Spectral graph analysis

In this section, we can also give an alternative explanation based on spectral graph theory [7] for the score function described above. The basic ideal of CCLS is that: a “good” feature must have strong locality preserving power, and a good global structure. Strong locality preserving power means that the two local structures constructed by only using this feature or using the complete feature set are consistent. A good global structure means that the instances of different classes are far from each other while instances of the same class are close to each other [18].

For locality preserving power, we first construct a similarity matrix to model the local geometric structure in a semi-supervised method. And then the locality preserving power of one feature can be regard as the degree it respects the similarity matrix. The detailed procedures are as follows:

Firstly, we construct three graphs G, G ^M, and G ^C all with N nodes, which represent the information of neighbors, must-link constraints and cannot-link constraints respectively. In these graphs, the i-th node corresponds to the i-th instance x _i . We put an edge between node i and node j in G if x _i and x _j are close to each other, i.e. if x _i is one of the k nearest neighbors of x _j or x _j is one of the k nearest neighbors of x _i , G _ij  = 1 . We put an edge between node i and node j in G ^M if there is a must-link constraint between x _i and x _j , which means if (x _i , x _j ) ∈ Ω _ML , ${G}_{ij}^M=1$. Similarly, We put an edge between node i and node j in G ^C if there is a cannot-link constraint between x _i and x _j , namely if (x _i , x _j ) ∈ Ω _CL , ${G}_{ij}^C=1$.

Once these graphs are constructed, we define the similarity matrix S whose elements are defined as follow:

$$ {\mathcal{S}}_{ij}=\left\{\begin{array}{l}1\kern7.6em \mathrm{if}\kern0.5em {G}_{ij}=1\kern0.5em \mathrm{and}\kern0.5em {G}_{ij}^M=1.\\ {}\left(1-\gamma \right){w}_{ij}\kern1.4em \mathrm{if}\kern0.5em {G}_{ij}=1\kern0.5em \mathrm{and}\kern0.5em {G}_{ij}^C=1.\\ {}\lambda \kern6.8em \mathrm{if}\kern0.5em {G}_{ij}=0\kern0.5em \mathrm{and}\kern0.5em {G}_{ij}^M=1.\\ {}0\kern7.3em \mathrm{otherwise}\kern0.5em \end{array}\right. $$

(14)

And define the Laplacian matrix as $\mathbf{L}=\mathbf{D}-\mathbf{\mathcal{S}}$, where D is the degree matrix with ${D}_{ii}={\sum}_j{\mathcal{S}}_{ij}$. Then, we can develop the numerator term of η _r in Eq. (9) as follows:

$$ \begin{array}{c}{T}_1={\sum}_{i,j}{\left({f}_{ri}-{f}_{rj}\right)}^2{\mathcal{S}}_{ij}\\ {}={\sum}_{i,j}\left({f}_{ri}^2-2{f}_{ri}{f}_{rj}+{f}_{rj}^2\right){\mathcal{S}}_{ij}\\ {}=2\left({\sum}_{i,j}{f}_{ri}^2{\mathcal{S}}_{ij}-{\sum}_{i,j}{f}_{ri}{\mathcal{S}}_{ij}{f}_{rj}\right)\\ {}=2\left({\mathbf{f}}_r^{\mathrm{T}}{\mathbf{Df}}_r-{\mathbf{f}}_r^{\mathrm{T}}\mathbf{\mathcal{S}}\mathbf{f}\right)\\ {}=2{\mathbf{f}}_r^{\mathrm{T}}{\mathbf{Lf}}_r\end{array} $$

(15)

The global structure is modeled by variance Σ _r of the whole dataset X, and both inner-class variance ${\Sigma}_r^w$ and inter-class variance ${\Sigma}_r^b$ of the labeled dataset X^l. To compute Σ _r , define 1 = [1, 1,  ⋯ , 1], let

$$ {\tilde{\mathbf{f}}}_r={\mathbf{f}}_r-\frac{{\mathbf{f}}_r^{\mathrm{T}}\mathbf{D}1}{1^{\mathrm{T}}\mathbf{D}1}1 $$

(16)

And according to [18],

$$ \begin{array}{c}{\Sigma}_r={\sum}_i{\left({f}_{ri}-{\mu}_r\right)}^2{D}_{ii}\\ {}={\sum}_i{\left({f}_{ri}-{\sum}_j{f}_{rj}\frac{D_{jj}}{\sum_k{D}_{kk}}\right)}^2{D}_{ii}\\ {}={\sum}_i{\left({f}_{ri}-\frac{1}{\sum_k{D}_{kk}}{\sum}_j{f}_{rj}{D}_{jj}\right)}^2{D}_{ii}\\ {}={\sum}_i{\left({f}_{ri}-\frac{{\mathbf{f}}_r^{\mathrm{T}}\mathbf{D}1}{1^{\mathrm{T}}\mathbf{D}1}\right)}^2{D}_{ii}\\ {}={\sum}_i{\tilde{f}}_{ri}^2{D}_{ii}\\ {}={\tilde{\mathbf{f}}}_r^{\mathrm{T}}\mathbf{D}{\tilde{\mathbf{f}}}_r\end{array} $$

(17)

To compute ${\Sigma}_r^w$ and ${\Sigma}_r^b$, a similarity matrix ${\mathbf{\mathcal{S}}}^l$ is defined, whose elements are as follows:

$$ {\mathcal{S}}_{ij}^l=\left\{\begin{array}{l}1/{n}_c\kern2.5em {y}_i={y}_j=c\\ {}0\kern3.4em \mathrm{otherwise}\end{array}\right. $$

(18)

To simplify, we assume the instances are ordered according to their labels and the unlabeled data points are appended after the labeled ones. Thus, ${\mathbf{\mathcal{S}}}^l$ can be written as follows:

$$ {\mathbf{\mathcal{S}}}^l=\left[\begin{array}{l}\begin{array}{c}\hfill {\mathbf{\mathcal{S}}}_1^l\hfill \\ {}\hfill 0\hfill \\ {}\hfill 0\hfill \end{array}\kern1em \begin{array}{c}\hfill 0\hfill \\ {}\hfill \ddots \hfill \\ {}\hfill 0\hfill \end{array}\kern1em \begin{array}{c}\hfill 0\hfill \\ {}\hfill 0\hfill \\ {}\hfill {\mathbf{\mathcal{S}}}_C^l\hfill \end{array}\kern1em 0\\ {}\kern3em 0\kern4em 0\end{array}\right] $$

(19)

where, ${\mathbf{\mathcal{S}}}_c^l$ is a n _c  × n _c matrix whose elements are 1/n _c and 0 is a matrix whose elements are all zero.

And define the Laplacian matrix as ${\mathbf{L}}^l={\mathbf{D}}^l-{\mathbf{\mathcal{S}}}^l$, where D ^l are the degree matrix with ${D}_{ii}^l={\sum}_j{\mathcal{S}}_{ij}^l$. Note that for each ${\mathbf{\mathcal{S}}}_c^l$, the raw sum is equal to 1, so

$$ {\mathbf{D}}^l=\left[\begin{array}{l}\begin{array}{c}\hfill {\mathbf{D}}_1^l\hfill \\ {}\hfill 0\hfill \\ {}\hfill 0\hfill \end{array}\kern1em \begin{array}{c}\hfill 0\hfill \\ {}\hfill \ddots \hfill \\ {}\hfill 0\hfill \end{array}\kern1em \begin{array}{c}\hfill 0\hfill \\ {}\hfill 0\hfill \\ {}\hfill {\mathbf{D}}_C^l\hfill \end{array}\kern1em 0\\ {}\kern3em 0\kern4em 0\end{array}\right]=\left[\begin{array}{cc}\hfill {\mathbf{I}}_L\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill \end{array}\right] $$

(20)

where, I _L is a L × L identity matrix in which L is the number of the labeled data as given in the Section 2, and ${\mathbf{D}}_c^l$ is a n _c  × n _c identity matrix.

Thus, the inner-class covariance ${\Sigma}_r^w$ can be developed as follows:

$$ \begin{array}{c}{\Sigma}_r^w={\sum}_c{n}_c{\left({\sigma}_r^{(c)}\right)}^2\\ {}={\sum}_c{n}_c\mathrm{c}\mathrm{o}\mathrm{v}\left({\mathbf{f}}_r^{(c)},{\mathbf{f}}_r^{(c)}\right)\\ {}={\sum}_c{\left({\mathbf{f}}_r^{(c)}\right)}^{\mathrm{T}}\left({\mathbf{D}}_c^l-{\mathbf{\mathcal{S}}}_c^l\right){\mathbf{f}}_r^{(c)}\\ {}={\mathbf{f}}_r^{\mathrm{T}}{\mathbf{L}}^l{\mathbf{f}}_r={\left({\tilde{\mathbf{f}}}_r^l\right)}^{\mathrm{T}}{\mathbf{L}}^l{\tilde{\mathbf{f}}}_r^l\end{array} $$

(21)

where, ${\mathbf{f}}_r^{(c)}$ is an N × 1 vector whose elements are as follows:

$$ {f}_{ri}^{(c)}=\left\{\begin{array}{l}{f}_{ri}\kern2.5em \mathrm{if}\kern0.5em {y}_i=c\\ {}0\kern3.4em \mathrm{otherwise}\end{array}\right. $$

(22)

and

$$ {\tilde{\mathbf{f}}}_r^l={\mathbf{f}}_r-\frac{{\mathbf{f}}_r^{\mathrm{T}}{\mathbf{D}}^l1}{1^{\mathrm{T}}{\mathbf{D}}^l1}1 $$

(23)

and the inter-class covariance ${\Sigma}_r^b$ can be develop as follows:

$$ \begin{array}{c}{\Sigma}_r^b={\sum}_c{n}_c{\left({\mu}_r^{(c)}-{\mu}_r^l\right)}^2\\ {}={\sum}_c\left({n}_c{\left({\mu}_r^{(c)}\right)}^2-2{n}_c{\mu}_r^{(c)}{\mu}_r^l+{n}_c{\left({\mu}_r^l\right)}^2\right)\\ {}={\sum}_c\frac{1}{n_c}{\left({n}_c{\mu}_r^{(c)}\right)}^2-2{\mu}_r^l{\sum}_c{n}_c{\mu}_r^{(c)}+{\left({\mu}_r^l\right)}^2{\sum}_c{n}_c\\ {}={\sum}_c\frac{1}{n_c}{\left({\mathbf{f}}_r^{(c)}\right)}^{\mathrm{T}}{11}^{\mathrm{T}}{\mathbf{f}}_r^{(c)}-2L{\mu}_r^l+L{\left({\mu}_r^l\right)}^2\\ {}={\left({\mathbf{f}}_r^{(c)}\right)}^{\mathrm{T}}{\mathbf{\mathcal{S}}}^l{\mathbf{f}}_r^{(c)}-{\left({\mathbf{f}}_r^{(c)}\right)}^{\mathrm{T}}\left(\frac{1}{L}{11}^{\mathrm{T}}\right){\mathbf{f}}_r^{(c)}\\ {}={\left({\mathbf{f}}_r^{(c)}\right)}^{\mathrm{T}}\left({\mathbf{D}}^l-{\mathbf{\mathcal{S}}}^l\right){\mathbf{f}}_r^{(c)}-{\left({\mathbf{f}}_r^{(c)}\right)}^{\mathrm{T}}\left({\mathbf{D}}^l-\frac{1}{L}{11}^{\mathrm{T}}\right){\mathbf{f}}_r^{(c)}\\ {}={\left({\tilde{\mathbf{f}}}_r^l\right)}^{\mathrm{T}}{\mathbf{L}}^l{\tilde{\mathbf{f}}}_r^l-{\left({\tilde{\mathbf{f}}}_r^l\right)}^{\mathrm{T}}{\mathbf{D}}^l{\tilde{\mathbf{f}}}_r^l\end{array} $$

(24)

Thus,

$$ {T}_2={\Sigma}_r+{\Sigma}_r^b-{\Sigma}_r^w={\tilde{\mathbf{f}}}_r^{\mathrm{T}}\mathbf{D}{\tilde{\mathbf{f}}}_r+2{\left({\tilde{\mathbf{f}}}_r^l\right)}^{\mathrm{T}}{\mathbf{L}}^l{\tilde{\mathbf{f}}}_r^l-{\left({\tilde{\mathbf{f}}}_r^l\right)}^{\mathrm{T}}{\mathbf{D}}^l{\tilde{\mathbf{f}}}_r^l $$

(25)

Subsequently, the CCLS can be computed as follows:

$$ {\eta}_r=\frac{2{\mathbf{f}}_r^{\mathrm{T}}{\mathbf{L}\mathbf{f}}_r}{{\tilde{\mathbf{f}}}_r^{\mathrm{T}}\mathbf{D}{\tilde{\mathbf{f}}}_r+2{\left({\tilde{\mathbf{f}}}_r^l\right)}^{\mathrm{T}}{\mathbf{L}}^l{\tilde{\mathbf{f}}}_r^l-{\left({\tilde{\mathbf{f}}}_r^l\right)}^{\mathrm{T}}{\mathbf{D}}^l{\tilde{\mathbf{f}}}_r^l} $$

(26)

The whole procedure of the proposed CCLS is summarized in Algorithm 1. Now we analyze the time complexity of Algorithm 1. Step 1 constructs the constraint set requiring O(L ²) operations. Step 2–3 build the graph matrices requiring O(N ²) operations. Step 4–6 evaluate the M features based on graphs, requiring O(MN ²) operations. Step 7 ranks the M features according to their scores requiring O(M log M) operations. Thus, the overall time complexity of Algorithm 1 is O(M ×  max (N ², logM)).

4.2 Feature redundancy

In this section, to evaluate the effectiveness of features, some measurements of redundancy between features are introduced firstly. Then, our strategy to measure similarity between features is given.

4.2.1 Measurements based on MI or correlation

Redundancy is usually characterized in terms of mutual information or correlation, in which the former one is the most widely used measure matric. MI is defined as Eq. (6), and as mentioned above, the MI is difficult to compute when at least one of the features is continuous though there have been many researches [19, 28] focusing on solving this problem.

If two features have a strong correlation between their values, it can be sure that they are redundant to each other. Thus, it is natural to use feature correlation to measure redundancy. Among the kinds of correlation coefficients, Pearson correlation coefficient is the most widely used measure. For two features F _r and F _v , the Pearson correlation coefficient between them is defined as follows:

$$ r\left({F}_r,{F}_v\right)=\frac{\sum_i\left({f}_{ri}-{\mu}_r\right)\left({f}_{vi}-{\mu}_v\right)}{\sqrt{\sum_i{\left({f}_{ri}-{\mu}_r\right)}^2}\sqrt{\sum_i{\left({f}_{vi}-{\mu}_v\right)}^2}} $$

(27)

The large |r(F _r , F _v )| means high correlation and redundancy. However, this coefficient can only measure the linear correlation properties, which may cause more errors when the relationship between features is non-linear.

4.2.2 GMM-based Bhattacharyya distance

Besides MI and correlation, redundancy can also be measured by the distance function. For a feature F _r can be regarded as a random variable, it’s easy to extract a probabilistic distance from some parameters of the corresponding feature vector f _r with the assumption of underlying distributions. It has been observed that Bhattacharyya distance is more effective than other distance functions like Euclidean, Kullback-Leibler, and Fisher [3, 20]. Moreover, The Bhattacharyya distance [13] has been used as a distance measure of vectors in feature extraction [6] and feature selection [26, 32]. Here we focus on Bhattacharyya-distance-based redundancy measurement.

In its simplest formulation, the Bhattacharyya distance between two Gaussian distributions ${g}_r\sim \mathcal{N}\left({\mathbf{m}}_r,{\boldsymbol{\Sigma}}_r\right)$ and ${g}_v\sim \mathcal{N}\left({\mathbf{m}}_v,{\boldsymbol{\Sigma}}_v\right)$ is defined as follows:

$$ {D}_B\left({g}_r,{g}_v\right)=\frac{1}{8}{\left({\mathbf{m}}_r-{\mathbf{m}}_v\right)}^{\mathrm{T}}{\left[\frac{{\boldsymbol{\Sigma}}_r+{\boldsymbol{\Sigma}}_v}{2}\right]}^{-1}\left({\mathbf{m}}_r-{\mathbf{m}}_v\right)+\frac{1}{2} \ln \frac{\left|\frac{{\boldsymbol{\Sigma}}_r+{\boldsymbol{\Sigma}}_v}{2}\right|}{\sqrt{\left|{\boldsymbol{\Sigma}}_r\right|\left|{\boldsymbol{\Sigma}}_v\right|}} $$

(28)

where, $\mathcal{N}\left({\mathbf{m}}_r,{\boldsymbol{\Sigma}}_r\right)$ represents a multi-dimensional Gaussian distributions with mean vector m _r and covariance matrix Σ _r :

$$ \mathcal{N}\left({\mathbf{m}}_r,{\boldsymbol{\Sigma}}_r\right)=\frac{1}{{\left(2\pi \right)}^{M^{\prime }/2}{\left|{\boldsymbol{\Sigma}}_r\right|}^{1/2}} \exp \left\{-\frac{{\left({\mathbf{o}}_r-{\mathbf{m}}_r\right)}^{\mathrm{T}}{\boldsymbol{\Sigma}}_r^{-1}\left({\mathbf{o}}_r-{\mathbf{m}}_r\right)}{2}\right\} $$

(29)

and o _r is the random variable and M ^′ is its dimension. So does $\mathcal{N}\left({\mathbf{m}}_v,{\boldsymbol{\Sigma}}_v\right)$.

The feature F _r (or F _v ) is naturally treated as a random variable which follows single Gaussian distribution which mean (m _r or m _v ) and variance (Σ _r or Σ _v ) can be estimated from f _r (or f _v ). Then, the Bhattacharyya distance D _B (g _r , g _v ) can be used to measure the redundancy between F _r and F _v .

However, it remains in doubt whether it is suitable to approximate the distribution of F _r by single Gaussian, because F _r contains data of at least two classes. Thus, a GMM-based Bhattacharyya distance to measure the feature redundancy is proposed, which can be stated as follows:

• (1) The unlabeled data in X^u is classified by using the nearest neighborhood (1-NN) classifier based on the labeled data in X^l. Then, the “labels” of the unlabeled data is Y^u = {y _L + 1, y _L + 2,  ⋯ , y _N | y _i  = 1, 2,  ⋯ , C}.

• (2) For the r-th feature F _r , we normalize its feature vector f _r to be a new vector ${\mathbf{f}}_r^{\mathbf{\prime}}$ with zero mean and unit variance:

  $$ {\mathbf{f}}_r^{\mathbf{\prime}}=\frac{{\mathbf{f}}_r-{\mu}_r1}{\sigma_r} $$

  (30)

• (3) Suppose ${F^{\prime}}_r^{(c)}$ is the r-th normalized feature of class c, we use a GMM estimated from ${{\mathbf{f}}^{\mathbf{\prime}}}_r^{(c)}=\left\{{f}_{ri}^{\prime}\left|{y}_i=c\right.\right\}$ to approximate its distribution:

  $$ {F^{\prime}}_r^{(c)}\sim \sum_{k=1}^{K^{(c)}}{\omega}_{r,k}^{(c)}{g}_{r,k}^{(c)} $$

  (31)

  where, K ^(c) is the number of Gaussians in the GMM for class c which is determined according to the number of instances in ${{\mathbf{f}}^{\mathbf{\prime}}}_r^{(c)}$. ${\omega}_{r,k}^{(c)}$ is the weight of the k ‐ th mixture component, and ${g}_{r,k}^{(c)}\sim \mathcal{N}\left({m}_{r,k}^{(c)},{\Sigma}_{r,k}^{(c)}\right)$ is the Gaussian distribution of the k ‐ th mixture component. Thus, the distribution of the r-th normalized feature ${F}_r^{\prime }$is:

  $$ {F}_r^{\prime}\sim \sum_c\frac{1}{C}\sum_{k=1}^{K^{(c)}}{\omega}_{r,k}^{(c)}{g}_{r,k}^{(c)} $$

  (32)

• (4) For any feature pairs (F _r , F _v ), the redundancy between them is defined as follows:

  $$ {\theta}_{rv}=\sum_c\frac{1}{C}\sum_{k=1}^{K^{(c)}}\sum_{\kappa =1}^{K^{(c)}}{\omega}_{r,k}^{(c)}{\omega}_{r,\kappa}^{(c)}{D}_B\left({g}_{r,k}^{(c)},{g}_{v,\kappa}^{(c)}\right) $$

  (33)

Define the redundancy matrix Θ whose element Θ _rv is as follows:

$$ {\Theta}_{rv}=\left\{\begin{array}{l}{\theta}_{rv}\kern2em r\ne v\\ {}0\kern2.8em r=v\end{array}\right. $$

(34)

4.3 The complete framework of SSMRMR

In this section, we will give a view of the complete framework of SSMRMR. Moreover, we will present the incremental search which obtains a near-optimal solution efficiently.

4.3.1 The objective function

Similar to mRMR, SSMRMR obtains the optimal feature set by maximum feature relevance and minimum feature redundancy simultaneously. Thus, the objective function of SSMRMR is defined as follows:

$$ \underset{\Lambda \subset \Omega}{ \min}\left\{{\sum}_{{\mathbf{f}}_r\in \Lambda}{\eta}_r^{\prime }-\frac{1}{\left|\Lambda \right|}{\sum}_{{\mathbf{f}}_r,{\mathbf{f}}_v\in \Lambda}{\Theta}_{rv}^{\prime}\right\} $$

(35)

where, ${\eta}_r^{\prime }={\eta}_r/ \max \left(\boldsymbol{\varPsi} \right)$ and ${\Theta}_{rv}^{\prime }={\Theta}_{rv}/ \max \left(\boldsymbol{\varTheta} \right)$. The normalization of these measurements is done to reduce the effect of differences in magnitude between feature relevance and redundancy.

4.3.2 Incremental search algorithm

The time complexity is O(M ^|Λ|) when the exact solution of the optimization in Eq. (35) is obtained. However, the incremental search algorithm can be used which obtains the near-optimal features with O(M ⋅ |Λ|) search. The algorithm steps are as follows:

• (1) The feature with the minimum constraint compensated Laplacian score is obtained as the first optimal feature:

  $$ {\overset{\frown }{\mathbf{f}}}_1=\underset{{\mathbf{f}}_r\subset \Omega}{ \arg \min }{\eta}_r $$

  (36)

  and ${\Lambda}_1=\left\{{\overset{\frown }{\mathbf{f}}}_1\right\}$.

• (2) To select the m-th feature, the corresponding incremental algorithm optimizes the following condition:

  $$ {\overset{\frown }{\mathbf{f}}}_m=\underset{{\mathbf{f}}_r\subset \Omega -{\Lambda}_{m-1}}{ \arg \min}\left\{{\eta}_r^{\prime }-\frac{1}{m-1}{\sum}_{{\mathbf{f}}_v\in {\Lambda}_{m-1}}{\Theta}_{rv}^{\prime}\right\} $$

  (37)

  where, Λ _m − 1 is the optimal feature set with m − 1 features.

• (3) Iterate step 2 until an expected feature number R have been obtained.

4.3.3 Complete framework

The whole procedure of SSMRMR algorithm is summarized in Algorithm 2. The relevancy vector and redundancy matrix are computed by using CCLS algorithm and GMM-based Bhattacharyya distance. Then, the optimal feature set is selected by using first-order incremental search algorithm.

5 Experimental study

In this Section, we firstly illustrate several features which have been widely used in audio classification. Then we evaluate the performance of relevance and redundancy measurements respectively. At last, we test our feature selection approach in audio classification.

5.1 Audio classification

Audio segmentation is a type of methods which split an audio stream into segments of homogeneous content. Given a predefined set of audio classes, some methods segment audios by executing iterative steps of segmentation and classification jointly, which means classification is embedded in audio segmentation in these methods. Assuming that an audio signal has been divided into a sequence of audio segments using fixed window segmentation, our works focus on categorizing these audio segments into a set of predefined audio classes. Although there may be some differences between the traditional definition of audio classification and that in our work, the essential issues are the same.

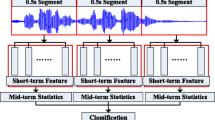
Figure 1 illustrates the process of audio classification. In an audio classification system, every audio signal is first divided into mid-length segments which duration range from 0.5 to 10 s. After this, the selected features are extracted for each segment using short-term overlapping frames. The sequence of short-term features in each segment is used to compute feature statistics, which are used as inputs to the classifier. In the final classification stage, the classifier determines a segment-by-segment decision.

Fig. 1

The audio classification framework

In audio analysis and classification there are dozens of features which can be used. Moreover, many novel feature extraction methods are proposed constantly [14, 25, 40]. In this paper, some classical and widely used acoustic features are selected for feature selection sources. Widely-used time-domain features [15] include short-term energy [22], zero-crossing rate [29], and entropy of energy [16]. Common frequency-domain features include spectral centroid, spectral spread, spectral entropy [21], spectral flux, spectral roll-off, MFCCs, and chroma vector [1].

In our system, the audio segment has been divided into 500 ms sub-segments without overlapping. And then, these sub-segments are split into overlapped 32 ms short-term frames with 10 ms frame shift, resulting 50 frames for each sub-segment. The 35 dimensional short-term feature vectors (shown in Table 1) are extracted from short-term frames. For each sub-segment, the mean and standard deviation of the corresponding 50 short-term feature vectors are computed and concatenated together, resulting 70 dimensional mid-term feature vectors which are used for classification.

Table 1 Classification accuracy of different features

5.2 Data and experimental setup

Experiments were performed using audio signals under telephone channel. Thus, each audio segment may contain speech, non-speech or silence, with more detailed classes as shown in Fig. 2. ‘Speech’ indicates direct dialogues between the calling and called users, when the call is connected, while ‘silence’ implies the segment with comfort noise. ‘Non-speech’ can be sub-classified into four types: ring, music, song, and other. ‘Ring’ contains the single-tone, dual-tone, or multi-tone used for dialing or waiting warning. ‘music’ and ‘song’ are the waiting music before the call is connected or the environmental noise when the phone is in call. ‘Other’ includes special sounds, such as laugh, barking, coughing, or other isolated sounds. To be specific, the mixed segments (speech over music) are not allowed.

Fig. 2

The audio classes in telephone channel

The database used here has been collected and manually labeled by Tsinghua University. It contains about 7 h audios with 837 real telephone recordings. The speaker in each recording is different, so does the waiting music. And the corpus consists of 204.4 min ‘speech’ data, 12.7 min ‘ring’ data, 6.3 min ‘music’ data, 6.6 min ‘song’ data, and 1.2 min ‘other’ data.

According to the label, an audio signal, which contains speech or non-speech, is divided into several 0.5 s segments. For each segment, all features mentioned in section 2 are extracted based on the short-term analysis, and the dimension of short-term feature is 35. The frame length and frame shift size are 32 ms and 10 ms, respectively. Then the two mid-term statistics, mean and standard deviation, are drawn per feature, therefore, the dimension of mid-term statistics vector is 70.

For feature selection, we choose 2000 speech segments and 2000 non-speech segments, with only 400 randomly chosen labeled segments. The γ value is set to 0.9 and λ = 0.5. We compare CCLS with existing unsupervised Laplacian Score, as well as supervised Constraint Score, Constrained Laplacian Score (CLS) [2], spectral feature selection (Spec) [38], and ReliefF [27]. The GMM-based Bhattacharyya distance is compared with MI-based and correlation-based measurements. We use a development dataset containing 200 speech segments and 200 non-speech segments to choose the optimal feature subset. And in the test dataset, there are 500 speech segments and 500 non-speech segments.

In all experiments, the k-nearest neighborhood (KNN) classifier with Euclidean distance is utilized for classification after feature selection and k = 5. To avoid the influence of the classifier, the training datasets of the classifier for all experiments are kept the same.

We use accuracy (Acc), average accuracy (Ave), optimized accuracy (Opt), and optimized number of feature (Num) to evaluate the performance of algorithms. The definitions are as follows:

$$ Acc=\frac{N_{\mathrm{correct}}}{N_{\mathrm{total}}}\times 100\% $$

(38)

where, N _correct is the number of segments which are classified correctly, and N _total is the total number of both speech segments and non-speech segments, namely N _total = 1000.

$$ Ave=\frac{1}{M}\sum_{R=1}^MAcc(R) $$

(39)

where, the mid-term feature dimension is M = 70, R is the number of selected features, and Acc(R) is the accuracy when using the selected R features for classification.

$$ Opt= \max Acc(R) $$

(40)

and

$$ Num=\underset{R}{ \arg } \max Acc(R) $$

(41)

The Num measurement is used to evaluate the redundancy of selected feature sets.

5.3 Experimental results

Ten types of short-term features extracted are listed in Table 1. Two statistics, mean and standard deviation (STD), are used as the mid-term representation of the audio segments. Table 1 shows the classification accuracies of different features for audio classification. The top 3 best features are MFCCs, chroma vector, and spectral centroid and the worst feature is short-term energy. Moreover, using all of these features does not improve but rather decreases the accuracy, as seen by comparing results using MFCC with that of all features, which indicates that there is redundant and even contradictory information among the features. Thus, it is valuable to use feature selection as a preprocessing module.

5.3.1 Feature relevance

To further illustrate the effectiveness of CCLS, it is compared with several established feature selection methods, which include Spec, ReliefF, LS, CS and CLS.

Table 2 gives comparisons of the averaged accuracy, optimized accuracy and the optimized number of features. In addition the value after the symbol ‘±’ denotes the standard deviation. It indicates that the performance is significantly improved by using the first d features selected from the ranking list of features generated by feature selection algorithms. It means that there is redundant and even contradictory information among original feature space, and feature selection algorithm can remove irrelevant and redundant features effectively.

Table 2 Averaged accuracy of different algorithms. (400 labeled segments)

The CCLS is superior to other evaluated methods not only in terms of averaged accuracy but also in terms of optimized accuracy. On the other hand, the CLS has the lowest averaged accuracy and optimized accuracy.

Figure 3 shows accuracy vs. number of selected features. It can be seen that the performance of CCLS is significantly better than that of Spec, Laplacian Score, Constraint Score and Constrained Laplacian Score. The results supports that combining supervised information with data structures to evaluate the relevance of features is very useful in feature selection.

Fig. 3

Accuracy vs. different numbers of selected features

To explore the influence of the numbers of labeled segments on the performance of the algorithm, different numbers of labeled data are used. The averaged accuracies, optimized accuracies and the optimal numbers of features of such methods on the condition of 200 and 800 labeled segments are summarized in Table 3 and Table 4 respectively. Comparing Table 2 with Tables 3 and 4, it is easy to conclude that the performance improves when the number of labeled data segments increases from 200 to 800. The CCLS is best in terms of averaged accuracy and optimized accuracy regardless of the number of labeled segments. The optimal feature number of ReliefF is always smaller than others. This may indicate that there are some redundant features in the optimum feature set selected by CCLS method.

Table 3 Performance of supervised and semisupervised methods with 200 labeled segments

Table 4 Performances of supervised and semisupervised methods with 800 labeled segments

Figure 4 shows the plots of accuracy vs. the number of selected features and the amount of labeled data. However, it should also be noticed that the performances of CCLS and ReliefF do not drop rapidly when decreasing the number of labeled data to 200, while the CS and Spec algorithms are unable to select relevant features.

Fig. 4

Accuracy vs. different numbers of selected features and different numbers of labeled data segments

5.3.2 Feature redundancy

To examine the effectiveness of GMM-based Bhattacharyya distance in measuring feature redundancy, some experiments have been done on the Waveform Database Generator (Version 2) Data Set [4]. This data set contains 5000 40-dimensional instances from 3 classes. Each class is generated from a combination of two of three base waveforms, h ₁(t), h ₂(t), and h ₃(t). Figure 5 shows graphs of these base waveforms.

Fig. 5

The base waveforms of waveform database generator data set

To generate a instance x _i , a single uniform random number u ∼ U(0, 1) and 40 normal random numbers ${e}_t\sim \mathcal{N}\left(0,{\sigma}^2\right)$, t = 1 , 2 ,  ⋯  , 40 are generated. Then, x _i is generated by combining two of the three base waveforms as follow:

$$ {\mathbf{x}}_i=u{\mathbf{h}}_1+\left(1-u\right){\mathbf{h}}_2+\mathbf{e} $$

(42)

where, for class 1, h ₁ = [h ₁(t)] and h ₂ = [h ₂(t)]. For class 2, h ₁ = [h ₁(t)] and h ₂ = [h ₃(t)] are selected to generate instances. For class 3, h ₁ = [h ₂(t)] and h ₂ = [h ₃(t)] are used similarly. And e = [e _t |t = 1, 2,  ⋯ , 40]^T. In all cases, there are many irrelevant features, almost half of them, which can be removed to achieve the best performance. This not only improves classification accuracy, but also reduces the time complexity of classification.

Obviously, the features f ₁ , f ₂₁ , f ₂₂ ,  ⋯  , f ₄₀ in this data set are white noise features for all of the corresponding values of base waveforms are 0. They are uncorrelated to each other or other relevant features. In other words, the redundancy corresponding to noise feature is quite low while using Pearson correlation coefficient as the measurement, shown in Fig. 6.

Fig. 6

The feature redundancy based on Pearson correlation coefficient

Similarly, the mutual information-based measurement faces the same defect as Pearson correlation, shown in Fig. 7.

Fig. 7

The feature redundancy based on mutual information. The mutual information is computed using Gaussian kernel-based estimator [31]

Figure 8 shows the graph of GMM-based Bhattacharyya distance measurement. In this graph, the larger value means smaller redundancy. It is easy to see that the redundancy related to noise feature is large enough, so it will be helpful for noise feature removal. Moreover, comparing Fig. 8 with Figs. 6 and 7, it’s not difficult to find the results in the region with vertices at about (6, 13), (6, 16), (9, 13), (9, 16) are quite the contrary. Figure 6 and Fig. 7 show that the redundancy values among these features are the highest while Fig. 8 indicates that these redundancy values are lowest. It is mainly because that the correlation among these features caused by the random variable is non-linear which cannot be represented properly by correlation-based or MI-based measurements. And the redundancy measurement proposed in this paper can prevent this type of problem.

Fig. 8

The feature redundancy measured by GMM-based Bhattacharyya distance. Note that the redundancy is inversely proportional to this measurement

We randomly choose 100 instances for each class from this dataset as training data. The MI between the feature and targeted classes is estimated using the nearest-neighbor method [28] and the MI between features is computed by Gaussian kernel-based estimator [31]. The GMM-based Bhattacharyya distance is calculated without Step 1 for all instances are labeled data.

Figure 9 shows the plots of mRMR algorithm with different redundancy measurements for accuracy vs. different numbers of selected features. It can be seen that the performance with GMM-based Bhattacharyya distance measurement is better than that with mutual information-based measurement. Table 5 shows the number of noise feature among the first 19 features. It can be concluded from these experimental results that mutual information-based measurement cannot represent the redundancy properly when the data set is affected by the random variable, which leads the algorithm to tend to preferentially choose the noise feature.

Fig. 9

Accuracy vs. different numbers of selected features using mRMR feature selection algorithm with different redundancy measurement

Table 5 The Number of Noise Feature Among the First 19 Features Selected by the mRMR Algorithm

5.3.3 Combination of feature relevance and redundancy

In this section, we will illustrate the performance of SSMRMR feature selection algorithm through a set of contrast experiments. In this first scenario, we compare the performance of mRMR, CCLS, and SSMRMR algorithms. In addition, we compare performances of SSMRMR with different number of labeled data.

Table 6 and Fig. 10 show the performance comparison among mRMR, CCLS, and SSMRMR algorithms. It can be seen in Table 6 that in terms of averaged accuracy gains, CCLS increases 2.53 percentage points and SSMRMR increases 2.7 percentage points, compared with mRMR algorithm. SSMRMR is better than CCLS with only 0.17 percentage points. However, in terms of optimized number of features, SSMRMR decreases 8 features compared with CCLS, which means redundancy elimination can help achieve a higher degree of dimensionality reduction without accuracy decrease.

Table 6 Performance Comparison of mRMR, CCLS, and SSMRMR Algorithm(400 labeled segments)

Fig. 10

Accuracy vs. different numbers of selected features using mRMR, CCLS, and SSMRMR feature selection algorithm

Figure 10 shows three curves of classification accuracy vs. different number of selected features. We can see that both the curves of CCLS and SSMRMR (black and blue) outperform the curve of mRMR (red). But the SSMRMR’s curve increases more rapidly and achieves good performance with a small number of features.

Figure 11 shows the plots of average accuracy vs. different number of labeled data. It can be concluded that the average accuracy increased with the addition of labeled data, but wouldn’t continue to increase when the labeled data reach a certain amount. Moreover, it is obvious that SSMRMR algorithm outperforms other algorithms significantly.

Fig. 11

Average accuracy vs. different numbers of labeled data

After the optimal feature subset has been selected, the classification is done on test data set. The results are listed in Table 7. From Table 7, it is easy to find the optimal feature subset selected from develop dataset can help improve the performance in test dataset. Through CCLS and SSMRMR still outperform other algorithms, the accuracy differences between algorithms are relatively small. However, the average accuracy of SSMRMR is much high than other algorithm, which means there are enough alternative optimal feature subsets of different feature numbers can be used, and we needn’t worry about that the selected optimal feature subset perform good only in develop dataset.

Table 7 Accuracy of different algorithms on test dataset. (400 labeled segments)

6 Conclusion

In this paper, we present a feature selection algorithm under the framework of mRMR algorithm. Rather than using mutual information to measure relevance and redundancy, a new score function named CCLS was developed to evaluate the relevance of features and the GMM-based Bhattacharyya distance was used to measure the redundancy between features. The CCLS algorithm evaluated feature relevance by making full use of locality preserving ability and constraint preserving power. The GMM-based Bhattacharyya distance evaluated redundancy more appropriately and is easier to extract than MI. SSMRMR optimized the minimum redundancy condition and the maximum relevance condition simultaneously and obtain better performance not only in classification accuracy but also in dimensionality reduction.

However, there are still some limitations in our experiments. The audio data used in our experiments is collected from telephone channel where the audio types are simple and without the mixed segments (speech over music). Audio classification and segmentation under broadcast channel are more challenging for the complex audio types, lower signal-to-noise ratio, and lots of mixed segments. Thus, How to extend our work to broadcast channel will be the focus in the further work.