A multiple watermarking scheme based on orthogonal decomposition

Abstract

This paper proposes a novel multiple watermarking scheme based on orthogonal decomposition (MWOD). In the first phase, based on orthogonal decomposition, the host data selected from multimedia data are divided into mutually independent multiple domains. Then multiple watermarks without need for considering the special correlation among them can respectively be embedded into these different domains even using different embedding algorithms. There is no mutual interference among watermarked domains so that multiple watermarks can be flexibly embedded in the distribution of the multimedia cover. Through theoretical analysis, the security of multiple watermarking operands is validated, which means that MWOD can ensure the security of watermarking operation domains. Therefore, media providers and service providers can embed their unique information step-by-step into digital multimedia using their own operation domain keys in MWOD, which can be used to identify media content’s ownership or trace the illegal redistributors. Experimental results and analysis demonstrate the feasibility and robustness of MWOD.

1 Introduction

Digital watermarking is a technique which allows a user to embed some marks into a digital content for protecting his/her copyright or tracing illegal redistributors [1]. With the rapid development of Internet and digital media sharing services, the distribution of digital works is becoming more and more popular. In the meantime, there are more chances for piracy. To keep the benefits of media providers and service providers earned from network media consumption, anti-piracy is regarded as an urgent issue. In a media distribution process, media providers and service providers need to embed their own unique information step-by-step into media content to protect their benefit. However, a classical single watermarking cannot satisfy this requirement. Therefore, a multi-watermarking scheme has become highly desirable.

Multiple watermarking can be used to not only identify media content’s owners or trace the illegal redistributors in media distributions, but also cope with different types of attacks, each of which may do harm to the media content from different perspectives [8]. Multi-watermarking scheme has more potential applications in the case of multiple content providers or users, such as in a cloud environment.

Current multi-watermarking schemes are as following. In [2], two watermarks are embedded simultaneously into two different sectors in the same DWT domain. They are used to verify the integrity and recover the tampered image. In [15], three different kinds of information: copyright management information, copy control information, and fingerprints are introduced as watermarks. The three kinds of information are embedded simultaneously into three different components of a single frame. These two schemes aim to simultaneously embed multiple watermarks into a same transform domain, but in fact, they are just a simple extension of single watermarking schemes to multiple watermarks embedding. In [18], a multiple watermarking model with side information is proposed. This model focuses on special correlations among watermarks. The correlation between the multimedia cover and watermarking, and the correlation among the watermarks themselves are considered as side information. Cox et al. [6] assumed that multiple watermarks are close to orthogonal and also applied a single watermark algorithm to embed multiple watermarks into multimedia data. Many more studies [14, 7, 9, 3] are similar. These schemes are based on an assumption of orthogonal relation among multiple watermarks. To overcome the restriction of orthogonal assumption, Peter H. W et al. [17] proposed a new multi-watermarking scheme, which embeds multiple watermarks in the same watermark space without orthogonal assumption among watermarks. But Peter’s scheme still has a limited situation that multiple watermarks should be embedded simultaneously, not step-by-step, which reduces the flexibility of multi-watermarking scheme to some extent.

Meanwhile, the correlation among watermarks is easy to cause another issue: security of multiple watermarking. In a multiple watermarking scheme, if watermarks are embedded step by step into the same watermarking domain, malicious watermarking operators could easily attack other watermarks in the same watermarking domain. On the other hand, if there is a strong correlation among watermarks, it may be easily used by attackers. For example, attackers can derive other unknown watermarks from a known one owing to the correlation among watermarks. Therefore, users should select watermarks independently without need for considering the special correlation among watermarks.

Additionally, embedding rule of watermarking is also an important aspect that needs to be considered. According to current studies, embedding rules of the watermarking can be classified into additive watermarking [19, 10], multiplicative watermarking [4], quantization watermarking [11], and hybrid watermarking [16]. However, for different applications, especially in multiple watermarking users, the users should have the right to choose their own embedded rule of multiple watermarks. Therefore, a multiple watermarking scheme without restriction on embedding rules is desired.

From the discussions above, a practical multi-watermarking scheme needs to satisfy the following three basic requirements.

• 1) Watermarks can be selected independently without need for considering the special correlation among them.

• 2) Watermarks can be operated independently. It means that the embedding domain of watermarks can be different and the operation (embedding and extraction) of watermarks can be processed independently.

• 3) Various embedded rules are compatible in the scheme. That is to say, the multiple watermarking users have the right to choose their own embedded rule.

However, the above-mentioned schemes are unable to satisfy the three requirements simultaneously. Hence, in this paper, a multiple watermarking scheme based on orthogonal decomposition (MWOD) is proposed that could satisfy the three requirements. In MWOD, orthogonal decomposition is used to divide the protected data into multiple mutually independent domains. Each domain can be used to embed unique watermark with different embedding rules. Finally, they can be formed as a whole data through orthogonal composition. Thus, MWOD can offer a seamless fusion of multiple watermarking, and enable the users to embed their watermarks in different domains without need for considering the relationship of embedded watermarks. Meanwhile the security of each watermark can be validated by different watermarking operands (domain keys). Therefore, the proposed scheme can offer adequate flexibility for users to satisfy the requirements of multiple watermarking applications.

The main contributions of this paper can be summarized as follows. Firstly, MWOD is proposed to realize multiple watermarking, in which watermarks are embedded into different domains using different domain keys without need for considering the correlation among them. Secondly, MWOD is proved that multiple watermarks can be flexibly embedded in the distribution of the multimedia cover by different embedding algorithms and the security among watermarking operands is validated through theoretical analysis.

The rest of the paper is organized as follows. The definition of MWOD scheme is introduced in Section 2. The performance analysis of MWOD, including security analysis, is described in Section 3, the experimental results and analyses are shown in Section 4. Some additional issues of MWOD scheme and conclusions are finally described and future works are listed in Section 5.

2 MWOD

In this section, we propose a MWOD scheme to embed multiple watermarks into different domains. At the same time, the conditions of practical multi-watermarking scheme are also proposed.

2.1 Conditions of practical multiple watermarking scheme

A practical multiple watermarking scheme for multimedia distribution should satisfy three conditions:

• Commutativity: it means that the processing order of watermarks should be commutative.

• Mixture: the operation results of multiple watermarking should be mixed for the end users.

• Applicability: multiple watermarking embedding algorithms should not be restricted, as are decided by users, such as various media providers and service providers.

Commutativity guarantees that the multiple watermarking orders do not affect the final result, and watermarks can be extracted from watermarked data. It provides the convenience for practical applications. The Mixture condition ensures a seamless fusion of multiple watermarking so that they can finally forms a whole. Applicability ensures that users have the right to choose their own embedding rule for multiple watermarking. Most current multiple watermarking schemes cannot fully satisfy the above conditions. So MWOD scheme is proposed as following.

2.2 MWOD scheme

We group some selected image pixels or transform coefficients to form a vector and define it a host vector. Let the host vector be X = (x ₁, x ₂, …, x _n )^T with length n. The i-th watermark W _i  = {w ₁, w ₂, ⋯, w _q } with number q, where q≪n. The bit sequence of watermark may be a meaningful image such as the logo of the image owner or the information related to the host images such as the owner’s name, image ID,…, etc. The watermark is modulated by the secret key which may be a pseudorandom bit sequence or other secret sequence for enhancing its security.

MWOD scheme consists of several multiple watermarking systems (MWS), each of which contains watermark embedded function ${\mathcal{W}}_i\left(\cdot, \cdot \right)$ corresponding with its key K _iw , extraction function ${\mathcal{V}}_i\left(\cdot, \cdot \right)$ corresponding with its key K _iv , and the i-th watermark W _i . In MWS, multiple watermarks W = {W ₁, W ₂, ⋯, W _u } with number u, multiple watermarking embedding functions $\mathcal{W}\left(\cdot, \cdot, \cdot \right)=\left\{{\mathcal{W}}_1\left(\cdot, \cdot, \cdot \right),{\mathcal{W}}_2\left(\cdot, \cdot, \cdot \right),\cdots, {\mathcal{W}}_u\left(\cdot, \cdot, \cdot \right)\right\}$ corresponding with its keys K _w  = {K _1w , K _2w , ⋯, K _uw }, extraction functions $\mathcal{V}\left(\cdot, \cdot \right)=\left\{{\mathcal{V}}_1\left(\cdot, \cdot \right),{\mathcal{V}}_2\left(\cdot, \cdot \right),\cdots, {\mathcal{V}}_u\left(\cdot, \cdot \right)\right\}$ corresponding with its keys K _v  = {K _1v , K _2v , ⋯, K _uv }.

Denoted X _iw as the X embedded the i-th watermark, W _i . ${\mathcal{W}}_i\left(\cdot, \cdot, \cdot \right)$ and ${\mathcal{V}}_i\left(\cdot, \cdot \right)$ are generic algorithms with no special requirements. Denote a transformation matrix $B=\left(\begin{array}{cccc}\hfill {b}_1,\hfill & \hfill {b}_2,\hfill & \hfill \dots, \hfill & \hfill {b}_n\hfill \end{array}\right)$, of size n × n, which satisfies the following:

$$ \left\{\begin{array}{c}\hfill {b}_i^T\cdot {b}_j\ne 0\hfill \\ {}\hfill {b}_i^T\cdot {b}_j=0\hfill \end{array}\right.\kern1.5em \begin{array}{c}\hfill if\kern0.5em i=j\hfill \\ {}\hfill otherwise\hfill \end{array}\kern1.75em 1\le i,j\le n $$

(1)

where b _i  = (b _i1, b _i2, …, b _in )^T is a n-dimensional column vector in B. X can be represented as X = B ⋅ Y or Y = B ^− 1 ⋅ X using orthogonal decomposition based on B.

Matrix B can be divided into multiple sub-matrixes, i.e., B = (S ₁, S ₂, ⋯, S _u ) corresponding to multiple watermarks, respectively. And Vector Y is also divided into multiple sub-vectors, i.e., Y = (Y ₁, Y ₂, ⋯, Y _u )^T. Then, X can be described as:

$$ X=B\cdot Y={S}_1\cdot {Y}_1+{S}_2\cdot {Y}_2+\cdots +{S}_u\cdot {Y}_u $$

(2)

In MWOD scheme, watermarking operation function $\mathcal{W}\left(\cdot, \cdot, \cdot \right)$ is represented as:

$$ {X}_w=\mathcal{W}\left(X,\mathbf{W},{K}_w\right)={\displaystyle \sum_{i=1}^u{\mathcal{W}}_i\left(X,{\mathbf{W}}_i,{K}_{iw}\right)} $$

Assuming Y _i is used to embed the watermark, then, $\mathcal{W}\left(\cdot, \cdot, \cdot \right)$ is defined as:

$$ {X}_w={\displaystyle \sum_{i=1}^u{\mathcal{W}}_i\left(X,{\mathbf{W}}_i,{K}_{iw}\right)}={\displaystyle \sum_{i=1}^u{S}_i\cdot {\mathcal{W}}_i\left({Y}_i,{\mathbf{W}}_i,{K}_{iw}\right)}={\displaystyle \sum_{i=1}^u{S}_i\cdot {Y}_{iw}}=B\cdot {Y}_w $$

(3)

where ${\mathcal{W}}_i\left({Y}_i,{\mathbf{W}}_i,{K}_{iw}\right)={Y}_{iw}$, Y _w  = (Y _1w , Y _2w , ⋯, Y _uw )^T.

Equation (3) means that, in MWOD, watermarking for X are applied to its orthogonal decomposition coefficients Y _i instead of directly applied to X itself. Similarly, watermarking extraction is applied to Y _iw . They are defined as follows:

$$ \begin{array}{l}{Y}_w={B}^{-1}\cdot {X}_w\hfill \\ {}{\mathbf{W}}_i={\mathcal{V}}_i\left({X}_w,{K}_{iv}\right)={\mathcal{V}}_i\left({Y}_w,{K}_{iv}\right)\hfill \\ {}\kern1.24em ={\mathcal{V}}_i\left({Y}_{iw},{K}_{iv}\right)\hfill \end{array} $$

(4)

The processing orders of multiple watermarking embedding in MWOD do not affect the final result.

From Eqs.(3) and (4), it show that the transform matrix B is required to participate in watermarking embedding and extraction operations, which is not suitable for distribution to multiple watermarking operators. If each watermarking operator can get B, watermarking operation domains of other operators are insecure. MWOD is a promising multi-watermarking scheme which can be used to build the infrastructure of digital rights management (DRM) and asymmetric fingerprinting systems, if its security is validated.

From a security point of view, two aspects are mainly concerned with the security of MWOD, the one is that the embedding/extraction keys of watermarking operation is secured, such as K _w and K _v ; the another is that the operands of multiple watermarking are expected to be secure, such as sub-matrix S _i . It is necessary that the sub-matrix S _i , by which the operation domain of each watermarking operator are defined, is regarded as a secret key to the i-th operator and other operators cannot obtain it (security analysis in Section 3). Based on these ideas, we provide the reconstruction of MWOD for its security analysis as follows.

For the convenience of description, we take the two watermarks embedding for example. Let S ₁ denotes the first watermark domain key and S ₂ denotes the second watermark domain key, S ₁ = (b ₁, b ₂, ⋯, b _m ) and S ₂ = (b _m + 1, b _m + 2, ⋯, b _n ), where B = (S ₁, S ₂).

From Eq. (1), assume that: b ^T _i  ⋅ b _i  = λ _i and λ _i  ≠ 0, where i ∈ [1, n]. Given that P = (B ^T B)^− 1, then P = diag(λ ^− 1₁ , λ ^− 1₂ , ⋯, λ ^− 1 _n ), and Y _w  = P ⋅ B ^T ⋅ X _w , based on Eq. (4). Similarly, assume the following:

${P}_{S_1}={\left({S}_1^T\cdot {S}_1\right)}^{-1}= diag\left({\lambda}_1^{-1},{\lambda}_2^{-1},\cdots, {\lambda}_m^{-1}\right)$ and ${P}_{S_2}={\left({S}_2^T\cdot {S}_2\right)}^{-1}= diag\left({\lambda}_{m+1}^{-1},{\lambda}_{m+2}^{-1},\cdots, {\lambda}_n^{-1}\right)$.

Assume the first watermarking domain is divided by S _1P , and the second watermarking domain is divided by S _2P , which satisfies: (S _1P , S _2P )^T = P ⋅ B ^T, Then, Eq. (5) is derived as follows:

$$ \left\{\begin{array}{l}Y={\left({S}_{1P},{S}_{2P}\right)}^T\cdot X\\ {}{Y}_w={\left({S}_{1P},{S}_{2P}\right)}^T\cdot {X}_w\end{array}\right. $$

(5)

Accordingly, P ⋅ (S ₁, S ₂)^T = (S _1P , S _2P )^T, ${S}_{1P}^T={P}_{S_1}\cdot {S}_1^T$ and ${S}_{2P}^T={P}_{S_2}\cdot {S}_2^T$. Then, the following is derived:

$$ \left\{\begin{array}{l}{Y}_1={S}_{1P}^T\cdot X={P}_{S_1}\cdot {S}_1^T\cdot X\\ {}{Y}_2={S}_{2P}^T\cdot X={P}_{S_2}\cdot {S}_2^T\cdot X\end{array}\right. $$

(6)

$$ \left\{\begin{array}{l}{Y}_{1w}={S}_{1P}^T\cdot {X}_w={P}_{S_1}\cdot {S}_1^T\cdot {X}_w\\ {}{Y}_{2w}={S}_{2P}^T\cdot {X}_w={P}_{S_2}\cdot {S}_2^T\cdot {X}_w\end{array}\right. $$

(7)

Finally, Eqs. (3) ~ (4) are redefined as follows:

$$ \begin{array}{l}{X}_{1w}={S}_1\cdot {\mathcal{W}}_1\left({Y}_1,{\mathbf{W}}_1,{K}_{1w}\right)+{S}_2\cdot {Y}_2\\ {}\kern1.75em ={S}_1\cdot {\mathcal{W}}_1\left({P}_{S_1}\cdot {S}_1^T\cdot X,{\mathbf{W}}_1,{K}_{1w}\right)+X-{S}_1\cdot {Y}_1\\ {}\kern1.75em ={S}_1\cdot {\mathcal{W}}_1\left({P}_{S_1}\cdot {S}_1^T\cdot X,{\mathbf{W}}_1,{K}_{1w}\right)+X-{S}_1\cdot {P}_{S_1}\cdot {S}_1^T\cdot X\\ {}\kern1.75em ={S}_1\cdot {\mathcal{W}}_1\left({\left({S}_1^T\cdot {S}_1\right)}^{-1}\cdot {S}_1^T\cdot X,{\mathbf{W}}_1,{K}_{1w}\right) + X-{S}_1\cdot {\left({S}_1^T\cdot {S}_1\right)}^{-1}\cdot {S}_1^T\cdot X\\ {}\kern2.12em ={\mathcal{W}}_1\left(X,{\mathbf{W}}_1,{S}_1,{K}_{1w}\right)\ \end{array} $$

(8)

Similarly,

$$ \begin{array}{l}{X}_{2w}={S}_2\cdot {\mathcal{W}}_2\left({\left({S}_2^T\cdot {S}_2\right)}^{-1}\cdot {S}_2^T\cdot X,{\mathbf{W}}_2,{K}_{2w}\right)+X-{S}_2\cdot {\left(\pi {S}_2^T\cdot {S}_2\right)}^{-1}\cdot {S}_2^T\cdot X\\ {}\kern2.5em ={\mathcal{W}}_2\left(X,{\mathbf{W}}_2,{S}_2,{K}_{2w}\right)\end{array} $$

(9)

$$ \begin{array}{l}{\mathbf{W}}_1={\mathcal{V}}_1\left({X}_w,{K}_{1v}\right)={\mathcal{V}}_1\left({Y}_{1w},{K}_{1v}\right)\\ {}\kern1em ={\mathcal{V}}_1\left({P}_{S_1}\cdot {S}_1^T\cdot {X}_w,{K}_{1v}\right)\\ {}\kern1em ={\mathcal{V}}_1\left({\left({S}_1^T\cdot {S}_1\right)}^{-1}\cdot {S}_1^T\cdot {X}_w,{K}_{1v}\right)\\ {}\kern1em ={\mathcal{V}}_1\left({X}_w,{S}_1,{K}_{1v}\right)\ \end{array} $$

(10)

$$ \begin{array}{l}{\mathbf{W}}_2={\mathcal{V}}_2\left({X}_w,{K}_{2v}\right)={\mathcal{V}}_2\left({Y}_{2w},K{}_{2v}\right)\ \\ {}\kern1em ={\mathcal{V}}_2\left({\left({S}_2^T\cdot {S}_2\right)}^{-1}\cdot {S}_2^T\cdot {X}_w,{K}_{2v}\right)\\ {}\kern1em ={\mathcal{V}}_2\left({X}_w,{S}_2,{K}_{2v}\right)\end{array} $$

(11)

According to Eqs. (8) - (11), through reconstruction, the MWOD scheme has following characteristics:

• 1) The redefined processing functions all depend on matrixes S ₁ or S ₂ in addition to their own keys (K _v , K _w ).

• 2) In addition to the existing keys, the first watermarking domain functions ${\mathcal{W}}_1\left(X,{\mathbf{W}}_1,{S}_1,{K}_{1w}\right)$ and ${\mathcal{V}}_1\left({X}_w,{S}_1,{K}_{1v}\right)$ are related to the matrix S ₁ only, and the second watermarking domain functions ${\mathcal{W}}_2\left(X,{\mathbf{W}}_2,{S}_2,{K}_{2w}\right)$ and ${\mathcal{V}}_2\left({X}_w,{S}_2,{K}_{2v}\right)$ are related to matrix S ₂ only.

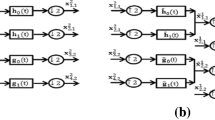
The first allows S ₁ or S ₂ to be regarded as a secret key for these functions. The second implies that S ₁ is the first watermarking domain key and S ₁ is the second watermarking domain key. Thus, the reconstruction of MWOD allows the introduction of S ₁ and S ₂ to the MWOD scheme as a hidden key system for enhanced security. The embedding framework of MWOD is shown in Fig. 1. The security analysis in Section 3 will validate the increase in security of this method.

Fig. 1

The embedding framework of MWOD

3 Performance analysis of MWOD

In performance analysis of previous multiple watermarking schemes, it has been more concerned about the potential use of the watermark. However, some performances, for example, the distortion and security of multiple watermarking operation domains, are not considered. So MWOD will be analyzed with respect to the robustness, distortion, capacity, and security of multiple watermarking operands, which can secure the security of watermarking operation domains.

3.1 Robustness analysis

The robustness of the multiple watermarking will be analyzed by focusing on the detection of watermark, i.e., cross correlation between the original watermark and decoded watermark in JPEG compression, high pass filter, median filter, low pass filter and noise.

To detect whether a modulated watermark W is present in a testing image, we decode all the K bits of watermark from the image as W′ and evaluate a score. A possible score is the traditional normalized the detection score (cross correlation), DS, between the original watermark and the decoded watermark as follows.

$$ DS=\frac{{\displaystyle {\sum}_{i=1}^q\left({w}_i-\overline{w}\right)\cdot \left({w}_i^{\prime }-{\overline{w}}^{\prime}\right)}}{\sqrt{{\displaystyle {\sum}_{i=1}^q{\left({w}_i-\overline{w}\right)}^2\cdot {\displaystyle {\sum}_{i=1}^q{\left({w}_i^{\prime }-{\overline{w}}^{\prime}\right)}^2}}}} $$

(12)

where w _i and w ^′ _i represent respectively original watermark bit and extracted watermark bit, $\overline{w}$ is the average of w and ${\overline{w}}^{\prime }$ is the average of w′. q is the size of W.

If it can be guaranteed that the increment of the detection score DS is greater than that of the threshold, the multiple watermarking increases the successful detection rate of the watermark, or else, the multiple watermarking decreases the successful detection rate of the watermark. If the detection score is higher than a pre-defined threshold, the watermark is considered to be present in the testing image. The experiments of robustness analysis and results are explicitly shown in section 4.

3.2 Distortion analysis

Whatever the watermarking is additive or multiplicative, Y _iw can be described as:

$$ {Y}_{iw}={Y}_i+{\tilde{\mathbf{W}}}_i\kern2.25em 1\le i\le n $$

(13)

Where ${\tilde{\mathbf{W}}}_i={\alpha}_i{\mathbf{W}}_i$ denotes additive watermarking, and ${\tilde{\mathbf{W}}}_i={\alpha}_i{Y}_i{\mathbf{W}}_i$ denotes multiplicative watermarking. α _i denotes the watermarking strength, w _i denotes the element of the i-th watermark sequence. So, from the Eqs. (2-3), we have:

$$ {X}_w=X+{\displaystyle \sum_{i=1}^u{S}_i{\tilde{\mathbf{W}}}_i} $$

(14)

In the distortion analysis, peak signal to noise ratio (PSNR) value is used to evaluate the distortion degree of multi-watermarking. Here, from Eq. (14), the PSNR is defined by

$$ \begin{array}{l}P=10 \lg \left(LM{255}^2/{\displaystyle {\sum}_{i=1}^L{\displaystyle {\sum}_{j=1}^M{\left(\pi {I}_{ij}^{\prime }-{I}_{ij}\right)}^2}}\right)\\ {}\kern0.75em \simeq 10 \lg \left(LM{255}^2/{\displaystyle {\sum}_{i=1}^u{S}_i^2{\tilde{\mathbf{W}}}_i^2}\right)\end{array} $$

(15)

Here, L and M denote the width and height of the cover, respectively. I′ and I denote the watermarking cover and the original cover, respectively. u denotes the number of watermarks.

It is shown in Eq. (15) that the multiple watermarking can only make the PSNR decreasing with the number of embedded watermarks (N_EW), that is to say, it degrades the image perceptual quality. This means that regardless of the embedding rules, the N_EW should be rationally set.

3.3 Capacity analysis

The capacity analysis of the multiple watermarking mainly aims at the capacity change with N_EW increasing. In this paper, the analysis is assumed that the whole image has uniform watermark power constraint and noise power constraint in all pixel locations. Therefore, the capacity can be described as

$$ C=\frac{1}{2}{ \log}_2\left(1+\left({P}_w/{P}_n\right)\right) $$

(16)

Here, P _w and P _n represent the uniform power of watermark and noise, respectively. In MWOD, the Eq. (16) can be written by

$$ \begin{array}{l}C=\frac{1}{2}{ \log}_2\left(1+\left({\displaystyle {\sum}_{j=1}^u{\sigma}_{wj}^2}/{\sigma}_X^2\right)\right)\\ {}\kern0.75em \simeq \frac{1}{2}{ \log}_2\left(1+\left({\displaystyle {\sum}_{i=1}^q{\displaystyle {\sum}_{j=1}^u{S}_{ij}^2{\tilde{\mathbf{W}}}_{ij}^2}}/m{\sigma}_X^2\right)\right)\end{array} $$

(17)

Here, P _w  = ∑ ^u _j = 1 σ ² _wj and P _n  = σ ² _X , S _ij denotes transformation sub-matrix, ${\tilde{\mathbf{W}}}_{ij}$ denotes embedded watermark, u denotes the number of watermarks, q denote the size of each watermark.

Actually, the block-wise embedding of multi-watermarking does not change total capacity of the final embedded watermark. But, for the scheme we proposed, the final embedded watermark is not equal to the straightforward superimposition of the each single watermark (see Eq. (17)), so the summation of capacity of single watermarks can be more than the capacity of the final embedded watermark under appropriate S _i .

3.4 Security analysis

The security of MWOD includes two aspects: Firstly, the external attacker cannot erase the watermark by obtaining multiple watermarking covers. Secondly, for the sake of ensuring the security of watermarking domain, the operation domain keys of multiple watermarking embedded cannot be deduced with each other. For the first case, Wang and Lian [16] proved that the greater N_EW can decrease the security of multi-watermarking scheme for the external attacker. Therefore, we can improve its security by setting rational the watermark number. For the second case, each watermark embedded operator cannot access the others watermark content. The security is analyzed as follows.

We take 2 watermarks embedding operation for example. S ₁ and S ₂ represent their watermarking operation domain keys, whose security depend on two conditions which will be validated as follows.

CONDITION 1:

As secret keys, S ₁ and S ₂ can be adjusted independently to satisfy any predetermined security threshold, i.e. their key space have large enough to resist the brute force attack.

CONDITION 2:

S ₁ and S ₂ are independent and cannot be mutually derived, i.e. it is difficult for the first operator to solve S ₂ and the second operator to solve S ₁.

As it mentioned in Section 2, there exists related constraint between S ₁ and S ₂ from Eq. (1). If n × n is the size of B, the Eq. (1) consisted of ${\scriptscriptstyle \frac{n\left(n-1\right)}{2}}$ quadratic polynomial simultaneous equations with n ² unknowns over a finite field F. The difference Δ is ${\scriptscriptstyle \frac{n\left(n+1\right)}{2}}$ between equations and unknowns. If the elements of B are k bits fix word-length integer, then F denotes the field of [−2^k − 1, 2^k − 1 − 1].

This is an underdefined multivariate quadratic equations problem, generally referred to as an MQ difficult problem [5]. MQ is NP-hard. Some algorithms have been proposed for solving MQ faster than using an exhaustive search, but most of them did not change the general exponential, thus increasing the complexity characteristics.

With respect to this problem, the attacker who does not know any of the MWOD keys is considered first. Assume an attack on B by Eq. (1). Then, the complexity can be expressed as follows:

$$ {d}_B={d}_{MQ}+{N}_{MQ}{d}_0 $$

(18)

where d _B denotes the total measure of complexity for attacking B, d _MQ denotes the complexity for solving the MQ solutions of B, N _MQ denotes the number of all the expected solutions of B, and d ₀ denotes the complexity for checking the solution is the correct solution.

Because there N _MQ possible solutions for B, the attacker must check the solutions one by one to find the true result. To do this, he has to substitute Eq. (4) with the candidates for B. However, K _1v or K _2v is unknown, thus the checking complexity nearly equals that of attacking K _1v or K _2v .

Equation (1) is an instance of MQ, where the number of unknowns is approximately 2 times the number of equations. In the practical application of Eq. (1), d _MQ can be roughly estimated as ${2}^{n^2k-{k}_m}$, where k _m is the factor that includes the efficiency improvement achieved over an exhaustive search by using a different algorithm. In most instances, k _m can be ignored because k _m  << n ² k if n and k are sufficiently large. N _MQ is approximately ${2}^{\varDelta k}={2}^{\frac{n\left(n+1\right)k}{2}}$. To ensure the security of K _1v or K _2v , assume there is a threshold, k ₀, that the keys should exceed, thus d ₀ can reasonably be set as ${2}^{k_0}$. Thus the complexity for attacking B tends to increase exponentially as O(n ² k) as follows:

$$ {d}_B \sim {2}^{n^2k-{k}_m}+{2}^{{\scriptscriptstyle \frac{n\left(n+1\right)k}{2}}+{k}_0} $$

(19)

From Eq. (19), it shows that S ₁ and S ₂, which are the B sub-matrixes, can be adjusted independently to satisfy any predetermined security threshold by set rational n and k. So the CONDITION 1 has been met.

If S ₁ and S ₂ cannot be mutually derived, the CONDITION 2 can be also met. We can prove THE CONDITION 2 as follows.

In MWOD, S ₁ is known by the first operator and S ₂ is known by the second operator, it is forbidden for the first operator to know S ₂. If the first operator knows S ₂, the second watermarking operation domain can be easily acquired, which would then lead to the breaking of the MWOD security. Similar reasoning is applied to S ₁ and the second operator. Hence, S ₁ and S ₂ must have a difficulty designed for mutual derivation.

If the first operator is attacking the second watermarking, Eq. (1) and the known S ₁ must be used to attack S ₂. If m denotes the number of columns in S ₁, and S ₁ is known, then applying Eq. (1) to solve S ₂ becomes the following:

$$ \left\{\begin{array}{l}{s}_{1i}^T\cdot {s}_{1j}=0\kern1.5em i\ne j,\kern0.75em 0\le i,j\le n-m\ \\ {}{s}_{1i}^T\cdot {s}_{2j}=0\kern1em 0\le i\le m,\kern0.75em 0\le j\le n-m\end{array}\right. $$

(20)

Equation system (20) consists of ${\scriptscriptstyle \frac{\left(n-m\right)\left(n-m-1\right)}{2}}$ quadratic equations and m(n − m) linear equations with n(n − m) unknowns. By using Gaussian elimination, m(n − m) unknowns can be eliminated using the linear equations, which results in the computational complexity, O(m ³(n − m)³). Then, the quadratic parts are underdefined multivariate quadratic equations, with ${\scriptscriptstyle \frac{\left(n-m\right)\left(n-m-1\right)}{2}}$ quadratic equations and (n − m)(n − m) unknowns. It is still a typical MQ equation system, similar to the equations of B, however, n is replaced by n − m. Referring to the result for B from Eq. (19), the complexity for attacking S ₂ with a known S ₁ can be estimated as follows:

$$ {d}_{S_2} \sim {2}^{3k{ \log}_2^{m\left(n-m\right)}+{\left(n-m\right)}^2k-{k}_m}+{2}^{{\scriptscriptstyle \frac{\left(n-m\right)\left(n-m+1\right)k}{2}}+{k}_0} $$

(21)

where 3k log₂ ^{m(n − m)} in the exponent arises from the Gaussian elimination calculations.

Similarly, the complexity for attacking S ₁ with a known S ₂ is estimated as follows:

$$ {d}_{S_1} \sim {2}^{3k{ \log}_2^{m\left(n-m\right)}+{m}^2k-{k}_m}+{2}^{{\scriptscriptstyle \frac{m\left(m+1\right)k}{2}}+{k}_0} $$

(22)

According to Eqs. (20–22), the complexity of attacking S ₁ and S ₂ are all exponential, increasing with O(m ² k) and O((n − m)² k), respectively, thus providing the criteria for the proper choice of the parameters S ₁ and S ₂ to achieve computational security of the MWOD scheme. For example, if n = 8, m = 4, and k = 16, the complexity for S ₁ and S ₂ must be of order ${2}^{448}+{2}^{160+{k}_0}$, ${2}^{448}+{2}^{160+{k}_0}$, respectively, which satisfies the security requirements of most applications. The parameter k _m is neglected in the latter two cases because all currently available QM accelerated algorithms are more effective than an exhaustive search only for massively large cases.

It is difficult for the malice operators to solve the operands of extraction functions ${\mathcal{V}}_1\left(\cdot, \cdot \right)$ and ${\mathcal{V}}_2\left(\cdot, \cdot \right)$ because of S ₁ and S ₂ cannot be mutually derivate. The above analysis proved that the CONDITION 2 can be also met.

What has been discussed above, the security of multiple watermarks embedding operands has been proved, which ensure the security of watermarking operation domains. So, this proof allows that multiple watermarks can be flexibly embedded in the distribution of the multimedia cover, which makes MWOD better practicability.

4 Experimental results

We tested the proposed scheme on many testing images selected from the USC-SIPI Image Database (freely available at http://sipi.usc.edu/database/). But only the experimental results of Lena and Baboon (in Fig. 2) will be given below due to the limited space. Four 32 × 32 binary logo images, as shown in Fig. 3, are used as perceptual meaningful watermarks in the experiments. The whole original image is transformed to DCT domain (suitable for other transform domains). The length of each watermark W _i is 32 × 32 = 1024. We choose partial low-frequency components of DCT to form the host vector X, in which these components tend to have large energies so that embedded watermark tend to be robust against different kinds of attacks. We generate an orthogonal matrix B = (b ₁, b ₂, ⋯, b ₈) with 8 by 8, which only satisfies Eq. (1). We divide B into 4 sub-matrixes, S ₁ = (b ₁, b ₂), S ₂ = (b ₃, b ₄), S ₃ = (b ₅, b ₆), S ₄ = (b ₇, b ₈) to embed 4 watermarks into images for facilitate description. The experiments use the hybrid watermarking embedding rule. We define $\mathcal{W}\left(\cdot, \cdot .\cdot \right)/\mathcal{V}\left(\cdot \right)$ as watermarking embedding/extraction.

Fig. 2

Original 256 × 256 “Lena” and “Baboon”

Fig. 3

Original logo “Alphabet” (Right)

Like most multiple watermarking schemes, PSNR of watermarked image was selected in this paper to demonstrate the impact of watermarking embedding, on the image quality, varies with N_EW. So the image degradation with respect to multiple watermarking is tested. The typical results of the experiments, the MWOD-watermarked Lena and Baboon images (4 watermarks), are shown in Figs. 4 and 5 respectively. The results show that the visual quality of 4-watermarked image is acceptable.

Fig. 4

MWOD-watermarked Lena image with 4 watermarks embedded. PSNR = 46.096 dB. 4 Extracted watermark (Right)

Fig. 5

MWOD-watermarked Baboon image with 4 watermarks embedded. PSNR = 43.428 dB. 4 Extracted watermark (Right)

In the condition of the same embedded information, we compared the PSNR of watermarked images of proposed MWOD scheme, with the schemes proposed by Wang and Lian [16] and Peter et al. [17]. The results are shown in Fig. 6. Though all PSNR curves with N_EW are descending obviously, but the proposed scheme has higher PSNR than Wang and Lian [16] and Peter et al. [17]. It generally means that the proposed scheme has better visual quality than others under the same conditions.

Fig. 6

PSNR versus N_EW

Additionally, for demonstrating the robustness of MWOD, the average detection scores of watermarks (ADS) vary with capacity and N_EW is considered for examination. The ADS is computed by Eq. (23). The following is ADS equation:

$$ ADS= mean\left(DS\left({\mathbf{W}}_1+{\mathbf{W}}_2+{\mathbf{W}}_3+{\mathbf{W}}_4\right)\right) $$

(23)

where W _i denotes the detection score of i-th watermark.

Certainly, the whole equivalent capacity of embedded watermarks is positively correlated to the N_EW. In the experiment, the N_EW in multi-watermarking is valued from 1 to 10, and each embedded watermark is restricted in equal size given as 16 × 16, 32 × 32, and 64 × 64 respectively. The ADS of watermarks in different size vary with the number watermarks for proposed scheme is shown in Fig. 7. It has been shown that, a greater N_EW result in the worse ADS of watermarks in same size of single watermark, and a larger capacity of single watermark has the lower of ADS under the same N_EW. It is also shown that, the proposed scheme has good ADS (>0.9) when N_EW less than 5. For a further insight of Fig. 7, it can be found that, under the same whole equivalent capacity of embedded watermarks, greater N_EW lead to a clearly lower ADS value. For example, 2 watermarks in the size of 32 × 32 and 8 watermarks in the size of 16 × 16, their ADS values are 0.9978 and 0.8813 respectively. The fact reminds us that the N_EW surely impact the ADS. The reason could be that there is a relative greater error caused by the finite word-length precision of orthogonal transform and watermarking extraction threshold when the N_EW is greater.

Fig. 7

Average detection score and capacity versus N_EW

From the perspective of the PSNR in Fig. 6 and average watermark detection scores in Fig. 7, we got the following results by testing various images: 4 watermarks were embedded into original images is acceptable. More than 4 watermarks may affect visual quality of watermarked image. From requirements of most multiple watermarking applications, 4 users are enough. So, we choose 4 watermarks to investigate the performance of multiple watermarking schemes with respect to JPEG compression, Additive Gaussian White Noise (AWGN), different filtering (high pass, median, low pass) and Geometric transformation attacks.

Several unintentional attacks are simulated for Lena image, including JPEG compression, high pass filter, median filter, low pass filter and noise. In the JPEG compression attack, the watermarked images are JPEG compressed with the default quantization matrix scaled by various the quality factor (QF) to achieve different compression ratio.

In the JPEG attack on MWOD, we compute the ADS by Eq. (23). In Fig. 8, if JPEG Quality Factor > = 40, there are little difference between MWOD and Wang et al. [16] in ADS value. In JPEG Quality Factor <= 40, the proposed scheme is clearly better. The results mean that the proposed scheme has better robustness than Peter et al. [17] and Wang and Lian [16].

Fig. 8

Average detection score versus JPEG quality factor

In the AGWN attacks on MWOD, the simulated results with different AGWN signal-to-noise ratio (SNR) are shown in Fig. 9. It can be seen that MWOD performs more and more remarkable robustness with the rise of AGWN SNR. The ADS of the proposed scheme is greater than Peter et al. [17] and Wang and Lian [16].

Fig. 9

Average detection score versus different AGWN SNR

In the usual filters attacks on MWOD, a Lena image embedded four watermarks is attacked by High Pass Filter, Median Filter and Low Pass Filter with 3 × 3 filter. The simulated results are listed in Table 1. It can be shown that the proposed scheme has the highest ADS and better robustness. The resisting filter attacks performance of the proposed scheme is better than Peter et al. [17] and Wang and Lian [16].

Table 1 Average watermark scores with 3 × 3 filter

In contrast to the above attacks, geometrical attacks do not attempt to remove the embedded watermark itself. Geometrical attacks usually make the watermark detector losing the synchronization information. The mostly well-known integrated tool for these kinds of attacks is StriMark [12, 13]. StriMark introduces the global distortions include scaling, rotation and cropping that belong to a class of general affine transformations.

For the scaling attacks on MWOD, the simulated results of various approaches for rescaling attacks with different sizes are list in Table 2. For example, the watermarked Lena with embedded 4 watermarks is scaled from 256 × 256 to 200 × 200. In order to recover the watermarks, the scaled image was rescaled to its original dimensions, and then extracting watermarks. The results show that the larger watermarked image scaling, the worse extracted watermark effect. It can be seen that the proposed scheme has the highest ADS and Peter et al. [17] scheme has the lowest ADS in every scale size.

Table 2 Average watermark scores with scaling attacks

For the rotation attacks on MWOD, the simulated results of various approaches for rotation attacks with different degrees are listed in Table 3. After the watermarked Lena image is rotated with various degrees (such as 5°, 15°, 20° and 30°), we selected the pixel densest portions and most complete image as watermarking extraction object. And the missing portions of the image were replaced with portions from the original unwatermarked Lena image. It can be seen that MWOD’s ADS is higher than Wang and Lian [16] and Peter et al. [17].

Table 3 Average watermark scores with rotation attacks

For the cropping attacks on MWOD, the simulated results of various approaches for cropping attacks with different cropping size are listed in Table 4. We cropped different sizes from watermarked Lena image. In order to extract the watermarks from this image, the cropped portions of the image were replaced with portions from the original unwatermarked Lena image. It can be shown that a less cropping size results in less impact on watermarking detection. MWOD’s ADS is higher than Wang and Lian [16] and Peter et al. [17].

Table 4 Average watermark scores with cropping attacks

From what has been discussed above, we could conclude that resisting geometric attacking performance of the proposed scheme is better than that of Wang and Lian [16] and Peter et al. [17].

In this section, unintentional and geometric attacking experiments have been accomplished. All results show that, MWOD can provide accepted visual quality under rational number of embedded watermarks, has better anti-attacks performance and watermarking robustness than Peter et al. [17] and Wang and Lian [16] in suffering various attacks.

5 Conclusions and future work

This paper proposes a multiple watermarking scheme based on orthogonal decomposition. The MWOD scheme can embed multiple watermarks into different domains using multiple orthogonal operation domain keys, without need for considering the correlation among them. Therefore, multiple watermarks can be flexibly embedded in the distribution of the multimedia cover. The security among watermarking operation domains was validated by theoretical analyses and the validity of the scheme was verified through experiments. The performance analysis and experimental results can also provide the reference information for user to select suitable algorithm and strategy for adapting different application scenarios and adjust rational parameters for optimizing the performance, such as the choice of watermarking number, hybrid watermarking strategy, setting rational the word length and dimension of transform matrix B etc. Through some comparative experiments, MWOD has been demonstrated a better robustness. That gives us the confidence that MWOD will be a promising practical protection tools for digital multimedia.

MWOD will have more application and prospects in the protection for multimedia in the scenario of multiple media providers or service providers, especially for cloud environment; there at least exists two basic application scenarios for multiple watermarking, the one based on different computing clouds and the other based on different servers in the same or different computing clouds. Meanwhile, MWOD has potential to combine re-encryption algorithm conveniently to construct a full protection scheme for digital multimedia in cloud. In the future, the combination of MWOD with re-encryption algorithm and the complete protocol based on MWOD for protecting digital multimedia in cloud will be the main research direction of our study.