1 Introduction

When dealing with huge amount of data, it is critical that one finds an efficient way for classifying them into relevant classes. Proper classification of the data has many potential applications in different domains. For instance, in text mining, it leads to faster textual data browsing and improved search results [35]. Human visual system is a strong object classifier [24, 32]. Whence it has been an ongoing trend among researchers to develop machine learning classification algorithms that work similar to human vision [4]. Development of such algorithms can lead to potentially vast number of applications such as improved content-based retrieval [11, 17], improved recognition, improved decision making, database summarization [7, 9, 14] and also various applications in biomedical imaging [25].

Traditionally the primary step in developing classification models is the training phase. Training phase is usually accomplished by the consideration of training data. In general, there are two categories of training data, supervised and unsupervised. The two training trends have been analyzed extensively in the past [12, 13]. In supervised training, one assumes that a certain amount of information is known about the training set. It could be the presence of a certain object inside an image for machine vision applications or the context of the training document in text mining. The embedded information is concordantly used to improve the learning process. For the unsupervised training sets, however, one assumes that no specific information is known about their content in advance. The advantage of the supervised sets to the unsupervised ones is that one can use the information available about the former to improve the learning process. The disadvantage of the supervised sets in comparison to the unsupervised ones is that, in general, creating large supervised training sets is far more resource demanding than creating unsupervised sets. Considering the size of the available training sets, one way to improve the learning process is through finding ways that one can use training sets interchangeably. The following example further elaborates the idea. Suppose that one decides to build a model that classifies different animal species. Considering two closely related but distinct bird species, such as falcons and hawks, and comparing them with land dwelling animals, such as horses and Kettles. The former pair shares many common features such as beaks, wings, talons, etc., that are either not present or are visually significantly different in the later. In order to exploit the class similarities to improve the classification process, one way is to create hierarchical structures based on visual similarities. The main idea is that the closely related classes are ought to have been generated from the same, unobserved, parental nodes. Therefore the same as siblings in a family tree share common traits [21], so do the neighboring nodes. The idea of using hierarchical structures for improving classification has already been analyzed in numerous works [1–3, 23, 27, 33]. In general the structure of the hierarchy is worked out in two different ways. Firstly by assuming a known in advance structure for the hierarchy, and secondly by assuming total ignorance about the hierarchical structure and proceeding with generating the hierarchy from the scratch based on the available data. The model that we propose in this work stands in the middle of the previous models. We therefore call it semisupervised online learning of hierarchical structures (SOLHS). The etymology comes from the following reasons. Semisupervised since it assumes a crude understanding of the hierarchical structure. Online learning because the model proceeds with improving its initial assumption of the hierarchical structure every time new data are introduced to it.

For machine vision applications, which is the focus of this work, often the models deal with the frequency of the occurrence of certain features inside objects, thus leading to count data modeling [15, 20]. Count data modeling approaches are divided into two main groups. The discriminative group of approaches such as support vector machines (SVM) [18] and the generative family of approaches [5]. There is a favorable trend for developing hierarchical classifiers based on generative models [29]. In comparison to discriminative models, generative models offer faster training speeds and are easier to expand. Another advantage of the generative models is that it is relatively an easy task, pendant certain conditions, to leverage flat statistical models to work in hierarchies. Previously Sivic et. al effectively used the hierarchical latent Dirichlet allocation [33], the hierarchical adaptation of the latent Dirichlet allocation (LDA) model [6]. Another example is using the hierarchical Dirichlet model for document classification [34] and the subsequent adoptions for improving the performance of the original model [1–3]. However, the cons in using hierarchical models is that since, they apply the training data attributed to their neighboring nodes to enhance their operation it leads to parameter mixing between neighboring classes. This in return results in the reduction of the model accuracy in distinguishing similar classes. This problem was observed in previous models developed for object classification. The main contribution of this work is proposing an efficient semisupervised online learning method for hierarchical structures through the development of effective and flexible hierarchical distributions for count data modeling. The contribution wavers the need for the prior assumption of the hierarchical structure. The second contribution of this work is, that the online learning model leads to better classification accuracy in comparison to the static structures. SOLHS in theory is applicable to all applications that deal with hierarchical count data modeling pendant that certain conditions, which will be explained in details, are met. We have observed the frequent occurrence of the necessary conditions in the field of hierarchical object classification, which will be the focus of this work. The main technical challenge of the proposed model is identifying features that strongly correlate in similar classes while in the same time offer distinction between non related classes.

The structure of the rest of this paper is as follows. In Section 2 we give a brief review of the previous hierarchical models, related to our work, that were developed for object classification. In Section 3 we describe SOLHS that we have developed in this work. In Section 4 we show the experimental results of applying SOLHS and we compare them with previously proposed models. In the last section we present our conclusions and possible future works.

2 Static hierarchical model

In this section we briefly describe the basic hierarchical model that we have used for developing our hierarchical semisupervised online learning approach. The model was originally proposed as a special case of the Dirichlet prior used in [34].

The description is as follows. Assuming that \(C=\left\{{{\bf C}_{\bf 1}},\ldots,{{\bf C}_{\bf N}} \right\}\) is a given set of count vectors, the model is assumed to be a generative multinomial with parameter space \({\boldsymbol{\theta}}_I=\left\{\theta_{I1},\ldots,\theta_{I(D+1)}\right\}\) as follows:

$$\label{multinomialhierarchical} p({\bf C}_n|{\boldsymbol{\theta}}_I)\propto \frac{\left(\sum_{d=1}^{D+1} C_{nd}\right)!}{\prod_{d=1}^{D+1}{C_{nd}}!}\prod\limits_{d=1}^{D+1}(\theta_{Id})^{C_{nd}} $$
(1)

In above D + 1 indicates the number of elements inside C n and C nd indicates the d-th element of C n .

The hierarchical Bayesian structure is maintained through the following assumptions. Firstly, the generative model parameter \({\boldsymbol{\theta}_{\bf I}}\) must be generated by a conjugate prior to the multinomial distribution. Secondly, the following condition has to be maintained:

$$\label{hierarchycondition} E[{\boldsymbol{\theta}}_I|{\boldsymbol{\theta}}_{pa(I)}]={\boldsymbol{\theta}}_{pa(I)} $$
(2)

In above, \({\boldsymbol{\theta}}_{pa(I)}\) is the generative parameter of the parent node of the I-th node. Through maintaining the above conditions, it was shown in [34] that a linear minimum mean square error (LMMSE) estimator can be used to find the estimation of \({\boldsymbol{\theta}}_{\!I}\) as follows

$$ \label{lmmsehierarchcial} {\boldsymbol{\theta}}_I= E[{\boldsymbol{\theta}}_I]+M^{-1} \times \begin{pmatrix} {\hat{\boldsymbol{\theta}}}_{ch(I1)}-E[{\boldsymbol{\theta}}_{ch(I1)}] \\ {\hat{\boldsymbol{\theta}}}_{ch(I2)}-E[{\boldsymbol{\theta}}_{ch(I2)}] \\. \\ {\hat{\boldsymbol{\theta}}}_{ch(Im)}-E[{\boldsymbol{\theta}}_{ch(Im)}] \\ \end{pmatrix} $$
(3)

where

$$ M = \begin{pmatrix} \Sigma({\boldsymbol{\theta}}_{ch(I1)}) &\Sigma({\boldsymbol{\theta}}_{ch(I1)},{\boldsymbol{\theta}}_{ch(I2)}) & . &\Sigma({\boldsymbol{\theta}}_{ch(I1)},{\boldsymbol{\theta}}_{ch(Im)}) \\ \Sigma({\boldsymbol{\theta}}_{ch(I2)},{\boldsymbol{\theta}}_{ch(I1)}) &\Sigma({\boldsymbol{\theta}}_{ch(I2)}) & . &\Sigma({\boldsymbol{\theta}}_{ch(I2)},{\boldsymbol{\theta}}_{ch(Im)}) \\ .&.&.&.\\ \Sigma({\boldsymbol{\theta}}_{ch(I1)},{\boldsymbol{\theta}}_{ch(I2)})&.&.&\Sigma({\boldsymbol{\theta}}_{ch(Im)}) \end{pmatrix} $$

In the above equation \(\Sigma({\boldsymbol{\theta}}_{ch(Ik)},{\boldsymbol{\theta}}_{ch(Ij)})\) is the correlation matrix between the parameter vectors of the k-th and j-th nodes from m children of the I-th node. It was shown in [34] that if the condition in (2) holds, the following simplifying relationships hold:

$$ E[{\boldsymbol{\theta}}_{ch(I)}]=E[{\boldsymbol{\theta}}_I] $$
(4)
$$ \Sigma({\boldsymbol{\theta}}_I,{\boldsymbol{\theta}}_{ch(Ij)})=\Sigma({\boldsymbol{\theta}}_I) $$
(5)
$$ \Sigma({\boldsymbol{\theta}}_{ch(Ij)},{\boldsymbol{\theta}}_{ch(Ik)})=\Sigma({\boldsymbol{\theta}}_I) $$
(6)
$$ \Sigma({\boldsymbol{\theta}}_{ch(Ik)})=\Sigma{\boldsymbol{\theta}}_I+E_{{\boldsymbol{\theta}}_I}[\Sigma({\boldsymbol{\theta}}_{ch(Ik)}|{\boldsymbol{\theta}}_I)] $$
(7)

The parameter vector \({\boldsymbol{\theta}_{\bf I}}\) is generated by a predetermined prior. In [1, 34] the prior was considered to be a Dirichlet distribution. In subsequent works we used generalized Dirichlet [2] and Beta-Liouville [3] distributions as replacement generating priors to improve the model efficiency.

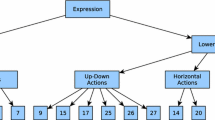
The schematic of the original model, is displayed in Fig. 1. A series of experiments for determining the classification and categorization of the models accuracies was performed in the past, the details of which are present in [1–3]. In Figs. 2 and 3 one can see the results of applying different priors on the original model. In the past works [1–3] we performed our experiments on the ETH-80 dataset (see Fig. 4) [28]. We assumed a known in advance hierarchical structure for our experiments (see Fig. 5). As an example we have also brought the confusion matrix of the model proposed in [3]. As one can see from Figs. 2, 3 and Table 1, the original model is quite capable of correctly categorizing different classes. However, when it comes to recognizing specific objects, the system accuracy fails to offer a strong outcome. Two reasons are thought to be behind the low accuracy. Firstly, since the models use visual words that are generated from a common pool they tend to be less sharp in distinguishing the differences. Secondly, the fact that the sibling nodes inherit common parameter generators from their parents makes the class vectors inherently similar to each other. In the next section we will show how by adapting the maximum likelihood threshold, introducing a saliency factor to it and adapting a learning hierarchical structure, we improve the efficiency of the model.

Fig. 1
figure 1

Flowchart of the static model learning and operation [1]

Full size image
Fig. 2
figure 2

Comparison of the classification success rate of the different models. The error bars are set at 90 % standard deviation of the relative graphs [3]

Full size image
Fig. 3
figure 3

Comparison of the second tier categorization success rate of the different models. The error bars are set at 90 % standard deviation of the relative graphs [3]

Full size image
Fig. 4
figure 4

Samples of the ETH-80 dataset

Full size image
Fig. 5
figure 5

The hierarchical model assumed for the image database classes in the previous works [1–3]. The choice of the hierarchy elements was based both on visual and conceptual similarities between the classes

Full size image
Table 1 Optimal confusion matrix for the hierarchical Beta-Liouville model [3]
Full size table

3 The model

Looking back at Table 1 gives us an overview of the problem that needs to be dealt with. If one looks, for example, at the row showing the attributions to the class “horse” one observes that the class has a tendency to absorb a great portion of the objects which have visual similarity to it. We call it an absorbing class. The original model uses maximum likelihood (ML) method for classification. Therefore, it is logical to assume that the absorbing node tends to have the higher likelihood in comparison to the neighboring nodes. In order to improve the classification process, it is necessary that one finds a way for penalizing the absorbing ML. To achieve this end we proceed with defining a saliency factor for each node. One factor to be considered as a relatively reliable saliency factor is that similar objects in general give somehow the same number of visual words. The number of features extracted from an object follows a natural process, therefore it is expectable to assume that it can be modeled by normal distribution. The histogram of the number of features in each category is shown in Fig. 6. As the first step we redefine the likelihood of the count vector to represent the I-th class as follows:

$$\label{multinomialhierarchical} p({{\bf C}}_n|{\boldsymbol{\theta}}_I, \Theta(I))\propto \frac{\left(\sum_{d=1}^{D+1} C_{nd}\right)!}{\prod_{d=1}^K{C_{n(D+1)}}!}\prod\limits_{d=1}^{D+1}(\theta_{Id})^{C_{nd}}\times p\left(\left(\sum({{\bf C}}_n)|\Theta(I)\right)\right) $$
(8)

In above Θ(I) represents the statistical characteristics of the I-th class. Therefore, assuming normal distribution for the number of feature occurrences in the I-th class, Θ(I) would be defined by the mean and the variance of the class histogram. It should be noted that Θ(I) is independent of \({\boldsymbol{\theta}_{\bf I}}\) and therefore acts solely as a weighing factor, penalizing deviations from the established characters of the class.

Fig. 6
figure 6

Histogram of the number of features present in each experimented class

Full size image

There is yet another factor that needs to be considered for improving the model. As it was discussed in the previous section, in the original model we encounter dominant classes that tend to bias the classification process towards themselves. Mathematically the bias happens because \({\boldsymbol{\theta}}_{I}\) of the dominant class, offers a broad histogram of likelihood with comparably long tails. Therefore theoretically there are always dominant classes present inside the model in the form of those classes which have stronger spreads on the log-likelihood spectrum. The model therefore finds out the hierarchical structure most efficiently when there is a strong similarity between the sibling classes and strong dissimilarity between the non related classes. In Fig. 7 we show the log-likelihood of the dominant classes in our experiments to further elaborate this fact.

Fig. 7
figure 7

Log liklihood of the count data for the dominant classes

Full size image

Unlike the previous case, however, as it can be seen in Fig. 7, the log likelihood of the count data does not clearly follow a Bell shaped Gaussian distribution and therefore it is analytically difficult to find a fitting function that covers all different shapes of the different log likelihoods. However, through observing the log likelihood of the dominant classes an effective boundary can be assumed where the majority of the likelihood instances occur. In our experiments we have observed that where normal fitting is possible the best results appear when the boundary is assumed to be one standard deviation from the mean of the training data likelihood. In theory The model accuracy suffers where the normal fitting fails to properly model the log likelihood. Still experiments show that the assumption is reliable in the majority of circumstances. By assigning this boundary on the dominant class, we devise an extra layer of protection against misplaced classification. As follows a new object is solely assigned to the dominant class when its likelihood falls in the acceptable boundary. If it doesn’t, even if it shows a higher likelihood than other classes in the same branch, it is rejected as an object belonging to the dominant class and the next highest likelihood is chosen as the assigned class.

3.1 Learning hierarchical structure

The presence of the dominant classes provides us with yet one more assumption easement. So far the hierarchical models proposed based on [34] have assumed a known hierarchical structure a priori. As an example the visual hierarchy used in [1] is brought in Fig. 8. In this work, however, we propose a learning hierarchical structure based on the presence of dominant classes. SOLHS starts from a crude sketch of the hierarchy, where only the dominant classes are placed in their relative positions inside the hierarchy. To derive the dominant classes we pledge to the naive Bayes classification over the training set. The dominant classes tend to give high likelihood not only to themselves but also to their sibling nodes, therefore they absorb the sibling entries in the confusion matrix. Theoretically there are always dominant classes, however the stronger the dominance of the class over its sibling classes gets the stronger the model efficiency in properly categorizing the data becomes. Here we need to define the difference between classification and categorization in our context. We define classification as the ability of the model to correctly identify different classes while we define categorization as the model ability to identify the concept the class belongs to. As an example a strong classifier can strongly tell the difference between a horse and a cow, while a strong categorizer can strongly depict that a horse or a cow belong to the animal class. As we described in this section the likelihood of the classes typically falls within a derivable boundary. Assuming that a new class appears which likelihood does not fall in the acceptable boundary of any of the dominant classes; SOLHS will decide that a new class of objects has been introduced. However, it is expectable to assume that the new class will have likelihood boundaries near to that of one of the dominant classes. In this step SOLHS compares the likelihood of the object with different dominant classes and decides where exactly the new branch of the hierarchy the new class must be placed. In this work, the assumption is that the new objects arrive in unlabeled classes. Totally random data arrival requires count data clustering as mentioned in the following works [8, 10]. SOLHS waits until enough new objects have arrived to form an appropriate training set. In the next step it assumes a new branch added to the hierarchy and it recalculates the model parameters [1–3] while including the new class. The process continues in the presence of coming data. Every time SOLHS decides that a new class has to be formed it adds the appropriate branch and recalculates the parameters accordingly. The following steps define the semisupervised online learning of the hierarchical structure phase:

  1. 1.

    From the training dataset extract the dominant classes.

  2. 2.

    From the training dataset extract the saliency and log likelihood of the dominant classes.

  3. 3.

    For each new entry find the nearest dominant class based on the maximum likelihood.

  4. 4.

    If the new entry does not fit within the salient boundaries of the dominant class flag the entry as belonging to an unidentified sibling node of the dominant class and repeat the process.

  5. 5.

    Once enough entries for the unidentified nodes is collected, re-estimate the model parameters with the inclusion of the unidentified nodes.

For the classification part we follow the following steps:

  1. 1.

    Use the ML estimation and if the ML remains within the salient boundaries of the dominant node with the highest ML select the dominant node as the class.

  2. 2.

    If the saliency fails enter the learning mode and perform the learning algorithm step 3–5.

Fig. 8
figure 8

An example of hierarchical object classification

Full size image

3.2 Different considered priors

In this work, we analyzed three different prior distributions to be used for our model. The three distributions are: Dirichlet distribution, generalized Dirichlet distribution and Beta-Liouville distribution. By appropriate considerations, the three distributions satisfy the conditions in (2). Also the three distributions are known to be conjugate priors to the multinomial distribution, which is the second necessary condition for creating the hierarchical structure of [34].

A random vector \({\boldsymbol{\theta}}_i\) follows a Dirichlet distribution with parameter vector \({\boldsymbol{\alpha}}_i=(\alpha_{i1},\ldots,\alpha_{i(D+1)})\) over the hyper plane \(\sum_{k=1}^{D+1}\theta_{ik}=1\), if its joint probability density function (PDF) is defined as follows [16]:

$$ p({\boldsymbol{\theta}}_i\vert{\boldsymbol{\alpha}}_i)=\frac{\prod_{k=1}^{D+1} \Gamma(\alpha_{ik})}{\Gamma\left(\sum_{k=1}^{D+1}\alpha_{ik}\right)}\prod\limits_{k=1}^{D+1}\theta_{ik}^{(\alpha_{ik}-1)} $$
(9)

where Γ is the Gamma function. Dirichlet distribution satisfies condition (2) unconditionally. Assuming n i  = (n i1,...,n i(D + 1)) to be the observed vector, the conjugacy with the multinomial distribution is derived as follows:

$$ p({\boldsymbol{\theta}}_i|{{\bf n}}_i) \propto \mathcal{D}(\alpha_{i1}+n_{i1},\ldots,\alpha_{i(D+1)}+n_{i(D+1)}) $$
(10)

Defining \({\boldsymbol{\alpha}}_{i}^{\prime}={\boldsymbol{\alpha}}_{i}+{{\bf n}}_i\), we obtain [22]:

$$ E({\boldsymbol{\theta}_{i}}|{{\bf n}}_i)=\frac{{\boldsymbol{\alpha}}_{i}^{\prime}}{\left|{\boldsymbol{\alpha}}_{i}^{\prime}\right|} \label{eqn:meanD} $$
(11)

The second distribution that we use in our model is the generalized Dirichlet distribution. Following the same terminology used for Dirichlet distribution a random vector \({\boldsymbol{\theta}}_i\) defined over the hyper plane \(\sum_{k=1}^D\theta_{ik}<1\) is said to follow a generalized Dirichlet distribution with parameter space \({\boldsymbol{\xi}}_i=(\alpha_{i1},\dots,\alpha_{iD},\beta_{i1},\dots,\beta_{iD})\), if its joint PDF is as follows:

$$ p({\boldsymbol{\theta}}_i\vert{\boldsymbol{\xi}}_i)=\prod\limits_{k=1}^D\frac{\Gamma(\alpha_{ik}+\beta_{ik})} {\Gamma(\alpha_{ik})\Gamma(\beta_{ik})} \theta_{ik}^{\alpha_{ik}-1}\left(1-\sum\limits_{j=1}^k\theta_{ij}\right)^{\gamma_{ik}} $$
(12)

Generalized Dirichlet distribution is also a conjugate prior to multinomial distribution and for \({\boldsymbol{\theta}}_i|{{\bf n}}_i\propto GD(\alpha_{i1}^{\prime},\ldots,\alpha_{iD}^{\prime},\beta_{i1}^{\prime},\ldots,\beta_{iD}^{\prime})\), where:

$$ \alpha_{ik}^{\prime}=\alpha_{ik}+n_{ik} $$
(13)
$$ \beta_{ik}^{\prime}=\beta_{ik}+\sum\limits_{l=k+1}^{D+1}n_{il} $$
(14)

and therefore we have [19]:

$$ E(\theta_{ik}|{{\bf n}}_i)=\frac{\alpha_{ik}^{\prime}}{\alpha_{ik}^{\prime}+\beta_{ik}^{\prime}}\prod\limits_{j=1}^{k-1}\frac{\beta_{ij}^{\prime}}{\alpha_{ij}^{\prime}+\beta_{ij}^{\prime}} \label{eqn:meanGD} $$
(15)

The following derivations provide the necessary conditions for maintaining the hierarchy:

$${\boldsymbol{\theta}}_i \sim \left \{ \begin{array}{cc} \mathcal{GD}(\eta,\ldots,\eta,\zeta,\ldots,\zeta) &\textrm{if \textit{i} is the f\/irst node }\\ \mathcal{GD}\big(\big(f\big({{\boldsymbol{\theta}}_{pa(i)}}\big),g({{\boldsymbol{\theta}}_{pa(i)}})\big)\big) &\textrm{otherwise}\\ \end{array}\right. $$
(16)

where \({\boldsymbol{\theta}}_{pa(i)}\) indicates the parent of the i-th node. The functions \(f({{\boldsymbol{\theta}}_{pa(i)}})\) and \(g({\boldsymbol{\theta}}_{pa(i)})\) depend on the parent node and must be determined in the way that the condition in (2) holds. By defining f i and g i functions as \({{\bf f}}_i=\left\{{f_{i1},\ldots,f_{iD}}\right\}\) and \({{\bf g}}_i=\left\{{g_{i1},\ldots,g_{iD}}\right\}\), it was shown in [2] that the following condition preserves the hierarchical structure:

$$ \label{eqn:alphabetarelation} g_i(k)=\frac{\big(1-\sum_{l=1}^k\theta_{pa(i)}(l)\big)}{\theta_{pa(i)}(k)}f_i(k) $$
(17)

It was shown in [2] that by choosing a linear relationship between f I and \({\boldsymbol{\theta}}_{pa(I)}\) the hierarchical generalized Dirichlet model is reduced to a simple hierarchical Dirichlet model. It was thus suggested that a nonlinear relationship between f I and \({\boldsymbol{\theta}}_{pa(I)}\) should be considered. Based on that assumption a square relationship between the parameters is considered as follows:

$${f_i(k)}\propto (\theta_{pa(i)}(k))^2 $$
(18)

The last prior that we consider for our model is the Beta-Liouville distribution. A random vector \({\boldsymbol{\theta}}_i\) defined over the hyper plane \(\sum_{k=1}^D\theta_{ik}<1\) is said to follow a Beta-Liouville distribution with parameter space \(\left(\left\{\alpha_1,\ldots,\alpha_D\right\},\alpha,\beta\right)\), if its joint PDF is as follows:

$$\begin{array}{lll} p\left({\boldsymbol{\theta}}_i|{\boldsymbol{\alpha}},\alpha,\beta\right)&=&\frac{\Gamma\sum_{d=1}^D\left.\alpha_d\right)\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\prod\limits_{d=1}^D \frac{\theta_{id}^{\alpha_d-1}}{\Gamma(\alpha_d)} \\ && \times \left(\sum\limits_{d=1}^D\theta_{id}\right)^{\alpha-\sum_{d=1}^D\alpha_d} \left(1-\sum\limits_{d=1}^D\theta_{id}\right)^{\beta-1} \end{array}$$

The condition for preserving the hierarchical structure with Beta-Liouville assumption was derived in [3] and is as follows:

$$ \label{hierarchcialBL} {\boldsymbol{\theta}}_i\sim BL\left(\sigma{\boldsymbol{\theta}}_{pa(i)},K\sigma\sum\limits_{d=1}^D\theta_{pa(id)}, \\ K\sigma\left(1-\sum\limits_{d=1}^D\theta_{pa(id)}\right)\right) $$

Beta-Liouville distribution is also a conjugate prior of the multinomial distribution and we have:

$$ \theta|({{\bf n}}_i,{\boldsymbol{\alpha}},\alpha,\beta) \sim BL({\boldsymbol{\alpha}}^{\prime},\alpha^{\prime},\beta^{\prime}) $$
(19)

where ~BL indicates a vector generated by the Beta-Liouville distribution and in the above \({\boldsymbol{\alpha}^{\prime}}={\boldsymbol{\alpha}}+(n_{i1},\ldots,n_{iD})\), \(\alpha^{\prime}=\alpha+\sum_{d=1}^Dn_{id}\) and \(\beta^{\prime}=\beta+n_{iD+1}\). And we therefore have [22]:

$$\label{posteriormean} E[{\boldsymbol{\theta}}_i|{{\bf n}}_i]=\frac{\alpha+\sum_{j=1}^Dn_{ij}}{\alpha+\beta+|{{\bf n}}_i|}\frac{{\boldsymbol{\alpha}}_i+{{\bf n}}_i}{\sum_{d=1}^D\alpha_{d}+\sum_{d=1}^Dn_{id}} $$
(20)

In the next section we show the results of applying SOLHS with three different prior assumptions and we compare its performances against the previously derived models.

4 Experimental results

4.1 Image dataset

To maintain consistency with previous works [1–3], we have chosen the ETH-80 dataset [28] for our experiments. The dataset is optimized for object classification purposes. It contains views and segmentation masks of 80 objects, each one photographed in more than 40 different poses. In total it contains more than 3,000 images. There are eight object classes, from which we choose seven categories to validate our work. The choice of classes is based on visual similarities. In general six of them can be classified in two unique categories: fruits and animals. It was shown in previous works that the visual similarities between the chosen classes contribute much to the efficiency of the hierarchical classification. Approximately 20 percent of the image database is randomly chosen as the training set, whilst the remaining images form the test dataset.

4.2 Feature extraction and visual words generation

We use scale invariant feature transform (SIFT) descriptors [30] to represent our objects. The high dimensionality of the SIFT descriptors and its comparably robustness towards changes in scaling, illumination, occlusion, etc, compared with other feature descriptors, have been shown to result in better classification results [31]. To generate the visual vocabulary, we extract SIFT descriptors over the entire dataset. Each SIFT descriptor has a dimension of 128 as described in [30]. In the next step the K-Means algorithm [26] is used to extract the centroides and then construct the visual vocabulary that we shall use.

4.3 Hierarchical model generation

In previous works the optimal hierarchical structure for the dataset was shown to be the one displayed in Fig. 5. In SOLHS, however, our assumption is that only a crude structure of the hierarchy in Fig. 5 is known and the model proceeds with learning the rest of the structure as described in the previous section. The class “cup” acts as a misplaced class to show the effect of class misplacement in the system accuracy. We analyze and compare the strengths and the weaknesses of the model in classification and categorization in comparison with static models proposed in previous works. It will be shown in the following subsection that the current model offers a more efficient classification rate in expense of slightly decreasing the categorization efficiency in comparison with the static hierarchical models.

4.4 Analysis of the recognition capability of the model

For recognition purposes the lowest branches of the hierarchy that show the individual object classes are analyzed. The main factor that affects the accuracy of the model is the number of chosen visual words. Each of the distributions has its own parent-children parameters that are extensively analyzed in previous works. In order to maintain the consistency we proceed with comparing the optimum results for each model against each other. The model recognition success rate is defined as the ratio between the total number of correctly classified images in all classes against the total number of images. Figure 9 compares the recognition success rates of the different models as a function of the number of visual words. As it can be seen from this figure SOLHS for all distributions show better classification accuracy in comparison with its static counterpart. This is mostly due to the fact that through applying the online learning algorithm we have created a deeper distance between the sibling nodes and therefore we have improved the classification accuracy.

Fig. 9
figure 9

Comparison of the recognition success rates of SOLHS against the static models for different prior assumptions. The error bars are set at 90 % standard deviation of the relative graphs

Full size image

Figure 10 shows the second tier categorization accuracy of SOLHS in comparison with the static hierarchical models. As it can be seen from this figure SOLHS in general acts less accurately when dealing with categorization task. The main reason behind the degradation of the categorization accuracy is due to the fact that the model starts from a crude understanding of the hierarchical structure. The static hierarchical models have the advantage of knowing in advance the parameters for the entire nodes inside the hierarchy. On the other hand the learning model is prone to placement errors while it learns the correct structure. Since we assume that an object is classified mistakenly once will not be classified again we thus end up with higher misplacement errors in comparison to static models. This is further visualized by looking at the relative confusion matrices in Tables 2, 3 and 4. As it can be seen from Tables 2–4 SOLHS progressively improves its performance through learning the hierarchical structure.

Fig. 10
figure 10

Comparison of the categorization success rates of the SOLHS against the static models for different prior assumptions. The error bars are set at 90 % standard deviation of the relative graphs

Full size image
Table 2 Optimal confusion matrix of SOLHS when considering the online hierarchical generalized Dirichlet model
Full size table
Table 3 Optimal confusion matrix of SOLHS when considering the online hierarchical Dirichlet model
Full size table
Table 4 Optimal confusion matrix of SOLHS when considering the online Beta-Liouville model
Full size table

5 Conclusion

In this paper we proposed a new adaptable general learning hierarchical model (SOLHS) dedicated to count data. As it was shown in the experimental results, SOLHS allows substantial improvement in hierarchical classification accuracy as compared to other models that we have described. The improvement is achieved through applying several saliency factors in SOLHS. In addition to that the learning algorithm proposed in SOLHS allows it to expand beyond the previously predefined hierarchical structures. SOLHS improves efficiency while dealing with unknown classes and as observed in the experiments succeeds in deciding the location of the new class within the hierarchy quite efficiently. SOLHS achieves this in return for a slight expense in its categorization capability. Therefore, an interesting idea for further work on this model could be the design of learning models that reduce the misplacement of the data in the early learning phases.